Generation, Transmission and Application of Orbital Angular Momentum in Optical Fiber: A Review

Optical orbital angular momentum (OAM) has become a hot research topic because of its unique properties due to its spiral distribution of phases. The production and transmission of OAM has also become a necessary condition for effective use of OAM. As an optical waveguide with good propagation properties, optical fibers are used in optical systems supporting OAM. This paper introduces the OAM generation and transmission system based on fiber, summarizes the current photonic crystal fiber, ring core fiber, fiber grating and other all-fiber systems that can support OAM modes, and explains some experimental principles. Finally, an outlook on OAM generation or transmission devices for all-fiber systems is presented, providing a useful reference for future related research.

Introduction

Since Allen et al. [1] discovered the orbital angular momentum (OAM) contained in the vortex beam, OAM has been widely used. Because the vortex beam has a phase factor of ${\text{e}}^{\text{i}l\phi }$, its phase distribution presents a spiral shape. Due to the unique properties, OAM beams have a wide range of applications in microscopy [2, 3], micromanipulation [4, 5], optical tweezers [6, 7], nonlinear optics [8, 9], quantum communication [10, 11], and so on. In the traditional optical communication, the multiplexing technology improves the communication capacity by multiplexing the optical wave from the aspects of wavelength, frequency and space, but the communication capacity is close to the Shannon limit [12]. OAM has a spirally distributed phase, and different OAM modes are orthogonal to each other. Theoretically, it provides an infinite set of orthogonal bases, which provides a new research direction for optical communication and information transmission [13–15]. Among them, the OAM-based modular multiplexing communication technology has received widespread attention. mode-division multiplexing (MDM) technology increases the efficiency of data transmission by simultaneously transmitting beams of different modes in the same transmission channel. The orthogonal property of OAM provides a degree of freedom for the multiplexing technique, increasing the capacity of the transmitted data. Moreover, the experiments of multiple-input multiple-output (MIMO) communication system based on OAM multiplexing technology are also gradually improved [16, 17]. In addition, OAM is also considered as a potential communication method of 6G technology [18].

The effective use of the OAM beam cannot be achieved without the generation and stable transmission of OAM. At present, OAM beam can be generated and propagated by optical fiber or spatial optical device. Commonly used spatial optical devices include cylindrical lens [19], spatial light modulator [20], Q plate [21], etc. Compared with spatial optical devices, optical fiber provides a binding transmission medium for OAM transmission, which can reduce external interference and increase transmission distance and efficiency [22]. In recent years, ring core fiber (RCF) and photonic crystal fiber (PCF) have become the main optical fibers for transmitting OAM. At present, the use of optical fiber transmission can achieve the stable propagation of thousands of OAM modes [23]. In addition, as the eigensolution of the optical fiber, OAM mode is formed by the coupling of the vector mode or scalar mode of the optical fiber, so the phase purity of OAM generated by the optical fiber is higher and the optical path complexity is lower. When OAM beam is generated in optical fiber, the vector mode or scalar mode of optical fiber is usually obtained first, and then the mode coupling is carried out with stress action or polarization controller (PC), etc. Therefore, fiber gratings and fiber mode selective couplers (MSCs) have attracted attention in the generation of OAM [24, 25]. The all-fiber OAM generation and transmission system provides a good carrier for OAM, which also provides a necessary condition for the effective use of OAM beam.

This review article discusses the principle, transmission, generation in optical fiber comprehensively, and introduces application of OAM. It’s expected to be of great significance for OAM fiber design and application.

The Principle of OAM Generation

Vortex Beam

Optical vortex is divided into polarization vortex and phase vortex. The former corresponds to the cylindrical vector beam (CVB) with polarization vortex characteristics, and the latter corresponds to the optical orbital angular momentum (OAM) with phase vortex characteristics [26].

Polarization Vortex

CVB corresponds to the polarization characteristics of vortex light. Polarized vortex light is generated by polarization singularities, and is also called vector beam [27], which is the solution of vector Maxwell’s equations. For general linearly polarized light, circularly polarized light, and elliptically polarized light, the polarization state is the same everywhere in the cross section of the beam propagation, but for CVB, the polarization state of the light changes as the azimuth angle [28]. For CVB, there are two mutually orthogonal modes, namely radial polarization and angular polarization, which correspond exactly to the TM mode and TE mode in the fiber vector mode. In addtion, the two CVBs mentioned above live in a four dimensional space spanned by the basis formed by the Cartesian product of the mode bases and the polarization vectors, this also means that in addition to the TM and TE modes, there are two bases with different dimensions. By applying a unitary transformation to TM and TE modes, we can obtain two other basis vectors. These two basis vectors correspond exactly to the odd and even modes of HE₂₁ in the fiber vector mode [29]. The intensity and polarization of these four basis vectors are shown schematically in Figure 1.

FIGURE 1

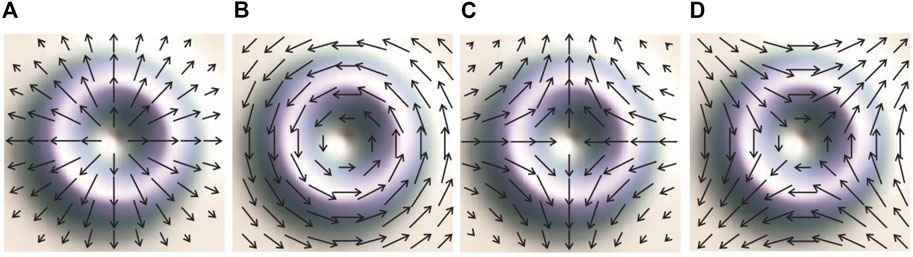
FIGURE 1. Polarization and light intensity of the four basis vectors (A) TM mode (B) TE mode (C) $\mathrm{H}{\mathrm{E}}_{21}^{\mathrm{even}}$ mode (D) $\mathrm{H}{\mathrm{E}}_{21}^{\mathrm{odd}}\mathit{ }$ mode [29].

Phase Vortex

Since the OAM has a phase factor of ${\text{e}}^{\text{i}l\phi }$, the phase distribution of the OAM is also related to the azimuth angle. $l$ represents the topological charge carried by the photon, the value is an integer, and each photon carries the OAM of $l\hslash$. The positive and negative values of $l$ will affect the vortex direction and phase distribution of OAM beam respectively. According to the direction of the vortex, the OAM beam is divided into left-handed vortex light ( $l$ is positive) and right-handed vortex light ( $l$ is negative), and the phase change of one circle is $2l\pi$ on the cross section of the beam propagation.

The Coupling Theory of OAM

The OAM beam can be formed by the coupling of the vector mode or the scalar mode in the optical fiber. The OAM formed by the two coupling methods contains different spin angular momentum, so the polarization characteristics of the OAM formed by the different coupling methods are different.

For OAM beam formed by vector mode coupling, its coupling principle is as follows:

$\left(\begin{array}{c}{\sigma }^{+}OA{M}_{+l}\\ {\sigma }^{-}OA{M}_{-l}\\ {\sigma }^{-}OA{M}_{+l}\\ {\sigma }^{+}OA{M}_{-l}\end{array}\right)=F_{l,m}\left(\begin{array}{cccc}1& i& 0& 0\\ 1& -i& 0& 0\\ 0& 0& 1& i\\ 0& 0& 1& -i\end{array}\right)\left(\begin{array}{c}H{E}_{l+\mathrm{1,1}}^{e\nu en}\\ H{E}_{l+\mathrm{1,1}}^{odd}\\ E{H}_{l-\mathrm{1,1}}^{e\nu en}\\ E{H}_{l-\mathrm{1,1}}^{odd}\end{array}\right)(1)$

Among them, $F_{l,m}$ represents the radial amplitude distribution, $\text{e}v\text{e}n$ and $odd$ represent even mode and odd mode. The positive and negative signs of $\sigma$ indicate left-hand and right-hand spin, correspondingly. $l$ represents topological charge. The spin of a photon is related to circular polarization, and the OAM formed by vector mode coupling has spin angular momentum, so it exhibits the characteristics of circular polarization.

For the OAM beam formed by scalar mode coupling, the corresponding relationship is [30]:

$\left\{\begin{array}{c}\widehat{x}{L}_{\pm l,m}\\ \widehat{y}{L}_{\pm l,m}\end{array}\right\}=\left\{\begin{array}{c}L{P}_{l,m}^{c,x}\pm iL{P}_{l,m}^{s,x}\\ L{P}_{l,m}^{c,y}\pm iL{P}_{l,m}^{s,y}\end{array}\right\}=F_{l,m}\left(r\right)\left\{\begin{array}{c}\widehat{x}{e}^{\pm \text{i}l\phi }\\ \widehat{y}{e}^{\pm \text{i}l\phi }\end{array}\right\},\left(l\ge 1\right)(2)$

Among them, $c$ and $s$ represent the phase form of cosine or sine contained in the scalar mode, and $\widehat{x}$ 、 $\widehat{y}$ represent the polarization direction. At this time, the spin angular momentum of the generated OAM is 0, and the beam exhibits linear polarization.

For OAM with different polarization states, they can be judged by the phenomenon after the beam passes through the optical element, as shown in Figure 2. A linearly polarized orbital angular momentum (LP-OAM) can only pass through a polarizer in the same direction as the light vector polarization. However, when the circularly polarized orbital angular momentum beam (CP-OAM) passes through the waveplate, it can pass through any angle of polarization because of the oscillating electromagnetic field at any angle of polarization, and the intensity distribution of transmitted light is still circular. When CP-OAM passes through the quarter-wave plate (QWP), it becomes linear polarization mode, and when it passes through the polarizer orthogonal to the light polarization direction, the beam cannot pass through.

FIGURE 2

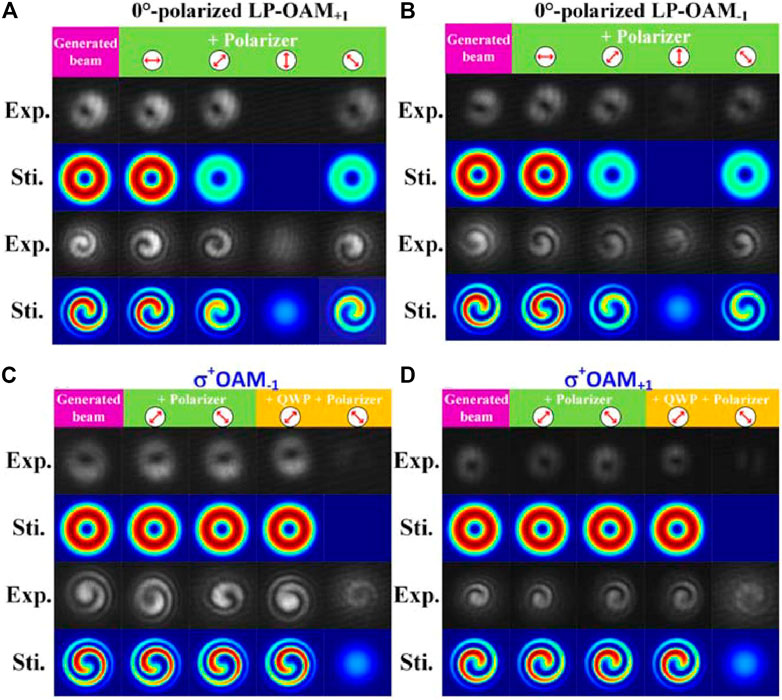
FIGURE 2. (A) (B) Schematic diagram of the phenomenon of LP-OAM passing through the polarizer (C) (D) Schematic diagram of the phenomenon of CP-OAM passing through the polarizer [31].

It is worth noting that both CP-OAM and LP-OAM are formed by coupling after generating a phase difference of $\pi /2$ between the corresponding vector modes or between the scalar modes. This also requires the system to be able to generate or provide a suitable phase difference to form or support OAM.

OAM Transmission in Optical Fiber

The long-distance transmission of OAM and optical communication multiplexing technology are inseparable from the stable transmission of OAM. As an excellent optical waveguide supporting beam transmission, optical fiber has become a research hotspot for effective transmission of OAM, but ordinary optical fiber is not suitable for OAM transmission [32]. Optical fibers that can transmit OAM stably, such as PCFs [33], RCFs [34], and microstructure fibers (MSFs) [35, 36], have received widespread attention.

Photonic Crystal Fiber

The PCF has attracted widespread attention due to its non-stop single-mode transmission, large mode area, and adjustable dispersion characteristics [37]. In 1996, Knight prepared the world’s first photonic crystal fiber (PCF) and achieved the property of having a single robust low-loss guiding mode over a wide spectrum [38]. Yang et al. [39] first proposed the use of PCF to transmit OAM. The proposed PCF supports two OAM modes, but there are problems include a small number of supported modes and large loss. Later, different structures of PCFs, such as circular air holes PCF [40–48], rectangular air holes PCF [49], and hybrid air hole PCF [50, 51], were proposed in some studies, and the performance of the fiber was optimized by changing the position and size of the air holes.

Circle Air-Hole Photonic Crystal Fiber

In 2015, Zhang et al. [40] proposed a four-ring cladding silicon dioxide circular photonic crystal fiber (C-PCF). The fiber supports 12 OAM modes. The cross-section structure, dispersion curve and nonlinear coefficient of proposed fiber are shown in Figure 3. It indicates the dispersion increases firstly and then decreases as wavelength, and the nonlinear coefficient is too high. None of these features are conducive to OAM lossless transmission.

FIGURE 3

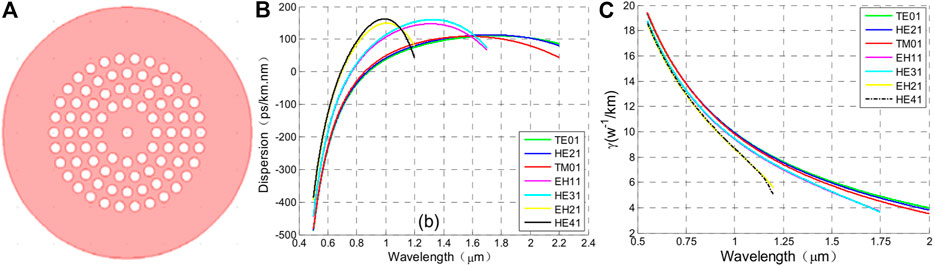
FIGURE 3. (A) Structure diagram of circular photonic crystal fiber made of silica material (B) Dispersion curve (C) Variation of the nonlinear coefficient with wavelength [40].

In some studies, the properties of the circular air hole PCF were changed by changing the position and size of holes [42–44], as shown in Figures 4A,B. Nandam et al. [46] proposed a PCF with spiral-shaped air holes and could support 14 OAM modes. Some transmission characteristics are shown in Figures 4C,D. It shows that the dispersion change is relatively gentle, and the nonlinear coefficient is reduced by nearly one order of magnitude compared with the C-PCF designed by Zhang et al. mentioned above. Jia et al. [41] proposed a PCF with large round air holes, whose diameter gradually increased. The fiber can transmit 38 OAM modes and has low confinement loss.

FIGURE 4

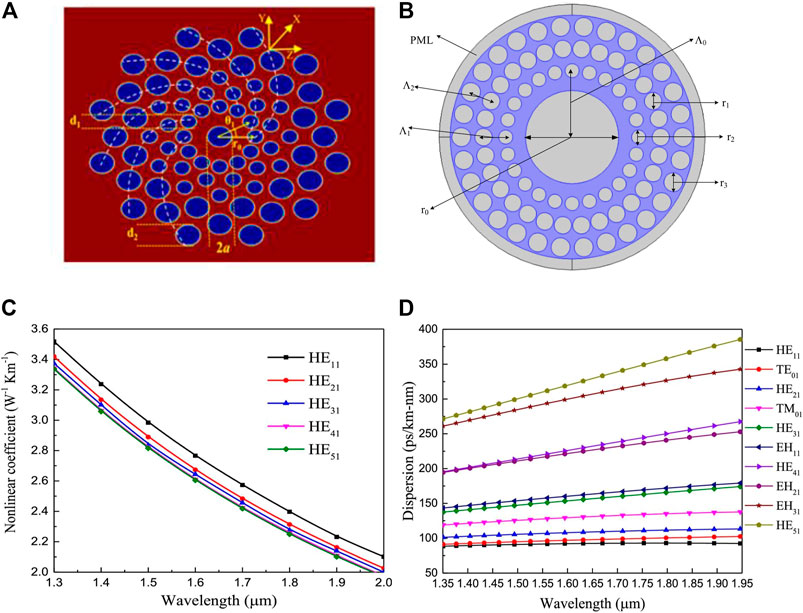
FIGURE 4. (A) and (B): Schematic diagram of some PCFs (A) Schematic diagram of spiral air pore arrangement [46] (B) Structure diagram of PCF with air holes of different sizes [41] (C) and (D): Characteristic parameters of PCF with spiral air hole arrangement [46] (C) Nonlinear coefficients with wavelength (D) Dispersion curves.

Non-circular Air-Hole Photonic Crystal Fiber

In recent years, with the improvement of optical fiber fabrication technology, the design of PCF’s holes is not limited to be circular. Several non-circular air-hole PCF are shown in Figure 5. Bai et al. [49] proposed the PCF of rectangular air holes, which can support up to 46 OAM modes, and the effective refractive index difference (ERID) between vector modes is all above ${10}^{-4}$. Figure 5B shows two kinds of air hole whose shapes are Bessel polygon [52, 53], which have very low confinement loss in the order of ${10}^{-10}$ dB/m.

FIGURE 5

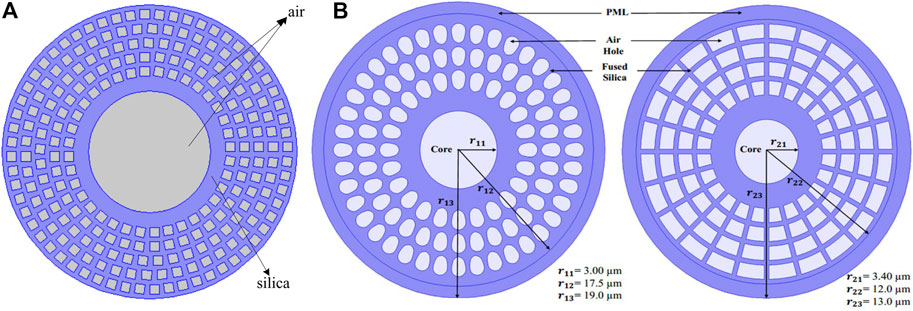
FIGURE 5. (A) Schematic diagram of PCF structure with rectangular air holes [49] (B) Schematic diagram of PCF structures with Bessel polygon air holes [53].

Now some studies have proposed some PCF combining air holes of different shapes [50, 51], which can support more OAM modes and have excellent characteristics. Table 1 summarizes the OAM transmission characteristics of several PCFs. Compared to PCF with circular air holes, PCFs with new shaped air holes are more complicated, but they provide a new direction for the study of PCF.

TABLE 1

TABLE 1. OAM transmission characteristics of several PCFs.

In order to make the PCF more suitable for transferring OAM, the central air hole of the PCF is usually designed to be larger, which allows the ring-shaped OAM to be transmitted outside the central air hole. If the central air hole is too small, the number of OAMs that PCF can support will decrease. In addition, the outer air holes also need to be able to effectively restrict the light beam. Too few air holes will cause beam leakage, resulting in higher loss.

At present, there are many research directions of OAM propagation using PCF. Based on space division multiplexing, some studies aim to improve the number of OAM mode in PCF [54–56]. In terms of filling materials for PCF, Tao He [57] filled the magnetic fluid into the large air hole of PCF. By changing the intensity of the applied magnetic field, the refractive index of the magnetic fluid changes correspondingly, and the nonlinear coefficient of the PCF is also reduced compared to that with no magnetic fluid.

Ring Core Fiber

In 2009, Ramachandran et al [58] demonstrated that the ERID is maximum when there is a mirror relationship between the refractive index distribution of the fiber and the intensity distribution of the propagation mode. The high ERID between modes will reduces the coupling, and different OAM mode groups (MGs) can achieve good transmission. The ring structure with high refractive index distribution restricts the OAM transmission within the ring, and the fabrication process of the RCF is simpler than that of other OAM fibers. By changing the refractive index distribution and composition materials of the fiber, the RCF can have different OAM transmission properties. Typical RCF such as step-index ring core fibers (SI-RCF) [59], graded index-ring core fiber (GI-RCF) [60], refractive-index-profile-modulated RCF (RIPM-RCF) [61], air core fiber(ACF) [62] are more widely used.

Step Index Ring Core Fiber

In 2014, Brunet et al. [63] conducted a theoretical analysis of the vector and scalar modes of SI-RCF, and gave an analytical expression for the cut-off conditions of SI-RCF. Based on this theory, they designed a set of SI-RCFs [64]. The effective index separation of the vector mode reaches above ${10}^{-4}$ and has a lower dispersion parameter. The refractive index distribution of the SI-RCF is shown in Figure 6. Wang et al. [65] has designed two SI-RCF supporting $\left|l\right|=3$ and $\left|l\right|=5$ respectively. The ERID between different modes reaches ${10}^{-3}$ magnitude, which reduces cross-talk between groups. At the same time, the transmission loss of the fiber is below 0.25 dB/km, which has excellent transmission characteristics.

FIGURE 6

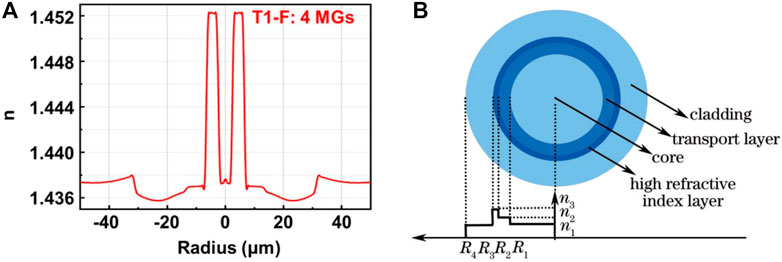
FIGURE 6. (A) Refractive index distribution of SI-RCF [65] (B) Refractive index distribution of modified SI-RCF [66].

However, in the actual propagation process, high refractive index materials will increase the transmission loss of the propagation process [67], so it is particularly important to balance the problem of mode degeneration and high refractive index transmission loss. Huang et al. [66] improved the SI-RCF by introducing a high refractive index material between the cladding and the transmission layer. Since the high refractive index material does not transmit OAM, the RCF can transmit the OAM more effectively.

Graded Index Ring Core Fiber

In order to prevent the high loss caused by high refractive index materials, it is effective to change the distribution pattern of refractive index to enhance the transmission properties of OAM. The graded index distribution of GI-RCF presents a gradual change, as shown in Figure 7A. The GI-RCF designed by Zhu et al. [68] supports 5 MGs with low coupling, and the average attenuation any mode is about 1 dB/km. Zhu et al. [69] proposed the GI-RCF, which suppressed the radial high-order mode effectively. The ERID between the fourth and fifth order OAM modes is $3.9\times {10}^{-3}$, which greatly separates the high-order OAM modes.

FIGURE 7

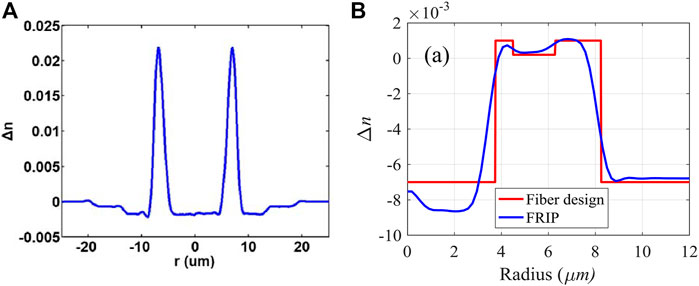
FIGURE 7. (A) Refractive index distribution of GI-RCF [69] (B) Refractive index distribution of RIPM-RCF [70].

Refractive-Index-Profile-Modulated RCF

In the real multiplexing system of OAM, the coupling between MGs can cause interference. In order to reduce the reference, Tan et al. designed RIPM-RCF [70]. Its refractive index distribution is shown in Figure 7B. The top of the ring core forms a numerical gap of effective refractive index. The optical fiber supports four low-order MGs, and the ERID between the MGs is more than $0.8\times {10}^{-3}$. Moreover, due to the large ERID between the mode and the cladding and the presence of notch modulation, the mode coupling from the guiding mode to the leaky cladding mode is effectively suppressed with low fiber attenuation about 0.2 dB/km. The RIPM-RCF proposed by Zhang et al. [71] can support four low-order MGs, and the ERID between the second and third-order modules is $2.5\times {10}^{-3}$. Group crosstalk is less than −36 dB/km.

Air Core Fiber

Some studies proposed ACF, one of which is shown in Figures 8A,B. Due to the huge ERID between air and the annular transmission layer, OAM can be confined to the transmission layer, so ACF has received extensive attention [23, 72–76]. The ACF proposed by Gregg et al. [72] can support up to three high-order MGs $\left(\left|l\right|=\mathrm{7,8,9}\right)$, and a large ERID is produced between different OAM modes. To a certain extent, the multi-path interference is reduced, and the purity of the transmission OAM is improved. Brunet et al [73, 74] added a low refractive index layer to the conventional ACF to increase the number of supported OAM modes, which can support up to 28 OAM modes for transmission.

FIGURE 8

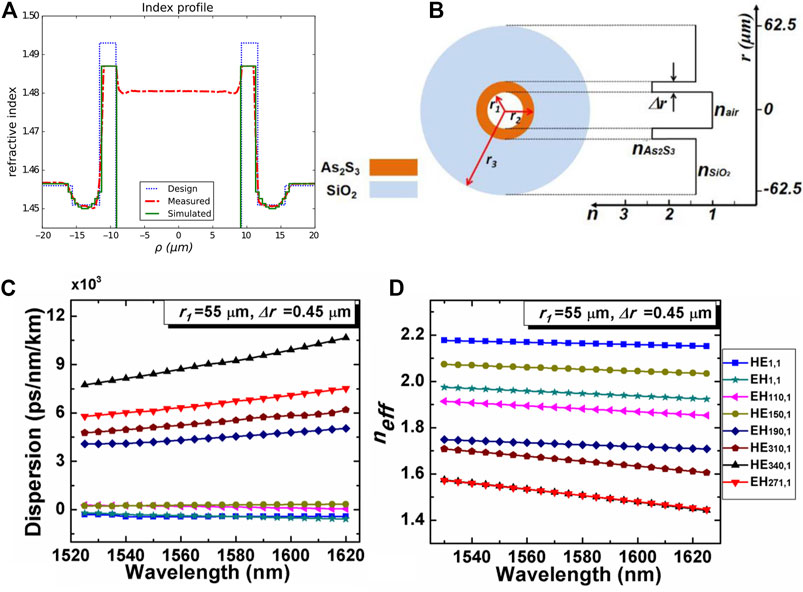
FIGURE 8. (A) and (B): Refractive index distribution of several ACFs [23, 74] (C) and (D): Characteristic parameters of ACF proposed by Wang et al. [23] (C) dispersion curve (D) effective refractive index variation curve with wavelength.

Wang et al. [23, 76] used $A{s}_2{S}_3$ as the material of the ring transmission layer in ACF, and the ERID between the transmission ring and the air hole was higher than that of the traditional ACF. Proposed fiber can support 1004 OAM modes in all O, E, S, C and L bands. The transmission characteristics of this fiber is shown in Figures 8C,D. The ERIDs of high-order vector modes keep is about ${10}^{-3}$ and the dispersion of the fiber changes smoothly. By adjusting the radius of the air hole, a double-frequency supercontinuum of 1,560–6,250 nm can be generated for the OAM_17,1 mode in the designed fiber.

In general, there are two design ideas that enable RCF to be more suitable for transmitting OAM. One is to add a high refractive index layer, and the other is to modulate the refractive index. For the first idea, the higher the refractive index and the smaller the width of the transmission layer added to the fiber, the greater the number of OAMs supported by the fiber. But this will cause higher losses. For the second idea, modulating the refractive index of the fiber according to the transmission characteristics can make the fiber obtain better transmission properties. The next experiment can combine idea one and idea two to modulate the refractive index of the fiber doped with a high refractive index layer.

Other Vortex Fiber

By changing the refractive index distribution in the fiber, some articles have also proposed other OAM fibers with good transmission performance.

B. Ung [77] proposed the inverse-parabolic graded-index fiber (IPGIF), and its refractive index profile is shown in Figure 9A. An ERID of $2.1\times {10}^{-4}$ is provided between the first-order mode, and the propagation of the first-order OAM mode can reach 1.1 km. Chen Yun [78] added a low refractive index layer between the core and the cladding to increase the ERID. The refractive index distribution is shown in Figure 9B. The simulation proves that the improved fiber can support the highest third-order OAM mode for effective transmission. Zhang et al. [79] performed a rotational twist on the designed IPGIF. Simulations show that the twisted IPGIF requires an order of magnitude less twist than the twisted air hole fiber. The twisted optical fiber can support 22 OAM modes in the entire C-band, and has excellent transmission characteristics with a small nonlinear coefficient.

FIGURE 9

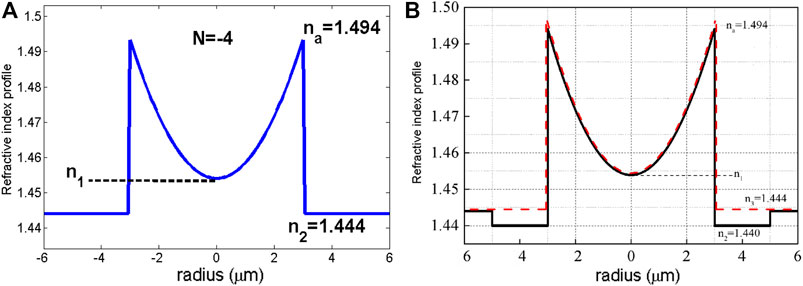
FIGURE 9. (A) Refractive index distribution of IPGIF [77] (B) Refractive index distribution of modified IPGIF [78].

The fibers mentioned above have different transmission properties due to differences in fiber structure and refractive index distribution. Taking into account the requirements of existing fabrication technology, RCF and PCF are more suitable for widespread production and use. From the perspective of optical communications, Optical fiber needs to meet the characteristics of low loss, large number of supported OAMs, and easy production. Therefore, the RCF with multiple transmission rings is more suitable for optical communications. The PCF is more suitable for transmitting OAM with special properties, such as adjustable dispersion and large mode field area. For the OAM fiber with a high refractive layer, although the number of supported OAMs is greatly increased, the loss is large. So this type of fiber is suitable for fiber lasers that generate high-order OAM. In addition to RCF and PCF, the manufacturing of some special structure optical fibers is limited by the technological level, but they exhibit excellent transmission characteristics, which provide a useful reference for the design of special fibers transmitting OAM.

The Generation of OAM in Fiber

OAM beam can be generated by spatial optical devices and optical fibers. Among them, OAM generated by spatial optical devices can be generated by helical phase plate [85], spatial light modulator [86], Q plate [87], etc. However, generating OAM through a spatial optical device will increase the complexity of the optical path. The vortex beam itself is an intrinsic solution of the fiber, so the generation of the OAM mode in the fiber will simplify the optical path and improve the phase purity of OAM [88]. The main optical fibers used to generate OAM modes in optical fibers are fiber gratings [89, 90], fiber MSCs [91], and helically twisted PCF (HT-PCF) [92–94].

Fiber Grating

Fiber gratings are divided into long-period fiber gratings and short-period fiber gratings (Bragg gratings) according to the length of their period. The fiber grating has a periodic distribution of refractive index. When the input meets the phase matching condition, mode coupling can be performed.

Long Period Fiber Grating

Long period fiber grating (LPFG) is a transmission grating [95]. The relationship between wavelength and grating period is [96]:

$\lambda =\left(n_{ef{f}_1}-n_{ef{f}_2}\right)\mathit{\Lambda }(3)$

Among them, $n_{ef{f}_1}$ and $n_{ef{f}_2}$ are the effective indices of the two coupled modes, respectively. $\lambda$ represents the resonant wavelength, and $\Lambda$ represents the period of the fiber grating. Due to the coupling and transmission characteristis of LPFG, Modes that satisfy the coupling conditions can be coupled to form LP modes or vector modes, thus further forming OAM. The experimental device in Ref. [97] contains a fiber grating for mode coupling, a vortex fiber for beam propagation, and a PC for forming OAM. The positive and negative conversion of the topological charge can be achieved by adjusting the pC. The schematic diagram is shown in Figure 10. Mode coupling of the input fundamental mode occurs within the fiber grating and generate a high-order mode. However, since the effective refractive index of the same order modes is approximately equal, the distribution of the same order modes generated at the same time is random and uneven. Therefore, PC or stress is usually added to adjust the amplitude and phase distribution of the same order mode, so the pure state vector mode or OAM mode can be output [98, 99].

FIGURE 10

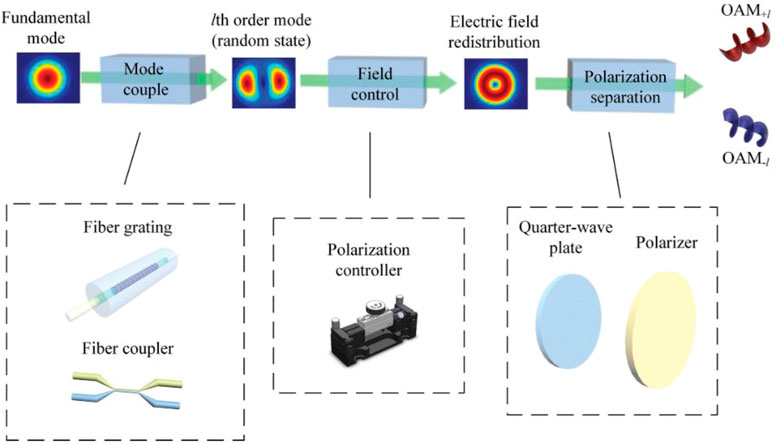
FIGURE 10. Schematic diagram of the coupling process [98].

Zhao et al. [100] designed a tilted LPFG (T-LPFG). In the T-LPFG, wave vector of the grating planes are tilted by angle θ with the Z axis. Compared with uniform LPFG, the grating period ${\Lambda }_T$ of T-LPFG is related to the tilt angle $\theta$, and ${\Lambda }_T=\Lambda \times \cos \theta$ is the actual grating period. By changing $\theta$, the grating period can be changed, and it can be seen from Eq. 4 that the resonant wavelength is related to the grating period, so the resonant wavelength and other parameters of TLPFG are adjustable. In the experiment, Zhao realized the mode coupling between LP₀₁ and LP₁₁ by calculating the relationship between the effective refractive index and the period of LP mode, and the coupling efficiency was greater than 99%. After that, a first-order OAM beam was generated by adjusting the PC in the optical path.

On the basis of the pattern coupling between LP₀₁ and LP₁₁, some studies realized the pattern coupling between LP₀₁ and LP₂₁ by cascading two LPFGs with different cycles [101, 102], as shown in Figure 11A. Through calculation, the designed two-stage LPFG meets the phase matching conditions of LP₀₁ and LP₁₁, LP₁₁ and LP₂₁ respectively, and the mode coupling is carried out. At the output end of the second-order LPFG, by adjusting PC, the vector mode of LP mode is degenerated and recombined to generate the second-order OAM beam.

FIGURE 11

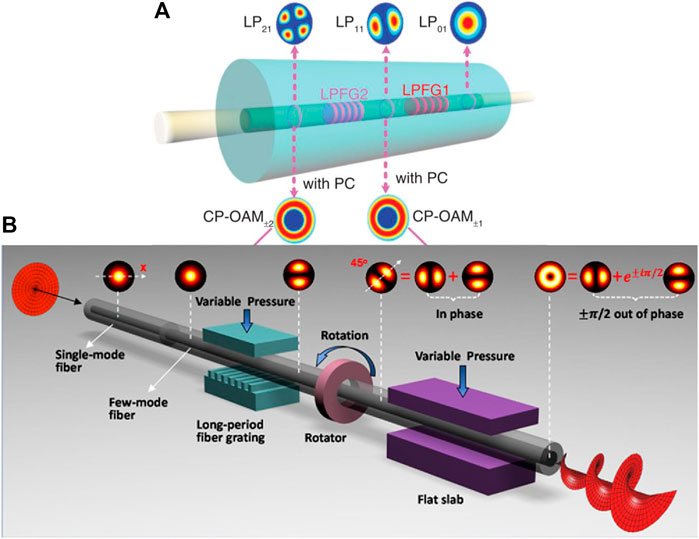
FIGURE 11. (A) Schematic diagram of two-stage long-period grating cascade structure [102] (B) Schematic diagram of the LP mode formation process [103].

It is worth noting that the generation of OAM based on LPFG above is all formed through the combination of vector modes. Some studies use LPFG system to synthesize OAM through LP mode. Li et al. [103] used mechanical LPFG to couple the input LP₀₁ into LP₁₁, and made the output of LP₁₁ at an angle of 45° with the X-axis of optical fiber cross section by rotation. LP₁₁ was decomposed into two orthogonal LP₁₁, and then the phase difference was generated through the pressure action of the plate to form OAM, as shown in Figure 11B. Wu et al. [104] used a four mode fiber-LPFG system such that LP₀₁ is coupled to form LP₂₁ directly. Then, by rotating LPFG, a phase difference of π∕2 was generated between the odd and even modes of LP₂₁ to produce a second-order OAM. Since the phase difference of π∕2 is difficult to achieve in some cases, Li et al. [105] proposed a scalar mode synthesis method and obtained OAM by synthesizing multiple LP modes with phase differences much smaller than π∕2. By distorting the few-mode fiber-LFPG (FMF-LFPG), a series of LP₁₁ modes with slight phase difference are generated, and the mode conversion is finally achieved with a power loss of 0.66 dB and a mode purity of 99%.

Both vector mode and LP mode coupling to OAM are based on the idea of mode coupling. Some studies have shown that it is possible to generate OAM patterns from a single CVB. Han et al. [106] firstly coupled the input beam into a single first-order CVB through the LPFG in tow mode fiber (TMF). After passing through QWP and the polarizer, the first-order OAM beam is generated by setting the angle of the polarizer. Compared to OAM synthesized from beams of two modes, a single CVB generates OAM with improved stability because it does not require a specific phase relationship between the two modes.

Considering the helical phase properties of OAM beams, helical long-period fiber gratings (HLPFG) are proposed [107–109]. Due to the special structure of HLPFG, the vortex phase can be directly excited without generating OAM beams through PC, stress and other operations. Moreover, the resonant wavelength of OAM can be adjusted when the HLPFG is twisted. The introduction of HLPFG can reduce the complexity of optical path, but the fabrication of grating is relatively complicated.

Fiber Bragg Grating

The fiber Bragg grating (FBG) is a reflective grating [95], and the relationship between the Bragg wavelength and the grating period is [96]:

$\lambda =\left(n_{ef{f}_1}+n_{ef{f}_2}\right)\mathit{\Lambda }(4)$

Similar to LPFG, the research on FBG mainly focuses on uniform period Bragg grating, tilted Bragg grating, and spiral Bragg grating.

Wang et al. [110] used FBG to characterize OAM transmitted in optical fibers. When the wavelength meets formula (4), the OAM beam is reflected by the grating. Topological charge reversal and circular polarization reversal can be observed. Wang et al. also showed that the Bragg grating could be applied to all fiber systems generating OAM.

Like TLPFG, the wavelength and period of the tilted FBG are also related to the cosine of the tilt angle. By adjusting the tilt angle, the resonant wavelength of the FBG can also be changed. The FMF-TFBG designed by Zhao et al. [111] realized the conversion of LP₀₁ mode to LP₁₁, LP₂₁, LP₀₂, LP₃₁ mode, and the conversion efficiency reached 90%. Then by controlling the PC, a phase difference of π∕2 is generated between the vector modes to form the corresponding OAM mode. Yang [112] et al. designed a ring-shaped FMF system containing TFBG. The ERID of the vector mode is very small, and this method can form a stable LP-OAM $\left(\left|l\right|=\mathrm{1,2,3}\right)$ mode. When the four degenerate vector modes are reflected, by adjusting the PC at the output end, the relative amplitude and phase between the degenerate modes are changed to generate a pure OAM mode.

The spiral FBG has the characteristic that the refractive index of the spiral can be modulated, and the refractive index in the lateral $x$ direction and $y$ direction has a phase shift of π∕2. Lin et al. [113] fabricated a spiral FBG using a phase mask. Among them, helical FBG is used for generating OAM beam, ytterbium-doped fiber is used for beam gain amplification, and two FM-FBGs are used to filter LP beams which cannot generate OAM mode. Huang [114] believe that the mode propagation in ordinary fiber will be degenerate, so they use RCF for transmission, which improves the ERID of the vector modes and makes the transmission of OAM more stable.

Mode Selective Coupler

The MSC is formed by splicing two kinds of fibers. The principle is that the modes are coupled through the evanescent wave between the fibers, and the fundamental mode is transmitted in the single-mode fiber through the MSC. High-order modes are coupled in the FMF. Similar to the fiber grating, the fiber MSC also couples the low-order mode to the high-order mode.

Due to the existence of degeneracy, at the output of some mode selection couplers, PC or stress is usually added to change the amplitude and phase relationship between high-order degenerate modes to generate OAM beams [31, 115, 116].

The SMF-FMF mode selection coupler designed by Wang et al. [115] realizes the coupling of LP₀₁, LP₁₁, and LP₂₁, and the principle is shown in Figure 12A. Based on this mode selector, Wang et al. designed an all-fiber mode-locked fiber femtosecond vortex beam laser, as shown in Figure 12B. Zhang et al [31] demonstrated theoretically that the system combined by SMF-FMF and squeezed PC can generate OAM in arbitrary polarization states. They passed the resulting beam through QWP and polarizing plates, demonstrating that the system can selectively produce LP-OAM and CP-OAM. There are other studies [116] that produced pure-state vector beams by controlling the PC at the output of the SMF-FMF. The pure-state vector beam was then passed through the QWP with the polarizer and the OAM beam was output. Changing the direction of the polarizer can obtain OAM with opposite vortex direction.

FIGURE 12

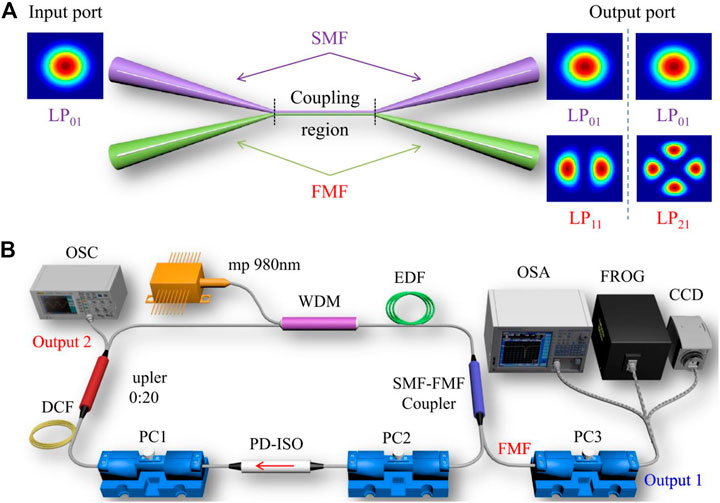
FIGURE 12. (A) Schematic diagram of the LP mode coupling performed by MSC (B) The vortex beam laser designed by wang et al. [115].

There are also some studies that replace the FMF in the mode selection coupler with other fibers which can generate the first-order OAM directly at the output, such as SMF-ACF [117], SMF-RCF [118], SMF-GIFMF [119] etc. The unique refractive index distribution that these fibers have provides a high ERID. Therefore it is possible to design MSCs so that the base mode is coupled to generate OAM modes directly. The high-order mode coupled out of the fundamental mode can be steadily propagated in the fiber, and a higher purity OAM can be produced without adding a PC at the output end.

In terms of fiber splicing, there is also a different method from the fiber splicing of the traditional mode selection coupler. Jin et al. [120] used SMF spliced with lateral offset to excite the HE₂₁ mode in the RCF, and discussed the relationship between the offset distance and the purity of the mode. This method enables the first-order OAM beam to be generated in a wide wavelength range of 1,540 nm–1580 nm. Li et al. [121] spliced SMF to TMF with a specific offset and tilt angle, and realized high-order fiber mode conversion through fundamental mode coupling. However, the coupling efficiency of this splicing method is only about 34%, and the structure needs to be optimized.

Helically Twisted PCF

Based on the three-dimensional structure of PCF, in 2012 Wong et al. [122] proved for the first time that HT-PCF can excite OAM. Due to the special structure of the helical twist, the loss, dispersion and polarization state of the fiber can be controlled by changing the twist rate and other parameters.

The HT-PCF designed by Fu et al. [93] stimulated OAM modes with topological charges of +5 and +6 in the experiment. They found that the leakage orbit resonance in the cladding is closely related to the twist rate and length of the spiral PCF. The fiber produced a high-quality OAM₊₆ at the resonant wavelength with a coupling efficiency of −22.27 dB.

Yan et al. [123] designed HT-PCF for filtering. When the distortion ratio reaches a certain value, the difference of transmission loss between positive and negative OAM beams will increase significantly. HT-PCF has the property of transmitting vortex beams with the same chirality as the hollow channels’, but dissipating vortex beams with opposite chirality. They also implemented the filtering of OAMs with different chirality in the experiment.

Acoustic-Induced Method

In 2006, Dashti et al. [124] studied the acousto-optic interaction in optical fibers from the perspective of optical vortices and acoustic vortices. The conversion of acoustic vortices and optical vortices is:

$\begin{array}{c}A{V}_{np}+C{V}_{l-n,k}^s\iff C{V}_{lm}^s\end{array}(5)$

Among them, $AV$ represents the OAM of the sound vortex. s indicates the spin of the photon. l denotes the order of the photon’s OAM. n indicates the order of the phonon’s OAM. p,k and m indicate the radial mode order of the phonon or photon. Based on this theory, Dashti conducted experiments to generate $A{V}_{\mp \mathrm{1,0}}$ by controlling the relative amplitude and phase of the radio frequency. When the fundamental mode passes through the acoustical driven generated AIFG, the fundamental mode will couple into the first-order OAM mode under acousto-optical conversion. However, due to the limitation of the acoustic resonance frequency under the acousto-optic phase matching, the device cannot generate high-order OAM modes. Zhang et al. [125] completed the coupling of the fundamental mode to the second-order OAM mode through the cascaded sound drive method, as shown in Figure 13. Two different frequencies of RF were used to induce two AIFGs simultaneously in the fiber. when the fundamental mode passed through, first-order and second-order OAM coupling occurred in the first- and second-order AIFGs, respectively.

FIGURE 13

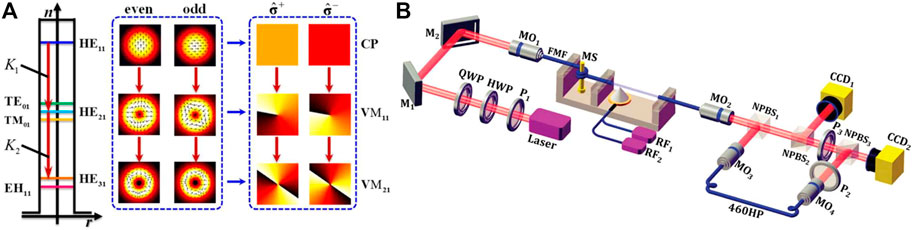
FIGURE 13. (A) Schematic diagram of the principle of the secondary acoustic drive cascade (B) Schematic diagram of the experimental setup by Zhang et al. [125].

By changing the radio frequency, the mode conversion after acousto-optic driving also shows wavelength tunability. Zhang et al. [126] realized the generation of the first-order vortex beam by means of acoustic drive in TMF, and achieved tunable wavelength in the 1,540 nm–1560 nm wavelength range by changing the radio frequency. In the entire wavelength tuning range, the mode conversion efficiency is maintained at about 95%.

Multi-Coherent Beam Synthesis

Yan et al. [127, 128] proposed a method of synthesizing OAM using input multiple coherent optical transmissions. As shown in Figure 14A, the fiber coupler consists of a central ring and four outer cores. The four coherent input lights pass through the four outer cores and are coupled into OAM beams, and the four coherent lights need to meet a certain phase difference. When the size of outer core changes, the OAM mode will also change. The purity of the OAM mode obtained by this coupling method is above 99%.

FIGURE 14

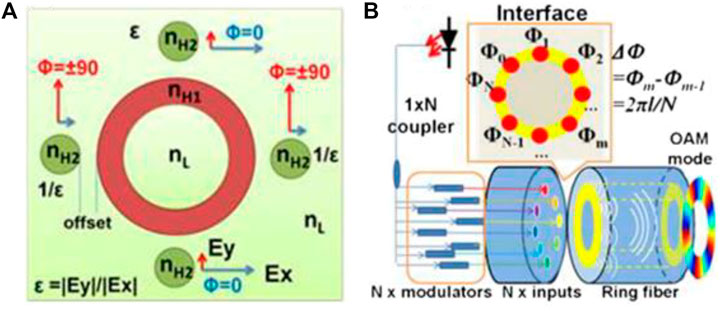
FIGURE 14. (A) Structure of the fiber coupler and the phase and polarization state of the input lights [127] (B) Generation of OAM modes of charge number $\mathit{l}$ in a ring fiber with N coherent Gaussian inputs [128].

In the other way, multiple coherent Gaussian fundamental modes are input to form OAM mode coupling, as shown in Figure 14B. Yan et al. found that controlling the phase relationship of multiple inputs can selectively generate OAM modes of different states. Theoretically, it is proved that there is a discrete Fourier transform relationship between the input Gaussian mode channel and the output OAM channel, which is suitable for OAM mode division multiplexing system. However, this method of coherent optical coupling into OAM mode requires high coherence for external light sources and needs to meet the phase difference, so the practicality is less.

In addition to the methods mentioned above, there are some other methods such as using a square-hole fiber to couple the input fundamental mode into OAM [129], using a system composed of a spiral symmetric fiber and a normal fiber to generate OAM [130], and other special structured fibers. However, the fabrication of these fibers is relatively complicated, and therefore most of them are in the simulation stage. Optical elements such as fiber gratings and MSCs can be effective in generating OAM, and different studies have also improved the ability of the system to generate OAM by changing the properties of these optical elements. The existing industrial level can manufacture fiber gratings and MSCs, and both belong to fiber components, so they can be used to construct fiber lasers for OAM. Besides, the acoustic-induced method excites vortex light from the perspective of acousto-optical interaction. The next experiment can start from the perspective of acousto-optic conversion, cascading multiple acoustic drivers to generate high-order OAM. In addition, special optical fibers generating OAM usually has strict requirements on fiber preparation and external light sources. Although it is difficult to achieve, it provides a new idea for the generation of OAM.

Application of OAM

OAM has the characteristics of infinite orthogonal basis and circular distribution of light intensity, which is different from Gaussian beam. These characteristics make the OAM beam closely related to cutting-edge disciplines, such as nonlinear optics [131], optical communication [132, 133], particle manipulation [134] and microscopic imaging [135].

Nonlinear Optics

The wavelength range of the OAM beam can be increased by nonlinear frequency conversion, shifting the OAM carried by fundamental frequency light to harmonics. In this process, both the frequency and topological charge of the new OAM may change [136]. Zhang et al. [8] proposed a method to generate a high-order OAM vortex beam using relativistic harmonics on a solid surface. And the first-order OAM beam was used to irradiate and generate a high-intensity ninth-order vortex beam. Wu [137] demonstrated theoretically and experimentally that the OAM transformation is modulated by a phase-matching mechanism for nonlinear effect. Fang et al [138] demonstrated that the phase-matching conditions of the OAM mode can be changed by varying the relative group velocity, and proposed a new vortex fiber that can manipulate the nonlinearity of the OAM beam.

In addition, Yang [139] proposed a novel OAM coding technique. He used computational holography for the design of nonlinear multiplexed holograms, which solved the multi-channel multiplexing problem in nonlinear holography.

Optical Communication

The orthogonal basis contained in the OAM provides an additional degree of freedom for communication coding, so MIMO systems provide a suitable method for practical information transmission. Based on MIMO, the transmission capacity of OAM can be greatly increased by using multiplexing methods such as space-division multiplexing (SDM) and wave-division multiplexing (WDM).

During the transmission of SDM, inter-ring crosstalk affects the transmission characteristics. Li et al. [140] designed an optical fiber suitable for SDM transmission. This fiber consists of seven uniformly arranged transmission rings, and each ring supports 18 OAM modes. The rings have high contrast ring structure, which can not only improve the number of OAM support, but also well limit the transmission of OAM crosstalk. The crosstalk between rings is small to −30 dB through 100 km. Subsequently, Li et al. [67] used a high contrast refractive index loop and groove design to integrate 19 transmission rings in a single fiber and each ring supports 18 OAM modes. The 100 km inter-ring crosstalk is less than −45 dB. As with normal RCF, the high contrast refractive index structure increases the ERID and constrains crosstalk, but increases transmission loss.

During the MDM transmission process, inter-mode crosstalk will occur, which will hinder the transmission of multi-mode OAM. Using MIMO technology can solve the problem of inter-mode crosstalk effectively [141]. By increasing the ERID between mode groups, the cross-talk between modes and complexity of MIMO technology can both be reduced. However, the use of MIMO will further increase the complexity of the system. Therefore, multiplexing systems without MIMO have become a hot spot. By using optical fibers, the transmission of MDM systems without MIMO can be realized, which simplifies the complexity of the system [69, 142, 143].

Particle Manipulation

With a deeper understanding of the microscopic world, the research on microorganism, single cell and other microscopic levels requires the control technology of particles. The trapping manipulation methods for particles include the traditional mechanical tweezers and the modern optical tweezers. Compared with mechanical tweezers, optical tweezers use non-contact operation, and has the characteristics of small damage to life and high repeatability. Gahagan et al. [144] used vortex beams to trap and manipulate particles in a low refractive index environment. Compared with traditional Gaussian beams, vortex beams can support more kinds of particles to be trapped and manipulated.

In the area of particle manipulation, there is also the optical wrench technology that enables the rotation of particles. The principle of conventional optical wrenches is to rotate the particles by using the interactions that occur when the particles absorb and reflect light and other processes. In contrast, the OAM optical wrenches transfer spin angular momentum and OAM to the captured particle directly, enabling three-dimensional translation and one-dimensional rotation of the particle [145]. Therefore, the OAM optical tweezers are convenient to operate and suitable for more particles. Gao et al. [146] realized the capture, translation and rotation of particles using OAM beams. Lehmuskero et al. [147] used a vortex beam to irradiate plasma gold particles, which rotated rapidly along a circular orbit. It was measured that there was a relationship between the particle rotation frequency and OAM, and a transfer of both occurred during the action.

In addition, OAM exhibit unique quantum entanglement properties due to the infinite dimensional Hilbert space constituted by the orthogonal basis of the OAM. Therefore OAM also has a wide range of applications in the quantum field [148, 149]. OAM has an important role in the field of optical microscopy because of its spiral phase feature that enhances the imaging of objects and its unique interference fringes [150, 151].

Conclusion

There are many research directions of fiber-based OAM transmission and generation systems, and some researches continue to make changes in fiber structure and optical devices to make the all-fiber system better support OAM mode. At present, PCF and RCF have become the hotspots of OAM fiber optic transmission system because of their good transmission characteristics. The number of modes, transmission efficiency and transmission distance of OAM need to be further improved to meet the needs of the information society.

For OAM fiber generation system, there are some generation systems with high requirements for fiber structure and external light source, which are not practical due to insufficient preparation process. Therefore, the use of fiber grating, MSC and other fiber structures with relatively mature preparation process is a hot research topic. The current all-fiber OAM generation system still has some problems for generating multiple OAM modes. A complete system for generating multiple high-purity OAM modes is also necessary to implement multiplexing technologies such as MDM and SDM.

Overall, there is a lot of room for improvement in fiber-based OAM transmission and generation systems. At the same time, the fiber system has great potential for OAM mode support [80–84].

Author Contributions

MM analyzed the data and wrote the manuscript, LY revised the manuscript, WY and LZ proposed the idea.

Funding

The authors gratefully acknowledge financial support from the National Natural Science Foundation of China (61905062, 62070506 and 61927815), China Postdoctoral Science Foundation (2020M670613), Hebei Postdoctoral Scholarship Project (B2020003026). Thanks for the support of the Key Laboratory of all Optical Networks and Advanced Communications Networks of Ministry of Education (Beijing Jiaotong University) (AON2019005).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are thankful to other colleagues in their laboratory for their understanding and help.

References

1. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fürhapter S, Jesacher A, Bernet S, Ritsch-Marte M. Spiral Interferometry. Opt Lett (2005) 30:1953–5. doi:10.1364/ol.30.001953

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Tamburini F, Anzolin G, Umbriaco G, Bianchini A, Barbieri C. Overcoming the Rayleigh Criterion Limit with Optical Vortices. Phys Rev Lett (2006) 97:163903. doi:10.1103/physrevlett.97.163903

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Friese MEJ, Nieminen TA, Heckenberg NR, Rubinsztein-Dunlop H. Optical Alignment and Spinning of Laser-Trapped Microscopic Particles. Nature (1998) 394:348–50. doi:10.1038/28566

CrossRef Full Text | Google Scholar

5. Toyoda K, Miyamoto K, Aoki N, Morita R, Omatsu T. Using Optical Vortex to Control the Chirality of Twisted Metal Nanostructures. Nano Lett (2012) 12:3645–9. doi:10.1021/nl301347j

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Dholakia K, Čižmár T. Shaping the Future of Manipulation. Nat Photon (2011) 5:335–42. doi:10.1038/nphoton.2011.80

CrossRef Full Text | Google Scholar

7. Padgett M, Bowman R. Tweezers with a Twist. Nat Photon (2011) 5:343–8. doi:10.1038/nphoton.2011.81

CrossRef Full Text | Google Scholar

8. Zhang X, Shen B, Shi Y, Wang X, Zhang L, Wang W, et al. Generation of Intense High-Order Vortex Harmonics. Phys Rev Lett (2015) 114:173901. doi:10.1103/PhysRevLett.114.173901

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ni R. Nonlinear Generation and Steering of Light in Second-Order Nonlinear Optical Materials. [dissertation/master’s thesis]. Nanjing(Jiangsu)]: Nanjing: Nanjing University (2017).

Google Scholar

10. Liu J, Nape I, Wang Q, Vallés A, Wang J, Forbes A. Multidimensional Entanglement Transport through Single-Mode Fiber. Sci Adv (2020) 6:eaay0837. doi:10.1126/sciadv.aay0837

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang X-L, Cai X-D, Su Z-E, Chen M-C, Wu D, Li L, et al. Quantum Teleportation of Multiple Degrees of freedom of a Single Photon. Nature (2015) 518:516–9. doi:10.1038/nature14246

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhao Y. Applied Basic Research on Multi-Scenario Short-Reach Optical Interconnects Based on Orbital Angular Momentum Modes. [dissertation/doctoral thesis]. [Wuhan(Hubei)]: Huazhong University of Science and Technology (2019).

Google Scholar

13. Wang J, Yang J-Y, Fazal IM, Ahmed N, Yan Y, Huang H, et al. Terabit Free-Space Data Transmission Employing Orbital Angular Momentum Multiplexing. Nat Photon (2012) 6:488–96. doi:10.1038/nphoton.2012.138

CrossRef Full Text | Google Scholar

14. Yan Y, Xie G, Lavery MPJ, Huang H, Ahmed N, Bao C, et al. High-capacity Millimetre-Wave Communications with Orbital Angular Momentum Multiplexing. Nat Commun (2014) 5:4876. doi:10.1038/ncomms5876

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ke X, Guo X. Realization of Optical Phase Information Encode by Using Orbital Angular Momentum of Light Beam. Chin J Quant Elect (2015) 32:69–76. doi:10.3969/j.issn.1007-5461.2015.01.010

CrossRef Full Text | Google Scholar

16. Randel S, Ryf R, Sierra A, Winzer PJ, Gnauck AH, Bolle CA, et al. 6×56-Gb/s Mode-Division Multiplexed Transmission over 33-km Few-Mode Fiber Enabled by 6×6 MIMO Equalization. Opt Express (2011) 19:16697–707. doi:10.1364/OE.19.016697

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Milione G, Huang H, Lavery M, Willner A, Padgett MJ. Orbital-Angular-Momentum Mode (De)Multiplexer: A Single Optical Element for MIMO-Based and Non-MIMO-based Multimode Fiber Systems[Conference Presentation]. San Francisco, California, United States: OFC 2014 (2014).

Google Scholar

18. Zhang Z, Xiao Y, Ma Z, Xiao M, Ding Z, Lei X, et al. 6G Wireless Networks: Vision, Requirements, Architecture, and Key Technologies. IEEE Veh Technol Mag (2019) 14:28–41. doi:10.1109/mvt.2019.2921208

CrossRef Full Text | Google Scholar

19. Yao AM, Padgett MJ. Orbital Angular Momentum: Origins, Behavior and Applications. Adv Opt Photon (2011) 3:161–204. doi:10.1364/aop.3.000161

CrossRef Full Text | Google Scholar

20. Curtis JE, Grier DG. Modulated Optical Vortices. Opt Lett (2003) 28:872–87. doi:10.1364/ol.28.000872

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yan L, Gregg P, Karimi E, Rubano A, Marrucci L, Boyd R, et al. Q-plate Enabled Spectrally Diverse Orbital-Angular-Momentum Conversion for Stimulated Emission Depletion Microscopy. Optica (2015) 2:900. doi:10.1364/optica.2.000900

CrossRef Full Text | Google Scholar

22. Liu J, Xing D, Zeng X, Lu J. Orbital Angular Momentum Multiplexing Technology Based on Optical Fiber. Laser Optoelectronics Prog (2018) 55:42–54. doi:10.3788/lop55.050005

CrossRef Full Text | Google Scholar

23. Wang Y, Bao C, Geng W, Lu Y, Fang Y, Mao B, et al. Air-Core Ring Fiber with >1000 Radially Fundamental OAM Modes across O, E, S, C, and L Bands. IEEE Access (2020) 8:68280–7. doi:10.1109/access.2020.2985776

CrossRef Full Text | Google Scholar

24. Zhang X, Wang A, Chen R, Zhou Y, Ming H, Zhan Q. Generation and Conversion of Higher Order Optical Vortices in Optical Fiber with Helical Fiber Bragg Gratings. J Lightwave Technol (2016) 34:2413–8. doi:10.1109/jlt.2016.2536037

CrossRef Full Text | Google Scholar

25. Wen J, He X, Xing J, Yang J, Pang F, Zeng X, et al. All-Fiber OAM Amplifier with High Purity and Broadband Spectrum Gain Based on Fused Taper Vortex-Beam Coupler. IEEE Photon J. (2018) 10:1–8. doi:10.1109/jphot.2018.2872040

CrossRef Full Text | Google Scholar

26. Tao R. Simulation and Realization of Vector Beam in Optical Fiber Waveguide. [dissertation/doctoral thesis]. [Hefei(Anhui)]: University of Science and Technology of China (2020).

Google Scholar

27. Zhou H. Research on Measurement Techniques of Optical Orbital Angular Momentum. [dissertation/doctoral thesis]. [Wuhan(Hubei)]: Huazhong University of Science and Technology (2017).

Google Scholar

28. Sun P. Generation of Vector Vortex Beams in an Optical Fiber. [dissertation/master’s thesis]. [Harbin(Heilongjiang)]: Harbin University of Science and Technology (2016).

Google Scholar

29. Holleczek A, Aiello A, Gabriel C, Marquardt C, Leuchs G. Classical and Quantum Properties of Cylindrically Polarized States of Light. Opt Express (2011) 19:9714–36. doi:10.1364/OE.19.009714

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Jiang Y, Ren G, Jin W, Xu Y, Jian W, Jian S. Polarization Properties of Fiber-Based Orbital Angular Momentum Modes. Opt Fiber Technol (2017) 38:113–8. doi:10.1016/j.yofte.2017.09.002

CrossRef Full Text | Google Scholar

31. Zhang H, Liu Y, Wang Z, Mao B, Han Y, Yang K. Generation of Arbitrary Polarized OAM Mode Based on a Fiber Mode Selective Coupler. J Opt (2019) 21:085705. doi:10.1088/2040-8986/ab2c4a

CrossRef Full Text | Google Scholar

32. Alexeyev AN, Fadeyeva TA, Fadeyeva TA, Volyar AV, Soskin MS. Optical Vortices and the Flow of Their Angular Momentum in a Multimode Fiber. Semiconductor Phys Quan Electron Optoelectronics (1998) 1:82–9. doi:10.15407/spqeo1.01.082

CrossRef Full Text | Google Scholar

33. Tian W, Zhang H, Zhang X, Xi L, Zhang W, Tang X. A Circular Photonic crystal Fiber Supporting 26 OAM Modes. Opt Fiber Technol (2016) 30:184–9. doi:10.1016/j.yofte.2016.07.009

CrossRef Full Text | Google Scholar

34. Nejad RM, Allahverdyan K, Vaity P, Amiralizadeh S, Brunet C, Messaddeq Y, et al. Mode Division Multiplexing Using Orbital Angular Momentum Modes over 1.4-km Ring Core Fiber. J Lightwave Technol (2016) 34:4252–8. doi:10.1109/jlt.2016.2594698

CrossRef Full Text | Google Scholar

35. Huang W, Liu Y-g., Wang Z, Zhang W, Luo M, Liu X, et al. Generation and Excitation of Different Orbital Angular Momentum States in a Tunable Microstructure Optical Fiber. Opt Express (2015) 23:33741–52. doi:10.1364/OE.23.033741

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Zhu G, Wang X, Chen Y, Hui C, Li S. Microstructured Optical Fibers for Transmitting Orbital Angular Momentum (OAM) Mode[Conference Presentation]. Hong Kong, China: ACP 2015 (2015).

Google Scholar

37. Wang W, Hou L. Present Situation and Future Development in Photonic Crystal Fibers. Las Optoelect Prog (2008) 45:43–58. doi:10.3788/lop20084502.0043

CrossRef Full Text | Google Scholar

38. Knight JC, Birks TA, Russell PSJ, Atkin DM. All-silica Single-Mode Optical Fiber with Photonic crystal Cladding. Opt Lett (1996) 21:1547–9. doi:10.1364/ol.21.001547

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Yue Y, Zhang L, Yan Y, Ahmed N, Yang J-Y, Huang H, et al. Octave-spanning Supercontinuum Generation of Vortices in an As_2S_3 Ring Photonic crystal Fiber. Opt Lett (2012) 37:1889–91. doi:10.1364/OL.37.001889

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Zhang H, Zhang W, Xi L, Tang X, Tian W, Zhang X. Design of a Circular Photonic Crystal Fiber Supporting OAM Modes[Conference Presentation]. Hong Kong, China: ACP 2015 (2015).

Google Scholar

41. Jia C, Jia H, Wang N, Chai J, Xu X, Lei Y, et al. Theoretical Analysis of a 750-nm Bandwidth Hollow-Core Ring Photonic Crystal Fiber with a Graded Structure for Transporting 38 Orbital Angular Momentum Modes. IEEE Access (2018) 6:20291–7. doi:10.1109/access.2018.2817577

CrossRef Full Text | Google Scholar

42. Hassan MM, Kabir MA, Hossain MN, Nguyen TK, Paul BK, Ahmed K, et al. Numerical Analysis of Circular Core Shaped Photonic crystal Fiber for Orbital Angular Momentum with Efficient Transmission. Appl Phys B (2020) 126:145. doi:10.1007/s00340-020-07497-2

CrossRef Full Text | Google Scholar

43. Huang W, You Y, Song B-b., Chen S-y. A Photonic crystal Fiber for Supporting 30 Orbital Angular Momentum Modes with Low Dispersion. Optoelectron Lett (2020) 16:34–9. doi:10.1007/s11801-020-9072-7

CrossRef Full Text | Google Scholar

44. Israk MF, Razzak MA, Ahmed K, Hassan MM, Kabir MA, Hossain MN, et al. Ring-based Coil Structure Photonic crystal Fiber for Transmission of Orbital Angular Momentum with Large Bandwidth: Outline, Investigation and Analysis. Opt Commun (2020) 473:126003. doi:10.1016/j.optcom.2020.126003

CrossRef Full Text | Google Scholar

45. Zhang L, Meng Y. Design and Analysis of a Photonic crystal Fiber Supporting Stable Transmission of 30 OAM Modes. Opt Fiber Technol (2021) 61:102423. doi:10.1016/j.yofte.2020.102423

CrossRef Full Text | Google Scholar

46. Nandam A, Shin W. Spiral Photonic crystal Fiber Structure for Supporting Orbital Angular Momentum Modes. Optik (2018) 169:361–7. doi:10.1016/j.ijleo.2018.05.055

CrossRef Full Text | Google Scholar

47. Hu Z-A, Huang Y-Q, Luo A-P, Cui H, Luo Z-C, Xu W-C. Photonic crystal Fiber for Supporting 26 Orbital Angular Momentum Modes. Opt Express (2016) 24:17285–91. doi:10.1364/OE.24.017285

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Jiao X, Zhang H, Zhang X, Li H, Wei J, Wang Z, et al. Performance of Circular Photonic crystal Fiber Transmitting Orbital Angular Momentum Modes under Macro-Bending. J Opt (2019) 21:065703. doi:10.1088/2040-8986/ab1c44

CrossRef Full Text | Google Scholar

49. Bai X, Chen H, Yang H. Design of a Circular Photonic crystal Fiber with Square Air-Holes for Orbital Angular Momentum Modes Transmission. Optik (2018) 158:1266–74. doi:10.1016/j.ijleo.2018.01.015

CrossRef Full Text | Google Scholar

50. Yang H. Design and Performance Analysis of a Novel Photonic crystal Fiber for OAM Mode Transmission. [dissertation/master’s thesis]. [Nanjing(Jiangsu)]: Nanjing University of Posts and Telecommunications (2018).

Google Scholar

51. Ke X, Wang S. Design of Photonic Crystal Fiber Capable of Carrying Multiple Orbital Angular Momentum Modes Transmission. Opt Photon J (2020) 10:49–63. doi:10.4236/opj.2020.104005

CrossRef Full Text | Google Scholar

52. Hassan MM, Kabir MA, Hossain MN, Biswas B, Paul BK, Ahmed K. Photonic crystal Fiber for Robust Orbital Angular Momentum Transmission: Design and Investigation. Opt Quant Electron (2019) 52:8. doi:10.1007/s11082-019-2125-0

CrossRef Full Text | Google Scholar

53. Kabir MA, Hassan MM, Hossain MN, Paul BK, Ahmed K. Design and Performance Evaluation of Photonic crystal Fibers of Supporting Orbital Angular Momentum States in Optical Transmission. Opt Commun (2020) 467:125731. doi:10.1016/j.optcom.2020.125731

CrossRef Full Text | Google Scholar

54. Wang W, Sun C, Wang N, Jia H. A Design of Nested Photonic crystal Fiber with Low Nonlinear and Flat Dispersion Supporting 30+50 OAM Modes. Opt Commun (2020) 471:125823. doi:10.1016/j.optcom.2020.125823

CrossRef Full Text | Google Scholar

55. Wang W, Wang N, Li K, Geng Z, Jia H. A Novel Dual Guided Modes Regions Photonic crystal Fiber with Low Crosstalk Supporting 56 OAM Modes and 4 LP Modes. Opt Fiber Technol (2020) 57:102213. doi:10.1016/j.yofte.2020.102213

CrossRef Full Text | Google Scholar

56. Al-Zahrani FA, Ahmed K. Novel Design of Dual Guided Photonic crystal Fiber for Large Capacity Transmission in High-Speed Optics Communications with Supporting Good Quality OAM and LP Modes. Alexandria Eng J (2020) 59:4889–99. doi:10.1016/j.aej.2020.09.004

CrossRef Full Text | Google Scholar

57. He T. Design of Photonic Crystal Fiber for Orbital Angular Momentum Mode and Study on its Magnetic Tunability. [dissertation/master’s thesis]. [Chengdu(Sichuan)]: University of Electronic Science and Technology of China (2020).

Google Scholar

58. Ramachandran S, Kristensen P, Yan MF. Generation and Propagation of Radially Polarized Beams in Optical Fibers. Opt Lett (2009) 34:2525–7. doi:10.1364/ol.34.002525

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Jung Y, Kang Q, Zhou H, Rui Z, Richardson DJ. Low-loss 25.3km Few-Mode Ring-Core Fibre for Mode-Division Multiplexed transmission[Conference Presentation]. Dusseldorf, Germany: ECOC 2016 (2016).

Google Scholar

60. Jin X, Gomez A, Shi K, Thomsen BC, Feng F, Gordon GSD, et al. Mode Coupling Effects in Ring-Core Fibers for Space-Division Multiplexing Systems. J Lightwave Technol (2016) 34:3365–72. doi:10.1109/jlt.2016.2564991

CrossRef Full Text | Google Scholar

61. Shen L, Zhang J, Liu J, Zhu G, Yu S. MIMO-free WDM-MDM Transmission over 100-KM Single-Span Ring-Core fibre[Conference Presentation]. Dublin, Ireland: ECOC 2019 (2019).

Google Scholar

62. Gregg P, Kristensen P, Rubano A, Golowich S, Marrucci L, Ramachandran S. Enhanced Spin Orbit Interaction of Light in Highly Confining Optical Fibers for Mode Division Multiplexing. Nat Commun (2019) 10:4707. doi:10.1038/s41467-019-12401-4

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Brunet C, Ung B, Belanger P-A, Messaddeq Y, LaRochelle S, Rusch LA. Vector Mode Analysis of Ring-Core Fibers: Design Tools for Spatial Division Multiplexing. J Lightwave Technol (2014) 32:4648–59. doi:10.1109/jlt.2014.2361432

CrossRef Full Text | Google Scholar

64. Brunet C, Vaity P, Ung B, Messaddeq Y, Larochelle S, Rusch LA. Design of a Family of Ring-Core Fiber for OAM[Conference Presentation]. Los Angeles, California, United States: OFC 2015 (2015).

Google Scholar

65. Wang H, Liang Y, Zhang X, Chen S, Shen L, Zhang L, et al. Low-loss Orbital Angular Momentum Ring-Core Fiber: Design, Fabrication and Characterization. J Lightwave Technol (2020) 38:1. doi:10.1109/jlt.2020.3012285

CrossRef Full Text | Google Scholar

66. Huang G, Zhou S, Qin Y, Xue L, Yan M. Modal Characteristics Analysis of Orbital Angular Momentum in a Modified Ring Fiber. Las Optoelect Prog (2015) 52:080604. doi:10.3788/lop52.080604

CrossRef Full Text | Google Scholar

67. Li S, Wang J. A Compact Trench-Assisted Multi-Orbital-Angular-Momentum Multi-Ring Fiber for Ultrahigh-Density Space-Division Multiplexing (19 Rings × 22 Modes). Sci Rep (2014) 4:3853. doi:10.1038/srep03853

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Zhu G, Hu Z, Wu X, Du C, Luo W, Chen Y, et al. Scalable Mode Division Multiplexed Transmission over a 10-km Ring-Core Fiber Using High-Order Orbital Angular Momentum Modes. Opt Express (2018) 26:594–604. doi:10.1364/OE.26.000594

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Zhu L, Zhu G, Wang A, Wang L, Ai J, Chen S, et al. 18 Km Low-Crosstalk OAM + WDM Transmission with 224 Individual Channels Enabled by a Ring-Core Fiber with Large High-Order Mode Group Separation. Opt Lett (2018) 43:1890–3. doi:10.1364/OL.43.001890

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Tan H, Zhang J, Liu J, Shen L, Yu S. Low-Loss Ring-Core Fiber Supporting 4 Mode Groups[Conference Presentation]. San Jose, California, United States: CLEO: Science and Innovations 2019 (2019).

Google Scholar

71. Zhang J, Liu J, Shen L, Zhang L, Luo J, Liu J, et al. Mode-division Multiplexed Transmission of Wavelength-Division Multiplexing Signals over a 100-km Single-Span Orbital Angular Momentum Fiber. Photon Res (2020) 8:1236. doi:10.1364/prj.394864

CrossRef Full Text | Google Scholar

72. Gregg P, Kristensen P, Golowich SE, Olsen JØ, Steinvurzel P, Ramachandran S. Stable Transmission of 12 OAM States in Air-Core Fiber[Conference Presentation]. San Jose, California, United States: CLEO: Science and Innovations 2013 (2013).

Google Scholar

73. Brunet C, Ung B, Messaddeq Y, Larochelle S, Rusch LA. Design of an Optical Fiber Supporting 16 OAM Modes [Conference Presentation]. San Francisco, California, United States: OFC 2014 (2014).

Google Scholar

74. Brunet C, Vaity P, Messaddeq Y, LaRochelle S, Rusch LA. Design, Fabrication and Validation of an OAM Fiber Supporting 36 States. Opt Express (2014) 22:26117–27. doi:10.1364/OE.22.026117

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Gregg P, Kristensen P, Ramachandran S. Conservation of Orbital Angular Momentum in Air-Core Optical Fibers. Optica (2015) 2:267. doi:10.1364/optica.2.000267

CrossRef Full Text | Google Scholar

76. Wang Y, Bao C, Jiang J, Fang Y, Geng W, Wang Z, et al. Two-Octave Supercontinuum Generation of High-Order OAM Modes in Air-Core As₂S₃ Ring Fiber. IEEE Access (2020) 8:114135–42. doi:10.1109/access.2020.3002767

CrossRef Full Text | Google Scholar

77. Ung B, Vaity P, Wang L, Messaddeq Y, Rusch LA, LaRochelle S. Few-mode Fiber with Inverse-Parabolic Graded-index Profile for Transmission of OAM-Carrying Modes. Opt Express (2014) 22:18044–55. doi:10.1364/OE.22.018044

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Chen Y. Design and Research of Transmission Fiber with High Order Orbital Angular Momentum Mode. [dissertation/master’s thesis]. [Xi’an(Shanxi)]: Xi’an University of Technology (2019).

Google Scholar

79. Zhang Z, Liu X, Wei W, Ding L, Tang L, Li Y. The Simulation of Vortex Modes in Twisted Few-Mode Fiber with Inverse-Parabolic Index Profile. IEEE Photon J. (2020) 12:1–8. doi:10.1109/jphot.2020.2994819

CrossRef Full Text | Google Scholar

80. Ma Y, Chen H, Bai X. A New Type Graded-index Ring Fiber Supporting Multi-OAM Modes. Study Opt Commun (2017) 02:47–50. doi:10.13756/j.gtxyj.2017.02.013

CrossRef Full Text | Google Scholar

81. Tu J, Gao S, Wang Z, Liu Z, Li W, Du C, et al. Bend-insensitive Grapefruit-type Holey Ring-Core Fiber for Weakly-Coupled OAM Mode Division Multiplexing Transmission. J Lightwave Technol (2020) 38:4497–503. doi:10.1109/jlt.2020.2987328

CrossRef Full Text | Google Scholar

82. Ma J, Xia F, Chen S, Li S, Wang J. Amplification of 18 OAM Modes in a Ring-Core Erbium-Doped Fiber with Low Differential Modal Gain. Opt Express (2019) 27:38087–97. doi:10.1364/OE.27.038087

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Liu J, Chen S, Wang H, Zheng S, Zhu L, Wang A, et al. Amplifying Orbital Angular Momentum Modes in Ring-Core Erbium-Doped Fiber. Research (2020) 2020:1–12. doi:10.34133/2020/7623751

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Jung Y, Kang Q, Sidharthan R, Ho D, Yoo S, Gregg P, et al. Optical Orbital Angular Momentum Amplifier Based on an Air-Hole Erbium-Doped Fiber. J Lightwave Technol (2017) 35:430–6. doi:10.1109/jlt.2017.2651145

CrossRef Full Text | Google Scholar

85. Beijersbergen MW, Coerwinkel RPC, Kristensen M, Woerdman JP. Helical-wavefront Laser Beams Produced with a Spiral Phaseplate. Opt Commun (1994) 112:321–7. doi:10.1016/0030-4018(94)90638-6

CrossRef Full Text | Google Scholar

86. Gibson G, Courtial J, Padgett MJ, Vasnetsov M, Pas'ko V, Barnett SM, et al. Free-space Information Transfer Using Light Beams Carrying Orbital Angular Momentum. Opt Express (2004) 12:5448–56. doi:10.1364/opex.12.005448

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Marrucci L, Karimi E, Slussarenko S, Piccirillo B, Santamato E, Nagali E, et al. Spin-to-orbital Conversion of the Angular Momentum of Light and its Classical and Quantum Applications. J Opt (2011) 13:064001. doi:10.1088/2040-8978/13/6/064001

CrossRef Full Text | Google Scholar

88. Zhang X. Generation and Conversion of Optical Vortices in Optical Fiber. [dissertation/doctoral thesis]. [Hefei(Anhui)]: University of Science and Technology of China (2016).

Google Scholar

89. Wu H. High-order Optical Vortex Generation and Modulation Based on Long-Period Grating in a Few-Mode Fiber. [dissertation/master’s thesis]. Guangzhou(Guangdong): Jinan University (2018).

Google Scholar

90. Zhang Y. The Generation and Regulation of Orbital Angular Momentum Mode Based on Few-Mode Fiber Grating. [dissertation/master’s thesis]. [Shenzhen(Guangdong)]: Shenzhen University (2019).

Google Scholar

91. Jiang Y, Ren G, Shen Y, Xu Y, Jin W, Wu Y, et al. Two-dimensional Tunable Orbital Angular Momentum Generation Using a Vortex Fiber. Opt Lett (2017) 42:5014–7. doi:10.1364/OL.42.005014

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Fujisawa T, Saitoh K. Geometric-phase-induced Arbitrary Polarization and Orbital Angular Momentum Generation in Helically Twisted Birefringent Photonic crystal Fiber. Photon Res (2020) 8:1278. doi:10.1364/prj.393255

CrossRef Full Text | Google Scholar

93. Fu C, Liu S, Wang Y, Bai Z, He J, Liao C, et al. High-order Orbital Angular Momentum Mode Generator Based on Twisted Photonic crystal Fiber. Opt Lett (2018) 43:1786–9. doi:10.1364/OL.43.001786

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Ye J, Li Y, Han Y, Deng D, Guo Z, Gao J, et al. Excitation and Separation of Vortex Modes in Twisted Air-Core Fiber. Opt Express (2016) 24:8310–6. doi:10.1364/OE.24.008310

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Fang L. Theoretical Study of Mode-Selective Couplers Based on Optical Fiber Gratings. [dissertation/master’s thesis]. [Shanghai]: University of Shanghai for Science and Technology (2014).

Google Scholar

96. Ge T. Theoretical and Experimental Reserch on the Use of Optical Fiber to Generate Vortex Beam. [dissertation/master’s thesis]. [Xi’an(Shanxi)]: Xi’an University of Technology (2018).

Google Scholar

97. Bozinovic N, Golowich S, Kristensen P, Ramachandran S. Control of Orbital Angular Momentum of Light with Optical Fibers. Opt Lett (2012) 37:2451–3. doi:10.1364/OL.37.002451

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Mao B, Liu Y, Zhang H, Yang K, Han Y, Wang Z, et al. Complex Analysis between CV Modes and OAM Modes in Fiber Systems. Nanophotonics (2018) 8:271–85. doi:10.1515/nanoph-2018-0179

CrossRef Full Text | Google Scholar

99. Zhang H, Mao B, Han Y, Wang Z, Yue Y, Liu Y. Generation of Orbital Angular Momentum Modes Using Fiber Systems. Appl Sci (2019) 9:1033. doi:10.3390/app9051033

CrossRef Full Text | Google Scholar

100. Zhao Y, Liu Y, Zhang L, Zhang C, Wen J, Wang T. Mode Converter Based on the Long-Period Fiber Gratings Written in the Two-Mode Fiber. Opt Express (2016) 24:6186–95. doi:10.1364/OE.24.006186

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Zhao Y, Liu Y, Zhang C, Zhang L, Zheng G, Mou C, et al. All-fiber Mode Converter Based on Long-Period Fiber Gratings Written in Few-Mode Fiber. Opt Lett (2017) 42:4708–11. doi:10.1364/OL.42.004708

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Han Y, Liu Y-G, Wang Z, Huang W, Chen L, Zhang H-W, et al. Controllable All-Fiber Generation/conversion of Circularly Polarized Orbital Angular Momentum Beams Using Long Period Fiber Gratings. Nanophotonics (2018) 7:287–93. doi:10.1515/nanoph-2017-0047

CrossRef Full Text | Google Scholar

103. Li S, Mo Q, Hu X, Du C, Wang J. Controllable All-Fiber Orbital Angular Momentum Mode Converter. Opt Lett (2015) 40:4376–9. doi:10.1364/OL.40.004376

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Wu H, Gao S, Huang B, Feng Y, Huang X, Liu W, et al. All-fiber Second-Order Optical Vortex Generation Based on strong Modulated Long-Period Grating in a Four-Mode Fiber. Opt Lett (2017) 42:5210–3. doi:10.1364/OL.42.005210

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Li Y, Jin L, Wu H, Gao S, Feng Y-H, Li Z. Superposing Multiple LP Modes with Microphase Difference Distributed along Fiber to Generate OAM Mode. IEEE Photon J. (2017) 9:1–9. doi:10.1109/jphot.2017.2674022

CrossRef Full Text | Google Scholar

106. Han Y, Chen L, Liu Y-G, Wang Z, Zhang H, Yang K, et al. Orbital Angular Momentum Transition of Light Using a Cylindrical Vector Beam. Opt Lett (2018) 43:2146–9. doi:10.1364/OL.43.002146

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Xu H, Yang L. Conversion of Orbital Angular Momentum of Light in Chiral Fiber Gratings. Opt Lett (2013) 38:1978–80. doi:10.1364/OL.38.001978

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Fu C, Yu B, Wang Y, Liu S, Bai Z, He J, et al. Orbital Angular Momentum Mode Converter Based on Helical Long Period Fiber Grating Inscribed by Hydrogen-Oxygen Flame. J Lightwave Technol (2018) 36:1683–8. doi:10.1109/jlt.2017.2787120

CrossRef Full Text | Google Scholar

109. Bai Z, Wang Y, Zhang Y, Fu C, Liu S, Li M, et al. Helical Long-Period Fiber Gratings as Wavelength-Tunable Orbital Angular Momentum Mode Generators. IEEE Photon Technol Lett (2020) 32:418–21. doi:10.1109/lpt.2019.2958385

CrossRef Full Text | Google Scholar

110. Wang L, Vaity P, Ung B, Messaddeq Y, Rusch LA, LaRochelle S. Characterization of OAM Fibers Using Fiber Bragg Gratings. Opt Express (2014) 22:15653–61. doi:10.1364/OE.22.015653

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Zhao Y, Wang C, Liu Z, Zhou K, Mou C, Liu Y. Generation of Multiple-Order OAM Modes Using a Tilted Few-Mode Fiber Bragg Grating[Conference Presentation]. Guangzhou, Guangdong, China: ACP 2017 (2017).

Google Scholar

112. Yang K, Liu Y-g., Wang Z, Li Y, Han Y, Zhang H-w., et al. Triple-order Orbital-Angular-Momentum Modes Generation Based on Single Tilted Fiber Bragg Grating in a Few-Mode Ring-Core Fiber. Opt Fiber Technol (2020) 55:102155. doi:10.1016/j.yofte.2020.102155

CrossRef Full Text | Google Scholar

113. Lin Z, Wang A, Xu L, Zhang X, Sun B, Gu C, et al. Generation of Optical Vortices Using a Helical Fiber Bragg Grating. J Lightwave Technol (2014) 32:2152–6. doi:10.1109/jlt.2014.2320539

CrossRef Full Text | Google Scholar

114. Huang G. Modal Characteristics of OAM in a Modified Ring Fiber. [dissertation/master’s thesis]. [Hangzhou(Zhejiang)]: Zhejiang University of Technology (2015).

Google Scholar

115. Wang T, Wang F, Shi F, Pang F, Huang S, Wang T, et al. Generation of Femtosecond Optical Vortex Beams in All-Fiber Mode-Locked Fiber Laser Using Mode Selective Coupler. J Lightwave Technol (2017) 35:2161–6. doi:10.1109/jlt.2017.2676241

CrossRef Full Text | Google Scholar

116. Zhang H, Mao B, Han Y, Yang K, Wang Z, Liu Y. Generation of Orbital Angular Momentum Mode Using a Single Cylindrical Vector Mode Based on Mode Selective Coupler. Opt Fiber Technol (2019) 52:101934. doi:10.1016/j.yofte.2019.101934

CrossRef Full Text | Google Scholar

117. Pidishety S, Khudus M, Gregg P, Ramachandran S, Brambilla G. OAM Beam Generation Using All-Fiber Fused Couplers[Conference Presentation]. San Jose, California, United States: CLEO: Science and Innovations 2016 (2016).

Google Scholar

118. Pidishety S, Pachava S, Gregg P, Ramachandran S, Brambilla G, Srinivasan B. Orbital Angular Momentum Beam Excitation Using an All-Fiber Weakly Fused Mode Selective Coupler. Opt Lett (2017) 42:4347–50. doi:10.1364/OL.42.004347

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Heng X, Gan J, Zhang Z, Li J, Li M, Zhao H, et al. All-fiber Stable Orbital Angular Momentum Beam Generation and Propagation. Opt Express (2018) 26:17429–36. doi:10.1364/OE.26.017429

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Jin X, Pang F, Zhang Y, Huang S, Li Y, Wen J, et al. Generation of the First-Order OAM Modes in Single-Ring Fibers by Offset Splicing Technology. IEEE Photon Technol Lett (2016) 28:1581–4. doi:10.1109/lpt.2016.2552223

CrossRef Full Text | Google Scholar

121. Li S, Xu Z, Zhao R, Shen L, Du C, Wang J. Generation of Orbital Angular Momentum Beam Using Fiber-To-Fiber Butt Coupling. IEEE Photon J. (2018) 10:1–7. doi:10.1109/jphot.2018.2856263

CrossRef Full Text | Google Scholar

122. Wong GKL, Kang MS, Lee HW, Biancalana F, Conti C, Weiss T, et al. Excitation of Orbital Angular Momentum Resonances in Helically Twisted Photonic crystal Fiber. Science (2012) 337:446–9. doi:10.1126/science.1223824

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Cui Y, Ye J, Li Y, Dai P, Qu S. Vortex Chirality-dependent Filtering in Helically Twisted Single-Ring Photonic crystal Fibers. Opt Express (2019) 27:20816–23. doi:10.1364/OE.27.020816

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Dashti PZ, Alhassen F, Lee HP. Observation of Orbital Angular Momentum Transfer between Acoustic and Optical Vortices in Optical Fiber. Phys Rev Lett (2006) 96:043604. doi:10.1103/PhysRevLett.96.043604

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Zhang W, Huang L, Wei K, Li P, Jiang B, Mao D, et al. High-order Optical Vortex Generation in a Few-Mode Fiber via Cascaded Acoustically Driven Vector Mode Conversion. Opt Lett (2016) 41:5082–5. doi:10.1364/OL.41.005082

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Zhang W, Wei K, Huang L, Mao D, Jiang B, Gao F, et al. Optical Vortex Generation with Wavelength Tunability Based on an Acoustically-Induced Fiber Grating. Opt Express (2016) 24:19278–85. doi:10.1364/OE.24.019278

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Yan Y, Wang J, Zhang L, Yang J-Y, Fazal IM, Ahmed N, et al. Fiber Coupler for Generating Orbital Angular Momentum Modes. Opt Lett (2011) 36:4269–71. doi:10.1364/OL.36.004269

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Yan Y, Yue Y, Huang H, Yang J-Y, Chitgarha MR, Ahmed N, et al. Efficient Generation and Multiplexing of Optical Orbital Angular Momentum Modes in a Ring Fiber by Using Multiple Coherent Inputs. Opt Lett (2012) 37:3645–7. doi:10.1364/OL.37.003645

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Yan Y, Zhang L, Wang J, Yang J-Y, Fazal IM, Ahmed N, et al. Fiber Structure to Convert a Gaussian Beam to Higher-Order Optical Orbital Angular Momentum Modes. Opt Lett (2012) 37:3294–6. doi:10.1364/OL.37.003294

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Li L, Zhu S, Li J, Shao X, Galvanauskas A, Ma X. All-in-fiber Method of Generating Orbital Angular Momentum with Helically Symmetric Fibers. Appl Opt (2018) 57:8182–6. doi:10.1364/AO.57.008182

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Lin Z. Nonlinear Frequency Conversion of Beams Carrying Orbital Angular Momentum. [dissertation/master’s thesis]. Nanjing(Jiangsu): Nanjing University (2019).

Google Scholar

132. Wang A, Zhu L, Chen S, Du C, Mo Q, Wang J. Characterization of LDPC-Coded Orbital Angular Momentum Modes Transmission and Multiplexing over a 50-km Fiber. Opt Express (2016) 24:11716–26. doi:10.1364/OE.24.011716

PubMed Abstract | CrossRef Full Text | Google Scholar

133. Zhu B, Taunay TF, Fishteyn M, Liu X, Chandrasekhar S, Yan MF, et al. 112-Tb/s Space-Division Multiplexed DWDM Transmission with 14-b/s/Hz Aggregate Spectral Efficiency over a 768-km Seven-Core Fiber. Opt Express (2011) 19:16665–71. doi:10.1364/OE.19.016665

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Lv W. Theoretical Research of Orbital Angular Momentum of Beam and Experimental Research of Optical Tweezers Sort Cell. [dissertation/master’s thesis]. [Qinhuangdao(Hebei)]: Yanshan University (2010).

Google Scholar

135. Fürhapter S, Jesacher A, Bernet S, Ritsch-Marte M. Spiral Phase Contrast Imaging in Microscopy. Opt Express (2005) 13:689–94. doi:10.1364/opex.13.000689

PubMed Abstract | CrossRef Full Text | Google Scholar

136. Padgett M, Courtial J, Allen L. Light's Orbital Angular Momentum. Phys Today (2004) 57:35–40. doi:10.1063/1.1768672

CrossRef Full Text | Google Scholar

137. Wu Y. Phase-Matching Controlled Nonlinear Frequency Conversion of Orbital Angular Momentum. [dissertation/master’s thesis]. [Nanjing(Jiangsu)]: Nanjing University (2019).

Google Scholar

138. Fang W-T, Tao R-X, Zhang Y-m., Zhou Z-Y, Yao P-j., Shi B-S, et al. Tailoring Nonlinear Processes of Orbital Angular Momentum with Dispersion Engineering in Vortex Fibers. Phys Rev Appl (2019) 12:034007. doi:10.1103/PhysRevApplied.12.034007

CrossRef Full Text | Google Scholar

139. Yang H. Nonlinear Multiplexing Holography Based on Orbital Angular Momentum of Light. [dissertation/master’s thesis]. [Nanjing(Jiangsu)]: Nanjing University (2020).

Google Scholar

140. Shuhui Li S, Jian Wang J. Multi-Orbital-Angular-Momentum Multi-Ring Fiber for High-Density Space-Division Multiplexing. IEEE Photon J. (2013) 5:7101007. doi:10.1109/jphot.2013.2272778

CrossRef Full Text | Google Scholar

141. Huang H, Milione G, Lavery MPJ, Xie G, Ren Y, Cao Y, et al. Mode Division Multiplexing Using an Orbital Angular Momentum Mode Sorter and MIMO-DSP over a Graded-index Few-Mode Optical Fibre. Sci Rep (2015) 5:14931. doi:10.1038/srep14931

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Zhang J, Zhu G, Liu J, Wu X, Zhu J, Du C, et al. Orbital-angular-momentum Mode-Group Multiplexed Transmission over a Graded-index Ring-Core Fiber Based on Receive Diversity and Maximal Ratio Combining. Opt Express (2018) 26:4243. doi:10.1364/oe.26.004243

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Feng F, Guo X, Gordon G, Jin X, Wilkinson TD. All-optical Mode-Group Division Multiplexing over a Graded-Index Ring-Core Fiber with Single Radial Mode[Conference Presentation]. Los Angeles, California, United States: OFC 2016 (2016).

Google Scholar

144. Gahagan KT, Swartzlander GA. Trapping of Low-index Microparticles in an Optical Vortex. J Opt Soc Am B (1998) 15:524. doi:10.1364/josab.15.000524

CrossRef Full Text | Google Scholar

145. O'Neil AT, MacVicar I, Allen L, Padgett MJ. Intrinsic and Extrinsic Nature of the Orbital Angular Momentum of a Light Beam. Phys Rev Lett (2002) 88:053601. doi:10.1103/PhysRevLett.88.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

146. Gao Ming-Wei M, Gao Chun-Qing C, He Xiao-Yan X, Li Jia-Ze J, Wei Guang-Hui G. Rotation of Particles by Using the Beam with Orbital Angular Momentum. Acta Physica Sinica (2004) 53:413–7. doi:10.7498/aps.53.413

CrossRef Full Text | Google Scholar

147. Lehmuskero A, Li Y, Johansson P, Käll M. Plasmonic Particles Set into Fast Orbital Motion by an Optical Vortex Beam. Opt Express (2014) 22:4349–56. doi:10.1364/OE.22.004349

PubMed Abstract | CrossRef Full Text | Google Scholar

148. Li L. The Analysis of High-Capacity Quantum Secure Direct Communication Using Polarization and Orbital Angular Momentum of Photons. [dissertation/master’s thesis]. [Beijing: Beijing University of Posts and Telecommunications (2020).

Google Scholar

149. Malik M, Erhard M, Huber M, Krenn M, Fickler R, Zeilinger A. Multi-photon Entanglement in High Dimensions. Nat Photon (2016) 10:248–52. doi:10.1038/nphoton.2016.12

CrossRef Full Text | Google Scholar

150. Lavery MPJ, Robertson DJ, Berkhout GCG, Love GD, Padgett MJ, Courtial J. Refractive Elements for the Measurement of the Orbital Angular Momentum of a Single Photon. Opt Express (2012) 20:2110–5. doi:10.1364/OE.20.002110

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Swartzlander GA. Peering into Darkness with a Vortex Spatial Filter. Opt Lett (2001) 26:497–9. doi:10.1364/ol.26.000497

PubMed Abstract | CrossRef Full Text | Google Scholar