- 1Peter Grünberg Institut and Institute for Advanced Simulation, Forschungszentrum Jülich and JARA, Jülich, Germany
- 2Science Institute of the University of Iceland, Reykjavík, Iceland
- 3Department of Mathematics and JARA FIT, RWTH Aachen University, Aachen, Germany
Chiral magnetic skyrmions, localized and topologically protected vortex-like magnetic textures that can be found in chiral magnets, are currently under intense study as an entity for information storage and processing. A recent study showed that so-called rank-one materials can host both skyrmions and antiskyrmions at the same energy. In such systems the Dzyaloshinskii-Moriya interaction, in general a tensorial quantity, is reduced to only one non-zero component. The presence of both skyrmions and antiskyrmions allows for the investigation of the possible interplay between them. Here, we investigate the stability and interaction of skyrmions and antiskyrmions as well as their transport properties subject to spin-orbit torque for a model system described by an atomistic spin-lattice Hamiltonian employing the simulation software Spirit. The spin-orbit torque driven spin-dynamics described by the Landau-Lifshitz-Gilbert equation is compared to the effective one of the Thiele equation. We demonstrate that, even though skyrmions and antiskyrmions can be seen as antiparticles, a rather dense arrangement of both along a memory track is possible, enabling their use as representations of the binary data bits “0” and “1” in a memory device.
1 Introduction
The increasing amount of digital data requires the development of new data storage devices with higher information density at lower energy consumption. So far, magnetic hard disks have been the backbone of mass storage applications in large data centers, where information is read and written using a read-write head that moves across the magnetic disk. However, this technology is approaching its limits, both in terms of information density and the mechanical effort of reading and writing data. A change of paradigm was suggested by the racetrack memory [1], a solid state shift register type memory in which the information is encoded in a pattern of magnetic domains separated by domain walls. These domain walls can be moved by spin-currents either applied in spin-transfer torque (STT) geometry, i.e., a current of spin-polarized electrons is passing in perpendicular geometry through the magnetic layer, or even more efficiently in spin-orbit torque (SOT) geometry, i.e., a charge current is passing through a nonmagnetic heavy metal substrate layer creating a perpendicularly flowing spin current or an accumulation of spin-polarized electrons at the interface to the magnetic domain.
Around 10 years ago, chiral magnetic skyrmions [2] were discovered [3–5], two-dimensional magnetic vortex-like spin textures of topological nature at the nanoscale. They can form in the presence of an applied magnetic field in ferromagnetic films that experience an interfacial Dzyaloshinskii-Moriya interaction [6, 7] (DMI) as a result of spin-orbit coupling and broken structure-inversion symmetry as introduced at the interface [8]. This finding led to an extension of the racetrack idea towards skyrmion racetracks [9], where the information is now encoded in the presence or absence of such skyrmions on a thin racetrack stripe. Those skyrmions can then be moved by ultra-low electric current densities [10]. Such a possible movement of skyrmions has been shown both theoretically [11, 12] and experimentally [13–16]. In the last years we witnessed significant progress towards the optimization of skyrmion design for technology [17, 18].
Like in ordinary racetrack memories, the information in skyrmion racetrack devices relies on the presence or absence of the skyrmion and the quantization of distances between adjacent skyrmions on a track. However, skyrmions are highly movable, interacting particles that can drift as a result of thermal fluctuations, making it difficult to maintain their distribution along a track. This can lead to difficulties, as e.g., thermal movement can change the distance between neighboring particles, destroying the encoded information. To overcome this problem, several suggestions have been made. One option would be to force the skyrmions to settle on discrete positions, e.g., realized by nano-fabricated arrays of notches or of artificial pinning centers acting as a periodic potential [19]. A more recent proposal is a two-lane racetrack [20], where the choice of track on which the skyrmion settles encrypts the binary information. Those lanes are separated by a finite energy barrier which prevents the loss of data. Both solutions to solve the problem rely on fabrication on the nanoscale. This is a serious challenge that is likely to lead to higher costs. Lately, a powerful alternative approach has been proposed that does not require fixed distances between moving bit carriers because the stream of binary data, which is a sequence of ones and zeros, has been encoded using a sequence of two distinguishable particles: single skyrmions and bobbers [21]. The proposed concept of data encoding promises the realization of a new generation of magnetic solid-state storage devices, where a higher data density can be achieved compared to the existing skyrmion-based racetrack storage concept.
Recently, it was shown on theoretical grounds that in magnetic thin layers of particular point-group symmetry classes, not only magnetic skyrmions but also antiskyrmions can exist [22, 23]. The latter can occur when symmetry allows an anisotropic Dzyaloshinskii-Moriya interaction (DMI), i.e., its strength is different in different spatial directions as experimentally evidenced for thin films of Co. on W (110) [24]. In this case, and resorting to the micromagnetic formulation of the energy landscape, the DMI can no longer be described by a single scalar quantity, the so-called spiralization D, but must be replaced by a two-dimensional spiralization tensor
Antiskyrmions [23, 25, 26], like skyrmions, are localized magnetic particles with a topologically non-trivial magnetization texture specified by the same magnitude of the topological charge, |Q| = 1, but an opposite sign and an opposite
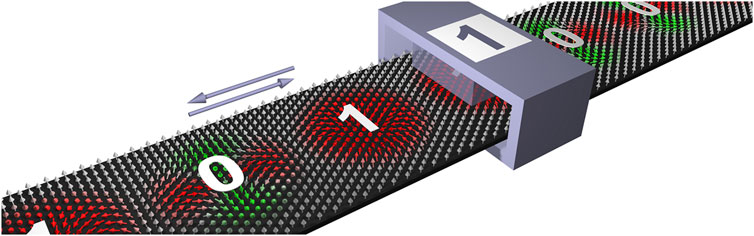
FIGURE 1. Schematic picture of a skyrmion-antiskyrmion racetrack. Information is encoded in the type of the magnetic particle, i.e., a skyrmion represents the bit “1” and an antiskyrmion represents the bit “0”. By applying a current, the magnetic particles can be moved towards a read/write head.
In this paper, we combine the two recent development strands: The skyrmion racetrack device and the simultaneous presence and energetic degeneracy of skyrmions and antiskyrmions in rank-one materials, and propose a new type of data storage device, namely a skyrmion-antiskyrmion racetrack memory (see Figure 1). It is an alternative to the skyrmion-bobber racetrack memory [21]. In this device, as in Ref. [21], information would be encoded by two distinguishable magnetic particles, e.g., a skyrmion represents the bit “1”, whereas an antiskyrmion represents the “0”. The distinction between the two is possible, for example, by measuring the sign of the topological Hall effect (THE) [29], which depends on the sign of the topological charge Q, which is opposite for skyrmions and antiskyrmions, or the strength of the chiral Hall effect (CHE) [30] or the noncollinear Hall effect (NHE) [31], which both vary in size depending on the type of particle. We show that skyrmions and antiskyrmions, although they carry the notion of antiparticles, can indeed coexist and even repel each other if the proper geometry of the racetrack is chosen. We focus on SOT driven particle motion as this is more energy efficient than STT. Using spin-dynamics simulations applied to a model system we demonstrate the feasibility of such a device by showing that a coherent motion of skyrmions and antiskyrmions along the same trackline can be achieved. In order to show the main effects efficiently and to provide a transparent analysis of our simulations, our model system is parameterized to match a ferromagnetic rank-one material with C2v-symmetry of monoatomic layer thickness deposited on a nonmagnetic heavy-metal substrate, e.g. having (110) oriented interfaces in mind, in analogy to atomic-scale skyrmions studied experimentally in the past for (111) oriented interfaces with C3v symmetry [5, 32]. Consistently, the models and simulations are on the atomistic scale.
2 Models and Methods
2.1 Atomistic Heisenberg Model and Model Parameters
In this paper we study ultrathin ferromagnetic films with an out-of-plane easy axis on a heavy-metal substrate. As underlying model we use the extended Heisenberg Hamiltonian to describe the interactions between localized classical vector spins Si of unit length placed on atomic sites i,
containing exchange and Dzyaloshinskii-Moriya interactions as well as uniaxial anisotropy. The sites i and j are limited to the magnetic film, but the model parameters Jij, Dij, and K⊥ include also the properties of the metal substrate. (J < 0) J > 0 describes (anti-)ferromagnetic exchange between the sites and K⊥ < 0 denotes a magnetic easy axis parallel to the z-direction. For ultrathin magnetic systems, the dipolar interaction between magnetic moments is typically of minor importance and is added as an additional on-site contribution to the magnetic anisotropy constant K⊥. We restrict ourselves to monolayers with a two-dimensional, centered rectangular Bravais lattice as this crystal structure with C2v symmetry offers the possibility of a DMI tensor of rank-one [23]. To obtain such a tensor,
all atomistic DMI vectors, Dij, have to be aligned in parallel along one of the two lattice vectors of the rectangular unit cell. Without loss of generality we assume that the x-axis is oriented parallel to one of the lattice vectors. The direction along the second lattice vector we call the y-direction. The orientation of the track of the racetrack device on which the information particles move relative to the orientation of the crystal lattice and subsequently the orientation of the DM vector is an important design aspect. This determines the relative chiral orientation of the antiskyrmion with respect to the skyrmion. We will see below that this bears important consequences for the interaction of skyrmions with antiskyrmions. For visualization purposes, we chose the same lattice parameter, a, for both directions of the corresponding rectangular superlattice with two atoms per unit cell.
Magnetic skyrmionic structures can be stabilized by different combinations of parameters in the Heisenberg model (1). On the one hand, it is sufficient to have only nearest neighbor interactions both for the DMI and the exchange interaction and to apply a magnetic field parallel to the ferromagnetic background. By choosing the proper DMI geometry, i.e., a rank-one spiralization tensor, both skyrmions and antiskyrmions can coexist. However, under these assumptions the stabilization of skyrmionic particles becomes problematic when the DMI is not isotropic but anisotropic. In the case of rank-one DMI, i.e., the most anisotropic case possible, the magnetic texture loses its axial symmetry, it becomes elliptically unstable to the point that it decays into a one-dimensional magnetic structure. To counteract, a strong external magnetic field is needed to stabilize the skyrmionic structure, making it unpractical for applications.
An alternative way to stabilize skyrmionic spin textures is to resort to systems with competing magnetic exchange interactions, i.e., systems where more than a nearest neighbor parameter J is needed to describe the system correctly. These Js compete between different neighbors by opposite signs, yet, the magnetic ground state still remains ferromagnetic. Skyrmion stabilization can then be achieved either by counteracting the previously discussed elliptical instability of the skyrmion by an anisotropic exchange interaction or by purely stabilizing the skyrmionic particles due to exchange. In the following, we will focus on this latter case, since it provides the possibility of studying both skyrmions and antiskyrmions as both of them can be stable independent of the occurring DM interactions. However, we will show later that even though the DMI is not directly responsible for the stabilization, it is quite important for the motion of skyrmions and antiskyrmions, especially the collective motion along a particular direction.
As model parameters for our racetrack ferromagnet, we used J1 > 0, J4 = − 0.25 J1,
2.2 Atomistic Spin Dynamics Simulations of Current-Driven Skyrmion and Antiskyrmion Propagation and Minimum Energy Paths
The time evolution of the atomistic spins subject to the current induced SOT [36] is followed by the numerical solution of the Landau–Lifshitz-Gilbert (LLG) equation presented here in the Landau–Lifshitz form at the atomistic level [37, 38] extend by the SOT,
were Si = μi/μi are normalized magnetic moments located at a lattice site i,
The LLG equation is used in two regimes: (i) the quasi-static regime to determine the minimum energy paths (MEP) and the corresponding energy barriers for the interaction of (anti-)skyrmions with track boundaries as well as the mutual interactions of skyrmions with antiskyrmions and (ii) the dynamical regime to study the current-induced motion of both particles on the track. The importance of the MEP lies in the identification of a transition-state saddle-point and also provides detailed information about the transition mechanism, important quantitative knowledge, which is not easily accessible in the spin dynamics. To follow a MEP means to rotate spins in an optimal way so that the energy is minimal with respect to all degrees of freedom perpendicular to the path. Technically we use the geodesic nudged elastic band (GNEB) method [42] to determine the MEP. The GNEB method gives us precise values for the energy barriers by finding the maximum along any stable transition path and by this also the energetically most favorable transition path. The GNEB is a quasi-static method by which a path is initialized by a set of spin-configurations, called images, that is iteratively optimized using the LLG equation (3) without the precession (1. st term on the rhs in (3)) and SOT term but additional constraints added to the effective field
In order to study the current-driven (anti-)skyrmion dynamics we express the SOT according to the two qualitatively distinct contributions, the field-like torque
To simplify things we work with the normalized polarization direction
In Supplementary Note 1 we demonstrate that the assumption of linear dependent prefactors does not result in a loss of generality when it comes to describing (anti-)skyrmion dynamics.
3 Results
3.1 Energy Barriers of Single Particles
In the following, we will discuss the relevant energy barriers present in the system. At first, energy barriers are discussed which involve only a single particle. To do this, we apply the GNEB method to investigate the minimum energy path for rotation and collapse of both the skyrmion and the antiskyrmion as well as for their disappearance by overcoming the repulsive potential at the boundaries. The latter is caused in our simulations by assuming additional ferromagnetically pinned spins at the boundary of the simulation box. By rotation we mean the local rotation of the atomistic magnetic moments, resulting in the case of the skyrmion in a change from Néel-type with the preferred chirality via Bloch-type to Néel-type with opposite chirality and back, while for the antiskyrmion this is equivalent to a real rotation of the antiskyrmionic structure around its origin on the lattice.
The resulting GNEB paths are illustrated in Figure 2. For the paths of the (anti-)skyrmion motion and the collapse, the transition states, i.e., the states at the saddle point of the energy landscape are shown on the right-hand side of Figure 2, marked by the same boundary color as the corresponding GNEB path. As can be seen, the energy of the initial state, the final states, the minimum energy paths and thus the energy barriers for the skyrmion and the antiskyrmion are identical, in accordance with the previous statement that in rank-one materials both particles are energetically degenerated. Furthermore, with the chosen parameter set, all relevant single particle energy barriers are in the same order of magnitude which leads to a rather strong robustness against both deformation and rotation. From those results, the influence of the DM interaction becomes obvious: while the stability with respect to the collapse is mainly a result of the competing exchange interactions, the stability with respect to rotation is purely enforced by the DMI.
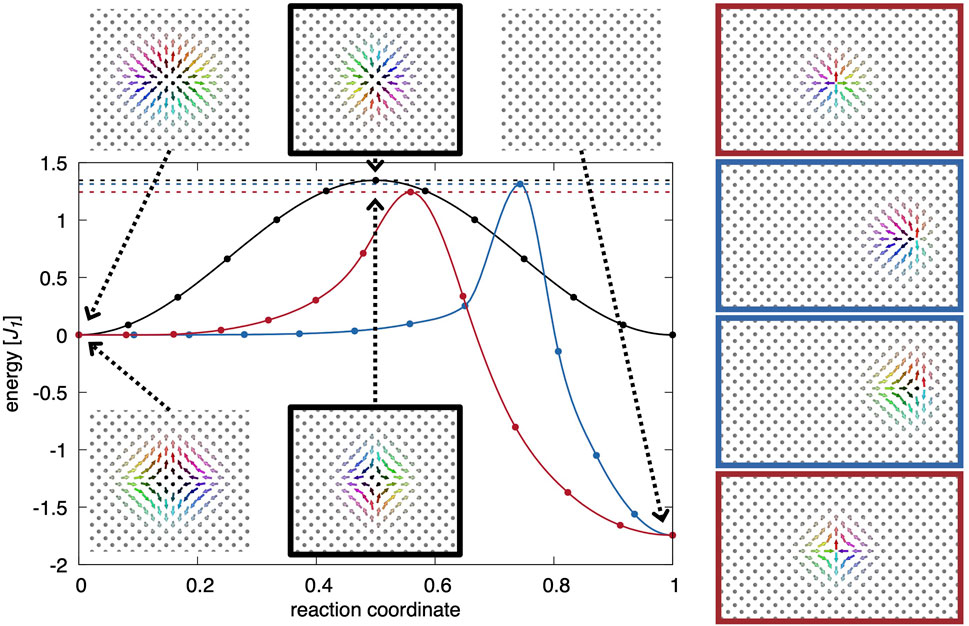
FIGURE 2. GNEB paths and energy barriers (indicated by dashed lines) given in units of the exchange parameter J1 for the rotation of an (anti-)skyrmion (black), the collapse of an (anti-)skyrmion (red) and the movement out of the system across the repulsive energy barrier at the boundary of our simulation box created by pinning the boundary spins ferromagnetically (blue). The insets show the relevant states. On the right, transition states are shown for the movement and the collapse. The colored boundary indicates the associated GNEB path degenerated for skyrmion and antiskyrmion. The reference energy refers to a single particle immersed in the ferromagnetic background.
3.2 Interaction Energies Between Two Particles
The representation of different bit combinations on the racetrack, e.g (0, 0), (0, 1), or (1, 1), requires the knowledge of the interaction behavior between equal and unequal kinds of particles. What might be surprising about the proposed skyrmion-antiskyrmion racetrack memory is the usage of antiparticles as information carriers. The question immediately arises to what extent these particles are mutual antiparticles and whether these particles would not simply annihilate mutually. As we see below, it turns out that the possible annihilation imposes a few restrictions on the fabrication of the resulting racetrack, namely the orientation of the atomistic lattice structure relative to the track direction, but does not prevent a possible realization of a skyrmion-antiskyrmion racetrack memory.
Recalling that an antiskyrmion is not rotationally invariant and thus possesses different properties along different spatial directions, these anisotropic properties need to be considered when one is interested in the interaction of skyrmions and antiskyrmions. As it can be seen in Figure 2, in our case the antiskyrmion can be obtained from the skyrmion by inverting the x-component of each atomistic spin, i.e.,
In Figure 3A the energy profiles for diskyrmionic interactions as a result of two single particles approaching along the x-axis (axis of direction of DM vector) is illustrated. Here and in the following, the distance between the centers of the particles is taken as measure for the reaction coordinate.
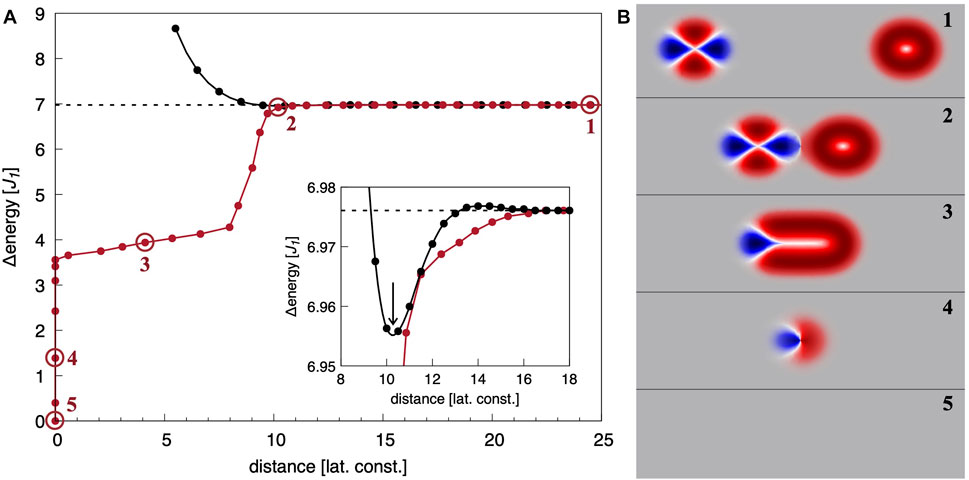
FIGURE 3. (A) Energy barriers for approaching (anti-)skyrmions along the x-direction. The MEP for the fusion of a skyrmion and an antiskyrmion is shown in red and the distance dependent energy for two equivalent particles (either skyrmions or antiskyrmions) is shown in black. The magnetic textures of exemplary intermediate states along the MEP are shown in (B). The corresponding points are highlighted by circles in (A) and labeled accordingly. The color code in (B) indicates the chirality of the particles. Red and blue represent Néel-type chirality (of opposite sign) while white highlights regions with Bloch-type chirality. State 5 indicates the ferromagnetic ground state, taken as energy zero reference and illustrated as grey background in (B). Distances are measured between the cores of the particles.
In the case of homoskyrmionic interactions, i.e., both particles are either skyrmions or antiskyrmions, the energy dependence on the distance of the two particles is shown by a black graph. To counteract the repulsive or attractive forces between two particles, we varied the size of the simulation box and placed the two particles such that their distance matched half of the box size along the x direction. By using periodic boundary conditions, this approach ensures that the particles remain at their initial position as no net force acts on them. The black graph in the inset of Figure 3A describes an energy profile typical for a fast and favorable formation of a homoskyrmionic “molecule,” a skyrmion-skyrmion-pair or an antiskyrmion-antiskyrmion-pair. It can be seen that the competing exchange interactions create a small repulsive energy barrier when the particles are approaching followed by the attractive binding potential for the homoskyrmionic molecule. The preferred distance of two particles in the homoskyrmionic molecule is about 10 a, slightly smaller than twice the skyrmion diameter of 6 a, with a being the lattice constant. If the distance between the two particles is decreased, the magnetization textures of the particles deform, and below a critical value of about 5.5 a, the pair interaction of the penetrating particles becomes so large that the (anti-)skyrmions become unstable and collapse to the ferromagnetic state. Since the chiral orientation of the antiskyrmion on the racetrack is determined by the DM vector of the underlying crystal lattice which remains unchanged across the racetrack memory, only antiskyrmion of the same chiral orientation will interact on the track.
To investigate the case of heteroskyrmionic interactions of one skyrmion and one antiskyrmion, the previously discussed simulational approach based on the total energy minimization of particles at a given distance is not applicable due to the fact that both particles attract each other and their static distance cannot be controlled anymore. Instead, we performed a GNEB calculation for the related path, meaning the initial state are well-separated particles (see state 1 in Figure 3B) at energy of two times the (anti-)skyrmion energy and the final state is the ferromagnetic state (state 5 in Figure 3B). The intermediate states represent the continuous nearing of the particles until they merge and finally collapse to the ferromagnetic state (see exemplary states 2-4 in Figure 3B). The resulting energy profile is shown by the red graph in Figure 3A. As before, the distance between the centers of the two particles is taken as measure for the reaction coordinate as long as they are well separated. Yet, during the merging process of two topologically nontrivial particles with opposite topological charge, a new elongated topologically trivial particle, i.e., with Q = 0, is formed (see state 3 in Figure 3B). The elongation of the core, i.e., the extend of the region with the magnetization pointing antiparallel to the ferromagnetic background (see central white line in Figure 3B, state 3), is taken as a new measure. The color code in Figure 3B indicates the chirality of the particles.
As it can be seen, no energy barrier exists if a skyrmion and an antiskyrmion approach along this x-direction visualized in state 1 of Figure 3B. Instead, the two particles can merge and mutually annihilate, the typical behavior of antiparticles. This is a direct consequence of the opposite chirality along the x-direction and is analogous to domain walls between ferromagnetic domains, which can also merge to lower the total energy of the system if they have opposite chirality. The opposite chirality of the antiskyrmion along the x-axis is a consequence of the racetrack material, for which we assumed a DMI vector D along the x-direction that favors in turn a Néel spin rotation along the y-direction. Consequently, these results show that a racetrack memory in which an antiskyrmion and a skyrmion are arranged in tandem in an orientation in which the spin chirality of the antiskyrmion is opposite to that of the skyrmion would not work because of data loss over time.
Figure 4 illustrates the energetic situation of a homochiral heteroskyrmionic interaction between an antiskyrmion and a skyrmion, i.e., the antiskyrmion and the skyrmion approach each other in a way that the chiral orientation of the two particles is the same along the reaction coordinate. This is realized by orienting the track direction, i.e., the reaction path in the language of our GNEB studies, along the y-axis of the crystal lattice keeping the direction of the DMI along the x-direction. Two distinct processes need to be considered for the description of such an interaction path: (i) This is an evasion of the particles by a sideways movement δx on their path along y, and (ii) the local change of the chirality of the particles. Both the sideways motion as well as the local rotation result in the possibility that the heteroskyrmionic interaction along the line connecting the centers of the two particles changes from a homo-to a heterochiral one, a condition for the merging and subsequently annihilation of the particles as discussed above. The observed sideways motion is similar to the one observed in Ref. [47] where the merging of two antiskyrmions and the formation of a higher-order state was investigated.
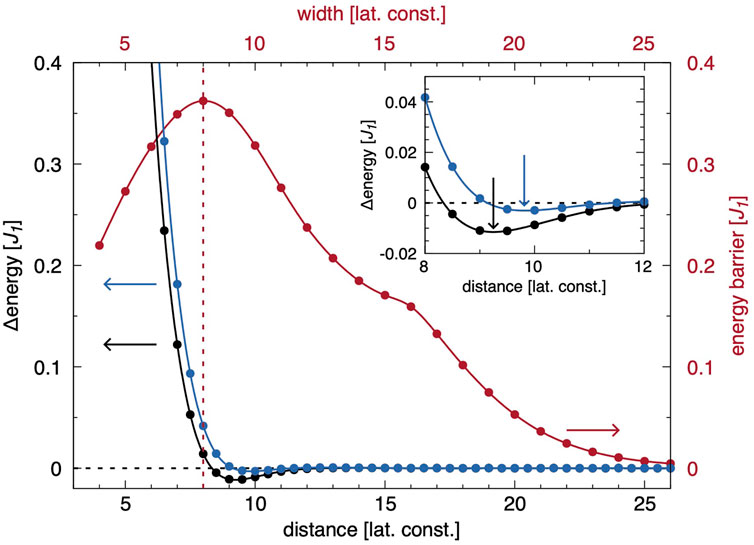
FIGURE 4. Energy barriers for approaching (anti-)skyrmions on a track oriented along the y-direction of the crystal lattice and of finite width in x-direction. In red, the energy barrier (right axis) for the fusion of a skyrmion and an antiskyrmion in dependence of the width (top axis) of the racetrack is given. The track width for which the energy barrier becomes maximum is highlighted by a red, vertical, dashed line. For this particular width, the distance dependent energy profile (left axis) for a skyrmion and an antiskyrmion located in the middle of the track is shown in blue calculated with the constraint of fixed chirality, i.e., preventing the local rotation of the atomistic moments within the particles. For two particles of equal type (either skyrmions or antiskyrmions) the profile is shown in black. The reference energy refers to infinitely separated particles at the same track width. The inset provides a higher energy resolution in the region around those two minima. The black and blue arrows indicate the distance of minimal energy.
In the case of an infinitely wide racetrack, the sideways movement δx, can become arbitrarily large to avoid the chirality change that would cost energy due to the DM interaction. Effectively, this means that the previously discussed case of the particles approaching along the x-axis is repeated, resulting in the situation of a vanishing energy barrier for particle annihilation. To restrict the sideways motion and thus δx, and to explore the optimal track width of a skyrmion-antiskyrmion racetrack memory, we simulate tracks with finite widths. The track boundary is again simulated by embedding the track in a ferromagnetically pinned background, technically achieved in our simulations by adding additional rows of pinned spins at each side of the track, to create the previously discussed repulsive potential, responsible for the discussed energy barrier to avoid the annihilation of the particles at the racetrack boundaries. For track widths between 4 and 26 lattice constants we performed 23 GNEB simulations in steps of one lattice parameter and determined the minimum energy potential barrier for the fusion of the skyrmion with the antiskyrmion. The resulting energy barrier depends on the width of the racetrack as can be seen in Figure 4 by the red graph. At finite widths, the repulsive force between the particles and the racetrack boundaries sets in. Yet, the skyrmion and antiskyrmion can still approach along the x-direction. By reducing the width further, the energy cost caused by the repulsive potential at the boundary gets too large and instead it becomes energetically more favorable to rotate the single particles additionally, which however now costs DMI energy and continues with decreasing width until finally almost no sideways motion occurs anymore. In that case, both in the skyrmion as well as in the antiskyrmion the atomistic magnetic moments need to rotate by 90° resulting in case of the skyrmion in a change from the preferred Néel-type chirality to Bloch-type chirality while the antiskyrmionic structure is effectively rotated by 45° around its origin. The chirality change is then solely responsible for the energy barrier. The energy barrier is about 0.36 J1, significantly lower than the expected barrier of 1.5 J1 as estimated based on the rotation barrier of a single particle discussed in Section 3.1. This can be understood as following: To reduce the energy cost due to DMI, the chirality change does not occur isotropically over the whole particles, but predominantly along the line connecting the centers of the particles while the chirality along the opposite direction is almost unchanged. Additionally, the particles are already squeezed by the repulsive potential caused by the track boundaries. This results in a destabilization and a reduction of the barrier against a change of chirality. This destabilization is enhanced for even smaller track width, manifesting in the reduction of the energy barrier at lower widths. As it can be seen in Figure 4, the optimal energy barrier for application purposes, i.e., the highest barrier as function of the track width, is reached for about 8 lattice constants. In the supplementary materials, we included movies of the annihilation path for different track widths. See Supplementary Note 2 and Supplementary Movies 1-5.
As a skyrmion-antiskyrmion pair feels an repulsive force, which is trying to separate both when they are too close to each other, the range of this repulsive interaction needs to be analyzed. Therefore, in addition, in Figure 4 the distance dependent energy for two identical particles and for one skyrmion and one antiskyrmion are shown in black and blue, respectively, the later under the constraints that no sidewards movement is allowed, i.e., δx = 0, and no rotation of the local moments occurs. The track width for those simulations was set to the previously obtained value of 8 lattice constants. As it can be seen, the competing exchange interactions create an optimal distance between the particles, and both a homo-as well as a heteroskyrmionic pair can be formed, a good side effect for application purposes as this reduces the time management for the reading process. The optimal distance varies from about 9.25 lattice constants for identical particles to about 9.8 lattice constants for different ones (see inset in Figure 4). The black curve of Figure 4 should be compared to the black curve in Figure 3. Both describe the binding energy of the homoskyrmionic molecules, the former for reaction paths along the y-direction and the latter along the x-direction of the lattice. We find that the binding energy and the bond length of homoskyrmionic pairs differ slightly due to the anisotropic DM interaction.
3.3 Motion of Skyrmions and Antiskyrmions Under the Effect of SOT
Here we turn to the atomistic simulation of the SOT enabled electric current induced motion of the skyrmion and the antiskyrmion. A particular challenge is to achieve a coherent and linear motion of the particles independent on the type considering that the skyrmion and the antiskyrmion show an opposite skyrmion Hall angle. Therefore, we simulated the dynamics of both particles by solving the LLG Equation 3 for SOTs 4) with different orientations of the spin current polarization Sp. We have chosen the current density or torque amplitude so that the relationship of particle velocity and current density stays in the linear regime, thus avoiding the breakdown that would result in a trochoidal motion of the particles [48]. However, it should be highlighted that the rank-one DMI increases the region where current-driven linear motion is possible both for the skyrmion and the antiskyrmion as the relevant energy barrier is increased equivalently for both particles. The results are shown in Figure 5, where the velocity components along the two crystallographic directions are plotted as function of the direction of the spin-polarization relative to the current direction. Since we are in the linear regime, both velocity components scale with the torque exerted on the spins or indirectly on the current density. For the simulations presented in Figure 5, we used a damping of αG = 0.7 and τ(j) = 0.003 meV. As it can be seen, the y-component of the velocity is equivalent for both the skyrmion and the antiskyrmion and follows a sinusoidal shape with respect to the direction of the spin polarization. The x-component, however, differs between the skyrmion and the antiskyrmion. More precisely, the velocity component along x is inverted for the two particles. Additionally, one can see that this results in a vanishing x-component of the velocity for both when the absolute value of the y-component is largest, in our case for an angle of the spin polarization relative to the x-axis of about 130°. Another important aspect to mention is the different maximal velocity which can be achieved along the two different crystallographic directions which can be explained by the ellipticity of the particles. Note, as before, we assumed the same lattice constant a in both directions.
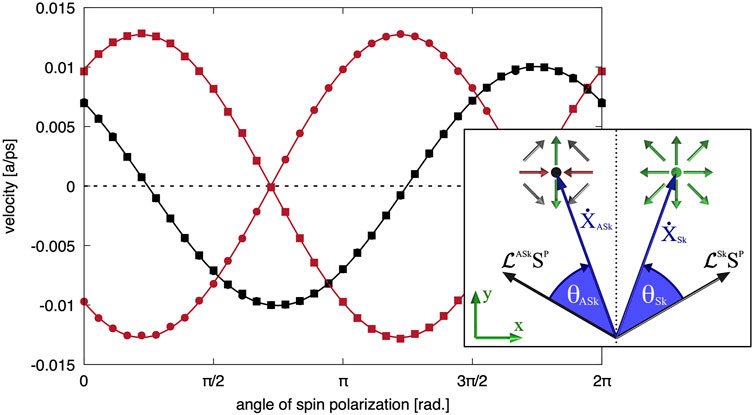
FIGURE 5. Velocity components along x-direction (red) and y-direction (black) for different orientations of the spin current polarization (angle measured from the x-axis). Circles (squares) represent the skyrmion (antiskyrmion). Inset: schematic representation of the resulting trajectories of skyrmions and antiskyrmions and their symmetry relation according to the Thiele-like Eq. 6.
To interpret the obtained results, we go back to the LLG Equation 3 which can be written in its implicit form as
In a first step, we go from the atomistic description to the micromagnetic one by replacing the discrete lattice of localized spins by a normalized continuous vector field, i.e., Si → m(r). Assuming that the shape of the magnetic structures remains unchanged during the motion in an applied spin current, i.e., staying within the rigid-body ansatz, m(r, t) = m(r − X(t)), and further neglecting the ellipticity of the skyrmion one can then find an equation of motion for the center of the (anti-)skyrmion similar to the Thiele equation (49) in an inplane current by projecting Eq. 5 onto the translational mode. The resulting Thiele-like equation for the position, X, of the particle reads as
(apply summation over common index β) with
where ϵαβ is the Levi-Civita symbol, α and β take the values of the x and y components of the magnetic film, α, β ∈ {x, y}. Q is the integer topological charge,
The Thiele-like equation states that the SOT-driven skyrmion dynamics depends not only on the topology, but also on the chirality. In the case of SOT, the skyrmion Hall effects can be controlled using special DMI and the resulting chiralities of the skyrmions, which we exploit to keep skyrmions and antiskyrmions on the track. The chirality tensor is different for Néel and Bloch-type skyrmions and antiskyrmions, which are typically described in terms of the helicity defined as the angle of the global rotation around the z-axis that relates various skyrmions to the Néel skyrmion by a smooth transformation. The limit of axial and nearly axial skyrmions was discussed by Ritzmann et al. in Ref. [48]. In this case, the chirality tensor becomes proportional to the helicity and thus for these systems the choice of the topological charge and the helicity determines the dynamics of skyrmions.
Eq. 6 has two fundamental consequences: (i) the Hall angle is inverted for skyrmions and antiskyrmions due to the opposite topological charge Q and (ii) the “effective” spin polarization,
Thus, one can conclude that a parallel motion of skyrmions and antiskyrmions is possible along the y-direction with the same speed and thus the necessary conditions for the possibility of a two-particle racetrack memory are fulfilled.
4 Discussion
A few important conditions need to be fulfilled if one uses more than one type of particles for such a device: i) Both particles should be energetically stable, i.e., they need to be (meta-) stable states of the system with a finite energy barrier preventing them from disappearing. ii) There should exist an energy barrier avoiding the fusion or annihilation of different particles. iii) The involved particles should move a) in the same direction and b) with the same velocity to avoid a change of the stored information for example due to annihilation or other effects.
In this paper we demonstrated, that rank-one DMI materials, materials where the DMI tensor possesses a zero determinant, are good candidates for the analysis of the interplay of skyrmions and antiskyrmions. Although the antiskyrmion carries the notion of the antiparticle of the skyrmion, we found the energy barrier for skyrmion-antiskyrmion annihilation can be large for particles on a track with proper track width and a track oriented properly with respect the anisotropy of the DM interaction of the crystal lattice. The energy profile as function of distant-dependent reaction coordinates for pairs of particles on a track shows the typical behavior for the formation of diskyrmionic molecules with very similar bond lengths, regardless of whether they are skyrmion-skyrmion, skyrmion-antiskyrmion or antiskyrmion-antiskyrmion pairs. This means any string of information encoded in a sequence of “0” and “1” can form a weakly bound chain of skyrmions and antiskyrmions with well-defined distances. This serves a simplification of the reading electronics. We showed, that a collective motion along one particular high-symmetry direction can be achieved if one applies a spin current in SOT geometry. This would allow for the creation of a skyrmion-antiskyrmion racetrack where the data is stored not in the presence or absence of particles but in their type itself, allowing for a more robust and time persistent way of information storage than it can be achieved if the information relies on predefined distances of information carriers. In Supplementary Movie 6 we show the simulation of such a skyrmion-antiskyrmion racetrack which confirms the collective motion of skyrmions and antiskyrmions as well as their even distribution along the racetrack.
The natural question arises whether such a model system of a perfect rank-one material occurs in nature. The main focus of both experimental measurements as well as theoretical investigations on magnetic thin films and multilayers was so far mainly on (111)-oriented surfaces and interfaces of fcc or bcc materials [5, 33, 50], meaning a hexagonal structure, and partially on (001) ones [51], i.e., square alignments. Those, however, do not allow for an anisotropic DM interaction due to their high symmetry, namely C3v and C4v, respectively. Only recently, the possibility of anisotropic DMI in low-symmetry systems was brought into focus [23, 24]. Thus, the determination of a particular rank-one material is still missing. However, it is worth noting that the proposed racetrack memory itself assumes only the possible coexistence of skyrmions and antiskyrmion. Such a coexistence does not rely on a perfect rank-1 DMI, but can be achieved even if the DMI deviates from the rank-1 behaviour. While larger deviations can in fact result in small changes of the velocity as well as the direction of motion, the overall motion is predominantly determined by the helicity of the magnetic object, and thus by the crystal symmetry, here C2v. However, as the deviation of the DMI from the rank-1 behaviour increases, either the stability of the skyrmion or antiskyrmion decreases, in particular with respect to helicity changes, eventually leading to the occurrence of trochoidal motion.
Yet, it should be highlighted that systems with C2v symmetry, and among these in particular those materials that have a rank-1 DMI, should be superior candidates for a skyrmion-antiskyrmion racetrack memory compared to material classes with higher symmetry. Recently, it was experimentally shown that in tetragonal inverse Heusler alloys, skyrmions and antiskyrmions can coexist [52, 53]. Presumably, however, the mechanism for the stability of the two particles is different, and so are their energetics. While again exchange frustration is the main stabilization mechanism, the DMI, however, exhibits D2d symmetry and thus intrinsically favors antiskyrmions over skyrmions. The observed elliptical deformation of the skyrmion suggests that the dipole interaction is a possible cause for the stability of the particle, and therefore leads to significantly different static and dynamic properties of the two particles.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
MH performed the spin dynamic simulations. CM provided the mathematical analysis of the micromagnetic functional. SB initiated and supervised this work. All authors took part in the analysis and the discussion of the results and contributed to the writing of the paper.
Funding
We acknowledge computing time on supercomputers provided by the Jülich Supercomputing Centre (JSC) and RWTH-Aachen University. We acknowledge funding from the DARPA TEE program (grant MIPR#HR0011831554) from DOI and from the Deutsche Forschungsgemeinschaft (DFG) through CRC 1238 (Project No. C01) and SPP 2137 (DFG grant no. BL 444/16). GM acknowledges funding from the Icelandic Research Fund (grant no.152483-052). CM acknowledges funding from Deutsche Forschungsgemeinschaft (DFG grant no. ME 2273/3-1). CM and SB acknowledge seed-fund support from JARA-FIT.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.769873/full#supplementary-material
References
1. Parkin SSP, Hayashi M, Thomas L. Magnetic Domain-Wall Racetrack Memory. Science (2008) 320:190–4. doi:10.1126/science.1145799
2. Bogdanov AN, Yablonskii D. Electrostatic Interaction of Neutral Semi-permeable Membranes. Zh Eksp Teor Fiz (1989) 95:178.
3. Mühlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A. Skyrmion Lattice in a Chiral Magnet. Science (2009) 323:915–9.
4. Yu XZ, Onose Y, Kanazawa N, Park JH, Han JH, Matsui Y. Real-space Observation of a Two-Dimensional Skyrmion crystal. Nature (2010) 465:901–4. doi:10.1038/nature09124
5. Heinze S, Von Bergmann K, Menzel M, Brede J, Kubetzka A, Wiesendanger R. Spontaneous Atomic-Scale Magnetic Skyrmion Lattice in Two Dimensions. Nat Phys (2011) 7:713–8. doi:10.1038/nphys2045
6. Dzyaloshinsky I. A Thermodynamic Theory of "weak" Ferromagnetism of Antiferromagnetics. J Phys Chem Sol (1958) 4:241–55. doi:10.1016/0022-3697(58)90076-3
7. Moriya T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys Rev (1960) 120:91–8. doi:10.1103/physrev.120.91
8. Bode M, Heide M, Von Bergmann K, Ferriani P, Heinze S, Bihlmayer G. Chiral Magnetic Order at Surfaces Driven by Inversion Asymmetry. Nature (2007) 447:190–3. doi:10.1038/nature05802
9. Fert A, Cros V, Sampaio J. Skyrmions on the Track. Nat Nanotech (2013) 8:152–6. doi:10.1038/nnano.2013.29
10. Jonietz F, Mühlbauer S, Pfleiderer C, Neubauer A, Münzer W, Bauer A. Skyrmion Lattice in a Chiral Magnet. Science (2010) 330:1648–51. doi:10.1126/science.1166767
11. Sampaio J, Cros V, Rohart S, Thiaville A, Fert A. Skyrmions on the Track. Nat Nanotechnol (2013) 8:839–44. doi:10.1038/nnano.2013.29
12. Koshibae W, Nagaosa N. Creation of Skyrmions and Antiskyrmions by Local Heating. Scientific Rep (2018) 8:6328. doi:10.1038/ncomms6148
13. Woo S, Litzius K, Krüger B, Im M-Y, Caretta L, Richter K. Observation of Room-Temperature Magnetic Skyrmions and Their Current-Driven Dynamics in Ultrathin Metallic Ferromagnets. Nat Mater (2016) 15:501–6. doi:10.1038/nmat4593
14. Hrabec A, Sampaio J, Belmeguenai M, Gross I, Weil R, Chérif SM. Current-induced Skyrmion Generation and Dynamics in Symmetric Bilayers. Nat Commun (2017) 8:15765. doi:10.1038/ncomms15765
15. Woo S, Song KM, Han HS, Jung MS, Im MY, Lee KS. Nat Commun (2017) 8:1–8. doi:10.1038/ncomms15573
16. Litzius K, Lemesh I, Krüger B, Bassirian P, Caretta L, Richter K. Skyrmion Hall Effect Revealed by Direct Time-Resolved X-ray Microscopy. Nat Phys (2017) 13:170–5. doi:10.1038/nphys4000
17. Back C, Cros V, Ebert H, Everschor-Sitte K, Fert A, Garst M. The 2020 Skyrmionics Roadmap. J Phys D: Appl Phys (2020) 53:363001. doi:10.1088/1361-6463/ab8418
18. Hoffmann M, Müller GP, Blügel S. Atomistic Perspective of Long Lifetimes of Small Skyrmions at Room Temperature. Phys Rev Lett (2020) 124:247201. doi:10.1103/physrevlett.124.247201
19. Kang W, Huang Y, Zheng C, Lv W, Lei N, Zhang Y. Voltage Controlled Magnetic Skyrmion Motion for Racetrack Memory. Sci Rep (2016) 6:23164. doi:10.1038/srep23164
20. Müller J. Magnetic Skyrmions on a Two-Lane Racetrack. New J Phys (2017) 19:025002. doi:10.1088/1367-2630/aa5b55
21. Zheng F, Rybakov FN, Borisov AB, Song D, Wang S, Li Z-A. Experimental Observation of Chiral Magnetic Bobbers in B20-type FeGe. Nat Nanotech (2018) 13:451–5. doi:10.1038/s41565-018-0093-3
22. Güngördü U, Nepal R, Tretiakov OA, Belashchenko K, Kovalev AA. , 93 (2016). p. 064428. doi:10.1103/physrevb.93.064428Phys Rev B
23. Hoffmann M, Zimmermann B, Müller GP, Schürhoff D, Kiselev NS, Melcher C. Antiskyrmions Stabilized at Interfaces by Anisotropic Dzyaloshinskii-Moriya Interactions. Nat Commun (2017) 8:308. doi:10.1038/s41467-017-00313-0
24. Camosi L, Rohart S, Fruchart O, Pizzini S, Belmeguenai M, Roussigné Y. Anisotropic Dzyaloshinskii-Moriya Interaction in Ultrathin Epitaxial Au/Co/W(110). Phys Rev B (2017) 95:214422. doi:10.1103/physrevb.95.214422
25. Koshibae W, Nagaosa N. Theory of Antiskyrmions in Magnets. Nat Commun (2016) 7:10542. doi:10.1038/ncomms10542
26. Kovalev AA, Sandhoefner S. Orbital Angular Momentum and Topological Charge of a Multi-Vortex Gaussian Beam. Front Phys (2018) 6 98:2296–424X. doi:10.1364/JOSAA.401561
27. Huang S, Zhou C, Chen G, Shen H, Schmid AK, Liu K. Stabilization and Current-Induced Motion of Antiskyrmion in the Presence of Anisotropic Dzyaloshinskii-Moriya Interaction. Phys Rev B (2017) 96(14):144412. doi:10.1103/physrevb.96.144412
28. Silva RC, Silva RL, Pereira AR. Magnus-force Induced Skyrmion-Antiskyrmion Coupling in Inhomogeneous Racetrack. J Phys Condens Matter (2020) 33:105802. doi:10.1088/1361-648x/abd1fa
29. Kumar V, Kumar N, Reehuis M, Gayles J, Sukhanov AS, Hoser A. Detection of Antiskyrmions by Topological Hall Effect in Heusler Compounds. Phys Rev B (2020) 101(1):014424. doi:10.1103/physrevb.101.014424
30. Lux FR, Freimuth F, Blügel S, Mokrousov Y. Chiral Hall Effect in Noncollinear Magnets from a Cyclic Cohomology Approach. Phys Rev Lett (2020) 124(9):096602. doi:10.1103/physrevlett.124.096602
31. Bouaziz J, Ishida H, Lounis S, Blügel S. Transverse Transport in Two-Dimensional Relativistic Systems with Nontrivial Spin Textures. Phys Rev Lett (2021) 126:147203. doi:10.1103/physrevlett.126.147203
32. Romming N, Hanneken C, Menzel M, Bickel JE, Wolter B, von Bergmann K. Writing and Deleting Single Magnetic Skyrmions. Science (2013) 341:636–9. doi:10.1126/science.1240573
33. Romming N, Kubetzka A, Hanneken C, von Bergmann K, Wiesendanger R. Field-Dependent Size and Shape of Single Magnetic Skyrmions. Phys Rev Lett (2015) 114(17):177203. doi:10.1103/physrevlett.114.177203
34. Rohart S, Thiaville A. Skyrmion Confinement in Ultrathin Film Nanostructures in the Presence of Dzyaloshinskii-Moriya Interaction. Phys Rev B (2013) 88:184422. doi:10.1103/physrevb.88.184422
35. Bessarab PF, Müller GP, Lobanov IS, Rybakov FN, Kiselev NS, Jónsson H. Lifetime of Racetrack Skyrmions. Scientific Rep (2018) 8:1–10. doi:10.1038/s41598-018-21623-3
36. Manchon A, Železný J, Miron IM, Jungwirth T, Sinova J, Thiaville A. Relativistic Néel-Order fields Induced by Electrical Current in Antiferromagnets. Rev Mod Phys (2019) 91(3):035004. doi:10.1103/revmodphys.91.035004
37. Schieback C, Kläui M, Nowak U, Rüdiger U, Nielaba P. Numerical Investigation of Spin-Torque Using the Heisenberg Model. Eur Phys J B (2007) 59:429–33. doi:10.1140/epjb/e2007-00062-2
38. Chureemart P, Evans RFL, Chantrell RW. Dynamics of Domain wall Driven by Spin-Transfer Torque. Phys Rev B (2011) 83:184416. doi:10.1103/physrevb.83.184416
39. Mentink JH, Tretyakov MV, Fasolino A, Katsnelson MI, Rasing T. Stable and Fast Semi-implicit Integration of the Stochastic Landau-Lifshitz Equation. J Phys Condens Matter (2010) 22:176001. doi:10.1088/0953-8984/22/17/176001
40.Spirit Spin Simulation Framework. Available at: https://spirit-code.github.io.
41. Müller GP, Hoffmann M, Dißelkamp C, Schürhoff D, Mavros S, Sallermann M. Spirit : Multifunctional Framework for Atomistic Spin Simulations. Phys Rev B (2019) 99:224414. doi:10.1103/physrevb.99.224414
42. Bessarab PF, Uzdin VM, Jónsson H. Method for Finding Mechanism and Activation Energy of Magnetic Transitions, Applied to Skyrmion and Antivortex Annihilation. Comp Phys Commun (2015) 196:335–47. doi:10.1016/j.cpc.2015.07.001
43. Henkelman G, Uberuaga BP, Jónsson H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J Chem Phys (2000) 113:9901–4. doi:10.1063/1.1329672
44. Hals KMD, Brataas A. Spin-Wave Driven Bidirectional Domain Wall Motion in Kagome Antiferromagnets. Phys Rev B (2013) 88(8):085423. doi:10.1103/physrevb.88.085423
45. Hanke JP, Freimuth F, Dupé B, Sinova J, Kläui M, Mokrousov Y. Theory of Current-Induced Angular Momentum Transfer Dynamics in Spin-Orbit Coupled Systems. Phys Rev B (2020) 101(1):014428. doi:10.1103/physrevb.101.014428
46. Železný J, Gao H, Manchon A, Freimuth F, Mokrousov Y, Zemen J. Relativistic Néel-Order fields Induced by Electrical Current in Antiferromagnets. Phys Rev B (2017) 95(1):014403. doi:10.1103/PhysRevLett.113.157201
47. Ritzmann U, Desplat L, Dupé B, Camley RE, Kim J-V. Asymmetric Skyrmion-Antiskyrmion Production in Ultrathin Ferromagnetic Films. Phys Rev B (2020) 102:174409. doi:10.1103/physrevb.102.174409
48. Ritzmann U, von Malottki S, Kim J-V, Heinze S, Sinova J, Dupé B. Trochoidal Motion and Pair Generation in Skyrmion and Antiskyrmion Dynamics under Spin-Orbit Torques. Nat Electron (2018) 1:451–7. doi:10.1038/s41928-018-0114-0
49. Thiele AA. Steady-State Motion of Magnetic Domains. Phys Rev Lett (1973) 30:230–3. doi:10.1103/physrevlett.30.230
50. Dupé B, Hoffmann M, Paillard C, Heinze S. Tailoring Magnetic Skyrmions in Ultra-thin Transition Metal Films. Nat Commun (2014) 5:4030. doi:10.1038/ncomms5030
51. Nandy AK, Kiselev NS, Blügel S. Interlayer Exchange Coupling: A General Scheme Turning Chiral Magnets into Magnetic Multilayers Carrying Atomic-Scale Skyrmions. Phys Rev Lett (2016) 116:177202. doi:10.1103/physrevlett.116.177202
52. Peng L, Takagi R, Koshibae W, Shibata K, Arima T-h., Nagaosa N. Real-Space Observation of a Transformation from Antiskyrmion to Skyrmion by Lorentz TEM. Microsc Microanal (2019) 25:1840–1. doi:10.1017/s1431927619009930
Keywords: skyrmion, antiskyrmion, racetrack memory, dzyaloshinskii-moriya interaction, spin-dynamics, Thiele equation
Citation: Hoffmann M, Müller GP, Melcher C and Blügel S (2021) Skyrmion-Antiskyrmion Racetrack Memory in Rank-One DMI Materials. Front. Phys. 9:769873. doi: 10.3389/fphy.2021.769873
Received: 02 September 2021; Accepted: 25 October 2021;
Published: 23 November 2021.
Edited by:
Xichao Zhang, Shinshu University, JapanReviewed by:
Alexey Kovalev, University of Nebraska-Lincoln, United StatesJoo-Von Kim, CNRS/Université Paris-Saclay, France
Copyright © 2021 Hoffmann, Müller, Melcher and Blügel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Markus Hoffmann, bS5ob2ZmbWFubkBmei1qdWVsaWNoLmRl
 Markus Hoffmann
Markus Hoffmann Gideon P. Müller1,2
Gideon P. Müller1,2 Christof Melcher
Christof Melcher Stefan Blügel
Stefan Blügel