Spatiotemporal Distribution Characterization for Terahertz Waves Generated From Plasma Induced by Two-Color Pulses

The spatiotemporal distribution of terahertz (THz) radiation from plasma has been demonstrated with the technology of THz focal-plane imaging. It has been found that the spatiotemporal distribution will vary with the frequency, as well as the length of plasma. A doughnut-shaped distribution appears in the lower frequency range, while the bell-shaped distribution corresponds to the higher frequency range. For plasmas with different lengths, their generated THz images in the time domain are similar, the THz images in the frequency domain as well. The spatiotemporal distributions are simulated with the off-axis-phase matching theory. All the findings will renew the understanding of the THz generation from plasma induced by two-color pulses.

Introduction

Terahertz (THz) wave generated from plasma has been proven to be a valuable tool in the field of nonlinear spectroscopy, imaging, and remote sensing [1–3]. The scheme of THz radiation from plasma induced by two-color laser pulses [4–7] has attracted more attention, and became popular owing to the emitted THz wave with broad spectrum and high intensity, as well as the good quality of polarization. With the widely application of THz radiation from two-color-induced plasma, its spatial characterization is desired. Many efforts have been put on this by using incoherent or coherent methods. The THz spatial distribution was deduced to be the shape of bell [8, 9] by raster scanning with the pyroelectric detectors or doughnut-shape [10] by raster scanning with Michelson interferometer; With a THz camera the transverse intensity of THz wave was captured and 3D-reconstructed to be the dumbbell shape [11]. There is also reported work contributing the conical hollow of THz distribution into the photo-induced carriers in the silicon wafer [12], which was used to filter the THz waves in the experiment. However, all these results seem incomplete for the comprehensive spatial characterization of THz waves. The influence of single-color plasma channel length on an angular THz radiation distribution was studied [13], yet its THz emission mechanism differs significantly from that of the two-color scheme. To fully understand the THz emission from two-color-induced plasma, it is necessary to characterize the spatiotemporal distribution of THz wave generated from plasma induced by two-color pulses.

In this work, the spatiotemporal distribution of THz wave radiated from plasma has been measured by using the technology of THz focal-plane imaging. For the plasma with unchanged length, THz spatial images in the time domain and frequency domain are presented, as well as their evolution. For plasmas with different lengths, the similarity and difference of the THz spatiotemporal distribution are also demonstrated. The experimental results are in accord with their simulations. These results are helpful in re-understanding the mechanism of the THz generation from plasma.

Experimental and Simulation Results

In the experiment, the technology of THz focal-plane imaging is used to obtain the spatiotemporal distribution of THz waves radiated from plasma induced by two-color pulses. The experimental setup is illustrated in Figure 1. A laser amplifier provides laser pulses with the central wavelength of 800 nm, repetition frequency of 1 kHz and pulse width of 35 fs. The femtosecond pulses are divided into two beams by a beam splitter (BS), one is used as the pump pulse and the other one is used as the probe pulse. The average pump and probe power are 700 and 13 mW, respectively. The pump pulse is focused by a lens with the focal length of 200 mm. With this lens, a relative uniform plasma about 7 mm is formed. There is a Barium Boron Oxide (BBO) crystal between the lens and its geometric focus. When the fundamental waves (800 nm) of femtosecond laser pass through the BBO crystal, their second harmonic waves generate. Both the fundamental ($\omega$) and second harmonic ($2\omega$) pulses ionize the air at the focus, which form a filament radiating THz waves. A 4f imaging system consisting of 2 THz lenses with the focal length of 100 mm and diameter of 75.8 mm is introduced in the THz beam. The front focal plane of the 4f imaging system coincides with the focus of the optical lens, while its back focal plane coincides with the ZnTe crystal (<110>, $10 mm\times 10 mm\times 1 mm$). With this 4f imaging system, THz images delivered from the front focal plane to the detection crystal. A silicon wafer is used to combine the probe pulses and THz waves. The probe pulses are subjected to the refractive index modulation of the crystal by the THz electric field, then they are captured by a CCD. In the measurement, the images of THz waves have been extracted by the technology of dynamic matching and subtraction [14]. For clarity, the THz time-domain signal and its Fourier-transformed spectrum are also shown in the inset of Figure 1, which was obtained by summing the values of four pixels in the center part of the CCD.

FIGURE 1

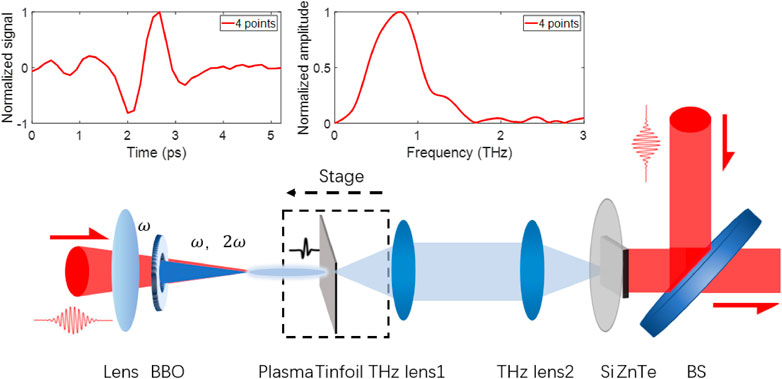
FIGURE 1. Schematic diagram of experimental setup. BS: Beam Splitter, BBO: Barium Boron Oxide Crystal. The dashed part is used to measure the spatiotemporal distribution of THz waves generated by plasma with different lengths. The insets are the THz time-domain signal and its Fourier-transformed spectrum, obtained by summing the values of four pixels in the center part of the CCD.

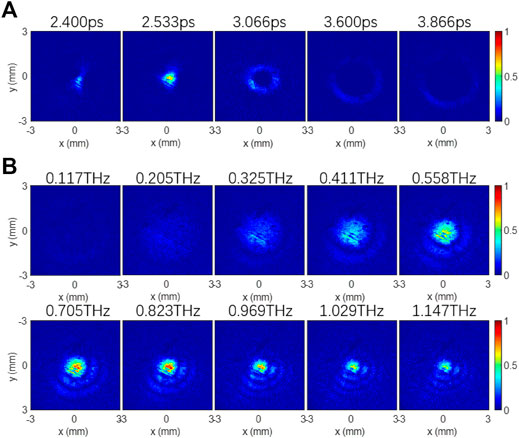
In the experiment, by selecting proper experimental parameters, such like the crystal axis angle of the BBO crystal and the distance to the geometric focus of the focusing lens, the generated THz signal was optimized. After that, the THz spatiotemporal distribution is measured and shown in Figure 2A. At the initial time of the THz pulse t ≤ 2.533 ps, the spatial intensity distribution obtained by the above system is mainly concentrated near the center of the optical axis, like a solid bright spot. Thereafter, it diffuses when t ≥ 3.066 ps, and the THz light spot diffuses into a hollow ring with the radius gradually increasing. In the process of diffusion, the amplitude of THz wave in the ring region decreases gradually due to the effect of divergence until the overall signal disappears. These THz temporal images were Fourier-transformed to obtain their field distributions at different frequencies. The results are shown in Figure 2B. For clearly, all images are normalized by the maximum value of the THz signal. It is clear that the THz field appears as a weak annular profile in the lower frequency range, while it appears in the region near the optical axis in the higher frequency range. With the frequency increasing, the annular side lobes gradually appear around the solid spot. Compared with that of the central spot the intensity of the annular side lobes becomes more and more obvious. It indicates that the radiation angle is corresponding to the frequency component of the radiated THz wave, which is consistent with the result reported in Ref. [15]. As illustrated in Figure 2, it seems that there are some nonuniform intensity distributions in these THz images, which was caused by some defects in the ZnTe crystal.

FIGURE 2

FIGURE 2. Normalized THz images in the time domain (A) and frequency domain (B).

As shown in Figure 2B, with the frequency increasing, the spatial distribution of THz wave changes from the shape of doughnut to bell mixed with dark ring lobes. Currently, there are many theoretical models used to describe THz generation from ionized plasma, including the model of pondermotive, photocurrent, four-wave mixing and off-axis phase matching [7, 16–18]. Considering this experimental system, we adopt an off-axis phase matching model for simulation, in which the parameters similar to that in the experiment was selected. Different from the work in Ref. [16], the near-field profile of THz emission from the plasma has been calculated. For the case of plasma length shorter than the dephasing length, the near-filed integration and their initial phases are also considered in the simulation. The simulation results are shown in Figure 3A. In the lower frequency range, $\nu \le 0.558$ THz, the spatial distribution of THz wave gradually changes from the shape of doughnut to bell, and the ring side lobes begin to appear; In the higher frequency range, $\nu \ge 0.705$ THz, the center spot of THz image becomes smaller and the annular side lobe becomes more obvious. According to the theory of off-axis phase matching, THz waves radiated from each point sources interfere constructively and accumulate continuously in the paraxial region; Away from the axis, THz waves interfere destructively and form alternative dark side ring lobes. For demonstration, we present the unnormalized experimental and simulated images at 0.117 THz, as shown in Figure 3B, the upper one is the experimental result, while the lower one is the simulated result. It is obviously that both the experimental and simulated spatial distributions are circular with the similar size, indicating that the theoretical simulation results are in good agreement with the experimental ones. To reveal the dependence of THz spatial distributions at different frequency, we extracted their THz amplitude information along the center line of the simulated images at different frequencies. The values of these curves were normalized by their own maximum, respectively, and plotted in Figure 3C. In Figure 3C, the left subfigure corresponds the lower frequency range $0.117\text{ THz}\le \text{ν}\le 0.558\text{ THz}$, while the right one corresponds the higher frequency range $0.705\text{ THz}\le \text{ν}\le 1.147\text{ THz}$. When$0.117\text{ THz}\le \text{ν}\le 0.325\text{ THz}$, the simulated distribution transits gradually from the shape of annular to bell with the frequency increasing; When $\nu =0.411 \text{THz}$, the ring side lobe appears. With the frequency increasing, the ring side lobe becomes more obvious, as shown in the right subfigure of Figure 3C. Comparing Figure 3 with Figure 2B, one may find that more ring side lobes in the simulation results than that in the experimental ones, it may be caused by an error of optical focus position between the experiment and simulation.

FIGURE 3

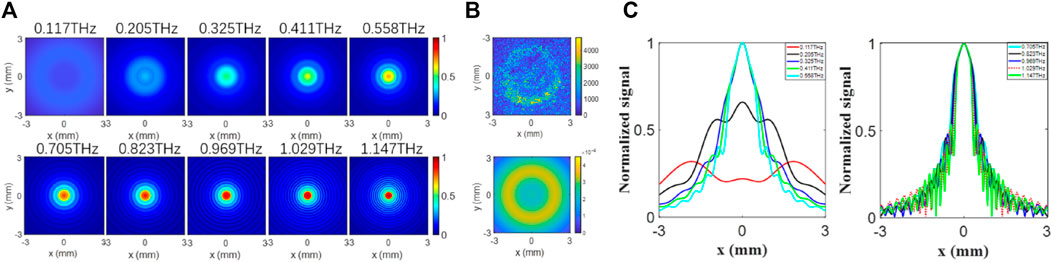
FIGURE 3. Simulation and experimental results of THz spatial distribution. (A) Simulation results by the off-axis phase matching model. (B) Unnormalized experimental (up) and simulation (bottom) images at 0.117 THz. (C) THz amplitude distributions at lower frequencies (left) and higher frequencies (right).

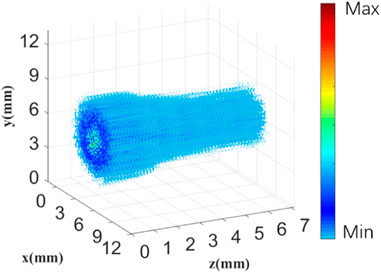
In addition, images of THz radiation from plasma with different lengths are also obtained. As shown in the dashed part of Figure 1, a tinfoil is placed slightly away from the end of the plasma. Moving the tinfoil to make it approach the plasma end, until the tinfoil is penetrated by the plasma. Since the diameter of the hole on the tinfoil is similar to that of the plasma, we believe that the THz wave radiated from the plasma at the left side of the foil can be blocked and only the THz wave radiated from the plasma on the right side can be detected. By moving the foil to the left, the electric field $E_i(i=1 , 2 , 3\dots )$ of THz waves radiated from plasma of different lengths can be obtained. For the case of plasma length comparable with the depth of field of the 4f system, the influence of the fixed front-focus of the 4f system on the experimental results is acceptable. In the experiment, we move the tinfoil across the plasma with the length of 7 mm by the step of 1 mm. The experimental results in the time domain and frequency domain are shown in Figures 4A,B, respectively. From Figure 4A, it can be found that the patterns of THz radiation from the plasmas with the same length diffuse from solid to hollow ring and then disappear over time. Moreover, the spatial shape and size of THz wave radiated from different lengths of plasma are maintained, but their intensities decrease with the plasma length shortened. Similarly, the images in Figure 4A are Fourier-transformed to obtain their frequency-domain images as shown in Figure 4B. For the plasmas of the same length, the spatial distribution of THz waves at different frequencies evolves from a doughnut-shape at low frequencies to a bell-shape at high frequencies; For the same frequency, the spatial distribution shape of THz waves radiated from different lengths of plasma is similar, while the intensity decreases with the decrease of plasma length. All these results indicate the accumulation effect of THz waves radiated from plasma.

FIGURE 4

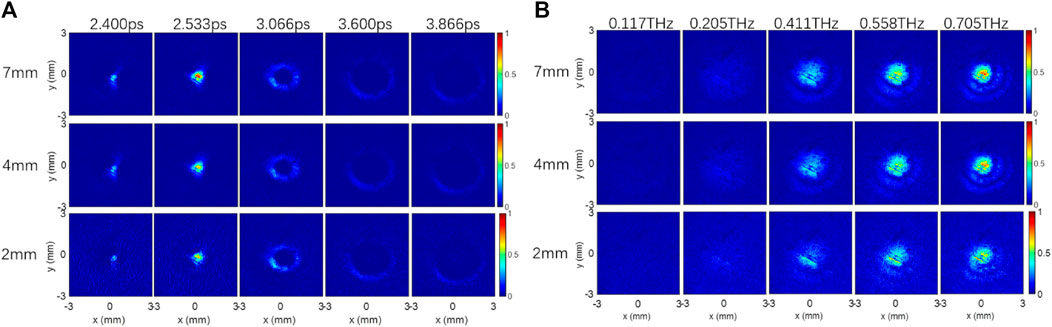
FIGURE 4. Experimental results of THz waves radiated from plasmas with different lengths. THz images in the time domain (A) and frequency domain (B).

It is known that the above THz electric fields $E_i(i=1,2,3\dots )$ are generated from plasma fragments with different lengths, and these fragments are obtained by separating from one and the same filament. Thus, it allows us to achieve the THz electric fields at different positions of the plasma by subtracting the electric fields generated from the adjacent plasma fragments,

$M{E}_{THzi}=E_i-E_{i-1}\left(i=1,2,3\dots \right)(1)$

$E_0$ is the THz electric field when the plasma length is 0, i.e., $E_0=0$. It is reported that the peak frequency of the THz emission was used in characterizing the plasma density [19], the THz frequency corresponds to the plasma frequency, which can be written as,

${\omega }_p=\sqrt{4\pi e^2{n}_e/m_e},(2)$

Where $n_e$ is the electron density and $m_e$ is the electron mass. The electric field$E_{THz}$ is proportional to the oscillation frequency of the plasma under the assumption of the appropriate laser field and gas density [20], meaning that $E_{THz}\propto \sqrt{n_e}$. Therefore, the electron density distributions at different positions of the plasma can be obtained, as shown in Figure 5. It can be found that the electron density of the plasma distributes symmetrically in the cross section. Additionally, the electron density is higher in the center of the plasma, and it decreases gradually with the increase of the diameter of the plasma. In the longitudinal direction, the electron density is also not uniform, and its density maximum locates near the beginning of the filament, which is in reasonable agreement with Refs. [19, 21–23].

FIGURE 5

FIGURE 5. Electron density distributions at different positions of the plasma.

Conclusion

The THz spatiotemporal distribution of THz radiation from plasma has been measured by the technology of THz focal-plane imaging. With the off-axis phase matching model, we obtained their simulation results, and the simulation results are in good agreement with the experimental ones. THz spatial distributions are doughnut-shape at low frequencies and bell-shape at high frequencies. The spatiotemporal distribution characteristics of THz wave from plasmas with different lengths are similar, but their intensities depend on the length of the plasma seriously. With the THz images radiated from plasmas of different lengths, the electric density inside of the plasma has been revealed.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

EW, YW, and WS contributed to experiment and simulation. WS designed the study. XW, SF, PH, JY, and YZ performed the theoretical analysis. All authors contributed to article revision, read, and approved the submitted version.

Funding

The National Natural Science Foundation of China (61735002, 11774243, 11774246, 11474206, 11404224); Youth Innovative Re-search Team of Capital Normal University (19530050146, 18530500155, 20530290053); Connotative Development Foundation for Distinguished Young Talents in Capital Normal University (2055105); Capacity Building for Science and Technology Innovation–Fundamental Scientific Research Funds (20530290072, 19530050170,19530050180,18530500186, 025185305000/142, 025185305000/142).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Reference

1. Kampfrath T, Sell A, Klatt G, Pashkin A, Mährlein S, Dekorsy T. Coherent Terahertz Control of Antiferromagnetic Spin Waves. Nat Photon (2011) 5:31–4. doi:10.1038/nphoton.2010.259

CrossRef Full Text | Google Scholar

2. Ulbricht R, Hendry E, Shan J, Heinz TF, Bonn M. Carrier Dynamics in Semiconductors Studied with Time-Resolved Terahertz Spectroscopy. Rev Mod Phys (2011) 83:543–86. doi:10.1103/revmodphys.83.543

CrossRef Full Text | Google Scholar

3. Liu J, Dai J, Chin SL, Zhang X-C. Broadband Terahertz Wave Remote Sensing Using Coherent Manipulation of Fluorescence from Asymmetrically Ionized Gases. Nat Photon (2010) 4:627–31. doi:10.1038/nphoton.2010.165

CrossRef Full Text | Google Scholar

4. Zhang XC, Shkurinov A, Zhang Y. Extreme Terahertz Science. Nat Photon (2017) 11:16–8. doi:10.1038/nphoton.2016.249

CrossRef Full Text | Google Scholar

5. Clerici M, Peccianti M, Schmidt BE, Caspani L, Shalaby M, Giguère M. Wavelength Scaling of Terahertz Generation by Gas Ionization. Phys Rev Lett (2013) 110:253901. doi:10.1103/physrevlett.110.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Siegel PH. Terahertz Technology in Biology and Medicine. IEEE Trans Microwave Theor Techn. (2004) 52(10):2438–47. doi:10.1109/tmtt.2004.835916

CrossRef Full Text | Google Scholar

7. Cook DJ, Hochstrasser RM. Intense Terahertz Pulses by Four-Wave Rectification in Air. Opt Lett (2000) 25(16):1210–2. doi:10.1364/ol.25.001210

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Akhmedzhanov RA, Ilyakov IE, Mironov VA, Suvorov EV, Fadeev DA, Shishkin BV. Generation of Terahertz Radiation by the Optical Breakdown Induced by a Bichromatic Laser Pulse. J Exp Theor Phys (2009) 109(3):370–8. doi:10.1134/s1063776109090027

CrossRef Full Text | Google Scholar

9. Zhong H, Karpowicz N, Zhang X-C. Terahertz Emission Profile from Laser-Induced Air Plasma. Appl Phys Lett (2006) 88(26):261103. doi:10.1063/1.2216025

CrossRef Full Text | Google Scholar

10. Andreeva VA, Kosareva OG, Panov NA, Shipilo DE, Solyankin PM, Esaulkov MN. Ultrabroad Terahertz Spectrum Generation from an Air-Based Filament Plasma. Phys Rev Lett (2016) 116(6):063902–5. doi:10.1103/physrevlett.116.063902

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Klarskov P, Strikwerda AC, Iwaszczuk K, Jepsen PU. Experimental Three-Dimensional Beam Profiling and Modeling of a Terahertz Beam Generated from a Two-Color Air Plasma. New J Phys (2013) 15(7):075012–3. doi:10.1088/1367-2630/15/7/075012

CrossRef Full Text | Google Scholar

12. Sørensen C, Guiramand L, Degert J, Tondusson M, Skovsen E, Freysz E. Conical versus Gaussian Terahertz Emission from Two-Color Laser-Induced Air Plasma Filaments. Opt Lett (2020) 7(45):2132–5. doi:10.1364/OL.390112

CrossRef Full Text | Google Scholar

13. Koribut AV, Rizaev GE, Mokrousova DV, Savinov SA, Reutov AA, Mityagin YA. Similarity of Angular Distribution for THz Radiation Emitted by Laser Filament Plasma Channels of Different Lengths. Opt Lett (2020) 45(45):4009–11. doi:10.1364/OL.394377

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang X, Cui Y, Sun W, Ye J, Zhang Y. Terahertz Real-Time Imaging with Balanced Electro-Optic Detection. Opt Commun (2010) 283(23):4626–32. doi:10.1016/j.optcom.2010.07.010

CrossRef Full Text | Google Scholar

15. Zhao J, Chu W, Wang Z, Peng Y, Gong C, Lin L. Strong Spatial Confinement of Terahertz Wave inside Femtosecond Laser Filament. ACS Photon (2016) 3(12):2338–43. doi:10.1021/acsphotonics.6b00512

CrossRef Full Text | Google Scholar

16. You YS, Oh TI, Kim KY. Off-axis Phase-Matched Terahertz Emission from Two-Color Laser-Induced Plasma Filaments. Phys Rev Lett (2012) 109(18):183902–5. doi:10.1103/physrevlett.109.183902

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Borodin AV, Panov NA, Kosareva OG, Andreeva VA, Esaulkov MN, Makarov VA. Transformation of Terahertz Spectra Emitted from Dual-Frequency Femtosecond Pulse Interaction in Gases. Opt Lett (2013) 38(38):1906–8. doi:10.1364/OL.38.001906

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Béjot P, Kasparian J, Wolf J-P. Dual-color Co-filamentation in Argon. Opt Express (2008) 16(18):14115–27. doi:10.1364/oe.16.014115

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Wang T-J, Ju J, Wei Y, Li R, Xu Z, Chin SL. Longitudinally Resolved Measurement of Plasma Density along Femtosecond Laser Filament via Terahertz Spectroscopy. Appl Phys Lett (2014) 105:051101. doi:10.1063/1.4892424

CrossRef Full Text | Google Scholar

20. Kim K-Y, Glownia JH, Taylor AJ, Rodriguez G. Terahertz Emission from Ultrafast Ionizing Air in Symmetry-Broken Laser fields. Opt Express (2007) 15(8):4577–84. doi:10.1364/oe.15.004577

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gaarde MB, Couairon A. Intensity Spikes in Laser Filamentation: Diagnostics and Application. Phys Rev Lett (2009) 103:043901. doi:10.1103/PhysRevLett.103.043901

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen Y, Théberge F, Kosareva O, Panov N, Kandidov VP, Chin SL. Evolution and Termination of a Femtosecond Laser Filament in Air. Opt Lett (2007) 32(24):3477–9. doi:10.1364/ol.32.003477

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Sun X, Xu S, Zhao J, Liu W, Cheng Y, Xu Z. Impressive Laser Intensity Increase at the Trailing Stage of Femtosecond Laser Filamentation in Air. Opt Express (2012) 20(4):4790–5. doi:10.1364/oe.20.004790

PubMed Abstract | CrossRef Full Text | Google Scholar