Narrow-Linewidth Laser Linewidth Measurement Technology

A narrow-linewidth laser with excellent temporal coherence is an important light source for microphysics, space detection, and high-precision measurement. An ultranarrow-linewidth output with a linewidth as narrow as subhertz has been generated with a theoretical coherence length over millions of kilometers. Traditional grating spectrum measurement technology has a wide wavelength scanning range and an extended dynamic range, but the spectral resolution can only reach the gigahertz level. The spectral resolution of a high-precision Fabry–Pérot interferometer can only reach the megahertz level. With the continuous improvement of laser coherence, the requirements for laser linewidth measurement technology are increasing, which also promotes the rapid development of narrow-linewidth lasers and their applications. In this article, narrow-linewidth measurement methods and their research progress are reviewed to provide a reference for researchers engaged in the development, measurement, and applications of narrow-linewidth lasers.

Introduction

Narrow-linewidth lasers with extremely low phase noise and a large coherence length have been widely used as a high-spectral-purity light source in gravitational wave detection [1, 2], optical atomic clocks [3, 4], lidar [5, 6], high-speed coherent optical communication [7, 8], and distributed optical fiber sensing [9, 10]. The main reason for the linewidth generation is the phase fluctuation caused by spontaneous radiation [11] and the noise induced by mechanical and temperature factors [12, 13]. Therefore, the laser linewidth reflects the physical and frequency stability of the laser. Scully and Lamb [14] proposed the laser quantum theory. They deduced that the spectral profile of the laser is Lorentzian and calculated its width (full width at half height). The linewidth value, an essential parameter of the laser, directly affects the accuracy of the narrow-linewidth laser in detection [15], sensitivity in sensing [16], and bit error rate in communication [17, 18]. Therefore, precise measurement of the linewidth value is a prerequisite for the application of narrow-linewidth lasers.

Different types of laser produce a broad coverage of linewidths, as large as tens of gigahertz [19, 20] and as small as subhertz [21, 22]. At present, the resolution of a commercial optical spectrum analyzer based on diffraction gratings is approximately 0.05 nm (gigahertz level)¹, and the resolution of Fabry–Pérot interferometers can reach a few megahertz². The rapid development and application of narrow-linewidth lasers have resulted in higher requirements for laser linewidth measurement technology. Specific devices must be built for lasers with a narrower linewidth (sub-megahertz) to measure the linewidth. In the past few decades, laser frequency stabilization [23, 24] and mode selection [25] have matured, and many narrow-linewidth measurement schemes are constantly being updated.

In this article, typical methods for measuring narrow-linewidth lasers are reviewed, and the characteristics of each method, as well as the status of its development, are summarized. Finally, a summary and an outlook for the future development of narrow-linewidth measurements are provided.

Narrow-Linewidth Laser Measurement Method

Two methods are mainly used for linewidth measurement: directly calculating the laser linewidth using the power spectrum density (PSD) of the laser and deducing the linewidth indirectly based on the relationship between the phase noise and linewidth. The power spectrum contains more-intuitive linewidth information, and it is relatively easy to obtain; therefore, a large proportion of linewidth measurement experiments focus on the former. Optical beat notes are necessary to obtain the PSD. The mixed signal of two incoherent lasers, each with a Lorentzian line shape, still has a Lorentzian line shape, and the PSD of the beat notes can be expressed as [26].

$s\left(v\right)=\frac{\Delta v}{2\pi \left[{\left(v-v_b\right)}^2+{\left(\Delta v/2\right)}^2\right]}(1)$

where $\Delta v=v_t+v_r$ , $v_t$ is the linewidth of the tested laser, $v_r$ is the linewidth of the reference laser, and $v_b$ is the difference between the output frequencies of the two lasers mentioned above (also the center frequency of the beat notes). Two lasers with the same or similar frequencies interfere and produce a beat signal with a lower frequency. The linewidth of the beat signal is the sum of the widths of the two lasers participating in the beat. There are usually two cases of beat notes suitable for linewidth measurement, as shown in Figure 1A. If $v_t=v_r$, the linewidth of the beat notes is twice the linewidth of the tested laser ($\Delta v=2v_t$, case 1). If $v_t\gg v_r$, (that is, the output spectrum of the reference laser is exceptionally narrow and the linewidth can be ignored compared with the tested laser), the linewidth value of the beat signal is approximately the value of the linewidth of the tested laser ($\Delta v\approx v_t$, case 2). These two cases are flexibly used in different measurement structures according to the specific conditions of the tested lasers. In this section, the focus is on four measurement structures based on the above two cases.

FIGURE 1

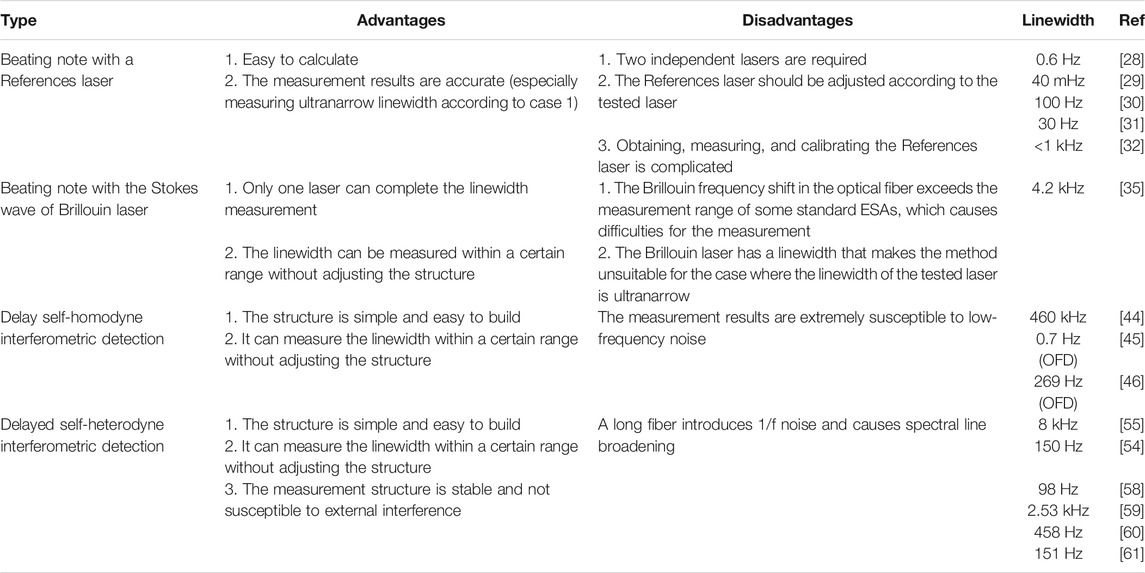
FIGURE 1. (A) Principle of optical beat notes, (B) beating note with a reference laser, (C) beating note with the Stokes wave of a Brillouin laser, (D) delayed self-homodyne interferometric detection, (E) delayed self-heterodyne interferometric detection, and (F) recirculating delayed self-heterodyne interferometer detection (PD, photodetector; ESA, electrical spectrum analyzer; RTC, resonance tracking circuit; PZT, piezoelectric transducer; AOM, acoustic optical modulator).

Beating Note With a Reference Laser

Figure 1B shows the measurement structure of using an additional laser to generate a reference laser beam and beating with the tested laser. The photodetector (PD) receives the mixed signal and transmits it to an electrical spectrum analyzer (ESA). Based on case 1, a laser with the same linewidth as the test is used to serve as the reference laser. In this case, any linewidth can be measured, but obtaining, measuring, and calibrating a reference laser is difficult. Based on case 2, using a reference laser whose linewidth value is negligible compared with the tested laser can meet the linewidth measurement requirements of most lasers; however, it is difficult to measure the ultranarrow linewidth in this case accurately. In addition, the two lasers participating in the beating should have the same amplitude, the same optical frequency (or a slight difference), and constant phase difference [27], which requires a stable experimental environment, increasing the difficulty and cost of testing.

Although this method has high requirements for the stability of the two lasers and the experimental environment, scientific researchers still favor it. In particular, ultranarrow-linewidth measurement based on case 1 does not require extra algorithm design, such as measuring the ultranarrow linewidth (see Delayed self-heterodyne interferometric detection), when analyzing beat notes. This avoids calculation errors, and the results are more convincing. In 1999, Young et al. [28] used a high-precision Fabry–Pérot cavity to realize a narrow-linewidth output. They built a second similar cavity for laser stability measurement (including linewidth measurement) and adjusted the laser frequency difference $v_b$ between the two cavities to 400 MHz to avoid low-frequency noise. They designed an independent vacuum chamber, temperature control system, and vibration isolation platform to ensure the stability of the two lasers. The measured linewidth was 0.6 Hz. In 2012, Kessler et al. [29] used two traditional cavity-stabilized lasers as reference laser sources to study a test laser. By analyzing the heterodyne signals among the three lasers, they concluded that the stability of the tested laser was the best, so the linewidth of the laser under test was the narrowest. The narrowest linewidth value obtained by the heterodyne signals between the tested laser and the other two lasers was 49 mHz, so they judged the linewidth of the tested laser to be less than 40 mHz. In 2013, Lee et al. [30] reported a chip-based resonator in the form of a spiral. It had a strong resistance to thermal noise and mechanical noise interference. Two identical fiber lasers were locked to the spiral resonator using a Pound–Drever–Hall locking system. The linewidth obtained by analyzing the beat notes of the two locked lasers was less than 100 Hz. In 2015, Liang et al. [31] built a laser identical to the tested laser to measure the narrow linewidth. They designed a thermal package and a sealed environment for the reference resonator to avoid technical noise caused by environmental and temperature fluctuations, and they concluded that the laser has an integrated linewidth of 30 Hz and a subhertz instantaneous linewidth. In 2018, Pavlov et al. [32] achieved a single-frequency output by using self-injection locking. They used a narrow-linewidth tunable fiber laser to perform heterodyne measurement with the tested laser and obtained a 340-Hz Lorentzian width and 1.7-kHz Gaussian width. According to Voigt linewidth theory [33], it was concluded that the laser linewidth was less than 1 kHz.

Beating Note With the Stokes Wave of Brillouin Laser

This approach does not require an additional reference laser, which solves the structural limitation that an additional laser must be used to provide a reference laser beam for linewidth measurement (see Beating note with a reference laser). As shown in Figure 1C, the tested laser was divided into two beams by a coupler. One beam is injected into the fiber ring cavity to form a Brillouin laser, and the other couples with the first-order Stokes wave propagating backward in the Brillouin laser. The coupling signal enters the PD to beat, and the beat note signal is fed into the ESA. The measurement principle is based on case 2. The tested laser is also the pump used to generate the Brillouin laser. The first-order Stokes beam linewidth $v_r$ of the Brillouin laser is usually much smaller than the pump linewidth, so the linewidth of the beat notes is approximately the linewidth of the tested laser ($\Delta v\approx v_r$). Compared with the structure discussed in Beating note with a reference laser, this scheme only requires the tested laser to complete the linewidth measurement and makes testing easier. Generally, the Brillouin frequency shift reaches 10–20 GHz [34] in the optical fiber. This frequency shift is the frequency difference $v_b$ between the Stokes wave and the tested laser. It is also the center frequency of the beat notes. Therefore, a large Brillouin frequency shift causes the center frequency of the beat signal to exceed the measurement range of the ESA, which causes difficulties in the measurement. In principle, this scheme is only suitable for 1–500-kHz linewidth measurement [35]. When the linewidth of the tested laser is extremely narrow, this scheme is no longer applicable, and significant errors occur.

In 1991, Smith [36] verified the good linewidth compression effect of the Brillouin laser by building a Brillouin fiber ring laser. In 1994, Boschung [37] realized a 3.84-Hz linewidth Brillouin laser output in a fiber ring cavity by using an incident laser with a linewidth of 100 kHz. These works provide a theoretical and experimental foundation for the beating frequency with the Stokes wave of the Brillouin laser. In 1996, Kueng [35] built the measurement structure shown in Figure 1C for the first time and obtained a linewidth of 4.2 kHz. In 2005, Dong et al. [38] proposed a scheme using a second-order Stokes wave in the fiber ring as the reference beam, which further improved the accuracy of the Brillouin laser first-order Stokes optical beat method.

Delayed Self-Homodyne Interferometric Detection

The delayed self-homodyne interferometric structure is shown in Figure 1D, and the measurement principle is based on case 1. This structure is based on the unbalanced Mach–Zehnder interferometer (UMZI) [39]. It does not have the measurement range limitation of the structure in Beating note with the Stokes wave of Brillouin laser and has the advantages of a simple structure, wide measurement range, and low optical transmission loss. However, the center frequency $v_b$ of the beat notes is 0 Hz; therefore, the low-frequency noise in the environment interferes with the measurement results. Considering the sensing characteristics of the optical fiber [40], the disturbance of environmental noise, temperature, pressure, and other factors can seriously affect the test results obtained by the optical fiber [41].

In 1986, Ryu [42] found that this method has the advantages of simple setting and high resolution when measuring narrow-linewidth lasers. In 1989, Nazarathy [43] derived the photocurrent power spectral density for this structure. In 1998, Ludvigsen [44] reported an optimized delay homodyne method in which the photocurrent signal was amplified by a low-noise amplifier and mixed with a stable 200 MHz local oscillator in a double-balanced mixer. They obtained a 460-kHz linewidth value with only 71.7 m of fiber. Because of its poor stability, this structure has rarely been used for direct linewidth measurement in recent years, but it often appears in optical frequency discriminators (OFDs) for linewidth measurement. The measurement principle of OFDs is no longer based on case 1 or case 2, and the linewidth information is calculated from the noise spectrum. In 2019, Gundavarapu [45] et al. reported a narrow-linewidth Brillouin laser output on an integrated Si₃N₄ waveguide platform. They measured the linewidth based on an OFD using a fiber-based UMZI and a balanced PD (the PD in Figure 1D is changed to a balanced PD), and the linewidth value was calculated to be 0.7 Hz. In 2021, Chauhan [46] et al. reported a visible-light photonic integrated Brillouin laser, and the measured laser linewidth value was 269 Hz using an OFD.

Delayed Self-Heterodyne Interferometric Detection

Delayed self-heterodyne interferometry (DSHI) overcomes the shortcoming that delayed self-homodyne interferometric structures are susceptible to low-frequency noise. The measurement principle is based on case 1. As shown in Figure 1E, an acousto-optic modulator (AOM) is introduced to shift the center frequency of the beat notes to a high frequency that is not affected by the environment to reduce system errors and improve measurement accuracy. Nevertheless, the DSHI method to measure narrow-linewidth lasers must be completed under the condition that the delay time is much longer than the coherence time. In theory, to test a 100-Hz linewidth, the fiber length required is as much as 1,590 km [47]. The long optical fiber increases the experimental volume and attenuation and introduces 1/f noise that can cause spectral line broadening [48], which results in larger measurement errors. Moreover, when the output power of the tested laser is large, the long-delay fiber generates stimulated Brillouin scattering, which is opposite to the direction of laser transmission; in this case, the incident pump energy is converted into Stokes wave and sound wave energy, increasing the transmission loss and even making the PD unable to detect the signal. The DSHI method was first proposed by Okoshi [49] in 1980. In 1986, Richter [50] derived the power spectral density function of the beat notes under the DSHI structure and reported that the measurement result would be more accurate with a delay time much longer than the coherence time of the tested laser. The spectral line of the beat signal is generally fitted by a Lorentzian function [51]. To offset the influence of 1/f noise introduced by long optical fiber, Chen [33] proposed a fitting scheme based on the Voigt profile. The Voigt function is the convolution of the Gaussian and Lorentz functions [52, 53]. Using this function to fit the collected data can effectively filter out the influence of 1/f noise.

To remove the 1/f noise from the root, researchers have proposed a short-fiber delayed self-heterodyne interferometer strategy for linewidth measurement. When the fiber is short, the PSD function is no longer expressed by Eq. 1, and the complete PSD function is expressed as [49, 54].

$S\left(f\right)=\frac{P_0^2}{4\pi }\frac{\Delta f}{\Delta f^2+{\left(f-f_1\right)}^2}\left\{1-exp\left(-2\pi {\tau }_d\Delta f\right)\left[\cos \left(2\pi {\tau }_d\left(f-f_1\right)\right)+\Delta f\frac{\sin \left(2\pi {\tau }_d\left(f-f_1\right)\right)}{f-f_1}\right]\right\}+\frac{\pi P_0^2}{2}exp\left(-2\pi {\tau }_d\Delta f\right)\delta \left(f-f_1\right)(2)$

where $P_0$ is the power of the beat signal, $\Delta f$ is the laser linewidth, $f_1$ is the AOM modulation frequency, ${\tau }_d$ is the delay time (proportional to the fiber length), and $\delta \left(f\right)$ is the impact function. According to the PSD function under a short optical fiber delay, different schemes have been designed to calculate the laser linewidth. In 2008, Jia [55] used polynomial fitting to eliminate the defect that caused the measurement accuracy to drop significantly when the delay time was insufficient and measured an 8-kHz linewidth with 25-km fiber. In 2015, Wei [56] obtained a numerical solution for the laser linewidth by measuring the frequency difference between the minimum points next to the maximum at the center frequency of the power spectrum. In principle, measuring a linewidth of 10 kHz requires only 300 m of delay fiber. In 2016, Huang [54, 57] reported an approach for contrasting the difference with the second peak and the second trough (CDSPST) of the coherence envelope to determine the laser linewidth. Only 3 km of fiber was used to measure a linewidth of 150 Hz. In 2018, Bai [58] successfully measured a laser with a linewidth of 98 Hz using the CDSPST method with a fiber delay of 2,950 m. In 2019, He [59] reported a linewidth demodulation scheme that achieved linewidth measurement by demodulating the coherent envelope of a short-delay self-heterodyne interference spectrum, and used this method to demodulate a 2.53-kHz linewidth. In 2020, Wang [60] reported a dual-parameter acquisition method and used it to calculate a 458-Hz linewidth by obtaining the frequency difference and amplitude difference of the coherence envelope. In 2021, Xue [61] reported a linewidth measurement method that combined long and short fibers. The measurement result of the long-delay fiber was used as the initial value, and the short-fiber self-heterodyne measurement results were demodulated. Xue used this method to demodulate a laser linewidth of 151 Hz successfully.

Other Measurement Methods

In addition to the above approaches, many other structures and optimization algorithms for narrow-linewidth laser measurements have been developed. The recirculating delayed self-heterodyne interferometer (RDSHI) method (see Figure 1F) is also widely used [62–65]. The unique fiber ring structure of this approach permits the delay fiber to increase the delay time by several times between two laser beams [66]. It is also an approach for improving the traditional DSHI method. Moreover, there is a close relationship between frequency noise and linewidth. Domenico et al. [67] proposed an approximate formula to show the relationship between the linewidth and frequency noise. Zhou et al. [68] reported a method to estimate the laser linewidth from its frequency power spectral density, called the “power-area method.” The β-separation line technique is an application of this relationship, which is convenient for calculating the laser linewidth after obtaining the laser frequency noise data [69]. Xu [70] et al.reported a method to measure the linewidth by using an unbalanced Michelson interferometer composed of a 3 × 3 optical fiber coupler. These structures can achieve a relatively accurate measurement of linewidth at a level of 1,000 Hz.

Conclusion and Outlook

Linewidth measurement technology is an essential part of the research and development process of narrow-linewidth lasers. Here, the typical methods for narrow-linewidth measurement were summarized, and the characteristics of various schemes were analyzed, as shown in Table 1. At present, measurement technology based on DSHI methods is developing rapidly, and its application is the most extensive among the methods. The method of beating notes with a reference laser is also used to test some ultranarrow-linewidth lasers owing to its excellent accuracy. The future renewal of linewidth compression technology is expected to place higher requirements on linewidth measurement technology. The RDSHI method has the advantages of the DSHI method. The multiorder beat signal measured by this scheme can avoid random errors and is expected to become the next research focus of narrow-linewidth measurement technology. In addition, Pollnau et al. [71, 72] questioned the traditional linewidth theory in recent studies, and they pioneered the theory that laser linewidth is a classical physics phenomenon, which may have an impact on linewidth measurement technology.

TABLE 1

TABLE 1. Comparison of laser linewidth measurement methods.

Author Contributions

ZB: Investigation, Writing—original draft, Writing—review and editing, Supervision. ZZ: Investigation, Writing—original draft. YQ: Investigation, Writing—review and editing. JD: Investigation, Writing—review and editing. SL: Investigation, Writing—review and editing. XY: Writing—review and editing. YW: Writing—review and editing, Supervision. ZL: Writing—review and editing, Supervision.

Funding

This work was supported by the National Natural Science Foundation of China (61905061, and 61927815), Natural Science Foundation of Hebei Province (F2019202337), and National Defense Science and Technology Key Laboratory Foundation (6142107190308).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://tmi.yokogawa.com.

²https://www.thorlabs.com.

References

1. Abbott BP, Abbott R, Adhikari R. LIGO: the Laser Interferometer Gravitational-Wave Observatory. Rep Prog Phys (2009) 72(7):076901. doi:10.1088/0034-4885/72/7/076901

CrossRef Full Text | Google Scholar

2. Abbott BP, Abbott R, Abbott TD, Abernathy MR, Acernese F, Ackley K, et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys Rev Lett (2016) 116(6):061102. doi:10.1103/PhysRevLett.116.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bloom BJ, Nicholson TL, Williams JR, Campbell SL, Bishof M, Zhang X, et al. An Optical Lattice Clock with Accuracy and Stability at the 10 ⁻¹⁸ Level. Nature (2014) 506(7486):71–5. doi:10.1038/nature12941

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ludlow AD, Boyd MM, Ye J. Optical Atomic Clocks. Rev Mod Phys (2015) 87(2):637–701. doi:10.1103/revmodphys.87.637

CrossRef Full Text | Google Scholar

5. Hostetler CA, Behrenfeld MJ, Hu Y, Hair JW, Schulien JA. Spaceborne Lidar in the Study of marine Systems. Annu Rev Mar Sci (2018) 10(1):121–47. doi:10.1146/annurev-marine-121916-063335

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Yang F, Ye Q, Pan Z, Chen D, Cai H, Qu R, et al. 100-mW Linear Polarization Single-Frequency All-Fiber Seed Laser for Coherent Doppler Lidar Application. Opt Commun (2012) 285(2):149–52. doi:10.1016/j.optcom.2011.09.030

CrossRef Full Text | Google Scholar

7. Guan H, Novack A, Galfsky T, Ma Y, Fathololoumi S, Horth A, et al. Widely Tunable, Narrow-Linewidth III-V/silicon Hybrid External-Cavity Laser for Coherent Communication. Opt Express (2018) 26(7):7920–33. doi:10.1364/oe.26.007920

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhou K, Zhao Q, Huang X, Yang C, Li C, Zhou E, et al. kHz-Order Linewidth Controllable 1550-nm Single-Frequency Fiber Laser for Coherent Optical Communication. Opt Express (2017) 25(17):19752–9. doi:10.1364/oe.25.019752

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhu T, He Q, Xiao X, Bao X. Modulated Pulses Based Distributed Vibration Sensing with High Frequency Response and Spatial Resolution. Opt Express (2013) 21(3):2953–63. doi:10.1364/oe.21.002953

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Juarez JC, Taylor HF. Field Test of a Distributed Fiber-Optic Intrusion Sensor System for Long Perimeters. Appl Opt (2007) 46(11):1968–71. doi:10.1364/ao.46.001968

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Schawlow AL, Townes CH. Infrared and Optical Masers. Phys Rev (1958) 112(6):1940–9. doi:10.1103/physrev.112.1940

CrossRef Full Text | Google Scholar

12. Renk KF. Basics of Laser Physics. Dordrecht London New York: Springer Heidelberg (2012).

Google Scholar

13. Siegman AE. Lasers. Sausalito,CA,United States: University Science Books (1986).

Google Scholar

14. Scully MO, Lamb WE. Quantum Theory of an Optical Maser. 1. General Theory. Phys Rev (1967) 159(2):208–26. doi:10.1103/physrev.159.208

CrossRef Full Text | Google Scholar

15. Li C, Wang T, Zhang H, Xie J, Liu L, Guo J. Effect of Laser Linewidth on the Performance of Heterodyne Detection. Acta Physica Sinica (2016) 65(8):084206. doi:10.7498/aps.65.084206

CrossRef Full Text | Google Scholar

16. Shi L, Zhu T, He Q, Huang S. Effect of Laser Linewidth on Phase-OTDR Based Distributed Vibration Sensing Regime. Proc SPIE (2014) 9157:91576H. doi:10.1117/12.2059448

CrossRef Full Text | Google Scholar

17. Savory S, Hadjifotiou A. Laser Linewidth Requirements for Optical DQPSK Systems. IEEE Photon Technology Lett (2004) 16(3):930–2. doi:10.1109/lpt.2004.823720

CrossRef Full Text | Google Scholar

18. Honjo T, Inoue T, Inoue K. Influence of Light Source Linewidth in Differential-Phase-Shift Quantum Key Distribution Systems. Opt Commun (2011) 284(24):5856–9. doi:10.1016/j.optcom.2011.08.056

CrossRef Full Text | Google Scholar

19. Bai Z, Williams RJ, Kitzler O, et al. Diamond Brillouin Laser in the Visible. APL Photon (2020) 5(3):031301. doi:10.1063/1.5134907

CrossRef Full Text | Google Scholar

20. O’Reilly JJ, Lane PM, Heidemann R, Hofstetter R. Optical Generation of Very Narrow Linewidth Millimetre Wave Signals. Electronics Lett (1992) 28(25):2309–11. doi:10.1049/el:19921486

CrossRef Full Text | Google Scholar

21. Al-Taiy H, Wenzel N, Preußler S, Klinger J, Schneider T. Ultra-narrow Linewidth, Stable and Tunable Laser Source for Optical Communication Systems and Spectroscopy. Opt Lett (2014) 39(20):5826–9. doi:10.1364/ol.39.005826

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hirata S, Akatsuka T, Ohtake Y, Morinaga A. Sub-hertz-linewidth Diode Laser Stabilized to an Ultralow-Drift High-Finesse Optical Cavity. Appl Phys Express (2014) 7(2):022705. doi:10.7567/apex.7.022705

CrossRef Full Text | Google Scholar

23. Drever RWP, Hall JL, Kowalski FV, Hough J, Ford GM, Munley AJ, et al. Laser Phase and Frequency Stabilization Using an Optical Resonator. Appl Phys B Photophysics Laser Chem (1983) 31(2):97–105. doi:10.1007/bf00702605

CrossRef Full Text | Google Scholar

24. Argence B, Chanteau B, Lopez O, Nicolodi D, Abgrall M, Christian C, et al. Quantum cascade Laser Frequency Stabilization at the Sub-hz Level. Nat Photon (2015) 9(7):456–60. doi:10.1038/nphoton.2015.93

CrossRef Full Text | Google Scholar

25. Shaykin AA, Burdonov KF, Khazanov EA. A Novel Technique for Longitudinal Mode Selection in Q-Switched Lasers. Laser Phys Lett (2015) 12(12):125001. doi:10.1088/1612-2011/12/12/125001

CrossRef Full Text | Google Scholar

26. Fang Z, Cai H, Chen G, QU R. Fundamentals of Semiconductor Lasers. Single Frequency Semiconductor Lasers (2017) 9(39). doi:10.1007/978-981-10-5257-6_2

CrossRef Full Text | Google Scholar

27.The Fact Factor. Global Threat Report (2021). Available at: https://thefactfactor.com/facts/pure_science/physics/formation-of-beats/6682/ (Accessed August 26, 2021).

Google Scholar

28. Young BC, Cruz FC, Itano WM. Visible Lasers with Subhertz Linewidths. Phys Rev Lett (1999) 82(19):3799–802. doi:10.1103/physrevlett.82.3799

CrossRef Full Text | Google Scholar

29. Kessler T, Hagemann C, Grebing C, Legero T, Sterr U, Riehle F, et al. A Sub-40-mHz-linewidth Laser Based on a Silicon Single-crystal Optical Cavity. Nat Photon (2012) 6(10):687–92. doi:10.1038/nphoton.2012.217

CrossRef Full Text | Google Scholar

30. Lee H, Suh MG, Chen T, Li J, Diddams SA, Vahala KJ. Spiral Resonators for On-Chip Laser Frequency Stabilization. Nat Commun (2013) 4(1):2468. doi:10.1038/ncomms3468

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Liang W, Ilchenko VS, Eliyahu D, Savchenkov AA, Matsko AB, Seidel D, Maleki L. Ultralow Noise Miniature External Cavity Semiconductor Laser. Nat Commun (2015) 6(1):7371. doi:10.1038/ncomms8371

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Pavlov NG, Koptyaev S, Lihachev GV, Voloshin AS, Gorodnitskiy AS, Ryabko MV, et al. Narrow-linewidth Lasing and Soliton Kerr Microcombs with Ordinary Laser Diodes. Nat Photon (2018) 12(11):694–8. doi:10.1038/s41566-018-0277-2

CrossRef Full Text | Google Scholar

33. Chen M, Meng Z, Wang J, Chen W. Ultra-narrow Linewidth Measurement Based on Voigt Profile Fitting. Opt Express (2015) 23(5):6803–8. doi:10.1364/oe.23.006803

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Yu J, Park Y, Oh K, Kwon I. Brillouin Frequency Shifts in Silica Optical Fiber with the Double Cladding Structure. Opt Express (2002) 10(19):996–1002. doi:10.1364/oe.10.000996

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Kueng A, Thevenaz L, Robert PA. Laser Linewidth Determination in the Sub-megahertz Range Using a Brillouin Fibre Laser. Proc Eur Conf Opt Commun (1996) 2:305–8. https://ieeexplore.ieee.org/abstract/document/715751

Google Scholar

36. Smith SP, Zarinetchi F, Ezekiel S. Narrow-linewidth Stimulated Brillouin Fiber Laser and Applications. Opt Lett (1991) 16(6):393–5. doi:10.1364/ol.16.000393

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Boschung J, Robert PA, Thévenaz L. High-accuracy Measurement of the Linewidth of a Brillouin Fibre Ring Laser. Electronics Lett (1994) 30(18):1488–9. doi:10.1049/el:19941053

CrossRef Full Text | Google Scholar

38. Dong Y, Lu Z, Lu Y, He W. A New Method of Measuring Ultra-narrow Laser Line-Width. J Harbin Inst Technology (2005) 37(5):670–3. https://en.cnki.com.cn/Article_en/CJFDTotal-HEBX200505028.htm

Google Scholar

39. Mach L. Ueber einen interferenzrefraktor. Z für Instrumentenkunde. (1982) 12(3):89–93. https://de.wikipedia.org/wiki/Mach-Zehnder-Interferometer

Google Scholar

40. Hocker GB. Fiber-optic Sensing of Pressure and Temperature. Appl Opt (1979) 18(9):1445–8. doi:10.1364/ao.18.001445

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Conforti E, Rodigheri M, Sutili T, Galdieri Flavio J. Acoustical and 1∕f Noises in Narrow Linewidth Lasers. Opt Commun (2020) 476:126286. doi:10.1016/j.optcom.2020.126286

CrossRef Full Text | Google Scholar

42. Ryu S, Yamamoto S. Measurement of Direct Frequency Modulation Characteristics of DFB-LD by Delayed Self-Homodyne Technique. Electronics Lett (1986) 22(20):1052–4. doi:10.1049/el:19860721

CrossRef Full Text | Google Scholar

43. Nazarathy M, Sorin WV, Baney DM, Newton SA. Spectral Analysis of Optical Mixing Measurements. J Lightwave Technology (1989) 7(7):1083–96. doi:10.1109/50.29635

CrossRef Full Text | Google Scholar

44. Ludvigsen H, Tossavainen M, Kaivola M. Laser Linewidth Measurements Using Self-Homodyne Detection with Short Delay. Opt Commun (1998) 155(1–3):180–6. doi:10.1016/s0030-4018(98)00355-1

CrossRef Full Text | Google Scholar

45. Gundavarapu S, Brodnik GM, Puckett M, Huffman T, Bose D, Behunin R, et al. Sub-hertz Fundamental Linewidth Photonic Integrated Brillouin Laser. Nat Photon (2019) 13(1):60–7. doi:10.1038/s41566-018-0313-2

CrossRef Full Text | Google Scholar

46. Chauhan N, Isichenko A, Liu K, Wang J, Zhao Q, Behunin RO, et al. Visible Light Photonic Integrated Brillouin Laser. Nat Commun (2021) 12(1):4685. doi:10.1038/s41467-021-24926-8

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Peng Y. A Novel Scheme for Hundred-Hertz Linewidth Measurements with the Self-Heterodyne Method. Chin Phys Lett (2013) 30(8):084208. doi:10.1088/0256-307x/30/8/084208

CrossRef Full Text | Google Scholar

48. Mercer LB. 1/f Frequency Noise Effects on Self-Heterodyne Linewidth Measurements. J Lightwave Technology (1991) 9(4):485–93. doi:10.1109/50.76663

CrossRef Full Text | Google Scholar

49. Okoshi T, Kikuchi K, Nakayama A. Novel Method for High Resolution Measurement of Laser Output Spectrum. Electronics Lett (1980) 16(16):630–1. doi:10.1049/el:19800437

CrossRef Full Text | Google Scholar

50. Richter L, Mandelberg H, Kruger M, McGrath P. Linewidth Determination from Self-Heterodyne Measurements with Subcoherence Delay Times. IEEE J Quan Electronics (1986) 22(11):2070–4. doi:10.1109/jqe.1986.1072909

CrossRef Full Text | Google Scholar

51. Saito S, Yamamoto Y. Direct Observation of Lorentzian Lineshape of Semiconductor Laser and Linewidth Reduction with External Grating Feedback. Electronics Lett (1981) 17(9):325. doi:10.1049/el:19810229

CrossRef Full Text | Google Scholar

52. Abrarov SM, Quine BM, Jagpal RK. A Simple Interpolating Algorithm for the Rapid and Accurate Calculation of the Voigt Function. J Quantitative Spectrosc Radiative Transfer (2009) 110(6–7):376–83. doi:10.1016/j.jqsrt.2009.01.003

CrossRef Full Text | Google Scholar

53. Bruce SD, Higinbotham J, Marshall I, Beswick PH. An Analytical Derivation of a Popular Approximation of the Voigt Function for Quantification of NMR Spectra. J Magn Reson (2000) 142(1):57–63. doi:10.1006/jmre.1999.1911

CrossRef Full Text | Google Scholar

54. Huang S, Zhu T, Cao Z, Liu M, Deng M, Liu J, et al. Laser Linewidth Measurement Based on Amplitude Difference Comparison of Coherent Envelope. IEEE Photon Technology Lett (2016) 28(7):759–62. doi:10.1109/lpt.2015.2513098

CrossRef Full Text | Google Scholar

55. Jia Y, Ou P, Yang Y, Chunxi Z. Short Fibre Delayed Self-Heterodyne Interferometer for Ultranarrow Laser Linewidth Measurement. J Beijing Univ Aeronautics Astronautics (2008) 34(05):568. https://en.cnki.com.cn/Article_en/CJFDTotal-BJHK200805021.htm

Google Scholar

56. Wei ZP. Measurement of the Narrow Linewidth Laser Spectrum Based on the Delayed Self-Heterodyne. Opt Optoelectronic Technology (2015) 13(3):38–40. http://www.cqvip.com/qk/87090x/201503/71887168504849534851484857.html

Google Scholar

57. Huang S, Zhu T, Liu M, Huang W. Precise Measurement of Ultra-narrow Laser Linewidths Using the strong Coherent Envelope. Scientific Rep (2017) 7(1):41988. doi:10.1038/srep41988

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Bai Q, Yan M, Xue B, Gao Y, Wang D, Wang Y, et al. The Influence of Laser Linewidth on the Brillouin Shift Frequency Accuracy of BOTDR. Appl Sci (2018) 9(1):58. doi:10.3390/app9010058

CrossRef Full Text | Google Scholar

59. He Y, Hu S, Liang S, Yiyue L. High-precision Narrow Laser Linewidth Measurement Based on Coherent Envelope Demodulation. Opt Fiber Technology (2019) 50:200–5. doi:10.1016/j.yofte.2019.03.024

CrossRef Full Text | Google Scholar

60. Wang Z, Ke C, Zhong Y, Xing C, Wang H, Yang K, et al. Ultra-narrow-linewidth Measurement Utilizing Dual-Parameter Acquisition through a Partially Coherent Light Interference. Opt Express (2020) 28(6):8484–93. doi:10.1364/oe.387398

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Xue M, Zhao J. Laser Linewidth Measurement Based on Long and Short Delay Fiber Combination. Opt Express (2021) 29(17):27118–26. doi:10.1364/oe.428787

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Gao J, Jiao D, Deng X, Liu J, Zhang L, Zang Q, et al. A Polarization-Insensitive Recirculating Delayed Self-Heterodyne Method for Sub-kilohertz Laser Linewidth Measurement. Photonics (2021) 8(5):137. doi:10.3390/photonics8050137

CrossRef Full Text | Google Scholar

63. Dawson JW, Park N, Vahala KJ. An Improved Delayed Self-Heterodyne Interferometer for Linewidth Measurements. IEEE Photon Technology Lett (1992) 4(9):1063–6. doi:10.1109/68.157150

CrossRef Full Text | Google Scholar

64. Han M, Wang A. Analysis of a Loss-Compensated Recirculating Delayed Self-Heterodyne Interferometer for Laser Linewidth Measurement. Appl Phys B (2005) 81(1):53–8. doi:10.1007/s00340-005-1871-9

CrossRef Full Text | Google Scholar

65. Chen X, Han M, Zhu Y, Dong B, Wang A. Implementation of a Loss-Compensated Recirculating Delayed Self-Heterodyne Interferometer for Ultranarrow Laser Linewidth Measurement. Appl Opt (2006) 45(29):7712–7. doi:10.1364/ao.45.007712

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Tsuchida H. Simple Technique for Improving the Resolution of the Delayed Self-Heterodyne Method. Opt Lett (1990) 15(11):640. doi:10.1364/ol.15.000640

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Di Domenico GD, Schilt S, Thomann P. Simple Approach to the Relation between Laser Frequency Noise and Laser Line Shape. Appl Opt (2010) 49(25):4801–7. doi:10.1364/ao.49.004801

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Zhou Q, Qin J, Xie W, Liu Z, Tong Y, Dong Y, et al. Power-area Method to Precisely Estimate Laser Linewidth from its Frequency-Noise Spectrum. Appl Opt (2015) 54(28):8282–9. doi:10.1364/ao.54.008282

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Xu D, Lu B, Yang F, Dijun C, Haiwen C, Qu R. Narrow Linewidth Single-Frequency Laser Noise Measurement Based on a 3×3 Fiber Coupler. Chin J Lasers (2016) 43(1):0102004. doi:10.3788/cjl201643.0102004

CrossRef Full Text | Google Scholar

70. Tran MA, Huang D, Bowers JE. Tutorial on Narrow Linewidth Tunable Semiconductor Lasers Using Si/III-V Heterogeneous Integration. APL Photon (2019) 4(11):111101. doi:10.1063/1.5124254

CrossRef Full Text | Google Scholar

71. Pollnau M, Eichhorn M. Spectral Coherence, Part I: Passive-Resonator Linewidth, Fundamental Laser Linewidth, and Schawlow-Townes Approximation. Prog Quan Electronics (2020) 72:100255. doi:10.1016/j.pquantelec.2020.100255

CrossRef Full Text | Google Scholar

72. Pollnau M. Phase Aspect in Photon Emission and Absorption. Optica (2018) 5(4):465–74. doi:10.1364/optica.5.000465

CrossRef Full Text | Google Scholar