A Local Search Algorithm for the Influence Maximization Problem

How to select a set of top k nodes (called seeds) in a social network, through which the spread of influence under some certain diffusion models can achieve the maximum, is a major issue considered in the social network analysis. This problem is known as the Influence Maximization Problem (IMP). Due to its NP-hard nature, designing a “good” algorithm for the IMP is a very challengeable work. In this paper, we propose an efficient local search algorithm called DomIM to solve the IMP, which involves two main ideas. The first one is an approach to constructing an initial solution based on a dominating set, while the second is a degree based greedy strategy in the local search phase. DomIM is evaluated on three real world networks, under three widely-used diffusion models, including independent cascade (IC) model, weighted cascade (WC) model, and linear threshold (LT) model. Experimental results show that DomIM is competitive and efficient, and under all of these diffusion models it can obtain the best performance (in terms of solution quality) on the networks we consider.

1 Introduction

A social network is an interconnected structure which consists of a set of socially relevant nodes (e.g., individuals, groups, organizations, or related systems) connected with one or more relations, such as shared ideas, social contacts, financial stock exchanges, and affinities [1,2]. Needless to say, exploring valuable information related to nodes and revealing relations between them are very meaningful and significant. For this, many topics have been introduced to analyze social networks, from a different perspective; please refer to [3,4] for an overview of social network analysis.

One of the most studied problems in the social network analysis is the influence maximization problem (IMP), whose task is to select a set of k nodes from a given social network, called seed set, through which the number of influenced nodes under some certain diffusion model can achieve the maximum. Due to its potential applications in practice, the IMP has attracted wide-spread attention. Especially, in today’s era, with the rapid development in the communication field, the size of social networks is becoming increasingly large. As a consequence, information exchange among users throughout social networks has become an indispensable part in our daily life, and meanwhile a large number of users may be influenced by such information diffusion. So, there is a growing body of literature analyzing the influence and information propagation in social networks [5–8].

The well-known application of the IMP is viral marketing, which aims to exploit the network value of customers, i.e., the potential influence of a customer who may recursively influence his neighbors (e.g., family members, colleagues, friends, friend’s colleagues, friend’s friends, and so on) to buy a product through the “word-of-mouth” propagation [9]. Clearly, a small number of highly influential customers can be specified as potential customers to market to, so that the expected profit can be maximized. Besides viral marketing, there are also many other applications, e.g., analyzing human behavior [10], target advertisement [11], rumor blocking [12], social recommendation [13], etc. Practically, the spread of influence can occur with the aid of some operational models. Three widely-used diffusion models are independent cascade (IC) model, weighted cascade (WC) model, and linear threshold (LT) model, where the WC model is a special case of the IC model [14]; see Section 2 for an detailed discussion of these models.

1.1 Related Works

The IMP in social networks was first studied in 2001 by [9], who regarded it as an algorithm problem. Since then, it has been studied extensively, especially after the work by [14] who proved that the IMP is NP-hard by defining it as a combinatorial optimization problem. Nevertheless, it is still challengeable to solve the IMP, due to the following two difficulties: the first one is how to accurately measure the influence of a given seed set, which has been shown to be ♯P-hard; the second is how to select a seed set with the maximum influence [15,16]. We make an overview of related works on the IMP from the following two aspects: greedy based approaches and heuristic approaches. For more detailed categories on this problem, please see the survey papers [17–19].

1.1.1 Greedy Based Approach

It is widely believed that the initial work using greedy based idea to solve the IMP is attributed to [14], who proposed a simple hill-climbing greedy algorithm to solve the IMP under the IC model and the LT model. Despite the algorithm can get a guarantee that obtains the optimal solution with a high probability (about 63%), it is very time-consuming, because it has to search for the whole network (every node) and implement tens of thousands Monte-Carlo simulations. To optimize the efficiency of the simple greedy algorithm, [20] proposed an improved greedy algorithm with an approximation ratio of $\frac{1}{2}(1-\frac{1}{\mathrm{e}})$, called CELF, which selects influential nodes leveraging the submodular property. They showed that CELF can achieve up to 700 times faster than the simple greedy algorithm. Whereas, CELF has a poor performance in large network since it has to compute the marginal influence spread of each alternative node repeatedly [21]. [22] designed new schemes to optimize the greedy algorithm under the IC model, by which they generated a faster greedy algorithm based on CELF. [23] developed an improved version of CELF, called CELF++, and showed that it is 35–55% faster than CELF. [24] proposed a deprecation based greedy algorithm for the IMP, called DGS. This algorithm first orders the nodes of a social network by applying three heuristic influence functions, and then selects the most influential nodes from a list of pre-ordered vertices. Although DGS takes less time than CELF, it is still time-consuming in large networks. In [25], Heidari et al. proposed a fast greedy algorithm SMG to solve the IMP. By reducing calculations in counting the traversing nodes and Monte-Carlo graph construction, SMG improves the efficiency of greedy algorithms. To deal with the time-consuming drawback of greedy algorithms, [26] proposed a CascadeDiscount algorithm for solving the IMP. The algorithm uses PageRank to measure the initial influence of nodes, measures node’s marginal gain of influence spread by considering the influence loss on their neighbors, and then selects the most influential nodes based on a greedy strategy. [27] proposed a community-based framework for the IMP, which was further improved in [28] by designing an objective function to evaluate the influence spread and then generating an efficient greedy algorithm to find the influential nodes.

A simple greedy algorithm can yield nearly optimal solutions, but it is often time-consuming, which limits its application on large-scale networks. As a useful technique to deal with NP-hard problems, heuristic approaches have been widely used in a variety of problems, such as partition coloring problem [29], network immunization [30], dominating set problem [31], etc. Also, heuristic algorithms for the IMP are proposed sequentially.

1.1.2 Heuristic Approach

To solve the low efficiency of simple greedy algorithms, [22] in 2009 proposed a degree discount heuristics to improve influence spread, by considering the degree discount of a candidate node caused by its seed neighbors. However, compared with greedy algorithms, the algorithm has a poor accuracy, though it reduces the running time. Later on, [32] introduced a heuristic approach called MIP to measure node’s influence from other nodes, by which a heuristic algorithm called PMIA was developed to solve the IMP on large-scale social networks. The drawback of PMIA is that it has to design different thresholds for different networks and there is no uniform method to set the thresholds, which may affect the accuracy of the algorithm. Since then, a large body of heuristic algorithms for the IMP are developed. In 2011, [33] designed a simulated annealing based algorithm for the IMP under the IC model, which integrates two heuristic approaches to optimize the convergence process and a method to speed up the selection of the most influential nodes. [34] proposed a scalable influence approximation algorithm IPA for the IMP under the IC model, which uses an independent influence path to estimate the influence of nodes. For the purpose of bridging the theory and practice in influence maximization, [35] proposed an algorithm called TIM. They showed that TIM runs in $O((k+\ell )(n+m)\log \frac{n}{{\epsilon }^2})$ time and guarantees an approximation ratio of $1-\frac{1}{\mathrm{e}}-\epsilon$ (with at least 1−n^−ℓ probability). By utilizing the genetic approach and the strength greedy algorithm, [36] proposed an efficient algorithm for solving the IMP in social networks. Based on evolutionary methods, [37] introduced a simple genetic algorithm for the IMP. In [38], Kim proposed a Random Walk and Rank Merge based algorithm, which uses a random walk method to speed up the algorithm. [39] analyzed the reason why the greedy approaches have low efficiency and proposed a degree-descending search strategy, based on which they designed an evolutionary algorithm. By eliminating the time-consuming simulations in a greedy algorithm, the efficiency of the algorithm is improved significantly. Recently, [16] proposed a discrete shuffled frog-leaping algorithm for the IMP, which selects influential nodes based on network topology characteristic. In [21], Qin et al. introduced a discount-degree descending technology and lazy-forward technology to identify a set of candidate nodes, based on which they designed a two-stage selection algorithm for the IMP in social networks. [6] proposed a path-based approach, which uses the degree and the independent influence path to estimate the influence spread and uses a heuristic method to reduce the computation volume.

The heuristic algorithms usually have better running time and scalability. But, they cannot provide any performance guarantee.

1.2 Contribution

In this paper, we propose an efficient local search algorithm named DomIM to solve the IMP in social networks. Our contributions mainly include the following three aspects.

(1) We propose a mechanism to construct a high quality initial solution based on dominating set, and an approach to building candidate set.

(2) A degree based greedy strategy is introduced in the local search.

(3) DomIM is evaluated on three real world graphs, under IC model, WC model, and LT model. Compared with four heuristic algorithms, DomIM is competitive and efficient, and obtains the best performance on these graphs.

The remainder of the paper is organized as follows. Section 2 introduces basic definitions, including the influence maximization problem and three diffusion models. Section 3 gives a brief overview of dominating set problem and a heuristic algorithm for finding minimum dominating set that we will quote. Section 4 describes our DomIM algorithm. Section 5 presents experimental results and Section 6 concludes this paper with future work.

2 Preliminaries

To study the IMP, we often abstract a social network as a graph, where the vertex set represents the set of nodes in the social network and edge set represents the social ties among nodes. From now on, we use the term “graphs” to replace “social networks”, and follow the standard terminologies in graph theory.

All graphs considered in this paper are simple undirected graphs. Let G = (V, E) be a graph with vertex set V and edge set E. We use a 2-length string uv to denote an edge connecting two vertices u and v. The two vertices u, v are called endpoints of edge uv. An edge is said to be incident with its two endpoints, and the two endpoints of an edge are said to be adjacent to each other. A vertex is called a neighbor of another vertex, if they are adjacent in G. Given a vertex v ∈ V, the neighborhood of v in G, denoted by N_G(v), is the set of neighbors of v, and let N_G [v] = N_G(v) ∪ {v}. The number of neighbors of v in G (or equally the number of edges incident with v), denoted by d_G(v), is called the degree of v in G. For a set S ⊆ V, we use G [S] to denote the subgraph of G induced by S, i.e., the resulting graph obtained from G by deleting all vertices in V \ S and their incident edges.

2.1 Influence Maximization Problem

Given a graph G = (V, E) and a positive number k, the task of the IMP is to find a set S of k vertices (called seed set) such that the influence spread by S [denoted by σ(S)], i.e., the number of influenced vertices triggered by S, reaches maximum under a given diffusion model. This problem was formulated as an optimization problem by [14], which is shown as follows.

$S^{*}=\arg \underset{S\subseteq V,|S|=k}{\max }\sigma (S)(1)$

In Equation 1, the maximum is taken over all seed sets S and S* is the best one that can maximize the spread of influence.

Now, we describe three widely-adopted diffusion models that we will use for the IMP.

2.2 Independent Cascade Model

As the simplest model of dynamic cascade models, the IC model was first investigated by [40]. In this model, the influence spread, starting with a set of active vertices (seed set), follows a randomized rule: an active vertex can activate its inactive neighbors only when it first becomes active. Specifically, let u be a vertex activated at step t. Then, for each inactive neighbor v ∈ N_G(u), there is a single change for v to be activated by u with probability p_u,v (a parameter independent of all previous attempts to active v). If u succeeds, then v will become active at step t + 1; otherwise, v is still inactive. Note that whether or not v is activated successfully, it cannot be further activated by u at subsequent steps. If at step t, an inactive vertex u has more than one newly activated neighbors, then they can activate u one by one in any order. In this way, the diffusion process stops when no more possible vertices will be activated.

2.3 Weighted Cascade Model

The WC model is a special IC model [14], in which a newly activated vertex u activates its inactive neighbor v with a probability related to the degree of v, i.e., $p_{u,v}=\frac{1}{d_G(v)}$. It is clear to see that a high-degree vertex may be activated by each of its activated neighbors with low probability. In a certain sense, this simulates the actual interpersonal relationships. Consider the case that if a person has only one friend, then suggestions from his unique friend will play a very important role in his decisions. In contrast, if a person has many friends, then suggestions from one of its friends may be less important to his decisions.

2.4 Linear Threshold Model

The LT model is different from the IC model and the WC model, which estimates the spread process by using vertex-specific thresholds [14]. In this model, an inactive vertex v is influenced by each of its active neighbor u with a weight b_v,u, under the limitation of ∑_ub_v,u ≤ 1, where u is taken over all active neighbors of v. Indeed, this limitation has its own significance, since the probability that u can be activated is at most one.

The dynamic process can be described as follows. We preassign randomly a threshold θ_v ∈ [0, 1] to each vertex v. Then, start with a seed set as an initial set of active vertices; in sept t ( ≥2), each active vertex in step t−1 (t ≥ 2) is still active and an inactive vertex v is activated successfully if the total weight of its active neighbors is at least θ_v, i.e.,

$\sum _{u\in N_G(v)isactiveatstept}{b}_{v,u}\ge {\theta }_v.$

It is intuitive that the thresholds of vertices represent the distinct potential tendencies of vertices to become active. Due to the lack of knowledge, we assign the same threshold to all vertices in the experiment.

3 Dominating Set

A dominating set of a given graph G = (V, E) is a subset S of vertices such that V \ S ⊆ N_G(S), where N_G(S) = {v|v has a neighbor in S}. The minimum dominating set problem (MDS) aims to find a dominating set with the minimum cardinality. The MDS is a classic NP-hard problem, which has been widely studied in both theoretical and application aspects [41,42], especially for designing efficient approximation algorithms [43,44]. Given that vertices in a dominating set may have some important properties, we have reason to believe that vertices from a (minimum) dominating set can have high influence. So, we can construct an initial solution based on a dominating set of a given social network.

In our algorithm DomIM which will be presented in the subsequent section, an algorithm finding a minimum dominating set will be used. We quote such an algorithm called ScBppw proposed by [31]. Here we present the local search framework of ScBppw for the reader’s convenience.

ALGORITHM 1

Algorithm 1. ScBppw [31].

Notice that Algorithm 1 integrates two sub-procedures, InitDS and ExchangeVertices, where InitDS is a simple greedy strategy to generate an initial solution and ExchangeVertices is an exchanging procedure based on a proposed tabu strategy. For more information about this algorithm, please refer to paper [31].

4 The DomIM Algorithm

We develop a local search algorithm for IMP named DomIM (Algorithm 2), which is based on dominating set and a degree-related rule for selecting vertices.

In the beginning, the algorithm finds a minimum dominating set, by which an initial solution will be constructed. Considering that the MDS problem is NP-hard, we adopt a fast heuristic algorithm (Algorithm 1) to approximatively find a minimum dominating set of the input graph (line 2). A key concept of our algorithm is the uncorrelated degree.

Definition 1. Let S be a subset of vertices in a graph G = (V, E), and v ∈ V be an arbitrary vertex. The S-uncorrelated neighborhood of v, denoted by $N_{\bar{S}}(v)$, is defined as the set of vertices in V \ S that are adjacent to v in G, and the S-uncorrelated degree of v is the cardinality of $N_{\bar{S}}(v)$, denoted by $d_{\bar{S}}(v)$, i.e., $d_{\bar{S}}(v)$ = $|N_{\bar{S}}(v)|$.For a fixed set S, the vertices with the maximum S-uncorrelated degree may have higher influence in some sense, since it can influence more vertices directly when vertices in S are not considered. This observation is used to construct an initial solution and design an approach to improving solutions by exchanging vertices.The algorithm utilizes a greedy strategy (related to the uncorrelated degree) based on dominating set to construct an initial solution. Notice that when the dominating set D contains less than k vertices, the algorithm selects k−|D| vertices from V \ D (according to the S-uncorrelated degree from large to small) to generate an initial solution by adding them into D (lines 3–5); otherwise, the algorithm chooses top k vertices from D in terms of the uncorrelated degrees (as large as possible) as an initial solution (line 7).After the construction of an initial solution S, the algorithm computes the minimum S-correlated degree of vertices in S, according to which a candidate set T is constructed for the local search phase (Line 9). Note that T may be not large enough to improve the current solution S by exchanging vertices repeatedly between T and S; if this happens, i.e., |T| < α|V|, the algorithm selects ⌊α|V|⌋ − |T| vertices from V \ (S ∪ T) with S-uncorrelated degree as high as possible and adds them to T, where α is a real number in the interval (0,1) related to the value of |V| and the type of the diffusion model (lines 10–12).

ALGORITHM 2

Algorithm 2. DomIM

Subsequently, a loop (lines 13–24) is executed until a given termination condition is reached. DomIM returns the best found seed set S* (line 25). In each iteration of the loop, a local search process is executed to exchange vertices between the current solution S and the candidate set T for improving the current solution (starting with the initial solution). Specifically, the algorithm chooses a vertex u ∈ S with the minimum S-uncorrelated degree (randomly select one when there is more than one vertices with the minimum value). Note that it is possible that u is not be selected for the first time; if so, u is reselected randomly (lines 15–16). Then, remove u from S, and select a vertex v from T randomly (for the diversity) and add it to S (lines 17–18). If the exchanging can produce more influence, then it is viewed as a valid process, and update S* by S and T by T ∪ {u} (for the diversity of solutions) (lines 19–21); otherwise, S is back to the previous state (lines 22–24).

5 Experiments

We evaluate DomIM on three real world (undirected) networks under the three diffusion models mentioned in Section 2, i.e., the LT model, the IC model, and the WC model. The data come from two databases: Network Repository¹ and SNAP (Stanford Large Network Dataset Collection)².

ia-email-univ (IEU) [45]: This network is from Network Repository, which is an email communication network at the University Rovira i Virgili in Tarragona in the south of Catalonia in Spain. There are in total 1,133 vertices and 5,451 edges. Each vertex represents a user and an edge connecting two users indicates that one sent at least one email to another.

soc-wiki-Vote (SWV) [45]: This network is also from Network Repository, which involves all the Wikipedia voting data from the inception of Wikipedia till January 2008. This graph contains 889 vertices and 2,914 edges, where vertices represent Wikipedia users and a direct edge from vertex i to vertex j represents that user i vote on user j. In our experiment, we consider only the underlying undirected graph of this graph.

feather-lastfm-social (FLS) [46]: This is a social network of LastFM users which was collected from the public API in March 2020. This graph is from SNAP, consisting of 7,624 vertices and 27,806 edges, where vertices represent LastFM users from Asian countries and edges are mutual follower relationships between them.

5.1 Experiment Setup

DomIM is implemented in C++ and complied by g++ 8.2.0. All experiments are run on a computer with Intel i7-8565U 1.80 GHz with 16 GB RAM under Windows 10.

We compare the overall performances of DomIM with four heuristic algorithms, including Degree [14], Random [14], CELFGreedy [20], and TreeCore [47]. Degree is a simple algorithm that selects high-degree vertices. Random chooses vertices randomly. CELFGreedy is a greedy algorithm with lazy-forward optimization, in which for each candidate seed set, it executes 10,000 simulations to obtain an accurate estimation of influence spread. Therefore, CELFGreedy is time-consuming. TreeCore is an approach based on a network connectivity parameter called tree coritivity.

For each instance, all algorithms are executed 3 times with seed set size from 1 to 50, from which we select the best solutions for each situation. The time limit of each run is at most 90 s, which is dependent on the size of networks.

5.2 Results on Real World Social Networks

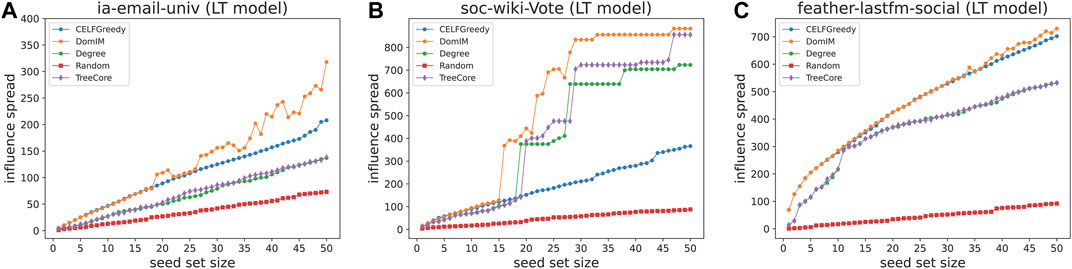
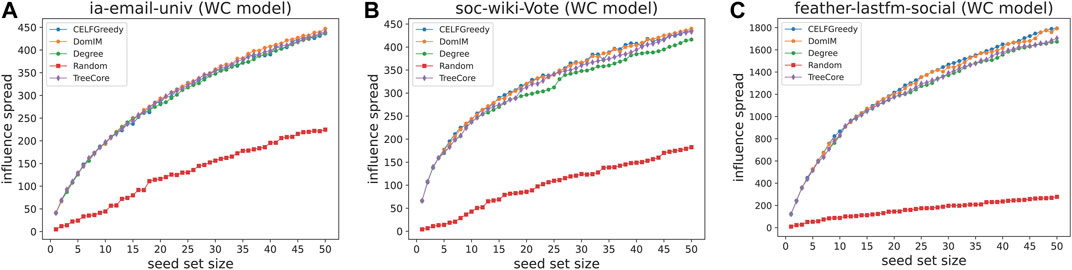
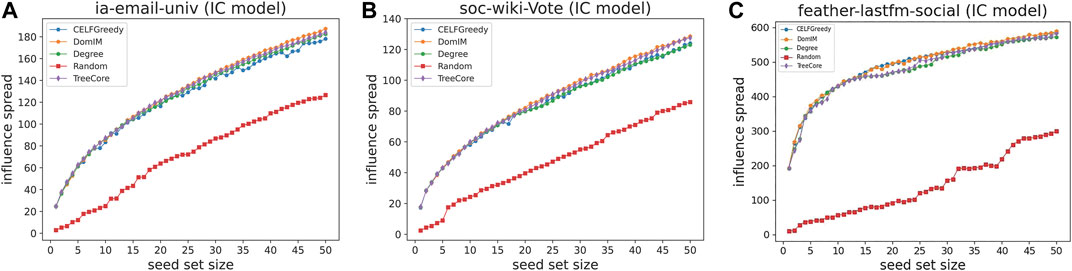
Experimental results under the three diffusion models are shown in three groups of figures (Figures 1–3), where each group contains three figures corresponding to the results on the three networks we consider, respectively [1) for the IEU network, 2) for the SWV network, and 3) for the FLS network]. In each figure, the x-axis represents the size of seed set (denoted by seed set size which is from 1 to 50) and the y-axis represents the number of all vertices that are activated at the end of the diffusion process (denoted by influence spread). Each figure depicts the results obtained by five different algorithms (represented by distinct colors), where CELFGreedy, Degree, Random, and TreeCore are the four approaches mentioned above, and DomIM is our algorithm.

FIGURE 1

FIGURE 1. Results of influence spread under LT model.

FIGURE 3

FIGURE 3. Results of influence spread under WC model.

5.2.1 Results Under the LT Model

Under the LT model, all vertices are assigned to the same threshold 0.5 in the experiment, and we assume that an inactive vertex v is influenced by each of its neighbor u with the same weight $b_{v,u}=\frac{1}{d_G(v)}$. In Figure 1 (a), α is set to 0.1 and cutoff is 10 s; in Figure 1 (b), α is set to 0.05 and cutoff is 15 s; and in Figure 1 (c), α is set to 0.06 and cutoff is 50 s.

In each figure, the trend of influence spread is on the rise as the seed set size increases, although some exceptions may occur due to the random selection in the local search phase. Of all these approaches, Random did worst on these instances. And the reason is simple because Random does not consider any network properties and does not use any strategy to improve the solution. We use Random here just for the sake of comparison. As a whole, our algorithm DomIM preforms the best in terms of solution quality, but Degree and TreeCore are worse on the IEU instance and CELF is worse on the SWV instance. In particular, for the IEU and SWV instances, DomIM is essentially better than the other algorithms. For the FLS instance, CELFGreedy performs slightly worse than DomIM, but Degree and TreeCore are worse.

5.2.2 Results Under IC Model

Under the IC model, for every two adjacent vertices u and v such that u is an active vertex and v is an inactive vertex, the probability p_u,v that v is activated by u is set to the same value 0.05 (this is based on the consideration that the networks we use are sparse). In Figure 2 (a), α is set to 0.01 and cutoff is 10 s; in Figure 1 (b), α is set to 0.01 and cutoff is 20 s; and in Figure 1 (c), α is set to 0.0015 and cutoff is 20 s.

FIGURE 2

FIGURE 2. Results of influence spread under IC model.

As shown in Figure 2, all of these algorithms (except for Random) can obtain a better influence spread, and they have a very similar performance on all the three instances. Our algorithm DomIM slightly outperforms Degree, TreeCore, and CELFGreedy (especially when the size of seed set increases), and TreeCore and CELFGreedy perform very closely to DomIM. Note that the result obtained by the simple approach Degree is also not bad. The reason is because the diffusion probability is not so large, which limits the propagation depth of an active vertex. So, vertices with high-degree may influence much more neighbors. This shows that selecting high-degree vertices as seed set is possible to produce a good influence spread for this case.

5.2.3 Results Under WCM

For the WC model, in Figure 3 (a), α is set to 0.01 and cutoff is 20 s; in Figure 1 (b), α is set to 0.01 and cutoff is 20 s; and in Figure 1 (c), α is set to 0.0065 and cutoff is 90 s.

As shown in Figure 3, all algorithms (except for Random) can achieve a similar influence spread. For the IEU instance, DomIM has the best performance under almost all cases (in terms of the seed set size); For the SWV and FLS instances, DomIM and CELFGreedy are better than other algorithms, and they have a similar performance. However, DomIM is efficient, while CELFGreedy is inefficient which will take a long time to obtain a better solution.

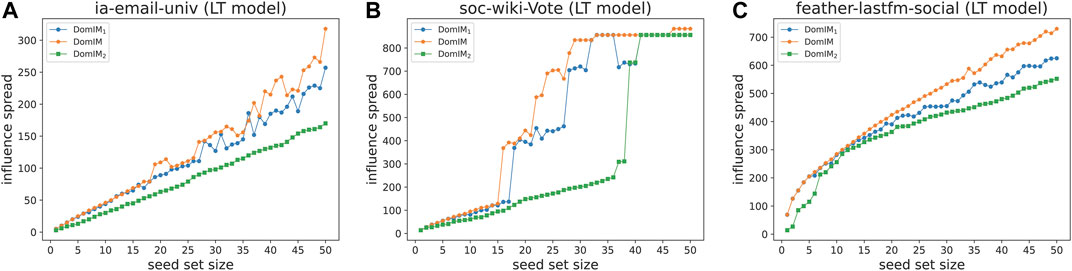
5.3 Analysis of Underlying Strategies

We also study the effectiveness of the key strategies of our algorithm. We modify DomIM to obtain two alternative approaches, denoted by DomIM₁ and DomIM₂, where DomIM₁ uses standard degree to replace the uncorrelated degree and DomIM₂ removes the local search procedure on the basis of DomIM.

The comparison experiment of DomIM and its alternatives on the three real-world instances is implemented under the LT model, and the results are presented in Figure 4, from which we see that DomIM is better than DomIM₁ and DomIM₂. This implies that these two strategies play an important role in our algorithm DomIM.

FIGURE 4

FIGURE 4. Comparison results between DomIM and its alternatives under LC model.

6 Conclusion

We proposed a local search algorithm DomIM for the IMP. Compared with four distinct types of algorithms, DomIM is efficient and robust, and obtains the best performance for all graphs and all diffusion models we use. However, for the purpose of obtaining an improved solution in the local search phase, our algorithm has to compute the influence of a newly constructed seed set in each iteration. This may slightly effect the efficiency of DomIM. We would like to consider this issue in our future work.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

EZ performed the measurements, analyzed the results, and wrote the paper. LY: performed the experiments and analyzed the results. YX: analyzed the results and refined our manuscript.

Funding

This work was supported in part by National Natural Science Foundation of China under Grant 61872101; in part by Natural Science Foundation of Guangdong Province of China under Grant 2021A1515011940.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹http://networkrepository.com

²https://snap.stanford.edu/data/feather-lastfm-social.html

References

1. Scott J, Carrington PJ. The SAGE Handbook of Social Network Analysis. 1st ed. London: Sage Publications Ltd (2011).

Google Scholar

2. Can U, Alatas B. A New Direction in Social Network Analysis: Online Social Network Analysis Problems and Applications. Physica A (2019) 355:122372. doi:10.1016/j.physa.2019.122372

CrossRef Full Text | Google Scholar

3. Tabassum S, Pereira FSF, Fernandes S, Gama J. Social Network Analysis: An Overview. WIREs Data Mining Knowledge Discov (2018) 8:e1256. doi:10.1002/widm.1256

CrossRef Full Text | Google Scholar

4. Han W, Tian Z, Huang Z, Li S, jia Y. Topic Representation Model Based on Microblogging Behavior Analysis. World Wide Web (2020) 23:11–2. doi:10.1007/s11280-020-00822-x

CrossRef Full Text | Google Scholar

5. Tong G, Wu W, Tang S, Du D-Z. Adaptive Influence Maximization in Dynamic Social Networks. IEEE/ACM Trans Networing (2017) 25:112–25. doi:10.1109/tnet.2016.2563397

CrossRef Full Text | Google Scholar

6. Kianian S, Rostamnia M. An Efficient Path-Based Approach for Influence Maximization in Social Networks. Expert Syst Appl (2021) 167:114168. doi:10.1016/j.eswa.2020.114168

CrossRef Full Text | Google Scholar

7. Li S, Jiang L, Wu X, Han W, Zhao D, Wang Z. A Weighted Network Community Detection Algorithm Based on Deep Learning. Appl Maths Comput (2021) 401:126012. doi:10.1016/j.amc.2021.126012

CrossRef Full Text | Google Scholar

8. Centola D. The Spread of Behavior in an Online Social Network experiment. Science (2010) 329:1194–7. doi:10.1126/science.1185231

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Domingos P, Richardson M. Mining the Network Value of Customers. In: Proceedings of the Seventh ACM SIGKDD international Conference on Knowledge Discovery and Data Mining; 2001 August 26–29; San Francisco, CA (2001) p. 57–66. doi:10.1145/502512.502525

CrossRef Full Text | Google Scholar

10. Bond RM, Fariss CJ, Jones JJ, Kramer ADI, Marlow C, Settle JE, et al. A 61-Million-Person experiment in Social Influence and Political Mobilization. Nature (2012) 489:295–8. doi:10.1038/nature11421

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Li Y, Zhang D, Tan K-L. Real-time Targeted Influence Maximization for Online Advertisements. Proc VLDB Endowment (2015) 8:1070–81. doi:10.14778/2794367.2794376

CrossRef Full Text | Google Scholar

12. Fan L, Lu Z, Wu W, Thuraisingham B, Ma H, Bi Y. Least Cost Rumor Blocking in Social Networks. In: Proceeding of the 2013 IEEE 33rd International Conference on Distributed Computing Systems; 2013 July 8–11; Philadelphia, PA. IEEE (2015). p. 540–9.

Google Scholar

13. Ye M, Liu X, Lee W-C. Exploring Social Influence for Recommendation-A Generative Model Approach. In: 35th International ACM SIGIR conference on research and development in information retrieval; 2012 August 12–16; Portland, OR. New York: ACM Press (2012). p. 671–80.

Google Scholar

14. Kempe D, Kleinberg J, Tardos É. Maximizing the Spread of Influence through a Social Network. In: Proceedings of the 9th ACM SIGKDD international Conference on Knowledge Discovery Data Mining; 2003 August 24–27; Washington, DC. Washington: ACM Press (2003) p. 137–46. doi:10.1145/956750.956769

CrossRef Full Text | Google Scholar

15. Lee JR, Chung CW. A Query Approach for Influence Maximization on Specific Users in Social Networks. IEEE Trans Knowledge Data Eng (2015) 27:340–53. doi:10.1109/tkde.2014.2330833

CrossRef Full Text | Google Scholar

16. Tang J, Zhang R, Wang P, Zhao Z, Fan L, Liu X. A Discrete Shuffled Frog-Leaping Algorithm to Identify Influential Nodes for Influence Maximization in Social Networks. Knowledge-Based Syst (2020) 187:104833. doi:10.1016/j.knosys.2019.07.004

CrossRef Full Text | Google Scholar

17. Banerjee S, Jenamani M, Pratihar DK. A Survey on Influence Maximization in a Social Network. Knowl Inf Syst (2020) 62:3417–55. doi:10.1007/s10115-020-01461-4

CrossRef Full Text | Google Scholar

18. Li Y, Fan J, Wang Y, Tan K-L. Influence Maximization on Social Graphs: A Survey. IEEE Trans Knowledge Data Eng (2018) 30:1852–72. doi:10.1109/tkde.2018.2807843

CrossRef Full Text | Google Scholar

19. Peng S, Zhou Y, Cao L, Yu S, Niu J, Jia W. Influence Analysis in Social Networks: a Survey. J Netw Comput Appl (2018) 106:17–32. doi:10.1016/j.jnca.2018.01.005

CrossRef Full Text | Google Scholar

20. Leskovec J, Krause A, Guestrin C, Faloutsos C, VanBriesen J, Glance N. Cost-effective Outbreak Detection in Networks. In: Proceedings of the 13th ACM SIGKDD international Conference on Knowledge Discovery Data Mining; 2007 August 12–15; San Jose, CA. San Jose: ACM Press (2007) p. 420–9. doi:10.1145/1281192.1281239

CrossRef Full Text | Google Scholar

21. Qiu L, Gu C, Zhang S, Tian X, Zhang M. Tsim: A Two-Stage Selection Algorithm for Influence Maximization in Social Networks. IEEE Access (2020) 8:12084–95. doi:10.1109/access.2019.2963100

CrossRef Full Text | Google Scholar

22. Chen W, Wang Y, Yang S. Efficient Influence Maximization in Social Networks. In: Proceedings of the 15th ACM SIGKDD international Conference on Knowledge Discovery Data Mining; 2009 June 28–July 1; Paris, France. Pairs: ACM Press (2009) p. 199–208. doi:10.1145/1557019.1557047

CrossRef Full Text | Google Scholar

23. Goyal A, Lu W, Lakshmanan L. Celf++: Optimizing the Greedy Algorithm for Influence Maximization in Social Networks. In: Proceedings of the 20th International Conference on World Wide Web, WWW 2011; March 28-April 1, 2011; Hyderabad, India (2011). Companion Volume.

Google Scholar

24. Kundu S, Pal S. Deprecation Based Greedy Strategy for Target Set Selection in Large Scale Social Networks. Inf Sci (2015) 316:107–22. doi:10.1016/j.ins.2015.04.024

CrossRef Full Text | Google Scholar

25. Heidari M, Asadpour M, Faili H. Smg: Fast Scalable Greedy Algorithm for Influence Maximization in Social Networks. Physica A (2015) 420:124–33. doi:10.1016/j.physa.2014.10.088

CrossRef Full Text | Google Scholar

26. Lu F, Zhang W, Shao L, Jiang X, Xu P, Jin H. Scalable Influence Maximization under Independent cascade Model. J Netw Comput Appl (2016) 86:15–23. doi:10.1016/j.jnca.2016.10.020

CrossRef Full Text | Google Scholar

27. Shang J, Zhou S, Li X, Liu L, Wu H. Cofim: A Community-Based Framework for Influence Maximization on Large-Scale Networks. Knowledge-Based Syst (2016) 117:88–100. doi:10.1016/j.knosys.2016.09.029

CrossRef Full Text | Google Scholar

28. Wu H, Shang J, Zhou S, Zhong J, Yong F, Qiang B. Impc: Influence Maximization Based on Multi-Neighbor Potential in Community Networks. Physica A. (2018) 512:1085–103. doi:10.1016/j.physa.2018.08.045

CrossRef Full Text | Google Scholar

29. Zhu E, Jiang F, Liu C, Xu J (2020). Partition Independent Set and Reduction-Based Approach for Partition Coloring Problem. IEEE Trans Cybernetics. 1–10. doi:10.1109/TCYB.2020.3025819

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Li S, Zhao D, Wu X, Tian Z, Li A, Wang Z. Functional Immunization of Networks Based on Message Passing. Appl Maths Comput (2020) 366:124728. doi:10.1016/j.amc.2019.124728

CrossRef Full Text | Google Scholar

31. Fan Y, Lai Y, Li C, Li N, Zongjie M, et al. Efficient Local Search for Minimum Dominating Sets in Large Graphs. In: 24th International Conference on Database Systems for Advanced Applications; 2019 April 22–25; Chiang Mai, Thailand (2019) p. 211–28. doi:10.1007/978-3-030-18579-4_13

CrossRef Full Text | Google Scholar

32. Chen W, Wang C, Wang Y. Scalable Influence Maximization for Prevalent Viral Marketing in Large-Scale Social Networks. In: Proceedings of the 16th ACM SIGKDD international Conference on Knowledge Discovery Data Mining; 2010 July 25–28; Washington, DC. Washington: ACM Press (2010) p. 1029–38. doi:10.1145/1835804.1835934

CrossRef Full Text | Google Scholar

33. Jiang Q, Song G, Cong G, Wang Y, Si W, Xie K. Simulated Annealing Based Influence Maximization in Social Networks. In: Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence; 2011 August 7–11; San Francisco, CA. San Francisco: AAAI Press (2011). p. 127–32.

Google Scholar

34. Kim J, Kim S-K, Yu H. Scalable and Parallelizable Processing of Influence Maximization for Large-Scale Social Networks? In: Data Engineering (ICDE), 2013 IEEE 29th International Conference on; 2013 April 8–12; Brisbane, QLD (2013). p. 266–77.

Google Scholar

35. Tang Y, Xiao X, Shi Y. Influence Maximization: Near-Optimal Time Complexity Meets Practical Efficiency. In: SIGMOD’14: Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data; 2014 June 22–27; Snowbird, UT. New York; ACM Press (2014). p. 75–86.

Google Scholar

36. Tsai C-W, Yang Y-C, Chiang M-C. A Genetic Newgreedy Algorithm for Influence Maximization in Social Network. In: 2015 IEEE International Conference on Systems, Man, and Cybernetics; 2015 October 9–12; Hong Kong, China. IEEE Press (2015) p. 2549–54. doi:10.1109/smc.2015.446

CrossRef Full Text | Google Scholar

37. Bucur D, Lacca G. Influence Maximization in Social Networks with Genetic Algorithms. In: 19th European Conference on the Applications of Evolutionary Computation; 2016 March 30–April 1; Porto, Portugal. Springer (2016). p. 379–92. doi:10.1007/978-3-319-31204-0_25

CrossRef Full Text | Google Scholar

38. Kim S, Kim D, Oh J, Hwang J-H, Han W-S, Chen W, et al. Scalable and Parallelizable Influence Maximization with Random Walk Ranking and Rank Merge Pruning. Inf Sci (2017) 415:171–89. doi:10.1016/j.ins.2017.06.018

CrossRef Full Text | Google Scholar

39. Cui L, Hu H, Yu S, Yan Q, Ming Z, Wen Z, et al. Ddse: A Novel Evolutionary Algorithm Based on Degree-Descending Search Strategy for Influence Maximization in Social Networks. J Netw Comput Appl (2018) 103:119–30. doi:10.1016/j.jnca.2017.12.003

CrossRef Full Text | Google Scholar

40. Goldenberg J, Libai B, Muller E. Talk of the Network: A Complex Systems Look at the Underlying Process of Word-Of-Mouth. Marketing Lett (2001) 12:211–23. doi:10.1023/a:1011122126881

CrossRef Full Text | Google Scholar

41. Liu C. A Note on Domination Number in Maximal Outerplanar Graphs. Discrete Appl Maths (2021) 293:90–4. doi:10.1016/j.dam.2021.01.021

CrossRef Full Text | Google Scholar

42. Wuchty S. Controllability in Protein Interaction Networks. Pnas (2014) 111:7156–60. doi:10.1073/pnas.1311231111

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Wang Y, Cai S, Chen J, Yin M. A Fast Local Search Algorithm for Minimum Weight Dominating Set Problem on Massive Graphs. In: Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18); 2018 July 13–19; Stockholm, Sweden (2018) p. 1514–22. doi:10.24963/ijcai.2018/210

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Cai S, Hou W, Wang Y, Luo C, Lin Q. Two-goal Local Search and Inference Rules for Minimum Dominating Set. In: Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence (IJCAI-20); 2021 January 7–15; Yokohama, Japan (2020) p. 1467–73. doi:10.24963/ijcai.2020/204

CrossRef Full Text | Google Scholar

45. Rossi RA, Ahmed NK. The Network Data Repository with Interactive Graph Analytics and Visualization. In: Proceedings of the 29th AAAI Conference on Artificial Intelligence; 2015 January 25–30; Austin, TX (2015).

Google Scholar

46. Rozemberczki B, Sarkar R. Characteristic Functions on Graphs: Birds of a Feather, from Statistical Descriptors to Parametric Models. In: Proceedings of the 29th ACM International Conference on Information and Knowledge Management (CIKM’ 20) (ACM); 2020 October 19–23 (2020) p. 1325–34. doi:10.1145/3340531.3411866

CrossRef Full Text | Google Scholar

47. Zhu E, Wu Y, Xu Y, Niu Y. Tree-coritivity-based Influence Maximization in Social Networks. Acta Electronica Sinica (2019) 47:161–8. doi:10.3969/j.issn.0372-2112.2019.01.021

CrossRef Full Text | Google Scholar