Effect of Space Fractional Parameter on Nonlinear Ion Acoustic Shock Wave Excitation in an Unmagnetized Relativistic Plasma

In this work, the model equation with space fractional-order (FO) is used to investigate the nonlinear ion acoustic shock wave excitations (NIASWEs) in an unmagnetized collisionless weakly relativistic plasma having inertial relativistic ions fluid with viscous effects, inertial-less non-thermal electrons and inertial-less Boltzmann positrons. To do it, the Korteweg-de Vries Burgers equation (KdVBE) is derived from the considered fluid model equations by implementing the standard reductive perturbation method. Accordingly, such equation is converted to space fractional KdVBE via Agrawal’s variational principle with the help of the beta fractional derivative and its properties. The exact analytical solutions of KdVBE with space FO are determined via the modified Kudryashov method. The influence of space fractional and other related plasma parameters on NIASWEs are investigated. The outcomes would be useful to understand the nature of shocks with the presence of non-local or local space in many astrophysical and space environments (especially in the relativistic wind of pulsar magnetosphere, polar regions of neutron stars, etc.) and further laboratory verification.

Introduction

It is well established that the relativistic electron-positron-ion (REPI) plasmas are not only existed in the evolution of the early Universe [1, 2] but also in many astrophysical and space environments (ASEs), especially in the relativistic wind of pulsar magnetosphere [3], polar regions of neutron stars [4], pulsar magnetospheres [5], inner regions of the accretion disks surrounding the central black holes [6], active galactic nuclei [7], the center of the Milky Way galaxy [8], laser–plasma interaction [9, 10], and so on. The production of electron-positron pair along with massive ions is confirmed in peculiar ASEs by Advanced Satellite for Cosmology and Astrophysics. When the oscillatory electron exceeds an energy of 2m_oc², the electron-positron pair along with the positive ions is also produced in such environments. Most of the physical issues in such plasmas are still not possible to examine in laboratories. But, it may easily describe by the tedious mathematical techniques [11–21]. On the other hand, the shock wave excitation (SWE) is one of the most credible structures based on the outward propagating in various ASEs. For instance, a shock wave is basically produced in some pulsar and magneto-sphere due to the relativistically spreading pulsar wind hits the sub-relativistically moving ejecta. REPI plasmas are also produced into radiation in gamma-ray bursts with the presence of relativistic kinetic energies with their arbitrary concentrations. In such a situation, the framework plasma with relativistic flows is produced the SWEs and pulsar wind nebulae due to the interactions of relativistic shells. Some of the basic features of physical scenarios in such plasmas have reported experimentally by a few authors [22, 23]. But, their growth rate mechanism is still now unfamiliar due to the limitation of laboratory studies. SWEs with the presence of heavy elements in the REPI plasmas have already reported theoretically by Atteya et al. [24], Hafez et. al [13, 16, 25, 26]. and Pakzad and Tribeche [27]. They have mentioned that SWEs are produced in such plasmas. Actually, SWEs are not generally occurred within the fluid description in collisionless regimes since the dissipative effects cannot be rationalized by the state of macroscopic change. But, it is possible to examine SWEs with the presence of kinetic influence at the shock front. Because, the kinetic influences are only responsible to examine an effective dissipation in such environments. Indeed, SWEs can be studied by balancing between nonlinear and dissipative terms that are involved in the nonlinear evolution equations (NLEEs). Basically, the electrostatic SWEs are exited in the collisionless unmagnetized plasmas when an electrostatic potential has only mediated at the discontinuity. At this stage, the dissipation mechanism is relied on the reflection of part of the ion population and trapping part of the electron population entering the shock front.

Further, NLEEs are widely applicable for understanding the formation of wave structures not only in plasma physics but also in water wave theories, optics, fluid dynamics, etc. Many kinds of NLEEs have already derived from the considered model equations by taking distinct ASEs into account [11–20, 25–27]. In all previous studies [16, 18, 24–27], the authors have reported the influence of plasma parameters on nonlinear ion acoustic shock wave excitations (NIASWEs) in the relativistic plasmas by deriving NLEEs of integer order for the case of the locality and conservative energies of plasma particles. They have reported that the structure of shock waves is strongly dependent on the temperature, relativistic streaming factor, density and viscosity coefficient of charged particles. Hafez et al. [25] have reported the oblique NIASWEs in REPI plasmas having nonthermal electrons and positrons with relativistic ions fluid by forming Korteweg-de Vries Burgers (KdVB) equation. Pakzad and Tribeche [27] have reported the propagation of NIASWEs in a dissipative relativistic plasma. Due to the complexity arises in a certain regimes of space or time for the impact of non-locality as well as non-conservative energies of plasma particles in such plasmas, it is sometimes not possible to examine the basic features of wave phenomena by deriving only integer order NLEEs. At these stages, NLEEs of fractional-order (FO) are only an arena to examine the physical issues in such plasmas. It is now fast-growing attention to the research community that fractional calculus has its huge applicability to study complex physical behavior in a diverse field of science and engineering. In another point of view, not only the model involving fractional-order derivatives (FDs) but also FO NLEEs abstracted from many physical problems [28–31] are applicable with the presence of any situations that arise in many branches of modern physics. The FO NLEEs, when compared to the integer order NLEEs, can more accurately explain the dynamic response of the actual system, boost dynamic system performance, and solve practical difficulties. It is important to note that NLEEs of FO are not only applicable with the presence of locality or non–locality but also the conservative or non–conservative system to study the wave propagation in ASEs. Recently, Atangana et al. [32] have provided the useful definition of beta FD for studying both of nonlocal and local behaviors in the physical system as

${}_0{}^{A}D_Z^{\beta }F\left(Z\right)=\underset{\mathrm{\Delta }Z\to 0}{\lim }\frac{F\left(Z+\mathrm{\Delta }Z{\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{1-\beta }\right)-F\left(Z\right)}{\mathrm{\Delta }Z},$

where one can use 0 < β < 1 and β = 1 as a nonlocal (fractional-order) and local (integer order) operator, respectively. They have also provided that the beta FD is followed all the entire fundamental properties of calculus, whereas some of other fractional derivatives, especially Riemann–Liouville FD doesn’t follow all the entire fundamental properties of calculus. Besides, researchers have devoted their effort to derive only NLEEs of integer order from the considered model equations for distinct ASEs. It is therefore necessary to derive the NLEEs of FO for investigating the basic features of wave dynamics in the plasmas for both cases of locality or non–locality.

Due to the importance of FDs, a few researchers [33–39] have concentrated their considerable momentous effort to study the nonlinear complex wave phenomena that may exists for a certain regimes of space or time in some plasma environments by deriving time or space or time-space fractional NLEEs. For instance, Liu and Chen [34] have studied the effects of fractional parameter along with the other plasma parameters on the propagation of electrostatic wave potential in ultra–relativistic plasmas by deriving (2 + 1) dimensional time-space fractional cylindrical Kadomtsev–Petviashvili equation and cylindrical-modified Kadomtsev–Petviashvili equation. Nazari-Golshan [36, 37] have investigated the wave propagation described by the space fractional modified Korteweg-de Vries equation and the time fractional Schamel equation for different plasma situations. Very recently, Nazari-Golshan [35] have investigated the SWEs in REPI plasmas dy deriving sapce fractional Korteweg-de Vries Burgers equation (KdVBE). In the aforementioned literatures, researchers have considered the Riemann–Liouville FD as a nonlocal operator. But, no one has been derived the NLEE involving beta FD and its useful solutions for studying the nature of nonlocal wave structures in the plasmas to best of our knowledge. Thus, the work explores the mathematical formation of space fractional KdVBE by using beta FD for examining the effect of nonlocal along with other plasma parameters on NISAWs in the REPI plasmas. Such plasma is composed of nonthermal distributed electrons, Boltzmann distributed positrons and the speed of ions fluid having kinematic viscosity effect is comparable to speed of light. The space fractional KdVBE is derived by forming Euler-Lagrange equation via Agrawal method [40, 41]. This work is also focused the modified Kudryashov method (MKM) [28, 42] for obtaining the analytical solutions of space fractional KdVBE.

Mathematical Model Equations

It is confirmed that electrons having sufficient energies and higher density than positrons are existed in many ASEs by Freja and Viking satellites [43, 44]. Besides, Yu and Luo [45] have reported that the plasma species are actually occurred in different regions of phase space with different temperatures for constructing quasi-stationary nonlinear structures in the plasmas. However, electrons can interact with IAWs during its evolution, and then be trapped. Guo et al. [46] have already reported that the trapped electrons produce the pattern of phase space hole, where the trapped electrons are not followed the Maxwellian distribution. Bettega et al. [47] have also experimentally shown that the growth rate of ion resonance diocotron instability are increased exponentially with the trapped electrons kinetic energy. In addition, the positrons having much higher temperature cannot be trapped by the wave and they stay free. In such situations, one can assume the nonthermal distributed electrons [48] and Boltzmann distributed positrons. Further, the hot electron-positron pairs are mainly produced in most of the astrophysical and cosmic plasmas, but the minority cold electrons and heavy ions are likely to be present, as observed in the outflows of electron-positron plasmas from the pulsars entering into interstellar colds. Besides, the ion kinematic viscosity for collsionless plasmas is widely applicable in many environments, particularly in pulsar wind, solar wind, etc. because it is dependent on the ion temperature, ion gyrofrequency, ion-ion collision time, and ion mass. Indeed, it is only responsible for the dissipative characteristics of the plasma under assumption. Very recently, Hafez [21] has been reported the electrostatic shock wave structures in an unmagnetized collisonless plasmas by composing of the generalized distributed electrons, Boltzmann distributed positrons and relativistic ions fluid having kinetic viscous effects. Hence, an unmagnetized relativistic plasma system having inertial relativistic ions fluid having viscous effects, inertial-less non-thermal electrons and inertial-less Boltzmann positrons is considered based on N_e0 = N_i0 + N_p0, where N_y0, y = e, i and p are respectively the unperturbed concentrations of electrons, positrons and ions. The continuity and momentum equations are obtained [26, 35] to study the nonlinear dynamics of propagating IAWs in such plasmas, as

$\frac{\partial N_i}{\partial t}+\frac{\partial }{\partial x}(N_i{V}_i)=0,(1)$

$\left(\frac{\partial }{\partial t}+V_i\frac{\partial }{\partial x}\right)\left(V_i{\gamma }_i\right)+\frac{\partial \mathrm{\Phi }}{\partial x}={\rho }_i\frac{{\partial }^2{V}_i}{\partial x^2},(2)$

The aforementioned plasma is bounded via the following Poisson’s equation:

$\frac{{\partial }^2\mathrm{\Phi }}{\partial x^2}={\gamma }_e\left(1-\frac{4{\alpha }_e}{1+3{\alpha }_e}\mathrm{\Phi }+\frac{4{\alpha }_e}{1+3{\alpha }_e}{\mathrm{\Phi }}^2\right)e^{\mathrm{\Phi }}-N_i-{\gamma }_p{e}^{-T_{ep}\mathrm{\Phi }},(3)$

where $N_e=N_{e0}\left[1-\frac{4{\alpha }_e}{1+3{\alpha }_e}\left(e\mathrm{\Phi }/T_e\right)+\frac{4{\alpha }_e}{1+3{\alpha }_e}{\left(e\mathrm{\Phi }/T_e\right)}^2\right]e^{\left(e\mathrm{\Phi }/T_e\right)}$ is the nonthermal electron density [48](see details in [48]),α_e is the nonthermality index, $N_p=e^{-\left(e\mathrm{\Phi }/T_p\right)}$ is the Boltzmann positron density, T_ep = T_e/T_p, γ_e = 1/(1 − N_p0/N_e0) and ${\gamma }_p=\left(N_{p0}/N_{e0}\right)/(1-N_{p0}/N_{e0})$. Eq. 1 and Eq. 2 is normalized to introduce the scaling as N_i → N_i/N_i0, $U_i\to U_i/C_s(C_s=\sqrt{T_i/m_i})$, Φ → eΦ/T_e, $x\to x{\lambda }_{De}({\lambda }_{De}=\sqrt{T_e/4\pi N_{eo}{e}^2})$ and $t\to t{\omega }_p({\omega }_p=\sqrt{4\pi N_{eo}{e}^2/m_i})$, respectively. Here, N_i, U_i, x, t, C_s, λ_De, ω_p and c are the ion density, ion fluid velocity, space variable, time variable, ion acoustic speed, electron Debye length, plasma frequency and speed of light, respectively. In addition, the ion viscosity coefficient ρ_i is normalized by introducing ${\rho }_i\to {\rho }_i{\lambda }_{De}^2{m}_i{N}_{i0}/{\omega }_i$, which is actually obtained for describing shock wave phenomena in the plasmas. Since, $V_i^2/c^2\ll 1$, the Lorentz relativistic factor ${\gamma }_i=1/\sqrt{1-V_i^2/c^2}$ can be expanded up to three terms [21] as

${\gamma }_i=\sum _{N=0}^2{e}_N{\left(\frac{V_i^2}{c^2}\right)}^N,(4)$

where e₀ = 1, e₁ = 1/2 and e₂ = 3/8. The aforementioned plasma system may also view as an outcome of the interactions of relativistic ions coming from the relativistic outflows or extra-galactic jets with interstellar clouds having nonthermal electrons and Boltzmann positrons.

Formation of Space Fractional NLEE via the Beta FD

To report for the continuation of nonlinear propagation of IAWs in the considered unmagnetized plasmas, the stretched coordinates and expanded perturbed quantities are respectively defined by implementing the reductive perturbation method [13, 26] as

$Z=ϵ\left(x-V_{0}t\right),T={ϵ}^{3}t,.(5)$

and

$\begin{array}{ccc}\hfill & \hfill & N_i=1+{ϵ}^2{N}_{i1}+{ϵ}^4{N}_{i2}+\dots ‥,\hfill \\ \hfill & \hfill & V_i=V_{i0}+{ϵ}^2{V}_{i1}+{ϵ}^4{V}_{i2}+\dots ‥,\hfill \\ \hfill & \hfill & \mathrm{\Phi }={ϵ}^2{\mathrm{\Phi }}_1+{ϵ}^4{\mathrm{\Phi }}_2+\dots ‥,\hfill \end{array}(6)$

where 0 < ϵ < 1 and V_i0 is the ion streaming velocity, respectively. One can also consider ρ_i = ρ₀ϵ for the case of weakly viscous effect. By implementing Eq 5, Eq 6 and Eqs 1–3 are converted to different power of ϵ. To the smallest power of ϵ yields

$N_{i1}=\frac{V_{i1}}{V_0-V_{i0}},(7)$

$V_{i1}=\frac{{\mathrm{\Phi }}_1}{\left(1+\frac{3}{2}\frac{V_{i0}^2}{c^2}+\frac{15}{8}\frac{V_{i0}^4}{c^4}\right)\left(V_0-V_{i0}\right)},(8)$

$N_{i1}=\frac{1}{1-N_{p0}/N_{e0}}\left(\frac{1-{\alpha }_e}{1+3{\alpha }_e}+T_{ep}\frac{N_{p0}}{N_{e0}}\right){\mathrm{\Phi }}_1,(9)$

In order to describe the behaviour of linear IAWs in the considered plasmas, the phase speed is determined as

$V_0=V_{i0}+\sqrt{\frac{1-N_{p0}/N_{e0}}{\left(1+\frac{3}{2}\frac{V_{i0}^2}{c^2}+\frac{15}{8}\frac{V_{i0}^4}{c^4}\right)\left(\frac{1-{\alpha }_e}{1+3{\alpha }_e}+T_{ep}\frac{N_{p0}}{N_{e0}}\right)}},(10)$

It is observed from Eq. 10 that V₀ is strongly dependent on the related plasma parameter but not on viscosity coefficient of ions, which is in good agrement with the earlier investigations [25]. In addition, V₀ is stable in the linear regime because of it is a positive quantity for all values of releated plasma parameters and α_e > − 1/3. After simplification the equations that are obtained by taking the next higher power of ϵ with the help of Eqs 7–9, the following NLEE is archived:

$\frac{\partial {\mathrm{\Phi }}_1}{\partial T}+P_1{\mathrm{\Phi }}_1\frac{\partial {\mathrm{\Phi }}_1}{\partial Z}+P_2\frac{{\partial }^3{\mathrm{\Phi }}_1}{\partial Z^3}-P_3\frac{{\partial }^2{\mathrm{\Phi }}_1}{\partial Z^2}=0,(11)$

which is known as the KdVBE. The nonlinear (P₁), dispersive (P₂) and dissipative (P₃) coefficients of Eq. 11 are respectively defined as

$\begin{array}{c}{P}_1=\left\{{\eta }_1-\frac{{\eta }_2\left(V_0-V_{i0}\right)}{V_{i0}}\right\}\frac{1}{2{\eta }_1^2\left(V_0-V_{i0}\right)}+\frac{1}{{\eta }_1\left(V_0-V_{i0}\right)}-\frac{B}{A}\left(V_0-V_{i0}\right),\hfill \\ P_2=\frac{{\eta }_1{\left(V_0-V_{i0}\right)}^3}{2},P_3=\frac{{\rho }_0}{2{\eta }_1},{\eta }_1=1+\frac{3}{2}\frac{V_{i0}^2}{c^2}+\frac{15}{8}\frac{V_{i0}^4}{c^4},{\eta }_2=3\frac{V_{i0}^2}{c^2}+\frac{15}{2}\frac{V_{i0}^4}{c^4},\hfill \\ A=\frac{1}{1-N_{p0}/N_{e0}}\left(\frac{1-{\alpha }_e}{1+3{\alpha }_e}+T_{ep}\frac{N_{p0}}{N_{e0}}\right),B=\frac{1}{2\left(1-N_{p0}/N_{e0}\right)}\left(1-T_{ep}^2\frac{N_{p0}}{N_{e0}}\right).\hfill \end{array}$

Eq. 11 is combined the contribution in the formation of shock wave excitation from dispersion and dissipation with nonlinearity. But, when the viscosity coefficient of ions is zero, Eq. 11 can be converted to the following well known KdVE:

$\frac{\partial {\mathrm{\Phi }}_1}{\partial T}+P_1{\mathrm{\Phi }}_1\frac{\partial {\mathrm{\Phi }}_1}{\partial Z}+P_2\frac{{\partial }^3{\mathrm{\Phi }}_1}{\partial Z^3}=0,(12)$

which is only responsible for soliton propagation in the considered plasmas. It is provided that the ions viscosity coefficient is only responsible for the formation of SWEs in the plasmas. Now, considering a potential function ϕ(Z, T), where ${\mathrm{\Phi }}_1(Z,T)=\frac{\partial \varphi (Z,T)}{\partial Z}$, yields Eq. 11 in the following form:

$\frac{{\partial }^2\varphi }{\partial T\partial Z}+P_1\frac{\partial \varphi }{\partial Z}\frac{{\partial }^2\varphi }{\partial Z^2}+P_2\frac{{\partial }^4\varphi }{\partial Z^4}-P_3\frac{{\partial }^2\mathrm{\Phi }}{\partial Z^2}=0,(13)$

The functional of Eq. 13 can be defined via the semi-invese method [40, 41] as

$J(\varphi )={\int }_{R}dZ{\int }_{T}dT\varphi \left(Z,T\right)\left[h_1\frac{{\partial }^2\varphi }{\partial T\partial Z}+h_2{P}_1\frac{\partial \varphi }{\partial Z}\frac{{\partial }^2\varphi }{\partial Z^2}+h_3{P}_2\frac{{\partial }^4\varphi }{\partial Z^4}-h_4{P}_3\frac{{\partial }^2{\mathrm{\Phi }}_1}{\partial Z^2}\right],(14)$

where h₁, h₂, h₃ and h₄ are the Lagrange’s multipliers to be determined later and R is the space. By integrating Eq. 14 with the conditions $\frac{\partial \varphi }{\partial Z}{|}_R=\frac{{\partial }^2\varphi }{\partial Z^2}{|}_R=\frac{{\partial }^3\varphi }{\partial Z^3}{|}_R=\frac{\partial \varphi }{\partial Z}{|}_T=0$ and employing the variation of this functional with respect to ϕ(Z, T), where $\frac{{\partial }^2\mathrm{\Phi }}{\partial Z^2}$ is considered as a fixed function, yields

$\delta J(\varphi )={\int }_{R}dZ{\int }_{T}dT\left[-h_1\frac{\partial \varphi }{\partial T}\frac{\partial \varphi }{\partial Z}-\frac{1}{2}{h}_2{P}_1{\left(\frac{\partial \varphi }{\partial Z}\right)}^3+h_3{P}_2{\left(\frac{{\partial }^2\varphi }{\partial Z^2}\right)}^2-h_4{P}_3\varphi \frac{{\partial }^2{\mathrm{\Phi }}_1}{\partial Z^2}\right],(15)$

Considering the variation of Eq. 15 with integrating each term by parts and make the variation optimum, that is δJ(ϕ) = 0, one can easily derive the following equation;

$h_1\frac{{\partial }^2\varphi }{\partial T\partial Z}+3h_2{P}_1\frac{\partial \varphi }{\partial Z}\frac{{\partial }^2\varphi }{\partial Z^2}+2h_3{P}_2\frac{{\partial }^4\varphi }{\partial Z^4}-h_4{P}_3\frac{{\partial }^2{\mathrm{\Phi }}_1}{\partial Z^2}=0,(16)$

which is must be equivalent to Eq. 13. Comparing Eq 13 and Eq 16, one can obtain the Lagrange’s multipliers as h₁ = 1, h₂ = 1/3, h₃ = 1/2 and h₄ = 1. Indeed, the functional as mentioned in Eq. 15 yields directly by taking the values of h₁, h₂, h₃ and h₄ into account in the following Lagrangian form:

$f_L({\varphi }_T,{\varphi }_Z,{\varphi }_{ZZ})=-{\varphi }_T{\varphi }_Z-\frac{1}{6}{P}_1{\varphi }_Z^3+\frac{1}{2}{P}_2{\varphi }_{ZZ}^2-P_3\varphi {\mathrm{\Phi }}_{1ZZ}.(17)$

where, the subscripts denote the partial differentiation of the function with respect to space (Z) and time (T). Eq. 17 can then be rewritten by including beta FD as

$\begin{array}{ccc}\hfill & \hfill & f_L(\varphi ,{\varphi }_T,{}_0^A{D}_Z^{\beta }\varphi ,{}_0^A{D}_Z^{2\beta }\varphi )=-\left({}_0^A{D}_Z^{\beta }\varphi \right){\varphi }_T-\frac{1}{6}{P}_1{\left({}_0^A{D}_Z^{\beta }\varphi \right)}^3\hfill \\ \hfill & \hfill & +\frac{1}{2}{P}_2{\left({}_0^A{D}_Z^{2\beta }\varphi \right)}^2-P_3\varphi \left({}_0^A{D}_Z^{2\beta }{\mathrm{\Phi }}_1\right).\hfill \end{array}(18)$

where ${}_0{}^{A}D_Z^{\beta }$ is denoted the beta FD operator. Based on the definition of beta FD [32], the derivative properties are obtained as follows:

$(i).{}_0{}^{A}D_Z^{\beta }\left\{mF\left(Z\right)+nG\left(Z\right)\right\}=m_0^A{D}_Z^{\beta }\left\{F\left(Z\right)\right\}+n_0^A{D}_Z^{\beta }\left\{G\left(Z\right)\right\}(19)$

$(ii).{}_0{}^{A}D_Z^{\beta }\left\{\mu \right\}=0(20)$

$(iii).{}_0{}^{A}D_Z^{\beta }\left\{F\left(Z\right).G\left(Z\right)\right\}={F\left(Z\right)}_0^A{D}_Z^{\beta }\left\{G\left(Z\right)\right\}+{G\left(Z\right)}_0^A{D}_Z^{\beta }\left\{F\left(Z\right)\right\}(21)$

$(iv).{}_0{}^{A}D_Z^{\beta }\left\{F\left(Z\right)/G\left(Z\right)\right\}=\frac{{G\left(Z\right)}_0^A{D}_Z^{\beta }\left\{F\left(Z\right)\right\}-{F\left(Z\right)}_0^A{D}_Z^{\beta }\left\{G\left(Z\right)\right\}}{G^2\left(Z\right)}(22)$

where, $m,n,\mu \in \mathfrak{R}$. G ≠ 0 and F are two functions β − differentiable with $\beta \in \left(\mathrm{0,1}\right]$. By introducing $ϵ={\left(\chi +\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{\beta -1}h$, when ϵ → 0, h → 0 in the definition of beta FD, one can derive another useful property as

${}_0{}^{A}D_Z^{\beta }F\left(Z\right)={\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{1-\beta }\frac{dF\left(Z\right)}{dZ}(23)$

From Eq. 18, one obtains

$\frac{\partial f_L}{\partial \varphi }=-P_3\left({}_0^A{D}_Z^{2\beta }{\mathrm{\Phi }}_1\right),\frac{\partial f_L}{\partial {\varphi }_T}=-{}_0^A{D}_Z^{\beta }\varphi ,\frac{\partial f_L}{{\partial }_0^A{D}_Z^{\beta }\varphi }=-\frac{1}{2}{P}_1{\left({}_0^A{D}_Z^{\beta }\varphi \right)}^2,\frac{\partial f_L}{{\partial }_0^A{D}_Z^{2\beta }\varphi }=P_2{\partial }_0^A{D}_Z^{2\beta }\varphi .(24)$

Again, J(ϕ) With the Inclusion of Beta FD Becomes

$J(\varphi )={\int }_{R}dZ{\int }_{\tau }dT{f}_L(\varphi ,{\varphi }_T,{}_0^A{D}_Z^{\beta }\varphi ,{}_0^A{D}_Z^{2\beta }\varphi ),(25)$

Based on the semi-inverse method [40, 41], the variational principle, that is, δJ(ϕ) = 0 yields

$\frac{\partial f_L}{\partial \varphi }-\frac{\partial }{\partial T}\left(\frac{\partial f_L}{\partial {\varphi }_T}\right){-}_0^A{D}_Z^{\beta }\left(\frac{\partial f_L}{{\partial }_0^A{D}_Z^{\beta }\varphi }\right){+}_0^A{D}_Z^{2\beta }\left(\frac{\partial f_L}{{\partial }_0^A{D}_Z^{2\beta }\varphi }\right)=0,(26)$

which is known as the Euler—Lagrange equation. Finally, the following space fractional KdVBE is derived by inserting Eq. 24 in Eq. 26 along with ${\mathrm{\Phi }}_1{=}_0^A{D}_Z^{\beta }\varphi$:

$\frac{\partial {\mathrm{\Phi }}_1}{\partial T}+P_1{\mathrm{\Phi }}_1{}_0^A{D}_Z^{\beta }{\mathrm{\Phi }}_1+P_2{}_0^A{D}_Z^{3\beta }{\mathrm{\Phi }}_1-P_3{}_0^A{D}_Z^{2\beta }{\mathrm{\Phi }}_1=0.(27)$

In Ref. [35], author has been derived the same equation by including the Riemann–Liouville (RL) fractional derivative, where such derivative is defined as

${}_0{}^{A}D_Z^{\beta }F\left(Z\right)=\frac{1}{\mathrm{\Gamma }(\lambda -\beta )}\times \frac{d^{\lambda }}{d{Z}^{\lambda }}\left({\int }_a^{Z}dx{(Z-x)}^{\lambda -\beta -1}f(x)\right),\lambda -1<\beta \le \lambda ,Z\in [a,b].$

Besides, the nonlinear, dispersive and dissipative coefficients are different from Ref. [35] because of the distinct plasma assumptions. It is noted that this derivative has also some drawbacks for satisfying the rule of fundamental calculus.

Analytical Solutions of Space Fractional KDVBE

To obtain the analytical solutions of Eq. 27, the stretched variables can be combined by introducing traveling wave transformation ast

${\mathrm{\Phi }}_1\left(Z,T\right)=\mathrm{\Xi }\left(\zeta \right),\zeta =\frac{1}{L_w}\left[\frac{1}{\beta }{\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{\beta }-V_{r}T\right],(28)$

where Ł_w and V_r are respectively related to the thickness and constant speed of moving reference frame with conditions Φ⁽¹⁾ → 0, dΦ⁽¹⁾/dχ → 0, d²Φ⁽¹⁾/dχ² → 0, … at ζ → ∞. It is noted that one can consider the wave transformation with the presence of RL derivative as

$\zeta =\frac{1}{L_w}\left[\frac{1}{\mathrm{\Gamma }(1+\beta )}{Z}^{\beta }-V_{r}T\right].$

Based on the above assumptions, Eq. 27 can be converted to

$-L_w^2{V}_r\mathrm{\Xi }+\frac{1}{2}{P}_1{L}_w^2{\mathrm{\Xi }}^2+P_2\frac{d^2\mathrm{\Xi }}{d{\zeta }^2}-P_3{L}_w\frac{d\mathrm{\Xi }}{d\zeta }=0.(29)$

Now, the analytical solutions of Eq. 29 based on the MKM [28, 42] can be written by taking the homogeneous balance between Ξ² and $\frac{d^2\mathrm{\Xi }}{d{\zeta }^2}$ into account as

$\mathrm{\Xi }\left(\zeta \right)=\sum _{n=0}^2{\kappa }_n{\left(\mathrm{\Psi }(\zeta )\right)}^n,{\kappa }_n\ne 0,(30)$

where $\mathrm{\Psi }\left(\zeta \right)=1/\left(1+d{r}^{\zeta }\right)$, r and d are real constants. $\mathrm{\Psi }\left(\zeta \right)$ is satisfied the following auxiliary equation:

$\frac{d\mathrm{\Psi }(\zeta )}{d\zeta }=\left({\mathrm{\Psi }}^2(\zeta )-\mathrm{\Psi }(\zeta )\right)\left(\ln r\right),r\ne \mathrm{0,1}.(31)$

By inserting Eq. 30 into Eq. 29, a set of algebraic equations in terms of physical and additional parameters by taking the coefficients of like power of (Ψ(ζ))ⁱ, i = 0, 1, … , 4 are obtained (ignored for simplicity). By simplifying the overlooked algebraic equations, four types of parametric values of κ₀, κ₁, κ₂, Ł_w and V_r are archived.

Type 1

$\begin{array}{ccc}\hfill & \hfill & {\kappa }_0=0,{\kappa }_1=\frac{24}{25}\left(\frac{P_3^2}{P_1{P}_2}\right),{\kappa }_2=-\frac{12}{25}\left(\frac{P_3^2}{P_1{P}_2}\right),\hfill \\ \hfill & \hfill & L_w=\frac{5P_2\ln (r)}{P_3},V_r=\frac{6P_3^2}{25P_2}.\hfill \end{array}(32)$

Therefore, the analytical solution of space fractional KdVBE based on Type 1 is obtained as

$\mathrm{\Phi }\left(Z,T\right)=\frac{12P_3^2}{25P_1{P}_2}\left\{-\frac{1}{{\left(1+d{r}^{\frac{P_3}{5P_2\ln (r)}\left[\frac{1}{\beta }{\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{\beta }-\frac{6P_3^2}{25P_2}T\right]}\right)}^2}+\frac{2}{\left(1+d{r}^{\frac{P_3}{5P_2\ln (r)}\left[\frac{1}{\beta }{\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{\beta }-\frac{6P_3^2}{25P_2}T\right]}\right)}\right\},(33)$

Type 2

$\begin{array}{ccc}\hfill & \hfill & {\kappa }_0=\frac{12}{25}\left(\frac{P_3^2}{P_1{P}_2}\right),{\kappa }_1=0,{\kappa }_2=-\frac{12}{25}\left(\frac{P_3^2}{P_1{P}_2}\right),\hfill \\ \hfill & \hfill & L_w=-\frac{5P_2\ln (r)}{P_3},V_r=\frac{6P_3^2}{25P_2}.\hfill \end{array}(34)$

Therefore, the analytical solution of space fractional KdVBE based on Type 2 is obtained as

$\mathrm{\Phi }\left(Z,T\right)=\frac{12P_3^2}{25P_1{P}_2}\left\{1-\frac{1}{{\left(1+d{r}^{-\frac{P_3}{5P_2\ln (r)}\left[\frac{1}{\beta }{\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{\beta }-\frac{6P_3^2}{25P_2}T\right]}\right)}^2}\right\},(35)$

Type 3

$\begin{array}{ccc}\hfill & \hfill & {\kappa }_0=-\frac{12}{25}\left(\frac{P_3^2}{P_1{P}_2}\right),{\kappa }_1=\frac{24}{25}\left(\frac{P_3^2}{P_1{P}_2}\right),{\kappa }_2=-\frac{12}{25}\left(\frac{P_3^2}{P_1{P}_2}\right),\hfill \\ \hfill & \hfill & L_w=\frac{5P_2\ln (r)}{P_3},V_r=-\frac{6P_3^2}{25P_2}.\hfill \end{array}(36)$

Therefore, the analytical solution of space fractional KdVBE based on Type 3 is obtained as

$\mathrm{\Phi }\left(Z,T\right)=\frac{12P_3^2}{25P_1{P}_2}\left\{-1-\frac{1}{{\left(1+d{r}^{\frac{P_3}{5P_2\ln (r)}\left[\frac{1}{\beta }{\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{\beta }+\frac{6P_3^2}{25P_2}T\right]}\right)}^2}+\frac{2}{\left(1+d{r}^{\frac{P_3}{5P_2\ln (r)}\left[\frac{1}{\beta }{\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{\beta }+\frac{6P_3^2}{25P_2}T\right]}\right)}\right\},(37)$

Type 4

$\begin{array}{ccc}\hfill & \hfill & {\kappa }_0=0,{\kappa }_1=0,{\kappa }_2=-\frac{12}{25}\left(\frac{P_3^2}{P_1{P}_2}\right),\hfill \\ \hfill & \hfill & L_w=-\frac{5P_2\ln (r)}{P_3},V_r=-\frac{6P_3^2}{25P_2}.\hfill \end{array}(38)$

Finally, the analytical solution of space fractional KdVBE based on Type 4 is obtained as

$\mathrm{\Phi }\left(Z,T\right)=\frac{12P_3^2}{25P_1{P}_2}\left\{-\frac{1}{{\left(1+d{r}^{\frac{-P_3}{5P_2\ln (r)}\left[\frac{1}{\beta }{\left(Z+\frac{1}{\mathrm{\Gamma }\left(\beta \right)}\right)}^{\beta }+\frac{6P_3^2}{25P_2}T\right]}\right)}^2}\right\}.(39)$

Parametric Investigations

It is well known that fractional partial differential equations involving real or complex order derivatives have proven to be a very effective tool in modeling anomalous dynamics of various physical processes. The immense improvement of such fractional derivative operator is that one can formulate models analyzing much-recovered systems with memory effects. On the other hand, one can consider a gracefully discretized illustration of the medium. In such nonlocal media, the complex and spatially connected heterogeneity is represented via a reformulation of the evolution equation that provided the related transport physics such that its coefficients are, instead, smooth but paired with fractional-order space derivatives. Further, He [49] has been shown that fractal theory can be adopted to describe various phenomena when space or time becomes discontinuous. Hence, the space fractional KdVBE by introducing the beta fractional derivative has been derived from the considered plasma system. The analytical solutions of this equation have evaluated by employing the MKM and the properties of beta FD. In addition, this work has also been demonstrated that how the features of shock waves solutions can be affected by the plasma parameters with the influence of nonlocal operator. The parametric effects of β, α_e, N_p0/N_e0, V_i0/c (relativistic streaming factor), T_ep = T_e/T_p and ρ₀ on the basic features of NIASWEs based on the obtained result as mentioned in Eq. 33 are displayed graphically along with the physical interpretations.

Figures 1A,B layouts the contour plots of electrostatic NIASWEs with respect to space (Z) and time (T) for β = 1 and β = 0.1, respectively by assuming the remaining parameters constant. It is found from the distinction of Figure 1 that the SWEs are existed both of positive and negative regions of Z with the presence of local operator (β = 1), but only existed in the positive regions of Z with the presence of nonlocal operator (0 < β < 1). In the physical point of views, the electrostatic SWEs are significantly changed when the space non-conservative or space non-locality are occurred in the plasmas. Figures 2A,B explore the influence of ρ₀ on electrostatic NIASWEs by considering β = 1 and β = 0.8, whereas Figures 2C,D explore the variation of electrostatic NIASWEs for different values of T by considering β = 1 and β = 0.5, respectively along with the constant values of the remaining parameters. It is observed from Figure 2 that the amplitude of NIASWEs are decreased with the decrease of weakly viscosity coefficient of ions. In addition, the SWEs are existed within the range − ∞ < Z < ∞ for only β = 1 but remarkably modified and existed only within the range of 0 < Z < ∞ for 0 < β < 1. Figure 3 displays the influences of positron to electron density ratio on SWEs by considering different values of β and the remaining parameters constant. It is observed the amplitudes of SWEs are growing with the increase of positron concentrations. This happens with the depopulation of ions because the driving force provided by the ion inertia is increased with the increase of positron concentration. The influence of electron to positron temperature ratio and electron nonthermality index on electrostatic SWEs taking both of local (β = 1) and non-local (0 < β < 1) parameter into account are explored in Figures 4, 5, respectively. It is found from Figures 4, 5 that the amplitude of SWEs are increased with the increase of electron temperature, but decreased with the increase of electrons nonthermality index. Finally, the influence of relativistic streaming factor on electrostatic SWEs taking β = 1 and 0 < β < 1 into account is displayed in Figure 6. It clearly observed from Figure 6 that the electrostatic SWEs lose energies due to the increase of a relativistic factor of ions, which is in good agreement with the previous study [22]. As a result, the amplitudes of SWEs are remarkably restrained with the increase of relativistic factor of ions. On the other hand, the displayed Figure 3 show that the compressive and rarefactive shock structures have supported in the considered plasmas with the presence of not only a nonlocal operator (0 < β < 1) but also local operator (β = 1) by depending on the parametric values of the related plasma parameters. It is noted here that the parametric effects on the other obtained solutions of space fractional KdVBE is ignored for simplicity. In addition, the typical values of the plasma parameters are considered based on the earlier investigations [13, 14, 16, 24, 25], which are very much relevant to some astrophysical and space environments. It is predicted from the above discussion that the peak amplitude of SWEs has not existed in the negative regimes of Z with the presence of the nonlocal operator. Whereas, the peak amplitude of SWEs has existed in both regimes of Z with the presence of the local operator.

FIGURE 1

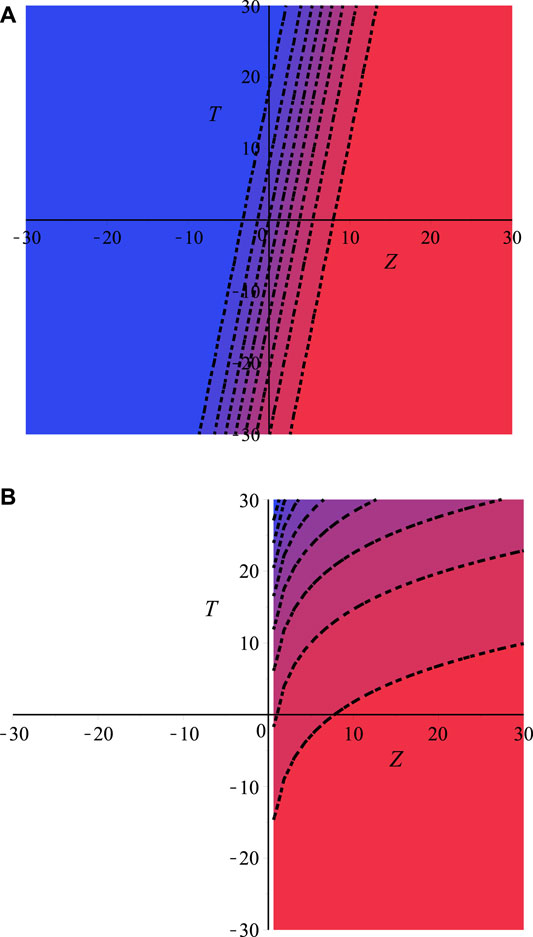
FIGURE 1. Contour plot of electrostatic NIASWEs with respect to space and time for (A) β = 1 and (B) β = 0.1. The remaining parameters are considered as d = 1, r = e, ρ = 0.96, α_e = 0.5, N_p0/N_e0 = 0.5, T_ep = 1 and V_i0/c = 0.1.

FIGURE 2

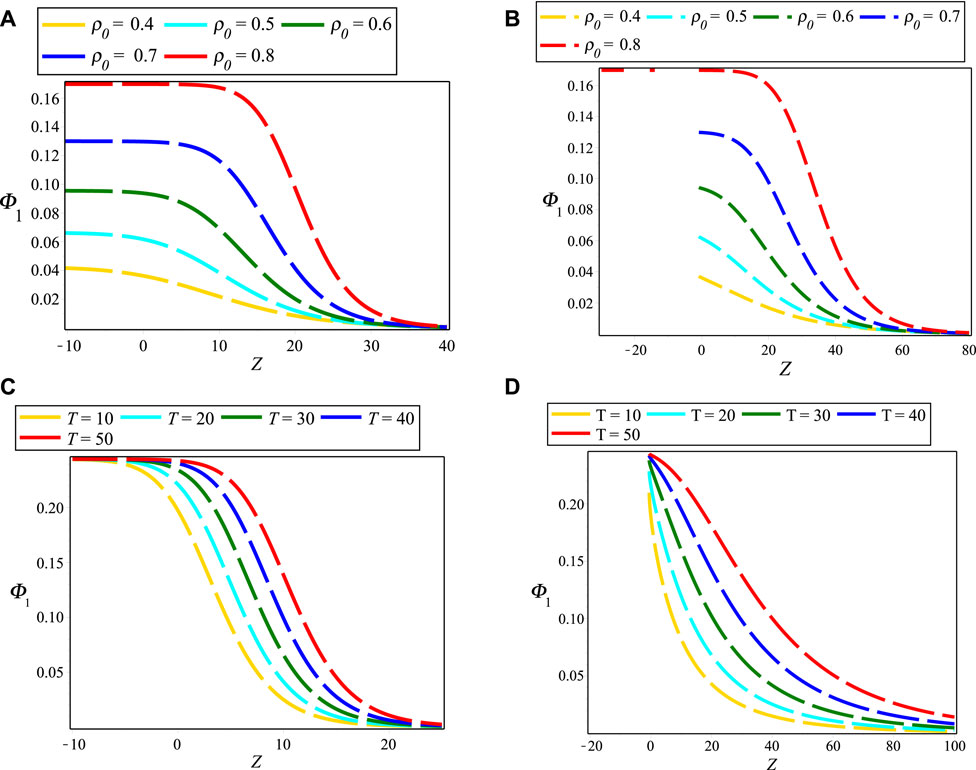
FIGURE 2. Electrostatic NIASWEs for (A) β = 1 and (B) β = 0.8 with the different of ρ₀ and T = 150, and (C) β = 1 and (D) β = 0.5 with the different values of T and ρ₀ = 0.96. The remaining parameters are considered as d = 1, r = e, α_e = 0.5, N_p0/N_e0 = 0.5, T_ep = 1 and V_i0/c = 0.1.

FIGURE 3

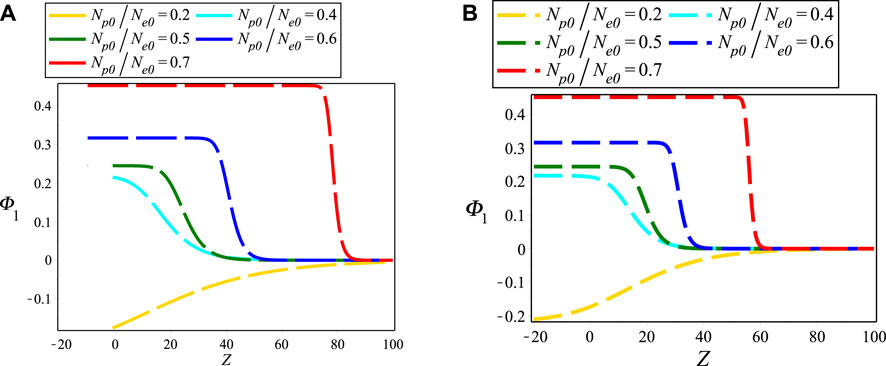
FIGURE 3. Electrostatic NIASWEs with respect to space (Z) and fixed time (T = 100) for (A) β = 0.9 and (B) β = 1 with different values of N_p0/N_e0. The remaining parameters are considered as d = 1, r = e, α_e = 0.5, ρ₀ = 0.96, T_ep = 1 and V_i0/c = 0.1.

FIGURE 4

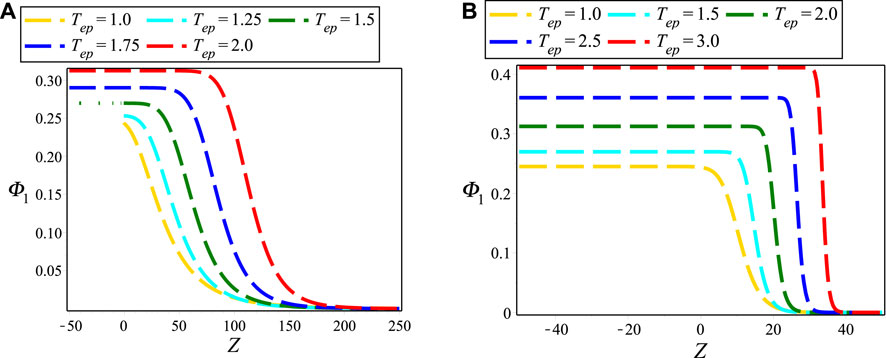
FIGURE 4. Electrostatic NIASWEs for different of (A) T_ep with d = 1, r = e, β = 0.9, α_e = 0.5, ρ₀ = 0.96, T_ep = 1, V_i0/c = 0.1, N_p0/N_e0 = 0.5 and T = 100; and (B) T_ep with the same typical values of (A) except β = 1.

FIGURE 5

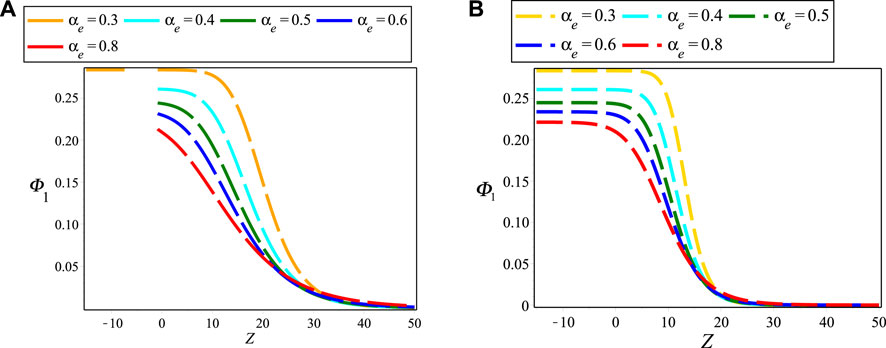
FIGURE 5. Electrostatic NIASWEs for different of (A) α_e with d = 1, r = e, β = 0.9, N_p0/N_e0 = 0.5, ρ₀ = 0.96, T_ep = 1, V_i0/c = 0.1 and T = 100; and (B) α_e with the same typical values of (A) except β = 1.

FIGURE 6

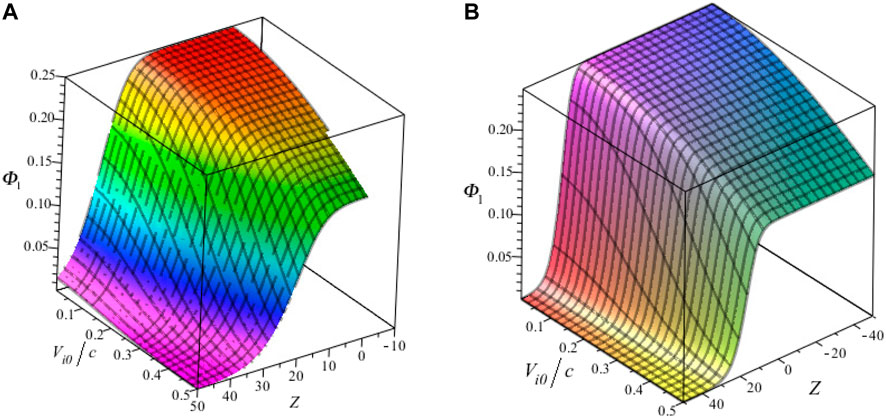
FIGURE 6. Effect of relativistic streaming factor on electrostatic NIASWEs for (A) β = 0.9 and (B) β = 1 with α_e = 0.5, N_p0/N_e0 = 0.5, d = 1, r = e, ρ₀ = 0.96, T_ep = 1 and T = 100.

In order to check the validity of the beta fractional derivative, the electrostatic potential with regards to space is displayed in Figure 7 by comparing it with the RL derivative. This figure is clearly shown that the electrostatic potential only exists in the positive regime of Z with the presence of both fractional derivatives, which is in good agreement with the investigations in Ref. [35]. It is also observed that beta fractional derivative minimizes the amplitude of electrostatic potential rather than RL fractional derivative. As it is expected because of some limitations of RL fractional derivative. Thus, the results obtained in this article would be very useful for better understanding the physical scenarios with the presence of non-locality as well as non-conservative energies of charged particles not only in astrophysical and space environments but also in plasma laboratories.

FIGURE 7

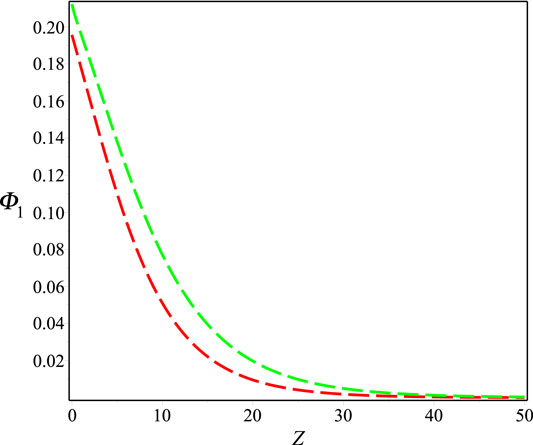
FIGURE 7. Electrostatic potential with the presence of beta (red color) and RL (green color) fractional derivatives with respect to space and T = 10. The remaining parameters are considered as d = 1, r = e, ρ = 0.96, α_e = 0.5, N_p0/N_e0 = 0.5, T_ep = 1, V_i0/c = 0.1, β = 0.8 and T = 10.

Concluding Remarks

The KdVBE including beta space FO has been proposed to report the unrevealed physical issues in the unmagnetized collisionless plasmas, where the non-locality as well as non-conservative systems play an essential role. The analytical solutions of this equation have obtained via the effective MKM. The proposed equation has been divulged the SWEs in the considered plasma system. The effects of beta fractional and other related parameters on NIASWEs have investigated. It is found that electrostatic NIASWEs are significantly modified with the presence of a nonlocal operator, like beta FD. This means that the nonlocal behaviors of electrostatic NIASWEs have only existed in the positive regimes of space with the influence of plasma parameters. From a physical point of view, this will happen only when the scale approaches a very small one. It is also observed that the beta FD is very useful to study the basic features of nonlinear dynamical wave phenomena because of the localized and non-localized nonlinear wave phenomena can be described very easily by considering β = 1 and 0 < β < 1, respectively. The considered plasma system is supported both of compressive and rarefactive shock wave excitations within the domain 0 < Z < ∞ with the presence of beta FD, which is another most important finding in this work. It would be concluded that one may be derived various types of beta fractional NLEEs for better understanding the unfamiliar physical scenarios not only in plasmas, but also in fluid dynamics, water wave theories, fluid-filled elastic tubes, nonlinear optics, etc.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

Conceptualization, MU and MH; methodology, MU and MH; data curation, MH; formal analysis, MU and MH; funding acquisition, IH; investigation, MU and MH; project administration, IH; resources, MH; software, MU and MH; supervision, MH; validation, MH; IH and CP; visualization, MU and MH; writing, original draft, MU and MH; review and editing, IH and CP All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Incheon National University Research Grant 2021–2022.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ress MJ. The Very Early Universe. Cambridge, U.K.: Cambridge University Press (1983).

Google Scholar

2. Peebles PJE. The Large-Scale Structure of the Universe. Princeton: Princeton University Press (1980).

Google Scholar

3. Gunn JE, Ostriker JP. On the Motion and Radiation of Charged Particles in strong Electromagnetic Waves. I. Motion in Plane and Spherical Waves. ApJ (1971) 165:523–41. doi:10.1086/150919

CrossRef Full Text | Google Scholar

4. Michel FC. Theory of Neutron Star Magnetospheres. Chicago, IL, USA: Chicago University Press (1991).

Google Scholar

5. Michel FC. Theory of Pulsar Magnetospheres. Rev Mod Phys (1982) 54:1–66. doi:10.1103/RevModPhys.54.1

CrossRef Full Text | Google Scholar

6. Weinberg S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York, USA: Wiley (1972).

Google Scholar

7. Miller HR, Wiita PJ. Active Galactic Nuclei. Berlin, Germany: Springer (1987).

Google Scholar

8. Burns ML. Positron-Electron Pairs in Astrophysics. Melville, NY, USA: American Institute of Physics (1983).

Google Scholar

9. Bhattacharyya B. Dominance of Ion Motion over Electron Motion in Some Intensity-Induced Wave Processes in a Magnetized Plasma. Phys Rev A (1983) 27:568–71. doi:10.1103/PhysRevA.27.568

CrossRef Full Text | Google Scholar

10. Bennaceur-Doumaz D, Djebli M. Modeling of Laser Induced Plasma Expansion in the Presence of Non-maxwellian Electrons. Phys Plasmas (2010) 17:074501. doi:10.1063/1.3458671

CrossRef Full Text | Google Scholar

11. Hafez MG. Face to Face Collisions of Ion Acoustic Multi-Solitons and Phase Shifts in a Dense Plasma. Braz J Phys (2019) 49:221–31. doi:10.1007/s13538-018-00620-x

CrossRef Full Text | Google Scholar

12. Alam MS, Hafez MG, Talukder MR, Hossain Ali M. Head-on Collision of Ion Acoustic Shock Waves in Electron-Positron-Ion Nonextensive Plasmas for Weakly and Highly Relativistic Regimes. Phys Plasmas (2018) 25:072904. doi:10.1063/1.5037788

CrossRef Full Text | Google Scholar

13. Hafez MG, Talukder MR, Hossain Ali M. Nonlinear Propagation of Ion-Acoustic Waves through the Burgers Equation in Weakly Relativistic Plasmas. Plasma Phys Rep (2017) 43:499–509. doi:10.1134/S1063780X17040031

CrossRef Full Text | Google Scholar

14. Hafez MG, Talukder MR, Ali MH. Nonlinear Propagation of Weakly Relativistic Ion-Acoustic Waves in Electron-Positron-Ion Plasma. Pramana - J Phys (2016) 87(70):1–10. doi:10.1007/s12043-016-1275-x

CrossRef Full Text | Google Scholar

15. Hafez MG, Talukder MR, Ali MH. Two-dimensional Nonlinear Propagation of Ion Acoustic Waves through KPB and KP Equations in Weakly Relativistic Plasmas. Adv Math Phys (2016) 2016:1–12. doi:10.1155/2016/9352148

CrossRef Full Text | Google Scholar

16. Hafez MG, Talukder MR, Hossain Ali M. Ion Acoustic Shock and Solitary Waves in Highly Relativistic Plasmas with Nonextensive Electrons and Positrons. Phys Plasmas (2016) 23:012902. doi:10.1063/1.4939750

CrossRef Full Text | Google Scholar

17. Mamun AA. Degenerate Pressure Driven Self-Gravito-Acoustic Solitary Waves in a Self-Gravitating Degenerate Quantum Plasma System. Phys Plasmas (2018) 25:022307. doi:10.1063/1.5013138

CrossRef Full Text | Google Scholar

18. Hafez MG, Talukder MR. Ion Acoustic Solitary Waves in Plasmas with Nonextensive Electrons, Boltzmann Positrons and Relativistic thermal Ions. Astrophys Space Sci (2015) 359:27. doi:10.1007/s10509-015-2480-7

CrossRef Full Text | Google Scholar

19. Saha A. Nonlinear Excitations for the Positron Acoustic Shock Waves in Dissipative Nonextensive Electron-Positron-Ion Plasmas. Phys Plasmas (2017) 24:034502. doi:10.1063/1.4977909

CrossRef Full Text | Google Scholar

20. Hafez MG, Talukder MR, Hossain Ali M. Comment on “Electrostatic Compressive and Rarefactive Shocks and Solitons in Relativistic Plasmas Occurring in Polar Regions of Pulsar”. Astrophys Space Sci (2016) 361:154. doi:10.1007/s10509-016-2738-8

CrossRef Full Text | Google Scholar

21. Hafez MG. Nonlinear Schamel Korteweg-De Vries-Burgers Equation to Report Ion-Acoustic Waves in the Relativistic Plasmas. IEEE Trans Plasma Sci (2019) 47(12):5314–23. doi:10.1109/TPS.2019.2949254

CrossRef Full Text | Google Scholar

22. Sarri G, Poder K, Cole JM, Schumaker W, Di Piazza A, Reville B, et al. Generation of Neutral and High-Density Electron-Positron Pair Plasmas in the Laboratory. Nat Commun (2015) 6:6747. doi:10.1038/ncomms7747

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Corde S, Adli E, Allen JM, An W, Clarke CI, Clayton CE, et al. Multi-gigaelectronvolt Acceleration of Positrons in a Self-Loaded Plasma wakefield. Nature (2015) 524:442–5. doi:10.1038/nature14890

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Atteya A, Behery EE, El-Taibany WF. Ion Acoustic Shock Waves in a Degenerate Relativistic Plasma with Nuclei of Heavy Elements. Eur Phys J Plus (2017) 132:109. doi:10.1140/epjp/i2017-11367-2

CrossRef Full Text | Google Scholar

25. Hafez MG, Roy NC, Talukder MR, Hossain Ali M. Oblique Propagation of Ion Acoustic Shock Waves in Weakly and Highly Relativistic Plasmas with Nonthermal Electrons and Positrons. Astrophys Space Sci (2016) 361:312. doi:10.1007/s10509-016-2903-0

CrossRef Full Text | Google Scholar

26. Hafez MG, Roy NC, Talukder MR, Hossain Ali M. Ion Acoustic Shock and Periodic Waves through Burgers Equation in Weakly and Highly Relativistic Plasmas with Nonextensivity. Plasma Sci Technol (2017) 19(1):015002. doi:10.1088/1009-0630/19/1/015002

CrossRef Full Text | Google Scholar

27. Pakzad HR, Tribeche M. Nonlinear Propagation of Ion-Acoustic Shock Waves in Dissipative Electron-Positron-Ion Plasmas with Superthermal Electrons and Relativistic Ions. J Fusion Energ (2013) 32:171–6. doi:10.1007/s10894-012-9543-3

CrossRef Full Text | Google Scholar

28. Uddin MF, Hafez MG, Hammouch Z, Baleanu D. Periodic and Rogue Waves for Heisenberg Models of Ferromagnetic Spin Chains with Fractional Beta Derivative Evolution and Obliqueness. Waves in Random and Complex Media (2020) 1–15. doi:10.1080/17455030.2020.1722331

CrossRef Full Text | Google Scholar

29. Uddin MF, Hafez MG. Interaction of Complex Short Wave Envelope and Real Long Wave Described by the Coupled Schrödinger-Boussinesq Equation with Variable Coefficients and Beta Space Fractional Evolution. Results Phys (2020) 19:103268. doi:10.1016/j.rinp.2020.103268

CrossRef Full Text | Google Scholar

30. Nourazar SS, Nazari-Golshan A, Soleymanpour F. On the Expedient Solution of the Magneto-Hydrodynamic Jeffery-Hamel Flow of Casson Fluid. Sci Rep (2018) 8:16358. doi:10.1038/s41598-018-34778-w

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Uddin MF, Hafez MG, Hammouch Z, Rezazadeh H, Baleanu D. Traveling Wave with Beta Derivative Spatial-Temporal Evolution for Describing the Nonlinear Directional Couplers with Metamaterials via Two Distinct Methods. Alexandria Eng J (2021) 60(1):1055–65. doi:10.1016/j.aej.2020.10.030

CrossRef Full Text | Google Scholar

32. Atangana A, Baleanu D, Alsaedi A. Analysis of Time-Fractional hunter-saxton Equation: a Model of Neumatic Liquid crystal. Open Phys (2016) 14(1):145–9. doi:10.1515/phys-2016-0010

CrossRef Full Text | Google Scholar

33. Nazari-Golshan A, Fallahi V. Positron Nonextensivity Effect on the Propagation of Dust Ion Acoustic Gardner Waves. Z für Naturforschung A (2021) 76:972–65. doi:10.1515/zna-2021-0012

CrossRef Full Text | Google Scholar

34. Liu Q, Chen L. Time-Space Fractional Model for Complex Cylindrical Ion-Acoustic Waves in Ultrarelativistic Plasmas. Complexity (2020) 2020:1–16. doi:10.1155/2020/9075823

CrossRef Full Text | Google Scholar

35. Nazari-Golshan A. Investigation of Shock Waves in Nonextensive Electron-Positron-Ion Plasma with Relativistic Ions. Plasma Phys Rep (2020) 46(9):943–9. doi:10.1134/S1063780X20090068

CrossRef Full Text | Google Scholar

36. Nazari-Golshan A. Derivation and solution of space fractional modified Korteweg de Vries equation. Commun Nonlinear Sci Numer Simulation (2019) 79:104904. doi:10.1016/j.cnsns.2019.104904

CrossRef Full Text | Google Scholar

37. Nazari-Golshan A. Investigation of Nonextensivity Trapped Electrons Effect on the Solitary Ion-Acoustic Wave Using Fractional Schamel Equation. Phys Plasmas (2016) 23:082109. doi:10.1063/1.4960668

CrossRef Full Text | Google Scholar

38. Nazari-Golshan A, Nourazar SS. Effect of Trapped Electron on the Dust Ion Acoustic Waves in Dusty Plasma Using Time Fractional Modified Korteweg-De Vries Equation. Phys Plasmas (2013) 20:103701. doi:10.1063/1.4823997

CrossRef Full Text | Google Scholar

39. Nazari-Golshan A. Investigation of Cylindrical Shock Waves in Dusty Plasma. Indian J Phys (2018) 92:1643–50. doi:10.1007/s12648-018-1260-y

CrossRef Full Text | Google Scholar

40. Agrawal OP. Formulation of Euler-Lagrange Equations for Fractional Variational Problems. J Math Anal Appl (2002) 272(1):368–79. doi:10.1016/S0022-247X(02)00180-4

CrossRef Full Text | Google Scholar

41. Agrawal OP. A General Formulation and Solution Scheme for Fractional Optimal Control Problems. Nonlinear Dyn (2004) 38:323–37. doi:10.1007/s11071-004-3764-6

CrossRef Full Text | Google Scholar

42. Akther S, Hafez MG, Ferdous F. Oblique Resonance Wave Phenomena for Nonlinear Coupled Evolution Equations with Fractional Temporal Evolution. Eur Phys J Plus (2019) 134:473. doi:10.1140/epjp/i2019-12832-6

CrossRef Full Text | Google Scholar

43. Bostrom R. Observations of Weak Double Layers on Auroral Field Lines. IEEE Trans Plasma Sci (1992) 20(6):756–63. doi:10.1109/27.199524

CrossRef Full Text | Google Scholar

44. Dovner PO, Eriksson AI, Boström R, Holback B. Freja Multiprobe Observations of Electrostatic Solitary Structures. Geophys Res Lett (1994) 21(17):1827–30. doi:10.1029/94gl00886

CrossRef Full Text | Google Scholar

45. Yu MY, Luo H. A Note on the Multispecies Model for Identical Particles. Phys Plasmas (2008) 15:024504. doi:10.1063/1.2854067

CrossRef Full Text | Google Scholar

46. Guo S, Mei L, He Y-L, Guo H, Zhao Y. The Effect of Trapped Electrons on the Three-Dimensional Ion-Acoustic Shock Wave in Magnetized Ionic-Pair Plasma. EPL (2016) 114(2):25002. doi:10.1209/0295-5075/114/25002

CrossRef Full Text | Google Scholar

47. Bettega G, Cavaliere F, Cavenago M, Illiberi A, Pozzoli R, Romé M. Experimental Investigation of the Ion Resonance Instability in a Trapped Electron Plasma. Plasma Phys Control Fusion (2005) 47(10):1697–708. doi:10.1088/0741-3335/47/10/007

CrossRef Full Text | Google Scholar

48. Cairns RA, Mamum AA, Bingham R, Boström R, Dendy RO, Nairn CMC, et al. Electrostatic Solitary Structures in Non-thermal Plasmas. Geophys Res Lett (1995) 22(20):2709–12. doi:10.1029/95GL02781

CrossRef Full Text | Google Scholar

49. He J-H. A Tutorial Review on Fractal Spacetime and Fractional Calculus. Int J Theor Phys (2014) 53:3698–718. doi:10.1007/s10773-014-2123-8

CrossRef Full Text | Google Scholar