Ultrafast Terahertz Complex Conductivity Dynamics of Layered MoS2 Crystal Probed by Time-Resolved Terahertz Spectroscopy

Introduction

Transition metal dichalcogenides (TMDs) are burgeoning layered semiconductors with a chemical formula of MX₂ (M represents transition metal elements, including Ti, V, Ta, Mo, W, and Re; X represents chalcogenide atoms, such as S, Se, and Te), in which the van der Waals force connects atomic sheets. Because of the superior properties such as high carrier mobility [1], strong optical nonlinearity [2], and high mechanical strength [3], TMDs materials are advancing the development of many optoelectronic devices, including photodetectors [4], light-emitting diodes [5], field-effect transistors [6], solar cells [7], etc. As one of the most typical and important TMDs, molybdenum disulfide (MoS₂) has been reported to have some unique properties. For example, MoS₂ has an indirect-to-direct bandgap transition when vary the layer number from bulk to monolayer [8]; MoS₂ transistor has a high on/off ratio up to 10⁸; MoS₂ has a strong spin-orbit coupling [9]. Therefore, many novel optical and electrical applications [2, 10, 11] are expected to be realized by MoS₂.

Clarifying the carrier dynamics mechanisms of MoS₂ is of key significance for developing MoS₂-based optoelectronic devices. Compared with the detection techniques that investigate the photoexcited carrier properties in a static state, such as photocurrent spectroscopy [12], photoluminescence spectroscopy [13], and electroluminescence spectroscopy [14], transient absorption spectroscopy based on the optical pump-probe technology is indispensable for studying the ultrafast carrier dynamics mechanisms [15]. Specifically, many valuable conclusions have been achieved on the ultrafast dynamic properties of MoS₂. For example, Wang et al. have reported the intervalley transfer, energy relaxation, and recombination of carriers in bulk MoS₂ crystal by resolving the dynamic process [16]. Huang et al. demonstrated that the exciton dynamics of monolayer and few-layer MoS₂ are remarkably different due to the quantum confinement effect and the surface defect effect [17]. Wang et al. proposed that the defect-assisted Auger relaxation of electron−hole recombination in MoS₂ is related to the strong Coulomb interaction and the electron-hole correlation in two-dimensional MoS₂ [18].

Compared with the optical pump-probe technology, optical pump-terahertz probe (OPTP) spectroscopy as another important method to probe the ultrafast process, is sensitive to terahertz (THz) conductivity instead of the static conductivity of materials. The sub-picosecond time resolution of OPTP is suitable to study the ultrafast dynamics of carrier, exciton, and phonon. Sood et al. have studied the dynamics of photoexcited carriers in a few-layered MoS₂ using OPTP spectroscopy [19]. They find that the fast relaxation time occurs due to the capture of electrons and holes by defects, and the slow relaxation time is related to bounded excitons which prevent the defect-assisted Auger recombination. For comparison, MoS₂ bulk crystal is an indirect bandgap semiconductor, which indicates that the position of electrons in the momentum space will change before and after the transition. In order to satisfy the conservation of momentum, there would be a large number of phonons and bounded excitons involved in the ultrafast process. Additionally, the exciton effect has been reported to be significant in TMDs [20, 21]. Therefore, understanding the exciton dynamics in MoS₂ crystals is of key importance for the application development.

In this work, we use the OPTP technique to explore the dynamics of photo-induced carriers in layered MoS₂ crystal. The complex photoconductivity is calculated from the pump-induced THz amplitude and phase changes. The real and imaginary parts of the photoconductivity is fitted by the exponential model. The real part-related time constant τ₁ of ∼80 ps is independent of the pump power, while the imaginary part-related time constant τ₂ increases from 110 to 260 ps as the pump power increases. The former is explained by the phonon-assisted carrier recombination process and the latter is induced by the defect-assisted exciton recombination. Additionally, with the increase of pump power, the peak values of the real and imaginary parts of the complex conductivity exhibit a trend of saturation, which is attributed to the many-body effect. These results deepen the understanding of carrier dynamics in MoS₂ crystals.

Experimental Section

The freestanding layered MoS₂ crystal sample (SPI Supplies) is 90 µm in thickness, and its size is approximately 8 × 8 mm. This crystal sample is hexagonal 2H polytype with good crystalline quality as proved from the X-ray diffraction measurement in our previous work [20]. The Raman spectrum (SmartRaman confocal-micro-Raman module) is used to investigate the phonon characteristics of samples. The light source for the OPTP experiment is a Ti:sapphire femtosecond laser, which has a repetition rate of 1 kHz, a central wavelength of 800 nm, and a pulse width of 35 fs. The beam generated by the femtosecond laser is divided into three parts for the THz wave generation, THz wave detection, and optical pump functions [21]. 1) The THz radiation is generated from the air plasma by a two-color method under 800 and 400 nm laser excitation. The generated THz wave was focused onto the sample by a pair of off-axis parabolic mirrors in a transmission configuration. 2) The THz wave is probed by an electro-optic sampling method using a zinc telluride (ZnTe) (110) crystal as the THz detector. A delay line is used to measure the time domain signal of THz electric field E(t). 3) The pump beam is focused onto the MoS₂ sample in a transmission geometry. A pump delay line is used to change the delay time (t_pump) between the pump and probe pulses. The sample is measured in a normal incident angle for both the THz wave and the pump laser. All experiments were measured in a nitrogen environment to avoid THz absorption by atmospheric water vapor.

Results and Discussion

The Raman spectrum of layered MoS₂ crystal under 532 nm excitation is shown in Figure 1A. The peaks E¹_2g and A_1g are two Raman modes, indicating in-plane and out-of-plane vibrations. The frequencies of these two modes are at around 379.2 and 403.8 m⁻¹, which are consistent with the characteristic peak positions of MoS₂ crystal according to previous report [22]. Since there is a close relationship between the photoexcitation process and the band structure of materials, first-principles calculation is performed to study the band structure of MoS₂ crystal (The calculation software is Quantum Espresso. The Perdew-Burke-Ernzerh of generalized gradient approximation is used for the exchange-correlation potential. We use the ultrasoft pseudopotential to describe the electron−ion interactions and the ultrasoft pseudopotential incorporate the electron orbital of Mo 4s5s4p5p4d and O 2s2p. The in-plane lattice constants are set as a = 3.166 Å and c = 18.41 Å. Monkhorst−Pack k-mesh of 15 × 15 × 15 is set for sampling the Brillouin zone. The kinetic energy cutoffs of the plane waves for charge density and basis function are set to 25 and 300 Ry. The van der Waals corrections are described by the vdW-DF method). As shown in Figure 1B, the valence band maximum is at the Γ point, and the conduction band minimum lies at the symmetry point between K and Γ. The transition from valence band maximum to conduction band minimum is indirect [8]. Thus, MoS₂ crystal is an indirect semiconductor with a bandgap energy of 1.29 eV. Additionally, there is a direct transition with bandgap energy of 1.9 eV from valence band K point to conduction band K point, which cannot be realized under the 800 nm (1.55 eV) laser excitation.

FIGURE 1

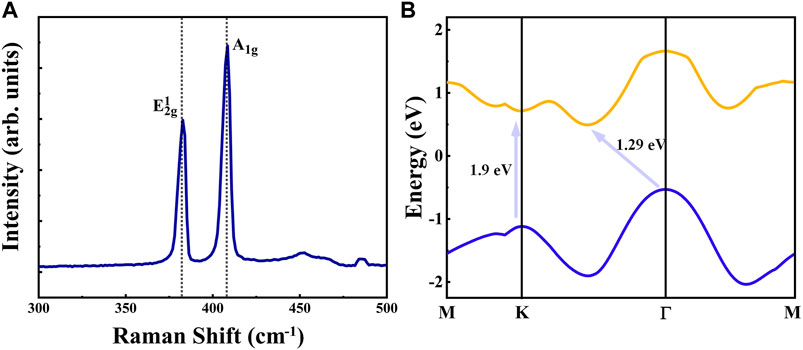
FIGURE 1. (A) Raman spectrum for layered MoS₂ crystal with 532 nm laser excitation. (B) Simplified energy band diagram based on first-principles calculation. The two arrows represent the direct and indirect transition from the valence band maximum to the conduction band minimum.

We will discuss the ultrafast THz complex conductivity dynamics of MoS₂ by using the OPTP technique in the following parts. The pump laser power is 20 mW. As shown in Figure 2A, the THz electric-field transmission waveform through the unexcited layered MoS₂ crystal E_ref is labeled as the blue curve, and the photo-induced THz waveform change ΔE at pump delay time t_pump = 20 ps is labeled as the yellow curve. The peak and zero-crossing values of the THz waveform are sensitive to absorption and phase change, respectively [23]. The former represents the real component of the complex conductivity and the latter represents the imaginary component of the complex conductivity. Specifically, the THz waveform changes at the peak and zero-crossing positions as a function of pump-probe delay time depict the photoexcitation dynamics of MoS₂ crystal, as shown in Figure 2B. Because the photon energy of the incident light is larger than the bandgap of MoS₂ crystal, real carriers will generate after excitation. We can see the THz waveform at both the peak and zero-crossing positions exhibit ultrafast optical response, indicating photo-induced carrier generation and recombination processes.

FIGURE 2

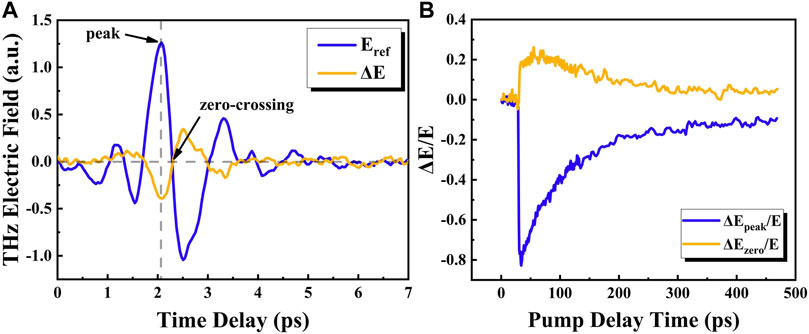
FIGURE 2. (A) Transmitted THz electric field E(t) (blue line) and photo-induced change of the THz waveform at pump delay time ΔE (t_pump = 20 ps) (yellow line) with the pump power of 20 mW for the MoS₂ crystal. (B) Pump-induced changes of the THz amplitude and phase of layered MoS₂ crystal at the peak and zero-crossing positions of the THz waveforms.

According to the peak and zero-crossing changes of the THz waveform, the photoconductivity can be calculated by the formula [24]:

$\Delta \sigma \left(t_{pump}\right)=-\frac{n_{air}+n_{THz}}{Z_{0}d}\frac{\Delta E\left(t,t_{pump}\right)}{E\left(t_{\max }\right)},(1)$

where n_air = 1 is the THz refractive index of air, n_THz = 2.95 is the THz refractive index of the MoS₂ crystal [22], Z₀ = 377 Ω is the free space impedance, and d = 90 μm is the thickness of the MoS₂ crystal. Using Eq. 1, the photoconductivity of MoS₂ with different pump power from 5 to 30 mW can be obtained. The real and imaginary parts of the photoconductivity are shown in Figures 3A,B, respectively. The sub-picosecond abrupt changes observed at ∼32 ps in Figures 3A,B are related to the process that the photo-induced carriers are excited from the valence band to the conduction band. Subsequently, the slow changes in Figure 3 correspond to the relaxation processes of photoconductivity. The real and imaginary parts of the complex conductivity reflect the absorption and chromatic dispersion properties of materials, respectively. According to previous reports, the THz absorption properties of MoS₂ are mainly decided by the photo-generated carriers [20], and the THz chromatic dispersion properties of MoS₂ could be contributed from the polarization effects of bound charges such as excitons [25, 26]. Here, the binding energy of exciton in MoS₂ crystals is approximately 0.1 eV [27], which is larger than the thermal energy (≈25 meV) at room temperature. Due to the strong Coulomb interactions among carriers, extraordinary exciton effects have been observed in TMDs such as MoS₂ [17], WSe₂ [21], and WS₂ [20]. Therefore, the exciton effect could be important for the imaginary part of photoconductivity of MoS₂ crystal due to the polarization effect.

FIGURE 3

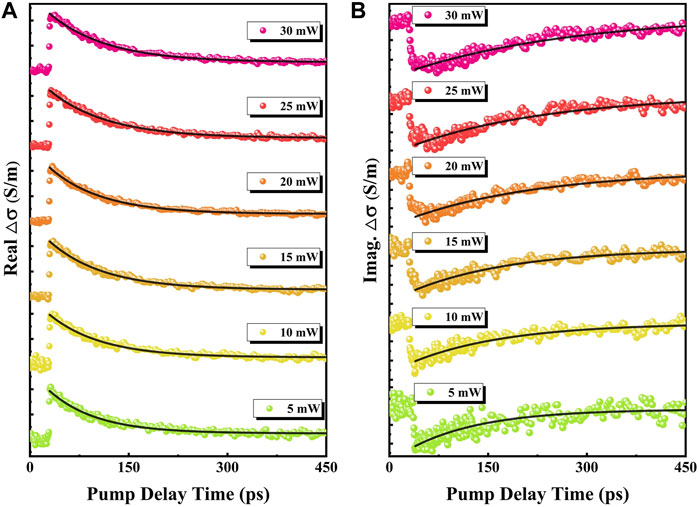
FIGURE 3. Transient photoinduced real (A) and imaginary (B) parts of the THz conductivity with different pump power. The dots are experimental data, and the solid lines are the exponential fitting.

Next, the time constants deduced from the pump delay time dependent complex conductivity are analyzed to reveal the relaxation dynamics of the photoexcited carriers and excitons in MoS₂ crystal. The experimental data in Figure 3 are exponentially fitted by $\Delta {\sigma }_{\mathit{RE}/\mathit{IM}}=\mathrm{Exp}((t-t_0)/{\tau }_{\mathrm{1,2}})$, where τ₁ (τ₂) is the time constant of the real (imaginary) part of the photoconductivity. The obtained τ₁ and τ₂ with different pump power are shown in Figure 4A as depicted by blue and yellow dots, respectively. The time constant τ₁ is approximately 80 ps, independent of the pump power. In comparison, the time constant τ₂ increases linearly from 110 to 260 ps with the increase of the pump power. In MoS₂ crystal, there are many possible relaxation processes. For the fast relaxation processes with a duration of sub-picosecond or several picoseconds, there are carrier-carrier scattering, carrier-phonon scattering, and exciton-exciton scattering in TMD materials [17, 28]. However, these fast processes cannot be identified from our experiment because of the limited time resolution. The time constant τ₁ and τ₂ can mainly be attributed to the slow relaxation processes. For the time constant τ₁, it has been reported that the phonon-mediated recombination time of free carriers is independent on the pump power in layered WSe₂ crystal, monolayer MoS₂, and suspended graphene [17, 21, 29]. Hence, the decay time τ₁ could be attributed to the phonon-assisted free carrier recombination. For the time constant τ₂, it has been reported that defect-assisted exciton recombination can result in an increase of decay time with pump power [20, 21]. The Auger processes for exciton capture by defects are believed to be important in most bulk semiconductors with high carrier densities [18]. Therefore, the time constant τ₂ could be governed by the exciton recombination via defect-assisted Auger process.

FIGURE 4

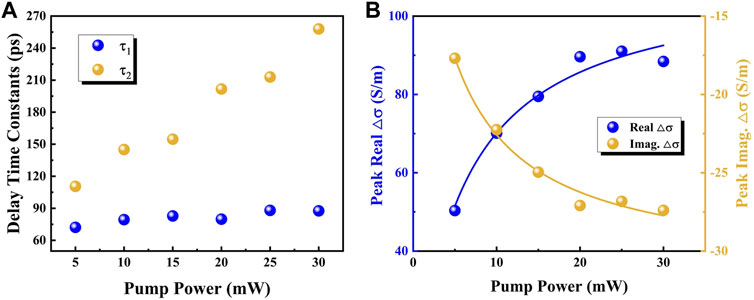
FIGURE 4. (A) Time constants extracted from the exponential fittings for the real and imaginary parts of the complex conductivity. (B) Real (imaginary) part of the complex conductivity at maximum (minimum) points as a function of pump power.

Additionally, the peak value of photoconductivity related to the carrier quantity has been discussed. Figure 4B shows the pump power dependence of the maximum (minimum) of the real (imaginary) part of photoconductivity. Both the real and imaginary parts exhibit enhanced absolute values with the increase of the pump power, and then present a saturable trend at the high pump power region. Because the photoconductivity is associated with the free carriers and excitons, the enhancement of the peak values indicates that the quantity of photo-induced carriers and excitons increase with the pump power. Then, equation $\Delta \sigma \propto P/(P+P_s)$ (P is the pump power and P_s is the saturation pump power) [21] is used to fit the experimental data. The saturation pump power P_s of the real and imaginary photoconductivity are 3.6 and 5.7 mW, respectively. These results suggest that both photo-induced carriers and excitons are generated before the pump power of 3.6 mW; then, the photo-induced carriers are saturated and excitons are continuously generated before 5.7 mW; at last, both the carriers and excitons become saturated due to the possible many-body effect at high carrier concentration [30, 31]. The carrier density is calculated as [16]:

$N_0=\left[1-\frac{{\left(n_0-1\right)}^2+{\kappa }_0^2}{{\left(n_0+1\right)}^2+{\kappa }_0^2}\right]{\alpha }_0{F}_0/ћ\mathit{\omega },(2)$

where n₀ = 4.83 is the real part of the refraction index, κ₀ = 0.78 is the imaginary part of the refraction index, and α₀ = 1.23×10⁷ m⁻¹ is the absorption coefficient [22, 32]. The F₀ is the peak energy fluence of the pump pulse, which can be calculated by $F_0=4\ln \left(2\right)P/\left(\pi f{w}^2\right)$, where P is average pump power, f = 1 kHz is the repetition rate of the laser, and w = 2.5 mm is the radius of focus pump spot. According to Eq. 2, the numbers of photo-induced carriers are calculated to be 1.95×10²⁵, 3.9×10²⁵, 5.85×10²⁵, 7.8×10²⁵, 9.75×10²⁵, 11.7×10²⁵ m⁻³, with 5, 10, 15, 20, 25, and 30 mW pump power, respectively.

Finally, the frequency-dependent photoconductivity is obtained by the fast Fourier transform of the time-domain signals. The real and imaginary parts of the photoconductivity are measured at the delay time of 5 ps with a variable pump power of 5, 10, 20, and 30 mW as shown in Figure 5. The Drude model can be used to describe the free carrier motion and the Smith term includes the carrier backscattering. In addition, the exciton effect in relaxation process can be described by the Lorentz model. Therefore, we use the Drude–Smith model (free charge species) combined with the Lorentz model (exciton species) to describe the photo-induced complex conductivity. The fitting formula of the Drude-Smith-Lorentz model is described as follows [21]:

${\sigma }_{D-S-L}=\frac{D_0\tau }{1-i\omega \tau }\left(1+\frac{C}{1-i\omega \tau }\right)+\frac{S\omega }{i\left({\omega }_0^2-{\omega }^2\right)+\omega \gamma },(3)$

where D₀ is the Drude weight, τ is the free carrier relaxation time, ω is the angular frequency, C ranging from -1 to 0 is related to the degree of carrier scattering, S is the oscillator strength, ω₀ is the resonant frequency, and γ is the damping coefficient. From Figure 5, the curves calculated with Eq. 3 fit well with the dot-denoted experimental data. The fitting coefficients are given in Table 1. The relaxation time τ increases with the increase of pump power. The constant C has no pump power dependence, suggesting that the carrier backscattering is not affected by the pump power. In addition, the frequency ω₀ of the oscillator response has no obvious change with the increase of pump power.

FIGURE 5

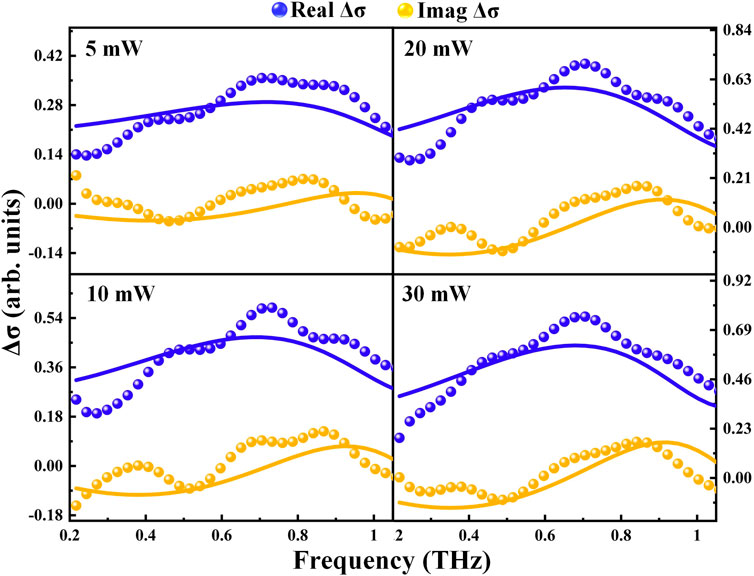
FIGURE 5. Frequency-dependent transient real and imaginary parts of the photoconductivity measured at the delay time of 5 ps with various pump power of 5, 10, 20, and 30 mW. The blue and yellow solid lines represent the fitting results of the real and imaginary parts of photoconductivity by Drude–Smith-Lorentz model, respectively.

TABLE 1

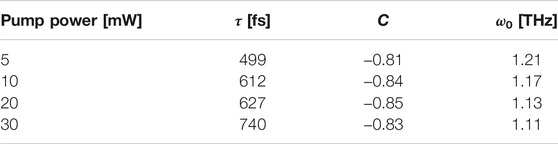
TABLE 1. Fitting parameters used in Figure 5.

Conclusion

We have studied the ultrafast photoconductivity response in MoS₂ crystal by OPTP spectroscopy. The time constant of the real part of the photoconductivity, which is independent of the pump power, demonstrates the photo-induced free carrier recombination via phonon-assistance of ∼80 ps. The time constant of the imaginary part of the photoconductivity increases with the pump power, revealing the excitons annihilated by a defect-assisted process of ∼110–260 ps. The peak values of both the real and imaginary parts of photoconductivity tend to saturate with the increase of pump power due to the many-body effect. This work unveils the relaxation processes of photo-generated carriers and excitons, which could be helpful for developing novel optoelectronic devices based on MoS₂.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

XX, CH, YZ, and YY contributed to conception and design of the study. CH, LZ, and YH designed and built the optics system. YH organized the database. YY wrote the first draft of the article. YY, CH, YZ, and XX wrote sections of the article. All authors contributed to article revision, read, and approved the submitted version.

Funding

This work was supported by National Natural Science Foundation of China (No. 12074311, 12004310, 11974279, and 11774288), Natural Science Foundation of Shaanxi Province (2019JC-25, 2020JQ-567).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Strait JH, Nene P, Rana F. High Intrinsic Mobility and Ultrafast Carrier Dynamics in Multilayer Metal-dichalcogenide MoS₂. Phys Rev B (2014) 90(24), 245402. doi:10.1103/PhysRevB.90.245402

CrossRef Full Text | Google Scholar

2. Huang Y, Zhu L, Yao Z, Zhang L, He C, Zhao Q, et al. Terahertz Surface Emission from Layered MoS₂ Crystal: Competition between Surface Optical Rectification and Surface Photocurrent Surge. J Phys Chem C (2017) 122(1):481–8. doi:10.1021/acs.jpcc.7b09723

CrossRef Full Text | Google Scholar

3. Mak KF, Lee C, Hone J, Shan J, Heinz TF. Atomically Thin MoS₂: A New Direct-Gap Semiconductor. Phys Rev Lett (2010) 105(13):136805. doi:10.1103/PhysRevLett.105.136805

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Koppens FHL, Mueller T, Avouris P, Ferrari AC, Vitiello MS, Polini M. Photodetectors Based on Graphene, Other Two-Dimensional Materials and Hybrid Systems. Nat Nanotech (2014) 9(10):780–93. doi:10.1038/nnano.2014.215

CrossRef Full Text | Google Scholar

5. Sherson JF, Krauter H, Olsson RK, Julsgaard B, Hammerer K, Cirac I, et al. Quantum Teleportation between Light and Matter. Nature (2006) 443(7111):557–60. doi:10.1038/nature05136

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Radisavljevic B, Radenovic A, Brivio J, Giacometti V, Kis A. Single-layer MoS₂ Transistors. Nat Nanotech (2011) 6(3):147–50. doi:10.1038/nnano.2010.279

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Singh E, Kim KS, Yeom GY, Nalwa HS. Two-dimensional Transition Metal Dichalcogenide-Based Counter Electrodes for Dye-Sensitized Solar Cells. RSC Adv (2017) 7(45):28234–90. doi:10.1039/c7ra03599c

CrossRef Full Text | Google Scholar

8. Cheng Y, Schwingenschlögl U. MoS₂: A First-Principles Perspective. In: ZM Wang, editor. MoS₂: Materials, Physics, and Devices. Cham: Springer International Publishing (2014). p. 103–28. doi:10.1007/978-3-319-02850-7_5

CrossRef Full Text | Google Scholar

9. Huang Y, Yartsev A, Guan S, Zhu L, Zhao Q, Yao Z, et al. Hidden Spin Polarization in the Centrosymmetric MoS₂ crystal Revealed via Elliptically Polarized Terahertz Emission. Phys Rev B (2020) 102(8):085205. doi:10.1103/PhysRevB.102.085205

CrossRef Full Text | Google Scholar

10. Radisavljevic B, Kis A. Mobility Engineering and a Metal-Insulator Transition in Monolayer MoS₂. Nat Mater (2013) 12(9):815–20. doi:10.1038/nmat3687

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Roy K, Padmanabhan M, Goswami S, Sai TP, Ramalingam G, Raghavan S, et al. Graphene-MoS₂ Hybrid Structures for Multifunctional Photoresponsive Memory Devices. Nat Nanotech (2013) 8(11):826–30. doi:10.1038/nnano.2013.206

CrossRef Full Text | Google Scholar

12. Klots AR, Newaz AKM, Wang B, Prasai D, Krzyzanowska H, Lin J, et al. Probing Excitonic States in Suspended Two-Dimensional Semiconductors by Photocurrent Spectroscopy. Sci Rep (2014) 4:6608. doi:10.1038/srep06608

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Tonndorf P, Schmidt R, Böttger P, Zhang X, Börner J, Liebig A, et al. Photoluminescence Emission and Raman Response of Monolayer MoS_2, MoSe_2, and WSe_2. Opt Express (2013) 21(4):4908–16. doi:10.1364/OE.21.004908

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Cheng R, Li D, Zhou H, Wang C, Yin A, Jiang S, et al. Electroluminescence and Photocurrent Generation from Atomically Sharp WSe2/MoS2 Heterojunction P-N Diodes. Nano Lett (2014) 14(10):5590–7. doi:10.1021/nl502075n

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang Q, Ge S, Li X, Qiu J, Ji Y, Feng J, et al. Valley Carrier Dynamics in Monolayer Molybdenum Disulfide from Helicity-Resolved Ultrafast Pump-Probe Spectroscopy. ACS Nano (2013) 7(12):11087–93. doi:10.1021/nn405419h

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kumar N, He J, He D, Wang Y, Zhao H. Charge Carrier Dynamics in Bulk MoS₂ crystal Studied by Transient Absorption Microscopy. J Appl Phys (2013) 113(13):133702. doi:10.1063/1.4799110

CrossRef Full Text | Google Scholar

17. Shi H, Yan R, Bertolazzi S, Brivio J, Gao B, Kis A, et al. Exciton Dynamics in Suspended Monolayer and Few-Layer MoS₂ 2D Crystals. ACS Nano (2013) 7(2):1072–80. doi:10.1021/nn303973r

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wang H, Zhang C, Rana F. Ultrafast Dynamics of Defect-Assisted Electron-Hole Recombination in Monolayer MoS₂. Nano Lett (2015) 15(1):339–45. doi:10.1021/nl503636c

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Kar S, Su Y, Nair RR, Sood AK. Probing Photoexcited Carriers in a Few-Layer MoS₂ Laminate by Time-Resolved Optical Pump-Terahertz Probe Spectroscopy. ACS Nano (2015) 9(12):12004–10. doi:10.1021/acsnano.5b04804

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Xing X, Zhao L, Zhang Z, Liu X, Zhang K, Yu Y, et al. Role of Photoinduced Exciton in the Transient Terahertz Conductivity of Few-Layer WS₂ Laminate. J Phys Chem C (2017) 121(37):20451–7. doi:10.1021/acs.jpcc.7b05345

CrossRef Full Text | Google Scholar

21. He C, Zhu L, Zhao Q, Huang Y, Yao Z, Du W, et al. Competition between Free Carriers and Excitons Mediated by Defects Observed in Layered WSe₂ Crystal with Time-Resolved Terahertz Spectroscopy. Adv Opt Mater (2018) 6(19):1800290. doi:10.1002/adom.201800290

CrossRef Full Text | Google Scholar

22. Huang Y, Zhu L, Zhao Q, Guo Y, Ren Z, Bai J, et al. Surface Optical Rectification from Layered MoS₂ Crystal by THz Time-Domain Surface Emission Spectroscopy. ACS Appl Mater Inter (2017) 9(5):4956–65. doi:10.1021/acsami.6b13961

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Cunningham PD. Accessing Terahertz Complex Conductivity Dynamics in the Time-Domain. IEEE Trans THz Sci Technol (2013) 3(4):494–8. doi:10.1109/tthz.2013.2258193

CrossRef Full Text | Google Scholar

24. Cunningham PD, Hayden LM, Yip H-L, Jen AK-Y. Charge Carrier Dynamics in Metalated Polymers Investigated by Optical-Pump Terahertz-Probe Spectroscopy. J Phys Chem B (2009) 113(47):15427–32. doi:10.1021/jp906454g

CrossRef Full Text | Google Scholar

25. Wang F, Shan J, Islam MA, Herman IP, Bonn M, Heinz TF. Exciton Polarizability in Semiconductor Nanocrystals. Nat Mater (2006) 5(11):861–4. doi:10.1038/nmat1739

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Jensen SA, Ulbricht R, Narita A, Feng X, Müllen K, Hertel T, et al. Ultrafast Photoconductivity of Graphene Nanoribbons and Carbon Nanotubes. Nano Lett (2013) 13(12):5925–30. doi:10.1021/nl402978s

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Komsa H-P, Krasheninnikov AV. Effects of Confinement and Environment on the Electronic Structure and Exciton Binding Energy of MoS₂ from First Principles. Phys Rev B (2012) 86(24), 241201. doi:10.1103/PhysRevB.86.241201

CrossRef Full Text | Google Scholar

28. Sun D, Rao Y, Reider GA, Chen G, You Y, Brézin L, et al. Observation of Rapid Exciton-Exciton Annihilation in Monolayer Molybdenum Disulfide. Nano Lett (2014) 14(10):5625–9. doi:10.1021/nl5021975

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Gao B, Hartland G, Fang T, Kelly M, Jena D, Xing H, et al. Studies of Intrinsic Hot Phonon Dynamics in Suspended Graphene by Transient Absorption Microscopy. Nano Lett (2011) 11(8):3184–9. doi:10.1021/nl201397a

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Chen K, Ghosh R, Meng X, Roy A, Kim J-S, He F, et al. Experimental Evidence of Exciton Capture by Mid-gap Defects in CVD Grown Monolayer MoSe₂. Npj 2d Mater Appl (2017) 1(1):15. doi:10.1038/s41699-017-0019-1

CrossRef Full Text | Google Scholar

31. Mai C, Barrette A, Yu Y, Semenov YG, Kim KW, Cao L, et al. Many-body Effects in Valleytronics: Direct Measurement of valley Lifetimes in Single-Layer MoS₂. Nano Lett (2014) 14(1):202–6. doi:10.1021/nl403742j

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Yan X, Zhu L, Zhou Y, E Y, Wang L, Xu X. Dielectric Property of MoS_2 crystal in Terahertz and Visible Regions. Appl Opt (2015) 54(22):6732. doi:10.1364/ao.54.006732

PubMed Abstract | CrossRef Full Text | Google Scholar