Pseudospin-dependent Acoustic Topological Insulator by Sonic Crystals With Same Hexagonal Rods

We report the experimental and numerical realization of a pseudospin-dependent acoustic topological insulator based on two sonic crystals constructed by the same regular hexagonal rods. Based on the zone folding mechanism, we obtain double Dirac cones with a four-fold deterministic degeneracy in the sonic crystal, and realize a band inversion and topological phase transition by rotating the rods. We observe the topologically protected one-way sound propagation of pseudospin-dependent edge states in a designed topological insulator composed of two selected sonic crystals with different rotation angles of the rods. Furthermore, we experimentally demonstrate the robustness of topological sound propagation against two types of defects, in which the edge states are almost immune to backscattering, and remain pseudospin-dependent characteristics. Our work provides a diverse route for designing tunable topological functional sound devices.

Introduction

In the past few years, acoustic topological insulators (ATIs) have become a hot topic in the area of acoustics for its great potential applications, such as acoustic-noise reduction [1], acoustic beam splitter [2] and acoustic communications [3]. However, the intrinsic difference between electrons and acoustics poses a challenge to realize a spin-like degree of freedom for acoustics due to the longitudinal polarization characteristics of sound. To overcome it, four types of ATIs have been proposed successively. To mimic the quantum Hall effect and break time-reversal symmetry, topologically protected edge states were observed in acoustic waveguides by introducing circular flowing air [4–9]. Later, analogous Floquet ATIs were proposed based on coupled acoustic trimers or strong coupling ring resonator waveguides [10–13]. Moreover, to realize acoustic valley Hall (AVH) states, the nonzero Berry curvature located near the valley K/Kʹ was obtained by breaking mirror or inversion symmetry, and valley-projected topological edge states were observed at the interface between two sonic crystals (SCs) with distinct AVH phases [14–28]. Furthermore, to mimic quantum spin Hall states in acoustics, the SCs with C₆ crystal symmetry were introduced to realize artificial pseudospins-1/2 states by hybridizing degenerate modes [29–39]. Generally, the observed double Dirac cones are accidental degeneracy in these pseudospin-dependent ATIs, and the sizes or shapes of rods in the SCs are different, which is still a challenge for practical applications.

Recently, by introducing the zone folding mechanism, a type of pseudospin-dependent ATI without depending on a fixed filling ratio was proposed [30, 31], in which the observed double Dirac cones were a deterministic degeneracy. These types of pseudospin-dependent ATIs were designed by fictitious soft metamaterial rods [30] and three circular rods with different radius [31], and the complex structures greatly limit their applications. Based on the SCs composed of same rods, the experimental realization of the pseudospin-dependent ATIs with a deterministic degeneracy is still a challenge.

In this work, we propose a pseudospin-dependent ATI constructed by two airborne SCs which consist of the same rods. Based on the zone folding mechanism, we obtain double Dirac cones with the deterministic degeneracy, and realize a band inversion by simply rotating the rods in the SCs. Moreover, we design an ATI composed of two SCs with different rotation angles of the rods, and observe a one-way sound propagation of topological edge states. Finally, we experimentally demonstrate the robustness of the topologically protected sound propagation against two types of defects of a disorder and a bend.

Results and Discussions

Figure 1A shows an airborne SC composed of regular hexagonal rods with the side length l = 14.4 mm. The proposed SC can be described by the unit A or B, in which the lattice constants of the units A and B are a₀ = 30 mm and a = 30$\sqrt{3}$mm, respectively. By simply rotating these rods, we obtain another type of SC composed of the unit B (shown in Figure 1B), in which the rotation angles of a central rod and six surrounding rods are θ₀ and θ, respectively. Figure 1C shows the folding mechanism of the Brillouin zones (BZs) for the units A and B. In the BZ, the point K₀ with high symmetry of the unit A can be folded into the point Γ of the unit B. Here, we use the COMSOL Multiphysics software to numerically simulate propagation characteristics of sound. The regular hexagon rods are fabricated with polymethyl methacrylate (PMMA), which is used to meet the condition of sound hard boundary in numerical models. The material parameters are adopted as follows: the density ρ = 1180 kg/m³, the longitudinal wave velocity c_l = 2730 m/s and the transversal wave velocity c_t = 1430 m/s for PMMA; the density ρ₀ = 1.18 kg/m³ and sound velocity c₀ = 346 m/s for air.

FIGURE 1

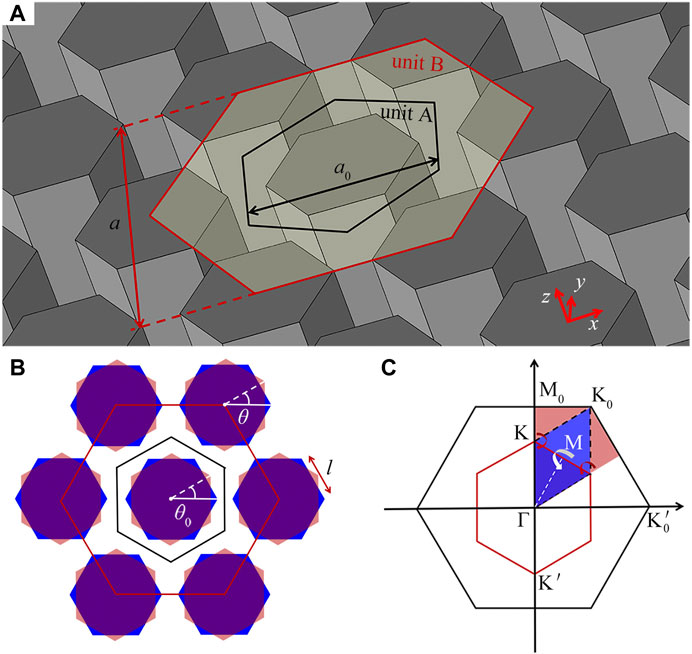
FIGURE 1. (A) Schematic of an airborne SC composed of regular hexagonal rods. Black and red open regular hexagons refer to the units A and B with the lattice constants a₀ and a, respectively. (B) Schematic of the unit B with two types of configurations. Red regular hexagons exhibit its rotation state, and the parameters θ₀ and θ are the rotation angles of a central rod and six surrounding rods, respectively. Blue regular hexagons represent its riginal configuration (θ₀ = θ = 0°). (C) Schematic of the folding mechanism of the BZs for the units A and B, corresponding to the black and red open regular hexagons, respectively.

Figures 2A, B show the dispersion relations of the units A and B in the SC-I (θ₀ = 0^o and θ = 0^o), respectively. As shown in Figure 2A, there exists a Dirac cone with the two-fold degeneracy at the point K₀ for the unit A, which is attributed to its C_6v symmetry. However, for the unit B, we observe double Dirac cones with a four-fold deterministic degeneracy at the point Γ (Figure 2B). The dispersion characteristics of both units agree well with the folding of the BZ.

FIGURE 2

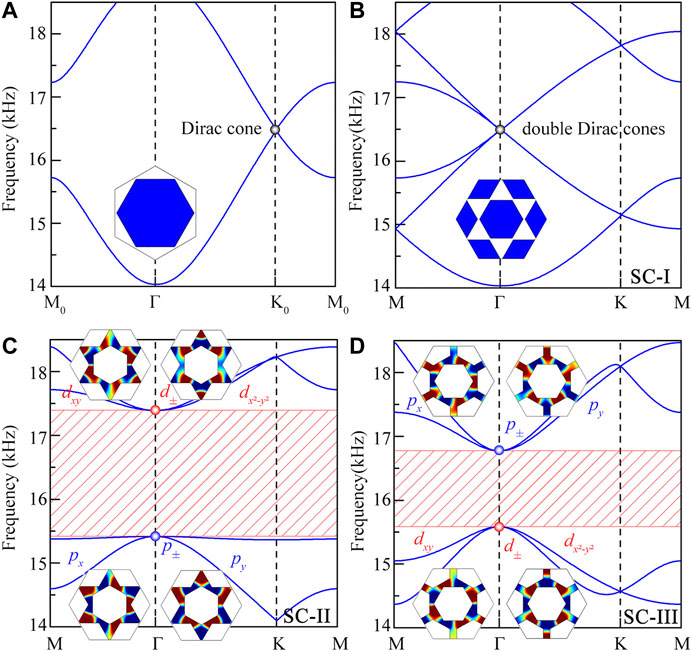
FIGURE 2. Dispersion relations of the units (A) A and (B) B in the SC-I (θ₀ = 0^o and θ = 0^o), and of the unit B in the (C) SC-II (θ₀ = 30^o and θ = 0^o) and (D) SC-III (θ₀ = 0^o and θ = 30^o). Black dots in Figures 2A,B represent the Dirac points. Eight insets in Figures 2C,D are the simulated pressure eigenfunctions of the pseudospin dipolar (p_x and p_y) and quadrupolar modes (d_xy and $d_{x^2-y^2}$) at the BZ center (red and blue dots) of the SC-II and SC-III, respectively.

Figures 2C,D show the dispersion relations of the unit B in the SC-II (θ₀ = 30^o and θ = 0^o) and SC-III (θ₀ = 0^o and θ = 30^o), respectively, in which the four-fold degeneracy is broken, and is divided into a double two-fold degeneracy (p and d types) for both cases. We can see that the bands of the d type are above the p type in the SC-II (Figure 2C), while the bands of the p type are above the d type in the SC-III. The phenomenon of band inversion arises from the increasing coupling strength between the hexagonal rods by changing the values of θ₀ and θ. Additionally, the pressure eigenfunctions of the dipolar (p_x and p_y) and quadrupolar (d_xy and $d_{x^2-y^2}$) modes which correspond to the blue and red dots are displayed in eight insets of Figures 2C,D, further showing a typical characteristic of the band inversion. Additionally, we also calculated the Chern numbers of SC-II and SC-III based on the Wilson-loop method (shown in the supplementary material), which further verify that both SCs have different topological phases. Here, it is worth mentioning that the pseudospin-1/2 modes of sound are the basis for imitating quantum spin Hall effect in acoustics, which can be realized by hybridizing both modes p and d as$p_{\pm }=\left(p_x\pm i{p}_y\right)/\sqrt{2}$and$d_{\pm }=\left(d_{x^2-y^2}\pm i{d}_{xy}\right)/\sqrt{2}$.

Figure 3A shows the dispersion relations of the designed ATI composed of the SC-II and SC-III, in which the SC-III is placed on the upside of the SC-II. We observe a pair of edge states (red and blue solid lines) in the overlapped bulk band gap of both SCs, which is located at the domain wall between the SC-II and SC-III. Here, the group velocity of the edge states is determined by the slope of the bands (red and blue solid lines), and thus the edge states have the same acoustic velocity, but propagate in the opposite directions. Moreover, it is obvious that there exists a mini gap located between the bands of two edge states, which mainly arises from the reduction of the C_6ν point group symmetry at the domain wall between SC-II and SC-III. Figure 3B shows the eigen-modes for the real (M₁) and imaginary (M₂) parts of the edge state at the point A. The edge states at the points A and B can be obtained by hybridizing the modes M₁ and M₂ as the forms of M₁+iM₂ and M₁−iM₂, respectively. To further exhibit the pseudospin-dependent characteristics, we simulate the distributions of energy flow around the domain wall of a supercell at the points A and B (shown in Figure 3C). We find that there exist energy vortexes around the domain wall, and the chirality of the vortex is clockwise at the point A, but is anticlockwise at the point B, which corresponds to the pseudospin− (red circular arrow) and pseudospin+ (blue circular arrow), respectively.

FIGURE 3

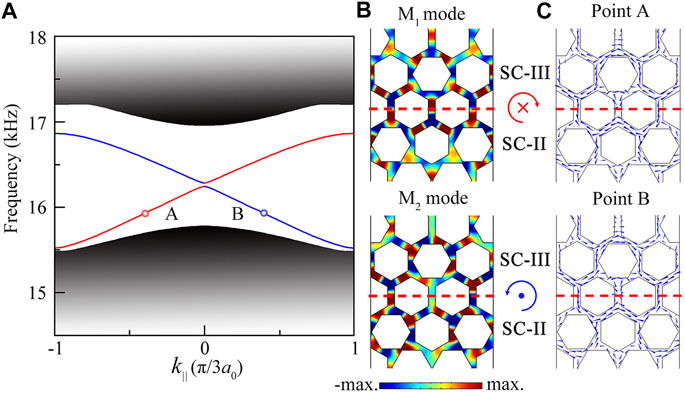
FIGURE 3. (A) Dispersion relations of the ATI composed of the SC-II and SC-III. (B) Simulated pressure eigenfunctions (M₁ and M₂ modes) of the supercell at the point A (k_|| = −0.4). (C) Simulated acoustic energy flow of the pseudospin-dependent edge states at the points A and B (k_|| = 0.4). Red dashed lines refer to the domain wall of the ATI.

Next, we simulate the pseudospin-dependent one-way propagation of sound in the ATI composed of the SC-II and SC-III, in which the intensity distributions excited by two types of chiral sources (green stars) with the opposite chirality at 16.0 kHz are shown in Figure 4. The chiral sources are realized by six point sound sources arranged in a circular array with different initial phase delays, which are placed at the center of the domain wall. As shown in Figure 4A, when the chirality of the source is anticlockwise, the edge state propagates toward the left side along the domain wall with almost negligible backscattering. In addition, it is found from the zoom of R1 that, the chirality of the energy vortex remains the same during its propagation along the domain wall, which further demonstrates the one-way propagation of the pseudospin + edge state. However, when the chirality of the source is clockwise, the pseudospin edge state is excited and propagates toward the right side. Therefore, we demonstrate the one-way sound propagation of the pseudospin-dependent edge states.

FIGURE 4

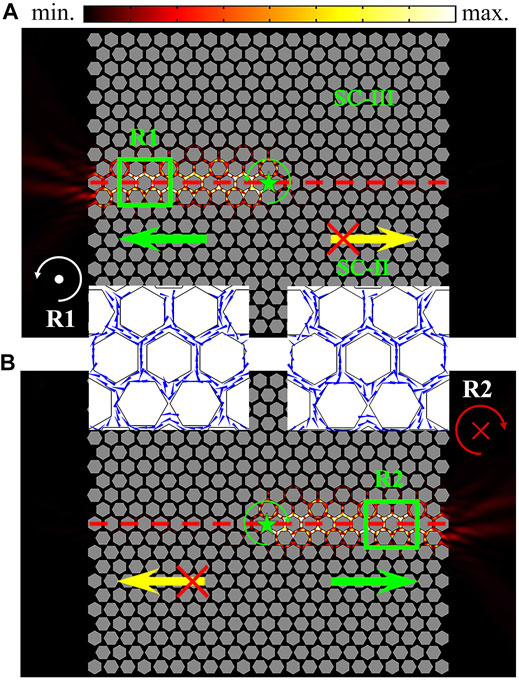
FIGURE 4. Simulated intensity distributions in the ATI at 16.0 kHz (within the bulk band gap). Two types of chiral sound sources (green stars) with the opposite chirality (green circular arrows) are placed at the center of the domain wall, realizing one-way sound propagation towards the (A) left and (B) right sides along the domain wall. Red dashed lines represent the domain wall, and blue arrows in the zooms R1 and R2 refer to the direction of energy flow.

To demonstrate the robustness feature of the pseudospin-dependent edge states, we separately introduce two kinds of defects (a lattice disorder and a bend) around the domain wall of the ATI. Figure 5A shows the photograph of the sample without the defects. The description of experimental set-up is displayed in the supplementary material. Figures 5B–D show the simulated intensity distributions in the ATIs without defects and with the defects of a disorder and a bend, respectively, in which a point source is placed at the left side of the domain wall. Meanwhile, the measured intensity distributions in the scanning region (green open rectangle) are shown at the right side. We find that the smooth propagations of the pseudospin edge states still exist with both types of defects (Figures 5C,D), and the corresponding intensity distributions are almost the same as those in Figure 5B. The experimental results agree well with the simulations. Beyond that, in the zooms of R3-R5 (Figures 5B–D), the chirality of edge states is not affected by both defects, showing high robustness of the pseudospin-dependent edge states.

FIGURE 5

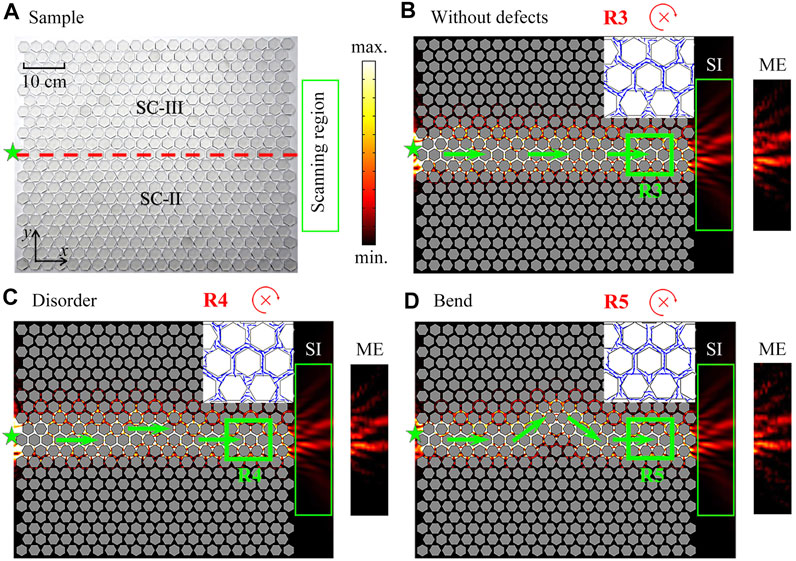
FIGURE 5. (A) Photograph of an ATI without defects. Green stars and red dashed lines represent the point sound source and domain wall, respectively. Green open rectangle is the scanning region in the measurement. Simulated (SI) and measured (ME) distributions of intensity field in the ATIs with three different configurations at 16.0 kHz, corresponding to (B) without defects, with (C) a lattice disorder and (D) a bend around the domain wall. Green arrows are the propagation paths of sound in the ATIs. Blue arrows in the zooms R3-R5 represent direction of energy flow.

Finally, to demonstrate the topologically protected sound propagation, we also experimentally measure the transmission spectra for the three types of ATIs in Figures 5B–D, which is shown in Figure 6. Note that the transmittance spectra for the three cases are almost the same, especially in the overlapped bulk band gap (black shaded region). Therefore, we further experimentally demonstrate the robustness of the pseudospin-dependent edge states.

FIGURE 6

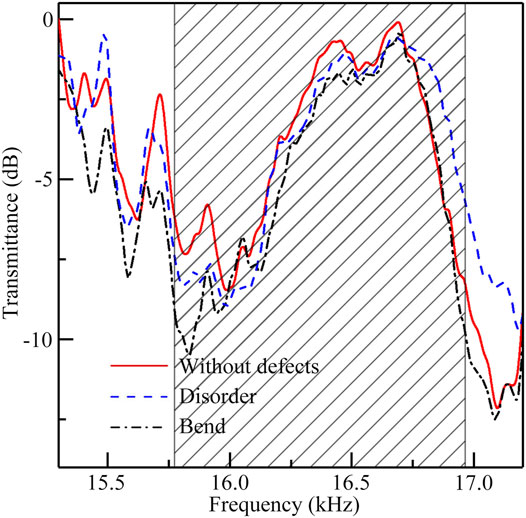
FIGURE 6. Measured transmittance spectra of the ATIs with and without defects. Black shaded region represents the overlapped bulk band gap.

Conclusions

In conclusion, we have demonstrated a pseudospin-dependent ATI composed of two SCs with the same regular hexagonal rods. The results show that, by using the zone folding mechanism, the double Dirac cones with a four-fold deterministic degeneracy are observed in the SC, and the band inversion is realized by rotating the rods. Moreover, the ATI composed of two SCs with different rotation angles of the rods is designed, and the one-way sound propagation of the pseudospin-dependent edge states excited by the chiral sound sources in the ATI is observed. Furthermore, by measuring the transmission spectra in the ATIs with and without defects, the robustness of sound propagation against two types of defects (a lattice disorder and a bend) is demonstrated. The simulated and measured results agree well with each other. Our work opens a new venue to design tunable pseudospin-dependent ATIs with various functionalities and applications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11774137, 51779107 and 12174159), the China Postdoctoral Science Foundation (Grant No. 2020M671351), and the Postdoctoral Research Funding Program of Jiangsu Province (Grant No. 2021K567C).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.762567/full#supplementary-material

References

1. He C, Ni X, Ge H, Sun X-C, Chen Y-B, Lu M-H, et al. Acoustic Topological Insulator and Robust One-Way Sound Transport. Nat Phys (2016) 12:1124–9. doi:10.1038/nphys3867

CrossRef Full Text | Google Scholar

2. Ye L, Qiu C, Lu J, Wen X, Shen Y, Ke M, et al. Observation of Acoustic valley Vortex States and valley-chirality Locked Beam Splitting. Phys Rev B (2017) 95(17):174106. doi:10.1103/physrevb.95.174106

CrossRef Full Text | Google Scholar

3. Zhang Z, Tian Y, Wang Y, Gao S, Cheng Y, Liu X, et al. Directional Acoustic Antennas Based on Valley-Hall Topological Insulators. Adv Mater (2018) 30(36):1803229. doi:10.1002/adma.201803229

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yang Z, Gao F, Shi X, Lin X, Gao Z, Chong Y, et al. Topological Acoustics. Phys Rev Lett (2015) 114(11):114301. doi:10.1103/physrevlett.114.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Khanikaev AB, Fleury R, Mousavi SH, Alù A. Topologically Robust Sound Propagation in an Angular-Momentum-Biased Graphene-like Resonator Lattice. Nat Commun (2015) 6:8260. doi:10.1038/ncomms9260

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Ni X, He C, Sun X-C, Liu X-p., Lu M-H, Feng L, et al. Topologically Protected One-Way Edge Mode in Networks of Acoustic Resonators with Circulating Air Flow. New J Phys (2015) 17(5):053016. doi:10.1088/1367-2630/17/5/053016

CrossRef Full Text | Google Scholar

7. Chen ZG, Wu Y. Tunable Topological Phononic Crystals. Phys Rev Appl (2016) 5(5):054021. doi:10.1103/physrevapplied.5.054021

CrossRef Full Text | Google Scholar

8. Ding Y, Peng Y, Zhu Y, Fan X, Yang J, Liang B, et al. Experimental Demonstration of Acoustic Chern Insulators. Phys Rev Lett (2019) 122:014302. doi:10.1103/PhysRevLett.122.014302

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Gao P, Zhang ZW, Christensen J. Sonic valley-Chern Insulators. Phys Rev B (2020) 101(2):020301. doi:10.1103/physrevb.101.020301

CrossRef Full Text | Google Scholar

10. Fleury R, Khanikaev AB, Alù A. Floquet Topological Insulators for Sound. Nat Commun (2016) 7:11744. doi:10.1038/ncomms11744

PubMed Abstract | CrossRef Full Text | Google Scholar

11. He C, Li Z, Ni X, Sun X-C, Yu S-Y, Lu M-H, et al. Topological Phononic States of Underwater Sound Based on Coupled Ring Resonators. Appl Phys Lett (2016) 108:031904. doi:10.1063/1.4940403

CrossRef Full Text | Google Scholar

12. Peng Y-G, Qin C-Z, Zhao D-G, Shen Y-X, Xu X-Y, Bao M, et al. Experimental Demonstration of Anomalous Floquet Topological Insulator for Sound. Nat Commun (2016) 7:13368. doi:10.1038/ncomms13368

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wei Q, Tian Y, Zuo SY, Cheng Y, Liu XJ Experimental Demonstration of Topologically Protected Efficient Sound Propagation in an Acoustic Waveguide Network. Phys Rev B (2017) 95:094305. doi:10.1103/physrevb.95.094305

CrossRef Full Text | Google Scholar

14. Lu J, Qiu C, Ye L, Fan X, Ke M, Zhang F, et al. Observation of Topological valley Transport of Sound in Sonic Crystals. Nat Phys (2016) 13:369–74. doi:10.1038/nphys3999

CrossRef Full Text | Google Scholar

15. Lu J, Qiu C, Deng W, Huang X, Li F, Zhang F, et al. Valley Topological Phases in Bilayer Sonic Crystals. Phys Rev Lett (2018) 120:116802. doi:10.1103/physrevlett.120.116802

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zhang ZW, Tian Y, Cheng Y, Wei Q, Liu XJ, Christensen J. Topological Acoustic Delay Line. Phys Rev Appl (2018) 9(3):034032. doi:10.1103/physrevapplied.9.034032

CrossRef Full Text | Google Scholar

17. Yang Y, Yang Z, Zhang B. Acoustic valley Edge States in a Graphene-like Resonator System. J Appl Phys (2018) 123(9):091713. doi:10.1063/1.5009626

CrossRef Full Text | Google Scholar

18. Wen X, Qiu C, Lu J, He H, Ke M, Liu Z. Acoustic Dirac Degeneracy and Topological Phase Transitions Realized by Rotating Scatterers. J Appl Phys (2018) 123(9):091703. doi:10.1063/1.5004073

CrossRef Full Text | Google Scholar

19. Zhang Z, Cheng Y, Liu X. Achieving Acoustic Topological valley-Hall States by Modulating the Subwavelength Honeycomb Lattice. Sci Rep (2018) 8:16784. doi:10.1038/s41598-018-35214-9

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Xie BY, Liu H, Cheng H, Liu ZY, Chen SQ, Tian JG. Acoustic Topological Transport and Refraction in a Kekulé Lattice. Phys Rev Appl (2019) 11:044086. doi:10.1103/physrevapplied.11.044086

CrossRef Full Text | Google Scholar

21. Zhu ZX, Huang XQ, Lu JY, Yan M, Li F, Deng WY, et al. Negative Refraction and Partition in Acoustic Valley Materials of a Square Lattice. Phys Rev Appl (2019) 12:024007. doi:10.1103/physrevapplied.12.024007

CrossRef Full Text | Google Scholar

22. Shen Y, Qiu C, Cai X, Ye L, Lu J, Ke M, et al. Valley-projected Edge Modes Observed in Underwater Sonic Crystals. Appl Phys Lett (2019) 114:023501. doi:10.1063/1.5049856

CrossRef Full Text | Google Scholar

23. Shan Q, Yu D, Li G, Yuan L, Chen X. One-way Topological States along Vague Boundaries in Synthetic Frequency Dimensions Including Group Velocity Dispersion (Invited). Pier (2020) 169:33–43. doi:10.2528/pier20083101

CrossRef Full Text | Google Scholar

24. Tian Z, Shen C, Li J, Reit E, Bachman H, Socolar JES, et al. Dispersion Tuning and Route Reconfiguration of Acoustic Waves in valley Topological Phononic Crystals. Nat Commun (2020) 11:762. doi:10.1038/s41467-020-14553-0

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zhao W, Xu Y, Yang Y, Tao Z, Hang ZH. Multiband Acoustic Waveguides Constructed by Two-Dimensional Phononic Crystals. Appl Phys Express (2020) 13:094001. doi:10.35848/1882-0786/abafc7

CrossRef Full Text | Google Scholar

26. Wang M, Zhou W, Bi L, Qiu C, Ke M, Liu Z. Valley-locked Waveguide Transport in Acoustic Heterostructures. Nat Commun (2020) 11:3000. doi:10.1038/s41467-020-16843-z

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yu L, Xue H, Zhang B. Antichiral Edge States in an Acoustic Resonator Lattice with Staggered Air Flow. J Appl Phys (2021) 129:235103. doi:10.1063/5.0050645

CrossRef Full Text | Google Scholar

28. Jia D, Ge Y, Xue H, Yuan S-q., Sun H-x., Yang Y, et al. Topological Refraction in Dual-Band valley Sonic Crystals. Phys Rev B (2021) 103:144309. doi:10.1103/physrevb.103.144309

CrossRef Full Text | Google Scholar

29. Mei J, Chen Z, Wu Y. Pseudo-time-reversal Symmetry and Topological Edge States in Two-Dimensional Acoustic Crystals. Sci Rep (2016) 6:32752. doi:10.1038/srep32752

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Zhang Z, Wei Q, Cheng Y, Zhang T, Wu D, Liu X. Topological Creation of Acoustic Pseudospin Multipoles in a Flow-free Symmetry-Broken Metamaterial Lattice. Phys Rev Lett (2017) 118:084303. doi:10.1103/PhysRevLett.118.084303

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Deng Y, Ge H, Tian Y, Lu M, Jing Y. Observation of Zone Folding Induced Acoustic Topological Insulators and the Role of Spin-Mixing Defects. Phys Rev B (2017) 96:184305. doi:10.1103/physrevb.96.184305

CrossRef Full Text | Google Scholar

32. Yves S, Fleury R, Lemoult F, Fink M, Lerosey G. Topological Acoustic Polaritons: Robust Sound Manipulation at the Subwavelength Scale. New J Phys (2017) 19(7):075003. doi:10.1088/1367-2630/aa66f8

CrossRef Full Text | Google Scholar

33. Chen JJ, Huang HB, Huo SY, Tan ZH, Xie XP, Cheng JC, et al. Self-ordering Induces Multiple Topological Transitions for In-Plane Bulk Waves in Solid Phononic Crystals. Phys Rev B (2018) 98(1):014302. doi:10.1103/physrevb.98.014302

CrossRef Full Text | Google Scholar

34. Jia D, Sun H-x., Xia J-p., Yuan S-q., Liu X-j., Zhang C. Acoustic Topological Insulator by Honeycomb Sonic Crystals with Direct and Indirect Band Gaps. New J Phys (2018) 20:093027. doi:10.1088/1367-2630/aae104

CrossRef Full Text | Google Scholar

35. You B, Dong M, Zhou J, Xu H. Performance Improvement and Antenna Design of Left-Handed Material Units Based on Topological Deformations. Pier (2019) 165:13–33. doi:10.2528/pier19011603

CrossRef Full Text | Google Scholar

36. Lee T, Iizuka H. Bragg Scattering Based Acoustic Topological Transition Controlled by Local Resonance. Phys Rev B (2019) 99(6):064305. doi:10.1103/physrevb.99.064305

CrossRef Full Text | Google Scholar

37. Ma G, Xiao M, Chan CT. Topological Phases in Acoustic and Mechanical Systems. Nat Rev Phys (2019) 1:281–94. doi:10.1038/s42254-019-0030-x

CrossRef Full Text | Google Scholar

38. Wang B, Huang Q, Chen K, Zhang J, Kurczveil G, Liang D, et al. Modulation on Silicon for Datacom: Past, Present, and Future (Invited Review). Pier (2019) 166:119–45. doi:10.2528/pier19102405

CrossRef Full Text | Google Scholar

39. Ji CY, Zhang Y, Liao Y, Zhou X, Jiang JH, Zou B, et al. Fragile Topologically Protected Perfect Reflection for Acoustic Waves. Phys Rev Res (2020) 2(1):013131. doi:10.1103/physrevresearch.2.013131

CrossRef Full Text | Google Scholar