The Robustness of Interdependent Directed Networks With Intra-layer Angular Correlations

The robustness of interdependent networks is a frontier topic in current network science. A line of studies has so far been investigated in the perspective of correlated structures on robustness, such as degree correlations and geometric correlations in interdependent networks, in-out degree correlations in interdependent directed networks, and so on. Advances in network geometry point that hyperbolic properties are also hidden in directed structures, but few studies link those features to the dynamical process in interdependent directed networks. In this paper, we discuss the impact of intra-layer angular correlations on robustness from the perspective of embedding interdependent directed networks into hyperbolic space. We find that the robustness declines as increasing intra-layer angular correlations under targeted attacks. Interdependent directed networks without intra-layer angular correlations are always robust than those with intra-layer angular correlations. Moreover, empirical networks also support our findings: the significant intra-layer angular correlations are hidden in real interdependent directed networks and contribute to the prediction of robustness. Our work sheds light that the impact of intra-layer angular correlations should be attention, although in-out degree correlations play a positive role in robustness. In particular, it provides an early warning indicator by which the system decoded the intrinsic rules for designing efficient and robust interacting directed networks.

1 Introduction

In the past few decades, increasing studies had proved that most real-world networks are multi-layered by dependency connectivity to interact with one another, and such structures are of great interest in the aspect of the robustness [1–6]. An emerging field is also called the robustness of interdependent networks, interconnected networks, or interdependent networks. Indeed, cascading failures of interdependent networks are possible to induce catastrophic consequences: the failure of a node in one network leads to the collapse of the dependent nodes in other networks, which in turn may cause further damage to the first network [7, 8]. Enhancing the understanding of the real-world dynamical process thus needs to focus on the structure of interdependent networks, which is of utmost importance for preventing crashes or for engineering more efficient and stalwart networked systems [9, 10].

The study of the robustness for interdependent networks has been widely investigated in across-layers and intra-layers features of topology structures, including the degree correlations [11, 19], the coupling strength between layers [12], the community structure [13, 14], the historic dependency [15], the degree heterogeneity [16], and so on. In particular, the correlated structures affect the structural robustness in diverse fashions: strong degree correlations across layers suppress susceptibility to a social cascade process [17] and be robust against targeted attacks [18]. For another branch of studies, attentions have shifted to understanding the dynamical process of interdependent networks by hidden geometric correlations [19–21]. The geometric correlation contains two parts: one, the radial correlation is equal to degree correlation, which has been widely discussed on its contribution to systems robustness; and two, the angular correlation is a novel statistical property. Angular correlations across layers can produce the lower outbreak threshold [21] and mitigate the breakdown of mutual connectivity under targeted attacks [20].

Even though the robustness of interdependent networks has received much research interest, few studies focus on interdependent directed networks. Taking the real-world scenes into consideration, network structures are generally asymmetric, which may cause a more enriched phenomenon in the critical behaviors of the robustness [22, 23]. For instance, different measures characterize the feature of nodes in directed systems: in-degrees, out-degrees, and their correlations (i.e., in-out degree correlations). The robustness of many real-world systems increases as the in-out degree correlations [22]. An open question is whether other correlations indexes affect the robustness of interdependent directed networks, even in the state of the high in-out degree correlations, or not?

Inspired by those studies, we argue for a need to study the robustness of interdependent directed networks in hyperbolic space. Here, we expand the concept of geometric correlations [19] to interdependent directed networks, defined as intra-layer geometric correlations which are derived from directed structures. Specifically, each layer of interdependent directed networks is represented by four hidden geometric features in hyperbolic space: in-radius, out-radius, in-angles, and out-angles [24]. To this end, intra-layer geometric correlations include intra-layer radial correlations (i.e., equivalent to in-out degree correlations) and intra-layer angular correlations. In this study, we will simulate and investigate the effects of intra-layer angular correlations on the robustness of artificial interdependent directed networks. Meanwhile, we analyze the intra-layer geometric correlation and its contribution to robustness in real-world systems by mapping interdependent directed networks into hyperbolic space.

This paper is structured as follows. Section 2 introduces the basic knowledge, including hyperbolic embedding methods, cascading failure model, and artificial geometric model for interdependent directed networks. In section 3, we analyze the influence of intra-layer angular correlations on robustness in both artificial networks and real-world networks. Section 4 concludes the paper finally.

2 Materials and Methods

2.1 Interdependent Networks

Interdependent networks can be defined as a sequence of graphs: G = {G_A, G_B…}. Usually, nodes in two or more monoplex networks are adjacent to each other via edges that are called dependency edges [1]. In our paper, interdependent directed networks contain two layers in terms of a layer A and a layer B, and each layer is a directed and unweighted scale-free network with the size N_A = N_B = N, as shown in Figure 1. Thus, the degree distributions of in-degree and out-degree are the power-law distribution in interdependent directed networks, where γ_in and γ_out are the power-law exponent of in-degree and out-degree, respectively. In Mathematics, it is sufficient to provide the adjacency matrix to formally characterize interdependent directed networks. For each layer (e.g., network A), and an asymmetric N × N matrix A whose generic entry a_ij = 1 if a link from node i to j exists, otherwise a_ij = 0.

FIGURE 1

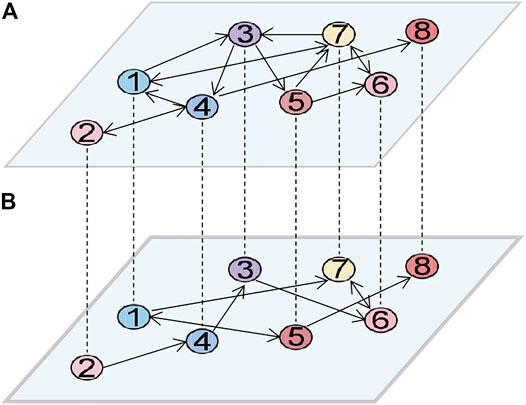
FIGURE 1. Illustration of interdependent directed networks. Directed networks A and B are coupled by dependency links (dotted lines).

2.2 Cascading Failure Model

One may observe cascades in interdependent directed networks, i.e., avalanches of failures triggered by the failure of one or more nodes, as the nodes are removed gradually with a specific order K. K is defined by K = max(k_A, k_B), where the degree of nodes in the network A or B are set by k_A = k_A,in + k_A,out or k_B = k_B,in + k_B,out. In practice, we begin removing a fraction 1 − p in network A and a fraction 1 − p in network B, and removing all the links connected to these removed nodes. For interdependent nodes across layers, if node i fails to function due to being attacked or isolated, node i also fails in another layer. We continue this process until no further new failed nodes can occur.

To measure the robustness for interdependent directed networks under targeted attacks, we compute its mutually connected components (MCC) in each step of removing nodes with fraction 1 − p. Each layer network fragments into MCC, within which each pair of nodes can reach each other by a path [7, 20]. Some nodes in the MCC of the layer A network will play an important function in the layer A network, but they may not exist in the MCC of layer B. Thus, we define the MCC of interdependent systems to be the average value of all layers. A similar definition also applies to calculate the second maximum connected component (2nd-MCC). By doing this, when the reserved fraction p is tuned increasingly from zero to a unit, at a certain critical fraction p_c, the MCC of networks shifts from zero to non-zero. When p < p_c, the interdependent networks have no MCC, and otherwise p > p_c. The critical fraction p_c thus reveals the robustness of interdependent directed networks, i.e., the smaller p_c, the higher network robustness.

2.3 The Intra-layer Geometric Correlations

Intra-layer geometric correlations are composed of intra-layer radial correlations and intra-layer angular correlations in a certain layer, obtained by embedding interdependent directed networks into hyperbolic space. Therefore, we introduce the A-PSO (the asymmetric popularity and similarity optimization) model to map each layer of interdependent directed networks into hyperbolic space [24].

In this model, each node i is firstly split into two sets (a_i in the set a and b_i in the set b), and a directed link goes from a node i to a node j, which will be transformed a link between a_i and b_j. Then, each pair of nodes a_i and b_j correspond to polar coordinates $\left.\right({(\theta }_{a,i}$ and $r_{a,i})$ and $({\theta }_{b,i}$ and $r_{b,i})$, respectively. The radial coordinates can be calculated by κ − r mapping: r = R − 2ln(κ/κ_min), where hidden variable κ_*,_i(* ∈ {a, b}) is derived from $\rho ({\kappa }_{*})=(\gamma -1){\kappa }_{min}^{(\gamma -1)}{\kappa }_{*}^{-\gamma }$, the minimum of hidden variable ${\kappa }_{min}=\bar{k}({\gamma }_{*}-1)/({\gamma }_{*}-2)$, and θ is drawn from uniform Probability Density Function (PDF). Finally, the directed link is created by any integrable function $f(\chi )={(1+{\chi }^{\beta })}^{-1}$ in hyperbolic space, where hyperbolic distance χ = r_a,i + r_b,j + 2ln(d_ai,bj/2), β is a model parameter.

In practice, we do not know the nodes’ coordinates by given the adjacency matrix A of a layer. We are interested in the conditional probability $\mathcal{P}(\theta ,\kappa |A)$ that the possibility of assigning a coordinate to each node, giving our observed network data. Following Bayes’ rule, we have

$\mathcal{P}(\{\kappa ,\theta \}|a_{ij})\propto \mathcal{P}(a_{ij}|\{\kappa ,\theta \})\mathcal{P}(\{\kappa ,\theta \}).(1)$

where the posterior distribution $\mathcal{P}(\{\kappa ,\theta \}|a_{ij})$ is proportional to two components: the likelihood $\mathcal{P}(a_{ij}|\{\kappa ,\theta \})$ of the network data a_ij, the prior probability $\mathcal{P}(\{\kappa ,\theta \})$ κ and θ are obtained by following some constraints mentioned above, and we write P({κ, θ}) = 1 if the constraint is satisfied and otherwise P({κ, θ}) = 0. Thus, the likelihood can be calculated as followed:

$\mathcal{P}(a_{ij}|\{\kappa ,\theta \})=\prod _{1\le i\ne j\le N}f{(\chi )}^{a_{ij}}{[1-f(\chi )]}^{1-a_{ij}},(2)$

where hidden variables are solved by κ_i = k_i − γ_/β and angular coordinates are inferred by using the localized Metropolis-Hastings (LMH) algorithm [25, 26].

To this end, we have the angular coordinate (θ_a; θ_b) and the radial coordinates (r_a; r_b) in according with giving a directed network layer. Then, we use mutual information to describe intra-layer geometric correlations. Formally, the mutual information about two random various X, Y is obtained by [27].

$I(X;Y)={\int }_Y{\int }_{X}p(x,y)ln\left(\frac{p(x,y)}{p(x)p(y)}\right)dxdy,(3)$

where p(x, y) is the joint probability density function of X, Y, and p(x), p(y) are marginal PDF of X and Y. In this paper, the intra-layer angular correlation of each layer is quantified by the normalized mutual information NMI_θ = I(θ_a; θ_b)/max{I(θ_a; θ_a), I(θ_b; θ_b)}. Similarly, the intra-layer radial correlation is defined as NMI_r = I(r_a; r_b)/max{I(r_a; r_a), I(r_b; r_b)}. The higher the NMI (NMI ∈ [0, 1]), the stronger are the intra-layer geometric correlations.

2.4 Artificial Geometric Model

We simulate targeted attacks on artificial networks to investigate the relationship between the robustness and intra-layer angular correlations. The geometric multiplex model (GMM, Ref. [19]) is applied to generate the artificial undirected interdependent networks with across-layer geometric correlations. Inspired by it, we use this framework to develop a single-layer directed network with an intra-layer geometric correlation. The difference between the GMM and our work is that we aim to obtain the out-direction and the in-direction coordinates in a specific correlation. In Figure 2, each directed layer is generated according to the following steps:

FIGURE 2

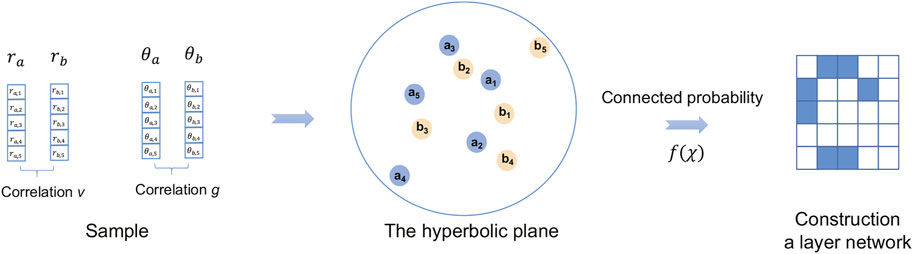
FIGURE 2. The flow diagram of construction teach layer of artificial interdependent networks. Yellow nodes and blue nodes are represented in-direction nodes and out-direction nodes, respectively.

Step 1. Determine the initial parameters: the network size N, the exponent β of the connection probability, the power-law exponent of out-degree γ_a, the power-law exponent of in-degree γ_b, the average degree $\bar{k}$, the intra-layer radial correlation v ∈ [0, 1], and the intra-layer angular correlation g ∈ [0, 1].

Step 2. Determine the hyperbolic coordinates with a certain correlation in each layer of interdependent directed networks.

First of all, each node is assigned in-direction hidden variables κ_b, θ_b in the set b, as sampled from $\rho ({\kappa }_b)=({\gamma }_b-1){\kappa }_{b,min}^{({\gamma }_b-1)}{\kappa }_b^{-{\gamma }_b}$ and uniform PDF, respectively.

Secondly, the out-direction angular coordinates are chosen from θ_a = mod[θ_b + 2πl_i/N, 2π], where l_i is an arc length of radius R in a hyperbolic disc, which is satisfied by zero-mean truncated Gaussian PDF, defined as $f_{\sigma }=\frac{1/\sigma \varphi (l/\sigma )}{\mathrm{\Phi }(N/2\sigma )-\mathrm{\Phi }(-N/2\sigma )}$, σ = σ₀(1/g − 1), σ₀ = min[100, N/4π]. ϕ(x) is normal distribution. Φ(x) is the PDF of ϕ(x).

Thirdly, each node of out-direction radial coordinates r_a is assigned. Notice that r_a is taken the place of the hidden variables κ_a to implement the algorithm easily. Specifically, the κ_a is derived from the copulas function $C_{\eta }(F({\kappa }_a),F({\kappa }_b))=e^{-{[\left.\right(-ln{(F({\kappa }_b))}^{\eta }+{(-ln(F{\kappa }_a))}^{\eta }]}^{1/\eta }}$, where $F({\kappa }_a)=1-{\kappa }_a^{(1-{\gamma }_a)}{\kappa }_{a,min}^{({\gamma }_a-1)}$, $F({\kappa }_b)=1-{\kappa }_b^{(1-{\gamma }_b)}{\kappa }_{b,min}^{({\gamma }_b-1)}$, η = 1/(1 − v), the minimum of hidden variable ${\kappa }_{a,min}=\bar{k}({\gamma }_a-1)/({\gamma }_a-2)$ and ${\kappa }_{b,min}=\bar{k}({\gamma }_b-1)/({\gamma }_b-2)$. We then transform hidden variables to radial coordinates r_a = R − 2ln(κ_a/κ_a,min) and r_b = R − 2ln(κ_b/κ_b,min).

In particular, when g = 1 and v = 1, the coordinates of each node is identical in the two directions (that is, θ_a = θ_b and κ_a = κ_b, respectively), and a generated network degenerates into a undirected network. To overcome this problem, we regard v = 0.99 and g = 0.99 as the full correlations (i.e., v = 1 and g = 1) in this paper and make sure to generate a directed network.

Step 3. Determine the artificial networks. Links are created by the connection probability, i.e., each node pair i, j is connected by probabilities $f({\chi }_{ij})={(1+{\chi }^{\beta })}^{-1}$, ${\chi }_{ij}=\frac{\mathrm{\Delta }\theta N\bar{k}}{\beta sin(\pi /\beta ){\kappa }_{ia}{\kappa }_{jb}}$ and Δθ = |π − |π − |θ_ia − θ_jb‖|. To do so, a layer of the artificial network has been constructed. The steps 1–3 are repeated to generate another layer.

3 Results

3.1 The Influence of Intra-layer Angular Correlations on Robustness in Artificial Networks

In this section, all artificial networks are double-layer directed networks, where a pair of nodes across layers are interdependent. The artificial geometric model is used to generate each layer which is a heterogeneous directed network with the power-law exponent of out-degree γ_a = 2.6, the power-law exponent of in-degree γ_b = 2.6, average node degree $\bar{k}=6$, and the parameter β = 3.5. The intra-layer angular correlation and the intra-layer radial correlation are denoted by the symbols ( g_A, v_A) in layer A and ( g_B, v_B) in layer B.

By doing this, three kinds of artificial networks have been generated to simulate targeted attacks, as shown in Figures 3A,B. Results reveal two geometric contributions to the robustness. One, the value of p_c in the orange line is larger than others, which shows that intra-layer angular correlations increase the vulnerability of interdependent directed networks. Notice that our results are in contrast to the situation on across-layer correlations between interdependent networks [20], which reveals that intra-layer angular correlations are hidden factors to understand complex systems. Two, such vulnerability will be exacerbated by the increase in the number of layers. Additionally, we also provide the behavior of cascading failures for the 2nd-MCC in different size systems. The largest 2nd-MCC achieves its extremum near the critical point, which is a way to estimate and compare p_c. Figure 3C illustrates the extreme value point p_c for interdependent directed networks with full angular correlations is always significantly higher than the case of the non-angular correlations. Multi-subsystem interaction and its hidden geometric structure thus should be considered designing network systems more robust. Additional, we analyze the fraction of coupling strength q ∈ [0, 1], where q = 0 represents that network systems become two single and independent networks, and q = 1 represents the mapping relationship of nodes between two layers is one to one. Figures 3D–F illustrates that the results of Figure 3A can expand to general cases (the inter-layer coupling of arbitrary proportions). Figure 3F shows their percolation behaviors with the fraction of remaining nodes p changing from 0 to 1 under intra-layer angular correlations and different coupling strengths q. The results show that decreasing coupling strength can mitigate the vulnerability of interdependent directed networks with the intra-layer angular correlation against targeted attacks.

FIGURE 3

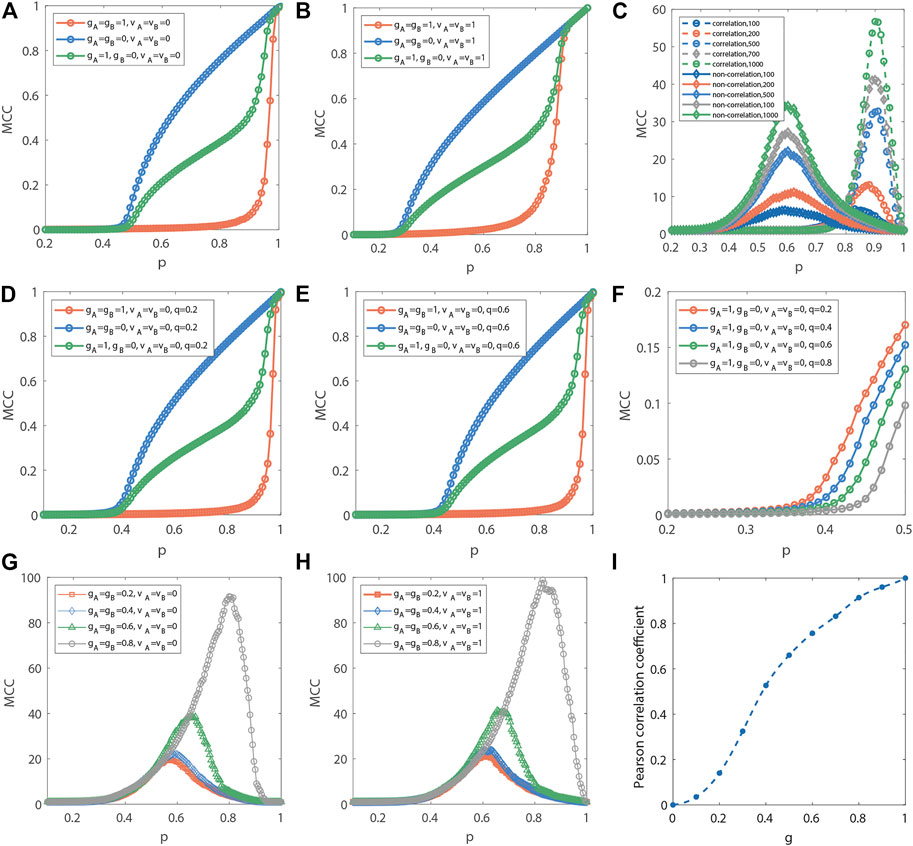
FIGURE 3. Targeted attack in artificial networks. (A,B) Targeted attacks on different kinds of synthetic networks with N = 5,000. (C) The size of the 2nd-MCC as a function of p for different sizes N. we set g_A = g_A = 1, r_A = r_A = 0 in the correlation case and g_A = g_A = 0, r_A = r_A = 0 in the non-correlation case. (D–F) Targeted attacks on three kinds of synthetic networks with coupling strengths q. (G,H) Simulate targeted attack with different intra-layer angular correlations, and N = 500. The results are averages over 100 realizations. (I) illustrates the relationship between parameter g and Pearson correlation coefficient in the artificial model.

To study this issue further, we examine the impact of different angular correlations on robustness by several variations of artificial networks, as shown in Figures 3G,H. As intra-layer angular correlations decrease, the vulnerability of directed systems is mitigated, irrespective of the effect of intra-layer radial correlations. This means that, although the contribution of in-out degree correlations is positive to robustness for interdependent directed networks, intra-layer angular correlations play an essential factor in undermining the robustness. Thus, intra-layer angular correlations have an early-warming function when interdependent directed networks face a sudden extreme attack. In addition, we also found that such an increasing trend is not apparent in low-correlation situations. To analyze the cause, we checked the relationship between parameter g and the Pearson correlation between intra-layer angular coordinates. Figure 3I suggests that the nonlinear relationship induces the phenomenon mentioned above.

3.2 Linking Intra-layer Angular Correlations to Robustness in Real Interdependent Networks

The influence of intra-layer angular correlations on the robustness in real-world interdependent networks is simulated in this subsection. Empirical networks are all derived from open databases and describe in detail, as followed. 1) C. elegans neural dataset describes the neural interconnection via chemical synapses and gap junctions, which can be obtained from the Wormatlas database [28]. The nodes are neurons, and each layer corresponds to a different type of synaptic connection. 2) International trade dataset considers different types of trade relationships among countries, obtained from Ref. [29]. The worldwide food import/export network is an economic network in which layers represent products, nodes are countries, and edges at each layer represent import/export relationships of a specific food product among countries. Each layer is directed and weighted networks with 214 nodes. 3) Arabidopsis interdependent Genetic networks are obtained from the Biological General Repository for Interaction Datasets (BioGRID, thebiogrid.org), a public database that archives and disseminates genetic and protein interaction data from humans and model organisms [30, 31]. Each layer is directed and unweighted networks with 1,449 nodes after removing the isolated nodes. 4) Social networks consist of 3 kinds of (Co-work, Friendship, and Advice) between partners and associates of a corporate law partnership [32, 33]. Each layer is directed and unweighted networks.

Secondly, we construct reshuffled counterparts (so-called reshuffled networks) from real-world networks (so-called original networks). The reshuffled counterpart is a variant of the original network to alter intra-layer geometric correlations. Specifically, each layer (a directed network) is transformed into a bipartite structure, as shown in Figure 4, and randomly reshuffled nodes’ ID of the set b in a way. Notably, interdependent nodes are also reshuffled in the same way in other layers if nodes’ ID is reshuffled at a layer. Node b₁ and node b₄ are also reshuffled in layer B, when node b₁ and node b₄ are reshuffled in layer A, To this end, the reshuffled counterparts are destroyed the intra-layer geometric correlation and preserved across-layers geometric correlations.

FIGURE 4

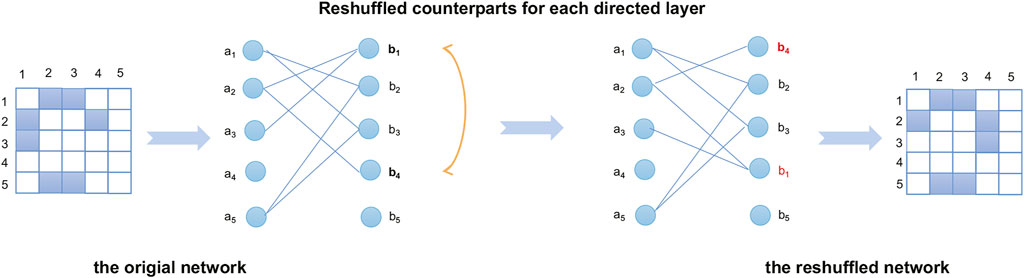
FIGURE 4. Illustration of the reshuffled counterpart of original networks. In the example, we exchanged the ids of nodes b₁ and b₄, thereby destroying the intra-layer topological similarity.

Then, each layer for these networks can be embedded into a hyperbolic space, where each layer is represented by a group of angular coordinates (θ_a, θ_b) and a group of radial coordinates (r_a, r_b). To validate the influence of intra-layer geometric correlations on this real-world multiplex network, we implement targeted attacks on the original networks and reshuffled networks for empirical networks, respectively. Figure 5 displays that the p_c of original networks is smaller than their reshuffled counterparts under targeted attacks. We also observe that the NMI_θ,ori is always larger than the NMI_θ,re for different real-world networks, as shown in Table 1. Linking those results, we find that the larger the value p_c, the stronger intra-layer angular correlations. It is the reason why interdependent directed networks are more robust after the reshuffle. Results also suggest our arguments and highlight the importance of intra-layer angular correlations.

TABLE 1

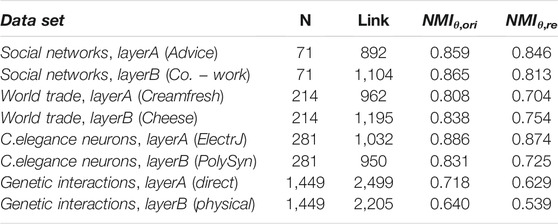
TABLE 1. The basic properties of empirical directed networks. NMI_θ,ori and NMI_θ,re present the strength of the intra-layer angular correlation in original networks and reshuffled networks, respectively.

FIGURE 5

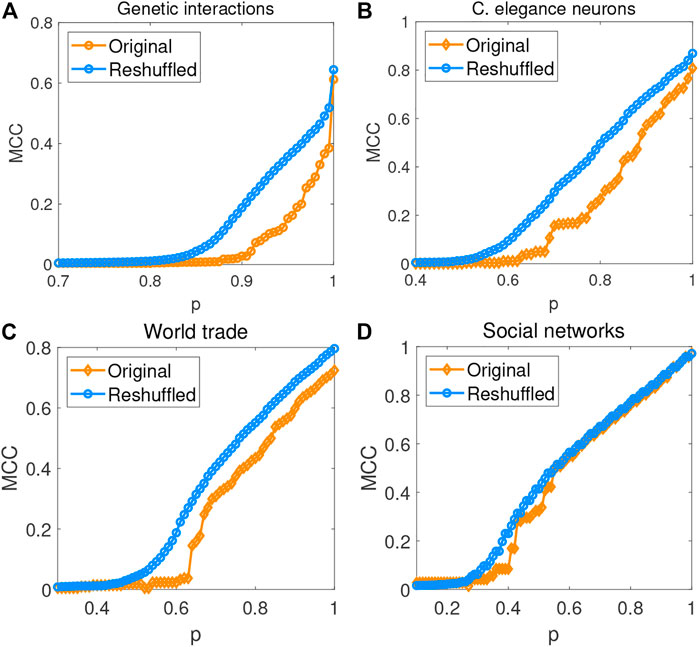
FIGURE 5. The relative size of the MCC against the remaining fraction p of nodes remaining in the system for real interdependent directed networks, including genetic interactions networks (A), C.elegance neurons networks (B), world trade networks (C), and social networks (D). The orange line and the blue line represent the results of real-world networks (Original) and their reshuffled counterparts (Reshuffled), respectively.

4 Conclusion

The hidden geometric structures of real-world networks provide a new perspective in revealing a relationship between topology and dynamical processes. Here, we examine the importance of intra-layer geometric correlations in understanding the robustness of interdependent directed networks from the perspective of hyperbolic embedding. For one thing, simulations are performed targeted attacks on artificial networks with diverse geometric correlations. Our main finding is that strong intra-layer angular correlations can quickly shift the sizes of the mutually connected components to fragmentation. The robustness will decrease as the increase in intra-layer angular correlations, even if in the case of in-out degree correlations. Couple strength q impacts the robustness: robustness of interdependent directed networks enhances as decrease of q. For another, we have studied two-layered empirical directed networks, validating that intra-layer geometric correlations also induce the vulnerability of real-world systems. Our results may help design a more robust network system and plan efficient protection strategies. However, it is also the beginning of clarifying the relationship between geometric structures and the dynamical process in interdependent directed networks. There are also some limitations in this work. For instance, the contribution of geometric correlations and coupling patterns across layers in the aspect of robustness has not yet been discussed. Exploring the failure mechanism of one-to-one correspondence nodes between layers may also offer new insights into studying the robustness of multilayer networks.

Data Availability Statement

Publicly available datasets were analyzed in this study. These data can be found in Section 3.2.

Author Contributions

ZNW performed the analysis, validated the analysis, and drafted the manuscript. ZRD and YF designed the research and reviewed the manuscript. All authors have read and approved the content of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 71731002 and 61573065).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kivelä M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer Networks. J complex networks (2014) 2:203–71. doi:10.1093/comnet/cnu016

CrossRef Full Text | Google Scholar

2. Boccaletti S, Bianconi G, Criado R, del Genio CI, Gómez-Gardeñes J, Romance M, et al. The Structure and Dynamics of Multilayer Networks. Phys Rep (2014) 544:1–122. doi:10.1016/j.physrep.2014.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Wu Z, Di Z, Fan Y. The Structure and Function of Multilayer Networks: Progress and Prospects. J Univ Electron Sci Technol China (2021) 50:106–20. doi:10.12178/1001-0548.2020068

CrossRef Full Text | Google Scholar

4. Gómez S, Díaz-Guilera A, Gómez-Gardeñes J, Pérez-Vicente CJ, Moreno Y, Arenas A. Diffusion Dynamics on Multiplex Networks. Phys Rev Lett (2013) 110:028701. doi:10.1103/PhysRevLett.110.028701

PubMed Abstract | CrossRef Full Text | Google Scholar

5. De Domenico M, Granell C, Porter MA, Arenas A. The Physics of Spreading Processes in Multilayer Networks. Nat Phys (2016) 12:901–6. doi:10.1038/nphys3865

CrossRef Full Text | Google Scholar

6. Wang W, Liu QH, Liang J, Hu Y, Zhou T. Coevolution Spreading in Complex Networks. Phys Rep (2019) 820:1–51. doi:10.1016/j.physrep.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Buldyrev SV, Parshani R, Paul G, Stanley HE, Havlin S. Catastrophic cascade of Failures in Interdependent Networks. Nature (2010) 464:1025–8. doi:10.1038/nature08932

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Gao J, Buldyrev SV, Stanley HE, Xu X, Havlin S. Percolation of a General Network of Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88:062816. doi:10.1103/PhysRevE.88.062816

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Yuan X, Hu Y, Stanley HE, Havlin S. Eradicating Catastrophic Collapse in Interdependent Networks via Reinforced Nodes. Proc Natl Acad Sci USA (2017) 114:3311–5. doi:10.1073/pnas.1621369114

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Duan D, Lv C, Si S, Wang Z, Li D, Gao J, et al. Universal Behavior of Cascading Failures in Interdependent Networks. Proc Natl Acad Sci U S A (2019) 116:22452–7. doi:10.1073/pnas.1904421116

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Reis SDS, Hu Y, Babino A, Andrade Jr JS, Canals S, Sigman M, et al. Avoiding Catastrophic Failure in Correlated Networks of Networks. Nat Phys (2014) 10:762–7. doi:10.1038/nphys3081

CrossRef Full Text | Google Scholar

12. Parshani R, Buldyrev SV, Havlin S. Interdependent Networks: Reducing the Coupling Strength Leads to a Change from a First to Second Order Percolation Transition. Phys Rev Lett (2010) 105:048701. doi:10.1103/PhysRevLett.105.048701

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Sun J, Zhang R, Feng L, Monterola C, Ma X, Rozenblat C, et al. Extreme Risk Induced by Communities in Interdependent Networks. Commun Phys (2019) 2:1–7. doi:10.1038/s42005-019-0144-6

CrossRef Full Text | Google Scholar

14. Shekhtman LM, Shai S, Havlin S. Resilience of Networks Formed of Interdependent Modular Networks. New J Phys (2015) 17:123007. doi:10.1088/1367-2630/17/12/123007

CrossRef Full Text | Google Scholar

15. Li M, Lü L, Deng Y, Hu M-B, Wang H, Medo M, et al. History-Dependent Percolation on Multiplex Networks. Natl Sci Rev (2020) 7:1296–305. doi:10.1093/nsr/nwaa029

CrossRef Full Text | Google Scholar

16. Sun S, Wu Y, Ma Y, Wang L, Gao Z, Xia C. Impact of Degree Heterogeneity on Attack Vulnerability of Interdependent Networks. Sci Rep (2016) 6:32983–9. doi:10.1038/srep32983

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Kim JY, Goh KI. Coevolution and Correlated Multiplexity in Multiplex Networks. Phys Rev Lett (2013) 111:058702. doi:10.1103/PhysRevLett.111.058702

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Min B, Yi SD, Lee KM, Goh KI. Network Robustness of Multiplex Networks with Interlayer Degree Correlations. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 89:042811. doi:10.1103/PhysRevE.89.042811

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Kleineberg K-K, Boguñá M, Ángeles Serrano M, Papadopoulos F. Hidden Geometric Correlations in Real Multiplex Networks. Nat Phys (2016) 12:1076–81. doi:10.1038/nphys3812

CrossRef Full Text | Google Scholar

20. Kleineberg KK, Buzna L, Papadopoulos F, Boguñá M, Serrano MÁ. Geometric Correlations Mitigate the Extreme Vulnerability of Multiplex Networks against Targeted Attacks. Phys Rev Lett (2017) 118:218301. doi:10.1103/PhysRevLett.118.218301

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Fan D, Jiang G-P, Song Y-R, Zhang X. Influence of Geometric Correlations on Epidemic Spreading in Multiplex Networks. Physica A: Stat Mech its Appl (2019) 533:122028. doi:10.1016/j.physa.2019.122028

CrossRef Full Text | Google Scholar

22. Liu X, Stanley HE, Gao J. Breakdown of Interdependent Directed Networks. Proc Natl Acad Sci USA (2016) 113:1138–43. doi:10.1073/pnas.1523412113

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Liu RR, Jia CX, Lai YC. Asymmetry in Interdependence Makes a Multilayer System More Robust against Cascading Failures. Phys Rev E (2019) 100:052306. doi:10.1103/PhysRevE.100.052306

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wu Z, Di Z, Fan Y. An Asymmetric Popularity-Similarity Optimization Method for Embedding Directed Networks into Hyperbolic Space. Complexity (2020) 2020(5):1–16. doi:10.1155/2020/8372928

CrossRef Full Text | Google Scholar

25. Newman M, Barkema G. Monte Carlo Methods in Statistical Physics. New York, USA: Clarendon Press (1999).

Google Scholar

26. Boguñá M, Papadopoulos F, Krioukov D. Sustaining the Internet with Hyperbolic Mapping. Nat Commun (2010) 1:62. doi:10.1038/ncomms1063

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kraskov A, Stögbauer H, Grassberger P. Estimating Mutual Information. Phys Rev E Stat Nonlin Soft Matter Phys (2004) 69:066138. doi:10.1103/PhysRevE.69.066138

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Varshney LR, Chen BL, Paniagua E, Hall DH, Chklovskii DB. Structural Properties of the caenorhabditis Elegans Neuronal Network. Plos Comput Biol (2011) 7:e1001066. doi:10.1371/journal.pcbi.1001066

PubMed Abstract | CrossRef Full Text | Google Scholar

29. De Domenico M, Nicosia V, Arenas A, Latora V. Structural Reducibility of Multilayer Networks. Nat Commun (2015) 6:6864. doi:10.1038/ncomms7864

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Stark C, Breitkreutz BJ, Reguly T, Boucher L, Breitkreutz A, Tyers M. Biogrid: A General Repository for Interaction Datasets. Nucleic Acids Res (2006) 34:D535–D539. doi:10.1093/nar/gkj109

PubMed Abstract | CrossRef Full Text | Google Scholar

31. De Domenico M, Porter MA, Arenas A. Muxviz: A Tool for Multilayer Analysis and Visualization of Networks. J Complex Networks (2015) 3:159–76. doi:10.1093/comnet/cnu038

CrossRef Full Text | Google Scholar

32. Lazega E. The Collegial Phenomenon: The Social Mechanisms of Cooperation Among Peers in a Corporate Law Partnership. Oxford: Oxford University Press (2001).

Google Scholar

33. Snijders TAB, Pattison PE, Robins GL, Handcock MS. New Specifications for Exponential Random Graph Models. Sociological Methodol (2006) 36:99–153. doi:10.1111/j.1467-9531.2006.00176.x

CrossRef Full Text | Google Scholar