- Department of Electrical Engineering, School of Electrical Engineering and Computer Science, Pennsylvania State University, University Park, PA, United States
Quantum machine learning (QML) is promising for potential speedups and improvements in conventional machine learning (ML) tasks. Existing QML models that use deep parametric quantum circuits (PQC) suffer from a large accumulation of gate errors and decoherence. To circumvent this issue, we propose a new QML architecture called QNet. QNet consists of several small quantum neural networks (QNN). Each of these smaller QNN’s can be executed on small quantum computers that dominate the NISQ-era machines. By carefully choosing the size of these QNN’s, QNet can exploit arbitrary size quantum computers to solve supervised ML tasks of any scale. It also enables heterogeneous technology integration in a single QML application. Through empirical studies, we show the trainability and generalization of QNet and the impact of various configurable variables on its performance. We compare QNet performance against existing models and discuss potential issues and design considerations. In our study, we show 43% better accuracy on average over the existing models on noisy quantum hardware emulators. More importantly, QNet provides a blueprint to build noise-resilient QML models with a collection of small quantum neural networks with near-term noisy quantum devices.
1 Introduction
Quantum computing (QC) is one of the major transformative technologies. The community is seeking computational advantages with quantum computers (i.e., quantum supremacy) for practical applications. Recently, Google has claimed quantum supremacy with a 53-qubit quantum processor to complete a computational task (of no practical relevance though) in 200 s that may take 10K years on the state-of-the-art supercomputers [1]. This experiment has been a significant milestone for quantum computing.
Quantum machine learning (QML) is a promising application domain to archive quantum advantage with noisy quantum computers in the near term. Numerous QML models built upon parametric quantum circuits (PQC) are already present in the literature [2–6]. A PQC is a quantum circuit with parameterized gates as shown in Figure 1 (w1, w2,…are the tunable parameters). The parameters can be tuned to create the desired output state. Quantum Neural Network (QNN) is one of the most promising QML models that has gained significant attention in the past few years [3–5, 7, 8]. A conventional QNN consists of a data encoding circuit and a PQC followed by measurement operations (Figure 1). The data encoder encodes the classical data as a quantum state. The quantum state is transformed by changing the parameters of the PQC. The output state is retrieved through the measurements. QNN models are claimed to be more expressive than the classical neural networks [8–10]. In other words, QNN models have a higher capability to approximate the desired functionality (e.g., classifying data samples) compared to the classical models of a similar scale (e.g., with the same number of tunable parameters/weights). Numerous choices exist for the encoding circuits, PQC, and measurements to build a QNN [9, 11–13]. Recent works have demonstrated application of QNN in image classification [14, 15], drug discovery [16, 17], finance [18, 19], and many other industrial problems [20].
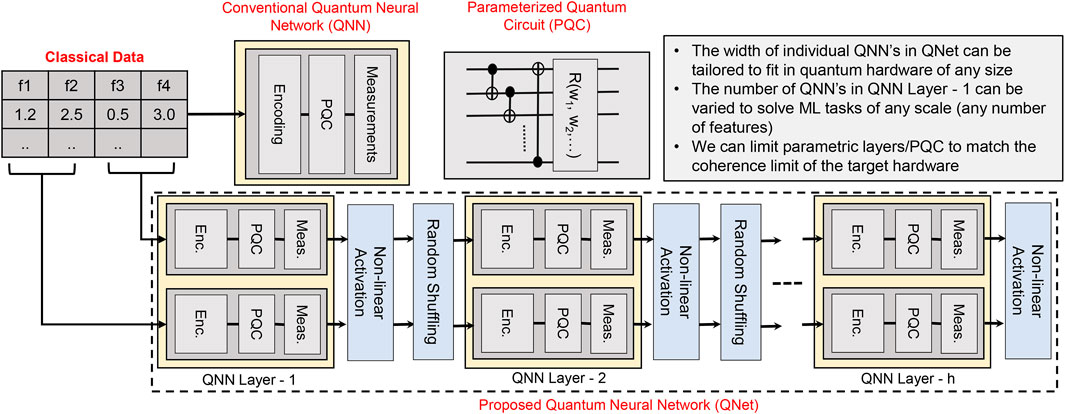
FIGURE 1. Conventional quantum neural network (QNN) and the proposed architecture (QNet). Each conventional QNN consists of a classical-to-quantum data encoding circuit followed by a parametric quantum circuit and measurement operations. QNet consists of several conventional QNN’s placed in different QNN layers. Each QNN layer is followed by classical non-linear activation and random shuffling of the output vector.
The near-term quantum devices have a limited number of qubits. Moreover, they suffer from various errors such as, decoherence, gate errors, measurement errors and crosstalk. John Preskill famously coined the term Noisy Intermediate-Scale Quantum or NISQ computers to refer to these machines [21]. The size of the quantum circuit (in terms of qubit count, gate count, and depth) that can be executed reliably on a quantum computer is limited by the hardware noise characteristics [22]. Therefore, the QNN models need to be small to exploit near-term devices for QML applications. However, the size of the conventional QNN model grows with the scale of the ML task. For example, we may require a 4-qubit QNN model to solve a 4-features ML task with 1 variable per qubit angle encoding (Figure 2B). A 1000-features problem will require a 1000-qubit circuit that may not fit in any near-term quantum devices. Even if the larger model fits in target hardware, it may not execute reliably due to a higher accumulation of gate errors and decoherence. Therefore, development of QNN models that use smaller quantum circuits is required.
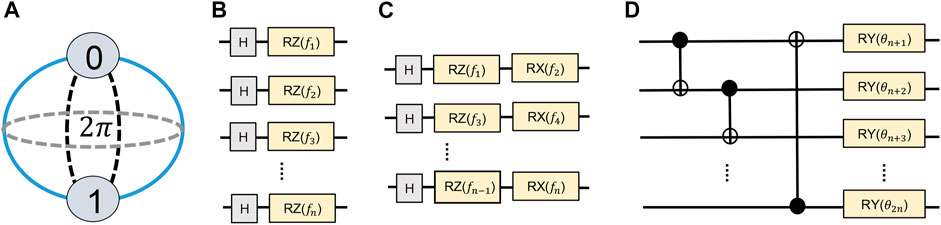
FIGURE 2. (A) Bloch sphere representation of a qubit. At any given point, a qubit can be rotated along the X, Y, or Z axis. The states repeat in 2π intervals, (B) angle encoding 1:1 (i.e., one continuous variable encoded in a single qubit state), (C) angle encoding 2:1 (i.e., two continuous variables encoded in a single qubit state), and (D) parametric layer used in this work (following [7, 8, 11]).
Two variants of the conventional QNN model are widely used to address the above scalability issue: 1) reduction of data dimension using a classical algorithm (e.g., PCA) before training a QML [17,23,24], and 2) repeatedly uploading the high-dimensional data in a small number of qubits using sequential rotation operations [25–27]. Technically, both these approaches can exploit arbitrarily small quantum hardware to solve ML tasks of any scale (a single qubit can be used to build a classification model involving 1,000 features). However, they have significant limitations that restrict their use in practical problems. For example, the performance of approach 1) will largely depend on the number of principal components (PC) taken from the PCA. A lower number of PC may not explain the variance in the data efficiently. This can affect the overall performance of this hybrid model. If we choose a large number of PCs, the succeeding QNN model may not be that small. It may not even fit in the target hardware. Uploading many features on a small number of qubits using approach 2) will easily cross the coherence limit of the quantum devices if the number of features is large. Therefore, the model will essentially generate random outputs on hardware and may not be trainable.
To address the above challenges, we propose QNet - a scalable quantum neural network architecture for small noisy quantum computers (Figure 1). We draw inspiration from classical multilayer perceptron network (MLP) [28]. QNet consists of several smaller QNN’s that are distributed in multiple QNN Layers (similar to the hidden layers in MLP). The number of qubits in a QNN and the circuit depth can be chosen based on the target hardware characteristics. Each QNN takes a fraction of the input vector as inputs and generates a transformed output. All the QNN’s in a QNN Layer together generates a new representation of the input vector. A QNN Layer is followed by classical non-linear activation functions to add more non-linearity to the system. A random shuffling layer is used to mix the outputs from different QNN’s before feeding them as inputs to the next layer. Note that, the random shuffling indexes are generated during model instantiation. These indexes remain the same throughout the training and inference steps. Every QNN can have a very small number of qubits, gates, and circuit depth. Therefore, they can show robustness against various types of quantum noises. Consequently, the overall QNet network can show greater resilience to noise compared to the conventional models. A large number of QNN’s can be used to solve large-scale ML problems which indicate the scalability aspect of QNet.
We make the following contributions in this paper: 1) present a scalable quantum neural network architecture (QNet) for noisy small quantum devices, 2) analyze the performance of QNet against a variety of design choices through numerical experiments, 3) compare the performance of QNet against conventional QNN, and two existing proposals to exploit small quantum computers for larger ML problems, and 4) discuss potential issues and future developments of QNet. We perform the numerical experiments using ideal simulators and hardware emulators (ibmq_melbourne, ibmq_bogota, ibmq_casablanca). An extensive set of classification datasets e.g., Iris, Wine, Breast Cancer, Digits, MNIST, and Fashion-MNIST is used to showcase the superior performance of QNet over the existing proposals.
We cover the basics on quantum computing and quantum neural networks in Section 2, discuss related works in Section 3, present our QNet architecture in Section 4, describe the results in Section 5, discuss potential issues, applications, and future development of QNet in Section 6, and draw our conclusions in Section 7.
2 Preliminaries
Qubits, Quantum Gates, and Measurements: Qubit is analogous to classical bits. However, unlike a classical bit, a qubit can be in a superposition state i.e., a combination of |0⟩ and |1⟩ at the same time. A variety of technologies exist to realize qubits such as, superconducting qubits, trapped-ions, neutral atoms, silicon spin qubits, to name a few [29]. Quantum gates (e.g., single qubit Pauli-X gate or 2-qubit CNOT gate) modulate the state of qubits and thus perform computations. These gates can perform a fixed computation (e.g., an X gate flips a qubit state) or a computation based on a supplied parameter (e.g. the RY(θ) gate rotates the qubit along the Y-axis by θ). A two-qubit gate changes the state of one qubit (target qubit) based on the current state of the other qubit (control qubit). For example, the CNOT gate flips the target qubit if the control qubit is in |1⟩ state. A quantum circuit contains many gate operations.
Qubits are measured to retrieve the final state of a quantum program. A complete state extraction requires the simultaneous computation of the position of a qubit along the X, Y, and Z-axis in the Bloch sphere. Unfortunately, it is impossible to simultaneously compute these components, thus requiring many executions of the same circuit. In addition, measurements are generally restricted to a computational basis (Z-basis in IBM quantum computers). Therefore, each qubit needs to be rotated to the standard Z-basis before measurement to access the X and Y components. Note that the majority of the existing quantum algorithms only require measurements in the computational Z-basis.
Expectation Value of an Operator: Expectation value is the average of the eigenvalues, weighted by the probabilities that the state is measured to be in the corresponding eigenstate. Mathematically, expectation value of an operator (σ) is defined as
Noise in Quantum Computation: Errors in quantum computing can be broadly classified into three categories: 1) Coherence errors: a qubit can retain its state for a short period (coherence time). The computation needs to be completed well within this limit. The coherence time restricts the depth of quantum circuits that can be executed reliably on any target hardware. 2) Gate errors: quantum gates are realized using microwave/laser pulses. It is impossible to generate and apply precise pulses in actual hardware. Hence, gate operations in quantum computers are erroneous. An intended rotation of θ along X-axis may end up being θ + δ or θ − δ when executed on the hardware. 3) Measurement errors: a |0⟩ state qubit can be measured as |1⟩ (or vice versa) due to imprecise measurement apparatus. In practice, the output state (e.g., Pauli-Z expectation value of a qubit) of a quantum circuit is approximated from a finite number of repeated circuit executions and measurements. The state approximation can be erroneous due to finite sampling. This error is often referred to as shot noise or finite sampling error in the literature [30].
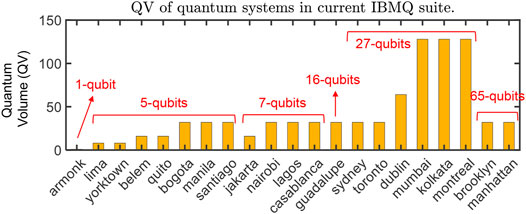
Quantum Volume (QV): QV is a metric to measure the computational power of physical quantum computers [22]. IBM measures QV using the following formula: log 2QV = arg maxn≤N{ min[n, d(n)]} where N is the total number of qubits in the hardware. Here, “n” and “d(n)” are the maximum width and depth of the circuit that can be executed reliably on the hardware, respectively. The output distributions of a set of random circuits are used to calculate these values [22]. In simple words, a QV of 32 signifies that we can run circuits with 5-qubits and a depth of 5 reliably on the hardware. If we go beyond this limit, the reliability will be severely compromised. Figure 3 shows the QV metric of the current generation of quantum systems in the IBMQ suite (7/28/2021).
Challenges in Scaling Quantum Computing Systems: The current generation of quantum computers operates in near-zero temperatures to minimize thermal noise. They are stored in dilution refrigerators while the control circuit operates at room temperature [31]. The Quantum Control Interface (QCI) between the qubits and the control circuitry is a major bottleneck in scaling quantum computers [31, 32]. The cables connecting the control chip with the qubits dissipate heat in the quantum chip adding thermal noise in computation. Large quantum systems are noisier due to larger QCI. Therefore, they may not provide a higher computational power compared to a small system. For instance, the 7-qubit ibmq_casablanca, ibmq_lagos, ibmq_nairobi systems have a quantum volume of 32 same as the 65-qubit ibmq_brooklyn or ibmq_manhattan systems. Significant research is underway to move control circuitry near the qubits using cryogenic control chips [33]. However, the most optimistic projection places their development at least a decade away [32]. Therefore, small quantum computers (≈10 qubits) may dominate in the near term.
Quantum Neural Network: QNN involves parameter optimization of a PQC to obtain a desired input-output relationship. QNN generally consists of three segments: 1) a classical to quantum data encoding (also referred to as embedding in the literature) circuit, 2) a parameterized circuit, and 3) measurement operations. A variety of encoding methods are available in the literature [12]. For continuous variables, the most widely used encoding scheme is angle encoding [7, 8, 12, 34] where a continuous variable input classical feature is encoded as a rotation of a qubit along the desired axis (X/Y/Z). For “n” classical features, we require “n” qubits. For example, RZ(f1) on a qubit in superposition (the Hadamard–H gate is used to put the qubit in superposition) is used to encode a classical feature “f1” in Figure 2B [8]. We can also encode multiple continuous variables in a single qubit using sequential rotations. For example, “f1” and “f2” are encoded using subsequent RZ(f1) and RX(f2) rotations on a single qubit in Figure 2C. As the states produced by a qubit rotation along any axis will repeat in 2π intervals (Figure 2A), features are generally scaled within 0 to 2π in a data pre-processing step. One can restrict the values between −π to π to accommodate features with both negative and positive values. Discrete/categorical variables can be encoded using rotations in discrete steps [35].
The parametric circuit has two components: entangling operations and parameterized single-qubit rotations. The entanglement operations are a set of multi-qubit operations between the qubits to generate correlated states [34]. The following parametric single-qubit operations search through the solution space. This combination of entangling and rotation operations is referred to as a parametric layer in the literature. Note that finding the optimal PQC architecture is an unresolved research problem. Descriptors such as, expressive power, entanglement capability, and effective dimension are proposed to measure the potency of various PQC choices [8, 9, 11]. Recent work indicates that these descriptors may have a significant correlation with the trainability of the quantum circuits [36]. In practical applications, such descriptors may be useful to choose better PQC architecture for the intended QML application. A widely used parametric layer architecture is shown in Figure 2D [8, 11]. Here, CNOT gates between neighboring qubits create the entanglement, and rotations along Y-axis using RY(θ) operations define the search space. Normally, these layers are repeated multiple times to extend the search space [7, 8]. We refer to this QNN model with a single PQC as our “Baseline.”
QNN Cost Functions: Qubits in a QNN circuit are measured in the computational basis to retrieve the output state. A cost function is derived from the measurements to train the network [6–8]. For example, in a binary classification problem, the authors measured all the qubits in the QNN model in Pauli-Z basis and associated class 0 with the probability of obtaining even parity, and class 1 with odd parity [8]. Then, the model is trained using binary cross-entropy loss (BCELoss).
Here, “N” is the number of samples in a batch, yi is the original class label of the ith sample (0 or 1), pi is the predicted probability of class 1.
In [37], the authors used the Pauli-Z expectation value of a single qubit (−1 associated with class 1 and +1 associated with class 0) for a binary classifier and trained it using mean-squared error loss (MSELoss).
Here, “N” is the number of samples in a batch, yi is the original class label of the ith sample (−1 or 1), E(Qi) is the Pauli-Z expectation value of the qubit.
Note that multiple one-vs-all classifiers are often used for multi-class classification problems, i.e., classification of more than two classes [7]. Huang et al. [24] fed the expectation values from the QNN to a classical neural network and trained it using binary cross-entropy loss function for binary classifications (Projected Quantum Kernel or PQK).
3 Related Works
Baseline QNN: The “Baseline” QNN is widely used in the literature where a single parametric quantum circuit is used as the QML model [7, 8, 12, 34]. Although they are quite useful to demonstrate various properties of QNN’s with toy datasets, they are not quite as useful for practical applications. The qubit requirements and the circuit depth/gate-count grows with the size (number of features) of the input dataset. The exact nature of this growth depends on the chosen encoding method and PQC architecture. For example, in angle encoding, qubit requirement and gate-count grow linearly while the depth remains constant for the encoding circuit [7, 8, 34]. In amplitude encoding, the qubit requirement grows logarithmically while the gate count/depth grows in O(2n) [38]. The gates in the entanglement layer in Figure 2D grows linearly with the number of qubits. In summary, either the qubit-count or the gate count/depth or both become high for large datasets. Due to the limited quantum volume of the NISQ-era quantum devices, the “Baseline” approach is infeasible for practical applications.
PCA + Baseline: A popular quantum-classical hybrid QNN model targetted for smaller quantum devices uses classical algorithm (e.g., PCA) to reduce data dimension to a level that is tractable for the “Baseline” model [15, 17, 23, 24] (Figure 4A). We refer to this model as “PCA + Baseline.” This hybrid model has some obvious issues. For instance, the chosen number of principal components in PCA will explain a fraction of the variance of the original dataset. Therefore, the hybrid model performance will depend on the number of chosen principal components. Increasing the number of components may improve the overall model performance. However, the quantum circuit may or may not fit in the small hardware if the number of components is high. Even if the circuit fits in the target hardware, it may not execute reliably if the gate count or depth is large.

FIGURE 4. Existing QNN models for small quantum computers. In (A), the high dimensional data is transformed to a lower dimension using a classical algorithm (e.g., PCA, LDA, etc.). The lower-dimensional data is used as inputs to the Baseline QNN model [17, 23, 24]. In (B), classical features are loaded repeatedly in a single-qubit using a series of rotation operations [25–27].
Data Re-Uploading Classifier: Data Re-Uploading Classifier (DRC) is proposed by Pérez-Salinas et al. [25] for small quantum computers. In DRC, classical data are sequentially uploaded in qubits with rotation angles. Each set of data uploads is followed by a PQC. This combination of data uploading and PQC is repeated many times. Note that one can implement a classifier with a single qubit for an arbitrary number of feature variables using DRC. For example, 4 features of a dataset (f1, f2, f3, f4) can be uploaded in a single qubit with alternating RZ and RY rotations [RZ(f1)–RY(f2)–RZ(f3)–RY(f4)] (Figure 4B). Adding a suitable PQC to this single qubit [e.g., trainable RX(θ)], and repeating this combination many times, one can use a single qubit to build a QNN classification model for the dataset with 4-features. However, the DRC model has obvious scalability issues. For instance, the number of gates in DRC increases linearly with the size of the dataset. For a 1000 feature dataset, a single data upload requires 1000 sequential single-qubit operations. In the current generation of IBM quantum computers, the coherence time is in the order of microseconds while gate operation time is in the order of nanoseconds [39]. The DRC classifier for the 1000 feature dataset can cross the coherence limit in a single data uploading step.
4 Proposed QNet Architecture
In this section, we present the architectural details of QNet which consists of several QNN Layers (Figure 1). Each QNN Layers contains multiple conventional QNN’s. A QNN processes/transforms a fraction of the input vector. A QNN Layer is followed by classical non-linear activation functions and random shuffling of the output vector. The final QNN Layer output is fed to a fully connected classical dense layer. The details of the architecture are discussed below.
Conventional QNN: The conventional QNN model lies at the heart of QNet. It consists of several conventional QNN models distributed in multiple QNN Layers. Unlike “Baseline” which encodes the whole input vector as a quantum state, each QNN in QNet encodes a fraction of the input vector in a quantum state and performs data transformation in the Hilbert space with a PQC. The width of the QNN (number of qubits) can be chosen based on the size of the target hardware. Each QNN in QNet can use any conventional data encoding technique, PQC architecture, and measurement operations. However, in this work, we use angle encoding (1 continuous variable per qubit as in Figure 2B) as our preferred encoding method and the entanglement layer shown in Figure 2D as our preferred PQC architecture following the recent trends in QML research [8, 11, 24]. We use Pauli-Z expectation values of the qubits as the output features from the QNN [6, 7]. In this chosen configuration, each QNN takes “k” continuous variables as inputs and generates “k” output features as qubit expectation values in the range of [−1, 1]. A toy example is shown in Figure 1. The toy dataset has 4 features. The “Baseline” processes all 4 features using a single quantum circuit. On the other hand, each QNN in QNet processes a fraction of the features (2).
QNN Layers: QNN’s are distributed in multiple QNN Layers (Figure 1). The number of parallel QNNs in a Layer is chosen based on the size of the input vector, and the width of individual QNN’s. For example, in a 30-feature tabular dataset, each QNN Layer can have five 6-qubit QNN’s or ten 3-qubit QNN’s. Increasing the number of QNN Layers raises the total number of QNN in the network. If each QNN has a similar number of trainable parameters, the total number of trainable parameters in the network grows linearly with increasing QNN Layers. It is quite similar to increasing hidden layers in a multi-layer perceptron network [28]. Note that the width of individual QNN’s in a QNN Layer can differ. Moreover, the number of QNN’s in different QNN Layers can be varied as well. For simplicity, we have kept these values constant across the layers in this work. In the remaining paper, we refer to the number of Qubits/QNN as QQ, the number of Parametric Layers/PQC as PL, and the number of QNN Layers in QNet as QL.
Non-linearity: Classical deep neural networks consists of many neurons that perform linear transformations on the input data. However, linear transformation alone is not sufficient to generate complex non-linear decision boundaries encountered in practical ML classification/regression problems. Therefore, non-linear activation functions (e.g., sigmoid, relu, tanh, etc.) are used to provide non-linearity in classical neural networks [28]. In the quantum domain, every gate operation is a linear transformation of the quantum state [29]. During measurements of the qubits in the computational Z-basis, we lose the phase information associated with the quantum state (X and Y components). It provides the required non-linearity in QNN models [40]. In our QNet architecture, we have added an optional classical non-linear activation layer at the end of every QNN Layer to increase non-linearity (Figure 1).
Random Shuffling: In classical neural networks, each fully connected neuron processes the entire input vector generated by the previous layer. However, in QNet, each QNN processes a fraction of the input vector. Therefore, the correlation between features at different fractions is not utilized. To circumvent this issue, we have added a shuffling layer at the end of every QNN Layer that randomly shuffles the input vector generated by the previous layer. Consequently, the QNN’s in subsequent QNN Layers processes a different fraction of the input (/transformed) vector. Note that the random shuffling order is generated when the QNet is instantiated. In the later training and inference steps, the order remains constant.
Output Layer and Cost Function: To date, the best QNN performance (accuracy/loss) has been reported by Huang et al. [24] using a hybrid quantum-classical architecture called Projected Quantum Kernel or PKQ. In PKQ, a “Baseline” QNN transforms the input data to a new feature space using a PQC. These new features are extracted through measurements of the quantum state in all three bases (X, Y, and Z). Next, these features are fed to an MLP. The classical network can be trained using any conventional loss function (e.g., cross-entropy loss).
Drawing inspiration from this work, we use a classical dense layer at the end of QNet. The final QNN Layer output is taken as the input to this classical layer. For classification problems, the number of neurons in this dense layer is equal to the number of classes in the input dataset. Unlike PKQ, which performs the quantum kernel transformation and training of the classical network separately, we train the whole network simultaneously. Moreover, PKQ uses a single large quantum circuit while QNet uses a collection of several small quantum circuits. We apply LogSoftmax activation at the output of the dense layer and use negative log-likelihood loss (NLLLoss) as our preferred loss function [41]. The LogSoftmax activation function transforms the output of the dense layer to class probabilities. This combination of LogSoftmax activation and NLLLoss is also known as Cross-Entropy Loss (CELoss) in the literature.
Here, “N” is the number of samples in a batch, “k” is the number of classes in the problem, yij is the truth label of the ith sample and jth class, and pij is the corresponding predicted probability. Note that one can choose any suitable loss function to train QNet (e.g., MSELoss).
Trainable Parameters: The number of trainable circuit parameters in QNet depends on chosen PL and QL. Since we have used identical QNN across the layers with single feature/qubit angle encoding, the total number of trainable circuit parameters is “f*PL*QL” where “f” is the number of features in the input dataset. Additionally, the network has “f*C” classical weights between the final QNN Layer and the output Dense layer where “C” is the number of classes in the dataset. Note that one can also add bias parameters/weights to the outputs of the QNN Layers and the classical dense layer.
Training and Inference: The QNet network can be trained using any gradient-based optimization algorithm such as, Adam or Adagrad [42, 43]. To apply backpropagation on QNet, QNN outputs have to be differentiable with respect to the inputs and the circuit parameters. Multiple methods exist to compute gradients in QNN [44–46]. However, not all of them are suitable for hardware. For instance, the adjoint method proposed by Luo et al. [44] requires the circuit intermediate state information to compute gradients which is not accessible when we execute the circuit on hardware. The parameter-shift rule is widely used to compute quantum gradients [45, 46]. It is quite similar to the age-old finite difference method which uses two evaluations of the target function at proximity to compute the gradients. However, in the parameter-shift rule, the two data points can be far from each other. It shows greater resilience to shot noise and measurement errors compared to finite difference [46]. It is also suitable for hardware. The PennyLane framework supports all these quantum gradient computation methods [47]. In this work, we use the Pytorch and the PennyLane frameworks to build and train QNet [41, 47].
Note that all the QNN’s in a QNN layer can go through the forward pass during training/inference at the same time as they do not have any dependency. Therefore, multiple hardware/simulators can be used to execute/simulate these QNN’s for faster computation both during training and inference. We can also use gradient-free optimizers such as, Nelder-Mead to train QNet [48]. However, they may perform poorly when the network has lots of parameters.
5 Evaluation
In this section, we present a numerical analysis of QNet performance with varying QQ, QL, and PL. We compare QNet with “Baseline” both in noiseless simulations and hardware emulations. We also compare QNet with PCA + Baseline and DRC. Note that this is not an exhaustive study. For instance, encoding methods, parametric layer architecture, measurements in the QNN’s are also major design choices. The field is continuously evolving, and there is a wide variety of choices for each of them. We stick to the same design choices throughout the study to prevent deviating from our key goals. Future research can focus on a comprehensive analysis that takes into account all of the variables.
5.1 Setup for Numerical Studies
Datasets: We use 6 classification datasets that are often used to evaluate the performance of QML models in contemporary works [3, 8, 23, 24]–Iris (150 samples, 4 features, 3 classes), Wine (178 samples, 13 features, 3 classes), Breast Cancer (569 samples, 30 features, 2 classes), Digits (1797 samples, 64 features, 10 classes), MNIST (70000 samples, 784 features, 10 classes) and Fashion-MNIST (70000 samples, 784 features, 10 classes). To limit simulation time, we pick 1200 samples from the MNIST and the Fashion-MNIST datasets. For MNIST, we pick 400 samples/digits of digits 3, 5, and 8 [49]. For Fashion-MNIST, we use samples of T-shirt/top, Trouser, and Pullover [50] classes. We also downsampled both MNIST and Fashion-MNIST datasets from 28 × 28 to 14 × 14 using 2d max-pooling [41]. The Iris, Wine, Breast Cancer, and Digits datasets are downloaded through the scikit-learn Python package [51]. We divide each dataset into two equal sets and use them for training and validation, respectively.
Metrics: We use the average loss and accuracy as our preferred metrics to measure the performance of the QML models [28]. Note that the average loss value is calculated by performing a forward pass through the networks with each of the data samples, measuring the corresponding loss value, and then averaging all the losses. Accuracy is the fraction of the samples that are classified correctly. The training loss and accuracy indicate the trainability of the models. The validation loss and accuracy indicate the generalization capability of the models on unseen data.
Simulation Framework: We have developed a Python framework using Pytorch, PennyLane, and Qiskit packages to build and train all the QML models used in this work [39, 41, 47]. We use the Adagrad optimizer with a learning rate of 0.5 [41, 43]. We use the default state vector simulator available in the PennyLane framework to simulate the quantum circuits in noiseless training [47]. Currently, we have limited access to actual quantum computers through cloud-based quantum computing services. It is not possible to present a statistically significant amount of data from the hardware since training and inference of QML models need frequent calls to quantum computers. Therefore, we resort to hardware emulators (simulated hardware with noise). IBM calibrates the hardware available in their cloud service twice a day. After each calibration, they provide the hardware characterization data through IBM Quantum [52]. Qiskit provides hardware emulation models (e.g., FakeMelbourne, FakeBogota, FakeCasablanca, etc.) that can replicate the output from the target hardware available in IBM Quantum [39]. These emulators use the noise models derived from the calibration data. We use these hardware emulators to compare the performance of various QML models under noise. The adjoint method is used for gradient computation in noiseless simulations because it is faster than parameter-shift. We use the parameter-shift rule in training QNet with hardware emulators as it is robust against shot noise and measurement errors. The QNN outputs are calculated (Pauli-Z expectation values of the qubits) from a finite number of samples of the circuit output. The number of samples is kept to 128 throughout our experiments. In the noiseless simulation, we calculate QNN outputs analytically. The simulations are done in a Windows machine with an Intel Core i7-10750H processor and 16 GB RAM. The datasets and Python framework are available through the following GitHub repository.1
Noise Simulation: We measure the impact of gate errors, decoherence, and measurement errors on QML models using Qiskit hardware emulators–FakeBogota, FakeMelbourne, and FakeCasablanca [39, 53, 54]. Several contemporary research works have also used these emulators [55–58]. Errors in single-qubit gate execution are simulated by applying a single qubit depolarizing error (gate error) followed by a single qubit thermal relaxation error (decoherence). Similarly, errors in two-qubit gate execution are simulated by applying a two-qubit depolarizing error (gate error) followed by single-qubit thermal relaxation errors on both qubits in the gate (decoherence). Each measured bit is flipped with a bit-flip probability to simulate the impact of measurement errors. The error parameter of the thermal relaxation errors is derived from T1 (longitudinal coherence time) and T2 (phase coherence time) parameters, and the gate execution time parameters [59]. Several characterization techniques are used in the IBM quantum systems to measure coherence time parameters (T1 and T2) such as Inversion Recovery, Ramsey Experiments, and Hahn Echoes. Gate errors are characterized using the Randomized Benchmarking protocol. Qubits are repeatedly prepared and measured in |0⟩ and |1⟩ states to calculate the corresponding bit-flip probabilities during measurements. IBM provides access to the hardware calibration data through its Qiskit framework [53]. During simulation, the hardware emulators load these noise models, decompose/compile the circuit with the basis/native gates of the hardware, and generate outputs under the aforementioned noises. Note that noise modeling is not the contribution of our work. One can use a different/more accurate noise model for comparative analysis of the QML models [60, 61, 62]. However, we believe that the conclusion will remain similar. The Supplementary Materials provide a more detailed overview of the noise models and attributes.
Note that these hardware emulators do not support simulation of crosstalk noise that stems from parallel/concurrent execution of gate operations on the same hardware. The smaller QNN’s in QNet run on different hardware or on the same hardware at different points in time. Therefore, there are fewer concurrent gate operations in one particular hardware compared to the Baseline. As a result, QNet may accumulate less crosstalk noise compared to the Baseline. On top of that, we use noise simulations for comparative studies between the models/architectures. Therefore, we believe that the exclusion of crosstalk noise simulation does not affect our conclusions.
Recent studies show a high degree of similarity between the distributions generated by hardware simulators and the original hardware [55–58]. The difference can be as little as ≈ 7% in terms of total variation distance [37]. The minor difference can be attributed to noises that are not simulated (e.g., crosstalk). Therefore, we believe the comparative analysis will yield similar conclusions if the experiments are done on actual hardware.
5.2 Results
5.2.1 QNet Design-Space Exploration
We sweep three major configurable attributes of QNet (PL, QL, and QQ) and train the networks for various classification tasks to gauge the impact of these attributes on training and validation. The training curves (over 100 epochs, averaged over 10 separate training runs) of Iris and Wine classifiers are shown in Figures 5A,D, respectively (QQ = 2, PL = 2, QL = 2). The training loss consistently goes down over training epochs, and the training accuracy improves for both these datasets. However, the validation loss decreases initially, and after a few epochs of training, it either goes up (Figure 5A) or remains at similar level (Figure 5D). This behavior resembles the classic overfitting issue of neural networks [28]. When a network is trained over a large number of epochs, the model tends to overfit. Consequently, it exhibits poor performance on unseen data. To avoid overfitting QNet, we can use the existing techniques such as early stopping [63].
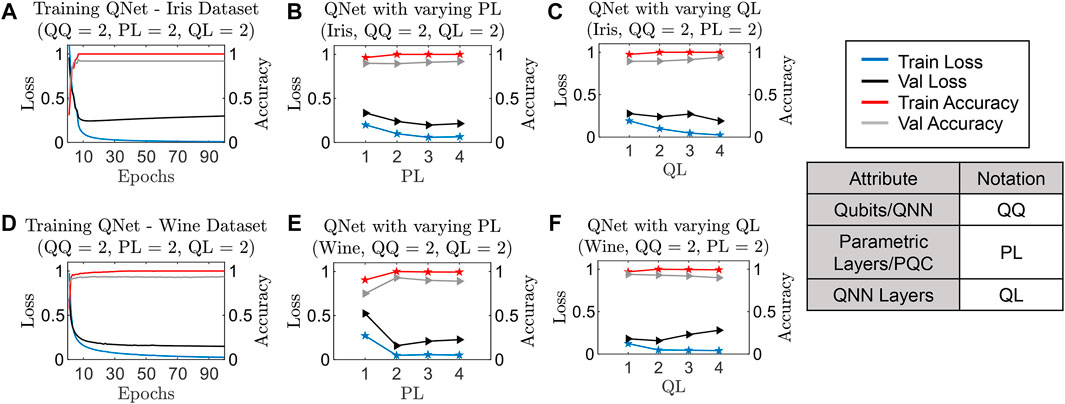
FIGURE 5. Performance (training loss, training accuracy, validation loss, and validation accuracy) of QNet on Iris and Wine datasets with a varying number of Parametric Layers/PQC (PL) and QNN Layers (QL). Qubits/QNN (QQ) is fixed at 2. (A,D) shows the performance over 100 epochs of training. (B,E) shows performance against varying PL after 20 training epochs. (C,F) shows performance against varying QL after 20 training epochs. All data points are an average of 10 different training runs that start with different seeds. The models tend to overfit (performance improves monotonically for the training set and worsens for the validation set) with an increasing number of epochs, PL and QL.
We vary PL from 1 to 4 (for QQ = 2, QL = 2) and train the corresponding QNet networks for Iris and Wine classification. The corresponding results are shown in Figures 5B,E, respectively. Note that increasing PL from 1 to 2 doubles the number of trainable circuit parameters in the network. In both cases, the training loss goes down and the training accuracy improves with increasing PL. However, the validation loss or accuracy improve initially, then they start to saturate (Figure 5B) or degrade (Figure 5E). We observe similar behavior when we vary QL from 1 to 4 (Figures 5C,F). Increasing QL from 1 to 2 doubles the number of trainable circuit parameters in the QNet network used in this work. This behavior also resembles the classic overfitting issue in neural networks due to over-parameterization [28]. In practical applications, the size of the network should be chosen judiciously to avoid this issue. It may be worthwhile to explore techniques that exist in the classical domain to avoid overfitting in over-parameterized neural networks and apply them to QNet [64].
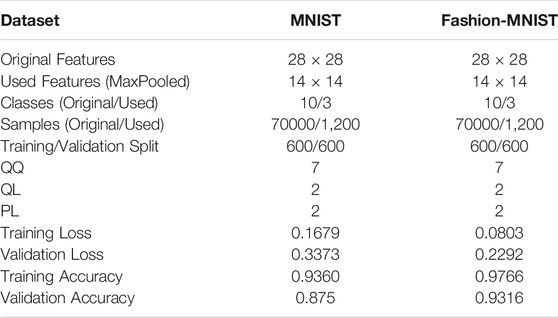
QNet performance metrics for the Wine, Breast Cancer and the Digits datasets with varying QQ’s and network sizes (PL = 2, QL = 2 Vs PL = 3, QL = 3) are shown in Table 1. Surprisingly, at lower QQ values, QNet performs better across all these datasets. The performance on the training set improves with increased network size. However, the validation performance deteriorates as expected due to overfitting. The performance on the truncated MNIST and Fashion-MNIST datasets are shown in Table 2. The performance metrics on both these datasets indicate the trainability and generalization capability of QNet on real-world datasets. Note that prior works on applying QML models on datasets such as MNIST or Fashion-MNIST reduced the input dimensions to an extremely low level (e.g., 30 in [24]). However, such reduction is not necessary for QNet. Nevertheless, we downsample the data from 28 × 28 (784) to 14 × 14 (196) to avoid large simulation time.
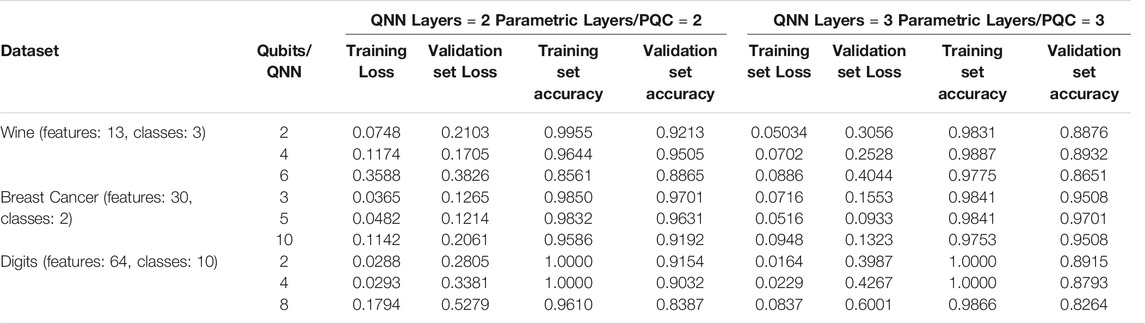
TABLE 1. QNet performance after 20 epochs of training on Wine, Breast Cancer, and Digits classification datasets with varying QQ, QL, and PL. QNet performs better with lower QQ. Larger networks tend to overfit, e.g., training performance improves from QL = 2, PL = 2 to QL = 3, PL = 3 while validation performance falls down.
5.2.2 QNet Vs. Baseline
We train the Iris and Wine classifiers using QNet and Baseline with a varying number of trainable circuit parameters (noiseless simulation). The results are shown in Figures 6A,B. Note that both these approaches provide similar performance in noiseless simulations. Baseline performs slightly better than QNet for the smaller Iris dataset (Figure 6A). QNet performs slightly better than Baseline for the bigger Wine dataset. Note that the Baseline models for Iris and Wine datasets require 4 and 13 qubits, respectively. We used QQ = 2, PL = 2, and QL = 2 in the QNet models. We can not train the Baseline models for other datasets (e.g., Breast Cancer, Digits, MNIST, Fashion-MNIST) in our computing environment due to the memory bottleneck of quantum simulation [29].

FIGURE 6. QNet and Baseline model performances in 10 training epochs on a simulator (noiseless) with similar network sizes (same number of trainable circuit parameters). (A,B) shows the performances on Iris and Wine datasets, respectively. These models exhibit similar performances in noiseless simulations.
The superior performance of QNet becomes evident when we train these models under noise with a hardware emulator (ibmq_16_melbourne) as shown in Figure 7. On the smaller Iris dataset (Figure 7A), the performances are similar. However, on the bigger Wine dataset, there is a significant gap (Figure 7B). The QNet network training loss and validation loss consistently goes down over training epochs. However, the Baseline models remain more or less constant. The Baseline model uses a 13-qubit circuit for the Wine dataset. The target device’s quantum volume (ibmq_16_melbourne) is 8, implying that 3-qubit (or similarly sized) circuits can be reliably executed on the hardware. Consequently, the Iris Baseline model performs well with this hardware emulator that uses a 4-qubit circuit. However, the 13-qubit Baseline QNN for the Wine dataset essentially generates random outputs, and therefore, this model does not train well as evident from Figure 7B. In both cases, QNet employs a sequence of 2-qubit circuits and is hardly affected by hardware noise.
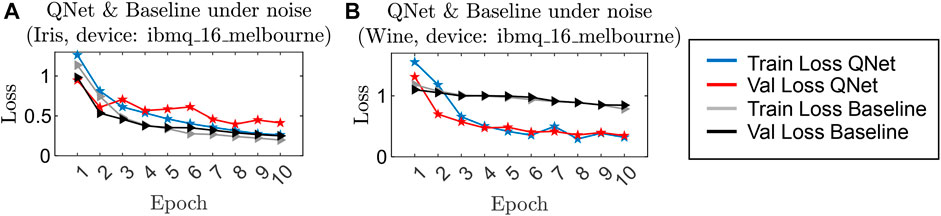
FIGURE 7. QNet and Baseline model performances in 10 training epochs on a quantum hardware emulator (simulated ibmq_16_melbourne) with similar network sizes (same number of trainable circuit parameters). (A,B) shows the performances on Iris and Wine datasets, respectively. On the smaller Iris dataset (4-features), the performance is comparable. However, on the larger Wine dataset (13-features), QNet shows significantly better performance under noise.
5.2.3 QNet Vs. PCA + Baseline
As mentioned earlier, the performance of PCA + Baseline will largely depend on the level of compression using PCA. To further illustrate this issue, we show the fraction of explained variance against the chosen number of principal components (PC) on the Digits dataset in Figure 8A [65]. The fraction improves with an increasing number of PC. For instance, 4 PC explains roughly 40% variance in the digits dataset compared to ≈ 70% in 8 PC. Therefore, the subsequent Baseline model in PCA + Baseline will work on a poor representation of the original dataset. Consequently, this PCA + Baseline model will perform poorly. The accuracy of the trained PCA + Baseline models and QNet models on the Digits dataset with varying PCs is shown in Figure 8B (noiseless simulation). Note that, when we choose n-PC’s, the subsequent Baseline QNN in the PCA + Baseline model uses n-qubit circuits. For QNet, we use QQ = 2 (2-qubit circuits), PL = 2, and QL = 2. The QNet models outperform the corresponding PCA + Baseline models in terms of accuracy. For instance, QNet accuracy is 68% greater than PCA + Baseline with 2 PC. The difference is 30% for PCA + Baseline with 16 PC. If we use a larger PC (e.g., 32), the PCA + Baseline model may perform at a similar level to QNet in the noiseless simulation. However, the quantum circuit will be much larger (32-qubit), and it may perform very poorly on the near-term hardware.

FIGURE 8. The PCA + Baseline model performance largely depends on the chosen number of principal components (PC). A higher number of PC captures more variance of the input data. (A) shows the fraction of explained variance with an increasing number of PC. (B) shows the performance of PCA + Baseline against QNet with varying numbers of PC (after 20 epochs of training in a noiseless simulator). n-qubit corresponds to n chosen PC for the PCA + Baseline models and QQ = n for the corresponding QNet models (both can be executed on n-qubit hardware). In QNet, we use PL = 2, QL = 2. For a fair comparison, we vary the number of trainable parameters in PCA + Baseline models and report the best-measured performance against QNet.
To compare the performance between QNet and PCA + Baseline on hardware, we use the 5-qubit ibmq_bogota and 7-qubit ibmq_casablanca hardware emulators and measure the trained QNet and PCA + Baseline models performance for Wine, Breast Cancer, Digits, MNIST, and Fashion-MNIST datasets. The results are shown in Figures 9A,B. We use 5 and 7 PC in the PCA + Baseline models for ibmq_bogota and ibmq_casablanca, respectively. In all these cases, QNet uses QQ = 2, PL = 2, QL = 2. QNet accuracy is 36–76% higher on ibmq_bogota and 32–62% higher on ibmq_casablanca across all these datasets. Note that both of these pieces of hardware have a QV of 32, indicating that they can run 5-qubit (or equivalent) circuits reliably. The PCA + Baseline models use 5/7 qubit circuits. We anticipate that noise will have less of an impact on these circuits. However, the PCA compression loses too much information and thus, damages the overall performance.
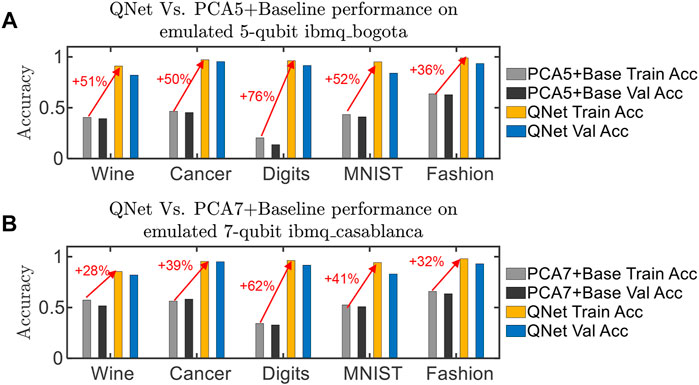
FIGURE 9. Measured performance of trained QNet and PCA + Baseline models on hardware emulators. (A) shows performance comparison on 5-qubit ibmq_bogota where the QNet models use QQ = 5 and the PCA + Baseline models use 5 principal components. (B) shows the performance comparison on 7-qubit ibmq_casablanca where the QNet models use QQ = 7 and the PCA + Baseline models use 7 principal components. For QNet, we use PL = 2, QL = 2. For a fair comparison, we vary the number of trainable parameters in PCA + Baseline models and report the best-measured performance against QNet.
5.2.4 QNet Vs DRC
As mentioned earlier, the DRC model exceeds the coherence time of the device when the number of features is large. It may be pointless to compare DRC with QNet for larger datasets on hardware emulators. Therefore, we choose the smallest Iris dataset for comparison. The measured performance of the trained QNet (QQ = 2, PL = 2, QL = 2) and two-qubit DRC models (on simulator and ibmq_bogota emulator) are shown in Figure 10. Note that the performances are similar in noiseless simulations (Figure 10A). However, the measured accuracy of QNet on noisy ibmq_bogota emulator is significantly higher on both the training (29%) and the validation (21%) sets (Figure 10B). Similarly, the loss is significantly lower in QNet.
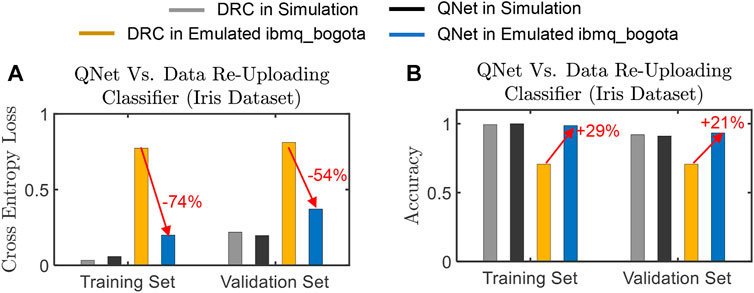
FIGURE 10. Performance comparison between QNet and DRC on Iris classification dataset. We report (A) loss and (B) accuracy of the trained QNet and DRC models in noiseless simulation and emulated hardware (ibmq_bogota). In the noiseless simulation, their performances are comparable. However, under noise, QNet significantly outperforms DRC. For QNet, we used QQ = 2, PL = 2, QL = 2. For a fair comparison, we vary the number of trainable parameters in a single-qubit DRC model and report the best-measured performance against QNet.
6 Discussion and Future Outlook
Why is QNet Noise-Resilient and Scalable?: Unlike Baseline, PCA + Baseline, and DRC models, the circuit sizes can be modulated arbitrarily in QNet. This flexibility provides noise resilience and scalability to QNet. Each QNN can have a small number of qubits (e.g., QQ = 2) and a small depth (e.g., PL = 2). One can execute these small circuits reliably in existing NISQ-machines. Due to the high accumulation of gate noise and decoherence in the Baseline and PCA + Baseline models, their corresponding QNN circuit outputs can be highly erroneous. Therefore these models may perform poorly on hardware. The circuits in DRC have a lower number of qubits. They are, however, too deep for larger datasets, so decoherence and gate errors can have a bigger impact on their outputs. To solve larger problems in the Baseline or PCA + Baseline models, we need to add more qubits to the QNN circuit, whereas in QNet, we only need to add more small noise-resilient QNN circuits. As a result, QNet models can be scaled to fit any size dataset. PCA + QNet could be another promising solution for reducing the use of quantum resources. The PCA + QNet variation, unlike PCA + Baseline, does not require significant data compression to fit the quantum circuit on the target hardware. As a result, its performance will be less affected than that of the PCA + Baseline model due to information loss during data compression.
Constructing QNN’s in QNet: Throughout this study, we use the same encoding method (Figure 2B), parametric layer architecture (Figure 2D), and measurement operations (Pauli-Z expectation values of qubits) in all the models. We also use the same number of QNN in different QNN Layers. All these choices can have a significant impact on the network size and performance. For example, if we choose a 2-variables/qubit angle encoding method instead of the 1-variable/qubit angle encoding method, the number of QNN’s in the network can reduce greatly. For example, the QNN circuits in a QNet network for an 8-feature dataset (QQ = 2, QL = 2) will reduce from 8 to 3 as shown in Figure 11. The Baseline and PCA + Baseline models will also have similar benefits. However, a detailed study on this front is beyond the scope of this paper.
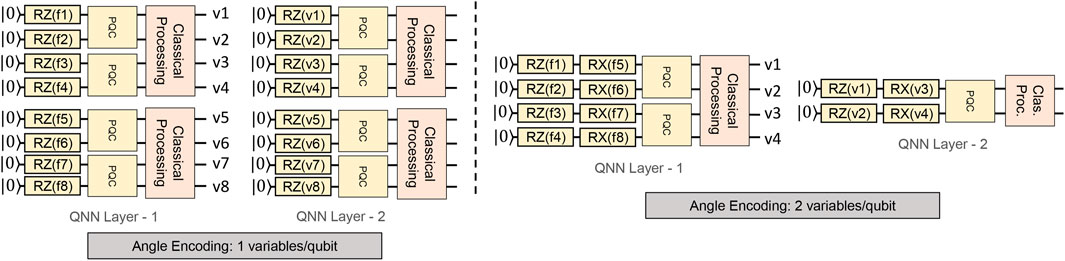
FIGURE 11. Throughout this work, we have used 1-variable/qubit angle encoding for all the QNN models. All these networks (QNet, Baseline, PCA + Baseline) can benefit from improved classical-to-quantum data encoding methods. Here, we show the impact of using the 2-variables/qubit angle encoding method on the QNet network for an 8-feature ML problem. We use QQ = 2, PL = 2, QL = 2. While the first network uses a total of 8 2-qubit circuits, the second one uses only 3. However, we may potentially lose information while loading too many variables in a single qubit, and that may affect the performance/trainability of these models [8]. We keep exploration on this front for future studies.
QNet on Small Quantum Systems: QNet enables the integration of multiple small and heterogeneous quantum computing systems in a single machine learning application. The QNNs in a QNN Layer can be executed sequentially on a small quantum computer (at the expense of increased run-time) or concurrently in different hardware during the training/inference step’s forward pass. Seven 5-qubit systems, four 7-qubit systems, and one single-qubit system are available in the current IBMQ suite. One can use the 64 qubits available in these chips to create QNet models to handle 64-feature ML problems (e.g., digits classification discussed in the previous section). To create QNet with this set of hardware, we can utilize seven 5-qubit QNNs, four 7-qubit QNNs, and one single-qubit QNN in each QNN Layer. Each QNN model (parametric layer, encoding, and so on) should be tailored to the hardware used in the backend. For example, if we want all the QNNs in a QNN Layer to have a comparable forward pass execution time, the QNNs with a larger number of qubits should have fewer Parametric Layers than the QNNs with lower qubit counts.
QNet on Heterogeneous Systems: It’s worth noting that hardware based on a different quantum computing technology (for example, IonQ’s 11-qubit trapped-ion system) can be added to the mix without sacrificing generality. Individual QNN models can be modified for unique hardware in these circumstances. QNN’s for trapped-ion computers can be built using the technology’s native gates (e.g., GPI, GPI2, GZ, and MS) [66]. For example, instead of the CNOT gate, which is the native 2-qubit gate in IBM’s superconducting quantum computers, we can entangle the qubits using the two-qubit MS gate in trapped-ion systems [22]. Again, if we want all the QNNs in a single QNN Layer in QNet to have a comparable forward pass time, the PQCs of individual QNNs will need to be customized accordingly.
QNet on Larger Quantum Systems: Furthermore, we can implement QNet with small QNN’s on large hardware (e.g., the 65-qubit ibmq_brookyn). Even if a Baseline fits in this large hardware, QNet might be preferred. The QV measure explains this. The ibmq_brookyn hardware has QV of 32. Even though it has 65 qubits, we can reliably execute circuits that have ≈ 5-qubits and a depth of ≈ 5. As a result, for an ML job including a 64-feature dataset, a QNet model with sixteen 4-qubit QNNs per QNN Layer will have a better chance of success than a Baseline QNN created with a 64-qubit circuit.
QNet in Simulation: Quantum simulation is limited by the memory bottleneck [29]. One can represent an n-qubit system state with a state vector that has 2n complex values. The memory requirement can easily go beyond the limit of classical simulation if we increase the number of qubits. Currently, the most powerful simulator available in the IBMQ suite can handle 32-qubits. Even QML applications based on classical simulators can benefit from QNet. Let’s say we’re solving a 64-feature dataset with QNet, and we’re employing 8-qubit QNNs. There will be eight such QNN’s in each QNN Layer. A quantum simulator will need to store 28 or 256 complex values to process these QNN’s sequentially. Eight instances of the simulator (e.g., employing multi-processing) can be used for concurrent simulation, requiring storage of 8*28 or 2048 complex values. In comparison, a 64-qubit Baseline QNN circuit will require storage of 264 complex values. It is far beyond the capabilities of existing supercomputers.
In this work, we have demonstrated QNet models on 196-feature datasets using quantum simulators available in the Pennylane [47] framework that runs on a single CPU-core of a standard computer (Intel Core i7-10750H, 16 GB RAM) reasonably fast. The simulation time can be improved by allocating QNN’s in a QNN Layer to different instances of the simulator using advanced computing techniques (e.g., multi-processing/multi-threading or distributed computing). QNet is not affected by the memory bottleneck as much as the Baseline when QQ is small. Figure 12 shows the single-epoch training time of QNet (Breast Cancer dataset) with varying QQ on our computing environment. At lower QQ, the simulation takes minutes. Therefore, QNet can be an exciting choice for simulation-based practical QML applications.
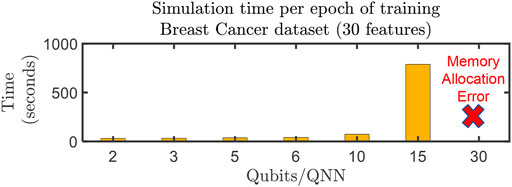
FIGURE 12. QNet models are suitable for simulation based QML applications where quantum simulators are used for training and inference of QNN models for practical applications. We report the time taken for 1 training epoch on the Breast Cancer classification dataset with varying QQ. This dataset contains 569 samples (30 features) and we use half of them (285) for training. The training is done on a standard desktop machine (Intel Core i7-10750H, 16 GB RAM) using a single computing core. We use the default state vector simulator available in the PennyLane framework. With lower QQ, the model can be trained in minutes. With higher QQ, the training time increases due to larger memory requirements by the simulator.
Other Applications of QNet: In this study, we exclusively employ classification datasets. By adjusting the cost functions, one can use QNet for different QML tasks (such as regression, auto-encoder, and so on). These can be worthwhile research topics for the future.
Quantum Supremacy: Quantum computing and quantum machine learning are still in their infancy. Existing classical ML algorithms have matured over a few decades of research. Therefore, we feel that seeking superior performance with QNet compared to the classical algorithms can be unfair. Nonetheless, the performance of QNet in this study is comparable to that of traditional neural networks. It may improve further with proper choice of encoding methods, parametric layer architecture, and measurements. QNet is a generic framework for creating quantum machine learning models that are noise-resistant. We believe it will have a profound impact on quantum machine learning research in the near term.
QNet Limiting Factors: QNet employs a large number of small QNNs, which can be advantageous if a user has access to a large number of small quantum computers for parallel processing. However, having only one piece of quantum hardware can be a bottleneck. In such circumstances, one needs to execute the QNNs in order. Furthermore, we will need to reset the qubits between each call to the quantum computers, which may raise the overall execution time of the QNet network because qubit resets can take much longer than actual gate executions [67]. Moreover, the number of qubit measurements increases with QL in QNet. A QNet with QL = 2 may have 2X measurements compared to QL = 1. Large measurement errors can affect QNet performance. However, measurement errors have decreased significantly in the IBM quantum devices in the past few years. For example, the 5-qubit ibmqx-2, a quantum device from the past generation, had an average measurement error of 8.2% while the current 5-qubit ibmq_bogota device has an average measurement error rate of 2.27%. On top of that, one can reduce measurement errors by applying classical post-processing [68–70]. The advantages of a reduced depth and gate-count may outweigh the additional measurement noise, as evidenced by comparison to prior approaches.
7 Conclusion
In this paper, we present QNet–a scalable and noise-resilient quantum neural network architecture. Through empirical study, we show that QNet outperforms existing techniques in terms of performance and noise resilience. We use six datasets (Iris, Wine, Breast Cancer, Digits, MNIST, Fashion-MNIST) and three noisy hardware emulators (ibmq_16_melbourne, ibmq_bogota, ibmq_casablanca) for this study. On average, trained QNet models show 43% better accuracy over the existing models on the hardware emulators. QNet also provides a framework for creating noise-resistant QML models using a collection of small quantum neural networks. In the not-too-distant future, it has the potential to have a significant impact on quantum machine learning research.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The work is supported in parts by NSF (CNS-1722557, CCF-1718474, OIA-2040667, DGE-1723687, DGE-1821766, and DGE-2113839) and seed grants from Penn State ICDS and Huck Institute of the Life Sciences.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We also thank Prof. Mehrdad Mahdavi from Penn State and Dr. Rasit Topaloglu from IBM Corp. for helpful discussions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.755139/full#supplementary-material
Footnotes
1https://github.com/mahabubul-alam/QNet
References
1. Arute F, Arya K, Babbush R, Bacon D, Bardin JC, Barends R, et al. Quantum Supremacy Using a Programmable Superconducting Processor. Nature (2019) 574:505–10. doi:10.1038/s41586-019-1666-5
2. Biamonte J, Wittek P, Pancotti N, Rebentrost P, Wiebe N, Lloyd S. Quantum Machine Learning. Nature (2017) 549:195–202. doi:10.1038/nature23474
3. Farhi E, Neven H. Classification with Quantum Neural Networks on Near Term Processors (2018). arXiv preprint arXiv:1802.06002.
4. Killoran N, Bromley TR, Arrazola JM, Schuld M, Quesada N, Lloyd S. Continuous-variable Quantum Neural Networks. Phys Rev Res (2019) 1:033063. doi:10.1103/physrevresearch.1.033063
5. Cong I, Choi S, Lukin MD. Quantum Convolutional Neural Networks. Nat Phys (2019) 15:1273–8. doi:10.1038/s41567-019-0648-8
6. Schuld M, Killoran N. Quantum Machine Learning in Feature hilbert Spaces. Phys Rev Lett (2019) 122:040504. doi:10.1103/PhysRevLett.122.040504
7. Schuld M, Bocharov A, Svore KM, Wiebe N. Circuit-centric Quantum Classifiers. Phys Rev A (2020) 101:032308. doi:10.1103/physreva.101.032308
8. Abbas A, Sutter D, Zoufal C, Lucchi A, Figalli A, Woerner S. The Power of Quantum Neural Networks. Nat Comput Sci (2021) 1:403–9. doi:10.1038/s43588-021-00084-1
9. Du Y, Hsieh M-H, Liu T, Tao D. Expressive Power of Parametrized Quantum Circuits. Phys Rev Res (2020) 2:033125. doi:10.1103/physrevresearch.2.033125
10. Wright LG, McMahon PL. The Capacity of Quantum Neural Networks. In: CLEO: QELS_Fundamental Science. Washington, DC: Optical Society of America (2020). p. JM4G–5. doi:10.1364/cleo_at.2020.jm4g.5
11. Sim S, Johnson PD, Aspuru‐Guzik A. Expressibility and Entangling Capability of Parameterized Quantum Circuits for Hybrid Quantum‐Classical Algorithms. Adv Quan Tech (2019) 2:1900070. doi:10.1002/qute.201900070
12. Schuld M, Sweke R, Meyer JJ. Effect of Data Encoding on the Expressive Power of Variational Quantum-Machine-Learning Models. Phys Rev A (2021) 103:032430. doi:10.1103/physreva.103.032430
13. Funcke L, Hartung T, Jansen K, Kühn S, Stornati P. Dimensional Expressivity Analysis of Parametric Quantum Circuits. Quantum (2021) 5:422. doi:10.22331/q-2021-03-29-422
14. Mari A, Bromley TR, Izaac J, Schuld M, Killoran N. Transfer Learning in Hybrid Classical-Quantum Neural Networks. Quantum (2020) 4:340. doi:10.22331/q-2020-10-09-340
15. Alam M, Kundu S, Topaloglu RO, Ghosh S. Iccad Special Session Paper: Quantum-Classical Hybrid Machine Learning for Image Classification (2021). arXiv preprint arXiv:2109.02862.
16. Li J, Alam M, Sha CM, Wang J, Dokholyan NV, Ghosh S. Drug Discovery Approaches Using Quantum Machine Learning (2021). arXiv preprint arXiv:2104.00746.
17. Batra K, Zorn KM, Foil DH, Minerali E, Gawriljuk VO, Lane TR, et al. Quantum Machine Learning Algorithms for Drug Discovery Applications. In: Chem Inf Model., 61 (2021). p. 2641–7. doi:10.1021/acs.jcim.1c00166
18. Sakuma T. Application of Deep Quantum Neural Networks to Finance (2020). arXiv preprint arXiv:2011.07319.
19. Pistoia M, Ahmad SF, Ajagekar A, Buts A, Chakrabarti S, Herman D, et al. Quantum Machine Learning for Finance (2021). arXiv preprint arXiv:2109.04298.
20. Luckow A, Klepsch J, Pichlmeier J. Quantum Computing: Towards Industry Reference Problems (2021). arXiv preprint arXiv:2103.07433.
21. Preskill J. Quantum Computing in the Nisq Era and beyond. Quantum (2018) 2:79. doi:10.22331/q-2018-08-06-79
22. Cross AW, Bishop LS, Sheldon S, Nation PD, Gambetta JM. Validating Quantum Computers Using Randomized Model Circuits. Phys Rev A (2019) 100:032328. doi:10.1103/physreva.100.032328
23. Grant E, Benedetti M, Cao S, Hallam A, Lockhart J, Stojevic V, et al. Hierarchical Quantum Classifiers. npj Quan Inf (2018) 4:1–8. doi:10.1038/s41534-018-0116-9
24. Huang HY, Broughton M, Mohseni M, Babbush R, Boixo S, Neven H, et al. Power of Data in Quantum Machine Learning. Nat Commun (2021) 12:2631–9. doi:10.1038/s41467-021-22539-9
25. Pérez-Salinas A, Cervera-Lierta A, Gil-Fuster E, Latorre JI. Data Re-uploading for a Universal Quantum Classifier. Quantum (2020) 4:226. doi:10.22331/q-2020-02-06-226
26. Easom-Mccaldin P, Bouridane A, Belatreche A, Jiang R. On Depth, Robustness and Performance Using the Data Re-uploading Single-Qubit Classifier. IEEE Access (2021) 9:65127–39. doi:10.1109/access.2021.3075492
27. Suzuki T, Katouda M. Predicting Toxicity by Quantum Machine Learning. J Phys Commun (2020) 4:125012. doi:10.1088/2399-6528/abd3d8
28. Anthony M, Bartlett PL. Neural Network Learning: Theoretical Foundations. Cambridge University Press (2009).
29. Nielsen MA, Chuang I. Quantum Computation and Quantum Information. American Association of Physics Teachers (2002).
30. Crawford O, Straaten Bv., Wang D, Parks T, Campbell E, Brierley S. Efficient Quantum Measurement of Pauli Operators in the Presence of Finite Sampling Error. Quantum (2021) 5:385. doi:10.22331/q-2021-01-20-385
31. Reilly D. Challenges in Scaling-Up the Control Interface of a Quantum Computer. In: 2019 IEEE International Electron Devices Meeting (IEDM). IEEE (2019). p. 31–7. doi:10.1109/iedm19573.2019.8993497
32. Clarke J. An Optimist’s View of the 4 Challenges to Quantum Computing. IEEE Spectrum (2019). Available at: https://spectrum.ieee.org/an-optimists-view-of-the-4-challenges-to-quantum-computing (Accessed November 30, 2021).
33. Pauka SJ, Das K, Kalra R, Moini A, Yang Y, Trainer M, et al. A Cryogenic Cmos Chip for Generating Control Signals for Multiple Qubits. Nat Electron (2021) 4:64–70. doi:10.1038/s41928-020-00528-y
34. Lloyd S, Schuld M, Ijaz A, Izaac J, Killoran N. Quantum Embeddings for Machine Learning (2020). arXiv preprint arXiv:2001.03622.
35. Yano H, Suzuki Y, Raymond R, Yamamoto N. Efficient Discrete Feature Encoding for Variational Quantum Classifier. In: 2020 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE (2020). p. 11–21. doi:10.1109/qce49297.2020.00012
36. Hubregtsen T, Pichlmeier J, Stecher P, Bertels K. Evaluation of Parameterized Quantum Circuits: on the Relation between Classification Accuracy, Expressibility, and Entangling Capability. Quan Machine Intelligence (2021) 3:1–19. doi:10.1007/s42484-021-00038-w
37. Alam M, Ash-Saki A, Ghosh S. Addressing Temporal Variations in Qubit Quality Metrics for Parameterized Quantum Circuits. In: 2019 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED). IEEE (2019). p. 1–6. doi:10.1109/islped.2019.8824907
38. Mottonen M, Vartiainen JJ, Bergholm V, Salomaa MM. Transformation of Quantum States Using Uniformly Controlled Rotations (2004). arXiv preprint quant-ph/0407010.
39. Cross A. The Ibm Q Experience and Qiskit Open-Source Quantum Computing Software. In: APS March Meeting Abstracts, 2018 (2018). p. L58–003.
40. Nghiem NA, Chen SY-C, Wei T-C. Unified Framework for Quantum Classification. Phys Rev Res (2021) 3:033056. doi:10.1103/physrevresearch.3.033056
41. Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, et al. Pytorch: An Imperative Style, High-Performance Deep Learning Library. Adv Neural Inf Process Syst (2021) 32:8026–8037.
42. Kingma DP, Ba J. Adam: A Method for Stochastic Optimization (2014). arXiv preprint arXiv:1412.6980.
43. Duchi J, Hazan E, Singer Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J machine Learn Res (2011) 12.
44. Luo X-Z, Liu J-G, Zhang P, Wang L. Yao.jl: Extensible, Efficient Framework for Quantum Algorithm Design. Quantum (2020) 4:341. doi:10.22331/q-2020-10-11-341
45. Banchi L, Crooks GE. Measuring Analytic Gradients of General Quantum Evolution with the Stochastic Parameter Shift Rule. Quantum (2021) 5:386. doi:10.22331/q-2021-01-25-386
46. Schuld M, Bergholm V, Gogolin C, Izaac J, Killoran N. Evaluating Analytic Gradients on Quantum Hardware. Phys Rev A (2019) 99:032331. doi:10.1103/physreva.99.032331
47. Bergholm V, Izaac J, Schuld M, Gogolin C, Alam MS, Ahmed S, et al. Pennylane: Automatic Differentiation of Hybrid Quantum-Classical Computations (2018). arXiv preprint arXiv:1811.04968.
48. Lavrijsen W, Tudor A, Müller J, Iancu C, de Jong W. Classical Optimizers for Noisy Intermediate-Scale Quantum Devices. In: 2020 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE (2020). p. 267–77. doi:10.1109/qce49297.2020.00041
49. Li Deng L. The Mnist Database of Handwritten Digit Images for Machine Learning Research [best of the Web]. IEEE Signal Process Mag (2012) 29:141–2. doi:10.1109/msp.2012.2211477
50. Xiao H, Rasul K, Vollgraf R. Fashion-mnist: A Novel Image Dataset for Benchmarking Machine Learning Algorithms (2017). arXiv preprint arXiv:1708.07747.
51. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: Machine Learning in python. J machine Learn Res (2011) 12:2825–30.
52.[Dataset] Ibm quantum. Real Quantum Computers. Right at Your Fingertips (2021). Available at: https://quantum-computing.ibm.com/ (Accessed July 28, 2021).
53.[Dataset] Ibm quantum. Qiskit/qiskit-terra (2021). Available at: https://github.com/Qiskit/qiskit-terra/tree/main/qiskit/test/mock/backends (Accessed July 28, 2021).
54.[Dataset] Ibm quantum. High-Performance Simulator Tutorials (2021). Available at: https://qiskit.org/documentation/tutorials/simulators/ (Accessed July 28, 2021).
55. Liu J, Zhou H. Reliability Modeling of Nisq-Era Quantum Computers. In: 2020 IEEE International Symposium on Workload Characterization (IISWC). IEEE (2020). p. 94–105. doi:10.1109/iiswc50251.2020.00018
56. Wang Y, Krstic PS. Prospect of Using grover’s Search in the Noisy-Intermediate-Scale Quantum-Computer Era. Phys Rev A (2020) 102:042609. doi:10.1103/physreva.102.042609
57. Azses D, Haenel R, Naveh Y, Raussendorf R, Sela E, Dalla Torre EG. Identification of Symmetry-Protected Topological States on Noisy Quantum Computers. Phys Rev Lett (2020) 125:120502. doi:10.1103/physrevlett.125.120502
58. Resch S, Gutierrez A, Huh JS, Bharadwaj S, Eckert Y, Loh G, et al. Accelerating Variational Quantum Algorithms Using Circuit Concurrency (2021). arXiv preprint arXiv:2109.01714.
59. Wood CJ. Special Session: Noise Characterization and Error Mitigation in Near-Term Quantum Computers. In: 2020 IEEE 38th International Conference on Computer Design (ICCD). IEEE (2020). p. 13–6. doi:10.1109/iccd50377.2020.00016
60. Ishizaki A, Fleming GR. Unified Treatment of Quantum Coherent and Incoherent Hopping Dynamics in Electronic Energy Transfer: Reduced Hierarchy Equation Approach. J Chem Phys (2009) 130:234111. doi:10.1063/1.3155372
61. Ishizaki A, Fleming GR. On the Adequacy of the redfield Equation and Related Approaches to the Study of Quantum Dynamics in Electronic Energy Transfer. J Chem Phys (2009) 130:234110. doi:10.1063/1.3155214
62. Wang B-X, Tao M-J, Ai Q, Xin T, Lambert N, Ruan D, et al. Efficient Quantum Simulation of Photosynthetic Light Harvesting. NPJ Quan Inf (2018) 4:1–6. doi:10.1038/s41534-018-0102-2
63. Ying X. An Overview of Overfitting and its Solutions. J Phys Conf Ser (2019) 1168:022022. doi:10.1088/1742-6596/1168/2/022022
64. Li M, Soltanolkotabi M, Oymak S. Gradient Descent with Early Stopping Is Provably Robust to Label Noise for Overparameterized Neural Networks. In: International conference on artificial intelligence and statistics. Palermo, Sicily, Italy: PMLR (2020). p. 4313–24.
65. Friedman J, Hastie T, Tibshirani R. The Elements of Statistical Learning, Vol. 1. New York: Springer series in statistics (2001).
66. Wright K, Beck KM, Debnath S, Amini JM, Nam Y, Grzesiak N, et al. Benchmarking an 11-qubit Quantum Computer. Nat Commun (2019) 10:5464–6. doi:10.1038/s41467-019-13534-2
67. Magnard P, Kurpiers P, Royer B, Walter T, Besse JC, Gasparinetti S, et al. Fast and Unconditional All-Microwave Reset of a Superconducting Qubit. Phys Rev Lett (2018) 121:060502. doi:10.1103/PhysRevLett.121.060502
68. Tannu SS, Qureshi MK. Mitigating Measurement Errors in Quantum Computers by Exploiting State-dependent Bias. In: Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture (2019). p. 279–90. doi:10.1145/3352460.3358265
69. Nachman B, Urbanek M, de Jong WA, Bauer CW. Unfolding Quantum Computer Readout Noise. npj Quan Inf (2020) 6:1–7. doi:10.1038/s41534-020-00309-7
70. Bravyi S, Sheldon S, Kandala A, Mckay DC, Gambetta JM. Mitigating Measurement Errors in Multiqubit Experiments. Phys Rev A (2021) 103:042605. doi:10.1103/physreva.103.042605
71. Murali P, Baker JM, Javadi-Abhari A, Chong FT, Martonosi M. Noise-adaptive Compiler Mappings for Noisy Intermediate-Scale Quantum Computers. In: Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (2019). p. 1015–29. doi:10.1145/3297858.3304075
72. Tannu SS, Qureshi MK. Not all Qubits Are Created Equal: a Case for Variability-Aware Policies for Nisq-Era Quantum Computers. In: Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (2019). p. 987–99.
73. Alam M, Ash-Saki A, Ghosh S. Circuit Compilation Methodologies for Quantum Approximate Optimization Algorithm. In: 2020 53rd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO). IEEE (2020). p. 215–28. doi:10.1109/micro50266.2020.00029
Keywords: quantum machine learning, quantum neural network, parameterized quantum circuit, noisy intermediate-scale quantum, quantum-classical hybrid algorithms
Citation: Alam M and Ghosh S (2022) QNet: A Scalable and Noise-Resilient Quantum Neural Network Architecture for Noisy Intermediate-Scale Quantum Computers. Front. Phys. 9:755139. doi: 10.3389/fphy.2021.755139
Received: 08 August 2021; Accepted: 05 November 2021;
Published: 05 January 2022.
Edited by:
Jingfu Zhang, Technical University Dortmund, GermanyReviewed by:
Che-Ming Li, National Cheng Kung University, TaiwanQing Ai, Beijing Normal University, China
Stefano Martina, University of Florence, Italy
Copyright © 2022 Alam and Ghosh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mahabubul Alam, bXhhODkwQHBzdS5lZHU=
 Mahabubul Alam
Mahabubul Alam Swaroop Ghosh
Swaroop Ghosh