Numerical Study on the Influence of the Plasma Properties on the Keyhole Geometry in Laser Beam Welding

Keyhole laser welding is the benchmark for deep-penetration joining processes. It needs high incident laser beam power densities at the workpiece surface to take place. The gaseous phase plays a fundamental role to keep the deep and narrow keyhole cavity open during the process. The plasma created in this process is a mixture of ionized metal vapors and the environmental gas and it develops inside the keyhole (keyhole plasma) and above the workpiece surface (plasma plume). The presence of plasma implicates absorption, scattering, and refraction of laser beam rays. These phenomena alter the power density of the laser beam irradiating the workpiece surface and thus affect the resulting welding process. In this work, a mathematical and numerical model has been developed to calculate the keyhole shape taking into account the plasma absorption effects. The model considers the keyhole walls as the liquid-vapor interface and computes the keyhole geometry applying a local energy balance at this interface. In addition, the model takes into account the multiple reflections effects inside the cavity through an iterative ray-tracing technique, and calculates the absorption mechanism due to inverse Bremsstrahlung for each ray along its segmented path inside the keyhole. Results show the effect of plasma properties on the keyhole shape and depth.

Introduction

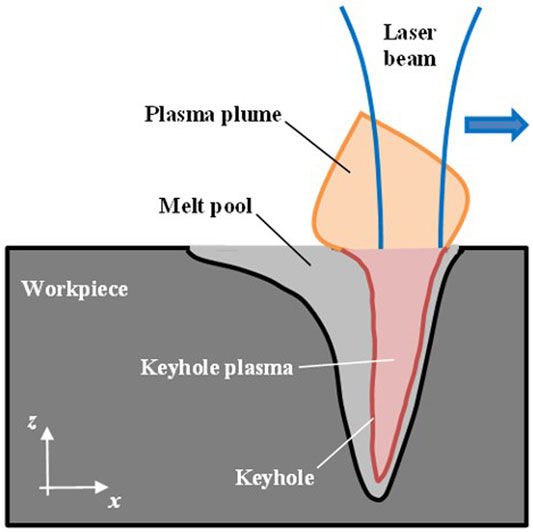
In the last decades, one of the most important developments of laser material processing in the field of advanced production methodologies regards joining processes. Metal joining through laser welding is by now a standardly used process for a wide range of applications in the automotive and aerospace industries. In this application, a laser beam is used as the heat source for the melting of the base material, eventually mixed with a filler one, forming a fused pool that becomes the weld seam when it solidifies. When the laser beam power intensity at the workpiece surface is sufficiently high [1] (≥10⁹ W/m² according to [2, 3]; ≥10¹⁰ W/m² according to [4–6]), a capillary called keyhole forms inside the melt metal pool (Figure 1).

FIGURE 1

FIGURE 1. Schematization of the keyhole laser welding process.

This long and very narrow channel follows the movements of the laser beam, permitting its deep penetration into the workpiece. Thus, the keyhole allows the formation of weld seams with high aspect ratios and small heat-affected zones. The keyhole cavity is formed and kept open thanks to the gaseous phase since the flow of the surrounding liquid and surface tension tend to close it [1]. In other conventional joining methods, the metal is simply heated up until melting, while the characteristic high laser beam density of keyhole welding provides a heating rate much higher than the heat extraction rate due to deeper heat conduction into the metal, convection, and back reflection mechanisms [2]. This implicates local heating of the metal up to temperatures higher than the boiling point, causing intensive metal evaporation and dispersion of the metal vapor. This intensive evaporation causes a reactive force in terms of vapor pressure, named recoil pressure, that bends and pierces the melted metal forming the keyhole cavity [2, 4]. The laser beam interacts with the evaporated metal vapor partially ionizing it. In addition, this ionized metal vapor mixes with the ambient, shielding, assisting gases creating plasma both inside the keyhole (usually named keyhole plasma) and above the workpiece surface (usually named plasma plume) [5, 6]. The resulting plasma is electrically neutral and consists of metal vapors, electrons, and excited neutral atoms and ions in both plasma plume and keyhole plasma [3]. The presence of plasma plays a fundamental role in the energy transport from the laser beam to the workpiece, affecting the welding process through several laser absorption, scattering, and refraction phenomena [3, 5]. The main absorption mechanism in the plasma is due to inverse Bremsstrahlung. This kind of absorption is quite relevant for CO₂ laser radiation due to its long wavelength of 10.6 µm. In this case, the absorption becomes stronger when the plasma temperature increases, due to the increasing ionization, until a maximum value of the related absorption coefficient is reached. Beyond this point, any further increase of the temperature causes a decrease of the absorption coefficient, which means a weakening of absorption effects, because of the reduction of plasma density [7]. Laser beams with shorter wavelengths of around 1 µm are much less sensitive to the inverse Bremsstrahlung mechanism, but the resulting energy absorption is still significant: the plasma plume attenuation of the beam radiation for Nd:YAG laser can reach up to 22% of the total power input [8]. In the last decades, many attempts of keyhole observation were conducted to better understand the several physical phenomena involved in laser keyhole welding. In some of them [9–11] high-speed cameras were employed, while others [12–16] adopted an X-ray transmission imaging system. The former method permits an observation limited only to the surface of the melt pool and the plasma plume, while the latter allows a deeper investigation of the dynamic phenomena into the keyhole and the molten pool; but both require generally complicated and expensive equipment, frequently without giving results with the desired level of detail [8]. For these reasons, in order to study keyhole laser welding, numerical and analytical models have been developed by assuming several hypotheses and simplifications for a tractable numerical computation, preserving the overall complexity of phenomena involved in the process [17–20]. The analytical calculation of the keyhole geometry is a key issue for the modeling of this process, even more than the transport phenomena of conduction and convection [8]. The simplest solution is to assume a cylindrical or conical keyhole [21–23], but in this way the change of the keyhole profile due to different process conditions is restricted only to its depth and not also to its shape. Finer solutions consist in considering energy, pressure, and velocity balance at the liquid-vapor interface (i.e., the keyhole wall) through a point-by-point in-depth calculation. This approach is often matched with the assumption of a rotational keyhole symmetry [24–27], which generally makes the modeling suitable only for low welding speeds. Instead, the keyhole shape modeling for higher welding speeds, which are much more commonly employed in manufacturing processes, needs the consideration of an asymmetric profile which could be achieved differentiating the balance calculations at the front keyhole wall (i.e., the half of the liquid-vapor interface which precedes the laser beam) from those at the rear keyhole wall (i.e., the other half which follows the laser beam) [7, 28–35]. All the applications of the asymmetric keyhole model consider the plasma absorption through inverse Bremsstrahlung assuming a constant value of the related absorption coefficient, which is temperature-dependent. Moreover, the modeling takes into account also multiple reflection effects inside the keyhole. The earliest applications of the energy balance model simplify the calculation of this mechanism considering the keyhole profile as a symmetric triangle and estimating a mean number of reflections inside the keyhole with a very simple formulation [7, 28]. More recent recoveries of the same model treat multiple reflections with more robust ray-tracing or similar approaches but consider only the downward orientated reflections [31, 35].

Keyhole laser welding is a complex multiphysical problem involving light-matter interaction, conduction, melting, vaporization, plasma generation, fluid flow, and surface deformation. Different approaches have been used for modeling laser-matter interaction in welding depending on the welding speed. In the case of moderate welding speed, keyhole physics could be considered decoupled from the resolution of the Navier-Stokes equations by calculating the heat flux into the cavity wall and using it as a source term for the fluid equations [18]. In this approach, stationary energy balance, including also the ray-tracing technique, can be adopted to calculate the keyhole profile [19]. The other approach extends to high welding speed and couples the ray-tracing method or the resolution of the electromagnetic field equation [20] with the resolution of the fluid equations.

In this paper, the keyhole shape of a laser welding process is calculated following an original and accurate steady-state energy balance model with an asymmetric profile [7, 28]. In the model, the evaluation of multiple reflections effects is improved by using a robust iterative ray-tracing technique in which the effective distance of the path covered by each ray is included and the absorption of each reflected ray depends on the effective incident angle on the front or rear keyhole wall. Moreover, plasma absorption due to inverse Bremsstrahlung is taken into account by investigating the effect of different values of the absorption coefficient on the keyhole profile and considering laser beams of different wavelengths. Finally, the resulting damping phenomena are analyzed.

Physical, Mathematical, and Numerical Model

Local Energy Balance at the Keyhole Interface

The keyhole geometry has been calculated by a semi-analytical approach starting from the assumptions made in [7]. In such approach, the energy balance is resolved by a point-to-point calculation discretizing the front (advancing side) and the rear (retreating side) wall of the vapor-liquid interface where the boiling point is assumed to be reached by the material due to the interaction with the laser beam. In Figure 2, a schematic representation of the local energy balance is depicted.

FIGURE 2

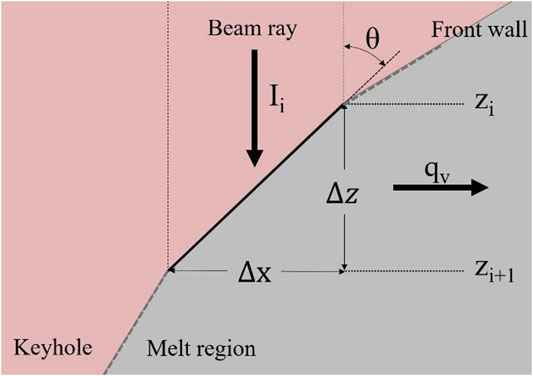
FIGURE 2. Schematization of a generic cell in the semi-analytical approach representing a small portion of the front wall (interface vapour-liquid along the welding advancing side).

The impinging beam ray, with its power density, hits the surface of the (front or rear) wall and the local energy balance determines the inclination angle of the wall itself. Imposing a constant spacing $\text{Δ}z$ along the vertical axis (z) parallel to the laser beam axis, the angle of the wall $\theta$ (both for the front and the rear side) can be calculated by the local energy balance:

$\frac{\mathit{\Delta }\mathit{x}}{\mathit{\Delta }\mathit{z}}\mathbf{=}\mathbf{tan}\mathbf{}{\mathit{\theta }}_{\mathit{i}}\mathbf{=}\frac{{\mathit{q}}_{\mathit{v}}}{\mathit{A}\mathbf{\left(}\mathit{\theta }\mathbf{\right)}\mathbf{\cdot }{\mathit{I}}_{\mathit{i}}}\mathbf{ }\mathbf{=}\frac{{\mathit{q}}_{\mathit{v}}}{{\mathit{I}}_{\mathit{a}}} (1)$

where $q_v$ is the heat flux of the losses due to heat conduction in the workpiece, A is the absorption coefficient, $I_i$ is the impinging power density (transmitted through the plasma) and $I_a$ is the power density absorbed in the material by the Fresnel absorption at the liquid-vapor interface. The plasma absorption inside the keyhole is taken into account as

${\mathit{I}}_{\mathit{i}}\mathbf{=}{\mathit{I}}_{\mathbf{0}}{\mathit{e}}^{\mathbf{-}{\mathit{\alpha }}_{\mathit{i}\mathit{B}}\mathit{l}}(2)$

being $I_0$ the power density directly irradiated by the laser (a Gaussian distribution is assumed), ${\alpha }_{iB}$ the plasma absorption coefficient due to inverse Bremsstrahlung and $l$ the length of the path the beam ray travels through the plasma inside the keyhole before hitting the wall surface. The damping effect due to the plasma plume was neglected.

Multiple Reflections in Local Energy Balance

Once the entire keyhole profile is initially defined by considering only the Fresnel absorption, multiple reflections were calculated by an original and iterative ray-tracing approach in which the energy deposited in each point by the reflected rays was stored and used in successive iterative steps where the energy balance is solved again including the contribution of the additional energy due to multiple reflections inside the keyhole. In Figure 3, a schematic representation of the energy balance of a generic calculation step is depicted.

FIGURE 3

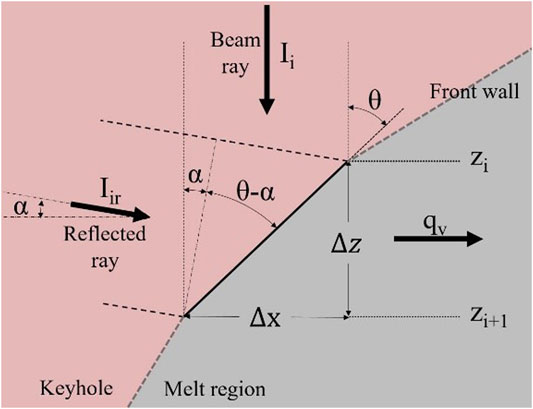
FIGURE 3. Schematization of a generic cell in the semi-analytical approach representing a small portion of the front wall (interface vapour-liquid along the welding advancing side).

During the iterative procedure, each portion of the surface on the front and the rear keyhole walls is irradiated by additional rays, with their own power density, that come from multiple reflections inside the keyhole. As it happens for the beam rays, the power density of reflected rays is attenuated by plasma absorption before hitting the keyhole wall and the effective power density $I_{a{r}_i}$ contributing to the energy balance is the one by the Fresnel absorption. Considering all the $N$ reflected rays, each with its inclination angle ${\alpha }_i$, hitting the same portion of wall surface, the new energy balance for that portion can be written as

$\mathbf{tan}\mathbf{}\mathit{\theta }\mathbf{=}\frac{{\mathit{q}}_{\mathit{v}}}{{\mathit{I}}_{\mathit{a}}\mathbf{+}{{\displaystyle \mathbf{\sum }}}_{\mathit{i}\mathbf{=}\mathbf{1}}^{\mathit{N}}{\mathit{I}}_{\mathit{a}{\mathit{r}}_{\mathit{i}}}\frac{\mathit{cos}\mathbf{\left(}\mathit{\theta }\mathbf{-}{\mathit{\alpha }}_{\mathit{i}}\mathbf{\right)}}{\mathit{sin}\mathbf{\left(}\mathit{\theta }\mathbf{\right)}}}(3)$

The keyhole profile and the consequent multiple reflections are iteratively calculated until a geometrical convergence is reached (deviations between two consecutive iterations under a threshold value).

Effects of Plasma Composition on Keyhole Profile

Focusing sufficiently high energy density laser beam on the surface of a metallic workpiece induces localized heating and evaporation of the material and, consequently, the formation of a partially ionized gas that can extend above the workpiece surface as a plasma plume composed by ambient air, shielding gas and metal vapors. The plasma could affect the welding processes due to absorption and refraction. In fact, the laser beam is partially absorbed due to inverse Bremsstrahlung when passing through the plasma and before impinging on the workpiece. Moreover, also during successive multiple reflections, the reflected beam intensity suffers inverse Bremsstrahlung due to the plasma generated by the laser. The absorption coefficient, mainly due to inverse Bremsstrahlung, is strictly dependent on the plasma temperature and consequently on plasma chemical compositions. Several approximations have been introduced to calculate the absorption coefficient, typically expressed by using the following expression [36, 37].

${\mathit{\alpha }}_{\mathit{i}\mathit{B}}\mathbf{\left(}{\mathit{n}}_{\mathit{e}}\mathbf{,}\mathit{T}\mathbf{\right)}\mathbf{=}\frac{\mathit{C}\mathbf{\cdot }{\mathit{n}}_{\mathit{e}}^{\mathbf{2}}\mathbf{\left[}\mathbf{1}\mathbf{-}{\mathit{e}}^{\mathbf{-}\mathit{D}\mathbf{/}\mathit{T}}\mathbf{\right]}}{\mathit{T}}(4)$

where C and D depend on the laser frequency and C depends also on the plasma frequency [36, 37], $\mathit{T}$ and ${\mathit{n}}_{\mathit{e}}$ are the plasma temperature and the electron density, respectively.

In order to get the plasma temperature field, simplified models [7, 28] or more accurate fluid dynamic approaches [5] which include continuity, momentum, and energy equations of the plasma can be used, assuming Local Thermodynamic Equilibrium (LTE) and laminar regime. The assumption of LTE of the vapor metal plasma has been widely discussed by several authors, both theoretically and experimentally. In particular, experimental tests [38], especially in the case of moderate laser power, have shown that electron density is two orders of magnitude greater than the critical electron density necessary to fulfill the criterion for LTE [39, 40] and time variations or spatial gradients in the plasma plume don’t break this assumption, being collisional terms greater than convection-diffusion terms. When the plasma temperature distribution function is known, chemical equilibrium and thermodynamic properties can be obtained starting from recent and accurate databases of atomic and molecular energy levels and collision integrals [41–47]. Due to the interaction between high-intensity laser and the metallic workpiece, the metallic vapors resulting from walls can significantly affect the characteristics and the properties of plasma. A lack or very partial results [48, 49] of properties of air/argon–metal plasmas (Cu, Fe, and Al) must be covered in order to obtain an accurate evaluation of the absorption coefficient. Both in the plasma plume and inside the keyhole, plasma temperature and electron number density in the plasma plume are always non-uniform, and electron density gradients (electron temperatures are from around 7,000 to over 15,000 K and densities between 10²¹ and 10²⁴ m⁻³) could reduce the power density of the laser beam arriving at the workpiece surface and may affect the laser welding process. In this paper, calculations have been made assuming a fixed spatial distribution of the absorption coefficient which typically could range between 0 and 300 m⁻¹ [5]. Further developments will include an accurate evaluation of plasma temperature distribution and the absorption coefficient, starting from the dependence of the absorption coefficient by the plasma temperature and electron densities. These calculations go beyond the scope of this paper, in which plasma effects have been accounted for by assuming a constant value of the absorption coefficient in the framework of a ray-tracing multiple reflection approach.

Numerical Procedure to Calculate the Keyhole Geometry

The iterative numerical procedure consists of the following steps:

1) The initial configuration of the keyhole shape is calculated by solving Eq. 1 in which only Fresnel absorption is included and ${\mathit{\alpha }}_{\mathit{iB}}=0$.

2) Simplified multiple reflection contribution is included by considering an averaged path length of a mean number of multiple reflections for a symmetric triangle keyhole geometry [7, 28].

3) By assuming a discretization grid along the radial direction for the laser light distribution, the ray-tracing procedure is applied and Eq. 3 is solved.

4) The power released on the front and rear walls is calculated for each ray until it comes out of the profile and step (3) is repeated up to the convergence is reached, i.e., when the relative error of the depth of the keyhole is less than 1%.

In order to get the converged solutions, approximately 20 iterations have been performed starting from the solution given by considering a mean number of multiple reflections as explained in [28]. The same results can be obtained starting from different initial conditions, even if the number of iterations could change considerably.

The aforementioned procedure has been applied for the calculation of the keyhole geometry assuming the laser welding process parameters and material specifications indicated in Table 1. In the simulations, $\mathit{\Delta z}={10}^{-7}\mathit{ }\text{m}$ was set and, consequently, depending on the keyhole depth, about 10⁴ grid points have been obtained in the z-direction. The laser source represented by the incident Gaussian intensity distribution of the light is decomposed into individual rays and the path of each ray is traced out during multiple reflections in order to evaluate the local absorbed intensity. The power released on the front and rear walls due to multiple reflections is affected by numerical noise which can be significantly reduced by considering the number of incident individual rays of the Gaussian intensity distribution of the light equal to the number of grid points in the z-direction.

TABLE 1

TABLE 1. Process specifications considered for the calculation of the keyhole profiles.

Results and Discussion

In all simulations, as the first step (step 1), calculations were conducted considering only Fresnel absorption and neglecting the plasma absorption, i.e. considering ${\alpha }_{iB}$ null. The red profile of Figure 4 was obtained considering the calculation of an averaged path length of a mean number of multiple reflections assuming the approximation of the keyhole geometry to a symmetric triangle, as already seen in the literature (step 2) [7, 28]. The same calculation was repeated adopting a ray-tracing approach for the multiple reflections neglecting upward-oriented ones (step 3). Great differences can be found between red and blue (dashed) profiles in Figure 4. The adoption of the ray-tracing technique, which ensures a more precise and robust calculation of multiple reflections paths, implicates a narrower and much deeper keyhole geometry than the approximated averaged solution, with also a more pronounced difference of slope between the front and rear keyhole walls. As already observed [7], the latter is mainly due to the heat conduction phenomenon inside the workpiece, whose effects are much stronger in the front wall because of the convective effects of the welding speed. Figure 5 shows results obtained for ${\alpha }_{iB}$ = 100 and 300 m⁻¹, also in this case multiple reflections are taken into account both with the averaged geometrical approximation and the ray-tracing technique. Results show that, when the geometrical approximation for multiple reflections is used, the two different ${\alpha }_{iB}$ values led to a difference of about 0.5 mm in the depth of the calculated keyhole (red curves in Figures 5A,B). Approximately the same absolute difference exists between the keyhole depth calculated by the proposed ray-tracing technique (blue dashed curves in Figures 5A,B). Nevertheless, for ${\alpha }_{iB}$ = 100 m⁻¹ (Figure 5A) the difference in the keyhole depth between the two approaches is 93% (from 2.55 to 4.93 mm) while for ${\alpha }_{iB}$ = 300 m⁻¹ (Figure 5B) the analogous difference approaches 115% (from 2.04 to 4.39 mm) highlighting a more pronounced sensitivity of the keyhole depth to plasma damping in the multiple reflections when higher plasma absorption is considered.

FIGURE 4

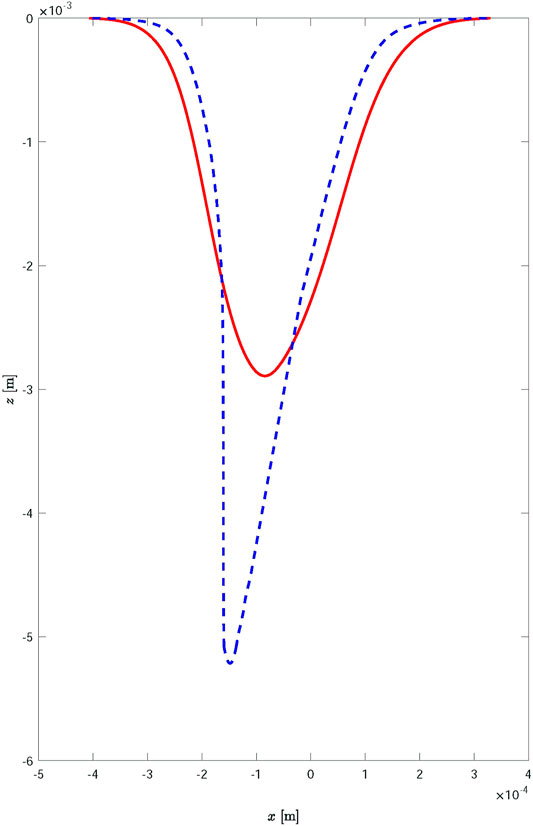
FIGURE 4. Keyhole profiles obtained neglecting the plasma absorption (${\alpha }_{iB}=0$) and modelling multiple reflections with averaged geometrical approximation (red curve), and with ray-tracing technique (dashed blue curve).

FIGURE 5

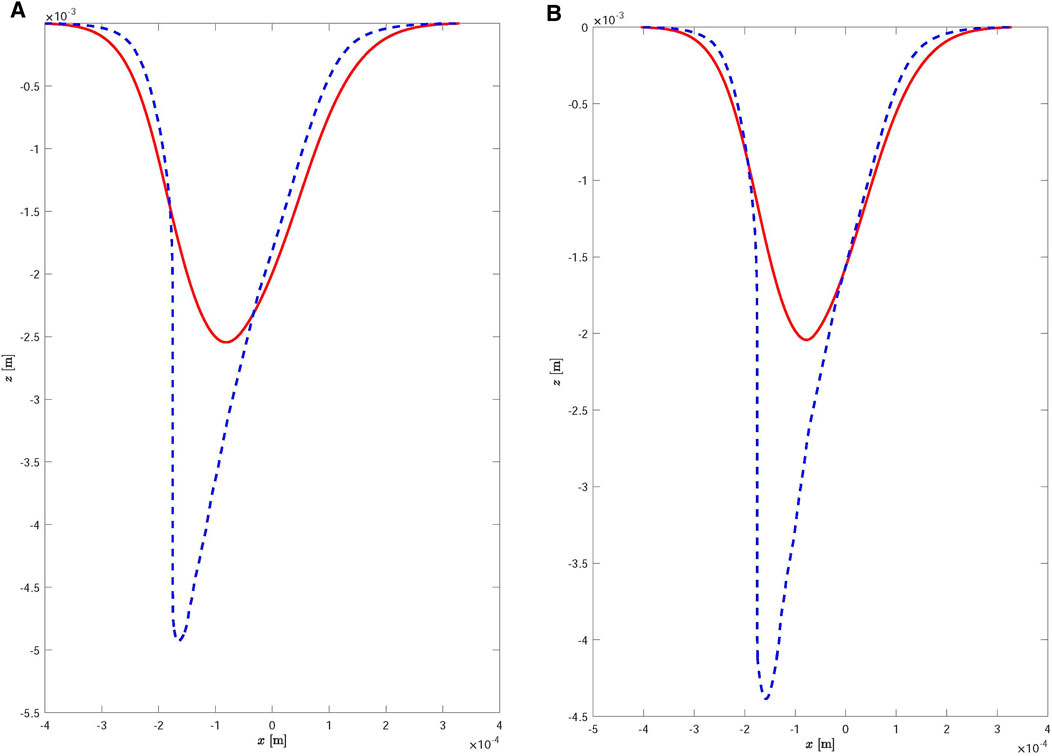
FIGURE 5. Keyhole profiles obtained for ${\text{α}}_{\text{iB}}=100$ (A) and 300 (B) m⁻¹ and modelling multiple reflections with averaged geometrical approximation (red curves), and with ray-tracing technique (dashed blue curves).

The influence of plasma properties on the keyhole shape and depth is shown more explicitly in Figure 6, where all the curves obtained with the ray-tracing technique and different values of the absorption coefficient ${\alpha }_{iB}$ are reported. The comparison highlights that plasma properties could affect considerably the keyhole shape and depth. Ranging from 0 to 300 m⁻¹ the keyhole depth obtained by the iterative procedure is in the range 4.38–5.5 10^–3 m with a difference of up to 26%. This agrees with the expectations because higher absorption coefficients implicate stronger damping effects of plasma on the laser beam, and this results in shallower keyholes. As already stated before, the absorption coefficient ${\alpha }_{iB}$ due to inverse Bremsstrahlung is directly related to plasma properties (temperature and chemical compositions), therefore its theoretical variation would mean the consideration of new welding conditions due to e.g., different welding process parameters, materials welded, shielding/assisting gases.

FIGURE 6

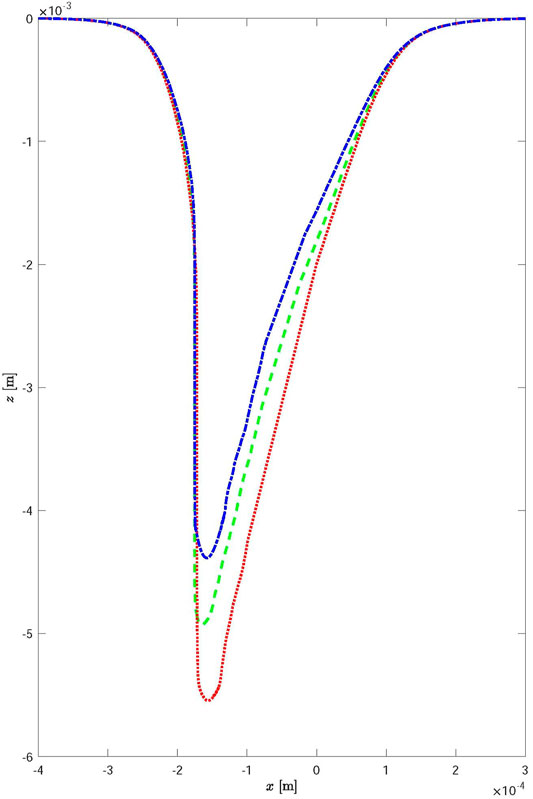
FIGURE 6. Keyhole profiles obtained for ${\alpha }_{iB}=0$ (red dotted), 100 (green dashed), 300 (blue dot-dashed) m⁻¹ and modelling multiple reflections with ray-tracing technique.

To better evaluate how the damping effect of the laser beam intensity is distributed along the segmented path, Figure 7 shows the damping factor ${\mathit{e}}^{-{\mathit{\alpha }}_{\mathit{iB}}{\mathit{l}}_{\mathit{ray}}}$ of the ith-reflection averaged on all rays of the laser beam. A damping factor in the order of magnitude of 10^–1 is registered for the first incoming reflection, but a drop of about seven orders of magnitude is observed moving to the second reflection. The factor decreases even more in the subsequent reflections, dropping to values in the order of 10^–12 for the sixth reflection. This proves that the main damping effect is related to the first incoming reflection, while those related to subsequent reflections are negligible.

FIGURE 7

FIGURE 7. Damping factors of the first six reflections averaged on all the rays of the laser beam.

The total contributions of the plasma damping equal to the products of the sequence of reflections as a function of the position of each ray are represented in Figure 8. The plasma damping due to multiple reflections is considered constant and equal to ${\mathit{e}}^{-{\mathit{\alpha }}_{\mathit{iB}}\mathit{d}/2}$ in the averaged geometrical approximation of multiple reflections [7, 28] assuming the averaged path length equal to half of the keyhole depth d. Instead, the one obtained with the ray-tracing technique is keyhole-shaped, with the lowest value (about 0.6) recorded at the same position of the deepest point of the keyhole. This confirms what was already observed, i.e., that most of the energy absorbed by plasma due to inverse Bremsstrahlung is at the first reflection of the incoming rays since the strongest damping effects occur at the longest first reflections.

FIGURE 8

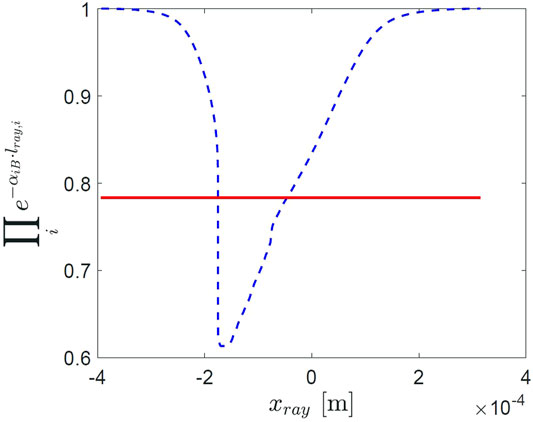
FIGURE 8. The total contributions of the plasma damping as a function of the position of the ray in the multiple reflections model: the averaged geometrical approximation (red curve) is compared with the ray-tracing technique (dashed blue curve).

Finally, the effect of laser wavelength on the keyhole profile was investigated. Figure 9 reports keyhole profiles obtained with the ray-tracing modeling of multiple reflections at different absorption coefficients ${\alpha }_{iB}$ with both a laser wavelength λ = 10.6 μm (i.e., a CO₂ laser source) and 1.06 μm (e.g., an Nd:YAG laser source). In the latter case, the keyholes are narrower and shallower, with a depth of 3.55 mm for ${\alpha }_{iB}$ = 100 m⁻¹, −28% compared to the case with λ = 10.6 μm, and 3.08 mm for ${\alpha }_{iB}$ = 300 m⁻¹, −30% compared to the same with higher wavelength. This confirms that the variation of the wavelength of the laser beam affects considerably the keyhole shape and dimensions, assuming the same values of other parameters. Nevertheless, the effects due to the plasma properties are similar regardless of the wavelength: the increase of ${\alpha }_{iB}$ from 100 to 300 m⁻¹ causes a decrease of keyhole depth with a difference of 13% considering the wavelength of 1.06 μm, while a decrease of 11% was observed for λ = 10.6 μm. This confirms that appropriate modeling of plasma properties is relevant to adequately consider damping effects due to inverse Bremsstrahlung also for laser sources with shorter wavelengths.

FIGURE 9

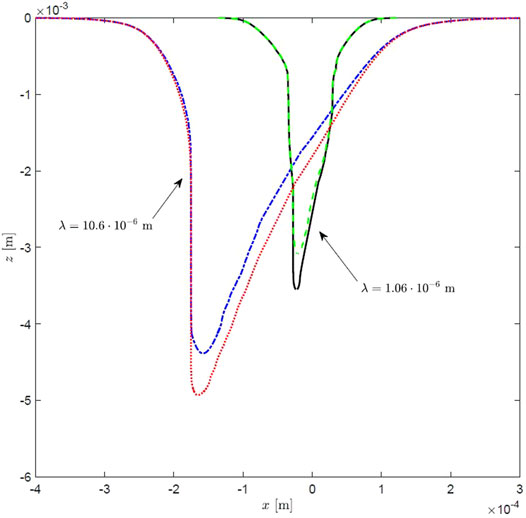
FIGURE 9. Keyhole profiles obtained at different laser wavelength for ${\alpha }_{iB}=100$ (red dotted for λ = 10.6 μm, black solid for λ = 1.06 μm), and 300 (blue dot-dashed for λ = 10.6 μm, green dashed for λ = 1.06 μm) m⁻¹, and modelling multiple reflections with ray-tracing technique.

Conclusion

A novel iterative approach for the calculation of the keyhole profile in laser-matter interaction was developed and used to analyze the damping effect related to the plasma absorption due to inverse Bremsstrahlung. This damping effect has been taken into account both in the first interaction between the beam ray and the plasma into the keyhole and in the following segmented path caused by multiple reflections by which every single ray repetitively moves inside the keyhole plasma hitting the liquid metal on the front and rear keyhole walls. The approach starts from an initial configuration of the keyhole shape calculated only by Fresnel absorption on the front and rear walls of the keyhole and an averaged approximated contribution of multiple reflections. Then the ray-tracing procedure is applied calculating the power density released on the front and rear walls. Noise reduction of the power densities is obtained by considering the number of individual rays of the laser source sufficiently high (one ray for each grid point in the z-direction). The local energy balance is then solved again and the procedure is repeated until convergence is reached, i.e., when the relative error of the depth of the keyhole is less than 1%.

The adoption of the ray-tracing technique including damping effects of the laser passing through the keyhole plasma led to a narrower and much deeper keyhole geometry than the approximated averaged solution, with also a more pronounced difference of slope between the front and rear keyhole walls. The effect of the absorption coefficient due to inverse Bremsstrahlung on the keyhole geometry was evaluated ranging its value from 0 to 300 m⁻¹. A difference of 26% in the keyhole depth was obtained when comparing the case with null absorption to the case with the maximum value of the absorption coefficient. Further analyses on the damping factor revealed that it assumes negligible values starting from the second reflection if compared to the first one. This is confirmed by the representation of the products of the sequence on reflections of the damping factor as a function of the position of the considered ray, which is keyhole-shaped because the longer the path of the first reflection is, the stronger the damping effect. Finally, the comparison of the 10.6 μm-long laser beam wavelength (i.e., a CO₂ laser source) with the 1.06 μm-long one (e.g., an Nd:YAG laser source) showed that the keyhole profiles obtained with the shortest wavelength are narrower and shallower (difference of depth of about 29%) than the same with the longest one. Nevertheless, the same effect due to the change of absorption coefficient was observed because a decrease of depth of about 12% was registered moving from ${\alpha }_{iB}$ = 100 to 300 m⁻¹ for both the wavelengths.

Further studies are needed to estimate the value of the absorption coefficient and its spatial distribution inside the keyhole and, consequently, improve the accurateness of the prediction of the keyhole geometry by the developed approach. In order to obtain an accurate spatial distribution of the absorption coefficient, both plasma temperature distribution and chemical equilibrium composition must be calculated. In particular, the calculation of the spatial distribution of the plasma temperature can be obtained by coupling simplified models or more accurate fluid dynamic approaches which include continuity, momentum, and energy equations of the plasma.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

DC, AD, and DS contributed to the conception and design of the study. DC, AD, and DS developed the theory. AD and DC performed the computations and performed the analysis. DC wrote the first draft of the manuscript. DC, AD, and DS wrote sections of the article. All authors contributed to article revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Klemens PG. Heat Balance and Flow Conditions for Electron Beam and Laser Welding. J Appl Phys (1976) 47:2165–74. doi:10.1063/1.322866

CrossRef Full Text | Google Scholar

2. Shcheglov P. Study of Vapour-Plasma Plume during High Power Fiber Laser Beam Influence on Metals. Berlin: BAM-Dissertationsreihe Band (2012).

Google Scholar

3. Rai R, Elmer JW, Palmer TA, Debroy T. Heat Transfer and Fluid Flow during Keyhole Mode Laser Welding of Tantalum, Ti-6Al-4V, 304L Stainless Steel and Vanadium. J Phys D Appl Phys (2007) 40:5753–66. doi:10.1088/0022-3727/40/18/037

CrossRef Full Text | Google Scholar

4. Svenungsson J, Choquet I, Kaplan AFH. Laser Welding Process - A Review of Keyhole Welding Modelling. Phys Proced (2015) 78:182–91. doi:10.1016/j.phpro.2015.11.042

CrossRef Full Text | Google Scholar

5. Wang H-X, Chen X. Three-dimensional Modelling of the Laser-Induced Plasma Plume Characteristics in Laser Welding. J Phys D Appl Phys (2003) 36:628–39. doi:10.1088/0022-3727/36/6/304

CrossRef Full Text | Google Scholar

6. Chen X, Wang H-X. Prediction of the Laser-Induced Plasma Characteristics in Laser Welding: A New Modelling Approach Including a Simplified Keyhole Model. J Phys D Appl Phys (2003) 36:1634–43. doi:10.1088/0022-3727/36/13/332

CrossRef Full Text | Google Scholar

7. Kaplan A. A Model of Deep Penetration Laser Welding Based on Calculation of the Keyhole Profile. J Phys D Appl Phys (1994) 27:1805–14. doi:10.1088/0022-3727/27/9/002

CrossRef Full Text | Google Scholar

8. Tan W, Bailey NS, Shin YC. Investigation of Keyhole Plume and Molten Pool Based on a Three-Dimensional Dynamic Model with Sharp Interface Formulation. J Phys D Appl Phys (2013) 46:055501. doi:10.1088/0022-3727/46/5/055501

CrossRef Full Text | Google Scholar

9. Semak VV, Bragg WD, Damkroger B, Kempka S. Transient Model for the Keyhole during Laser Welding. J Phys D Appl Phys (1999) 32:L61–L64. doi:10.1088/0022-3727/32/15/103

CrossRef Full Text | Google Scholar

10. Ki H, Mazumder J, Mohanty PS. Modeling of Laser Keyhole Welding: Part II. Simulation of Keyhole Evolution, Velocity, Temperature Profile, and Experimental Verification. Metall Mat Trans A (2002) 33:1831–42. doi:10.1007/s11661-002-0191-5

CrossRef Full Text | Google Scholar

11. Fabbro R. Melt Pool and Keyhole Behaviour Analysis for Deep Penetration Laser Welding. J Phys D Appl Phys (2010) 43:445501. doi:10.1088/0022-3727/43/44/445501

CrossRef Full Text | Google Scholar

12. Matsunawa A, Kim J-D, Seto N, Mizutani M, Katayama S. Dynamics of Keyhole and Molten Pool in Laser Welding. J Laser Appl (1998) 10:247–54. doi:10.2351/1.521858

CrossRef Full Text | Google Scholar

13. Seto N, Katayama S, Matsunawa A. High-speed Simultaneous Observation of Plasma and Keyhole Behavior during High Power CO2 Laser Welding: Effect of Shielding Gas on Porosity Formation. J Laser Appl (2000) 12:245–50. doi:10.2351/1.1324717

CrossRef Full Text | Google Scholar

14. Kaplan AFH, Mizutani M, Katayama S, Matsunawa A. Unbounded Keyhole Collapse and Bubble Formation during Pulsed Laser Interaction with Liquid Zinc. J Phys D Appl Phys (2002) 35:1218–28. doi:10.1088/0022-3727/35/11/319

CrossRef Full Text | Google Scholar

15. Kawahito Y, Mizutani M, Katayama S. Elucidation of High-Power Fibre Laser Welding Phenomena of Stainless Steel and Effect of Factors on weld Geometry. J Phys D Appl Phys (2007) 40:5854–9. doi:10.1088/0022-3727/40/19/009

CrossRef Full Text | Google Scholar

16. Kawahito Y, Matsumoto N, Abe Y, Katayama S. Relationship of Laser Absorption to Keyhole Behavior in High Power Fiber Laser Welding of Stainless Steel and Aluminum alloy. J Mater Process Techn (2011) 211:1563–8. doi:10.1016/j.jmatprotec.2011.04.002

CrossRef Full Text | Google Scholar

17. Pang S, Chen X, Zhou J, Shao X, Wang C. 3D Transient Multiphase Model for Keyhole, Vapor Plume, and weld Pool Dynamics in Laser Welding Including the Ambient Pressure Effect. Opt Lasers Eng (2015) 74:47–58. doi:10.1016/j.optlaseng.2015.05.003

CrossRef Full Text | Google Scholar

18. Cho JH, Na SJ. Three-dimensional Analysis of Molten Pool in GMA-Laser Hybrid Welding. Weld J (2009) 88:35–44.

Google Scholar

19. Ki H, Mohanty PS, Mazumder J. Modelling of High-Density Laser-Material Interaction Using Fast Level Set Method. J Phys D Appl Phys (2001) 34:364–72. doi:10.1088/0022-3727/34/3/320

CrossRef Full Text | Google Scholar

20. Courtois M, Carin M, MassonLe PL, Gaied S, Balabane M. A New Approach to Compute Multi-Reflections of Laser Beam in a Keyhole for Heat Transfer and Fluid Flow Modelling in Laser Welding. J Phys D Appl Phys (2013) 46:505305. doi:10.1088/0022-3727/46/50/505305

CrossRef Full Text | Google Scholar

21. Lankalapalli KN, Tu JF, Gartner M. A Model for Estimating Penetration Depth of Laser Welding Processes. J Phys D Appl Phys (1996) 29:1831–41. doi:10.1088/0022-3727/29/7/018

CrossRef Full Text | Google Scholar

22. Ye X-H, Chen X. Three-dimensional Modelling of Heat Transfer and Fluid Flow in Laser Full-Penetration Welding. J Phys D Appl Phys (2002) 35:1049–56. doi:10.1088/0022-3727/35/10/313

CrossRef Full Text | Google Scholar

23. Kroos J, Gratzke U, Simon G. Towards a Self-Consistent Model of the Keyhole in Penetration Laser Beam Welding. J Phys D Appl Phys (1993) 26:2066–74. doi:10.1088/0022-3727/26/3/021

CrossRef Full Text | Google Scholar

24. Andrews JG, Atthey DR. Hydrodynamic Limit to Penetration of a Material by a High-Power Beam. J Phys D Appl Phys (1976) 9:2181–94. doi:10.1088/0022-3727/9/15/009

CrossRef Full Text | Google Scholar

25. Dowden J, Postacioglu N, Davis M, Kapadia P. A Keyhole Model in Penetration Welding with a Laser. J Phys D Appl Phys (1987) 20:36–44. doi:10.1088/0022-3727/20/1/006

CrossRef Full Text | Google Scholar

26. Wei PS, Wu TH, Chow YT. Investigation of High-Intensity Beam Characteristics on Welding Cavity Shape and Temperature Distribution. J Heat Transfer (1990) 112:163–9. doi:10.1115/1.2910339

CrossRef Full Text | Google Scholar

27. Kar A, Rockstroh T, Mazumder J. Two‐dimensional Model for Laser‐induced Materials Damage: Effects of Assist Gas and Multiple Reflections inside the Cavity. J Appl Phys (1992) 71:2560–9. doi:10.1063/1.351072

CrossRef Full Text | Google Scholar

28. Zhao H, DebRoy T. Macroporosity Free Aluminum alloy Weldments through Numerical Simulation of Keyhole Mode Laser Welding. J Appl Phys (2003) 93:10089–96. doi:10.1063/1.1573732

CrossRef Full Text | Google Scholar

29. Rai R, Debroy T. Tailoring weld Geometry during Keyhole Mode Laser Welding Using a Genetic Algorithm and a Heat Transfer Model. J Phys D Appl Phys (2006) 39:1257–66. doi:10.1088/0022-3727/39/6/037

CrossRef Full Text | Google Scholar

30. Rai R, Kelly SM, Martukanitz RP, DebRoy T. A Convective Heat-Transfer Model for Partial and Full Penetration Keyhole Mode Laser Welding of a Structural Steel. Metall Mat Trans A (2008) 39:98–112. doi:10.1007/s11661-007-9400-6

CrossRef Full Text | Google Scholar

31. Xu GX, Wu CS, Qin GL, Wang XY, Lin SY. Adaptive Volumetric Heat Source Models for Laser Beam and Laser + Pulsed GMAW Hybrid Welding Processes. Int J Adv Manuf Technol (2011) 57:245–55. doi:10.1007/s00170-011-3274-x

CrossRef Full Text | Google Scholar

32. Kaplan AFH. Influence of the Beam Profile Formulation when Modeling Fiber-Guided Laser Welding. J Laser Appl (2011) 23:042005. doi:10.2351/1.3633221

CrossRef Full Text | Google Scholar

33. Kaplan AFH. Fresnel Absorption of 1μm- and 10μm-Laser Beams at the Keyhole wall during Laser Beam Welding: Comparison between Smooth and Wavy Surfaces. Appl Surf Sci (2012) 258:3354–63. doi:10.1016/j.apsusc.2011.08.086

CrossRef Full Text | Google Scholar

34. Chowdhury S, Nirsanametla Y, Manapuram M. Investigation on Keyhole Mode Fiber Laser Welding of SS 316 in a Self-Protected Atmosphere. Proc Inst Mech Eng C J Mech Eng Sci (2019) 233:6602–15. doi:10.1177/0954406219864137

CrossRef Full Text | Google Scholar

35. Jahn M, Montalvo-Urquizo J. Modeling and Simulation of Keyhole-Based Welding as Multi-Domain Problem Using the Extended Finite Element Method. Appl Math Model (2020) 82:731–47. doi:10.1016/j.apm.2020.01.072

CrossRef Full Text | Google Scholar

36. Pert GJ. Plasmas and Laser Light: T. P. Hughes Adam Hilger (London, UK) 1975, Pp 544, £35.00. Opt Laser Technol (1976) 8:142. doi:10.1016/0030-3992(76)90032-3

CrossRef Full Text | Google Scholar

37. Ready J. Effects of High-Power Laser Radiation. New York: Academic Press (1971). p. 448.

Google Scholar

38. Szymanski Z, Kurzyna J, Kalita W. The Spectroscopy of the Plasma Plume Induced during Laser Welding of Stainless Steel and Titanium. J Phys D Appl Phys (1997) 30:3153–62. doi:10.1088/0022-3727/30/22/014

CrossRef Full Text | Google Scholar

39. Huddlestone RH, Leonard SL. Plasma Diagnostic Techniques. New York: Academic Press (1965).

Google Scholar

40. Loureiro J, Amorim J. Kinetics and Spectroscopy of Low Temperature Plasmas. Cham: Springer International Publishing (2016). doi:10.1007/978-3-319-09253-9

CrossRef Full Text | Google Scholar

41. Colonna G, D'Angola A. A Hierarchical Approach for Fast and Accurate Equilibrium Calculation. Comput Phys Commun (2004) 163:177–90. doi:10.1016/j.cpc.2004.08.004

CrossRef Full Text | Google Scholar

42. Colonna G, D’Angola A, Laricchiuta A, Bruno D, Capitelli M. Analytical Expressions of Thermodynamic and Transport Properties of the Martian Atmosphere in a Wide Temperature and Pressure Range. Plasma Chem Plasma Process (2013) 33:401–31. doi:10.1007/s11090-012-9418-4

CrossRef Full Text | Google Scholar

43. Colonna G, D'Angola A. EquilTheTA: Thermodynamic and Transport Properties of Complex Equilibrium Plasmas. AIP Conf Proc (2012) 1501:1110–5. doi:10.1063/1.4769665

CrossRef Full Text | Google Scholar

44. Colonna G, D’Angola A, Pietanza LD, Capitelli M, Pirani F, Stevanato E. Thermodynamic and Transport Properties of Plasmas Including Silicon-Based Compounds. Plasma Sourc Sci. Technol. (2018) 27:015007. doi:10.1088/1361-6595/aa9f9b

CrossRef Full Text | Google Scholar

45. D'Angola A, Colonna G, Gorse C, Capitelli M. Thermodynamic and Transport Properties in Equilibrium Air Plasmas in a Wide Pressure and Temperature Range. Eur Phys J D (2008) 46:129–50. doi:10.1140/epjd/e2007-00305-4

CrossRef Full Text | Google Scholar

46. D’Angola A, Colonna G, Bonomo A, Bruno D, Laricchiuta A, Capitelli M. A Phenomenological Approach for the Transport Properties of Air Plasmas. Eur Phys J D (2012) 66:205. doi:10.1140/epjd/e2012-30147-8

CrossRef Full Text | Google Scholar

47. D’Angola A, Colonna G, Gorse C, Capitelli M. Thermodynamic Properties of High Temperature Air in Local Thermodynamic Equilibrium: II Accurate Analytical Expression for Electron Molar Fractions. Eur Phys J D (2011) 65:453–7. doi:10.1140/epjd/e2011-20424-5

CrossRef Full Text | Google Scholar

48. Zhong L, Wang X, Cressault Y, Teulet P, Rong M. Influence of Metallic Vapours on Thermodynamic and Transport Properties of Two-Temperature Air Plasma. Phys Plasmas (2016) 23:093514. doi:10.1063/1.4963245

CrossRef Full Text | Google Scholar

49. Cressault Y, Gleizes A, Riquel G. Properties of Air-Aluminum thermal Plasmas. J Phys D Appl Phys (2012) 45:265202. doi:10.1088/0022-3727/45/26/265202

CrossRef Full Text | Google Scholar

50. Kaars J, Mayr P, Koppe K. Determining Material Data for Welding Simulation of Presshardened Steel. Metals (2018) 8:740. doi:10.3390/met8100740

CrossRef Full Text | Google Scholar