Empirical Formulas of Shear Modulus and Damping Ratio for Geopolymer-Stabilized Coarse-Grained Soils

The contribution of gravel fraction on the maximum shear modulus (G_max), dynamic shear modulus ratio (G/G_max), and damping ratio (λ) of cementitious coarse-grained soils has not been fully understood yet. Large-scale triaxial cyclic tests for geopolymer-stabilized coarse-grained soils (GSCGSs) were conducted with different volumetric block proportions (VBPs) under various confining pressures (CPs) for investigating their dynamic behaviors and energy dissipation mechanisms. Results indicate that the G_max of GSCGS increases linearly with VBPs but nonlinearly with CP. High VBPs will probably result in a gentle decrease in G/G_max and a rapid increase in normalized λ (λ_nor), while the opposite is the case for a high CP. With the shear strain amplitude being normalized, the G/G_max and λ_nor are distributed in a narrow band with low dispersion and thus can be well-described by empirical functions of the normalized shear strain amplitude.

Introduction

Cementitious coarse-grained soils (CCGSs) are widely used as filling materials in infrastructure projects such as high-speed railway subgrades, earth dams, and highways [1,2]. However, the design and construction of engineering structures on CCGS are always challenging for engineers due to parameter determination difficulties. Dynamic soil properties including the maximum shear modulus (G_max), dynamic shear modulus ratio (G/G_max), and damping ratio (λ) from small to large shear strain amplitude (γ) are crucial indices for the seismic design and stability evaluation of geotechnical structures subjected to periodic random loads. Previous studies showed that CCGS was inhomogeneous and heterogeneous geotechnical materials [1,2]. Their cyclic shear behaviors were affected by gravel fraction, cementation, interparticle contact stiffness, void ratio, curing period, and deformation within individual particles [3–6]. Of these factors, the gravel fraction and cementation played a particularly significant role in the shear behavior of CCGS. However, no consensus exists on their effects up to now. Geopolymer binders (GBs) are alkali-activated aluminosilicate gel materials with enormous advantages in high strength, fast hardness, weak shrinkage, etc. Their primary raw materials are solid wastes, such as fly ash, glass waste, red mud, metakaolin (MK), and combinations of two or more of these materials [7]. The coarse-grained soil stabilized with GBs (GSCGS) thus can also be a better choice for engineering practices, regardless of safety performance in seismic resistance and durability or feasibilities in resource acquisition and cost control. This study conducted large-scale undrained triaxial cyclic tests on GSCGS with different volumetric block proportions (VBPs) under various confining pressures (CPs). The evolution of G_max, G/G_max, and λ was investigated, and their relationships with γ were discussed.

Experiments

The dynamic behaviors of GSCGS in this study were investigated via a large-scale triaxial cyclic shear instrument (HCA300) developed by the American company GCTS. Each GSCGS cylindrical specimen was 100 mm in diameter and 200 mm in height. For the convenience of sample preparation, coarse-grained soils were considered a mixture of the soil matrix and rock blocks. The soil matrix was fine-grained residual soil, with a maximum grain size of 2 mm. The natural dry density was 1.64 g/cm³. The maximum dry density and optimum water content were 1.72 g/cm³ and 18.3%, respectively. The rock blocks mainly comprised crushed stones with a dry density of 2.42 g/cm³. The maximum rock block size was limited to be 0.2 times the diameter of the specimen to avoid the grain size effect, namely, the rock block size used in sample preparation was 2–20 mm.

Considering that the VBP greater than 60% may result in considerable hollow phenomena among rock blocks and significant difficulties in packing GSCGS samples in the mold, only five VBPs (0/15/30/45/60, %) combined with four CPs (0.05/0.10/0.20/0.40, MPa) were considered in this study. The previous study showed that GBs could synthesize from MK, CaO, and NaHCO₃ with a mass ratio of 4:1:1, and their optimal mixing ratio in fine-grained soil was 15 wt% [7]. Therefore, the dosage of GBs in the coarse-grained soil samples was determined by the relative content of the soil matrix because of the cementation of GB functions primarily in the fine-grained soil. In other words, once the VBP is selected, the dosage of fine-grained soil in a GSCGS specimen is known, and the dosage of GBs can be determined. The water consumption for sample preparation was the sum of the amount of water required for the fine-grained soil to reach its maximum dry density and an extra water compensation of 5% for rock blocks’ water absorption. All the specimens were cured in a humid environment at room temperature for 7 days and saturated by a vacuum extractor on GCTS until the B-value reached 0.95 at least before loading. The axial strain amplitude was increased from 1 × 10^–5 to 1 × 10^–2 in a level-by-level manner. The number of cyclic loadings for each strain amplitude was 5. The loading frequency was 0.5 Hz.

Results and Discussion

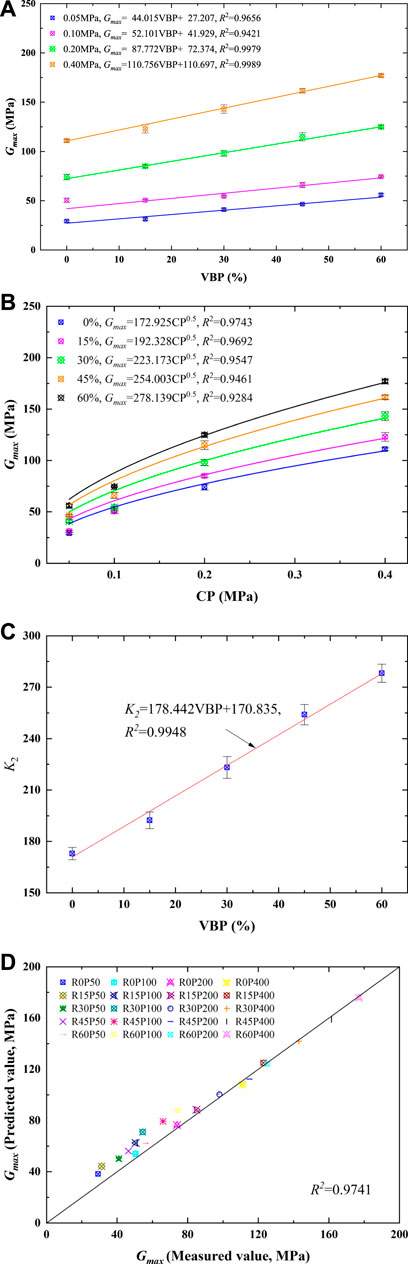
Dynamic soil properties, including G and λ, were achieved by following the calculation methods for symmetrical and asymmetric hysteresis loops suggested by Kumar et al. [8]. Figure 1A presents the relationship between the G_max of GSCGS and the VBP. The G_max always increases linearly with the VBP, despite GSCGS being subjected to tensile or compressive stress. The increasing gradient of fitting curves suggests that there is a positive correlation between the G_max and CP. Hence, the relationship of the G_max and VBP can be described as follows:

$G_{max}=k_{p}VBP+G_{matrix},(1)$

where k_p is the gradient of fitting curves and G_matrix is the intercept denoting the fundamental stiffness of the soil matrix under a specified CP. The fitting results based on Eq. 1 illustrate that the k_p increases with the CP, namely, high CP will result in larger values in G_max. Figure 1B presents the relationship between the G_max of GSCGS and the CP. The G_max increases nonlinearly with the CP at the same VBP. Seed et al. [9] proposed a simplified relationship between the G_max and CP for gravelly soil as follows:

$G_{max}=K_2{\left(CP\right)}^{0.5},(2)$

where K₂ is a regression coefficient. Rollins et al. [10] reported that K₂ was a function of relative density for soils. Since the GSCGS is regarded as the soil matrix and rock blocks, the density of GSCGS can be summarized as a function of the VBP. Therefore, K₂ is related to the VBP of GSCGS. Figure 1C illustrates an excellent linear correlation between K₂ and VBP. Thus, a new empirical formula for the G_max of GSCGS is defined as follows:

$G_{max}=\left(k_{0}VBP+C\right){\left(CP\right)}^{0.5},(3)$

where k₀ and C are regression coefficients. Figure 1D presents the measured and predicted G_max of GSCGS. Both are close to the bisecting line with a high correlation coefficient (R²) of 0.9741, which indicates that the proposed empirical formula can predict the G_max of GSCGS well.

FIGURE 1

FIGURE 1. Relationships of the G_max of GSCGS with the VBP and CP.

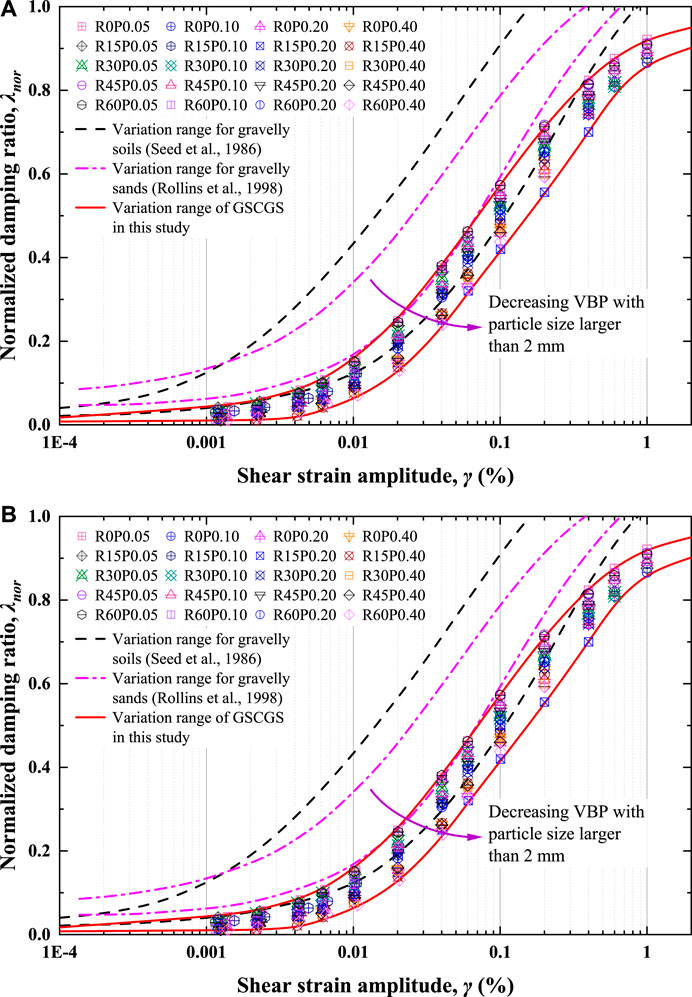
Figure 2A presents the G/G_max envelope curves of GSCGS with different VBPs under various CPs. The G/G_max is distributed within a band on the whole. The shape of the curves is very close as γ is less than the order of 10⁻⁴%. When γ lies between 10^–4% and 0.01%, the G/G_max is scattered. When γ lies between 0.01 and 1.0%, the G/G_max decreases significantly. The reduction rate of G/G_max slows down once γ is higher than 1.0%. As a whole, the G/G_max of GSCGS is more likely to be characterized following a hyperbolic G/G_max function proposed by Hardin and Drnevich [11], which is given in the following equation:

$G/G_{max}=1/{\left(1+\gamma /{\gamma }_r\right)}^n,(4)$

where γ_r is the reference shear strain and n is the curvature coefficient. It can be observed that the envelope region of G/G_max overlaps with the bounds proposed by Rollins et al. [10] when the VBP of GSCGS is higher than 45%. However, when the VBP is less than 45%, they have not overlapped anymore, especially when γ ranges between 0.01 and 1.0%. Seed et al. [9] pointed out that the G/G_max of sands always decreased faster than gravelly soils as γ increased, namely, high VBP would result in a gentle decrease in G/G_max of gravelly soils. This discovery explains why the G/G_max envelope curves of GSCGS are relatively higher than those of gravelly soils used in studies by Seed et al. [9] and Rollins et al. [10].

FIGURE 2

FIGURE 2. G/G_max and λ envelope curves of GSCGS with different VBPs under various CPs.

Figure 2B shows the normalized λ (λ_nor) envelope curves of GSCGS with different VBPs under various CPs, wherein the empirical model proposed by Chen et al. [12] is applied.

${\lambda }_{nor}={\lambda }_0{\left(1-G/G_{max}\right)}^n/\left({\lambda }_{\max }-{\lambda }_{\min }\right),(5)$

where λ_min and λ_max are the minimum and maximum λ, respectively, and λ₀ and n are regression parameters related to soil properties. It can be observed that λ_nor is distributed in a narrower band overall. The shape of the curves becomes unanimous when γ is less than the order of 10⁻³%. This result implies that the VBP and CP might have a minimal impact on λ_nor. The reason why the λ_nor envelope curves of GSCGS are lower than those of gravelly soils examined by Seed et al. [9] and Rollins et al. [10] maybe that a high VBP is more likely to result in significant difficulties in compaction of coarse-grained soils, while cementation improves the integrity of CGS significantly, and thereby results in relatively low λ_nor when subjected to cyclic loadings.

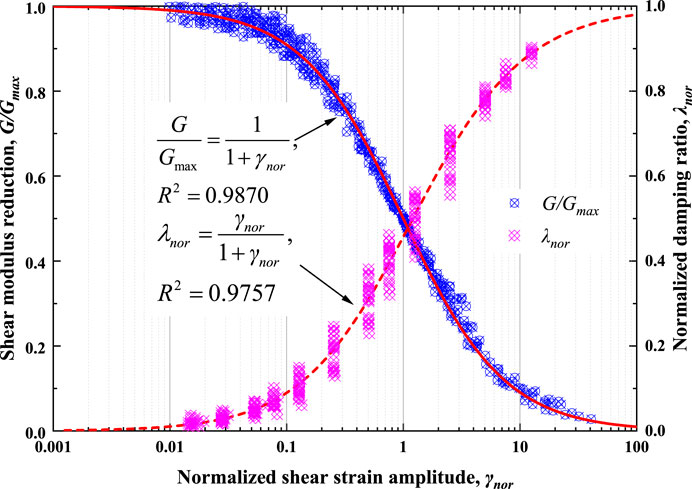
Figure 3 presents the relationship of the G/G_max and λ_nor of GSCGS vs. normalized γ (γ_nor = γ/γ_r). It can be observed that both G/G_max and λ_nor are distributed within a narrow band, namely, both of them are insensitive to the VBP and CP via γ_nor. Martin and Seed [13] had summarized a nonlinear elastic model for gravel soils with γ_nor, which is

$G/G_{max}=1-{\left[{\gamma }_{nor}^{2\beta }/\left(1+{\gamma }_{nor}^{2\beta }\right)\right]}^{\alpha },(6)$

where α and β are regression parameters. The fitting results of G/G_max show that this nonlinear model is also available to GSCGS with an excellent correlation coefficient of 0.9870 and can be simplified as follows:

$G/G_{max}=1/\left(1+{\gamma }_{nor}\right).(7)$

Substituting Eqs 4, 6 into Eq. 5 yields

${\lambda }_{nor}={\left[{\gamma }_{nor}^{2\beta }/\left(1+{\gamma }_{nor}^{2\beta }\right)\right]}^{\alpha n}.(8)$

The fitting results of λ_nor show a perfect correlation of 0.9757 with γ_nor, and can be rewritten as follows:

${\lambda }_{nor}={\gamma }_{nor}/\left(1+{\gamma }_{nor}\right).(9)$

This empirical formula thus can characterize λ of GSCGS under cyclic loadings.

FIGURE 3

FIGURE 3. Relationships of the G/G_max and λ_nor of GSCGS with γ_nor.

Conclusion

The dynamic properties of GSCGS were investigated via large-scale triaxial cyclic tests in this study. Outcomes illustrate that the G_max of GSCGS increases linearly with the VBP but nonlinearly with CP. Thus, new empirical formulas of G_max referring to the VBP and CP are proposed. A high VBP may result in a gentle decrease in G/G_max and a rapid increase in λ_nor, while the opposite is the case for a high CP. G/G_max and λ_nor are insensitive to VBP and CP via γ_nor so that they can be described by empirical formulas of γ_nor. The proposed empirical formulas can provide a reference to understand the dynamic behaviors of GSCGS and other similar cementitious geomaterials.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

Funding acquisition and formal writing of the work, SW; investigation and data analysis of the work, XG; review and editing of the work, WM, GL, CS, and PZ. All authors have read and agreed to the published version of the manuscript.

Funding

This study was financially supported by the National Natural Science Foundation of China (41902282) and State Key Laboratory of Frozen Soil Engineering (SKLFSE201809).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang T-l., Wang H-h., Song H-f., Yue Z-r., Guo Z-h. Effects of Cement Content and Grain-Size Composition on Engineering Properties of High-Speed-Railway Macadam Subgrade. Cold Regions Sci Tech (2018) 145:21–31. doi:10.1016/j.coldregions.2017.09.009

CrossRef Full Text | Google Scholar

2. Fu Z, Chen S, Han H. Large-scale Triaxial Experiments on the Static and Dynamic Behavior of an Artificially Cemented Gravel Material. Eur J Environ Civil Eng (2020) 2020:1–21. doi:10.1080/19648189.2020.1792350

CrossRef Full Text | Google Scholar

3. Pestana JM, Salvati LA. Small-Strain Behavior of Granular Soils. I: Model for Cemented and Uncemented Sands and Gravels. J Geotech Geoenviron Eng (2006) 132(8):1071–81. doi:10.1061/(asce)1090-0241(2006)132:8(1071)

CrossRef Full Text | Google Scholar

4. Wang H-L, Cui Y-J, Lamas-Lopez F, Calon N, Saussine G, Dupla J-C, et al. Investigation on the Mechanical Behavior of Track-Bed Materials at Various Contents of Coarse Grains. Construction Building Mater (2018) 164:228–37. doi:10.1016/j.conbuildmat.2017.12.209

CrossRef Full Text | Google Scholar

5. Liu X, Zhang X, Wang H, Jiang B. Laboratory Testing and Analysis of Dynamic and Static Resilient Modulus of Subgrade Soil under Various Influencing Factors. Construction Building Mater (2019) 195:178–86. doi:10.1016/j.conbuildmat.2018.11.061

CrossRef Full Text | Google Scholar

6. Xu D-s., Liu H-b., Rui R, Gao Y. Cyclic and Postcyclic Simple Shear Behavior of Binary Sand-Gravel Mixtures with Various Gravel Contents. Soil Dyn Earthquake Eng (2019) 123:230–41. doi:10.1016/j.soildyn.2019.04.030

CrossRef Full Text | Google Scholar

7. Wang S, Xue Q, Zhu Y, Li G, Wu Z, Zhao K. Experimental Study on Material Ratio and Strength Performance of Geopolymer-Improved Soil. Construction Building Mater (2021) 267:120469. doi:10.1016/j.conbuildmat.2020.120469

CrossRef Full Text | Google Scholar

8. Kumar SS, Krishna AM, Dey A. Evaluation of Dynamic Properties of sandy Soil at High Cyclic Strains. Soil Dyn Earthquake Eng (2017) 99:157–67. doi:10.1016/j.soildyn.2017.05.016

CrossRef Full Text | Google Scholar

9. Seed HB, Wong RT, Idriss IM, Tokimatsu K. Moduli and Damping Factors for Dynamic Analyses of Cohesionless Soils. J Geotechnical Eng (1986) 112(11):1016–32. doi:10.1061/(asce)0733-9410(1986)112:11(1016)

CrossRef Full Text | Google Scholar

10. Rollins KM, Evans MD, Diehl NB, Iii WDD. Shear Modulus and Damping Relationships for Gravels. J Geotechnical Geoenvironmental Eng (1998) 124(5):396–405. doi:10.1061/(asce)1090-0241(1998)124:5(396)

CrossRef Full Text | Google Scholar

11. Hardin BO, Drnevich VP. Shear Modulus and Damping in Soils: Design Equations and Curves. J Soil Mech Foundations Div (1972) 98(sm7):667–92. doi:10.1061/jsfeaq.0001760

CrossRef Full Text | Google Scholar

12. Chen G, Zhou Z, Sun T, Wu Q, Xu L, Khoshnevisan S, et al. Shear Modulus and Damping Ratio of Sand-Gravel Mixtures over a Wide Strain Range. J Earthquake Eng (2019) 23(8):1407–40. doi:10.1080/13632469.2017.1387200

CrossRef Full Text | Google Scholar

13. Martin PP, Seed HB. One-dimensional Dynamic Ground Response Analyses. J Geotech Engrg Div (1982) 108(7):935–52. doi:10.1061/ajgeb6.0001316

CrossRef Full Text | Google Scholar