Abstract
Optical quantum network plays an important role in large scale quantum communication. However, different components for photon generation, transmission, storage and manipulation in network usually cannot interact directly due to the wavelength and bandwidth differences, and thus interfaces are needed to overcome such problems. We propose an optical interface for frequency down-conversion and bandwidth compression based on the counter-propagating quasi-phase-matching difference frequency generation process in the periodically-poled lithium niobate on insulator waveguide. We prove that a separable spectral transfer function can be obtained only by choosing proper pump bandwidth, thus relaxing the limitation of material, dispersion, and working wavelength as a result of the counter-propagation phase-matching configuration. With numerical simulations, we show that our design results in a nearly separable transfer function with the Schmidt number very close to 1. With proper pump bandwidth, an photon at central wavelength of 550 nm with a bandwidth ranging from 50 GHz to 5 THz can be converted to a photon at central wavelength of 1,545 nm with a much narrower bandwidth of 33 GHz.
1 Introduction
Photons play an important role in quantum information science, such as long distance quantum communication [1,2], linear optical quantum computation [3,4] and interface to quantum memories [5,6]. However, in these applications, different devices and systems usually require different photon central frequencies and bandwidths. In order to combine all these systems in one quantum network, photon frequency interface capable of converting frequency and bandwidth is indispensable.
Electro-optical modulation is an efficient way to shift photon frequency [7–9], which is commonly used in pulse manipulation, however, its conversion range is limited to several GHz. Sum frequency generation (SFG) [10–12] and difference-frequency generation (DFG) [13] in nonlinear optical process are beneficial to frequency conversion between different frequency bands and have been utilized as an interface between the visible and communication wavelength bands [14–16]. Moreover, a bandwidth compression factor of 40 was achieved by utilizing SFG process with chirped input photon and anti-chirped strong pump laser [17]. However, interfaces generated by this way usually suffer from low conversion efficiency due to the need of ultra wide phase-matching bandwidth. How to convert frequency and compress bandwidth effectively at the same time is a big challenge. Recently, Allgaier et al. made an approach towards both goals with dispersion-engineered SFG [18], where photon at communication wavelength was converted to the visible range with a bandwidth compression factor of 7.47 and an internal conversion efficiency of 61.5%. Such method relies on modulating the dispersion and group velocity relationship among the input, pump, and output photons, and thus has limited choices on the working wavelengths and materials.
On the other hand, counter-propagating quasi-phase-matching (QPM) spontaneous parametric down-conversion (SPDC) process has been extensively studied due to its unique spectral properties [19,20], such as narrow bandwidth [21,22] and frequency uncorrelated [23–26] photon pairs. In contrast to the traditional co-propagating process, in the counter-propagating process the phase-matching function is greatly affected by the counter propagation of the signal and idler photons, and hence such method can be applied in a large range of nonlinear materials and working wavelengths. In this paper, we propose to use the counter-propagating QPM DFG to realize an optical interface for frequency down-conversion and bandwidth compression. We design an experimental feasible waveguide structure based on the thin-film lithium niobate on insulator (LNOI) platform, which has been considered as a revolutionary platform for integrated photonics [27] and aroused a great deal of interest in recent years, as it allows a strong optical confinement and thus brings strong nonlinear effects [28–30].
2 Methods
The configuration of a counter-propagating QPM DFG process is shown in Figure 1. With a pulse laser as the pump in a y-direction waveguide, a co-propagating high-frequency input photon is converted into a low-frequency output photon in the counter-propagation direction. In the undepleted pump approximation, the effective Hamiltonian describing the DFG process can be written as [31].where θ is the coupling parameter having absorbed all the constants, and the frequencies are constrained by the energy-conservation relation of ωi − ωp = ωo, with the subscripts i, p, and o representing the input, pump, and output photons, respectively. The normalized DFG transfer function can be expressed as f (ωi, ωo) = α(ωi − ωo)Φ(ωi, ωo), where α(ωi − ωo) is the spectral amplitude of pump light and Φ(ωi, ωo) denotes the phase matching function.
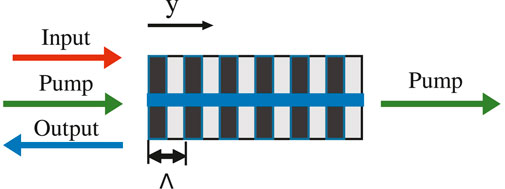
FIGURE 1
Geometry of a counter-propagating quasi-phase-matching difference frequency generation process in a y-direction waveguide with a poling period of Λ. The input and pump light propagate in the same direction, while the output light propagates in the opposite direction.
With broadband pump laser, the transfer function can be written as Schmidt decomposition form [32].where {ϕj (ωi)} and {ψj (ωo)} are two sets of orthogonal spectral amplitude functions and κj are the real Schmidt coefficients satisfying . Thus the effective Hamiltonian can be rewritten aswith broadband mode operators and . Compared with the effective Hamiltonian of an optical beam splitter (BS) .[33], the DFG process can be considered as a set of independent BSs which convert Aj to Cj with effective coupling parameter θκj, namely, Aj → cos (θκj)Aj + i sin (θκj)Cj with conversion efficiency sin2 (θκj) [31]. Hence, for the multi-mode input photon , with , the total conversion efficiency is given by ∑j|αj|2sin2 (θκj). We can see that, given a fixed pump light power, the maximum total conversion efficiency is achieved when the Schmidt number K = 1, i.e., the transfer function is separable, according to the Cauchy-Schwarz inequality. Hence, it is important to design a separable transfer function for efficient frequency conversion. In the following, we propose a method to obtain a separable transfer function by using the counter-propagating QPM DFG process.
The phase matching function can be expressed aswith L denoting the poling length. For the counter-propagating DFG process, the phase mismatch Δk is given bywhere kG = 2πm/Λ is the mth order reciprocal wave vector with Λ denoting the poling period.
We define frequency offsets Δωj ≡ Ωj − ωj, with j = i, p, o, where Ωj are central frequencies satisfying perfect phase-matching condition Δk = 0. Thus, according to the energy-conservation relation, we have Ωi − Ωp = Ωo, and Δωi − Δωp = Δωo. Then, by expanding Δk to the first order in Δωj and Δωo around central frequencies, we obtainwhere uj, j = i, o, p are the group velocities at central frequencies. For comparison, the phase mismatch of the co-propagating DFG process given by Δkco = ki − kp − ko − kG, can be expanded as
We can see that in the traditional co-propagating process the coefficients of frequency offsets only depend on the difference of the reciprocal of group velocities, and thus in such process the phase-matching function is usually engineered by selecting working frequencies and structures to control the dispersion and group velocities [34]. While, in the counter-propagating process, the coefficients also depend on the sum of the group velocities, enabling intrinsic features for phase-matching engineering [20–26].
To further characterize the transfer function, we define two characteristic bandwidth scales
Thus, the phase matching function given by Eq. 4 can be rewritten aswhere we defined a function of . By rewriting the pump amplitude function α(ωi − ωo) as , we can write the transfer function against frequency offsets as
In the following, we prove that when the pump light bandwidth δωp satisfies δω2 ≪ δωp ≪ δω1, the transfer function can approach a separable function of Δωi, Δωo. In analogy to the analysis in Ref. [20], we first recast the argument of function withwhere Δωp/δω1 has been neglected because it is on the order δωp/δω1 ≪ 1. Then we recast the argument of function aswhere Δωi/δω1 + Δωo/δω2 is the argument of the sinc function in as given in Eq. 9, and thus it is limited to values on the order of ∼ 10, namely, inside the bandwidth of sinc function, due to the product relationship of and shown in Eq. 10. Consequently, provided that δω2/δωp is small enough, we can have δω2 (Δωi/δω1 + Δωo/δω2) much smaller than δωp, the bandwidth of , and therefore this term is negligible in the argument of . Hence we have the following approximation
In addition, considering δω2/δω1 ≪ 1, we can further make approximation on Eq. 14 as
Consequently, the transfer function given by Eq. 10 approaches the factorized form
Such separable function also means that the correlation between the input and output photons is eliminated. It is clear that the frequency of the input photon can vary within the bandwidth of the pump light, and thus the bandwidth of the input photon can be as large as that of the pump light, namely, δωi = δωp. While, the bandwidth of the output photon is only determined by the phase-matching function irrespective of the pump bandwidth, which can be obtained from the full width at half maximum of the spectral density function , given by
Hence, we can get the bandwidth compression factor as
3 Results
The schematic of the LNOI waveguide is shown in Figure 2 consisting of three layers of silicon (Si), silica (SiO2), and lithium niobate (LN), respectively. The LN layer is made from X-cut LNOI film and the waveguide propagates in y-direction with a sidewall angle of φ = 60°, and a length of L = 10 mm. The waveguide height h and its bottom ridge width w restrict the transverse distribution of the guide mode and can be adjusted in structure design and fabrication process. By varying the height and width, light dispersion can be tuned in the LNOI waveguide. In order to characteristic the property of the bandwidth compressor, numerically simulations of group index and effective refractive index are obtained by utilizing the Mode Solution software with the material dispersion of LN given by Ref. [35].
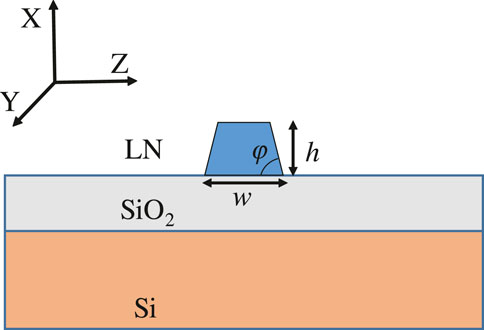
FIGURE 2
Schematic of the X-cut LNOI waveguide structure. The parameters φ, w, and h denote sidewall angle, bottom ridge width, and hight of the waveguide, respectively.
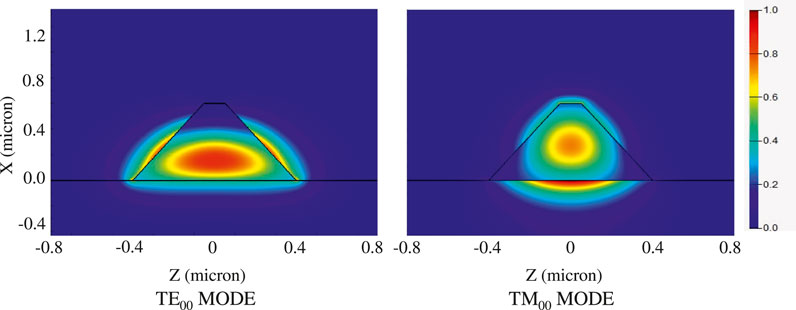
Here we aim to design a counter-propagating DFG process that converts the broadband input photons centered at 550 nm in TE00 mode to narrowband output photons centered at 1,545 nm in TM00 mode with a pulsed laser light centered at 854 nm in TM00 mode as the pump. Such frequency conversion process with the chosen wavelengths may connect the quantum communication channels with single-photon emitters around 550 nm, such as the charge-neutral nitrogen-vacancy center in diamond [36] and the CdSe quantum dots [37, 38]. The structure parameters are h = 0.6 μm and w = 0.8 μm. Single mode condition can be achieved at 1,545 nm with the field distribution of TE00 and TE00 modes shown in Figure 3. With simulated effective index of the waveguide, we can calculate the poling period to be Λ = 0.402 μm for satisfying the first-order QPM condition of Δk = 0 according to Eq. 5. The simulated results of group index ng = c/u of TE00 and TM00 modes with wavelength ranging from 500 to 1,600 nm are shown in Figure 4. Explicitly, the simulated group indexes of the pump light at 854 nm in TM00 mode, the input light at 550 nm in TE00 mode, and the output light at 1,545 nm in TM00 mode are ng,p = 2.533, ng,i = 2.532, and ng,o = 2.401, respectively. Therefore, we can obtain δω1 = 60 THz and δω2 = 12.2 GHz.
FIGURE 3
Field distribution of TM00 mode and TE00 mode at 1,545 nm.
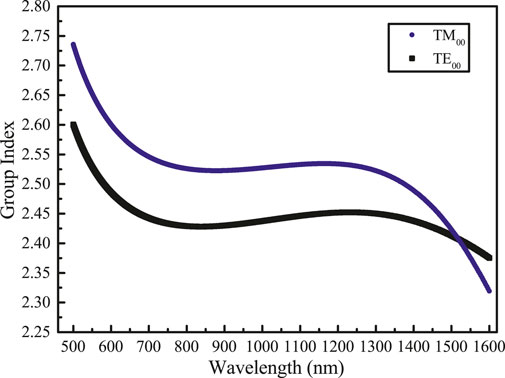
FIGURE 4
Group index of TE00 and TM00 modes in LNOI waveguide with wavelength ranging from 500 to 1,600 nm.
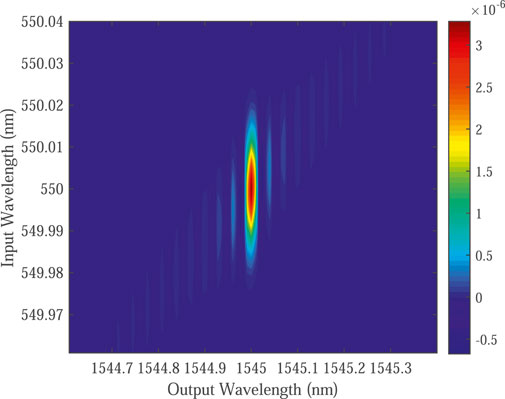
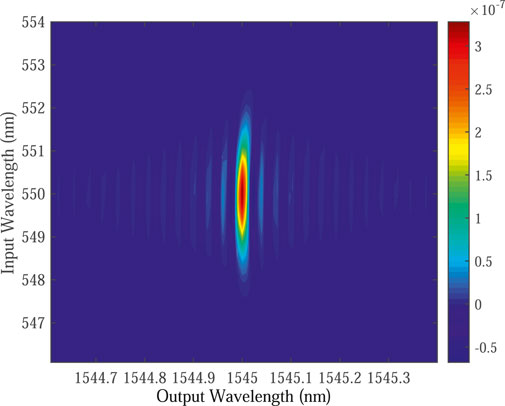
In order to show the spectrum relation between the input and output photons, we simulate the transfer function given by Eq. 10. By assuming a Gaussian spectrum pump, the simulation results when pump bandwidths δωp = 50 GHz and δωp = 5 THz are shown in Figure 5, 6, respectively. The corresponding Schmidt numbers K are estimated to be 1.037, and 1.041, respectively. Hence, we can see that the transfer function is very close to a separable one. The bandwidth of the output photon can be estimated from Eq. 17, namely, δωo = 33 GHz. Then according to Eq. 18 we can express the bandwidth compression factor asand consequently, in our simulation range of δωp = 50 GHz ∼ 5 THz, we can obtain a compression factor ranging from 1.5 to 150.
FIGURE 5
Simulated transfer function when the pump bandwidth δωp is 50 GHz.
FIGURE 6
Simulated transfer function when the pump bandwidth δωp is 5 THz.
Then we give a simulation of the conversion efficiency. The DFG process with a separable transfer function can be treated as a BS model and the conversion efficiency is given by sin2θ [31]. Here the coupling parameter can be expressed aswhere d = 2d31/(mπ) is the nonlinear coefficient, and Pp is the pump peak power, with nj (j = p, i, o) representing the effective refractive index of pump, input and output lights at central frequencies, respectively. The parameter N is the normalization factor of transfer function given by
The effective interaction area B can be written aswhere gj (x, z) (j = p, i, o) is the normalized spatial distribution of the cross-sectional area of pump, input and output fields, respectively. Through numerical simulation using the Mode solution software, we estimated B to be 0.472 μm2. With these calculations, we can estimate a pump peak power of 2.04 W in the case of unity conversion efficiency. If setting the pump pulse width to be 200 fs with a repetition rate of 80 MHz, we can calculate the average pump power to be 0.032 mW, which is much lower than the previous experiment results [39, 40].
It should be noted that the ideal unity conversion efficiency in a single process could be achieved only in the limit of short interaction length or long pump pulse [41]. In broadband mode case, time-ordering corrections may affect the conversion efficiency [42, 43], which are resulted from the noncommutativity of the interaction Hamiltonian at different times. A maximum conversion efficiency of 87.7% has been obtained in a SFG process [44]. Moreover, Reddy et al. [45] proposed a scheme to overcome the time-ordering correction limitation by cascading two frequency conversion processes with 50% conversion efficiency.
4 Discussion
We would like to discuss the experimental feasibility of our design. The LNOI waveguide structure is experimentally feasible with current LNOI fabrication techniques [27–30]. The poling period on the order of 0.402 μm is still challenging at present. However, we can use a higher-order reciprocal wave vector to obtain a bigger poling period at the cost of lower efficiency. For example, if using the third-order reciprocal wave vector, we would get a poling period of 1.206 μm with the nonlinear coefficient reduced to d/3. Such poling period is possible with current fabrication techniques [46].
In conclusion, we proposed a scheme to realize optical frequency down-conversion and bandwidth compression via the counter-propagating QPM DFG process, which can provide a quantum network interface for devices working at different central frequencies and bandwidths. We proved that, due to the counter-propagation configuration, a separable spectrum transfer function can be obtained only by choosing the pump bandwidth in a range between two characteristic bandwidth scales, rather than satisfying constrained dispersion and group velocity relations, and thus this method is not strictly limited by the material, dispersion, and working wavelength. Moreover, under this condition, the input photon can have a bandwidth the same with that of the pump light, while the bandwidth of the out photon is only determined by the phase-matching function irrespective of the pump bandwidth. Such feature enables a large bandwidth compression factor as well as facilitates the application in the interface between photons with different spectral shapes. We designed a periodically-poled LNOI waveguide to realize the scheme. The simulation result shows a nearly separable transfer function with the Schmidt number estimated very close to 1. By changing the pump bandwidth, a bandwidth compression factor ranging from 1.5 to 150 can be obtained. We also calculate a pump average power of 0.032 mW to achieve unit conversion efficiency. In addition, the counter-propagating output feature is also of great benefit to compressing co-propagating noises. Finally, our approach opens up a way for efficient optical interface connecting photons with different frequency and spectrum bandwidth benefiting from the counter-propagating nonlinear process. We hope our approach can stimulate more such investigations.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
D-JG designed the scheme and performed the calculations with the help of RY. Y-XG, and ZX supervised the project. All authors discussed the results and reviewed the manuscript.
Funding
This work was supported by the National Key R&D Program of China (No. 2019YFA0705000), Key R&D Program of Guangdong Province (No. 2018B030329001), Leading-edge technology Program of Jiangsu Natural Science Foundation (No. BK20192001), National Natural Science Foundation of China (51890861, 11690031, 11674169, 11974178).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
DuanL-MLukinMDCiracJIZollerP. Long-distance Quantum Communication With Atomic Ensembles and Linear Optics. Nature (2001) 414:413–8. 10.1038/35106500
2.
BoaronABosoGRuscaDVulliezCAutebertCCalozMet alSecure Quantum Key Distribution Over 421 Km of Optical Fiber. Phys Rev Lett (2018) 121:190502. 10.1103/PhysRevLett.121.190502
3.
KnillELaflammeRMilburnGJ. A Scheme for Efficient Quantum Computation With Linear Optics. nature (2001) 409:46–52. 10.1038/35051009
4.
KokPMunroWJNemotoKRalphTCDowlingJPMilburnGJ. Linear Optical Quantum Computing With Photonic Qubits. Rev Mod Phys (2007) 79:135–74. 10.1103/RevModPhys.79.135
5.
LvovskyAISandersBCTittelW. Optical Quantum Memory. Nat Photon (2009) 3:706–14. 10.1038/nphoton.2009.231
6.
KozhekinAEMølmerKPolzikE. Quantum Memory for Light. Phys Rev A (2000) 62:033809. 10.1103/PhysRevA.62.033809
7.
KarpińskiMJachuraMWrightLJSmithBJ. Bandwidth Manipulation of Quantum Light by an Electro-Optic Time Lens. Nat Photon (2017) 11:53–7. 10.1038/nphoton.2016.228
8.
WrightLJKarpińskiMSöllerCSmithBJ. Spectral Shearing of Quantum Light Pulses by Electro-Optic Phase Modulation. Phys Rev Lett (2017) 118:023601. 10.1103/PhysRevLett.118.023601
9.
SośnickiFKarpińskiM. Large-Scale Spectral Bandwidth Compression by Complex Electro-Optic Temporal Phase Modulation. Opt Express (2018) 26:31307–16. 10.1364/OE.26.031307
10.
VandevenderAPKwiatPG. High Efficiency Single Photon Detection via Frequency Up-Conversion. J Mod Opt (2004) 51:1433–45. 10.1080/09500340408235283
11.
AlbotaMAWongFNC. Efficient Single-Photon Counting at 155 Μm by Means of Frequency Upconversion. Opt Lett (2004) 29:1449–51. 10.1364/ol.29.001449
12.
KobayashiTIkutaRYasuiSMikiSYamashitaTTeraiHet alFrequency-Domain Hong-Ou-Mandel Interference. Nat Photon (2016) 10:441–4. 10.1038/nphoton.2016.74
13.
IkutaRKobayashiTYasuiSMikiSYamashitaTTeraiHet alFrequency Down-Conversion of 637 Nm Light to the Telecommunication Band for Non-Classical Light Emitted From Nv Centers in diamond. Opt Express (2014) 22:11205–14. 10.1364/OE.22.011205
14.
VollmerCEBauneCSamblowskiAEberleTHändchenVFiurášekJet alQuantum Up-Conversion of Squeezed Vacuum States from 1550 to 532 Nm. Phys Rev Lett (2014) 112:073602. 10.1103/PhysRevLett.112.073602
15.
RakherMTMaLSlatteryOTangXSrinivasanK. Quantum Transduction of Telecommunications-Band Single Photons From a Quantum Dot by Frequency Upconversion. Nat Photon (2010) 4:786–91. 10.1038/nphoton.2010.221
16.
WalkerTMiyanishiKIkutaRTakahashiHVartabi KashanianSTsujimotoYet alLong-Distance Single Photon Transmission From a Trapped Ion via Quantum Frequency Conversion. Phys Rev Lett (2018) 120:203601. 10.1103/physrevlett.120.203601
17.
LavoieJDonohueJMWrightLGFedrizziAReschKJ. Spectral Compression of Single Photons. Nat Photon (2013) 7:363–6. 10.1038/nphoton.2013.47
18.
AllgaierMAnsariVSansoniLEignerCQuiringVRickenRet alHighly Efficient Frequency Conversion With Bandwidth Compression of Quantum Light. Nat Commun (2017) 8:1–6. 10.1038/ncomms14288
19.
HarrisSE. Proposed Backward Wave Oscillation in the Infrared. Appl Phys Lett (1966) 9:114–6. 10.1063/1.1754668
20.
GattiACortiTBrambillaE. Temporal Coherence and Correlation of Counterpropagating Twin Photons. Phys Rev A (2015) 92:053809. 10.1103/physreva.92.053809
21.
GongYXXieZDXuPYuXQXuePZhuSN. Compact Source of Narrow-Band Counterpropagating Polarization-Entangled Photon Pairs Using a Single Dual-Periodically-Poled Crystal. Phys Rev A (2011) 84:053825. 10.1103/physreva.84.053825
22.
DuanJ-CZhangJ-NZhuY-JSunC-WLiuY-CXuPet alGeneration of Narrowband Counterpropagating Polarization-Entangled Photon Pairs Based on Thin-Film Lithium Niobate on Insulator. J Opt Soc Am B (2020) 37:2139–45. 10.1364/josab.395108
23.
ChristAEcksteinAMosleyPJSilberhornC. Pure Single Photon Generation by Type-I Pdc With Backward-Wave Amplification. Opt Express (2009) 17:3441–6. 10.1364/OE.17.003441
24.
LuoK-HAnsariVMassaroMSantandreaMEignerCRickenRet alCounter-Propagating Photon Pair Generation in a Nonlinear Waveguide. Opt Express (2020) 28:3215–25. 10.1364/OE.378789
25.
CaiW-HWeiBWangSJinR-B. Counter-propagating Spectrally Uncorrelated Biphotons at 1550 Nm Generated From Periodically Poled MTiOXO4 (M = K, Rb, Cs; X = P, as). J Opt Soc Am B (2020) 37:3048–54. 10.1364/JOSAB.401157
26.
LiuY-CGuoD-JRenK-QYangRShangMZhouWet alObservation of Frequency-Uncorrelated Photon Pairs Generated by Counter-propagating Spontaneous Parametric Down-Conversion. Sci Rep (2021) 11:1–6. 10.1038/s41598-021-92141-y
27.
BoesACorcoranBChangLBowersJMitchellA. Status and Potential of Lithium Niobate on Insulator (Lnoi) for Photonic Integrated Circuits. Laser Photon Rev (2018) 12:1700256. 10.1002/lpor.201700256
28.
WangCLangrockCMarandiAJankowskiMZhangMDesiatovBet alUltrahigh-Efficiency Wavelength Conversion in Nanophotonic Periodically Poled Lithium Niobate Waveguides. Optica (2018) 5:1438–41. 10.1364/optica.5.001438
29.
ChenJ-YMaZ-HSuaYMLiZTangCHuangY-P. Ultra-Efficient Frequency Conversion in Quasi-Phase-Matched Lithium Niobate Microrings. Optica (2019) 6:1244–5. 10.1364/OPTICA.6.001244
30.
LuJSuryaJBLiuXBruchAWGongZXuYet alPeriodically Poled Thin-Film Lithium Niobate Microring Resonators With a Second-Harmonic Generation Efficiency of 250,000%/w. Optica (2019) 6:1455–60. 10.1364/OPTICA.6.001455
31.
EcksteinABrechtBSilberhornC. A Quantum Pulse Gate Based on Spectrally Engineered Sum Frequency Generation. Opt Express (2011) 19:13770–8. 10.1364/OE.19.013770
32.
LawCKWalmsleyIAEberlyJH. Continuous Frequency Entanglement: Effective Finite hilbert Space and Entropy Control. Phys Rev Lett (2000) 84:5304–7. 10.1103/PhysRevLett.84.5304
33.
PrasadSScullyMOMartienssenW. A Quantum Description of the Beam Splitter. Opt Commun (1987) 62:139–45. 10.1016/0030-4018(87)90015-0
34.
BaronavskiAPLadouceurHDShawJK. Analysis of Cross Correlation, Phase Velocity Mismatch and Group Velocity Mismatches in Sum-Frequency Generation. IEEE J Quan Electron. (1993) 29:580–9. 10.1109/3.199312
35.
ZelmonDESmallDLJundtD. Infrared Corrected Sellmeier Coefficients for Congruently Grown Lithium Niobate and 5 mol.% Magnesium Oxide–Doped Lithium Niobate. JOSA B (1997) 14:3319–22. 10.1364/JOSAB.14.003319
36.
AharonovichICastellettoSSimpsonDASuC-HGreentreeADPrawerS. Diamond-Based Single-Photon Emitters. Rep Prog Phys (2011) 74:076501. 10.1088/0034-4885/74/7/076501
37.
ChenOZhaoJChauhanVPCuiJWongCHarrisDKet alCompact High-Quality CdSe-CdS Core-Shell Nanocrystals With Narrow Emission Linewidths and Suppressed Blinking. Nat Mater (2013) 12:445–51. 10.1038/nmat3539
38.
LinXDaiXPuCDengYNiuYTongLet alElectrically-Driven Single-Photon Sources Based on Colloidal Quantum Dots With Near-Optimal Antibunching at Room Temperature. Nat Commun (2017) 8:1132–7. 10.1038/s41467-017-01379-6
39.
TanzilliSTittelWHalderMAlibartOBaldiPGisinNet alA Photonic Quantum Information Interface. Nature (2005) 437:116–20. 10.1038/nature04009
40.
RoussevRVLangrockCKurzJRFejerMM. Periodically Poled Lithium Niobate Waveguide Sum-Frequency Generator for Efficient Single-Photon Detection at Communication Wavelengths. Opt Lett (2004) 29:1518–20. 10.1364/OL.29.001518
41.
DonohueJMMazurekMDReschKJ. Theory of High-Efficiency Sum-Frequency Generation for Single-Photon Waveform Conversion. Phys Rev A (2015) 91:033809. 10.1103/PhysRevA.91.033809
42.
ChristABrechtBMauererWSilberhornC. Theory of Quantum Frequency Conversion and Type-Ii Parametric Down-Conversion in the High-Gain Regime. New J Phys (2013) 15:053038. 10.1088/1367-2630/15/5/053038
43.
QuesadaNSipeJE. High Efficiency in Mode-Selective Frequency Conversion. Opt Lett (2016) 41:364–7. 10.1364/ol.41.000364
44.
BrechtBEcksteinARickenRQuiringVSucheHSansoniLet alDemonstration of Coherent Time-Frequency Schmidt Mode Selection Using Dispersion-Engineered Frequency Conversion. Phys Rev A (2014) 90:030302. 10.1103/physreva.90.030302
45.
ReddyDVRaymerMGMcKinstrieCJ. Efficient Sorting of Quantum-Optical Wave Packets by Temporal-Mode Interferometry. Opt Lett (2014) 39:2924–7. 10.1364/ol.39.002924
46.
YounesiMKumarPStanickiBJGeissRChangWKChenYH. Periodic Poling With Short Period for Thin Film Lithium Niobate Waveguides. In: Lasers and Electro-Optics Europe & European Quantum Electronics Conference (2019) IEEE. 10.1109/cleoe-eqec.2019.8871472
Summary
Keywords
frequency conversion, bandwidth compression, counter-propagating quasi-phase-matching, periodically-poled lithium niobate on insulator waveguide, difference frequency generation
Citation
Guo D-J, Yang R, Liu Y-C, Duan J-C, Xie Z, Gong Y-X and Zhu S-N (2021) Optical Frequency Down-Conversion With Bandwidth Compression Based on Counter-Propagating Phase Matching. Front. Phys. 9:752137. doi: 10.3389/fphy.2021.752137
Received
02 August 2021
Accepted
15 September 2021
Published
30 September 2021
Volume
9 - 2021
Edited by
Bao-Sen Shi, University of Science and Technology of China, China
Reviewed by
Qiang Zhang, University of Science and Technology of China, China
Yunfeng Huang, University of Science and Technology of China, China
Updates
Copyright
© 2021 Guo, Yang, Liu, Duan, Xie, Gong and Zhu.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhenda Xie, xiezhenda@nju.edu.cn; Yan-Xiao Gong, gongyanxiao@nju.edu.cn
This article was submitted to Optics and Photonics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.