Angle-Multiplexing Nonlinear Holography for Controllable Generations of Second-Harmonic Structured Light Beams

Nonlinear multiplexing holography emerges as a powerful tool to produce structured lights at new wavelengths. In this work, we propose and experimentally demonstrate an angle-multiplexing nonlinear holography in an angular noncritical phase-matching configuration. In experiment, various types of structured light beams, such as vortex beam, Airy beam and Airy vortex beam, are simultaneously output at second-harmonic waves along different paths. Because of the large angular acceptance bandwidth of noncritical phase-matching, one can achieve high conversion efficiency of angle-multiplexing nonlinear holography. Our method has potentially applications in high-capacity holographic storage and security encryption.

Introduction

Structured light has attracted widespread attentions because of its spatial distributions of amplitude, phase, and polarization [1]. For example, vortex beam has a unique spiral phase $\exp \left(il\varphi \right)$, featuring a phase singularity at the center and a donut-shaped intensity profile [2–8]. Airy beam is capable to remain its transverse profile during propagation, and it also has self-accelerating and self-healing characteristics [9, 10]. Airy vortex beam has been realized experimentally [11–14], which combines the propagation dynamics of Airy beam and the singularity of vortex beam [15–17]. The rapid development of structured light beam significantly boosts the applications in optical manipulation, quantum communications, and super-resolution microscopy [18, 19].

Holography has many important applications in numerous areas [20–26], including data storage [20], optical encryption [21], holographic interferometry [22], microscopy [23] and dynamic holography [24–26]. Because of its powerful wavefront shaping capability, holography has recently been used in nonlinear optics to enable the generations of various structured light beams at new optical frequencies [27–34]. By utilizing the orthogonal physical dimensions of light, nonlinear holography is capable to reconstruct multiple wavefront information from a single hologram, i.e., nonlinear multiplexing holography [28, 35]. Generally, only one wavefront channel can be output at a time when the corresponding phase matching condition is satisfied in nonlinear holography. It is still difficult for nonlinear holography to output various types of structured light beams efficiently, controllably, and simultaneously.

In this paper, we propose and experimentally demonstrate an angle-multiplexing nonlinear holography in an angular noncritical phase-matching (A-NCPM) configuration. By encoding proper holograms into the fundamental waves, multiple second-harmonic (SH) beams with the desired wavefronts can be simultaneously output along different paths. High conversion efficiency is guaranteed by the large angular acceptance bandwidth of A-NCPM. In experiment, we use the angle-multiplexing nonlinear holography to generate vortex beam, Airy beam and Airy vortex beam at SH waves for example.

Methods and Experiment

We consider two fundamental fields, i.e., $E_1\left(\omega \right)=E_1\exp \left(i{\varphi }_1\right)$ and $E_2\left(\omega \right)=E_2\exp \left(i{\varphi }_2\right)$, which have the same optical frequencies ($\omega$) but carry different holograms (${\varphi }_1$ and ${\varphi }_2$). These fields pass through a nonlinear crystal, which experience three birefringence phase matching (BPM) processes. First, 2 s harmonic generation (SHG) processes happen, in which each fundamental field is frequency-doubled with itself. Second, the two fundamental fields interact with each other through a sum-frequency-generation (SFG) process. Therefore, three fields at SH waves are generated, which can be calculated by using nonlinear three-wave mixing equation,

$E_1\left(2\omega \right)=C{\left(E_1\right)}^2\exp \left(2i{\varphi }_1\right)\exp \left(-i\text{Δ}{k}_1\left(z\right)z\right)(1)$

$E_2\left(2\omega \right)=C{\left(E_2\right)}^2\exp \left(2i{\varphi }_2\right)\exp \left(-i\text{Δ}{k}_2\left(z\right)z\right)(2)$

$E_3\left(2\omega \right)=C\left(E_1{E}_2\right)\exp \left[i\left({\varphi }_1+{\varphi }_2\right)\right]\exp \left(-i\text{Δ}{k}_3\left(z\right)z\right)(3)$

Here, $E_i\left(2\omega \right) \text{ with} i=\mathrm{1,2,3},\dots$ represents the generated SH fields. $C$ is a constant that is proportional to nonlinear coefficient of the nonlinear crystal. $z$ is the propagation direction. The phase mismatch between the interacting fields is defined as $\text{Δ}{k}_1=k_1\left(2\omega \right)-2k_1\left(\omega \right), \text{Δ}{k}_2=k_2\left(2\omega \right)-2k_2\left(\omega \right),\text{ and} \text{Δ}{k}_3=k_3\left(2\omega \right)-k_1\left(\omega \right)-k_2\left(\omega \right)$. When the BPM conditions are all satisfied, i.e., $\text{Δ}{k}_1\left(z\right)=\text{Δ}{k}_2\left(z\right)=\text{Δ}{k}_3\left(z\right)=0$, high conversion efficiency of nonlinear multiplexing holography can be achieved.

Figure 1A shows a collinear type-I BPM configuration, in which two horizontally-polarized fundamental fields propagate collinearly along the z axis. Three vertically-polarized SH fields [$E_1\left(2\omega \right),E_2\left(2\omega \right), \text{and} E_3\left(2\omega \right)$ as described in Eqs 1–3] are produced through three collinear BPM processes. Because $E_1\left(\omega \right)$ and $E_2\left(\omega \right)$ have the same wave vectors, it is easy to simultaneously satisfy the phase matching conditions $\text{Δ}{k}_1\left(z\right)=\text{Δ}{k}_2\left(z\right)=\text{Δ}{k}_3\left(z\right)=0$. However, this leads to overlapping of these SH fields at the image plane, as shown in Figure 1A. To effectively separate the generated SH fields, we add an additional term of $\exp \left(i\Delta k\right)$ to $E_1\left(\omega \right)$, and an additional term of $\exp \left(-i\Delta k\right)$ to $E_2\left(\omega \right)$, i.e., the fundamental fields of $E_1\left(\omega \right)$ and $E_2\left(\omega \right)$ are noncollinear. As a result, the SH fields $E_1\left(2\omega \right)$ and $E_2\left(2\omega \right)$ are output along the axisymmetric direction, while the SH field $E_3\left(2\omega \right)$ is still output along the z axis (Figure 1B). Clearly, the generated SH fields under such noncollinear configuration propagate along different paths in space, which can be well distinguished on the image plane.

FIGURE 1

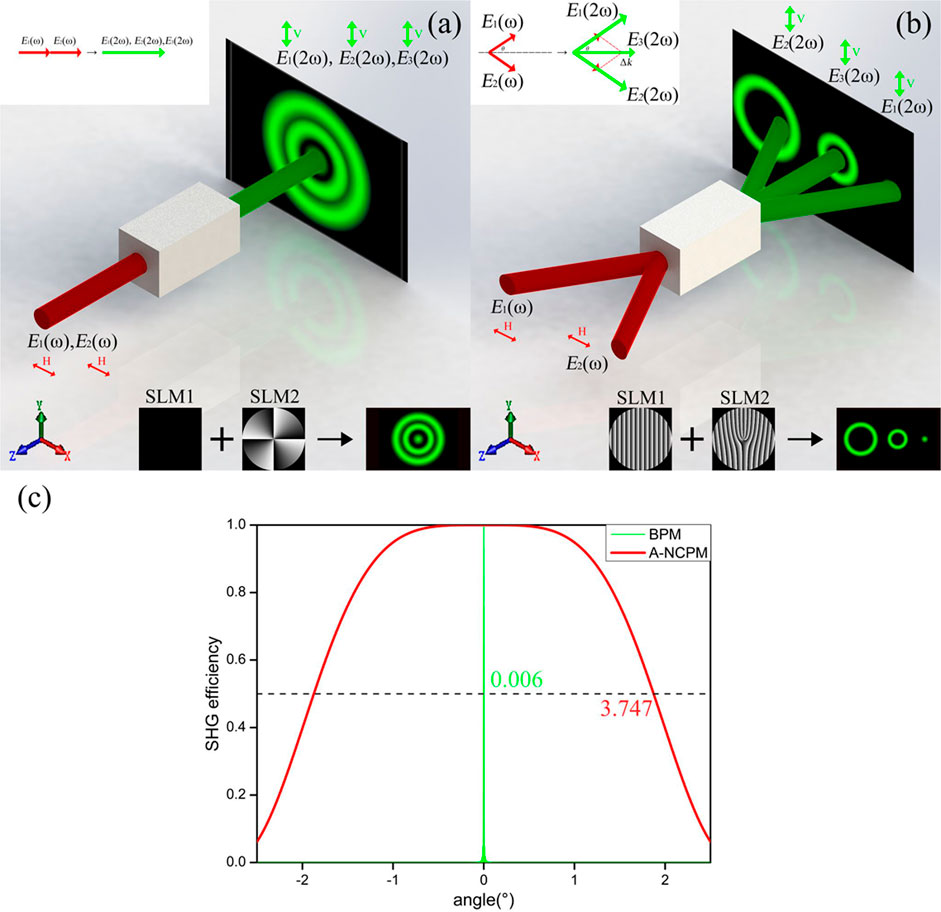
FIGURE 1. Comparison of collinear and noncollinear BPM configurations. We load the holograms of a plane wave and a l = -4 vortex phase respectively on SLM1 and SLM2 for example. (A) shows the collinear BPM process, in which the generated SH fields are mixed together. (B) shows the noncollinear case by introducing an additional phase of exp(iΔk) (or exp(−iΔk)) on SLM1 (or SLM2). Clearly, the SH fields can be well separated. (C) shows the angle dependence of the normalized SHG efficiency. Here, we use 15-mm-long barium borate (BBO) crystal and lithium boric oxide (LBO) crystal for the calculations of BPM and A-NCPM processes, respectively. The acceptance angular bandwidth is 0.006° in a traditional BPM process, while it is significantly increased is 3.741° in the A-NCPM configuration. Here, we define the angular bandwidth by using the full width at half maximum (FWHM) of the curves.

This noncollinear scheme can well solve the problem of SH field overlap. However, the phase mismatch becomes $\text{Δ}{k}_1\left(z\right)=\text{Δ}{k}_2\left(z\right)\ne \text{Δ}{k}_3\left(z\right)$, which cannot be simultaneously compensated in a traditional BPM crystal. Here, we propose A-NCPM to solve this problem [36]. A-NCPM is a popular phase-matching configuration, in which the input field generally propagates along the optical principal axis of nonlinear crystal. Under A-NCPM configuration, one can obtain a large angular acceptance bandwidth. By use of A-NCPM scheme, the conversion efficiency of the SHG process can be well maintained even the input fundamental beam is tilted by a certain angle. Figure 1C compares the normalized SHG conversion efficiencies of BPM and A-NCPM at different incident angles [36, 37]. In a traditional BPM process, the angular acceptance bandwidth is typically less than 0.1°. In contrast, the angular acceptance bandwidth is significantly enhanced to about 3.7° under an A-NCPM configuration in our experiment.

Figure 2 shows the experimental setup used in this work. In the optical alignment, the fundamental wave is derived from a 1,064 nm laser with a pulse repetition frequency of 20 kHz and a pulse width of 100 ns A polarizing beam splitter (PBS) is used to select a horizontally-polarized light. The fundamental wave is then shaped using a 4-f system consisting of two lenses (L1 and L2 with f1 = 200 mm and f2 = 75 mm) and a pinhole. After passing through a 50:50 beam splitter (BS), the fundamental wave is equally divided into two beams. These two beams are separately modulated by using two spatial light modulators (SLM1, BNS, P1920-600-1300-HDMI; and SLM2, Holoeye, Pluto-2-NIR-011) to carry the designed holograms. Because SLM1 used in the experiment only works for vertically-polarized light, we add a half-wave plate (HWP) between BS and SLM1. After modulation, they are combined via the 50:50 BS and then shaped using another 4-f system consisting of lenses L3 and L4 (with f3 = 500 mm and f4 = 50 mm). Then, the fundamental beams are incident into an LBO crystal (type-Ⅰ, θ = 0, φ = 90°, 4 × 4 × 15 mm³). A filter is placed after the LBO crystal to filter out the fundamental wave, and a lens L5 (f5 = 200 mm) is then used to perform the Fourier transform of the generated SH fields. Finally, the SH beams are recorded using a charge-coupled device (CCD) camera (Newport, LBP2-HR-VIS2). The SH vortex beams is tested by using a cylindrical lens [38].

FIGURE 2

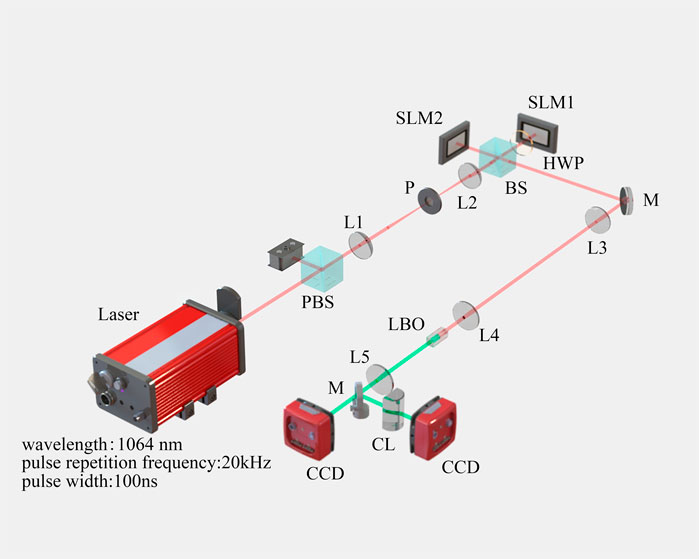
FIGURE 2. Schematic of the experiment setup. PBS, polarization beam spitter; L, lens; P, pinhole; BS, beam splitter; HWP, half-wave plate; M, mirror; LBO, lithium boric oxide crystal; CCD, charge-coupled device; CL, cylindrical lens.

In experiment, we first demonstrate the generations of multiple SH vortex beams. First, vortex holographic phase holograms with l = −4 and l = 4 are loaded onto SLM1 and SLM2, respectively. Here, the hologram is designed according to binary computer-generated-hologram (CGH) theory [39]. Besides, a blazed grating phase is superimposed on each hologram to introduce the additional spatial phase $\exp \left(i\Delta k\right)$ or $\exp \left(-i\Delta k\right)$. Here,$\Delta k$ is chosen to ensure the incident angle lies in the acceptance angular bandwidth of A-NCPM. In our experiment, the incident angle of the fundamental wave is measured to be 0.78°. Then, the two fundamental waves $E_1\mathrm{(\omega )}$ and $E_2\mathrm{(\omega )}$ interact in the LBO crystal to produce three SH beams. The conversion of the orbital-angular momentum (OAM) in nonlinear optical process obeys $l\left(2\omega \right)=l\left(\omega \right)+l^{\text{'}}\left(\omega \right)$[40, 41]. Figure 3A shows the experimental result. The two donut-shaped SH beams on the sides correspond to the SHG processes in which $E_1\mathrm{(\omega )}$ (or $E_2\mathrm{(\omega )}$) is frequency-doubled with itself. The generated $E_1\left(2\omega \right)$ (or $E_2\left(2\omega \right)$) carries an OAM of l = −8 (or l = 8), which is measured by using a cylindrical lens, as shown in Figure 3C. The central Gaussian spot results from the SFG process between $E_1\mathrm{(\omega )}$ and $E_2\mathrm{(\omega )}$. Because the interacting fundamental waves have topological charges of opposite sign, the spiral phase is cancelled in the generated SH wave. In addition, we replace the hologram loaded on SLM2 to a l = 1 vortex holographic phase hologram while keeping the hologram on SLM1 unchanged. As shown in Figure 4A, three SH vortex beams of l = −8, l = −3, and l = 2 present from left to right on the image plane. Their OAMs are also measured by a cylindrical lens as shown in Figure 4C, which is consistent with the OAM conservation law. Figures 3B, 4B show the numerical simulations, which are in good agreement with the experimental results in Figures 3A, 4A, respectively.

FIGURE 3

FIGURE 3. By using two fundamental waves of l = -4 and l = 4, three SH beams of l = -8, l = 0, and l = 8 (from left to right) are simultaneously generated. (A,B) show the experimental and simulated results, respectively. (C) shows the transformed patterns after a cylindrical lens, from which the OAM number can be measured by counting the dark strips.

FIGURE 4

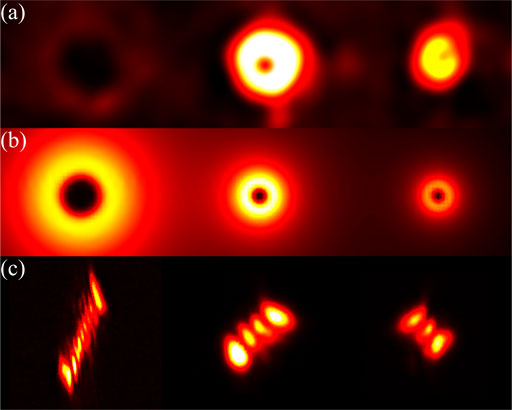
FIGURE 4. By using two fundamental waves of l = -4 and l = 1, three SH beams of l = -8, l = -3, and l = 2 (from left to right) are produced at the same time. (A,B) show the experimental and simulated results, respectively. (C) shows the transformed patterns after a cylindrical lens for OAM measurements.

Next, we produce various types of spatial light beams simultaneously. In this experiment, we load the holograms for the generations of a 2D Airy beam and a l = 1 vortex beam on SLM1 and SLM2, respectively. Notably, if a fundamental Airy beam is directly frequency-doubled with itself in the nonlinear crystal, one achieves the product of two Airy beams rather than the SH Airy beam [42]. In the experiment, we use the Fourier transform (FT) of the Airy beam as the hologram on SLM1, which is imaged into the nonlinear crystal and performs SHG. Then, the generated SH field is converted to an SH Airy beam after FT through a lens. Under such experimental configuration, three different types of SH beams, i.e., SH vortex beam, SH Airy beam, and SH Airy vortex beam, are produced along different paths. The experimental results are shown in Figure 5A, which agree well with the simulated results as shown in Figure 5B. Notably, the SH intensities in Figures 3–5 are not the same because the conversion efficiencies of SHGs involving various structured light beams are different.

FIGURE 5

FIGURE 5. The experimental (A) and simulated (B) generations of Airy beam, Airy vortex beam and vortex beam (from left to right) at SH waves.

Conclusion

In conclusion, we propose an angle-multiplexing nonlinear holography to produce multiple structured light beams simultaneously under an A-NCPM configuration. In experiment, we demonstrate a three-channel output of various SH beams, which can be further extended to more output channels within the angular acceptance bandwidth of A-NCPM. The angle-multiplexing nonlinear holography can also be applied in nonlinear photonic crystals and nonlinear metasurfaces [43–47]. Our work provides a feasible solution to enhance the capacity of nonlinear holography for multi-wavelength display, multi-dimensional optical storage, optical encryption, all-optical diffractive neuron networks [48], and optical communications.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

WY, CZ, TW, and PC performed the experiments under the guidance of YZ and MX, WY, and YZ wrote the manuscript with contributions from all

Funding

National Key R&D Program of China (2017YFA0303703), the National Natural Science Foundation of China (NSFC) (91950206 and 11874213), and Fundamental Research Funds for the Central Universities (021314380191 and 021314380105).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Forbes A Structured Light from Lasers. Laser Photon Rev (2019) 13(11):1900140. doi:10.1002/lpor.201900140

CrossRef Full Text | Google Scholar

2. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45(11):8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Coullet P, Gil L, Rocca F Optical Vortices. Opt Commun (1989) 73(5):403–8. doi:10.1016/0030-4018(89)90180-6

CrossRef Full Text | Google Scholar

4. Djordjevic IB, Arabaci M LDPC-coded Orbital Angular Momentum (OAM) Modulation for Free-Space Optical Communication. Opt Express (2010) 18(24):24722–8. doi:10.1364/OE.18.024722

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Yan L, Gregg P, Karimi E, Rubano A, Marrucci L, Boyd R, et al. Q-plate Enabled Spectrally Diverse Orbital-Angular-Momentum Conversion for Stimulated Emission Depletion Microscopy. Optica (2015) 2(10):900–3. doi:10.1364/OPTICA.2.000900

CrossRef Full Text | Google Scholar

6. Chong A, Wan C, Chen J, Zhan Q Generation of Spatiotemporal Optical Vortices with Controllable Transverse Orbital Angular Momentum. Nat Photon (2020) 14(6):350–4. doi:10.1038/s41566-020-0587-z

CrossRef Full Text | Google Scholar

7. Wei D, Zhu Y, Zhong W, Cui G, Wang H, He Y, et al. Directly Generating Orbital Angular Momentum in Second-Harmonic Waves with a Spirally Poled Nonlinear Photonic crystal. Appl Phys Lett (2017) 110(26):261104. doi:10.1063/1.4990527

CrossRef Full Text | Google Scholar

8. Wei D, Cheng Y, Ni R, Zhang Y, Hu X, Zhu S, et al. Generating Controllable Laguerre-Gaussian Laser Modes through Intracavity Spin-Orbital Angular Momentum Conversion of Light. Phys Rev Appl (2019) 11(1):014038. doi:10.1103/PhysRevApplied.11.014038

CrossRef Full Text | Google Scholar

9. Siviloglou GA, Broky J, Dogariu A, Christodoulides DN Observation of Accelerating Airy Beams. Phys Rev Lett (2007) 99(21):213901. doi:10.1103/PhysRevLett.99.213901

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Efremidis NK, Chen Z, Segev M, Christodoulides DN Airy Beams and Accelerating Waves: an Overview of Recent Advances. Optica (2019) 6(5):686–701. doi:10.1364/OPTICA.6.000686

CrossRef Full Text | Google Scholar

11. Wei B-Y, Liu S, Chen P, Qi S-X, Zhang Y, Hu W, et al. Vortex Airy Beams Directly Generated via Liquid crystal Q-Airy-Plates. Appl Phys Lett (2018) 112(12):121101. doi:10.1063/1.5019813

CrossRef Full Text | Google Scholar

12. Singh BK, Remez R, Tsur Y, Arie A Measurement of Acceleration and Orbital Angular Momentum of Airy Beam and Airy-Vortex Beam by Astigmatic Transformation. Opt Lett (2015) 40(22):5411–4. doi:10.1364/OL.40.005411

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhou J, Liu Y, Ke Y, Luo H, Wen S Generation of Airy Vortex and Airy Vector Beams Based on the Modulation of Dynamic and Geometric Phases. Opt Lett (2015) 40(13):3193–6. doi:10.1364/OL.40.003193

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Liu Y, Chen W, Tang J, Xu X, Chen P, Ma CQ, et al. Switchable Second‐Harmonic Generation of Airy Beam and Airy Vortex Beam. Adv Opt Mater. (2021) 9(4):2001776. doi:10.1002/adom.202001776

CrossRef Full Text | Google Scholar

15. Dai HT, Liu YJ, Luo D, Sun XW Propagation Properties of an Optical Vortex Carried by an Airy Beam: Experimental Implementation. Opt Lett (2011) 36(9):1617–9. doi:10.1364/OL.36.001617

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wei B, Qi S, Liu S, Li P, Zhang Y, Han L, et al. Auto-transition of Vortex- to Vector-Airy Beams via Liquid crystal Q-Airy-Plates. Opt Express (2019) 27(13):18848–57. doi:10.1364/OE.27.018848

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Xu C, Wu Y, Deng D Multioptical Bottles from Second-Order Chirped Symmetric Airy Vortex Beams. Opt Lett (2020) 45(13):3502–5. doi:10.1364/OL.388569

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hell SW, Wichmann J Breaking the Diffraction Resolution Limit by Stimulated Emission: Stimulated-Emission-Depletion Fluorescence Microscopy. Opt Lett (1994) 19(11):780–2. doi:10.1364/OL.19.000780

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Klar TA, Hell SW Subdiffraction Resolution in Far-Field Fluorescence Microscopy. Opt Lett (1999) 24(14):954–6. doi:10.1364/OL.24.000954

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Heanue JF, Bashaw MC, Hesselink L Volume Holographic Storage and Retrieval of Digital Data. Science (1994) 265(5173):749–52. doi:10.1126/science.265.5173.749

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Li J, Kamin S, Zheng G, Neubrech F, Zhang S, Liu N Addressable Metasurfaces for Dynamic Holography and Optical Information Encryption. Sci Adv (2018) 4(6):eaar6768. doi:10.1126/sciadv.aar6768

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Powell RL, Stetson KA Interferometric Vibration Analysis by Wavefront Reconstruction. J Opt Soc Am (1965) 55(12):1593–8. doi:10.1364/JOSA.55.001593

CrossRef Full Text | Google Scholar

23. Gabor D Microscopy by Reconstructed Wave-Fronts. Proc R Soc Lond A (1949) 197(1051):454–87. doi:10.1098/rspa.1949.0075

CrossRef Full Text | Google Scholar

24. Luc J, Bouchouit K, Czaplicki R, Fillaut J-L, Sahraoui B Study of Surface Relief Gratings on Azo Organometallic Films in Picosecond Regime. Opt Express (2008) 16(20):15633–9. doi:10.1364/OE.16.015633

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Bartkiewicz S, Miniewicz A, Sahraoui B, Kajzar F Dynamic Charge-Carrier-Mobility-Mediated Holography in Thin Layers of Photoconducting Polymers. Appl Phys Lett (2002) 81(20):3705–7. doi:10.1063/1.1512824

CrossRef Full Text | Google Scholar

26. Matczyszyn K, Bartkiewicz S, Sahraoui B A New Holographic System: Liquid crystal Doped with Photochromic Molecules. Opt Mater (2002) 20(1):57–61. doi:10.1016/S0925-3467(02)00047-2

CrossRef Full Text | Google Scholar

27. Fang X, Wang H, Yang H, Ye Z, Wang Y, Zhang Y, et al. Multichannel Nonlinear Holography in a Two-Dimensional Nonlinear Photonic crystal. Phys Rev A (2020) 102(4):043506. doi:10.1103/PhysRevA.102.043506

CrossRef Full Text | Google Scholar

28. Chen P, Wang C, Wei D, Hu Y, Xu X, Li J, et al. Quasi-phase-matching-division Multiplexing Holography in a Three-Dimensional Nonlinear Photonic crystal. Light Sci Appl (2021) 10(1):1–7. doi:10.1038/s41377-021-00588-5

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Liu S, Switkowski K, Xu C, Tian J, Wang B, Lu P, et al. Nonlinear Wavefront Shaping with Optically Induced Three-Dimensional Nonlinear Photonic Crystals. Nat Commun (2019) 10(1):1–7. doi:10.1038/s41467-019-11114-y

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Liu S, Mazur LM, Krolikowski W, Sheng Y Nonlinear Volume Holography in 3D Nonlinear Photonic Crystals. Laser Photon Rev (2020) 14(11):2000224. doi:10.1002/lpor.202000224

CrossRef Full Text | Google Scholar

31. Wang H, Wei D, Xu X, Wang M, Cui G, Lu Y, et al. Controllable Generation of Second-Harmonic Vortex Beams through Nonlinear Supercell Grating. Appl Phys Lett (2018) 113(22):221101. doi:10.1063/1.5050423

CrossRef Full Text | Google Scholar

32. Wei D, Wang C, Xu X, Wang H, Hu Y, Chen P, et al. Efficient Nonlinear Beam Shaping in Three-Dimensional Lithium Niobate Nonlinear Photonic Crystals. Nat Commun (2019) 10(1):1–7. doi:10.1038/s41467-019-12251-0

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wu Y, Liu H, Chen X Three-dimensional Nonlinear Optical Holograms. Phys Rev A (2020) 102(6):063505. doi:10.1103/PhysRevA.102.063505

CrossRef Full Text | Google Scholar

34. Zhu B, Liu H, Liu Ya., Yan X, Chen Y, Chen X Second-harmonic Computer-Generated Holographic Imaging through Monolithic Lithium Niobate crystal by Femtosecond Laser Micromachining. Opt Lett (2020) 45(15):4132–5. doi:10.1364/OL.394162

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Fang X, Yang H, Yao W, Wang T, Zhang Y, Gu M, et al. High-dimensional Orbital Angular Momentum Multiplexing Nonlinear Holography. Adv Photon (2021) 3(1):015001. doi:10.1117/1.AP.3.1.015001

CrossRef Full Text | Google Scholar

36. Liu Y, Wang Z, Yu F, Qi H, Yang X, Yu X, et al. Angular Non-critical Phase-Matching Second-Harmonic-Generation Characteristics of RECOB (RE = Tm, Y, Gd, Sm, Nd and La) Crystals. Opt Express (2017) 25(10):11867–93. doi:10.1364/OE.25.011867

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Wu FT, Zhang WZ Consideration of Angular Acceptance Angle in BBO crystal on a Highly Efficient Second Harmonic Generation. Opt Laser Tech (1998) 30(3-4):189–92. doi:10.1016/S0030-3992(98)00032-2

CrossRef Full Text | Google Scholar

38. Volyar A, Bretsko M, Akimova Y, Egorov Y Measurement of the Vortex and Orbital Angular Momentum Spectra with a Single Cylindrical Lens. Appl Opt.Applied Opt (2019) 58(21):5748–55. WH. Binary computer-generated holograms1979182136613669. doi:10.1364/AO.58.005748Leedoi:10.1364/AO.18.003661

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Lee W-H Binary Computer-Generated Holograms. Appl Opt (1979) 18(21):3661–9. doi:10.1364/AO.18.003661

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Courtial J, Dholakia K, Allen L, Padgett MJ Second-harmonic Generation and the Conservation of Orbital Angular Momentum with High-Order Laguerre-Gaussian Modes. Phys Rev A (1997) 56(5):4193–6. doi:10.1103/PhysRevA.56.4193

CrossRef Full Text | Google Scholar

41. Li Y, Zhou Z-Y, Ding D-S, Shi B-S Sum Frequency Generation with Two Orbital Angular Momentum Carrying Laser Beams. J Opt Soc Am B (2015) 32(3):407–11. doi:10.1364/AO.58.00574810.1364/josab.32.000407

CrossRef Full Text | Google Scholar

42. Dolev I, Arie A Frontiers in Optics. Rochester, NY, United States: Optical Society of America (2010). p. FThA1. doi:10.1364/FIO.2010.FThA1 Second Harmonic Generation of Airy Beams in Quadratic Nonlinear Photonic Crystals.

CrossRef Full Text | Google Scholar

43. Wei D, Wang C, Wang H, Hu X, Wei D, Fang X, et al. Experimental Demonstration of a Three-Dimensional Lithium Niobate Nonlinear Photonic crystal. Nat Photon (2018) 12(10):596–600. doi:10.1038/s41566-018-0240-2

CrossRef Full Text | Google Scholar

44. Xu T, Switkowski K, Chen X, Liu S, Koynov K, Yu H, et al. Three-dimensional Nonlinear Photonic crystal in Ferroelectric Barium Calcium Titanate. Nat Photon (2018) 12(10):591–5. doi:10.1038/s41566-018-0225-1

CrossRef Full Text | Google Scholar

45. Li G, Zhang S, Zentgraf T Nonlinear Photonic Metasurfaces. Nat Rev Mater (2017) 2(5):1–14. doi:10.1038/natrevmats.2017.10

CrossRef Full Text | Google Scholar

46. Zhang Y, Sheng Y, Zhu S, Xiao M, Krolikowski W Nonlinear Photonic Crystals: from 2D to 3D. Optica (2021) 8(3):372–81. doi:10.1364/OPTICA.416619

CrossRef Full Text | Google Scholar

47. Segal N, Keren-Zur S, Hendler N, Ellenbogen T Controlling Light with Metamaterial-Based Nonlinear Photonic Crystals. Nat Photon (2015) 9(3):180–4. doi:10.1038/nphoton.2015.17

CrossRef Full Text | Google Scholar

48. Lin X, Rivenson Y, Yardimci NT, Veli M, Luo Y, Jarrahi M, et al. All-optical Machine Learning Using Diffractive Deep Neural Networks. Science (2018) 361(6406):1004–8. doi:10.1126/science.aat8084

PubMed Abstract | CrossRef Full Text | Google Scholar