Application of Generalized Cauchy Process on Modeling the Long-Range Dependence and Self-Similarity of Sea Surface Chlorophyll Using 23 years of Remote Sensing Data

Understanding the temporal characteristics of sea surface chlorophyll (SSC) is helpful for marine environmental management. This study chose 10 time series of remote daily sea surface chlorophyll products from the European Space Agency during the period from July 29, 1998 to December 31, 2020. A generalized Cauchy model was employed to capture the local and global behaviors of sea surface chlorophyll from a fractal perspective; the fractal dimension D measures the local similarity while the Hurst parameter H measures the global long-range dependence. The generalized Cauchy model was fitted to the empirical autocorrelation function values of each SSC series. The results showed that the sea surface chlorophyll was multi-fractal in both space and time with the D values ranging from 1.0000 to 1.7964 and H values ranging from 0.6757 to 0.8431. Specifically, regarding the local behavior, 9 of the 10 series had low D values (<1.5), representing weak self-similarity; on the other hand, regarding the global behavior, high H values represent strong long-range dependence that may be a general phenomenon of daily sea surface chlorophyll.

Introduction

Sea surface chlorophyll (SSC) is an important bio-indicator, representing the biomass of the phytoplankton in the surface layer of the ocean [1–3]. On one hand, phytoplankton have made significant contributions to capture greenhouse gas from the atmosphere and balance the carbon cycle globally [4,5]; on the other hand, under a suitable living environment condition (such as temperature, nutrients, etc.), the phytoplankton will grow rapidly and cause blooms, leading to the degradation of the water environment and ecosystem corruption [6–8]. Therefore, understanding the evolution and pattern of SSC is of great significance to ocean environmental management.

With the development of remote sensing technology, the sensors equipped on satellites can provide long-term SSC products at a global scale, which is conducive to the studies of SSC. For example, the pattern of global ocean primary production can be investigated at a large scale [9–12]. Likewise, the regional SSC variations were studied using remote sensing data. Yamada et al. [13] employed the Ocean Color and Temperature Scanner (OCTS) and the Sea-Viewing Wide Field of View Sensor (SeaWiFS) remote sensing data to study the SSC variation in the East China Sea and the Sea of Japan and found the interannual variability of the spring bloom and the weak temporal transition of the fall bloom. In the Bohai Sea and the North Yellow Sea of China, Zhai et al. [14] found the SSC exhibited a spatially coherent increasing trend over 2003–2011 and a decreasing trend over 2012–2018 by using Moderate Resolution Imaging Spectroradiometer (MODIS) data; specifically, the decreasing trend was more obvious than the increasing trend. Further, the Ocean Colour Climate Change Initiative (OC-CCI) standard products with locally modified SSC was also used to detect four types of SSC annual cycle in the East China Sea, i.e., the summer bloom, spring and autumn bloom, early spring bloom, and low SSC [15]. In summary, the studies mentioned above only focused on the trends and made simple statistics for exploring the space-time SSC patterns.

Recently, specific SSC variation modeling has been implemented in several studies. He et al. [16] chose the optimal theoretical model (such as Exponential model, Spherical model, Gaussian model, and their combinations) to fit the spatial covariance of the SSC distribution in the Gulf of St. Lawrence, and found that the highest SSC variability occurred in November while it changed a lot during the period from August to November. Despite this, few studies have modeled the temporal variance or pattern of SSC. The long-range correlation (or dependence) of SSC was detected in the South China Sea with time scales ranging from a few weeks to 2 years [17]. However, the long-term mathematical modeling of the long-range dependence (LRD) and self-similarity of SSC is still lacking.

In general, several important parameters are used to characterize the complex behavior and dynamics of a time series, such as the Hurst parameter and the fractal dimension/index. Further, some methodologies have been developed to estimate these two parameters separately. Traditionally, the fractal dimension or index can be estimated by counting the number of level crossings, using increments, or the relationship between power variations and the fractal dimension [18–20]; besides this, some other fractal dimensions, such as number-based fragmentation fractal dimension and mass fractal dimension for soil properties can be calculated as shown in other studies [21–23]. Regarding the Hurst parameter, the variance-plot with various block sizes were fitted to obtain the slope $\beta$ and the Hurst parameter can be calculated subsequently by $\beta =2H-1$; Kettani and Gubner [24] developed a variogram-based method to calculate the Hurst parameter and found the new method was superior to the wavelet method; Li [25] used the generalized fractional Gaussian noise to fit the autocorrelation function (ACF) of the traffic and further obtain the Hurst parameter; moreover, modified multifractal Gaussian noise theory was also developed to calculate the Hurst parameter of the sea level across the study period [26]. Given that the two parameters denote various fractal characteristics of the time series, it is important to seek ways to simultaneously obtain the fractal dimension and Hurst parameter. Luckily, the generalized Cauchy model provides a potential way to achieve this goal. It can be used to model the ACF of the studied time series, and it proves that the two parameters were independent of each other [27]. In the past few decades, the generalized Cauchy process has been successfully applied to model the sea-level fluctuations, teletraffic, and network traffic [27,28].

Given the above considerations, the objective of this work is to use the generalized Cauchy process to model the ACF of remote SSC data and explore the fractal characteristics of SSC, which will benefit local SSC monitoring, controlling, and policy-making.

Methods and Materials

Data Collection

The long-term daily SSC data was collected from the European Space Agency (ESA). It merged remote sensing reflectance (Rrs) from several satellites, including SeaWiFS, MERIS (Medium Resolution Imaging Spectrometer), Aqua-MODIS, VIIRS (Visible and Infrared Imager/Radiometer Suite), and OLCI (Ocean and Land Color Instrument) [29]. Then, the SSC products are generated using Algorithm Theoretical Baseline Document (Optical Classification and Algorithm Blending) [30]. In the present study, the daily SSC products with spatial resolution 1° × 1° were integrated during the period from July 29, 1998 to December 31, 2020 (8,192 days in total), and 10 locations were selected for further analysis, see Figure 1. Of the 10 locations, 7 are located in the Gulf of California (Figure 1B), with 2 and 1 located in the western coastal regions of Madagascar and South Africa, respectively.

FIGURE 1

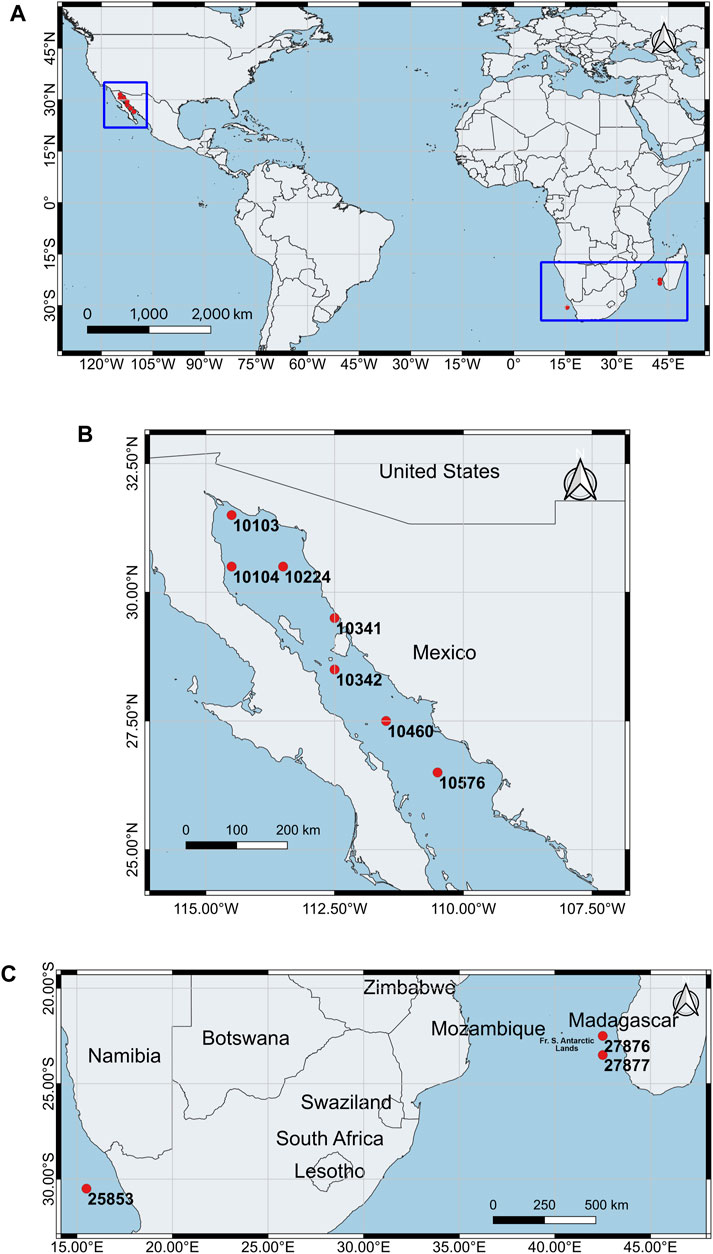
FIGURE 1. 10 sea surface chlorophyll data locations. (A) shows the distribution of the 10 data locations at a global scale, while the zoom-in views of the two rectangles are shown in (B) and (C). The number represents the identity of each data location.

Basic Theories

Long-Range Dependence

Let $x\left(t\right)$ and $r\left(\tau \right)$ denote the time series of the studied natural attribute and its ACF, i.e., $r\left(\tau \right)=E\left[x\left(t\right)x\left(t+\tau \right)\right]$, where E represents the expectation operator. Thus, LRD or long memory is used to depict the situation that the ACF decays slowly with the characteristic as $\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}r\left(\tau \right)d\tau =\infty$ [31–33], i.e., the values of the studied natural attribute with large temporal lag show a strong correlation. Further, the asymptotic form of ACF with LRD can be expressed as Eq. 1 with the help of the Hurst parameter [34].

$\{\begin{array}{c}r\left(\tau \right)\sim c{\tau }^{\beta } \left(\tau \to \infty \right) \\ \beta =2H-2\end{array}$(1a-1b)-1b)

Where the Hurst parameter H ranges from 0.5 to 1 under the LRD condition, representing the global property of the time series $x\left(t\right)$, a larger value of H implies that the LRD is stronger.

Self-Similarity

The ACF is self-similar when it remains the same through aggregating the sub-series of $x\left(t\right)$ with nonoverlapping blocks [35], i.e., part of the time series is locally approximately similar to the entire time series. According to the literature [36,37], the fractal index ($\alpha$) was employed to measure the local self-similarity, as follows:

$\{\begin{array}{c}r\left(0\right)-r\left(\tau \right)\sim c|\tau {|}^{\alpha }\\ D=2-\frac{1}{2}\alpha \end{array}$(2a-2b)-2b)

where $c>0$ and $0<\alpha \le 2$. The fractal dimension, D, belongs to $[\mathrm{1,2})$. A larger value of D means that the local self-similarity of the studied time series is stronger [27].

Generalized Cauchy Process

The generalized Cauchy process is applied when the time series $x\left(t\right)$ and its ACF are of the form of the following equation, subject to $1<\alpha \le 2$ and $\beta \ge 0$ [28,38]:

$C\left(\tau \right)={\psi }^2{\left(1+|\tau {|}^{\alpha }\right)}^{-\frac{\beta }{\alpha }}(3)$

where ${\psi }^2$ is the intensity of $x\left(t\right)$. The following comments discuss features of the two parameters in Eq. 3. Regarding the parameter $\beta$, it defines the dependence of $x\left(t\right)$ by setting $\tau \to \infty$: (a) if $0\le \beta <1$, $\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\left[\underset{\tau \to \infty }{\lim }C\left(\tau \right)\right]d\tau =\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}{\psi }^2|\tau {|}^{-\beta }d\tau =\infty$, i.e., it represents the LRD with respect to $\beta$; (b) if $\beta >1$, $\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}{\left(1+|\tau {|}^{\alpha }\right)}^{-\frac{\beta }{\alpha }}d\tau =\frac{2}{\alpha }B\left(\frac{1}{\alpha },\frac{\beta -\alpha }{\alpha }\right)<\infty$, where B is the beta function, i.e., it represents short-range dependence (SRD). Regarding the parameter $\alpha$, it defines the self-similarity of $x\left(t\right)$ by setting $\tau \to 0$, thus $\underset{\tau \to 0}{\lim }C\left(\tau \right)={\psi }^2|\tau {|}^{\alpha }$ with respect to $\alpha$. In short, the LRD and self-similarity of $x\left(t\right)$ only rely on the parameters $\beta$ and $\alpha$, respectively. In this case, with the definition of Eq. 1b and Eq. 2b, the generalized Cauchy process can be written as

$C\left(\tau \right)={\psi }^2{\left(1+|\tau {|}^{4-2D}\right)}^{-\frac{1-H}{2-D}}(4)$

For modeling purpose, the intensity ${\psi }^2$ can be set to 1, and Eq. 4 becomes

$C\left(\tau \right)={\left(1+|\tau {|}^{4-2D}\right)}^{-\frac{1-H}{2-D}}.(5)$

In this case, the generalized Cauchy process can simultaneously depict the LRD (global property) and self-similarity (local property) of $x\left(t\right)$ by using the two parameters H and D, respectively. Regarding the Hurst parameter H, if $0\le \beta <1$, i.e., $0.5<H<1$, it represents LRD, and the values of ACF remain high even over large temporal lag; whereas if $\beta >1$, i.e., $0<H<0.5$, it represents SRD, and the value of ACF usually decays quickly, e.g., the value of ACF may decline to zero over a lag of several days. With various values of H and D, the ACFs were plotted in Figure 2. It was found that the ACF value of the generalized Cauchy process decreases as the temporal lag $\tau$ increases. Moreover, the ACF value increases when the value of H increases and the value of D is fixed, while the ACF value decreases a little when the value of D increases and the value of H is fixed. Among the six lines shown in the sub-figures, the three blue represent the LRD cases, and three red lines represent the SRD cases. Specifically, when the temporal lag, H value, and D value are equal to 7.2 days, 0.05, and 1.7 respectively, the value of ACF declines to 0.01, representing SRD characteristics; see the dark red line of the bottom right sub-figure in Figure 2. On the other hand, when the temporal lag, H value, and D value are equal to 31 days, 0.75, and 1.1 respectively, the value of ACF is still greater than 0.179, representing LRD characteristics; see the middle blue line of the top left sub-figure in Figure 2.

FIGURE 2

FIGURE 2. Simple examples of the generalized Cauchy model with various values of D and H.

Autocorrelation Function Fitting Process

The original time series of SSC at each location was divided equally into 16 sub-series with no overlapping cases, each containing 512 data points. Considering that the value of the autocorrelation function may decay to zero with a 1-month temporal lag in some parts of the world [39,40], the theoretical autocorrelation function values for temporal lags between 0 and 32 was calculated by averaging the 16 autocorrelation functions of each sub-series. Then, the generalized Cauchy model (Eq. 5) was employed to fit each of the theoretical autocorrelation function values using the “lsqnonlin” function embedded in MATLAB software. Then, the fractal dimension D and the Hurst parameter H were estimated. The fitting performance of the generalized Cauchy model was evaluated by R², MAE, and RMSE, as follows:

$R^2=1-\frac{S{S}_{res}}{S{S}_{tot}}=1-\frac{{{\displaystyle \sum }}^{\text{}}{\left[Y\left(\tau \right)-\widehat{Y}\left(\tau \right)\right]}^2}{{{\displaystyle \sum }}^{\text{}}{\left[Y\left(\tau \right)-\overline{Y}\right]}^2}(6)$

$MAE=\frac{1}{n}{\displaystyle \sum }_{\tau =1}^n\left|Y\left(\tau \right)-\widehat{Y}\left(\tau \right)\right|(7)$

$RMSE=\sqrt{\frac{{\Sigma }_{\tau =1}^n{\left[Y\left(\tau \right)-\widehat{Y}\left(\tau \right)\right]}^2}{n}}(8)$

where $Y\left(\tau \right)$ and $\widehat{Y}\left(\tau \right)$ represent the empirical ACF value and fitted ACF value at temporal lag τ respectively, $\overline{Y}$ represents the mean value of the ACF series, $n$ represents the length of the series, and $S{S}_{res}$ and $S{S}_{tot}$ represents the sum of squared residuals and the sum of squares of deviation from mean respectively.

Results

Descriptive Statistics

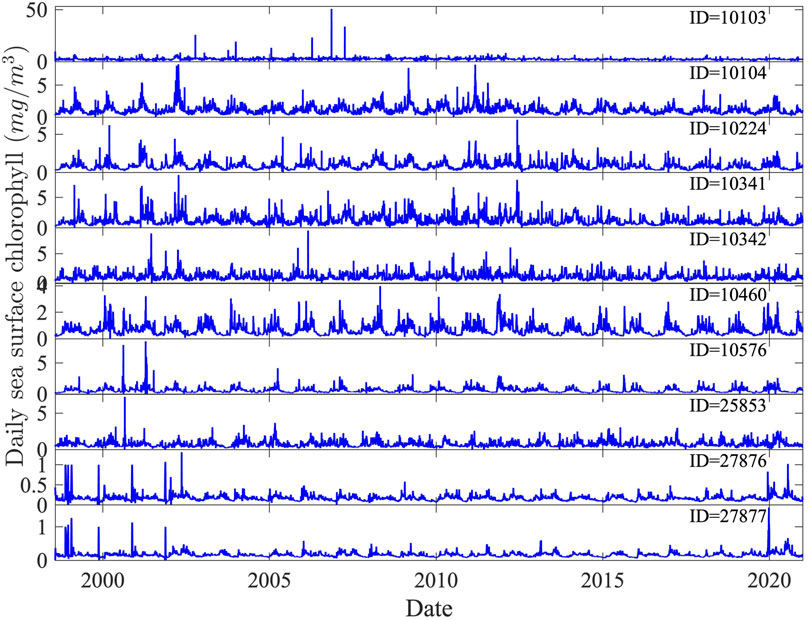
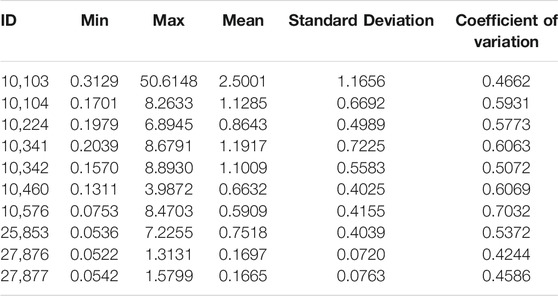
The proportion of missing daily SSC data from ESA at the 10 locations ranges from 8.02 to 11.56% over the entire period. Given that the missing values were discretely distributed in each SSC time series, they were interpolated by using the “spline” function in MATLAB software for further analysis. The SSC time series with full length (including 8192 SSC data) at the considered 10 locations are plotted in Figure 3 and the corresponding descriptive statistical results are presented in Table 1. The statistical results indicate that the SSC has the highest range (i.e., from 0.3129 to 50.6148 mg/m³) in the location with ID 10103 during the studied period; while the values of SSC at the other six locations around the Mexico offshore regions range from 0.0753 to 8.8930 mg/m³. On the other hand, similar ranges (i.e., from 0.0522 to 1.5799 mg/m³) are found in the two locations around the offshore of Madagascar. The values of SSC at the last location with ID 25853 range from 0.0536 to 7.2255 mg/m³.

FIGURE 3

FIGURE 3. Sea surface chlorophyll time series at the 10 chosen locations.

TABLE 1

TABLE 1. Descriptive statistics of the considered 10 time series of SSC.

Generalized Cauchy Process Fitting Results

Figure 4 shows the theoretical autocorrelation values and the corresponding fitted generalized Cauchy model with the fitting performance at each of the 10 daily SSC series. Our findings are as follows: 1) The autocorrelation functions of SSC can be well fitted by the generalized Cauchy model with R² ranging from 0.9469 to 0.9875, MAE ranging from 0.0143 to 0.0358, and RMSE ranging from 0.0187 to 0.0434. 2) The values of the fractal dimension D and the Hurst parameter H vary at different locations. 3) A high value for the fractal dimension D (1.7964) with strong self-similarity was only found at the location with ID = 10,103, while the D values at other locations are lower than 1.5 and 5 of the 10 locations have D values approximately equal to 1. This shows that most of the 10 daily SSC series have weak self-similarity. 4) The values of the Hurst parameter H of the 10 daily SSC series range from 0.6757 to 0.8431, indicating that the daily SSC series at the 10 locations have strong long-range dependence.

FIGURE 4

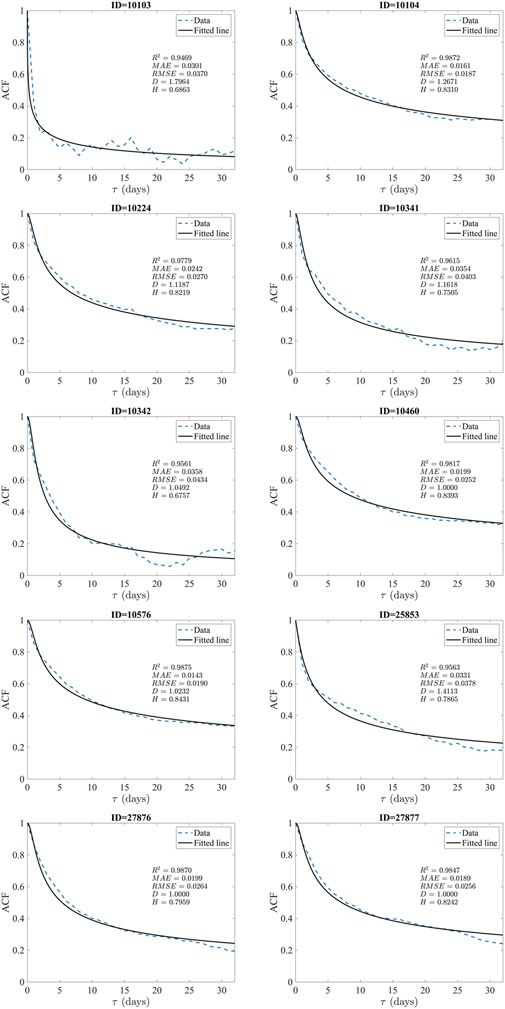
FIGURE 4. The empirical autocorrelation function values (dash blue line) and the fitted generalized Cauchy model (black line) for each of the 10 data points.

Discussion

The present work employed the generalized Cauchy process to model the ACF of daily remote SSC data during a 23-year period and good performance of the fitting was obtained, indicating that the SSC in the 10 chosen locations follows a heavy-tailed distribution [41]. Compared to the generalized Gaussian noise model, the outstanding ability of the generalized Cauchy model is that it can simultaneously estimate both independent variables (Hurst parameter and fractal dimension). This means that it can describe the global correlation and local self-similarity of the considered natural attribute [27,42], such as the SSC in the present work. To the best of my knowledge, the present effort is one of the earliest studies in obtaining the LRD and self-similarity of the SSC in view of fractal statistics.

Impacts of Environmental Factors on the Fractal Characteristics of Sea Surface Chlorophyll

Relatively low self-similarity and high LRD of the SSC series at the 10 locations can be summarized. A rather different case was found in a lake study, i.e., the chlorophyll-a was autocorrelated over lags of five or 6 days [43], indicating SRD. The nutrients and aquatic environment (light, temperature, salinity, etc.) impact the algae growth and further influence the SSC variability [44–48]. With the continuous variation of these factors, the variation of SSC across time is also smooth according to the algae growth, causing the weak irregularity characteristics with low values of the fractal dimension and strong LRD with high values of the Hurst parameter. This phenomenon leads to the empirical values of ACF (blue dash line shown in Figure 4) being slightly higher than the theoretical values of ACF (black line shown in Figure 4) with the temporal lags between 2 and 10 days at most locations. However, with the temporal lag increasing from 10 to 25 days, the empirical values become smaller than the theoretical values, because the SSC may be influenced by the global climatic dynamics, such as the Southern Pacific Oscillation Index [49], which is different from algae’s own growth condition. Moreover, there may be another situation that algae blooms with enough nutrient inputs [50], leading to extremely high SSC values, e.g., the SSC value increases rapidly and peaks for one or 2 days (as some peaks shown in Figure 3); and that may be the reason that the value of the fractal dimension is the highest among the 10 series, i.e., D = 1.7964 with the highest maximum SSC value and standard deviation across the study period. On the other hand, the values of the fractal dimension and Hurst parameter varied at various locations, indicating that the environmental conditions are rather different from each other. Moreover, various species of algae may exist at various locations and their growth response to the environmental conditions are rather different [51,52]. Compared to the values of the fractal dimension (varies from 1.7244 to 1.7838) of SSC in the Chesapeake Bay [45], the values of the fractal dimension obtained in the current study are rather low; this may due to the fact that the river discharge and the nutrients it carries are not as large as the rivers (e.g., Susquehanna River and Potomac River) that run into the Chesapeake Bay. However, the values of the Hurst parameters in the current study are greater than that in the Chesapeake Bay study with LRD characteristics, indicating that a large nutrient load in the Chesapeake Bay may lead to weak LRD. Therefore, the LRD may be a general feature of SSC variations in oceans.

Besides this, the aquatic environment will also influence the behavior of the zooplankton, e.g., warm waters will favor the consumption of the zooplankton, causing the reduction of SSC [53–55]. On the other hand, the upwelling system and surface currents around the coastal areas play important roles in shaping the distribution of zooplankton and further influence the variation of SSC [56]. The upwelling system on the California coast shows seasonal variabilities and can be summarized into four types: “Winter Storms” season (Dec-Jan-Feb), “Upwelling Transition” period (Mar and Jun), “Peak Upwelling” season (Apr-May), “Upwelling Relaxation” season (Jul-Aug-Sep), and “Winter Transition” season (Oct-Nov), so the impacts of upwelling system on the SSC are also seasonally continuous. That may be one of the reasons that SSC has LRD characteristic [57].

Long-Range Dependence of Sea Surface Chlorophyll at the Studied Locations

The present study employed ACF to describe the fractal characteristics (especially the long-range dependence) of SSC with temporal lags of 32 days. The empirical values of the ACF at the 10 studied locations range from 0.1160 to 0.3351, and the mean and standard deviation of the empirical values are 0.2319 and 0.0764, respectively. These results show that strong long-range dependence can be detected within a temporal lag of 1 month. Robles-Tamayo et al. [49] detected seasonal, semi-annual, and annual cycles of SSC in the Gulf of California using the Level 3 products of MODIS remote sensing data. In other words, the SSC variation may experience peak and valley values in a season (3 months). Moreover, the SSC values of the four seasons vary a lot with high values of the standard deviation. Regarding the seasonal variation, Escalante-Almazán [58] found that the mean values of SSC in the central gulf were 1.09, 1.20, 0.44, and 0.60 mg/m³ for winter, spring, summer, and autumn, respectively. The large variation between seasons suggests that the SSC may not have long-range dependence at an annual or semi-annual scale. On the other hand, in the warm period the mean ± standard deviation values of SSC in the south, central midriff islands, and north sub-regions of the Gulf of California are 0.79 ± 0.89, 0.55 ± 0.37, 1.19 ± 0.83, and 0.63 ± 0.39 mg/m³ respectively, and in the cold period, the values are 2.05 ± 1.20, 1.84 ± 0.73, 2.80 ± 1.40, and 1.50 ± 0.61 mg/m³ respectively [49]. The large standard deviations represent large variations of SSC, indicating that the SSC may not have large LRD at a semi-annual or annual scale. To test the LRD of SSC at a seasonal scale, the empirical values of ACF at the 10 studied locations were calculated with a temporal lag of 128 days. The results show that the value of empirical ACF at the 10 locations first reached 0 at the temporal lags of 49, 75, 89, 59, 47, 85, 89, 69, 70, and 67 days, respectively. Otherwise, with large temporal lags, the values of ACF will fluctuate around zero. Hence, long-range dependence at a seasonal scale (i.e., with temporal lag larger than 90 days) is relatively weak compared to the monthly scale.

Comparisons to Previous Works

Comparisons between the current study and previous studies were conducted as follows. Some ACFs of teletraffic was rather high, above 0.98 with even 128 days lag [27], but the ACF value of SSC in the current study fall below 0.5 with 31 days lag. This may be the reason why very high values of the Hurst parameter (larger than 0.99) were detected with teletraffic rather than SSC. In addition, the values of the fractal dimension of teletraffic were much larger than that of SSC, demonstrating that stronger self-similarity was found in teletraffic series than SSC. This may be due to the fact that values for teletraffic are more random in occurrence while the values for SSC are more like a continuous series associated with several environmental factors mentioned above. In another study [28], the generalized Cauchy process was used to model the ACF of sea level fluctuations with a temporal resolution of 1 h, and found that the value of the fractal dimension was approximately equal to 1 at several locations while the most of them were larger than 1.8; the values of Hurst parameter were larger than 0.98. Interestingly, the locations with low fractal dimension values are located in the Gulf of Mexico, which is similar to the seven locations studied in the current study, i.e., the weak self-similarity may occur in a stable environment.

Limitations and Future Work

Certain limitations of the current study should be acknowledged: 1) Although there may be a relationship between the fractal characteristics of SSC and the living environment, rigorous proof and statistical analysis was not conducted in the current study due to lack of data. Therefore, future work can focus on quantitatively exploring the impacts of nutrients and temperature on the fractal dimension or Hurst parameters of SSC. 2) Even SSC products with high spatiotemporal coverage were used in the current study, there still exist missing values from other locations. Hence, spatiotemporal interpolation methods should be employed to obtain a more complete remote SSC dataset for mapping the global fractal dimension or Hurst parameter of SSC, such as the Bayesian maximum entropy approach [59–61], so that the spatial pattern of the fractal dimension and Hurst parameter can be further studied. 3) Taking into consideration the stochastic differential equations, the evolution pattern (or law) of SSC can be further explored, such as the fractional Brownian motion pattern [62,63].

Conclusion

The present study applied a novel generalized Cauchy model to depict the variations of SSC and good performance was obtained. The fractal characteristics of the SSC vary at different locations in terms of the fractal dimension and Hurst parameter; weak self-similarity was found in most locations with low values of the fractal dimension while strong LRD was detected across all locations with reactively high value of the Hurst parameter.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JH contributed to conception and design of the study, organized the database, performed the statistical analysis, wrote the first draft of the manuscript. The author contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is supported by the China Postdoctoral Science Foundation (2020M681825) and National Natural Science Foundation of China (No. 42171398).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

I would like to thank Prof. Ming Li for his guidance in modeling the generalized Cauchy process and Chen, Bairu for his assistant in improving the manuscript.

References

1. Hayashida H, Matear RJ, Strutton PG. Background Nutrient Concentration Determines Phytoplankton Bloom Response to Marine Heatwaves. Glob Change Biol (2020) 26:4800–11. doi:10.1111/gcb.15255

CrossRef Full Text | Google Scholar

2. Liu C, Sun Q, Xing Q, Wang S, Tang D, Zhu D, et al. Variability in Phytoplankton Biomass and Effects of Sea Surface Temperature Based on Satellite Data From the Yellow Sea, China. Plos One (2019) 14:e0220058. doi:10.1371/journal.pone.0220058

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Shafeeque M, Sathyendranath S, George G, Balchand AN, Platt T. Comparison of Seasonal Cycles of Phytoplankton Chlorophyll, Aerosols, Winds and Sea-Surface Temperature off Somalia. Front Mar Sci (2017) 4:386. doi:10.3389/fmars.2017.00386

CrossRef Full Text | Google Scholar

4. Chu S. Carbon Capture and Sequestration. Science (2009) 325:1599. doi:10.1126/science.1181637

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Nair A, Sathyendranath S, Platt T, Morales J, Stuart V, Forget M-H, et al. Remote Sensing of Phytoplankton Functional Types. Remote Sensing Environ (2008) 112:3366–75. doi:10.1016/j.rse.2008.01.021

CrossRef Full Text | Google Scholar

6. Brooks BW, Lazorchak JM, Howard MDA, Johnson M-VV, Morton SL, Perkins DAK, et al. Are Harmful Algal Blooms Becoming the Greatest Inland Water Quality Threat to Public Health and Aquatic Ecosystems? Environ Toxicol Chem (2016) 35:6–13. doi:10.1002/etc.3220

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Riebesell U, Aberle-Malzahn N, Achterberg EP, Algueró-Muñiz M, Alvarez-Fernandez S, Arístegui J, et al. Toxic Algal Bloom Induced by Ocean Acidification Disrupts the Pelagic Food Web. Nat Clim Change (2018) 8:1082–6. doi:10.1038/s41558-018-0344-1

CrossRef Full Text | Google Scholar

8. Watson SB, Whitton BA, Higgins SN, Paerl HW, Brooks BW, Wehr JD. Harmful Algal Blooms. In: JD Wehr, RG Sheath, and JP Kociolek, editors. Freshwater Algae of North America (Second Edition), Aquatic Ecology. Boston: Academic Press (2015) p. 873–920. doi:10.1016/B978-0-12-385876-4.00020-7

CrossRef Full Text | Google Scholar

9. Eppley RW, Stewart E, Abbott MR, Heyman U. Estimating Ocean Primary Production From Satellite Chlorophyll. Introduction to Regional Differences and Statistics for the Southern California Bight. J Plankton Res (1985) 7:57–70. doi:10.1093/plankt/7.1.57

CrossRef Full Text | Google Scholar

10. Gregg WW, Rousseaux CS. Global Ocean Primary Production Trends in the Modern Ocean Color Satellite Record (1998-2015). Environ Res Lett (2019) 14:124011. doi:10.1088/1748-9326/ab4667

CrossRef Full Text | Google Scholar

11. Longhurst A, Sathyendranath S, Platt T, Caverhill C. An Estimate of Global Primary Production in the Ocean From Satellite Radiometer Data. J Plankton Res (1995) 17:1245–71. doi:10.1093/plankt/17.6.1245

CrossRef Full Text | Google Scholar

12. Platt T, Sathyendranath S. Oceanic Primary Production: Estimation by Remote Sensing at Local and Regional Scales. Science (1988) 241:1613–20. doi:10.1126/science.241.4873.1613

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Yamada K, Ishizaka J, Nagata H. Spatial and Temporal Variability of Satellite Primary Production in the Japan Sea From 1998 to 2002. J Oceanogr (2005) 61:857–69. doi:10.1007/s10872-006-0005-2

CrossRef Full Text | Google Scholar

14. Zhai F, Wu W, Gu Y, Li P, Song X, Liu P, et al. Interannual-Decadal Variation in Satellite-Derived Surface Chlorophyll-A Concentration in the Bohai Sea Over the Past 16 Years. J Mar Syst (2021) 215:103496. doi:10.1016/j.jmarsys.2020.103496

CrossRef Full Text | Google Scholar

15. Hao Q, Chai F, Xiu P, Bai Y, Chen J, Liu C, et al. Spatial and Temporal Variation in Chlorophyll a Concentration in the Eastern China Seas Based on a Locally Modified Satellite Dataset. Estuarine, Coastal Shelf Sci (2019) 220:220–31. doi:10.1016/j.ecss.2019.01.004

CrossRef Full Text | Google Scholar

16. He J, Chen Y, Wu J, Stow DA, Christakos G. Space-Time Chlorophyll-A Retrieval in Optically Complex Waters that Accounts for Remote Sensing and Modeling Uncertainties and Improves Remote Estimation Accuracy. Water Res (2020) 171:115403. doi:10.1016/j.watres.2019.115403

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhan H, Shi P, Mao Q, Zhang T. Long-Range Correlations in Remotely Sensed Chlorophyll in the South China Sea. Chin Sci Bull (2006) 51:45–9. doi:10.1007/s11434-006-9045-7

CrossRef Full Text | Google Scholar

18. Feuerverger A, Hall P, Wood ATA. Estimation of Fractal Index and Fractal Dimension of a Gaussian Process by Counting the Number of Level Crossings. J Time Ser Anal (1994) 15:587–606. doi:10.1111/j.1467-9892.1994.tb00214.x

CrossRef Full Text | Google Scholar

19. Gneiting T, Ševčíková H, Percival DB. Estimators of Fractal Dimension: Assessing the Roughness of Time Series and Spatial Data. Stat Sci (2012) 27:247–77. doi:10.1214/11-sts370

CrossRef Full Text | Google Scholar

20. Kent JT, Wood ATA. Estimating the Fractal Dimension of a Locally Self-Similar Gaussian Process by Using Increments. J R Stat Soc Ser B Methodol (1997) 59:679–99. Available at: https://www.jstor.org/stable/2346018

Google Scholar

21. Rieu M, Sposito G. Fractal Fragmentation, Soil Porosity, and Soil Water Properties: I. Theory. Soil Sci Soc America J (1991) 55:1231–8. doi:10.2136/sssaj1991.03615995005500050006x

CrossRef Full Text | Google Scholar

22. Tyler SW, Wheatcraft SW. Fractal Scaling of Soil Particle-Size Distributions: Analysis and Limitations. Soil Sci Soc America J (1992) 56:362–9. doi:10.2136/sssaj1992.03615995005600020005x

CrossRef Full Text | Google Scholar

23. Young IM, Crawford JW. The Fractal Structure of Soil Aggregates: its Measurement and Interpretation. J Soil Sci (1991) 42:187–92. doi:10.1111/j.1365-2389.1991.tb00400.x

CrossRef Full Text | Google Scholar

24. Kettani H, Gubner JA. A Novel Approach to the Estimation of the Hurst Parameter in Self-Similar Traffic. In: 27th Annual IEEE Conference on Local Computer Networks, 2002. Proceedings. LCN 2002. Presented at the 27th Annual IEEE Conference on Local Computer Networks, 2002. Proceedings. Piscataway: LCN 2002. (2002). p. 160–5.

Google Scholar

25. Li M. Generalized Fractional Gaussian Noise and its Application to Traffic Modeling. Physica A: Stat Mech its Appl (2021) 579:126138. doi:10.1016/j.physa.2021.126138

CrossRef Full Text | Google Scholar

26. Li M. Modified Multifractional Gaussian Noise and its Application. Phys Scr (2021) 96:125002. doi:10.1088/1402-4896/ac1cf6

CrossRef Full Text | Google Scholar

27. Li M. Long-Range Dependence and Self-Similarity of Teletraffic With Different Protocols at the Large Time Scale of Day in the Duration of 12 years: Autocorrelation Modeling. Phys Scr (2020) 95:065222. doi:10.1088/1402-4896/ab82c4

CrossRef Full Text | Google Scholar

28. Li M, Li J-Y. Generalized Cauchy Model of Sea Level Fluctuations With Long-Range Dependence. Physica A: Stat Mech its Appl (2017) 484:309–35. doi:10.1016/j.physa.2017.04.130

CrossRef Full Text | Google Scholar

29.ESA. Alfresco» D4.2 - Product User Guide for v5.0 dataset.Pdf. Plymouth: Eur. Space Agency (2020). Available from https://docs.pml.space/share/s/okB2fOuPT7Cj2r4C5sppDg (Accessed June 26, 2021).

30.ESA. Alfresco » OC-CCI_D2.1_ATBC_OCAB_v1.0.Pdf. Plymouth: Eur. Space Agency (2020). Available from https://docs.pml.space/share/s/fpEzM3HNR6CmdiclAnDtrA (accessed June 26, 2021).

31. Beran J. Statistics for Long-Memory Processes. Boca Raton: Routledge (2017). doi:10.1201/9780203738481

CrossRef Full Text

32. Beran J. Statistical Methods for Data With Long-Range Dependence. Stat Sci (1992) 7:404–16. doi:10.1214/ss/1177011122

CrossRef Full Text | Google Scholar

33. Beran J, Feng Y, Ghosh S, Kulik R. Long-memory Processes. Berlin, Heidelberg: Springer Berlin Heidelberg (2013) doi:10.1007/978-3-642-35512-7

CrossRef Full Text

34. Hurst HE. Long-Term Storage Capacity of Reservoirs. T Am Soc Civ Eng (1951) 116:770–99. doi:10.1061/taceat.0006518

CrossRef Full Text | Google Scholar

35. Crovella ME, Bestavros A. Self-Similarity in World Wide Web Traffic: Evidence and Possible Causes. Ieee/acm Trans Networking (1997) 5:835–46. doi:10.1109/90.650143

CrossRef Full Text | Google Scholar

36. Hall P. On the Effect of Measuring a Self-Similar Process. SIAM J Appl Math (1995) 55:800–8. doi:10.1137/s0036139992236566

CrossRef Full Text | Google Scholar

37. Hall P, Wood A. On the Performance of Box-Counting Estimators of Fractal Dimension. Biometrika (1993) 80:246–51. doi:10.1093/biomet/80.1.246

CrossRef Full Text | Google Scholar

38. Li M. Multi-Fractional Generalized Cauchy Process and its Application to Teletraffic. Physica A: Stat Mech its Appl (2020) 550:123982. doi:10.1016/j.physa.2019.123982

CrossRef Full Text | Google Scholar

39. Uz B, Yoder J. High Frequency and Mesoscale Variability in SeaWiFS Chlorophyll Imagery and its Relation to Other Remotely Sensed Oceanographic Variables. Deep Sea Res Part Topical Stud Oceanography (2004) 51:1001–17. doi:10.1016/s0967-0645(04)00097-9

CrossRef Full Text | Google Scholar

40. Feng J, Durant JM, Stige LC, Hessen DO, Hjermann DØ, Zhu L, et al. Contrasting Correlation Patterns Between Environmental Factors and Chlorophyll Levels in the Global Ocean. Glob Biogeochem. Cycles (2015) 29:2095–107. doi:10.1002/2015gb005216

CrossRef Full Text | Google Scholar

41. Li M. Fractal Time Series-A Tutorial Review. Math Probl Eng (2010) 2010:1–26. doi:10.1155/2010/157264

CrossRef Full Text | Google Scholar

42. Liu H, Song W, Zio E. Generalized Cauchy Difference Iterative Forecasting Model for Wind Speed Based on Fractal Time Series. Nonlinear Dyn (2021) 103:759–73. doi:10.1007/s11071-020-06150-z

CrossRef Full Text | Google Scholar

43. Malkin SY, Silsbe GM, Smith REH, Howell ET. A Deep Chlorophyll Maximum Nourishes Benthic Filter Feeders in the Coastal Zone of a Large Clear lake. Limnol Oceanogr (2012) 57:735–48. doi:10.4319/lo.2012.57.3.0735

CrossRef Full Text | Google Scholar

44. Dodds WK. Nutrients and the “Dead Zone”: the Link Between Nutrient Ratios and Dissolved Oxygen in the Northern Gulf of Mexico. Front Ecol Environ (2006) 4:211–7. doi:10.1890/1540-9295(2006)004[0211:natdzt]2.0.co;2

CrossRef Full Text | Google Scholar

45. He J, Christakos G, Wu J, Li M, Leng J. Spatiotemporal BME Characterization and Mapping of Sea Surface Chlorophyll in Chesapeake Bay (USA) Using Auxiliary Sea Surface Temperature Data. Sci Total Environ (2021) 794:148670. doi:10.1016/j.scitotenv.2021.148670

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Lee HS, Lee JHW. Continuous Monitoring of Short Term Dissolved Oxygen and Algal Dynamics. Water Res (1995) 29:2789–96. doi:10.1016/0043-1354(95)00126-6

CrossRef Full Text | Google Scholar

47. Rhee G-Y. Effects of N:P Atomic Ratios and Nitrate Limitation on Algal Growth, Cell Composition, and Nitrate Uptake 1. Limnol Oceanogr (1978) 23:10–25. doi:10.4319/lo.1978.23.1.0010

CrossRef Full Text | Google Scholar

48. Singh SP, Singh P. Effect of Temperature and Light on the Growth of Algae Species: A Review. Renew Sustainable Energ Rev (2015) 50:431–44. doi:10.1016/j.rser.2015.05.024

CrossRef Full Text | Google Scholar

49. Robles-Tamayo CM, García-Morales R, Valdez-Holguín JE, Figueroa-Preciado G, Herrera-Cervantes H, López-Martínez J, et al. Chlorophyll a Concentration Distribution on the Mainland Coast of the Gulf of California, Mexico. Remote Sensing (2020) 12:1335. doi:10.3390/rs12081335

CrossRef Full Text | Google Scholar

50. Damar A, Prismayanti AD, Rudianto BY, Ramli A, Kurniawan F. Algae Bloom Phenomenon in Jakarta Bay as Symptoms of Severe Eutrophication: Monitoring Results of 2014-2016. IOP Conf Ser Earth Environ Sci (2021) 744:012009. doi:10.1088/1755-1315/744/1/012009

CrossRef Full Text | Google Scholar

51. Butterwick C, Heaney SI, Talling JF. Diversity in the Influence of Temperature on the Growth Rates of Freshwater Algae, and its Ecological Relevance. Freshw Biol (2005) 50:291–300. doi:10.1111/j.1365-2427.2004.01317.x

CrossRef Full Text | Google Scholar

52. Righetti D, Vogt M, Gruber N, Psomas A, Zimmermann NE. Global Pattern of Phytoplankton Diversity Driven by Temperature and Environmental Variability. Sci Adv (2019) 5:eaau6253. doi:10.1126/sciadv.aau6253

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Chou W-R, Fang L-S, Wang W-H, Tew KS. Environmental Influence on Coastal Phytoplankton and Zooplankton Diversity: a Multivariate Statistical Model Analysis. Environ Monit Assess (2012) 184:5679–88. doi:10.1007/s10661-011-2373-3

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Fernandes LDd. A, Quintanilha J, Monteiro-Ribas W, Gonzalez-Rodriguez E, Coutinho R. Seasonal and Interannual Coupling Between Sea Surface Temperature, Phytoplankton and Meroplankton in the Subtropical South-Western Atlantic Ocean. J Plankton Res (2012) 34:236–44. doi:10.1093/plankt/fbr106

CrossRef Full Text | Google Scholar

55. George JA, Lonsdale DJ, Merlo LR, Gobler CJ. The Interactive Roles of Temperature, Nutrients, and Zooplankton Grazing in Controlling the winter-spring Phytoplankton Bloom in a Temperate, Coastal Ecosystem, Long Island Sound. Limnol Oceanogr (2015) 60:110–26. doi:10.1002/lno.10020

CrossRef Full Text | Google Scholar

56. Messié M, Chavez FP. Nutrient Supply, Surface Currents, and Plankton Dynamics Predict Zooplankton Hotspots in Coastal Upwelling Systems. Geophys Res Lett (2017) 44:8979–86. doi:10.1002/2017gl074322

CrossRef Full Text | Google Scholar

57. Walter RK, Armenta KJ, Shearer B, Robbins I, Steinbeck J. Coastal Upwelling Seasonality and Variability of Temperature and Chlorophyll in a Small Coastal Embayment. Continental Shelf Res (2018) 154:9–18. doi:10.1016/j.csr.2018.01.002

CrossRef Full Text | Google Scholar

58. Escalante-Almazán F. Temporal and Spatial Variation of Sea Surface Temperature, Chlorophyll a, and Primary Productivity in the Gulf of California. CiencMar (2013) 39:203–15. doi:10.7773/cm.v39i2.2233

CrossRef Full Text | Google Scholar

59. Christakos G. Spatiotemporal Random fields: Theory and Applications. Amsterdam: Elsevier (2017).

60. He J, Kolovos A. Bayesian Maximum Entropy Approach and its Applications: a Review. Stoch Environ Res Risk Assess (2018) 32:859–77. doi:10.1007/s00477-017-1419-7

CrossRef Full Text | Google Scholar

61. Wu J, He J, Christakos G. Quantitative Analysis and Modeling of Earth and Environmental Data. Amsterdam: Elsevier (2021). In press.

62. Heydari MH, Mahmoudi MR, Shakiba A, Avazzadeh Z. Chebyshev Cardinal Wavelets and Their Application in Solving Nonlinear Stochastic Differential Equations With Fractional Brownian Motion. Commun Nonlinear Sci Numer Simulation (2018) 64:98–121. doi:10.1016/j.cnsns.2018.04.018

CrossRef Full Text | Google Scholar

63. Heydari MH, Avazzadeh Z, Mahmoudi MR. Chebyshev Cardinal Wavelets for Nonlinear Stochastic Differential Equations Driven With Variable-Order Fractional Brownian Motion. Chaos, Solitons & Fractals (2019) 124:105–24. doi:10.1016/j.chaos.2019.04.040

CrossRef Full Text | Google Scholar