Spin Seebeck Effect in a Hybridized Quantum-Dot/Majorana-Nanowire With Spin Heat Accumulation

Properties of spin Seebeck effect (SSE) in a quantum dot (QD) connected to a topological superconductor or semiconductor nanowire with strong spin-orbit interaction are theoretically studied by the noneqilibrium Green’s function method combined with Dyson equation technique. At low temperatures, Majorana zero modes (MZMs) are prepared at the ends of topological superconductor or semiconductor nanowire, and are hybridized to the QD with spin-dependent strength. We consider that the QD is coupled to two leads in the presence of spin heat accumulation (SHA), i.e., spin-dependent temperature in the leads. We find that the thermopower is spin-polarized when the hybridization strength between the QD and one mode of the MZMs depends on electron spin direction, and its spin-polarization can be effectively adjusted by changing the magnitude of SHA. By proper variation of the spin-polarization of the QD-MZM hybridization strength, magnitude of the SHA, dot level, or the direct coupling between the MZMs, 100% spin-polarized or pure thermopower can be generated. Our results may find real usage in high efficiency spintronic devices or detection of the MZMs, which are under current extensive study. The present model is within the reach of current nano-technologies and may by used in high efficiency spin caloritronics devices.

1 Introduction

In the last decades, generating and manipulating spin current in closed circuits or spin bias in open ones by thermal bias have been successfully realized in experiments. This interdisciplinary subject of thermoelectric effect and spintronics is referred to as spin caloritronics aiming at spin control in terms of thermal means [1, 2]. In the usual thermoelectric effect, the Seebeck effect known as generation of electrical current or bias voltage in response to a temperature difference between two ends of a system is the most frequently investigated issue [3, 4]. The measured quantity is the thermopower S = ∑_σS_σ with S_σ = −ΔV_σ/ΔT the spin-resolved one denoting induced spin bias voltage ΔV_σ by a temperature gradient ΔT. In spin caloritronics, the counterpart of Seebeck effect is the spin Seebeck effect (SSE) [5]. It refers to the generation of pure spin current in the absence of charge electrical current, or spin bias denoting spin-resolved chemical potentials. Since the interaction strength between electron spins is much weaker as compared to the electrostatic force, and then the SSE suggests a possibility of high-efficiency and low-energy nano-scale thermoelectric devices. It is also promising in the detection of small temperature difference in low-dimensional systems [5], and has been extensively investigated in the fields of spin current rectifier [6], magnetic heat valves [7], quantum cooling [8], thermal spin-transfer torque [9], thermovoltaic transistor [10], thermal logic gates and thermal memory for quantum information processing [11]. After the pioneering work of K. Uchida in 2008 [5], the SSE has been continuously observed in various materials [12–21], including magnetic metals, ferromagnetic insulators, ferromagnetic metals, ferromagnetic semiconductors, nonmagnetic materials with a magnetic field, paramagnetic materials, antiferromagnetic materials, and even topological insulators.

In the definition of spin-dependent thermopower S_σ, the generated spin bias voltage ΔV_σ denotes the split mechanical potentials as $\mathrm{\Delta }{V}_{\sigma }=\hslash ({\mu }_{\sigma }-{\mu }_{\bar{\sigma }})/2$, and the spin-up and spin-down electrons are individually at different states μ_σ due to the existence of thermal bias ΔT. The spin bias is the driving force for electron transport and induces spin-polarized currents. In fact, from the Fermi-Dirac function f_σ = 1/{ exp [(ɛ − μ_σ)/k_BT_σ] + 1}, one can expect that the driving force for spin-dependent electronic transport to come from a spin-dependent electrons’ temperatures T_σ, whose function is similar to the spin bias μ_σ. This is called as spin heat accumulation (SHA) realizable by an electric current from a ferromagnet into a nonmagnetic material [7, 22–26]. Usually, the SHA emerges with the accompany of spin bias voltage and is quite weak as compared to the latter. In recent experiment [24], the magnitude of SHA can be enhanced to as high as about several kelvins.

Very recently, thermoelectric effect [27–31] was proposed to be used for detecting Majorana zero modes (MZMs), a kind of quasi-particles of Majorana fermions having zero energy that can be realized in nano-scale topological superconductors [32, 33]. They are of their own antiparticle and charge neutral [32–35], and have potential applications in fault-tolerant quantum computation and energy-saving spintronic devices [36]. Due to their exotic zero-energy, chargeless properties, the detection of them is the central topic in studies relating to MZMs. Currently, the most important detection means is the electrical tunnel spectroscopy by applying a voltage ΔV across the nanowire with MZMs and to observe the associate current. The MZMs induce a zero-bias anomaly in the differential of electrical conductance [32, 33, 37], which is viewed as the evidence of MZMs. But this zero-bias anomaly in the conductance may also induced by some other mechanisms, for example, the Kondo effect [35]. Therefore, some other schemes, including the thermoelectric effect tuned by MZMs, were then continuously proposed in recent years. It was proved that the electron-hole symmetric nature of the MZMs which results in null thermoelectric effect can be effectively broken in a structure with a quantum dot (QD) coupled to topological superconductor hosting MZMs [27, 28]. Large value of thermopower satisfying Mott formula was proposed for detecting temperature of MZMs [19]. Such a system is possible to deduce information of the dissipative decay of MZMs [29]. In a two-terminal structure with a QD sandwiched between two leads and side-coupled to MZMs, a global sign reversion of the thermopower induced by MZMs was studied by López et. al. Such a phenomenon is caused by the direct MZM-MZM coupling [28]. The sign change and abnormal enhancement of thermopower by coupling between the QD and MZMs were also studied in some subsequent works [30, 31].

In our recent work, we have proposed a scheme composing of a QD side-coupled to MZMs to detect the SHA in terms of sign change of thermopower [38]. The mechanism is that the thermopowers of different spin components will change signs at different temperatures due to the QD-MZMs coupling. The SHA denoting spin-dependent temperature then can be inferred by the change of spin-polarized thermopower varying with respect to the magnitude of SHA. This task can also be fulfilled by observing the charge thermpower, which is much easier to be measured in experiments. In the previous work [38], we proved that the transition temperature of the thermopower depends on the QD-MZMs coupling strength, and the ferromagnetism of the two leads connected to the QD. Above or below the transition temperature, both 100% spin-polarized or pure spin thermopower will emerge due to the influences of SHA and MZMs. In the present paper, we study the properties of thermopower in a QD connected to the left and right leads with SHA, and also to a topological superconductor nanowire hosting MZMs. We focus our attention of the spin-resolved thermopower induced by the existence of MZMs, which are coupled to electrons on the QD with spin-dependent coupling strength. Our numerical results show that 100% spin-polarized and pure spin thermopower can be obtained by varying several system parameters, such as spin-polarization of the QD-MZM hybridization interaction, inter-MZM coupling strength, magnitude of the SHA, and the dot levels.

2 Model and Methods

The system Hamiltonian we study can be written in the following form [30, 31, 38].

$H=\sum _{k\beta \sigma }{\epsilon }_{k\beta }{c}_{k\beta \sigma }^{†}{c}_{k\beta \sigma }+\sum _{\sigma }{\epsilon }_d{d}_{\sigma }^{†}{d}_{\sigma }+U{d}_{\uparrow }^{†}{d}_{\uparrow }{d}_{\downarrow }^{†}{d}_{\downarrow }+\sum _{k\beta \sigma }(V_{k\beta }{c}_{k\beta \sigma }^{†}{d}_{\sigma }+H.c)+H_{MZMs},(1)$

where $c_{k\beta \sigma }^{†}(c_{k\beta \sigma })$ is the creation (annihilation) operator for an electron with momentum k, energy ɛ_kβ in the non-interacting leads β = L, R. $d_{\sigma }^{†}(d_{\sigma })$ is the electron creation (annihilation) operator having gate voltage tunable energy level ɛ_d, spin-σ and intradot Coulomb interaction U. The coupling strength between the QD and the leads is described by V_kβ. The last term H_MZMs in Eq. 1 is for the MZMs formed at the ends of a topological superconductor nanowire. Here we assume that the QD is side-coupled to one mode of the MZMs and [39],

$H_{MZMs}=i{\mathrm{\Delta }}_M{\eta }_1{\eta }_2+\sum _{\sigma }{\lambda }_{\sigma }(d_{\sigma }-d_{\sigma }^{†}){\eta }_1,(2)$

in which Δ_M is the inter-MZM coupling strength with ${\eta }_j={\eta }_j^{†}(j=\mathrm{1,2})$ and {η_i, η_j} = δ_i,j. The spin-dependent hybridization strength between the MZM and electrons on the QD is λ_σ. We transform the Majorana operator η_j to the regular fermionic operators f as [39] ${\eta }_1=(f^{†}+f)/\sqrt{2}$ and ${\eta }_2=i(f^{†}-f)/\sqrt{2}$, and then H_MZMs is rewritten as

$H_{MZMs}={\mathrm{\Delta }}_M\left(f^{†}f-\frac{1}{2}\right)+\frac{1}{\sqrt{2}}\sum _{\sigma }{\lambda }_{\sigma }(d_{\sigma }-d_{\sigma }^{†})(f^{†}+f).(3)$

In this paper, we study the thermopower in linear response regime (infinitesimal bias voltage ΔV and temperature bias ΔT) which is calculated from S_σ = −K_1,σ/(eT_σK_0,σ), where the integrals are [28–31],

$K_{n,\sigma }=\frac{1}{\hslash }\int {(\epsilon -\mu )}^n\left[-\frac{\partial f_{\sigma }(\epsilon )}{\partial \epsilon }\right]{\zeta }_{\sigma }(\epsilon )\frac{d\epsilon }{2\pi },(4)$

in which ℏ is the reduced Planck’s constant, and μ = 0 is the leads’ chemical potential. The spin-dependent equilibrium Fermi distribution function is written as f_σ(ɛ) = 1/{1 + exp [(ɛ − μ)/k_BT_σ]} with k_B the Boltzmann constant and T_σ the spin-dependent equilibrium temperature known as SHA in the leads. Here we set the spin-resolved temperatures in the leads to be T_↑ = T + δT/2 and T_↓ = T − δT/2 with T the system equilibrium temperature. The transmission coefficient ζ_σ(ɛ) in the above equation can be obtained by using the Dyson equation method combined with Keldysh nonequilibrium Green’s function technique as [28–31], ${\zeta }_{\sigma }(\epsilon )=-2\tilde{\mathrm{\Gamma }}\mathrm{I}\mathrm{m}{G}_{e,\sigma }^r(\epsilon )$, where $\tilde{\mathrm{\Gamma }}={\mathrm{\Gamma }}_L{\mathrm{\Gamma }}_R/({\mathrm{\Gamma }}_L+{\mathrm{\Gamma }}_R)$ and the line-width function Γ_L(R) = 2π∑_k|V_kL(R)|²δ[ɛ −ɛ_kL(R)] is independent of electron spin for normal metal leads. The electron retarded Green’s function in the transmission coefficient can be calculated by the Dyson equation method as [40, 41].

$\mathbf{G}={\left[\begin{array}{cccccc}\hfill g_{e,\uparrow }^{r-1}+i\mathrm{\Gamma }/2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\lambda }_{\uparrow }}{\sqrt{2}}\hfill & \hfill \frac{{\lambda }_{\uparrow }}{\sqrt{2}}\hfill \\ \hfill 0\hfill & \hfill g_{h,\uparrow }^{r-1}+i\mathrm{\Gamma }/2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{{\lambda }_{\uparrow }}{\sqrt{2}}\hfill & \hfill -\frac{{\lambda }_{\uparrow }}{\sqrt{2}}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill g_{e,\downarrow }^{r-1}+i\mathrm{\Gamma }/2\hfill & \hfill 0\hfill & \hfill \frac{{\lambda }_{\downarrow }}{\sqrt{2}}\hfill & \hfill \frac{{\lambda }_{\downarrow }}{\sqrt{2}}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill g_{h,\downarrow }^{r-1}+i\mathrm{\Gamma }/2\hfill & \hfill -\frac{{\lambda }_{\downarrow }}{\sqrt{2}}\hfill & \hfill -\frac{{\lambda }_{\downarrow }}{\sqrt{2}}\hfill \\ \hfill \frac{{\lambda }_{\uparrow }}{\sqrt{2}}\hfill & \hfill -\frac{{\lambda }_{\uparrow }}{\sqrt{2}}\hfill & \hfill \frac{{\lambda }_{\downarrow }}{\sqrt{2}}\hfill & \hfill -\frac{{\lambda }_{\downarrow }}{\sqrt{2}}\hfill & \hfill \epsilon -{\delta }_M\hfill & \hfill 0\hfill \\ \hfill \frac{{\lambda }_{\uparrow }}{\sqrt{2}}\hfill & \hfill -\frac{{\lambda }_{\uparrow }}{\sqrt{2}}\hfill & \hfill \frac{{\lambda }_{\downarrow }}{\sqrt{2}}\hfill & \hfill -\frac{{\lambda }_{\downarrow }}{\sqrt{2}}\hfill & \hfill 0\hfill & \hfill \epsilon +{\delta }_M\hfill \\ \hfill \hfill \end{array}\right]}^{-1},(5)$

where Γ = Γ_L + Γ_R, and the electron (hole) free retarded Green’s function is calculated from the equation of motion method as [40, 41].

$g_{e(h),\sigma }^r=\frac{1-n_{\bar{\sigma }}}{\epsilon \mp {\epsilon }_d}+\frac{n_{\bar{\sigma }}}{\epsilon \mp {\epsilon }_d\mp U}.(6)$

The interacting electron Green’s function then is obtained as $G_{e,\uparrow (\downarrow )}^r={\mathbf{G}}_{11(33)}^r$. The occupation number n_σ in the above free retarded Green’s function needs to be calculated self-consistently from the equation of $n_{\sigma }=-2\tilde{\mathrm{\Gamma }}\int d\epsilon f_{\sigma }(\epsilon )G_{e,\sigma }^r(\epsilon )/2\pi$.

3 Results and Discussion

In the following numerical calculations, we set the band width in the leads D = 40 as the energy unit, and fix Γ_L = Γ_R = 0.1. Other constants are e = ℏ = k_B = 1, with the leads’ chemical potentials μ_L = μ_R = μ = 0. Figure 1 shows the influences of QD-MZM coupling strength on the electrical conductance and thermopower without SHA (δT = 0). In numerical calculations, the spin-dependent hybridization λ_σ is set to be λ_↑ = λ(1 − P) and λ_↓ = λP, with P the spin-polarization of the QD-MZM hybridization [40]. For the particular arrangement of λ_σ, we only present G_↑ in Figure 1A and S_↑ in Figure 1B, the behaviors of the spin-down component can be easily deduced. For P = 0, λ_↑ = λ whereas λ_↓ = 0, and G_↑ in Figure 1A shows the typical double-peak configuration due to the Coulomb-blockade effect [30, 31]. The peaks’ height is half of its quantum value e²/h. With increasing P, the magnitude of λ_↑ decreases and the peak’ height of G_↑ increases, accordingly. For p = 1, the spin-up electrons on the QD are totally decoupled from the MZM as λ_↑ = 0 and then the peak of G_↑ = e²/h. If the QD is coupled to a regular fermion, the peak value of the electrical conductance is zero, which is not shown here [39]. Such a change of the conductance G induced by the QD-MZM coupling originates from the half-fermionic properties of MZM and was first found by Liu et. al., and is a strong evidence of the existence of MZMs. [39].

FIGURE 1

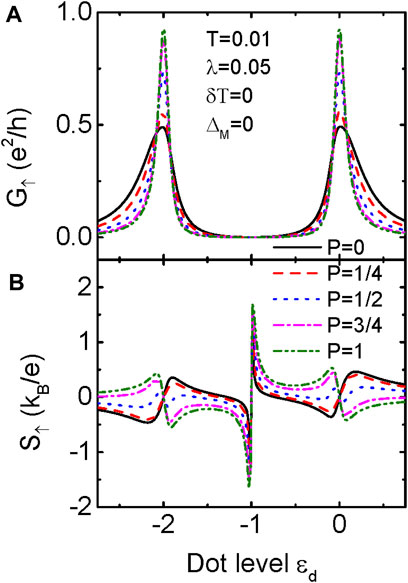
FIGURE 1. The spin-up electrical conductance G_↑ in (A), and thermopower S_↑ in (B) as functions of the dot level ɛ_d for indicated parameters, respectively. Due to the arrangement of λ_σ, G_↑,P=0 = G_↓,P=1, G_↑,P=1/4 = G_↓,P=3/4, and G_↑,P=1/2 = G_↓,P=1/2. The same holds true for the thermopower, and then we only illustrate the results of spin-up component.

Figure 1B shows the spin-up thermopower S_↑varying with respect to the dot levelɛ_d for different value of spin-polarization of QD-MZM coupling strength. For λ_↑ = 0 (P = 1), the thermpower has three zero points individually at ɛ_d = 0, ɛ_d = −U/2, and ɛ_d = −U as shown by the green dash-dot-dot line [30, 31]. At the two sides of each zero point, S_↑ develops two sharp peaks with opposite signs. From the calculation formulae of the thermopower and K_n,σ, one can see that the integrand of K_1,σ is antisymmetric with respective to the chemical potential for symmetrical transmission coefficient ζ_σ(ɛ). This indicates that, for λ_σ = 0 the magnitude of S_σ will be obviously suppressed in left-right symmetrical system as the tunneling of electrons will be compensated by the holes at the three zero points [27–30], which leads to null thermoelectric effect, i.e., zero thermopower. With increasing λ_↑ (decreasing P), the value of the thermopower at the zero points keep unchanged, whereas at other dot level except for the electron-hole symmetric point ɛ_d = −U/2, it fist decreases, reaching zero and then changes its sign. Such a sign change of the thermpower induced by QD-MZM coupling was also predicted by Chi et. al. in a recent work [30, 31]. We emphasize that in their work, the spin-up and spin-down electrons couple to the MZM with equal strength, i.e., the coupling strength between the QD and the MZM is spin-independent, and then the thermpower changes sign in the whole dot level regime. In the present paper, however, the consider the case of the spin-dependent QD-MZM coupling and find that the thermopower will not change its sign around S_σ = −U/2. The sign of S_σ can be reversed by varying the value of P indicates that the electron or hole tunneling direction is tunable by the MZM. As is known that the thermoelectric effect arises from the thermal bias applied between the two leads. We assume the left lead is hotter as compared to the right one, and then there are more electrons above the chemical potential in the left lead and more empty states below the chemical potential. If the dot energy level is below the chemical potential, electrons in the right lead will transport to the left one and occupy the empty states. This induces a positive thermopower. If the dot level is above the chemical potential, electrons in the left lead will tunnel into the right one and induces negative thermopower [27–29]. For non-zero λ_σ, the electron energy levels are modified by the QD-MZM coupling [39]. Therefore, electron transport is converted into that of holes at different energy states, inducing sign change of the thermopower. It is worth noting that the sign change of the thermopower induced by MZM-MZM coupling Δ_M was early predicted [28] and proposed to be an detection means for the existence of Majorana fermions. The sign change of the thermpower by QD-MZM coupling may provide a more feasible means to probe the existence of the MZMs as compared to the direct coupling between the MZMs. This is because that in experiments the value of Δ_M is adjusted by the length of nanowire hosting MZMs [32, 33]. For long enough nanowire, Δ_M vanishes. The strength of QD-MZM coupling, however, can be adjusted in experiments by the capacitive coupling of the tunnel-gate between QD and MZMs [32, 33]. The sign change of the thermpower can be explained as follows: in definition of the thermopower and K_1,σ, one can see that S_σ is proportional to ∫ɛdɛ and is zero for symmetric ζ_σ(ɛ) when ɛ_d = 0 or − U. Because − ∂f_σ(ɛ)/∂ɛ is symmetric with respective to ɛ = 0 and − U, the peaks of the ζ_σ(ɛ) induced by QD-MZM coupling in the positive (negative) energy regime moves toward (away from) the chemical potential. At low temperatures, the Sommerfeld expansion of the Fermi function shows that the thermopower obey the relationship of $S_{\sigma }=S_0{\epsilon }_d/2{\lambda }_{\sigma }^2$, and induces negative (positive) thermopower at the corresponding dot level. Note this relationship between S_σ and λ_σ is valid for only nonzero λ_σ.

Figure 2 presents spin-up conductance G_↑ in (a) and S_↑ in (b) varying with the system temperature T for different values of P (λ_↑) and fixed λ = 0.05. Since S_↑ = 0 at ɛ_d = 0, we then fix ɛ_d = −0.1. Figure 2A indicates that at ultra-low temperature, the conductance for p = 0 is G_↑ = e²/2h showing the exotic half-fermionic character of the MZMs [39], see the solid line. It is worth of noting that the property of G_↑ = e²/2h is independent on the value of dot level. With increasing temperature, the thermal motion of electrons becomes stronger and the impacts of QD-MZM coupling is weakened. As a result of it, the value of conductance is suppressed accordingly. When P > 0, the coupling between spin-up electrons on the QD with MZM becomes weaker, and then the conductance is also suppressed. For P = 1, the spin-up electrons is free from interaction with the MZM, and the conductance becomes normal as shown by the green dash-dot-dot line. The thermopower in Figure 2B shows a clear sign reversion at a particular system temperature T for small spin-polarization of the dot-MZM coupling strength P [or, equivalently large λ_↑ = λ(1 − P)]. It is found that the transition temperature of S_↑ become lower with smaller λ_↑. For very weak λ_↑, S_↑ is positive in the whole temperature regime. As was explained in our previous work, the sign reversion of the thermopower is induced by the asymmetric transmission in the presence of the QD-MZM coupling. Since the sign reversion of the thermopower depends on both the system temperature and magnitude of QD-MZM coupling, it enable that one spin component thermopower is zero whereas the other component is finite. In this way, a 100% spin polarized thermopower can be obtained. It is also possible that the thermopowers of the two spin components are of the same amplitude but have opposite signs, i.e., a pure spin thermpower without the accompany of charge thermopower. In spintronics, 100% spin-polarized and pure spin thermopowers are the corresponding currents or bias voltages.

FIGURE 2

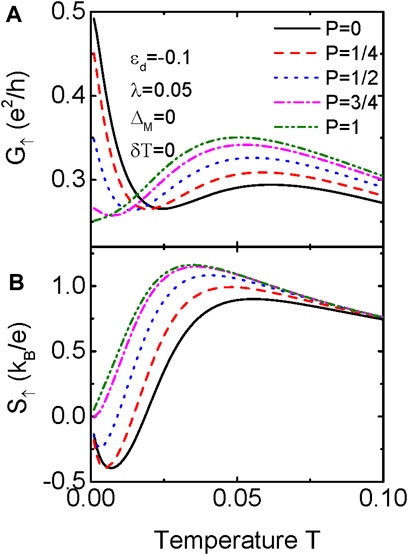
FIGURE 2. G_↑ in (A) and thermopower S_↑ in (B) as functions of system equilibrium temperature T for the given parameters. The thermpower changes sign by varying the temperature with the help of the MZMs.

We study influences of the SHA denoted by δT [7, 23, 24] on the thermopowers at different dot levels in Figure 3. Here we set p = 0.5 so as to λ_↑ = λ_↓ and S_↑ = S_↓ for δT = 0. It is found that S_↑ in Figure 3A and S_↓ in (Figure 3B) respectively approach to positive and negative values with increasing δT [38]. This is because the spin-up and spin-down electrons are in different temperatures for finite value of δT, and then have corresponding different transition temperature of the thermpower. The charge thermopower S_c = S_↑ + S_↓ in Figure 3C may also change its sign at dot levels of ɛ_d = −0.3 and −0.2, whereas it keeps positive at ɛ_d = −0.1. Interestingly, the charge thermpowerS_c = 0 at about δT = 3T/4 for both ɛ_d = −0.3 and −0.2, which provides a feasible way of changing the charge thermopower. In Figure 3D we present the result of pure spin thermpower S_s = S_↑− S_↓. There are three characters worth to be pointing out: one is that S_s shows the perfect linear relationship with δT, which is ideal in detecting the strength of SHA; and the other is that S_s is positive in the whole range of δT. This indicates that a pure spin thermopower in the absence of charge thermopower can be generated by properly adjusting some system parameters, such as the dot level, magnitude of SHA, QD-MZM coupling strength or its spin polarization. At last, the magnitude of S_s is comparable to that of the charge one, which is important in thermospin devices.

FIGURE 3

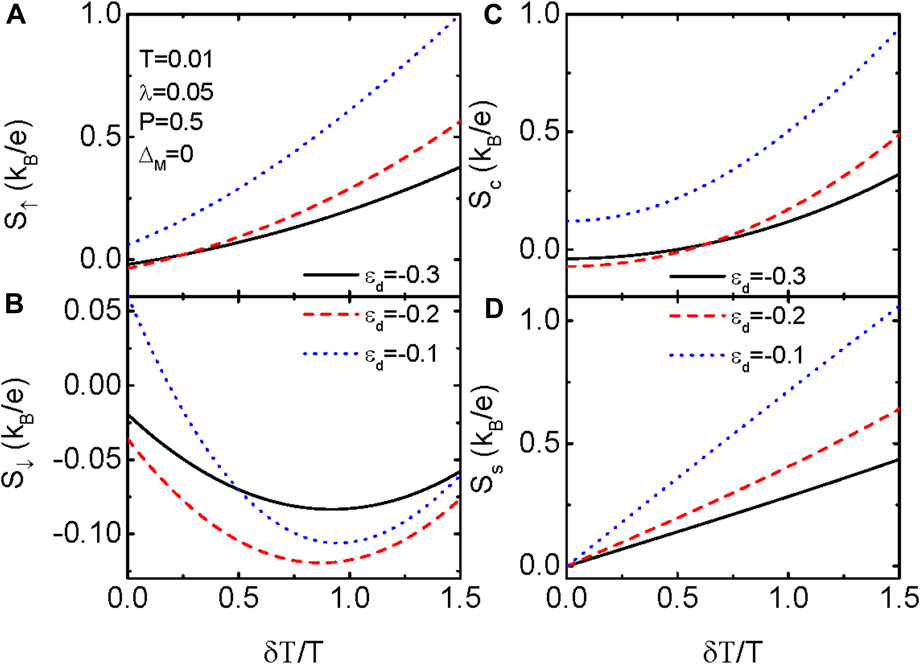
FIGURE 3. Spin-up thermopower in (A), spin-down thermopower in (B), charge thermopower in (C) and spin thermopower in (D) as functions of SHA magnitude δT for indicated parameters.

Finally in Figure 4 we present the influences of MZM-MZM coupling strength Δ_M on the spin-dependent thermopower. The most important property of the spin-up thermpower in Figure 4A is the sign change induced by Δ_M, which has also been found in some previous work [28, 30, 31, 38]. The sign change of the thermopower by Δ_M can also been explained in terms of the shape of the electronic transmission function ζ_σ(ɛ), [1, 2] which not shown here. For the particular value of P, the spin-down thermopower in Figure 4B keeps unchanged. From the two figures one can see that S_↑ and S_↓ of the same amplitude may be opposite in sign, which enable the emerge of 100% spin polarized or pure spin thermpowers.

FIGURE 4

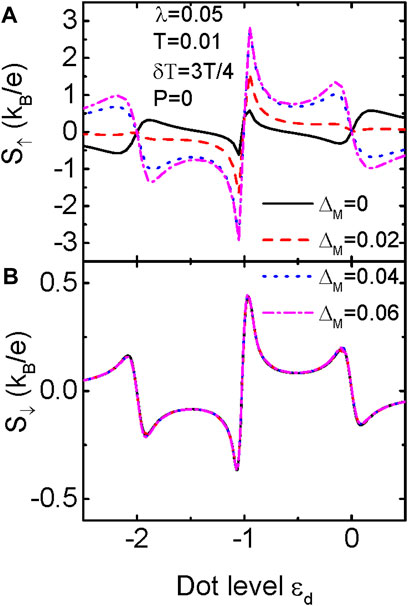
FIGURE 4. Thermopower for spin-up electrons in (A) and spin-down ones in (B) as functions of the dot level for varying MZM-MZM coupling strength Δ_M for indicated parameters.

4 Summary

In conclusion, we study properties of spin-dependent thermopower adjusted by MZMs in a QD connected to two normal metal leads. Our numerical results show that the spin-polarized thermopower will change its sign by varying the system equilibrium temperature with the help of interaction between the dot and one mode of the MZMs, which is useful in generating 100% spin-polarized or pure spin thermopowers. The SHA will change the signs of spin-up and spin-down thermpowers with enhanced magnitude. By the combined effect of the SHA and hybridization between the dot and MZM, the spin-polarized thermpower can be fully adjusted and enhanced, which is vital in energy-saving nanoscale devices.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

L-LS derived the formulae, performed partial numerical calculations, and wrote the original manuscipt. Z-GF discussed the physical model, performed partial numerical calculations, and contributed in the paper writting.

Funding

This work was supported by Research Funds for Beijing Universities (NO.KM201910009002).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Johnson M. Spin Caloritronics and the Thermomagnetoelectric System. Solid State Commu (2010) 150:543. doi:10.1016/j.ssc.2009.10.027

CrossRef Full Text | Google Scholar

2. Bauer G, Saitoh E, van Wees B. Spin Caloritronics. Nat Mater (2012) 11:391. doi:10.1038/nmat3301

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dresselhaus M, Dresselhaus G, Sun X, Zhang Z, Cronin S, Koga T. Low-dimensional Thermoelectric Materials. Phys Solid State (1999) 41:679. doi:10.1134/1.1130849

CrossRef Full Text | Google Scholar

4. Dubi Y, Ventra M. Colloquium: Heat Flow and Thermoelectricity in Atomic and Molecular Junctions. Rev Mod Phys (2011) 83:131. doi:10.1103/RevModPhys.83.131

CrossRef Full Text | Google Scholar

5. Uchida K, Takahashi S, Harii K, Ieda J, Koshibae W, Ando K, et al. Observation of the Spin Seebeck Effect. Nat (2008) 455:778. doi:10.1038/nature07321

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Ren J, Fransson J, Zhu J. Nanoscale Spin Seebeck Rectifier: Controlling thermal Spin Transport across Insulating Magnetic Junctions with Localized Spin. Phys Rev B (2014) 89:214407. doi:10.1103/PhysRevB.89.214407

CrossRef Full Text | Google Scholar

7. Heikkilä T, Hatami M, Bauer G. Spin Heat Accumulation and its Relaxation in Spin Valves. Phys Rev B (2010) 81:100408. doi:10.1103/PhysRevB.81.100408

CrossRef Full Text | Google Scholar

8. Hatami M, Bauer G, Zhang Q, Kelly P. Thermoelectric Effects in Magnetic Nanostructures. Phys Rev B (2009) 79:174426. doi:10.1103/PhysRevB.79.174426

CrossRef Full Text | Google Scholar

9. Yu H, Granville S, Yu D, Ansermet J. Evidence for thermal Spin-Transfer Torque. Phys Rev Lett (2010) 104:146601. doi:10.1103/PhysRevLett.104.146601

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gu L, Fu H, Wu R. How to Control Spin-Seebeck Current in a Metal-Quantum Dot-Magnetic Insulator junction. Phys Rev B (2016) 94:115433. doi:10.1103/PhysRevB.94.115433

CrossRef Full Text | Google Scholar

11. Ren J. Predicted Rectification and Negative Differential Spin Seebeck Effect at Magnetic Interfaces. Phys Rev B (2013) 88:220406. doi:10.1103/PhysRevB.88.220406

CrossRef Full Text | Google Scholar

12. Uchida K, Adachi H, Ota T, Nakayama H, Maekawa S, Saitoh E. Observation of Longitudinal Spin-Seebeck Effect in Magnetic Insulators. Appl Phys Lett (2010) 97:172505. doi:10.1063/1.3507386

CrossRef Full Text | Google Scholar

13. Uchida K, Xiao J, Adachi H, Ohe J, Takahashi S, Ieda J, et al. Spin Seebeck Insulator. Nat Mater (2010) 9:894. doi:10.1038/nmat2856

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bosu S, Sakuraba Y, Uchida K, Saito K, Ota T, Saitoh E, et al. Spin Seebeck Effect in Thin Films of the Heusler Compound Co2mnsi. Phys Rev B (2011) 83:224401. doi:10.1103/PhysRevB.83.224401

CrossRef Full Text | Google Scholar

15. Jaworski C, Yang J, Mack S, Awschalom D, Heremans J, Myers R. Observation of the Spin-Seebeck Effect in a Ferromagnetic Semiconductor. Nat Mater (2010) 9:898. doi:10.1038/nmat2860

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Jaworski C, Myers R, Johnston-Halperin E, Heremans J. Giant Spin Seebeck Effect in a Non-magnetic Material. Nat (2012) 487:210. doi:10.1038/nature11221

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wu SJE, Pearson , Bhattacharya A. Paramagnetic Spin Seebeck Effect. Phys Rev Lett (2015) 114:186602. doi:10.1103/PhysRevLett.114.186602

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wu S, Zhang W, Kc A, Borisov P, Pearson J, Jiang J, et al. Antiferromagnetic Spin Seebeck Effect. Phys Rev Lett (2016) 116:097204. doi:10.1103/PhysRevLett.116.097204

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tang G, Chen X, Ren J, Wang J. Rectifying Full-Counting Statistics in a Spin Seebeck Engine. Phys Rev B (2018) 97:081407. doi:10.1103/PhysRevB.97.081407

CrossRef Full Text | Google Scholar

20. Chang P, Mahfouzi F, Nagaosa N, Nikolić B. Spin-seebeck Effect on the Surface of a Topological Insulator Due to Nonequilibrium Spin-Polarization Parallel to the Direction of Thermally Driven Electronic Transport. Phys Rev B (2014) 89:195418. doi:10.1103/physrevb.89.195418

CrossRef Full Text | Google Scholar

21. Okuma N, Masir M, MacDonald A. Theory of the Spin-Seebeck Effect at a Topological-Insulator/ferromagnetic-Insulator Interface. Phys Rev B (2017) 95:165418. doi:10.1103/PhysRevB.95.165418

CrossRef Full Text | Google Scholar

22. Hatami M, Bauer G, Zhang Q, Kelly P. Thermal Spin-Transfer Torque in Magnetoelectronic Devices. Phys Rev Lett (2007) 99:066603. doi:10.1103/PhysRevLett.99.066603

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Dejene F, Flipse J, Bauer G, van Wees B. Spin Heat Accumulation and Spin-dependent Temperatures in Nanopillar Spin Valves. Nat Phys (2013) 9:636. doi:10.1038/nphys2743

CrossRef Full Text | Google Scholar

24. Vera-Marun I, van Wees B, Jansen R. Spin Heat Accumulation Induced by Tunneling from a Ferromagnet. Phys Rev Lett (2014) 112:056602. doi:10.1103/PhysRevLett.112.056602

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kimling J, Wilson R, Rott K, Kimling J, Reiss G, Cahill D. Spin-dependent thermal Transport Perpendicular to the Planes of Co/cu Multilayers. Phys Rev B (2015) 91:144405. doi:10.1103/PhysRevB.91.144405

CrossRef Full Text | Google Scholar

26. Kimling J, Cahill D. Spin Diffusion Induced by Pulsed-Laser Heating and the Role of Spin Heat Accumulation. Phys Rev B (2017) 95:014402. doi:10.1103/PhysRevB.95.014402

CrossRef Full Text | Google Scholar

27. Hou C, Shtengel K, Refael G. Thermopower and mott Formula for a Majorana Edge State. Phys Rev B (2013) 88:075304. doi:10.1103/PhysRevB.88.075304

CrossRef Full Text | Google Scholar

28. López R, Lee M, Serra L, Lim J. Thermoelectrical Detection of Majorana States. Phys Rev B (2014) 89:205418. doi:10.1103/PhysRevB.89.205418

CrossRef Full Text | Google Scholar

29. Leijinse M. Thermoelectric Signatures of a Majorana Bound State Coupled to a Quantum Dot. New J Phys (2014) 16:015029. doi:10.1088/1367-2630/16/1/015029

CrossRef Full Text | Google Scholar

30. Hong L, Chi F, Fu Z, Hou Y, Wang Z, Li K, et al. Large Enhancement of Thermoelectric Effect by Majorana Bound States Coupled to a Quantum Dot. J Appl Phys (2020) 127:124302. doi:10.1063/1.5125971

CrossRef Full Text | Google Scholar

31. Chi F, Fu Z, Liu J, Li K, Wang Z, Zhang P. Thermoelectric Effect in a Quantum Dot Side-Coupled to Majorana Bound States. Nanoscale Res Lett (2020) 15:79. doi:10.1186/s11671-020-03307-y

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Mourik V, Zuo K, Frolov S, Plissard S, Bakkers E, Kouwenhoven L. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science (2012) 336:1003. doi:10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Ricco L, de Souza M, Figueira M, Shelykh I, Seridonio A. Spin-dependent Zero-Bias Peak in a Hybrid Nanowire-Quantum Dot System: Distinguishing Isolated Majorana Fermions from Andreev Bound States. Phys Rev B (2019) 99:155159. doi:10.1103/PhysRevB.99.155159

CrossRef Full Text | Google Scholar

34. Qi X, Zhang S. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057. doi:10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

35. Nayak C, Simon S, Stern A, Freedman M, Sarma S. Non-abelian Anyons and Topological Quantum Computation. Rev Mod Phys (2008) 80:1083. doi:10.1103/RevModPhys.80.1083

CrossRef Full Text | Google Scholar

36. Alicea J, Oreg Y, Refael G, von Oppen F, Fisher M. Non-abelian Statistics and Topological Quantum Information Processing in 1d Wire Networks. Nat Phys (2011) 7:412. doi:10.1038/nphys1915

CrossRef Full Text | Google Scholar

37. Pikulin D, Dahlhaus J, Wimmer M, Schomerus H, Beenakker C. A Zero-Voltage Conductance Peak from Weak Antilocalization in a Majorana Nanowire. New J Phys (2012) 14:125011. doi:10.1088/1367-2630/14/12/125011

CrossRef Full Text | Google Scholar

38. Sun LL, Chi F. Detecting Spin Heat Accumulation by Sign Reversion of Thermopower in a Quantum Dot Side-Coupled to Majorana Bound States. J Low Temp Phys (2021) 203:381. doi:10.1007/s10909-021-02593-9

CrossRef Full Text | Google Scholar

39. Liu D, Baranger H. Detecting a Majorana-Fermion Zero Mode Using a Quantum Dot. Phys Rev B (2011) 84:201308. doi:10.1103/PhysRevB.84201308

CrossRef Full Text | Google Scholar

40. Gorski G, Kucab K. The Spin-dependent Coupling in the Hybrid Quantum Dot–Majorana Wire System. Phys Status Solidi B (2019) 256:1800492. doi:10.1002/pssb.201800492

CrossRef Full Text | Google Scholar

41. Chi F, Wang J, He TY, Fu ZG, Zhang P, Zhang XW, et al. Quantum Interference Effects in Quantum Dot Molecular with Majorana Bound States. Front Phys 8 (2021) 631031. doi:10.3389/fphy.2020.631031

CrossRef Full Text | Google Scholar