A Power Dispatch Optimization Method to Enhance the Resilience of Renewable Energy Penetrated Power Networks

With the wide deployment of renewable energies, future power grids become more vulnerable to extreme environments. This paper investigates enhancing the resilience of power systems with high penetrations of renewable energies under emergencies. The resilience enhancement firstly is defined as maintaining as much electric energy to critical loads in a fixed number of post-disaster periods by properly coordinating the available resources. Then, an optimal decision-making method is proposed to maximize the power supply of critical loads and to minimize the instability risks due to the randomness of the output power of renewable energies. The power consumption of loads, charging/discharging power of power storage plants, power generation of generators, and spinning reserve ratios of the renewable energy at each period are taken as decision variables. Constraints include spinning reserve, power flow constraints, and power consumption/generation limits. The interior-point algorithm is used to solve the formulated optimization problem. Numerical simulations verified the effectiveness and superiority of the proposed optimization method in boosting grid resilience after disasters. It is also found that a balance should be sought between decreasing stability risks and increasing the power supply benefit in extreme environments.

1 Introduction

1.1 Backgrounds

Power networks are essential infrastructures that support almost all kinds of activities in modern society. Their ability to maintain a reliable electricity supply to the consumers under various emergencies is crucial to society’s day-to-day operations. Due to the broad geographical coverage and exposure to wild and adverse environments, the power network is subject to various disturbances. Extreme environments will seriously affect the normal operation of the power network, reducing the network connectivity and functions. Damage to the network topology will lower the supply of load and seriously endangering economic development and social stability [1]. Thus, increasing the power grid resilience in face to extreme conditions has profound significance.

The study on network resilience has been an popular topic in the filed of complex networks since the publication of [2–6]. Being a typical complex network, the power network’s resilience has also attracted the interest of many scholars [7, 8]. The resilience of the power network refers to the ability of the power grid to resist interference and restore power promptly under inclement weather such as typhoons, heavy rain/snow, and earthquakes, or artificial attacks such as graphite bombs, high-altitude nuclear magnetic explosions, and computer viruses [9, 10]. Reference [11] comprehensively reviewed the evolution and current status of the U.S. power network, and exploreed ways to improve the resilience of the power network. Based on the understanding of the resilience recovery process of the power network, Refs. [12, 13] proposed a simulation model for the power system and addressed indexes to evaluate the network resilience. The model considered a series of equipment failures and repair events in the resilience process, in which the probability of equipment failure was expressed as a function of weather parameters, and the length of time from failure to repair of the failed equipment was set to obey an exponential distribution.

Motivated by energy and environmental requirements, the power network is entering a new era due to increasing penetrations of renewable energies. Making full use of existing available resources to achieve the maximum power supply capacity (the maximum power system sufficiency) by power dispatch and topology adjustments is an effective means to improve the resilience of the power system, and it is beneficial to alleviating the negative impact of extreme environments on social stability [14]. However current research on power network resilience fails to incorporate the increasing trend of the proportion of new energy sources connected to the power system and lacks sufficient control that considers the intermittent output of new energy sources and the reduction in the proportion of spinning reserve.

Differing from traditional power sources, the power outputs of renewable power units are random and fluctuant, which are determined by the weather. Renewable energy power units connect to the grid via electronic equipment with zero inertia and low tolerance. Though renewable energies bring huge environmental and social benefits, they also bring challenges to the safe operation of the power grid and the recovery of the system after severe damage under inclement weather. First, under inclement weather, the components and pieces of equipment of the power system are likely to be physically damaged, and it takes a long time to repair them or build new equipment [15]. Second, the randomness and fluctuantions of renewable power units are detrimental to maintaining the power balance in the power system, which requires traditional generators to keep an appropriate amount of reserve. In this case, higher amounts of reserve from traditional generators will reduce the power supplied to loads, while lower amounts of reserve from traditional generators will increase the operation risk.

1.2 An Insight to Enhance the Grid Resilience

When the power network is affected by inclement weather, its load-supply capacity is reduced. Moreover, it is difficult to repair electrical components that are physically damaged in the short term after the impact of extreme conditions. Therefore, it is practically feasible to boost the resilience of the damaged power grid by making full use of the remaining available resources to maximize the power supply benefit of the damaged power system, which can help significantly alleviate the negative impact of extreme environments on social stability.

Under inclement weather, it is hard for the power network to satisfy the power supply requirements of all loads. Thus the power consumption of each node should be reorganized by the dispatch center to maximize the power supply benefit of the power network. At the same time, during the special period of insufficient power supply after disasters, the power supply should also be prioritized to some certain consumers, e.g., government, hospitals, etc., should be higher than the power supply priority of some factories. Therefore, the weighted sum of the loads, which serves as the main part of the power supply benefit, is the objective function of the optimization model considered in this paper.

To maintain safety and stability, a certain amount of spinning reserve needs to be reserved for the conventional generators to cope with randomness and intermittent in the power network. Under normal circumstances, there are two main sources of randomness and volatility in power networks with high penetrations of renewable energies: load and renewable energy generators. Under inclement weather, the system only needs to plan conventional generators to reserve a certain amount of spinning reserve to balance the fluctuation of the renewable energy generators if loads are controlled without randomness and volatility. The total power generation of renewable energy generators in the network and the spinning reserve ratio during each period serve as the spinning reserve capacity of the system for each period. Therefore, the amount of the spinning reserve ratio of the network at each time will also affect the power supply capacity of the system in extreme environments. For example, if the spinning reserve ratio is too large, the power of the conventional generators for load supply will be reduced, which will affect the power supply benefit. In contrast, if the ratio is too small, once the actual output of the renewable energy generators is much smaller than the planned output, the planned load power will not be supplied. As a result, the power network will even lose balance, and a series of cascading failures will occur, which will heavily deprive the power supply of the network in extreme environments. Therefore, it is necessary to optimize the spinning reserve ratio for each period. In addition, the spinning reserve ratio of the system for each period is also an important factor that needs to be considered for flexibility optimization.

Inspired by this, an optimization model is proposed to enhance the resilience of the power network with high penetrations of renewable energies. The main contributions are as follows:

• The resilience of the power network with high penetrations of renewable energies is studied. Specifically, the stochastic properties of the renewable power units’ output are considered.

• A new resilience metric for the power network is proposed and defined as the amount of electric energy maintained to critical loads within a fixed number of periods. Then an optimization model aiming to maximize the power supply of critical loads and minimize the instability risks is proposed, and the power consumption of loads, power generation of generators, and spinning reserve ratios of the renewable energy at each period are taking as decision variables to coordinate the available resources properly;

• Two cases study based on the real power network are implemented, showing that the proposed optimization method can effectively boost grid resilience after disasters.

The remainder of this paper is organized as follows. The detailed optimization model is formulated in Section 2; two cases studied are carried out in Section 3 to verify the proposed model, and Section 4 concludes this work.

2 Model Formulation

2.1 Disposal of the Uncertainty of Renewable Energy Power

In this paper, the time duration of the resilience optimization considered for the power system is a short time (a few hours) after disasters, so the uncertainty of the renewable energy output in a short time needs to be considered [16,17]. The current renewable energy power generation mainly consists of wind power and photovoltaic power generation. Wind power accounts for the highest proportion (about 70%) of renewable energy power, and the short-term forecast error models of wind power photovoltaic power are similar. Thus the disposal of the uncertainty of renewable energy power in this paper mainly refers to the short-term forecast error model of wind power output for simplicity.

As renewable energy power generation is affected by weather and other factors, it is random and volatile and cannot be accurately predicted. The forecast error of renewable energy output is defined as:

${\tilde{P}}_{re}(t)=P_{re}(t)+\mathrm{\Delta }{P}_{re}(t),(1)$

where ${\tilde{P}}_{re}(t)$, P_re(t) and ΔP_re(t) are the actual value, the forecasted value, and the forecasted error of renewable energy power output, respectively. The wind power output forecast errors basically follows the Gaussian distribution according to the statistitics [18, 19]. In this paper, the short-term forscast errors of the reneable energy follows the Gaussian distribution $N(0,{\sigma }_{re}^2)$, whose standard deviation is defined as:

${\sigma }_{re}(t)=K\ast P_{re}(t)+R{E}_I/50,(2)$

where K is the forecast error factor for renewable energy power, which is always set as 0.2; RE_I is the total installed capacity of renewable energy power supply.

2.2 Decision Variables

In the optimization model, the decision variables are composed of the following parts:

• The output of each conventional power generator node in each period P_i(t)

• The power of each load node in each period P_l(t)

• The output of each renewable energy generator node in each period P_re(t)

• The power of each power storage node in each period P_sto(t)

• The spinning reserve ratio of the renewable energy in each period r(t)

2.3 Objective Function

The objective of the power system resilience optimization studied in this paper is to get the maximum power supply benefit by supplying power to various loads according to their priority in the short term under extreme environments without considering the cost through the remaining generation resources. Apart from the power supply to loads, the stability of the power system also plays an important role in the evaluation of the benefit. Therefore, due to the randomness of renewable energy power generation, conventional generator nodes are required to provide a certain amount of upward spinning reserve to deal with the situation where the actual output of the renewable energy is lower than the planned output to avoid causing the failure to supply load as planned power and cascading failure caused by power grid instability. In conclusion, the objective function of the optimization problem is:

$\mathrm{m}\mathrm{a}\mathrm{x}F=\sum _{t=1}^m(P_L(t)-Q(t))\ast \mathrm{\Delta }t,(3)$

where P_L(t) is the weighted sum of the power of all load nodes of the period t, Q(t) is the loss rate of the power supply benefit caused by the insufficient actual output of renewable energy power generator nodes and insufficient spinning reserve of the period t, Δt is the duration of a period. The specific formula P_L(t) is defined as follows:

$P_L(t)=\sum _{l=1}^L{w}_l{P}_l(t)(4)$

where P_l(t) is the planned power of load l during the period t, w_l is the power supply weight factor of the load l. The larger the value, the higher the power supply priority of the load under extreme environments.

The analysis of Q(t), which is the loss rate of the power supply benefit caused by the insufficient actual output of the renewable energy and insufficient spinning reserve during the period t, is shown in Figure 1. As shown in Figure 1, assuming that the actual power of renewable energy during the period t obeys the Gaussian distribution, the abscissa $P_t^{\sum }$ is the actual value of the total output of the renewable energy during the period t, and $P_f^{\sum }(t)$ is the average value, which is the forecasted output during the period t; $P_{pl,t}^{\sum }$ is the planned total output of the renewable energy power during the period t. The shaded part in the figure is the range of renewable energy output that can be balanced by the spinning reserve reserved by the system and P_d(t) is the minimum value of the actual total output of the renewable energy allowed by the spinning reserve. Therefore, when the renewable energy output is less than P_d(t), the spinning reserve is insufficient, resulting in the power supply to the load node not reaching the expected amount. Under extreme environmental conditions, failure to supply load as planned power is likely to cause serious economic losses and even cause more serious cascading failures. The specific formula Q(t) is:

$Q(t)=K_{loss}\ast {\int }_0^{P_d(t)}\phi \left({P_t}^{\sum }\right)\left(P_d(t)-{P_t}^{\sum }\right)d{P_t}^{\sum }(5)$

where K_loss is the benefit loss factor. The larger the value, the more serious the loss of the power supply benefit caused by insufficient renewable energy output and insufficient spinning reserve. $\phi ({P_t}^{\sum })$ is the Gaussian distribution function of renewable energy power. P_d(t) is the integral upper limit, which is the minimum value of the actual total output of the renewable energy allowed by the spinning reserve, and it can be calculated by the formula as follow:

$P_d(\mathrm{t})=(1-r(t))\left(\sum _{re=1}^{RE}{P}_{re}(t)\right),(6)$

where P_re(t) is the planned output of the renewable energy generator node re, and RE contains all the renewable energy generator nodes.

FIGURE 1

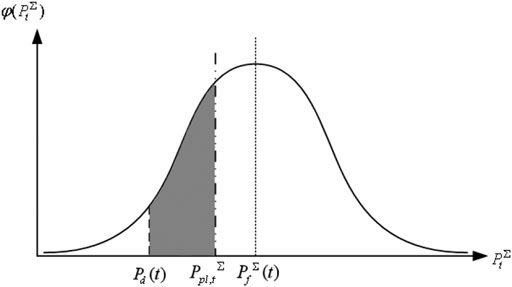
FIGURE 1. Probability density distribution of the total output of the renewable energy during the period t.

In summary, the reaction of P_L(t) and Q(t) in each period of the objective function to the change of the spinning reserve ratio in each period is the same. Still, the changes of the two variables have opposite effects on the value of the objective function. Therefore, the objective function of the optimization model in this paper will drive the optimization algorithm to find a balance value in the determination of the spinning reserve ratio in each period for the system so that the system can maximize its power supply capacity while maintaining a certain degree of reliability under extreme environments to achieve the greatest power supply benefit.

2.4 Constraints

Constraints include active power balance constraint (Eq. 7), spinning reserve constraint (Eq. 8), power flow constraint of lines (Eq. 9), output constraint of the conventional generator nodes (Eq. 10), constraints of the output rate of change of the conventional generator nodes (Eqs 11, 12), load power constraint (Eq. 13), output constraint of renewable energy generator nodes (Eq. 14), power constraints of energy storage nodes (Eq. 15), and capacity constraints of power storage nodes (Eq. 16).

$\sum _{i=1}^N{P}_i(t)+\sum _{re=1}^{\mathrm{R}\mathrm{E}}{P}_{re}(t)+\sum _{sto=1}^{STO}{P}_{sto}(t)=\sum _{l=1}^L{\mathrm{P}}_l(t)(7)$

$\sum _{i=1}^N\min (P_{i,\max }-P(t),P_{i,up}\ast \mathrm{\Delta }t)\ge r(t)\ast \sum _{re=1}^{\mathrm{R}\mathrm{E}}{P}_{re}(t)(8)$

$-L_{ij,\max }\le L_{ij}(t)\le L_{ij,\max }(9)$

$P_{i,\min }\le P_i(t)\le P_{i,\max }(10)$

$P_i(t+1)-P_i(t)\le \mathrm{\Delta }{P}_{i,up}(11)$

${\mathrm{P}}_i(t)-P_i(t+1)\le \mathrm{\Delta }{P}_{i,down}(12)$

$P_{l,\max }\le P_l(t)\le 0(13)$

$0\le P_{re}(t)\le P_{re,f}(t)(14)$

$P_{sto,\max }^{in}\le P_{sto}(t)\le P_{sto,\max }^{out}(15)$

$0\le \sum _{t=1}^{t\le t_1}{P}_{sto}(t)\cdot \mathrm{\Delta }t\le S_{sto,\max },t_1\in T(16)$

where P_i,max and P_i,min are the upper limit and lower limit of output of conventional generator node i, respectively; P_i(t) is the output of conventional generator node i during the period t; N contains the conventional generator nodes in the system; ΔP_i,up and ΔP_i,down are the maximum upward ramp rate and the maximum downward ramp rate of conventional generator node i, respectively; P_l,max is the maximum absorbed power of load node i, which is a negative value; P_re,f(t) is the predicted output of the renewable energy power generator node re of the period t; $P_{sto,\mathrm{m}\mathrm{a}\mathrm{x}}^{\text{in}}$ and $P_{sto,\mathrm{m}\mathrm{a}\mathrm{x}}^{\text{out}}$ are respectively the maximum input and output power of the power storage node sto; S_sto,max is the maximum capacity of the power storage node sto; t is any period in the entire research time range T.

The spinning reserve constraint is specifically the upward spinning reserve constraint. The principle is that when the actual output of the renewable energy unit cannot reach the planned output, a certain amount of upward spinning reserve is required to make up for the lack of renewable energy output. Corresponding to downward rotation is upward rotation. To obtain the maximum power supply benefit within a short term, its planned output should be controlled below its forecasted output to avoid potential safety hazards of the power grid caused by the upward fluctuation of renewable energy output and the burden of the downward spinning reserve. Therefore, the downward spinning reserve is not taken into consideration in this paper.

3 Cases Study

Two kinds of cases are considered in this section to verify the effectiveness of the proposed model. The details are shown in follows.

3.1 Case 1 (Power System Without Power Storage Plants)

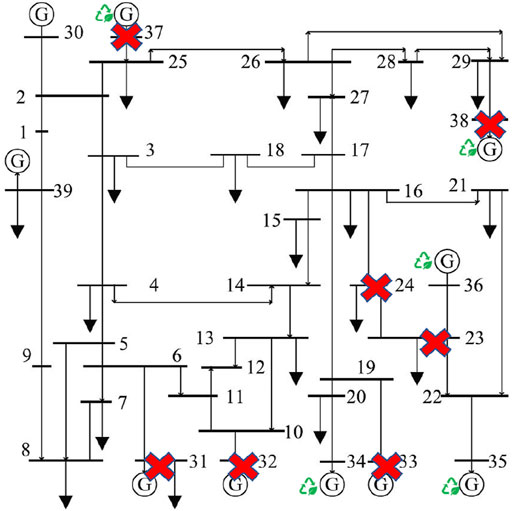
The simulations in this paper are based on the IEEE 39-Bus Test Case, as shown in Figure 2. Node 34, 35, 36, 37, 38 are selected as wind power generator nodes. It is assumed that nodes whose index are 23, 24, 31, 32, 33, 37, 38 are damaged due to extreme environments and are unavailable for the power dispatching center.

FIGURE 2

FIGURE 2. The power network used based on the IEEE 39-Bus system.

The DC power flow model is adopted in the simulation to improve the computational efficiency. The nodes in the system model are divided into four types: conventional power generator nodes, renewable energy generator nodes, load nodes, and power storage nodes (in case 2). The main parameters of conventional power generator nodes, load nodes, and power storage nodes are shown in Supplementary Appendix Tables S2, S3, S4.

A set of forecasted values of the renewable energy output is drawn up regarding the actual output data of the renewable energy in a certain place. The time scale of the renewable energy ultra-short-term forecast is 4-h and the time resolution is 15-min, and the time range studied in this paper is 2-h (8-period) after the disaster. The forecasted output values of renewable energy generator nodes are shown in Supplementary Appendix Table S4 in the appendix. The simulation is coded in Matlab based on the functions provided by Matpower [20].

The benefit loss factor is set to 10, the load priority weight is set to two levels of 1 and 10, and the standard deviation of the short-term forecast error of renewable energy output is set to 0.2 times the output of renewable energy generation. The results of the optimization are as follows.

3.1.1 Results of Optimal Variables

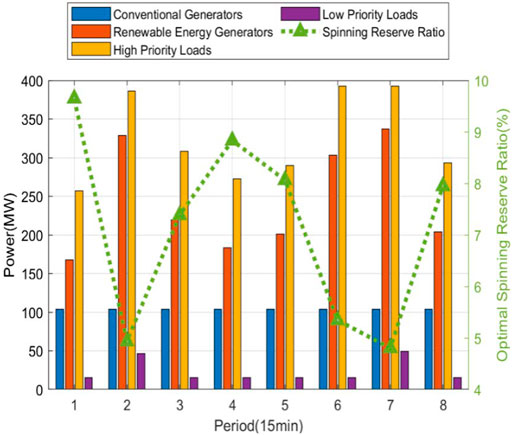
The results of the spinning reserve ratio in each period and the planned power of nodes are shown in Figure 3.

FIGURE 3

FIGURE 3. Results of optimal variables.

The relationship between the optimal spinning reserve ratio in each period and the total output of renewable energy generator nodes are shown in Figure 4.

FIGURE 4

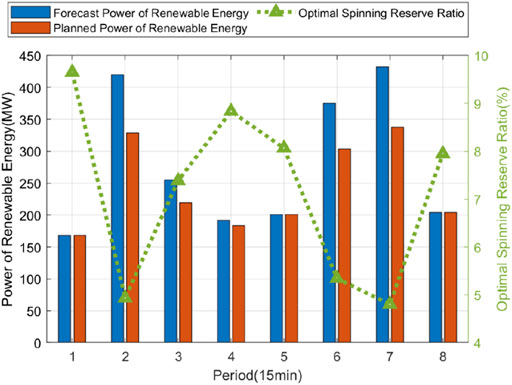
FIGURE 4. The relationship between the optimal ratio of renewable energy reserve of each period and the forecast power and planned power of the renewable energy.

Through analyzing the results of the optimization variables, it can be seen that the optimal spinning reserve ratio in each period has an inverse relationship with the renewable energy output in that period. That is to say, the higher the renewable energy output in a period, the smaller the optimal spinning reserve ratio in that period. The reason is that when the renewable energy output is high during the period, the same reserve ratio means that more reserve capacity will be reserved by the conventional generators. The excessive spinning reserve will occupy the scarce conventional generation resources of the post-disaster power system, resulting in a decline in the power supply efficiency of the system. Therefore, the optimization method in this paper can flexibly determine the spinning reserve rate in each period when the output of renewable energy fluctuates in different periods under extreme environments to maximizes the power supply benefit. Besides, the results show that loads with high priority fluctuate less with renewable energy output and have a high degree of satisfaction. In contrast, loads with low priority fluctuate more with the output of renewable energy and are almost zero when renewable energy output is low.

Under extreme environments, renewable energy generator nodes’ planned output is often lower than the forecast output to maximize the power supply benefit. The reason is that the topology of the post-disaster network is different from that of normal conditions, and constraints such as power flow constraint and active power balance constraint restrict the power of each node, including renewable energy generator nodes.

3.1.2 Improvement of Power Supply Benefit

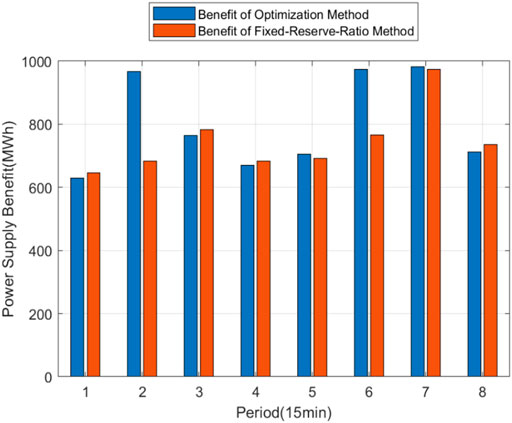
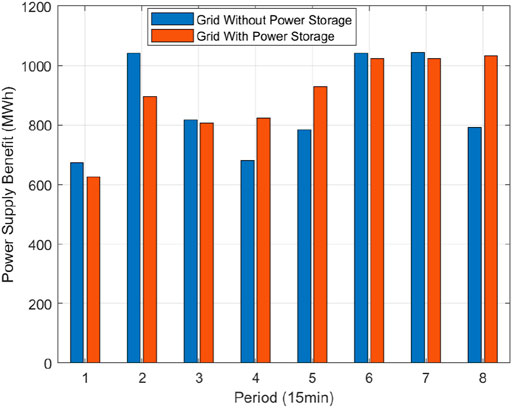
The reserve ratio is set to a fixed value (between 5 and 10%) by the traditional reserve configuration method [20]. The optimization method in this paper is compared with the traditional reserve configuration with a fixed ratio of 5%. And the power supply benefits in each period of the two methods are shown in Figure 5 for comparison.

FIGURE 5

FIGURE 5. Power supply benefits of the two methods in each period.

As for the total power supply benefit of 8 periods, the total benefit of the optimization method is 6405.471 MWh, while the total benefit of the traditional fixed-reserve-ratio method is 5961.039 MWh. Compared with the traditional method, the method proposed in this paper has significantly improved the power supply benefit by attaining a 7.45% increase in the total power supply benefit. However, as for the power supply benefit in some periods (such as periods 1 and 3), the optimization method behaves worse than the fixed-reserve-ratio method. The reason is that the objective function of the optimization method is the total benefit of all periods, and there are constraints of the output rate of change of the conventional generator nodes (Eqs 11, 12). As a result, the optimization method may try to obtain the optimal total benefit by sacrificing the benefit of some period.

3.2 Case 2 (Power System With Power Storage Plants)

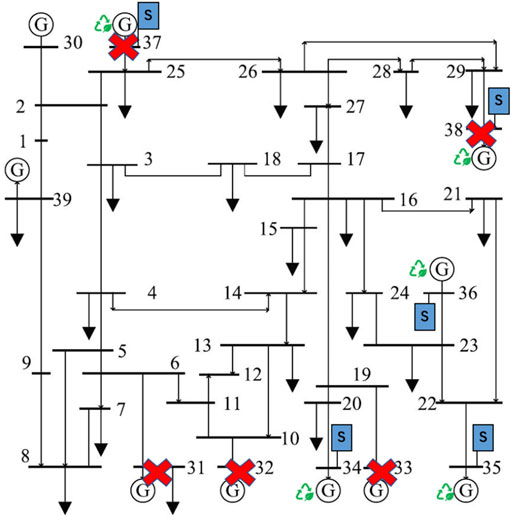
To analyze the impact of power storage plants on the power supply benefits for power networks with high penetrations of renewable energies under extreme environments, this paper implements another case study on a power network with power storage plants. Based on the power network in case 1, power storage nodes attached to renewable energy generator nodes are added to the grid, and load nodes are not assumed to be destroyed by disasters. The main parameters of nodes are the same as in case 1. The power network for case 2 is shown in Figure 6.

FIGURE 6

FIGURE 6. The power network with power storage nodes based on the IEEE 39-Bus system for case 2.

3.2.1 Results of Optimal Variables

This paper compares the power supply benefits of the two systems and the input power of loads with different power supply priorities in each period to analyze the influence of power storage nodes. The results are shown in Table 1, Figures 7, 8. The benefit loss factor is set to 10, the load priority weight is set to two levels of 1 and 10, and the standard deviation of the ultra short-term forecast error of the renewable energy output is set to 0.2 times the output of renewable energy generation. The optimized results are as follows.

TABLE 1

TABLE 1. Power Supply Benefit of the two systems.

FIGURE 7

FIGURE 7. Power supply benefits in each period of the two systems.

FIGURE 8

FIGURE 8. Input power of loads in each period of the two systems.

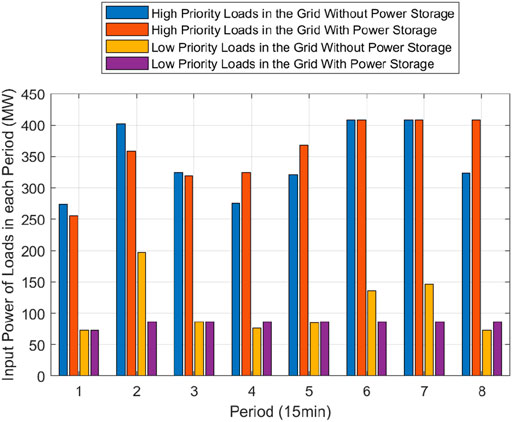
From Table 1 and Figure 7, it can be concluded that from the perspective of the power supply benefit in each period, the system with power storage does not always perform better than the original system without power storage. The reason is that a part of the generator nodes’ power in the system with power storage is absorbed by power storage nodes in certain periods, so the power supply benefits of these periods are often lower than the original system without power storage. However, the total power supply benefit of the power network with power storage increased by 4.2% than that of the original power system, showing the advantages of adding power storage. Besides, it can be seen from Figure 8 that the input power of high-priority loads in the system with power storage is higher than that of the system without power storage in most periods, while the input power of low-priority loads is lower than that of the system without power storage in most periods, indicating that loads with high power supply priority in the system with power storage account for a larger proportion of power supply. It can be concluded that the power system with power storage nodes guarantees the continuous power supply of critical loads at the expense of the power supply of low-priority loads, improving the total power supply benefit.

3.2.2 The Relationship Between the Output of Renewable Energy Generator Nodes and the Power of Storage Nodes in Each Period

To study the mechanism of how power storage plants improve the power supply benefit of power network with high penetration of renewable energies under extreme environments, this paper analyses the relationship among the forecasted output of renewable energy generator nodes, the planned output of renewable energy generator nodes, and the power of power storage nodes in the system with power storage nodes in each period, as shown in Figure 9.

FIGURE 9

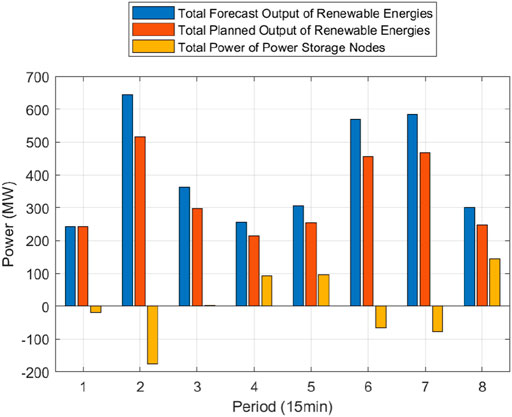
FIGURE 9. Relationship between the output of renewable energy generator nodes and the power of power storage nodes in each period.

It can be concluded from Figure 9 that the power storage can help regulate the fluctuant output of the renewable energy generation, like “cutting the peak and filling the valley.” When the output of the renewable energy generation is high, power storage plants act as loads by absorbing electricity power, while the output of the renewable energy generation is low, power storage plants act as generators by releasing electricity power. Unlike the power system under normal circumstances, the load is considered controllable in extreme environments, so the load is not volatile. The peak shaving effect of the power storage node in the optimization model is based on the extreme environment where the power supply is insufficient, and loads have a difference in power supply priority. When the output of the renewable energy generation is high, the power supply of the high-priority load may be saturated. During this time, the power supply benefit of supplying the remaining power to a low-priority load is poor. Thus the power storage plants store the electric power, which is relatively sufficient. When the output of the renewable energy generation is low, the power storage plants act as generators by releasing power, which can help high-priority loads getting better power supply when the power supply capacity is insufficient, ensuring the continuous power supply of the critical load. As a result, the power storage plants can help promote the short-term power supply benefits after disasters.

4 Conclusion

The problem of optimizing the power supply to critical loads after disasters considering the uncertainty of renewable energy output for a power network is studied in this paper. The overall power supply benefit of the power network with high penetrations of renewable energies in several post-disaster periods is identified as a resilience indicator of the power system with the consideration of the priority of different loads and safety risks. An optimization model for obtaining the total maximum power supply benefit is established with the spinning reserve ratio in each period, and the power of each node is taken as decision variables. The priority difference of each load and the negative impact of the failure to supply load as planned caused by the insufficient actual output of the renewable energy and insufficient spinning reserve is comprehensively considered in the objective function. Simulations on the IEEE 39-Bus Test Case are performed to verify the superior performance of the proposed method. The results show that the optimization method can flexibly determine the spinning reserve ratio and the power of each node in extreme environments, and increase the total power supply by 7.45%. Besides, another case studied is implemented to analyze the impact of power storage plants on the power supply benefits for power networks with high penetrations of renewable energies in extreme environments. Results show that the system with power storage guarantees the continuous power supply of critical loads by sacrificing the power supply for low-priority loads and improving the system’s total power supply benefit.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://matpower.org/.

Author Contributions

YH is responsible for the conceptualization and direction of the work. PL is for the problem formulation and validation of the method. XZ is responsible for the editing of the paper and funding acquisition. BM is responsible for the writing of the paper, data collection, and simulations. XM and ZL are responsible for simulation results analysis.

Funding

This paper is supported by Open Fund of State Key Laboratory of Operation and Control of Renewable Energy and Storage Systems (China Electric Power Research Institute) No. NYB51202001596.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.743670/full#supplementary-material

References

1. Panteli M, Trakas DN, Mancarella P, Hatziargyriou ND. Power Systems Resilience Assessment: Hardening and Smart Operational Enhancement Strategies. Proc IEEE (2017) 105:1202–13. doi:10.1109/jproc.2017.2691357

CrossRef Full Text | Google Scholar

2. Dong G, Gao J, Du R, Tian L, Stanley HE, Havlin S. Robustness of Network of Networks under Targeted Attack. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 87:052804. doi:10.1103/PhysRevE.87.052804

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Gao J, Barzel B, Barabási A-L. Universal Resilience Patterns in Complex Networks. Nature (2016) 530:307–12. doi:10.1038/nature16948

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Dong G, Fan J, Shekhtman LM, Shai S, Du R, Tian L, et al. Resilience of Networks with Community Structure Behaves as if under an External Field. Proc Natl Acad Sci USA (2018) 115:6911–5. doi:10.1073/pnas.1801588115

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Wu X, Dong H, Tse CK, Ho IWH, Lau FCM. Analysis of Metro Network Performance from a Complex Network Perspective. Physica A: Stat Mech its Appl (2018) 492:553–63. doi:10.1016/j.physa.2017.08.074

CrossRef Full Text | Google Scholar

6. Wu X, Dong H, Chi KT. A Three-Layer Model for Studying Metro Network Dynamics. IEEE Trans Syst Man, Cybernetics: Syst (2019) 51:2665–75. doi:10.1109/tsmc.2019.2915928

CrossRef Full Text | Google Scholar

7. Zhang X, Tu H, Guo J, Ma S, Li Z, Xia Y, et al. Braess Paradox and Double-Loop Optimization Method to Enhance Power Grid Resilience. Reliability Eng Syst Saf (2021) 215:107913. doi:10.1016/j.ress.2021.107913

CrossRef Full Text | Google Scholar

8. Wu J, Chen Z, Zhang Y, Xia Y, Chen X. Sequential Recovery of Complex Networks Suffering from Cascading Failure Blackouts. IEEE Trans Netw Sci Eng (2020) 7:2997–3007. doi:10.1109/tnse.2020.3008799

CrossRef Full Text | Google Scholar

9. Council NR. The Resilience of the Electric Power Delivery System in Response to Terrorism and Natural Disasters: Summary of a Workshop. Washington, D.C.: National Academies Press (2013).

10. Wu J, Fang B, Fang J, Chen X, Tse CK. Sequential Topology Recovery of Complex Power Systems Based on Reinforcement Learning. Physica A: Stat Mech its Appl (2019) 535:122487. doi:10.1016/j.physa.2019.122487

CrossRef Full Text | Google Scholar

11.National Academies of Sciences, E., Medicine. Enhancing the Resilience of the Nation’s Electricity System. Washington, D.C.: National Academies Press (2017).

12. Panteli M, Pickering C, Wilkinson S, Dawson R, Mancarella P. Power System Resilience to Extreme Weather: Fragility Modeling, Probabilistic Impact Assessment, and Adaptation Measures. IEEE Trans Power Syst (2016) 32:3747–57. doi:10.1109/tpwrs.2016.2641463

CrossRef Full Text | Google Scholar

13. Panteli M, Mancarella P, Trakas DN, Kyriakides E, Hatziargyriou ND. Metrics and Quantification of Operational and Infrastructure Resilience in Power Systems. IEEE Trans Power Syst (2017) 32:4732–42. doi:10.1109/tpwrs.2017.2664141

CrossRef Full Text | Google Scholar

14. Gao H, Chen Y, Mei S, Huang S, Xu Y. Resilience-oriented Pre-hurricane Resource Allocation in Distribution Systems Considering Electric Buses. Proc IEEE (2017) 105:1214–33. doi:10.1109/jproc.2017.2666548

CrossRef Full Text | Google Scholar

15. Zhang X, Guo J, Wang T, Zeng S, Ma S, Wu G. Identifying Critical Elements to Enhance the Power Grid Resilience. In: 2020 IEEE International Symposium on Circuits and Systems (ISCAS). IEEE (2020). p. 1–5. doi:10.1109/iscas45731.2020.9180814

CrossRef Full Text | Google Scholar

16. Hodge B-M, Milligan M. Wind Power Forecasting Error Distributions over Multiple Timescales. In: 2011 IEEE power and energy society general meeting. IEEE (2011). p. 1–8. doi:10.1109/pes.2011.6039388

CrossRef Full Text | Google Scholar

17. Bludszuweit H, Domínguez-Navarro JA, Llombart A. Statistical Analysis of Wind Power Forecast Error. IEEE Trans Power Syst (2008) 23:983–91. doi:10.1109/tpwrs.2008.922526

CrossRef Full Text | Google Scholar

18. Chaiyabut N, Damrongkulkamjorn P. Uncertainty Costs of Wind Power Generation Considering Expected Energy Not Supplied under Different Spinning reserve Levels. In: The Second IASTED International Conference OnPower and Energy Systems and Applications (2012). p. 1–5. PESA. doi:10.2316/p.2012.788-052

CrossRef Full Text | Google Scholar

19. Bouffard F, Galiana FD. Stochastic Security for Operations Planning with Significant Wind Power Generation. In: 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century. Pittsburgh, PA: IEEE (2008). p. 1–11. doi:10.1109/pes.2008.4596307

CrossRef Full Text | Google Scholar

20. Zimmerman RD, Murillo-Sánchez CE, Thomas RJ. Matpower: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans Power Syst (2010) 26:12–9. doi:10.1109/tpwrs.2010.2051168

CrossRef Full Text | Google Scholar