Normalized Shear Modulus and Damping Ratio of Soil–Rock Mixtures With Different Volumetric Block Proportions

Introduction

Soil–rock mixtures (SRMs) are inhomogeneous and heterogeneous geological materials widely used in infrastructure projects such as road foundations, earth dams, and slopes [1]. However, since their mechanical and physical properties are significantly determined by the interaction and properties of rock blocks, SRM belongs to neither the category of soil nor rock [2]. Great difficulties in parameter determination represent a significant challenge in engineering practice and thus have attracted the attention of scholars from home and abroad.

Soil dynamic parameters, including dynamic shear modulus (G), dynamic shear modulus ratio (G/G₀, G₀ was initial shear modulus), and damping ratio (λ) from small to large shear strain amplitude (γ_a), are significant indexes for the seismic design and stability analysis of structures and geo-structures subjected to seismic/repeated loading. Seed et al. [3], Rollins et al. [4], and Hardin and Kalinski [5] examined the G and λ of gravelly soils by cyclic triaxial tests. However, only a few tests were performed on gravel and gravelly soils due to the large size of the testing apparatus required. Lin et al. [6] pointed out that the large proportion of gravels and the unusual gap grading were the causes for the differing behavior of gravelly deposits. Tanaka [7] found that the G/G₀-γ_a relation of an undisturbed soil could be approximately described by that of the reconstituted soil sample. Araei et al. [8] believed that the dynamic characteristics of reconstituted gravelly soils were significantly affected by gravel content, confining pressure, and loading frequency. Wang et al. [9] further indicated that the dynamic soil properties showed significant changes when VBP was higher than 30%. Alhassan and VandenBerge [10] proposed a better distinguish between the behavior of compacted sand and gravel soils in normalized dynamic shear modulus and damping ratio with shear strain. Zhang et al. [11] studied the dynamic properties and damage evolution of silty soils with different volumetric block proportions (VBPs). Xu et al. [12] investigated the dynamic properties of sand–gravel mixtures with varying contents of gravel, loading cycles, and loading frequencies. Ye et al. [13] summarized the empirical models of dynamic shear modulus and the range of reduction curves for coarse-grained soils. It is not a stretch to infer that VBPs will significantly affect the dynamic properties of SRM. This study conducted undrained cyclic triaxial tests on SRM with different VBPs and confining pressures (CPs) to investigate their dynamic characteristic evolution. The relationships of G and λ with shear strain amplitude (γ_a) were discussed in detail.

Experiments

The Large-Scale Cyclic Triaxial System (GCTS HCA-300) was used to study the dynamic behavior of SRM. SRM samples were prepared with fine-grained soil and rock blocks. The fine-grained soil with particle size less than 2 mm was a residual soil formed in Quaternary, collected at Nanjing Tech University’s campus. The dry density of this soil was 1.63 g/cm³. The natural water content was 21.58%. The maximum dry density was 1.91 g/cm³, and the optimum moisture content was 12%. Considering that the sizes of cylindrical samples were 100 mm in diameter and 200 mm in height, the maximum diameter of rock blocks was limited to 20 mm to avoid the size effect. The natural density of dry rock blocks with particle sizes ranging from 2 to 20 mm was 2.36 g/cm³. Since the aerial phenomenon of rock blocks would result in significant difficulties in packing SRM samples into the mold when VBP was higher than 60%, only five VBP (0/15/30/45/60, %) combined with four CP (100/200/400/800, kPa) were considered in undrained cyclic triaxial tests. Given the water absorption of rock blocks, the extra 5% of water was mixed into SRM to avoid rock blocks absorbing water from the fine-grained soil. When SRM specimens were ready, they were saturated by a vacuum extractor until Skempton’s B achieved 0.95. The axial strain amplitude during loading process increased from 1 × 10^–5 to 1 × 10^–2 level by level. The specimen was reconsolidated at the same confining pressure for 15 min at least to achieve an effective pore water pressure dissipation as each strain loading level ended. The loading frequency was 0.5 Hz, and the loading cycle was 5.

Results and Discussion

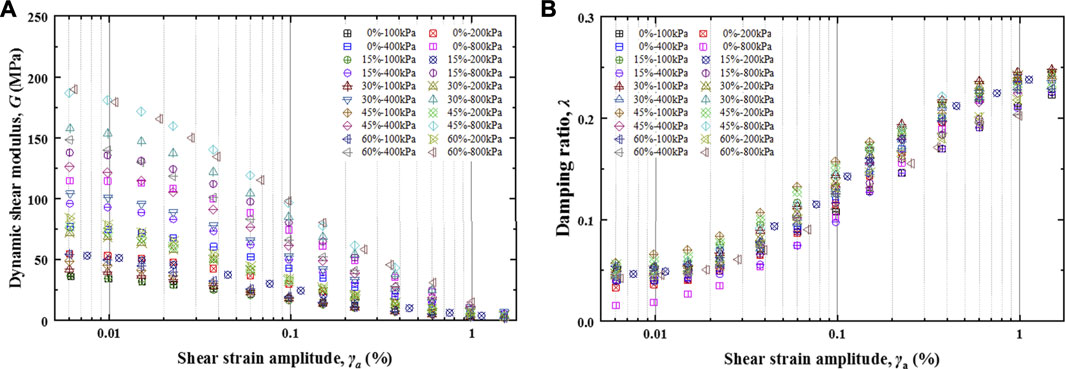
Figure 1A shows the G of SRM with different VBPs and CPs. The G of SRM exhibits degradation with γ_a on the whole. High CP always results in larger G values for SRM with the same VBP. The more significant deviation in CP, the more tremendous difference in the G of SRM. The G of SRM at low CP illustrates a slight discrepancy of G regardless of VBP. However, when CP increases, the difference in the G of SRM increases with VBP. These variations should be due to specimens’ compaction. High VBP may cause significant overhead phenomena in SRM. The higher CP can compact SRM specimens effectively, thereby resulting in denser structures with higher stiffness. The G₀ shows that both VBP and CP can positively impact soils’ fundamental stiffness.

FIGURE 1

FIGURE 1. G and λ of SRM with different VBPs and CPs.

Figure 1B shows the λ of SRM with different VBPs and CPs. The λ of SRM increases with γ_a and shows a zonal distribution on the whole. The whole growth process of λ can divide into the initial stage (γ_a < 0.01%), the growth stage (0.01% ≤ γ_a ≤ 1.0%), and the stable stage (γ_a > 1.0%). High VBP always results in λ growing earlier in the initial stage. The growth rate of λ is approximately the same at the growth stage, no matter what VBP is. Results of SRM with the same VBP show that high CP can narrow the distribution of λ.

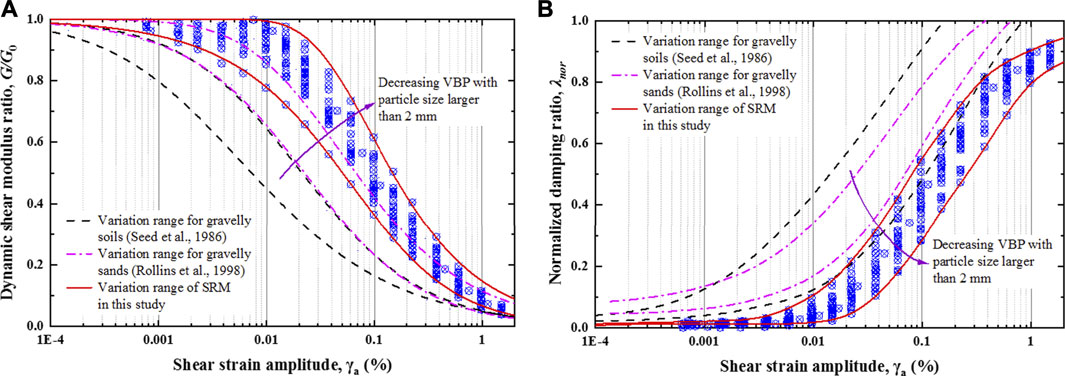
Figure 2A presents the envelope curves of G/G₀ of SRM with different VBP and CP, which exhibits a similar behavior identified by previous researchers. The G/G₀ falls within a relatively narrow band at the γ_a of 5 × 10^–4% but has almost no effect on the curve shape of G/G₀ in γ_a less than the order of 10⁻⁴%. In 1972, Hardin and Drnevich [14] proposed a hyperbolic shear modulus reduction function for soils. Darendeli [15] further proposed a modified hyperbolic model based on testing of sand and gravel samples as

$G/G_0=1/\left(1+{\left({\gamma }_a/{\gamma }_r\right)}^{\alpha }\right),(1)$

where γ_r is the reference shear strain and is determined as the shear strain when G/G₀ = 0.5; α is the regression parameter. The G/G₀ of SRM thus can be characterized by following this hyperbolic model. It can also be found that when VBP in SRM is higher than 45%, the G/G₀ curve begins to overlap with the bounds proposed by Rollins et al. [4]. When VBP in SRM is less than 45%, the G/G₀ curve almost does not overlap anymore, especially in γ_a between 0.01 and 0.1%. Seed et al. [3] indicated that the curve characteristics of G/G₀ for natural gravel deposits with VBP of 92% at least were similar to that of sandy soil but gentler. This find also highlights that the envelope curves of G/G₀ for gravelly soils are below that of SRM.

FIGURE 2

FIGURE 2. Envelope curves of G/G₀ and λ of SRM with different VBPs and CPs.

Figure 2B shows the envelope curves of normalized λ (λ_nor) of SRM with different VBP and CP, following the empirical model proposed by Chen et al. [16].

${\lambda }_{nor}={\lambda }_0{\left(1-G/G_0\right)}^{\beta }/\left({\lambda }_{\max }-{\lambda }_{\min }\right),(2)$

where λ_min and λ_max are the minimum and maximum damping ratios, λ₀ and β are regression parameters related to soil properties. Similarly, the variation of λ_nor falls within a relatively narrow band at the γ_a of 5 × 10^–3% and has almost no effect on the shape of λ_nor with γ_a < 10^–3%. The reason why the envelope curves of λ_nor for SRM is lower than gravelly soils examined by Seed et al. [3] and Rollins et al. [4] may be that the soil with high VBP is harder to compact but more likely to form a loose structure in low CP when subjected to cyclic loadings, thereby resulting in a faster increase of λ_nor.

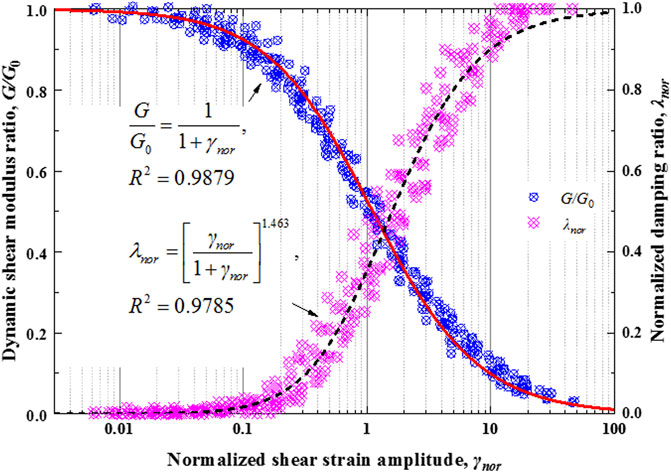
Figure 3 illustrates the G/G₀ and λ_nor of SRM with normalized shear strain amplitude (γ_nor = γ_a/γ_r). Both of them are falling within the relatively narrow bands. Namely, the G/G₀ and λ_nor of SRM with γ_nor are not sensitive to VBP and CP. According to the modified hyperbolic model as Eq. 1 proposed by Darendeli [15], the nonlinear relationship of G/G₀ with γ_nor for SRM was fitted. It can be found that this modified hyperbolic model is also appropriate to SRM with an excellent correlation coefficient up to 0.9879.

FIGURE 3

FIGURE 3. G/G₀ and normalized λ of SRM with γ_nor.

Taking Eq. 1 into Eq. 2 yields the following:

${\lambda }_{nor}={\left[{\mathit{\gamma }}_{nor}^{\alpha }/\left(1+{\gamma }_{nor}^{\alpha }\right)\right]}^{\beta }.(3)$

The fitting result of λ_nor shows that it has a high correlation of 0.9789 with γ_nor. So the empirical correlation can also be used to characterize the changes in the λ of SRM under cyclic loadings.

Conclusion

Cyclic triaxial tests were conducted to understand the dynamic properties of SRM further. Outcomes indicate that both VBP and CP can positively impact the fundamental stiffness (G₀) and λ of SRM. High VBP in coarse-grained soils is more likely to result in a gentler reduction in G/G₀ and a faster increase of λ_nor. Both G/G₀ and λ_nor of SRM can be evaluated by functions of γ_nor regardless of VBP and CP. This study’s results can provide a valuable reference to understand the dynamic response characteristics and energy dissipation mechanisms of SRM and other similar geo-materials.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

Funding acquisition and formal writing of the work, SW and XG; investigation and data analysis of the work, HH; review and editing of the work, WM, CS, and PZ. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (No. 41902282), the Natural Science Foundation of Jiangsu Province (No. BK20171006), and the State Key Laboratory of Frozen Soil Engineering (No. SKLFSE201809).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang H, Cui Y, Lamas-Lopez F, Dupla J, Canou J, Calon N, et al. Effects of Inclusion Contents on the Resilient Modulus and Damping Ratio of Unsaturated Track-Bed Materials. Can Geotechnical J (2017) 54(12):1672–81. doi:10.1139/cgj-2016-0673

CrossRef Full Text | Google Scholar

2. Wang S, Li Y, Gao X, Xue Q, Zhang P, Wu Z. Influence of Volumetric Block Proportion on Mechanical Properties of Virtual Soil-Rock Mixtures. Eng Geology (2020) 278:105850. doi:10.1016/j.enggeo.2020.105850

CrossRef Full Text | Google Scholar

3. Seed HB, Wong RT, Idriss IM, Tokimatsu K. Moduli and Damping Factors for Dynamic Analyses of Cohesionless Soils. J geotechnical Eng (1986) 112(11):1016–32. doi:10.1061/(asce)0733-9410(1986)112:11(1016)

CrossRef Full Text | Google Scholar

4. Rollins KM, Evans MD, Diehl NB, Daily WD. Shear Modulus and Damping Relationships for Gravels. J Geotechnical Geoenvironmental Eng (1998) 124(5):396–405. doi:10.1061/(asce)1090-0241(1998)124:5(396)

CrossRef Full Text | Google Scholar

5. Hardin BO, Kalinski ME. Estimating the Shear Modulus of Gravelly Soils. J Geotechnical Geoenvironmental Eng (2005) 131(7):867–75. doi:10.1061/(ASCE)1090-0241(2005)131:7(867)

CrossRef Full Text | Google Scholar

6. Lin S, Lin PS, Luo H, Juang CH. Shear Modulus and Damping Ratio Characteristics of Gravelly Deposits. Can Geotechnical J (2000) 37(3):638–51. doi:10.1139/t99-133

CrossRef Full Text | Google Scholar

7. Tanaka Y. Evaluation of Undrained Cyclic Strength of Gravelly Soil by Shear Modulus. Soils and Foundations (2003) 43(4):149–60. doi:10.3208/sandf.43.4_149

CrossRef Full Text | Google Scholar

8. Araei AA, Razeghi HR, Tabatabaei SH, Ghalandarzadeh A. Dynamic Properties of Gravelly Materials. Scientia Iranica (2010) 17(4):245–61.

Google Scholar

9. Wang Y, Li X, Zheng B. Stress-strain Behavior of Soil-Rock Mixture at Medium Strain Rates – Response to Seismic Dynamic Loading. Soil Dyn Earthquake Eng (2017) 93:7–17. doi:10.1016/j.soildyn.2016.10.020

CrossRef Full Text | Google Scholar

10. Alhassan MM, VandenBerge DR. Shear Modulus and Damping Relationships for Dynamic Analysis of Compacted Backfill Soils. Innovative Infrastructure Solutions (2018) 3:43. doi:10.1007/s41062-018-0152-5

CrossRef Full Text | Google Scholar

11. Zhang D, Li Q, Liu E, Liu X, Zhang G, Song B. Dynamic Properties of Frozen Silty Soils with Different Coarse-Grained Contents Subjected to Cyclic Triaxial Loading. Cold Regions Sci Technol (2019) 157:64–85. doi:10.1016/j.coldregions.2018.09.010

CrossRef Full Text | Google Scholar

12. Xu D, Liu H, Rui R, Gao Y. Cyclic and Postcyclic Simple Shear Behavior of Binary Sand-Gravel Mixtures with Various Gravel Contents. Soil Dyn Earthquake Eng (2019) 123:230–41. doi:10.1016/j.soildyn.2019.04.030

CrossRef Full Text | Google Scholar

13. Ye Y, Cai D, Yao J, Wei S, Yan H, Chen F. Review on Dynamic Modulus of Coarse-Grained Soil Filling for High-Speed Railway Subgrade. Transportation Geotechnics (2021) 27:100421. doi:10.1016/j.trgeo.2020.100421

CrossRef Full Text | Google Scholar

14. Hardin BO, Drnevich VP. Shear Modulus and Damping in Soils: Design Equations and Curves. J Soil Mech Foundations Div (1972) 98:667–92. doi:10.1061/jsfeaq.0001760

CrossRef Full Text | Google Scholar

15. Darendeli MB. Development of a new family of normalized modulus reduction and material damping curves. Texas: University of Texas at Austin (2011).

16. Chen G, Zhou Z, Sun T, Wu Q, Xu L, Khoshnevisan S, et al. Shear Modulus and Damping Ratio of Sand-Gravel Mixtures over a Wide Strain Range. J earthquake Eng (2019) 23(8):1407–40. doi:10.1080/13632469.2017.1387200

CrossRef Full Text | Google Scholar