Actively Controlled Frequency-Agile Fano-Resonant Metasurface for Broadband and Unity Modulation

The active control to the local resonant mode of metasurface is a promising route for improving the operation bandwidth limitation of metasurface. Here, we propose and experimentally demonstrated the active tunabilities in a frequency-agile Fano-resonant metasurface. The metasurface with a pair of asymmetric split ring resonators is integrated with double varactor diodes for active control of the sharp Fano resonance. It is found that the sharp Fano-type spectrum appears due to the near-field interferences between the collective electric and magnetic dipole modes. The physical insight is revealed through local field analysis, multipole decomposition and temporal coupled-mode theory. It is also found that the metasurface can be employed as a broadband and unity modulator. Hopefully, our results could inspire sophisticated electrically controlled photonic devices with novel functions.

Introduction

Metamaterials are artificial engineered subwavelength structures with tailorable properties superior to the natural materials, which have shown unprecedented capability in exterior light manipulations [1–5]. Since three-dimensional metamaterials are difficult to design and fabricate, their two-dimensional (2D) counterpart, metasurfaces [6–10], constructed by subwavelength metallic or dielectric particles in a planar platform, have attracted considerable attention in recent years for the arbitrary control of electromagnetic waves [11–13]. Metasurfaces have inspired extraordinary light manipulations such as invisibility cloak [14], broadband achromatic metalens [15], arbitrary orbital angular momentum generation [16], enhanced nonlinear photonics [17], and meta-hologram [18]. Compared with 3D complex metamaterials, planar metasurfaces with subwavelength-thickness monolayer or few functional layers [19, 20] are easier to fabricate by utilizing sophisticated processing techniques. Besides, the subwavelength thickness of metasurfaces along the propagating direction is beneficial for miniaturizing optical systems and improving working efficiency [21, 22].

Fano resonance appears when a discrete localized state interferences with a continuum band of states [23]. In general, Fano resonance is always accompanied by a high-Q factor and significant local field enhancement, showing a sharp transmission or reflection curves [24, 25]. Recently, metasurfaces with so-called bright and dark modes are designed to resemble the original physical mechanism of Fano resonance [26–28], i.e., interference between a narrow discrete resonance with a broadband spectral line in a quantum system. The bright and dark modes have different scattering pathways for the incident waves. The bright mode can be directly excited by incident waves in free space, while the dark mode is weakly coupled to incident waves and can be excited through near field coupling with the bright mode by breaking the geometric symmetry [29–31]. Fano resonances with high quality factors can be generated through the interference between the new-emergent narrow dark mode and the original continuum mode [32–34]. The Fano metasurfaces are generally accompanied with extremely sharp reflection or transmission curves and are widely studied due to the attractive feature of high-Q response [35–38].

Fano metasurfaces have been proven and considered as a very promising platform for the high-Q response with enhanced light-matter interactions, but the intrinsic narrow operation bandwidth may significantly hinder them towards practical applications due to their resonant natures. Although it can be optimized by incorporating changeable materials [39–42] or employing reconfigurable structures [43, 44] to extend the bandwidth, this greatly complicates the manufacturing process and also makes it more expensive/difficult to embed into increasingly integrated photonic systems. Here in this paper, we experimentally demonstrated an electrically tunable frequency-agile Fano-resonant metasurface with a pair of asymmetric split ring resonators (ASRRs) configuration. The ASRRs metasurface is integrated with double varactor diodes for active control of the sharp Fano resonance. Remarkable blue shift on the Fano resonance frequency was demonstrated by increasing the bias voltage from 0 to 8 V to electrically tune the capacitances of the varactor diodes. The sharp Fano-type spectrum appears due to the near-field couplings between the collective electric and magnetic dipole modes, and its physical insight is revealed through local field analysis, multipole decomposition and temporal coupled-mode theory (TCMT). Moreover, we also found that the metasurface can be employed as a broadband and unity modulator. The proposed strategy provides an alternative way to overcome the limited bandwidth of conventional meta-devices, which may facilitate the development of low-cost and high-performance active photonic applications.

Results and Discussion

The schematic of our designed metasurface is shown in Figure 1A. It consists of a pair of asymmetric split ring resonators (ASRRs) with different side lengths. To realize the electrically tunable frequency-agile Fano resonance, double varactor diodes (BBY52-02W, Infineon) are soldered at the middle gap of the ASRRs pair and are biased through four copper wires. The varactor diodes have a series resistance of 0.9 Ω and inductance of 0.6 nH, respectively. Four inductors are located between the bias wires and ASRRs to effectively avoid the cross talk. By applying external bias voltage on the varactor diodes, their capacitance can be significantly changed and the Fano resonance can be dynamically modulated accordingly. The photograph of a fabricated sample is shown in Figure 1B. The metallic pattern is 0.035 mm thick copper on a 1 mm thick Teflon base and is fabricated through standard printed circuit board (PCB) technology. The Teflon substrate was cut to a dimension of 72.14 × 34.04 mm² corresponding to the cross-section of a standard waveguide WR284, and simultaneously ensuring the metallic patterns at the center of the substrate. In our experiments, the scattering parameters of the metasurface are measured inside a standard waveguide of WR284, where the TE₁₀ mode with an electric field polarizing along the y direction is normally incident on the metasurface, and are recorded through a vector network analyzer (AV3629D).

FIGURE 1

FIGURE 1. Front view of the frequency-agile Fano-resonant metasurface. Schematic diagram (A) and photograph (B) of the fabricated sample. The metasurface is composed of a pair of asymmetric split ring resonators (ASRRs) on a Teflon substrate. Double varactor diodes are soldered in the middle gap of the asymmetric rings. Four inductors and four bias copper wires are integrated into the metasurface. The geometric parameters are: a = 13 mm, b = 14 mm, w = 2 mm, g = 1.3 mm, and δ = 8 mm.

To understand the design strategy of the Fano-resonant metasurface, we would like to firstly consider the spectral response of the coupled metasurface design (see Figure 2A). The calculations were carried out within a perfect electric conductor (PEC) around an air box to simulate a standard waveguide of WR284. In the simulations, PEC boundaries are set along x and y directions, and open boundaries are set along z direction. An excitation source is applied at the boundary of z direction. For a metasurface with only left split ring resonator (SRR), a typical symmetric Lorentz-type resonance dip appears at f₁ (2.99 GHz), while for a metasurface with only right SRR, another typical symmetric Lorentz-type resonance dip occurs at frequency f₂ (2.77 GHz). These resonators show electric dipolar resonances arising from the current induced by the incident electric field in the asymmetric metallic sides of SRR, which are further confirmed by the electric field and surface current distributions shown in Figures 2C,D. Since their resonant frequencies are close to each other, we may expect some interesting phenomena when we set the asymmetric SRRs in a close proximity, resulting from the near-field interference.

FIGURE 2

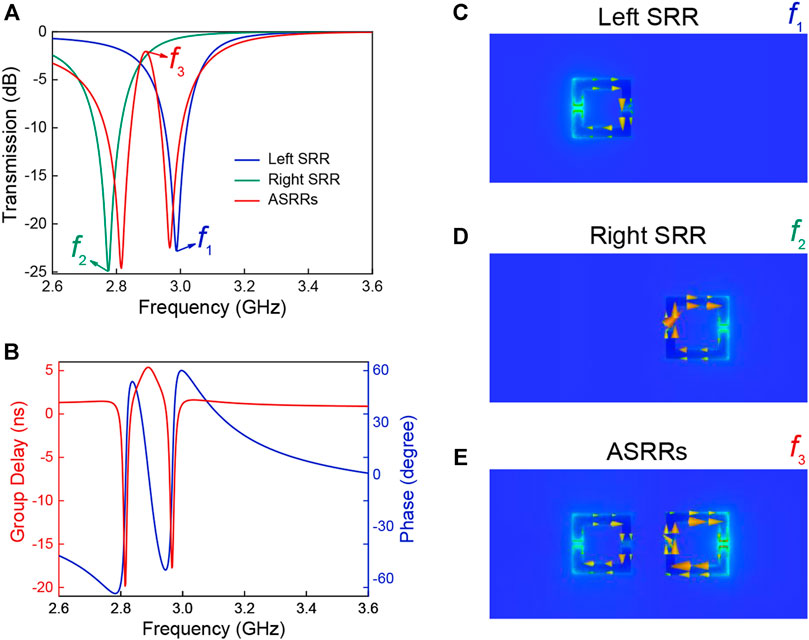
FIGURE 2. (A) Calculated transmission spectra of the left SRR only (blue curve), right SRR only (green curve), and the asymmetric SRR pair (red curve). (B) Calculated transmission group delay (red curve) and phase (blue curve) of the metasurface. (C–E) Instantaneous distributions of the out-of-plane electric field and the induced surface current corresponding to the resonant frequencies at f₁, f₂, and f₃ in section (A). Arrows indicate the instantaneous directions of the current flow. All these results are obtained when the capacitance of varactor diodes is 2.63 pF.

The red curve in Figure 2A shows the calculated transmission spectrum of the ASRRs metasurface. The near field coupling between the ASRRs leads to an asymmetric Fano-shaped profile with a sharp change between the dip and peak. The destructive interference between the ASRRs also results in a sharp transparency window around frequency f₃ (2.89 GHz), which is similar to the analogy of the electromagnetically induced transparency [28]. Note that the transparency peak of the metasurface is quite sharp with a full width at half-maximum (FWHM) of 0.0558 GHz, reaching a high quality factor of 52. The calculated transmission group delay and phase are shown in Figure 2B, from which we can see that around the transparency peak, the transmission phase experiences an abrupt variation, leading to strong dispersion of the effective parameters and a large group delay of 5.4 ns. To explore the underlying mechanism of the Fano-type resonance and the sharp transmission window, we calculated the surface current and electric field distribution at the transmission peak f₃ (see Figure 2E). The induced surface currents on the ASRRs are oscillating in-phase, forming a collective magnetic mode M_z. This new emergent mode M_z, as a non-radiative dark state (sharp discrete mode), is weakly coupling with the incident electromagnetic field, and destructively interfering with the background electric dipole mode P_y (broadband continuum mode), resulting in the sharp transparency window.

To further understand the near-field coupling mechanism of the metasurface, we calculated the contributions of various multipole moments induced in the metasurface. The electric and magnetic dipole moments of the metasurface can be quantitatively evaluated with the following formula [45].

$\mathbf{P}=\frac{1}{i\omega }\int \mathbf{j}{\mathit{d}}^3\mathbf{r}(1)$

$\mathbf{M}=\frac{1}{2c}\int \left(\mathbf{r}\times \mathrm{j}\right)d^3\mathbf{r}(2)$

where j is the current density, ω is the angular frequency, and c is the speed of light in vacuum. The multipole moments can be calculated by integrating spatially distributed current density extracted from the simulation. The calculated normalized magnitude and the corresponding phase of the electric dipole moment P_y and the magnetic dipole moment M_z are presented in Figures 3A,B, respectively.

FIGURE 3

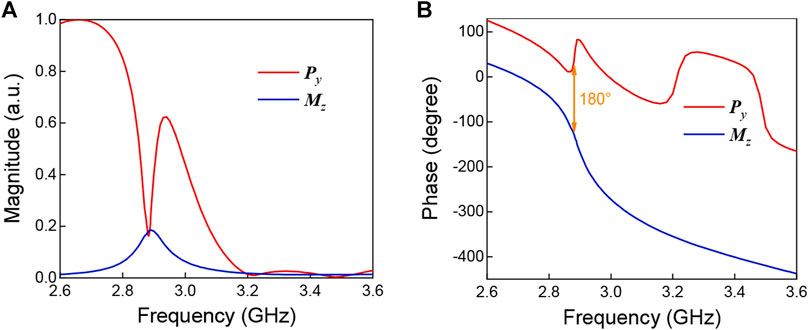
FIGURE 3. Normalized magnitude (A) of multipole moments P_y and M_z, and their corresponding phase (B) induced in the ASRRs metasurface with the capacitance 2.63 pF: the electric dipole (red curve), and magnetic dipole (blue curve).

We can find that the electric dipole P_y, as a bright mode resonance, shows strong scattering over the entire interesting frequency band, indicating that the ASRRs metasurface strongly couples to the y-polarized electric field component in the waveguide. The collective oscillations of the electric dipoles can be considered as a broadband continuum mode. Around the transparency peak frequency f₃, the P_y is significantly suppressed, while the M_z is excited and enhanced to a similar magnitude as P_y, and the phase difference between the P_y and M_z is about 180°, which further confirms the fact that these two modes interference destructively, and their scattering cancellation results in the non-radiating configuration and the sharp transparency window. We notice that the collective magnetic dipole mode cannot be directly excited by the incident wave, as the metasurface is placed in a standard rectangular waveguide where only the fundamental TE₁₀ mode can propagate in the frequency band of interest. However, the collective magnetic dipole mode can be excited through near-field coupling, leading to the collective oscillation of the ASRRs and the suppression of electric dipolar mode, and forming the dark mode resonance.

To quantitatively evaluate the interaction between the incident wave and the metasurface, we also employed TCMT to analyze the mode coupling between the collective electric and magnetic dipoles. The transmission spectrum of the metasurface excited by a monochromatic wave can be expressed as below [46, 47].

$t=\frac{\left(j\omega -j{\omega }_1+{\mathrm{\Gamma }}_{i1}\right)\left(j\omega -j{\omega }_2+{\mathrm{\Gamma }}_{i2}\right)+k^2}{\left(j\omega -j{\omega }_1+{\mathrm{\Gamma }}_{i1}+{\mathrm{\Gamma }}_{e1}\right)\left(j\omega -j{\omega }_2+{\mathrm{\Gamma }}_{i2}\right)k^2}.(3)$

where ω₁, Γ_e1, and Г_i1 (or ω₂, Γ_e2, and Г_i2) are the resonant frequency, radiative decay rate, and non-radiative decay rate of the bright (or dark) resonator, respectively, and κ is the coupling coefficient. We can obtain the characteristic parameters of the resonator system through fitting the expression of |t| to the simulated transmission spectrum of the metasurface (red curve in Figure 2A), as follows:

${\omega }_1=2\pi \times 2.88\times {10}^{9}rad/s,$

${\omega }_{12}=2\pi \times 2.891\times {10}^{9}rad/s,$

${\mathrm{\Gamma }}_{e1}=2\pi \times 0.197\times {10}^{9}rad/s,$

${\mathrm{\Gamma }}_{i1}=2\pi \times 0.0035\times {10}^{9}rad/s,$

${\mathrm{\Gamma }}_{i2}=2\pi \times 0.009\times {10}^{9}rad/s,$

$k=2\pi \times 0.076\times {10}^{9}rad/s.$

It can be found that the ω₁ and ω₂ correspond to the dip of electric dipole moment P_y (as bright mode) and the peak of magnetic dipole moment of M_z (as dark mode), respectively, (Figure 3A), indicating that our metasurface systems are dominated by these two modes. For the collective electric dipole mode, the radiative decay rate, Г_e1, is about 56 times larger than the non-radiative decay rate, Г_i1. Both the radiative and non-radiative decay rate of collective magnetic dipole mode, Г_e2 and Г_i2 are much less than Г_e1 and Г_i1, so they are negligible. The frequency interval between the two transmission dips of our metasurface is only 0.15 GHz, since the coupling coefficient κ is much less than the resonant frequencies, ω₁ and ω₂, and even the radiative decay rate, Г_e1. The TCMT accurately predicts the transmission spectrum of the metasurface, as shown in Figure 4.

FIGURE 4

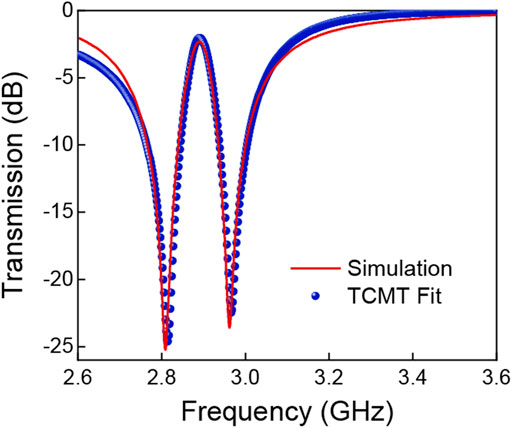
FIGURE 4. Transmission spectra of the metasurface predicted by the TCMT (blue points) and simulated through FDTD (red curve) with the capacitance 2.63 pF.

The tunabilities of the metasurface can be understood as a LC circuit with changeable capacitances. The electric resonance frequency is determined by $\omega ={\left(LC\right)}^{-1/2}$. So the resonance frequency of SRR and the Fano-type resonance frequency can be manipulated significantly by applying voltage to alter the capacitance of varactor diodes. Next, the transmission properties of the SRR alone under different bias voltages are investigated. The measured and calculated transmission spectra of the single SRR with different voltages (capacitances in simulations) are shown in Figure 5. As the bias voltage gradually increases from 0 to 8 V, the capacitance of the varactor diode decreases from 2.63 to 0.76 pF, and the corresponding transmission spectrum undergoes a remarkable blue shift; the experimental resonant frequency of the left SRR alone undergoes a blue shift of 0.22 GHz from 3.09 to 3.31 GHz (see Figure 5A), and similarly, the experimental resonant frequency of the right SRR alone undergoes a blue shift of 0.21 GHz from 2.93 to 3.14 GHz (see Figure 5B). The calculated trend (Figures 5C,D) agrees well with the measured results, implying the effective frequency-agile tunability by the integrated varactor diodes.

FIGURE 5

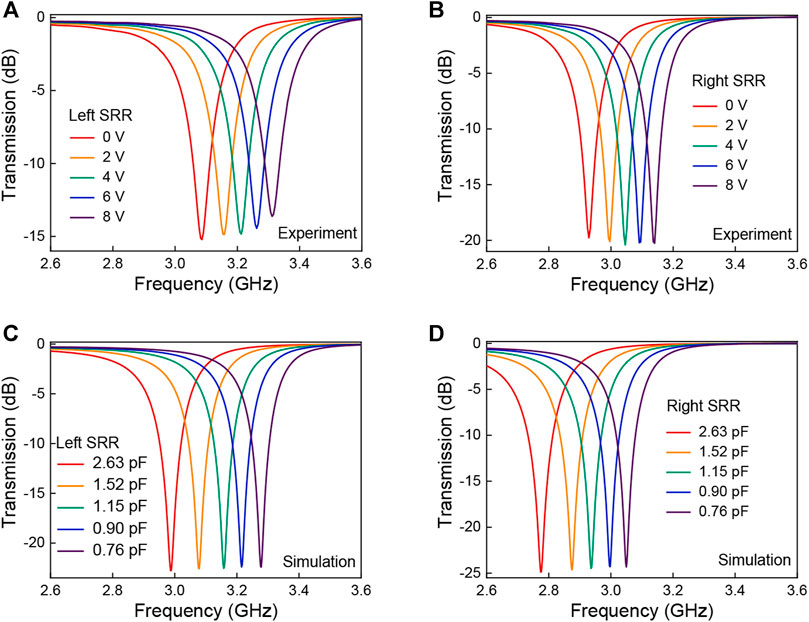
FIGURE 5. Measured (A), (B) and calculated (C), (D) transmission spectra of the SRR alone with different bias voltages (from 0 to 8 V) and corresponding capacitances (from 2.63 to 0.76 pF): the left SRR alone (A), (C), and right SRR alone (B), (D).

To actively control the Fano-type resonance, double varactor diodes are then integrated into the ASRRs metasurface system. The dynamic modulation on Fano resonance of the frequency-agile metasurface is illustrated in Figure 6. When no voltage is applied, the measured Fano resonance peak occurs at 2.98 GHz (see Figure 6A). As the bias voltage gradually increases from 0 to 8 V, the Fano resonance peak gradually shifts from 2.98 to 3.2 GHz, exhibiting a blue shift of 0.22 GHz. Although there is a small amplitude variation, the significant sharp transmission feature is preserved. Meanwhile, the transmission dips of the Fano resonance also exhibit blue shifts of 0.2 and 0.22 GHz, respectively. The calculated results (Figure 6B) show good agreement with our measured results. It is worth mentioning that the lower frequency dip completely exceeds the upper frequency dip when the applied voltage is changed from 0 to 8 V, thanks to the sharp dispersion characteristic of Fano resonance. It indicates that our metasurface can be employed not only for a frequency-agile device, but also for a broadband and unity amplitude modulator.

FIGURE 6

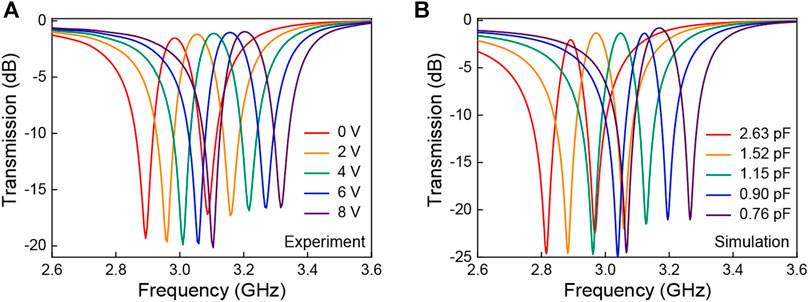
FIGURE 6. Measured (A) and calculated (B) transmission spectra of the frequency-agile metasurface with different bias voltages (from 0 to 8 V) and corresponding capacitances (from 2.63 to 0.76 pF).

To show the amplitude modulation performance of our metasurface, we here plot the transmission with different bias voltages, as shown in Figure 7. Remarkable modulation on transmission can be realized through electric biasing at several frequency points. For example, the measured transmission curves at three selected frequencies of 2.89, 3.10 and 3.32 GHz with different voltages are plotted. As the voltage changes from 0 to 8 V, the transmittance at 2.89 GHz monotonously increases from −19.31 dB to −1.63 dB (red curve), while at 3.32 GHz monotonously decreases from −0.59 dB to −16.29 dB (blue curve), showing a remarkable modulation performance. In particular, the transmittance at 3.10 GHz (green curve), shows a growing trend from −14.31 dB to −1.16 dB with the voltage increased from 0 to 4 V, while a downward trend from −1.16 dB to −19.62 dB when further increasing the voltage to 8 V. Note that although our results were obtained in a waveguide system, the similar modulation performance can also be achieved with periodic structures in free space.

FIGURE 7

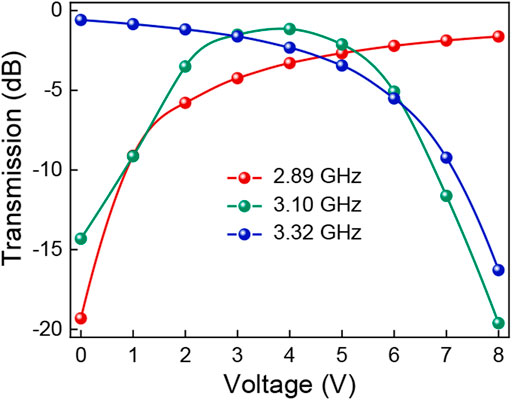
FIGURE 7. Measured transmission of the metasurface with different bias voltages ranging from 0 to 8 V at 2.89 GHz (red), 3.10 GHz (green), and 3.32 GHz (blue).

Conclusion

In conclusion, we have experimentally demonstrated the active tunabilities in a frequency-agile Fano-resonant metasurface. The sharp Fano resonance can be dynamically modulated by integrating a pair of varactor diodes in the metasurface. We found that the non-radiative collective magnetic dipole mode was excited in our metasurface and its physical insight is uncovered through local field analysis, multipole decomposition and TCMT. We also found significant manipulation on both frequency tuning and amplitude modulation by applying bias voltage on the varactor diodes. The demonstrated frequency-agile Fano-resonant metasurface is promising for realizing sophisticated electrically controlled microwave devices with novel functions, which may facilitate the development of high-performance active photonic applications in, e.g., smart sensing or signal processing.

Methods

Numerical Simulation: Numerical simulations are carried out using the finite-element frequency-domain solver. The metallic pattern with a conductivity of 5.8 × 10⁷ S/m is standing on a Teflon substrate with a relative permittivity of 2.65 and a tangent loss of 0.0004. In the simulations, PEC conditions are applied in both the x and y directions and open boundaries are set along z direction. An excitation source is applied at the boundary of z direction. The multipole moments P_y and M_z can be calculated by integrating spatially distributed current density extracted from the simulation utilizing the commonly used formulas (Eqs. 1, 2).

Experiments: The printed circuit board (PCB) technique was used to fabricate the metallic ASRRs pattern. The Teflon substrate was cut to a dimension of 72.14 × 34.04 mm² corresponding to the cross-section of a standard waveguide WR284, and simultaneously ensuring the metallic patterns at the center of the substrate. In the measurements, the sample was placed inside a WR284 rectrangular waveguide, and was measured through a vector network analyzer (AV3629D).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

QF, YF, and FZ conceived the idea and guided the research. RY designed the metasurface, characterized the samples, and wrote the article. JX, WZ and WC contributed to the final version of the article. All authors discussed the results and commented on the paper.

Funding

The authors would like to acknowledge financial support from Natural Science Foundation of China (NSFC) (Grants No. 12074314, 11774057, 11674266, 61771402), NPU AoXiang New Star program, Science, Technology and Innovation Commission of Shenzhen Municipality (JCYJ20170817162221169), Shaanxi Province Postdoctoral Science Foundation (No. 2018BSHEDZZ64), and Natural Science Basic Research Plan in Shaanxi Province of China (Nos. 2018JM6024, 2020JM-145).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Linden S, Enkrich C, Wegener M, Zhou J, Koschny T, Soukoulis CM. Magnetic Response of Metamaterials at 100 Terahertz. Science (2004) 306:1351–3. doi:10.1126/science.1105371

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Smith DR, Pendry JB, Wiltshire MC. Metamaterials and Negative Refractive Index. Science (2004) 305:788–92. doi:10.1126/science.1096796

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Chen H-T, Padilla WJ, Zide JMO, Gossard AC, Taylor AJ, Averitt RD. Active Terahertz Metamaterial Devices. Nature (2006) 444:597–600. doi:10.1038/nature05343

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Zhao Q, Zhou J, Zhang F, Lippens D. Mie Resonance-Based Dielectric Metamaterials. Mater Today (2009) 12:60–9. doi:10.1016/S1369-7021(09)70318-9

CrossRef Full Text | Google Scholar

5. Yang R, Xu J, Shen NH, Zhang F, Fu Q, Li J, et al. Subwavelength Optical Localization With Toroidal Excitations in Plasmonic and Mie Metamaterials. InfoMat (2021) 3:577–97. doi:10.1002/inf2.12174

CrossRef Full Text | Google Scholar

6. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, et al. Light Propagation With Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science (2011) 334:333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sun S, He Q, Xiao S, Xu Q, Li X, Zhou L. Gradient-Index Meta-Surfaces as a Bridge Linking Propagating Waves and Surface Waves. Nat Mater (2012) 11:426–31. doi:10.1038/NMAT3292

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Glybovski SB, Tretyakov SA, Belov PA, Kivshar YS, Simovski CR. Metasurfaces: From Microwaves to Visible. Phys Rep (2016) 634:1–72. doi:10.1016/j.physrep.2016.04.004

CrossRef Full Text | Google Scholar

9. Ding F, Pors A, Bozhevolnyi SI. Gradient Metasurfaces: a Review of Fundamentals and Applications. Rep Prog Phys (2017) 81:026401. doi:10.1088/1361-6633/aa8732

CrossRef Full Text | Google Scholar

10. Shaltout AM, Shalaev VM, Brongersma ML. Spatiotemporal Light Control with Active Metasurfaces. Science (2019) 364:eaat3100. doi:10.1126/science.aat3100

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Kildishev AV, Boltasseva A, Shalaev VM. Planar Photonics With Metasurfaces. Science (2013) 339:1232009. doi:10.1126/science.1232009

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Chen H-T, Taylor AJ, Yu N. A Review of Metasurfaces: Physics and Applications. Rep Prog Phys (2016) 79:076401. doi:10.1088/0034-4885/79/7/076401

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chen WT, Zhu AY, Capasso F. Flat Optics With Dispersion-Engineered Metasurfaces. Nat Rev Mater (2020) 5:604–20. doi:10.1038/s41578-020-0203-3

CrossRef Full Text | Google Scholar

14. Zhang F, Li C, Fan Y, Yang R, Shen NH, Fu Q, et al. Phase‐Modulated Scattering Manipulation for Exterior Cloaking in Metal-Dielectric Hybrid Metamaterials. Adv Mater (2019) 31:1903206. doi:10.1002/adma.201903206

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Chen WT, Zhu AY, Sanjeev V, Khorasaninejad M, Shi Z, Lee E, et al. A Broadband Achromatic Metalens for Focusing and Imaging in the Visible. Nat Nanotech (2018) 13:220–6. doi:10.1038/s41565-017-0034-6

CrossRef Full Text | Google Scholar

16. Devlin RC, Ambrosio A, Rubin NA, Mueller JPB, Capasso F. Arbitrary Spin-To-Orbital Angular Momentum Conversion of Light. Science (2017) 358:896–901. doi:10.1126/science.aao5392

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Koshelev K, Kruk S, Melik-Gaykazyan E, Choi J-H, Bogdanov A, Park H-G, et al. Subwavelength Dielectric Resonators for Nonlinear Nanophotonics. Science (2020) 367:288–92. doi:10.1126/science.aaz3985

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wen D, Yue F, Li G, Zheng G, Chan K, Chen S, et al. Helicity Multiplexed Broadband Metasurface Holograms. Nat Commun (2015) 6:8241. doi:10.1038/ncomms9241

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Cheng H, Liu Z, Chen S, Tian J. Emergent Functionality and Controllability in Few-Layer Metasurfaces. Adv Mater (2015) 27:5410–21. doi:10.1002/adma.201501506

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Chen S, Li Z, Liu W, Cheng H, Tian J. From Single‐Dimensional to Multidimensional Manipulation of Optical Waves with Metasurfaces. Adv Mater (2019) 31:1802458. doi:10.1002/adma.201802458

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Khorasaninejad M, Chen WT, Devlin RC, Oh J, Zhu AY, Capasso F. Metalenses at Visible Wavelengths: Diffraction-Limited Focusing and Subwavelength Resolution Imaging. Science (2016) 352:1190–4. doi:10.1126/science.aaf6644

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhu W, Yang R, Geng G, Fan Y, Guo X, Li P, et al. Titanium Dioxide Metasurface Manipulating High-Efficiency and Broadband Photonic Spin Hall Effect in Visible Regime. Nanophotonics (2020) 9:4327–35. doi:10.1515/nanoph-2020-0290

CrossRef Full Text | Google Scholar

23. Fano U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys Rev (1961) 124:1866–78. doi:10.1103/PhysRev.124.1866

CrossRef Full Text | Google Scholar

24. Luk'yanchuk B, Zheludev NI, Maier SA, Halas NJ, Nordlander P, Giessen H, et al. The Fano Resonance in Plasmonic Nanostructures and Metamaterials. Nat Mater (2010) 9:707–15. doi:10.1038/NMAT2810

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Limonov MF, Rybin MV, Poddubny AN, Kivshar YS. Fano Resonances in Photonics. Nat Photon (2017) 11:543–54. doi:10.1038/NPHOTON.2017.142

CrossRef Full Text | Google Scholar

26. Liu N, Langguth L, Weiss T, Kästel J, Fleischhauer M, Pfau T, et al. Plasmonic Analogue of Electromagnetically Induced Transparency at the Drude Damping Limit. Nat Mater (2009) 8:758–62. doi:10.1038/NMAT2495

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Gu J, Singh R, Liu X, Zhang X, Ma Y, Zhang S, et al. Active Control of Electromagnetically Induced Transparency Analogue in Terahertz Metamaterials. Nat Commun (2012) 3:1151. doi:10.1038/ncomms2153

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yang Y, Kravchenko , Briggs DP, Valentine J. All-dielectric Metasurface Analogue of Electromagnetically Induced Transparency. Nat Commun (2014) 5:5753. doi:10.1038/ncomms6753

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Fedotov VA, Rose M, Prosvirnin SL, Papasimakis N, Zheludev NI. Sharp Trapped-Mode Resonances in Planar Metamaterials With a Broken Structural Symmetry. Phys Rev Lett (2007) 99:147401. doi:10.1103/PhysRevLett.99.147401

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wu C, Khanikaev AB, Adato R, Arju N, Yanik AA, Altug H, et al. Fano-Resonant Asymmetric Metamaterials for Ultrasensitive Spectroscopy and Identification of Molecular Monolayers. Nat Mater (2012) 11:69–75. doi:10.1038/NMAT3161

CrossRef Full Text | Google Scholar

31. Cui C, Zhou C, Yuan S, Qiu X, Zhu L, Wang Y, et al. Multiple Fano Resonances in Symmetry-Breaking Silicon Metasurface for Manipulating Light Emission. ACS Photon (2018) 5:4074–80. doi:10.1021/acsphotonics.8b00754

CrossRef Full Text | Google Scholar

32. Zhang F, Huang X, Zhao Q, Chen L, Wang Y, Li Q, et al. Fano Resonance of an Asymmetric Dielectric Wire Pair. Appl Phys Lett (2014) 105:172901. doi:10.1063/1.4900757

CrossRef Full Text | Google Scholar

33. Fu Q, Zhang F, Fan Y, He X, Qiao T, Kong B. Electrically Tunable Fano-type Resonance of an Asymmetric Metal Wire Pair. Opt Express (2016) 24:11708–15. doi:10.1364/OE.24.011708

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Fan Y, Qiao T, Zhang F, Fu Q, Dong J, Kong B, et al. An Electromagnetic Modulator Based on Electrically Controllable Metamaterial Analogue to Electromagnetically Induced Transparency. Sci Rep (2017) 7:40441. doi:10.1038/srep40441

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Lassiter JB, Sobhani H, Fan JA, Kundu J, Capasso F, Nordlander P, et al. Fano Resonances in Plasmonic Nanoclusters: Geometrical and Chemical Tunability. Nano Lett (2010) 10:3184–9. doi:10.1021/nl102108u

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Khanikaev AB, Wu C, Shvets G. Fano-resonant Metamaterials and Their Applications. Nanophotonics (2013) 2:247–64. doi:10.1515/nanoph-2013-0009

CrossRef Full Text | Google Scholar

37. Yang Y, Wang W, Boulesbaa A, Kravchenko II, Briggs DP, Puretzky A, et al. Nonlinear Fano-Resonant Dielectric Metasurfaces. Nano Lett (2015) 15:7388–93. doi:10.1021/acs.nanolett.5b02802

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Lou J, Liang J, Yu Y, Ma H, Yang R, Fan Y, et al. Silicon‐Based Terahertz Meta‐Devices for Electrical Modulation of Fano Resonance and Transmission Amplitude. Adv Opt Mater. (2020) 8:2000449. doi:10.1002/adom.202000449

CrossRef Full Text | Google Scholar

39. Zhu W, Fan Y, Li C, Yang R, Yan S, Fu Q, et al. Realization of a Near-Infrared Active Fano-Resonant Asymmetric Metasurface by Precisely Controlling the Phase Transition of Ge2Sb2Te5. Nanoscale (2020) 12:8758–67. doi:10.1039/c9nr09889e

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gupta M, Srivastava YK, Singh R. A Toroidal Metamaterial Switch. Adv Mater (2018) 30:1704845. doi:10.1002/adma.201704845

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Fan Y, Shen NH, Zhang F, Zhao Q, Wu H, Fu Q, et al. Graphene Plasmonics: A Platform for 2D Optics. Adv Opt Mater (2019) 7:1800537. doi:10.1002/adom.201800537

CrossRef Full Text | Google Scholar

42. Gholipour B, Zhang J, MacDonald KF, Hewak DW, Zheludev NI. An All-Optical, Non-Volatile, Bidirectional, Phase-Change Meta-Switch. Adv Mater (2013) 25:3050–4. doi:10.1002/adma.201300588

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Manjappa M, Pitchappa P, Singh N, Wang N, Zheludev NI, Lee C, et al. Reconfigurable MEMS Fano Metasurfaces With Multiple-Input-Output States for Logic Operations at Terahertz Frequencies. Nat Commun (2018) 9:4056. doi:10.1038/s41467-018-06360-5

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Ren Z, Chang Y, Ma Y, Shih K, Dong B, Lee C. Leveraging of MEMS Technologies for Optical Metamaterials Applications. Adv Opt Mater. (2020) 8:1900653. doi:10.1002/adom.201900653

CrossRef Full Text | Google Scholar

45. Fan Y, Zhang F, Shen N-H, Fu Q, Wei Z, Li H, et al. Achieving a High- Q Response in Metamaterials by Manipulating the Toroidal Excitations. Phys Rev A (2018) 97:033816. doi:10.1103/PhysRevA.97.033816

CrossRef Full Text | Google Scholar

46. Fu Q, Zhang F, Fan Y, Dong J, Cai W, Zhu W, et al. Weak Coupling Between Bright and Dark Resonators With Electrical Tunability and Analysis Based on Temporal Coupled-Mode Theory. Appl Phys Lett (2017) 110:221905. doi:10.1063/1.4984596

CrossRef Full Text | Google Scholar

47. Yang R, Fu Q, Fan Y, Cai W, Qiu K, Zhang W, et al. Active Control of EIT-like Response in a Symmetry-Broken Metasurface With Orthogonal Electric Dipolar Resonators. Photon Res (2019) 7:955–60. doi:10.1364/PRJ.7.000955

CrossRef Full Text | Google Scholar