Collisions of Nucleons with Atoms: Calculated Cross Sections and Monte Carlo Simulation

After a summary description of the theory of elastic collisions of nucleons with atoms, we present the calculation of a generic database of differential and integrated cross sections for the simulation of multiple elastic collisions of protons and neutrons with kinetic energies larger than 100 keV. The relativistic plane-wave Born approximation, with binding and Coulomb-deflection corrections, has been used to calculate a database of proton-impact ionization of K-shell and L-, M-, and N-subshells of neutral atoms These databases cover the whole energy range of interest for all the elements in the periodic system, from hydrogen to einsteinium (Z = 1–99); they are provided as part of the penh distribution package. The Monte Carlo code system penh for the simulation of coupled electron-photon-proton transport is extended to account for the effect of the transport of neutrons (released in proton-induced nuclear reactions) in calculations of dose distributions from proton beams. A simplified description of neutron transport, in which neutron-induced nuclear reactions are described as a fractionally absorbing process, is shown to give simulated depth-dose distributions in good agreement with those generated by the Geant4 code. The proton-impact ionization database, combined with the description of atomic relaxation data and electron transport in penelope, allows the simulation of proton-induced x-ray emission spectra from targets with complex geometries.

1 Introduction

Motivated by the specific needs of protontherapy and proton-induced x-ray emission, we have recently extended the penelope code system [1] to introduce the simulation of interactions and transport of protons [2, 3]. The resulting code, named penh, performs class-II Monte Carlo simulation of coupled electron-photon-proton transport in material structures consisting of homogeneous bodies limited by quadric surfaces. In class II simulation schemes, hard interactions (that is, interactions involving scattering angles or energy losses larger than preselected cutoffs) are simulated by random sampling from their restricted differential cross sections (DCSs) while the cumulative effect of soft (sub-cutoff) interactions is described by means of a multiple-scattering approach. Class II simulation has distinct advantages in front of conventional condensed simulation (see, e.g., Ref. [1]).

The penh code accounts for elastic and inelastic collisions of protons with atoms, as well as for nuclear reactions induced by proton impact. Elastic collisions of protons with nuclei are described by means of numerical DCSs obtained as the product of the DCS for scattering by the bare nucleus, which was computed by the method of partial-waves with the global optical-model potential of Koning and Delaroche [4], and a screening factor accounting for the effect of the screening of the Coulomb field of the nucleus by the atomic electrons, which was calculated from the eikonal approximation for the Dirac-Hartree-Fock-Slater potential of neutral atoms [2, 3, 5]. Proton-induced electronic excitations are simulated by means of DCSs obtained from the Born approximation with the Sternheimer-Liljequist model of the generalized oscillator strength (GOS) [1], which is modified by rescaling the relative contributions of the various electron subshells to give cross sections for the impact ionization of inner subshells equal to unpublished results obtained from accurate atomic GOSs [2]. Nuclear reactions induced by proton impact are simulated by using information from data files in ENDF-6 format [6], which provide cross sections, multiplicities, and angle-energy distributions of all reaction products: light ejectiles (up to alphas), gammas, as well as recoiling heavy residuals.

Although electromagnetic interactions are faithfully described for protons in the energy range from 100 keV up to 1 GeV, the unavailability of nuclear reaction data for energies higher than about 200 MeV, limit the possible applications of the code. Simulations with penh are also limited by the fact that the code can only follow electrons/positrons, photons, and protons. To lessen the effect of this limitation, light charged ejectiles other than protons (deuterons, tritons, ³He, and alphas) are tracked as weighted protons [3]. Neutrons and heavy products are not followed and their kinetic energies were assumed to be deposited at the reaction site. Comparison with results from other codes shows that, as one could predict, the calculated dose distributions from proton beams are generally accurate in the volume swept by the protons, but are generally too low outside that volume, mostly because of the neglect of neutron transport. In this respect, it is worth recalling that neutrons practically do not interact with electrons and, as a consequence, they have large mean free paths. In the energy range covered by the proton simulation code, nominally from 100 keV to 1 GeV, the mean free path of neutrons in water ranges from about 5 cm at 100 keV to ∼ 66 cm at 1 GeV.

The aim of the present article is twofold. First, we present the theory and computational aspects of the calculation of the DCSs for elastic collisions of neutrons and protons, and of the cross sections for ionization of inner electron subshells of atoms by proton impact. We also describe the structure and contents of the associated numerical databases, which completely define the interaction models used in penh for nucleons. Second, we present a simplified algorithm for the simulation of the effect of neutron transport in Monte Carlo calculations of dose distributions from proton beams, which only uses the information provided in the calculated elastic-scattering database, that is, the total and DCS for elastic collisions and the reaction cross section, which is one of the basic parameters used to set the nuclear optical-model potential. The main simplification is that neutron-induced nuclear reactions are described as purely absorptive, that is, when the transported neutron induces a reaction, the simulation of the neutron is discontinued and a fraction of its kinetic energy is assumed to be locally absorbed. It will be shown that, in spite of its crudeness, this transport algorithm accounts for the contribution of neutrons to the spatial dose distribution fairly accurately. Although random histories of neutrons with protontherapy energies (say, from 100 keV to ∼ 300 MeV) may be simulated detailedly (i.e., interaction by interaction) we adopt a class II tracking scheme, which is analogous to the ones used in penelope-penh for electrons/positrons and protons, because it allows speeding up simulations of high-energy neutrons.

The present article is organized as follows. In Section 2 we describe the calculation of DCSs for elastic collisions of nucleons and protons with atoms (nuclei), the structure of the numerical database for elastic scattering of these particles, and the implementation of a class II algorithm for the simulation of multiple elastic scattering of neutrons. Section 3 deals with the ionization of inner electron subshells of atoms by impact of protons, which is based on total cross sections calculated from the relativistic plane-wave Born approximation with corrections for binding/polarization and Coulomb deflection effects. After a brief presentation of the theory and sample results, the associated numerical database is described. The validation of the penh calculation of dose distributions from proton beams is considered in Section 4. Section 5 illustrates the simulation of proton-induced x-ray emission from solid targets. Finally, in Section 6 we offer a few concluding remarks.

2 Elastic Collisions

We consider elastic collisions of nucleons with atoms of the element of atomic number Z. In order to cover the range of kinetic energies of interest in proton therapy, up to about 300 MeV, we shall use relativistic collision kinematics. The simulation code transports particles in the laboratory (L) frame, where the material is at rest and the projectile moves with kinetic energy E before the collision. For simplicity, we consider that the z axis of the reference frame is parallel to the linear momentum of the projectile, which is given by

$\mathbf{p}=c^{-1}\sqrt{\left.E\left(E+2m{c}^2\right.\right)}\widehat{\mathbf{z}},(1)$

where c is the speed of light in vacuum and m is the projectile mass (= m_p for protons, and = m_n for neutrons). The total energy of the projectile is

$\mathcal{W}=E+m{c}^2=\sqrt{m^2{c}^4+c^2{p}^2}.(2)$

We recall the general relations

$p=\beta \gamma mc\text{and}E=\left(\gamma -1\right)m{c}^2(3)$

where

$\beta =\frac{v}{c}=\frac{\sqrt{E\left(E+2m{c}^2\right)}}{E+m{c}^2}(4)$

is the speed of the particle in units of c and

$\gamma =\sqrt{\frac{1}{1-{\beta }^2}}=\frac{E+m{c}^2}{m{c}^2}(5)$

is the particle’s total energy in units of its rest energy.

Elastic collisions involve a certain transfer of kinetic energy to the target atom, which is easily accounted for by sampling the collisions in the center-of-mass (CM) frame, which moves relative to the L frame with velocity

${\mathbf{v}}_{\mathrm{C}\mathrm{M}}={\mathit{\beta }}_{\mathrm{C}\mathrm{M}}c=\frac{c^2\mathbf{p}}{E+m{c}^2+M_{\mathrm{A}}{c}^2},(6)$

where M_A is the mass of the atom. In the CM frame the linear momenta of the projectile and the atom before the collision are, respectively, ${\mathbf{p}}_{\mathrm{i}}^{\prime }={\mathbf{p}}_0^{\prime }$ and ${\mathbf{p}}_{\mathrm{A}\mathrm{i}}^{\prime }=-{\mathbf{p}}_0^{\prime }$, with

${\mathbf{p}}_0^{\prime }=\frac{M_{\mathrm{A}}{c}^2}{\sqrt{{\left(m{c}^2+M_{\mathrm{A}}{c}^2\right)}^2+2M_{\mathrm{A}}{c}^{2}E}}\mathbf{p}.(7)$

Quantities in the CM frame are denoted by primes. After the elastic collision, in CM the projectile moves with momentum $p_{\mathrm{f}}^{\prime }=p_0^{\prime }$ in a direction defined by the polar scattering angle θ′ and the azimuthal scattering angle ϕ′, and the target atom recoils with equal momentum $p_{\mathrm{A}\mathrm{f}}^{\prime }=p_0^{\prime }$ in the opposite direction. The final energies and directions of the projectile and the atom in the L frame are obtained by means of a Lorentz boost with velocity − v_CM. Thus, elastic collisions are completely determined by the DCS dσ/dΩ′ in the CM frame.

We follow the approach described in our previous work on proton transport [3], i.e., we assume that the interaction potential in the CM frame is central, because this is a prerequisite for applying the partial-wave expansion method to compute the DCS. Our approach can be qualified as semi-relativistic, because we are using strict relativistic kinematics but we do not account for the breaking of the central symmetry of the interaction when passing from the L to the CM frame.

2.1 Interaction Potential

The interaction of the incident nucleon with a bare nucleus of the isotope ^AZ having atomic number Z and mass number A can be described by a phenomenological complex optical-model potential

$V_{\mathrm{n}\mathrm{u}\mathrm{c}}\left(r\right)=V_{\mathrm{o}\mathrm{p}\mathrm{t}}\left(r\right)+\mathrm{i}{W}_{\mathrm{o}\mathrm{p}\mathrm{t}}\left(r\right),(8)$

where the first term is a real potential, which in the case of projectile protons includes the Coulomb interaction, and the second term, iW_opt(r), is an absorptive (negative) imaginary potential, which accounts for the loss of nucleons in the elastic channel caused by inelastic processes. Parameterizations of optical-model potentials are generally expressed as a combination of Woods–Saxon volume terms,

$f\left(R,a;r\right)=\frac{1}{1+\exp \left[\left(r-R\right)/a\right]},(\mathrm{9a})$

and surface derivative (d) terms,

$\begin{array}{ll}\hfill g\left(R,a;r\right)& =\frac{\mathrm{d}}{\mathrm{d}\mathit{r}}f\left(R,a;r\right)\hfill \\ \hfill & =\frac{1}{a}f\left(R,a;r\right)\left[f\left(R,a;r\right)-1\right].\hfill \end{array}(\mathrm{9b})$

The parameters in these functions are the radius R and the diffuseness a; typically, the radius is expressed as R = r₀A^1/3. We consider global model potentials of the type

$\begin{array}{ccc}\hfill V_{\mathrm{n}\mathrm{u}\mathrm{c}}\left(r\right)& =\hfill & V_{\mathrm{v}}\left(E;r\right)+V_{\mathrm{d}}\left(E;r\right)+V_{\mathrm{c}}\left(r\right)+V_{\mathrm{s}\mathrm{o}}\left(E;r\right)2\mathbf{L}\cdot \mathbf{S}\hfill \\ \hfill & \hfill & +\mathrm{i}\left[W_{\mathrm{v}}\left(E;r\right)+W_{\mathrm{d}}\left(E;r\right)+W_{\mathrm{s}\mathrm{o}}\left(E;r\right)2\mathbf{L}\cdot \mathbf{S}\right]\hfill \end{array}(10)$

with the following terms:

1) Real volume potential:

$V_{\mathrm{v}}\left(E;r\right)=V_{\mathrm{v}}\left(E\right)f\left(R_{\mathrm{v}},a_{\mathrm{v}};r\right).(\mathrm{11a})$

2) Real surface potential:

$V_{\mathrm{d}}\left(E;r\right)=V_{\mathrm{d}}\left(E\right)4a_{\mathrm{d}}g\left(R_{\mathrm{d}},a_{\mathrm{d}};r\right).(\mathrm{11b})$

3) Coulomb potential: approximated by the electrostatic potential of a uniformly charged sphere of radius R_c,

$V_{\mathrm{c}}\left(r\right)=\frac{z_{0}Z{e}^2}{r}\left\{\begin{array}{cc}\frac{r}{2R_{\mathrm{c}}}\left(3-\frac{r^2}{R_{\mathrm{c}}^2}\right)\hfill & \text{if}r<R_{\mathrm{c}},\hfill \\ 1\hfill & \text{if}r\ge R_{\mathrm{c}},\hfill \end{array}\right.(\mathrm{11c})$

where e is the elementary charge and z₀e the nucleon charge (z₀ = 1 for protons and = 0 for neutrons).

4) Real spin-orbit potential:

$V_{\mathrm{s}\mathrm{o}}\left(E;r\right)=V_{\mathrm{s}\mathrm{o}}\left(E\right){\left(\frac{\hslash }{m_{\pi }c}\right)}^2\frac{1}{r}g\left(R_{\mathrm{s}\mathrm{o}},a_{\mathrm{s}\mathrm{o}};r\right),(\mathrm{11d})$

where the quantity in parentheses is the pion Compton wavelength, ℏ/(m_πc) ≃ 1.429 502 fm.

5) Imaginary volume potential:

$W_{\mathrm{v}}\left(E;r\right)=W_{\mathrm{v}}\left(E\right)f\left(R_{\mathrm{w}},a_{\mathrm{w}};r\right).(11e)$

6) Imaginary surface potential:

$W_{\mathrm{d}}\left(E;r\right)=W_{\mathrm{d}}\left(E\right)4a_{\mathrm{w}\mathrm{d}}g\left(R_{\mathrm{w}\mathrm{d}},a_{\mathrm{w}\mathrm{d}};r\right).(\mathrm{11f})$

7) Imaginary spin-orbit potential:

$W_{\mathrm{s}\mathrm{o}}\left(E;r\right)=W_{\mathrm{s}\mathrm{o}}\left(E\right){\left(\frac{\hslash }{m_{\pi }c}\right)}^2\frac{1}{r}g\left(R_{\mathrm{w}\mathrm{s}\mathrm{o}},a_{\mathrm{w}\mathrm{s}\mathrm{o}};r\right).(\mathrm{11g})$

The operators L and S are, respectively, the orbital and spin angular momenta (both in units of ℏ) of the projectile nucleon. We have indicated explicitly that the strengths of the potential terms are functions (usually expressed as polynomials) of the kinetic energy E of the projectile in the L frame. Except for the Coulomb term of protons, the potential is of finite-range, it vanishes when the distance r from the projectile to the nucleus is larger than about twice the “nuclear radius”, R_nuc ∼ 1.2 A^1/3 fm. In the calculations we use the parameterization of the global optical-model potential of Koning and Delaroche [4].

2.2 Scattering Amplitudes and Cross Sections

The scattering of nucleons by nuclei in the CM frame is described by using the partial-wave expansion method. The underlying physical picture is that of a stationary process represented by a distorted plane wave, i.e., by an exact solution of the time-independent relativistic Schrödinger equation for the potential V_nuc(r),

$\left(-\frac{{\hslash }^2}{2{\mu }_{\mathrm{r}}}{\nabla }^2+V_{\mathrm{n}\mathrm{u}\mathrm{c}}\left(r\right)\right)\psi \left(\mathbf{r}\right)=\frac{p_0^{\prime 2}}{2{\mu }_{\mathrm{r}}}\psi \left(\mathbf{r}\right),(12)$

which asymptotically behaves as a plane wave with an outgoing spherical wave. The quantity μ_r is the relativistic reduced mass of the projectile and the target atom, defined as

${\mu }_{\mathrm{r}}=c^{-2}\frac{{\mathcal{W}}_{\mathrm{n}\mathrm{i}}^{\prime }{\mathcal{W}}_{\mathrm{A}\mathrm{i}}^{\prime }}{{\mathcal{W}}_{\mathrm{n}\mathrm{i}}^{\prime }+{\mathcal{W}}_{\mathrm{A}\mathrm{i}}^{\prime }},(13)$

where

${\mathcal{W}}_{\mathrm{n}\mathrm{i}}^{\prime }=\sqrt{m^2{c}^4+c^2{p}_0^{\prime 2}}\text{and}{\mathcal{W}}_{\mathrm{A}\mathrm{i}}^{\prime }=\sqrt{M_{\mathrm{A}}^2{c}^4+c^2{p}_0^{\prime 2}}(14)$

are, respectively, the total energies of the projectile and the atom before the collision.

As the potential (10) contains spin-orbit terms, the wave function is a two-component spinor. Assuming that before the interaction the projectile moves in the direction of the z axis, the asymptotic, large-r behavior of the distorted plane wave is

$\psi \left(\mathbf{r}\right)\begin{array}{c}\hfill \sim \hfill \\ \hfill r\to \infty \hfill \end{array}{\left(2\pi \right)}^{-3/2}\exp \left(\mathrm{i}kr\cos {\theta }^{\prime }\right)\chi +{\left(2\pi \right)}^{-3/2}\frac{\exp \left(\mathrm{i}kr\right)}{r}\mathcal{F}\left({\theta }^{\prime },{\varphi }^{\prime }\right)\chi .(15)$

where χ is a spinor, which defines the spin state of the incident nucleon, $k=p_0^{\prime }/\hslash$ is the projectile’s wave number, and θ′ and ϕ′ are the polar and azimuthal scattering angles, i.e., those of the direction $\widehat{\mathbf{r}}$. The factor $\mathcal{F}({\theta }^{\prime },{\varphi }^{\prime })$ is a 2 × 2 matrix independent of r,

$\mathcal{F}\left({\theta }^{\prime },{\varphi }^{\prime }\right)=\left(\begin{array}{cc}\hfill f\left({\theta }^{\prime }\right)\hfill & \hfill -\exp \left(-\mathrm{i}{\varphi }^{\prime }\right)g\left({\theta }^{\prime }\right)\hfill \\ \hfill \exp \left(\mathrm{i}{\varphi }^{\prime }\right)g\left({\theta }^{\prime }\right)\hfill & \hfill f\left({\theta }^{\prime }\right)\hfill \end{array}\right).(16)$

The functions f (θ′) and g (θ′) are called the “direct” and “splin-flip” scattering amplitudes, respectively. Evidently, these functions determine the final spin state of the scattered nucleon.

The scattering amplitudes can be calculated in terms of the phase shifts δ_ℓj of spherical waves with orbital and total angular momenta ℓ and j, respectively. Calculations are performed by using the Fortran subroutine package radial of Salvat and Fernández-Varea [7], which implements a robust power series solution method that effectively avoids truncation errors and yields highly accurate radial functions. The calculation for protons is complicated by the fact that the atomic electrons screen the long-range Coulomb potential of the nucleus, resulting in an affective electrostatic potential that decreases in magnitude as the radial distance r increases. This screened atomic potential extends up to radial distances of the order of the atomic radius, R_at ∼ 10⁵R_nuc and, because of the small wavelengths of protons and heavier projectiles, the numerical calculation of phase-shifts for the screened nuclear potential is unfeasible. The DCSs for elastic scattering of protons can be calculated by combining a partial-wave calculation of the scattering by the bare nucleus with an electronic screening correction derived from the eikonal approximation [3]. Here we describe the calculation of the DCS for elastic collisions of neutrons, which is less demanding than for protons because, due to the absence of the Coulomb term, the interaction potential has a finite range.

The reduced radial functions, P_ℓj(r) are the regular solutions of the radial wave equation

$-\frac{{\hslash }^2}{2\mu }\frac{{\mathrm{d}}^2}{\mathrm{d}{r}^2}{P}_{\ell j}\left(r\right)+V_{\ell j}\left(r\right)P_{\ell j}\left(r\right)=\frac{p_0^{\prime 2}}{2\mu }{P}_{\ell j}\left(r\right)(17)$

with the “radial” potential

$\begin{array}{ccc}\hfill V_{\ell j}\left(r\right)& =\hfill & V_{\mathrm{v}}\left(E;r\right)+V_{\mathrm{d}}\left(E;r\right)+\mathrm{i}\left[W_{\mathrm{v}}\left(E;r\right)+W_{\mathrm{d}}\left(E;r\right)\right]\hfill \\ \hfill & \hfill & +\left[V_{\mathrm{s}\mathrm{o}}\left(E;r\right)+\mathrm{i}{W}_{\mathrm{s}\mathrm{o}}\left(E;r\right)\right]\left(j\left(j+1\right)-\ell \left(\ell +1\right)-\frac{3}{4}\right)+\frac{{\hslash }^2}{2\mu }\frac{\ell \left(\ell +1\right)}{r^2}.\hfill \end{array}(18)$

The radial functions are normalized so that

$P_{\ell j}\left(r\right)\begin{array}{c}\hfill \sim \hfill \\ \hfill r\to \infty \hfill \end{array}\sin \left(kr-\ell \frac{\pi }{2}+{\delta }_{\ell j}\right),(19)$

where δ_ℓj is the complex phase shift. The radial subroutines determine each phase shift by integrating the corresponding radial equation from r = 0 outwards up to a radius r_m larger than the range of the nuclear interaction, and matching the numerical solution at r_m with a linear combination of the regular and irregular Bessel functions. It is worth mentioning that in the case of charged projectiles (protons and alphas), when electronic screening is ignored, the inner solution is matched to a combination of the regular and irregular Coulomb functions, and the phase shift is the sum of the calculated “inner” phase shift and the Coulomb phase shift (see, e.g., Ref. [7]). All phase shifts with absolute values larger than 10^–9 are calculated. In the following the phase shifts are denoted by the abridged notation δ_ℓa with a = sign (j − ℓ), i.e., δ_ℓ+ ≡ δ_{ℓ,j=ℓ+1/2} and δ_ℓ−≡ δ_{ℓ,j=ℓ−1/2}.

From the calculated phase shifts, the direct and spin-flip scattering amplitudes are evaluated from their partial-wave expansions

$f\left({\theta }^{\prime }\right)=\frac{1}{2\mathrm{i}k}\sum _{\ell }\left[\left(\ell +1\right)\left(S_{\ell +}-1\right)+\ell \left(S_{\ell -}-1\right)\right]P_{\ell }\left(\cos {\theta }^{\prime }\right)(\mathrm{20a})$

and

$g\left({\theta }^{\prime }\right)=\frac{1}{2\mathrm{i}k}\sum _{\ell }\left(S_{\ell -}-S_{\ell +}\right)P_{\ell }^1\left(\cos {\theta }^{\prime }\right),(\mathrm{20b})$

where P_ℓ(cos θ′) and $P_{\ell }^1(\cos {\theta }^{\prime })$ are Legendre polynomials and associated Legendre functions of the first kind [8], respectively, and

$S_{\ell a}=\exp \left(2\mathrm{i}{\delta }_{\ell a}\right),(21)$

are the S-matrix elements.

For spin-unpolarized neutrons, the elastic DCS per unit solid angle in the CM frame is given by

$\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}={\left|f\left({\theta }^{\prime }\right)\right|}^2+{\left|g\left(\theta \prime \right)\right|}^2.(22)$

Owing to the assumed spherical symmetry of the target nucleus, the angular distribution of scattered neutrons is axially symmetric about the direction of incidence, i.e., independent of the azimuthal scattering angle in both the CM and L frames.

The total elastic cross section is obtained as the integral of the DCS,

${\sigma }_{\mathrm{e}\mathrm{l}}=\int \frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}d{\mathrm{\Omega }}^{\prime }=2\pi {\int }_{-1}^1\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}\mathrm{d}\left(\cos {\theta }^{\prime }\right).(23)$

The grand total cross section σ_T, accounting for both elastic scattering and inelastic interactions or reactions, can be obtained from the optical theorem,

${\sigma }_{\mathrm{T}}={\sigma }_{\mathrm{e}\mathrm{l}}+{\sigma }_{\mathrm{R}}=\frac{4\pi }{k}\mathrm{I}\mathrm{m}f\left(0\right),(24)$

where σ_R denotes the reaction cross section, i.e., the total cross section for inelastic interactions.

2.3 Elastic-Scattering Database

A Fortran program named panelastic has been written to calculate differential and integrated cross sections for elastic collisions of protons, neutrons, and alphas with neutral atoms. It is assumed that the target atom is neutral and the calculated cross sections for each element are obtained as an average over those of the naturally occurring isotopes, weighted by their respective natural abundances [9]. Consistently, in the simulations we consider that the mass of a target atom is the average atomic mass of the element

$M_{\mathrm{A}}=\frac{A_{\mathrm{w}}}{\mathrm{g}/\mathrm{m}\mathrm{o}\mathrm{l}}\mathrm{u}(25)$

where A_w is the molar mass of the element, and u = m (¹²C)/12 is the atomic mass unit. This simplification permits reducing the required information for each element to a single cross section table, irrespective of the number of isotopes of that element. Panelastic uses the nuclear optical model potentials of Koning and Delaroche [4] for protons and neutrons, and that of Su and Han [10] for alphas. The parameters of the global potential for nucleons are determined for 24 ≤ A ≤ 209 and E ≤ 200 MeV. Owing to the lack of more accurate approximations, because the potential values vary smoothly with A, Z and E, we use those parameters for all isotopes and for energies up to 300 MeV, for higher energies the potential parameters at E = 300 MeV are employed.

In the case of protons (and also alphas) the screening of the Coulomb potential of the nucleus by the atomic electrons is described by means of the Dirac-Hartree-Fock-Slater analytical screening function [5], and the screening correction to the nuclear DCS is evaluated by means of the eikonal approximation [3]. Since scattering of charged particles is dominated by the long-range Coulomb interaction, the extrapolation of the nuclear optical-model potential to high energies has a small effect on proton transport calculations.

The program panelastic calculates cross sections for elastic collisions of a projectile particle with a given isotope ^AZ for the kinetic energies of the projectile specified by the user. Alternatively, it can produce a complete database of DCSs and integrated cross sections for collisions of projectiles of a given type, with laboratory kinetic energies covering the range from 100 keV to 1 GeV for each element from hydrogen (Z = 1) to einsteinium (Z = 99). The database grid of energies is logarithmic, with 35 points per decade. For each energy the program calculates the DCS in CM, Eq. 22, for a grid of 1,000 polar angles θ′. In order to reduce the size of the database, and also to improve the accuracy of interpolation in energy, the DCS is considered as a function of the variable

$Q\equiv 4{\left(c{p}_0^{\prime }\right)}^2{\sin }^2\left(\theta \prime /2\right),(26)$

c² times the square of the momentum transfer in CM. The original table is “cleaned”, by removing points in regions where the DCS varies smoothly, to define a reduced grid that allows accurate cubic spline interpolation in Q. The DCS interpolated in this way is estimated to be accurate to four or more digits. For each projectile energy, the database includes the values of the total elastic cross section, Eq. 23, the reaction cross section obtained from Eq. 24, the first transport cross section (or momentum transfer cross section),

${\sigma }_{\mathrm{t}\mathrm{r},1}^{\prime }\equiv \int \left(1-\cos {\theta }^{\prime }\right)\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}d{\mathrm{\Omega }}^{\prime },(27)$

and the second transport cross section

${\sigma }_{\mathrm{t}\mathrm{r},2}^{\prime }\equiv \int \frac{3}{2}\left(1-{\cos }^2{\theta }^{\prime }\right)\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}d{\mathrm{\Omega }}^{\prime }.(28)$

The values of these integrated cross sections serve to assess the accuracy of the DCS interpolation scheme adopted in the simulation. We recall that the total elastic cross section and the reaction cross section have the same values in the CM and the L frames.

2.4 Simulation of Neutron Elastic Collisions

The kinematics of elastic collisions of a neutron with laboratory energy E is completely determined by the polar scattering angle θ′ in CM. In the CM frame, after an elastic collision the magnitudes of the linear momenta of the projectile and the target atom are the same as before the collision, and the scattering angles θ′, ϕ′ determine the directions of motion of the two particles in CM. As mentioned above, the final kinetic energy E_nf and the polar scattering angle θ of the projectile neutron in the L frame are obtained by a Lorentz boost with velocity − v_CM, which gives

$E_{\mathrm{n}\mathrm{f}}={\gamma }_{\mathrm{C}\mathrm{M}}\left(W_{\mathrm{n}\mathrm{i}}^{\prime }+{\beta }_{\mathrm{C}\mathrm{M}}c{p}_0^{\prime }\cos {\theta }^{\prime }\right)-m_{\mathrm{n}}{c}^2(29)$

and

$\cos \theta =\frac{\tau +\cos {\theta }^{\prime }}{\sqrt{{\left(\tau +\cos {\theta }^{\prime }\right)}^2+{\gamma }_{\mathrm{C}\mathrm{M}}^{-2}{\sin }^2{\theta }^{\prime }}},(30)$

where

${\gamma }_{\mathrm{C}\mathrm{M}}\equiv \sqrt{\frac{1}{1-{\beta }_{\mathrm{C}\mathrm{M}}^2}}=\frac{E+m_{\mathrm{n}}{c}^2+M_{\mathrm{A}}{c}^2}{{\left(m_{\mathrm{n}}{c}^2+M_{\mathrm{A}}{c}^2\right)}^2+2M_{\mathrm{A}}{c}^{2}E}(31)$

and τ is the ratio of speeds of the CM and of the scattered neutron (in CM), $v_{\mathrm{n}}^{\prime }=c^2{p}_0^{\prime }/{\mathcal{W}}_{\mathrm{n}\mathrm{f}}^{\prime }$,

$\tau =\frac{v_{\mathrm{C}\mathrm{M}}}{v_{\mathrm{n}}^{\prime }}=\sqrt{{\left(\frac{m_{\mathrm{n}}}{M_{\mathrm{A}}}\right)}^2{\left(1-{\beta }_{\mathrm{C}\mathrm{M}}\right)}^2+{\beta }_{\mathrm{C}\mathrm{M}}}.(32)$

Notice that the azimuthal angle of the neutron direction in L is the same as in the CM frame. After the collision, in the L frame the target atom recoils with kinetic energy E_A = E − E_nf and direction in the scattering plane with the polar angle

$\cos {\theta }_{\mathrm{A}}=\frac{1-\cos {\theta }^{\prime }}{\sqrt{{\left(1-\cos \theta \prime \right)}^2+{\gamma }_{\mathrm{C}\mathrm{M}}^{-2}{\sin }^2{\theta }^{\prime }}}.(33)$

The DCS can also be expressed in terms of the scattering angles in the L frame by making use of the inverse of the relation (30),

$\cos {\theta }^{\prime }=\frac{-\tau {\gamma }_{\mathrm{C}\mathrm{M}}^2{\sin }^2\theta \pm \cos \theta \sqrt{{\cos }^2\theta +{\gamma }_{\mathrm{C}\mathrm{M}}^2\left(1-{\tau }^2\right){\sin }^2\theta }}{{\gamma }_{\mathrm{C}\mathrm{M}}^2{\sin }^2\theta +{\cos }^2\theta }.(34)$

If τ is less than unity only the plus sign before the square root has to be considered. For τ > 1, there are two values of the CM deflection θ′, given by Eq. 34, for each value of θ, which correspond to different final energies of the neutron in L. The DCS in the L frame is given by

$\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}\mathrm{\Omega }}=\left|\frac{\mathrm{d}\left(\cos {\theta }^{\prime }\right)}{\mathrm{d}\left(\cos \theta \right)}\right|\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}(35)$

where the last factor is the DCS in the CM frame. Using the relation (34), we obtain

$\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}\mathrm{\Omega }}=\frac{{\gamma }_{\mathrm{C}\mathrm{M}}^2{\left[\tau \cos \theta \pm \sqrt{{\cos }^2\theta +{\gamma }_{\mathrm{C}\mathrm{M}}^2\left(1-{\tau }^2\right){\sin }^2\theta }\right]}^2}{{\left({\gamma }_{\mathrm{C}\mathrm{M}}^2{\sin }^2\theta +{\cos }^2\theta \right)}^2\sqrt{{\cos }^2\theta +{\gamma }_{\mathrm{C}\mathrm{M}}^2\left(1-{\tau }^2\right){\sin }^2\theta }}\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}.(36)$

If τ < 1 only the plus sign is valid and the scattering angle θ varies from 0 to π. When τ ≥ 1, the DCS vanishes for angles θ larger than

${\theta }_{\max }=\arctan \left(\sqrt{\frac{1}{{\gamma }_{\mathrm{C}\mathrm{M}}^2\left({\tau }^2-1\right)}}\right);(37)$

for angles θ < θ_max, Eq. 34 yields two values of θ′ in (0, π), the expression on the right-hand side of Eq. 36 must then be evaluated for these two angles, and the resulting values added up to give the DCS in L. In class-II simulations formula (36) allows determining the contributions of soft elastic interactions to the first and second transport cross sections.

The elastic collision involves the transfer of energy W = E_A from the projectile to the target atom. The energy loss can be expressed in terms of the scattering angle in CM,

$W=W_{\max }\frac{1-\cos {\theta }^{\prime }}{2},(38)$

where

$W_{\max }=\frac{2M_{\mathrm{A}}{c}^{2}E\left(E+2m_{\mathrm{n}}{c}^2\right)}{{\left(M_{\mathrm{A}}{c}^2+m_{\mathrm{n}}{c}^2\right)}^2+2M_{\mathrm{A}}{c}^{2}E}(39)$

is the maximum energy loss in a collision, which occurs when θ′ = π. The energy-loss DCS is

$\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}W}=2\pi {\left|\frac{dW}{d\left(\cos {\theta }^{\prime }\right)}\right|}^{-1}\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}=\frac{4\pi }{W_{\max }}\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}.(40)$

The nuclear stopping cross section is defined as

$\begin{array}{ccc}\hfill {\sigma }_{\mathrm{s}\mathrm{t}}& =\hfill & {\int }_0^{W_{\max }}W\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}W}\mathrm{d}W\hfill \\ \hfill & =\hfill & \frac{W_{\max }}{2}\left(2\pi {\int }_{-1}^1\left(1-\cos {\theta }^{\prime }\right)\frac{\mathrm{d}{\sigma }_{\mathrm{e}\mathrm{l}}}{\mathrm{d}{\mathrm{\Omega }}^{\prime }}d\left(\cos {\theta }^{\prime }\right)\right)=\frac{W_{\max }}{2}{\sigma }_{\mathrm{t}\mathrm{r},\mathrm{1}}^{\prime }.\hfill \end{array}(41)$

The code penh simulates the transport of neutrons by using a class II tracking scheme that is analogous to the one employed for protons. The transport of neutrons is simplified by the fact that these particles only experience elastic collisions and nuclear reactions. The cross sections for these two processes are obtained from the partial-wave calculations of elastic scattering. The simulation of neutron-induced nuclear reactions is difficult because of the wide variety of open reaction channels, which are explicitly described in evaluated libraries for neutrons, although only for energies below 20 MeV. Since a detailed description of reactions induced by neutrons down to thermal energies is beyond the capabilities of a dose-calculation code, we consider nuclear reactions as a purely absorptive process that terminates the neutron trajectory and a fraction $\mathtt{F}\mathtt{N}\mathtt{A}\mathtt{B}\mathtt{S}$ of the kinetic energy of the absorbed neutron is deposited locally. Comparison with simulation results from the codes fluka [11] and Geant4 [12–14], which do include proper descriptions of neutron production and transport, shows that $\mathtt{F}\mathtt{N}\mathtt{A}\mathtt{B}\mathtt{S}$ should be given a value less than unity, indicating that neutron reactions produce high-energy gammas that propagate to large distances from the reaction site. In spite of its crudeness, this procedure is found to provide a realistic correction to the simulated dose whenever the actual flux of neutrons is in “radiative equilibrium” (i.e., when the number and average energy of neutrons that enter a small probe volume equal the number and average energy of those that leave that volume). Under these circumstances, a fraction $\mathtt{F}\mathtt{N}\mathtt{A}\mathtt{B}\mathtt{S}$ of the energy absorbed through neutron-induced reactions remains on average at the reaction site.

3 Ionization of Inner Electron Shells by Proton Impact

The slowing down of fast protons in matter is mostly due to inelastic collisions, i.e., collisions causing electronic excitations of the material. Protons also slow down due to elastic collisions with nuclei (the so-called nuclear stopping), an effect that is automatically accounted for by the simulation scheme adopted in penh. The plane-wave Born approximation (PWBA) [15, 16] is suited for describing inelastic collisions of protons with velocities much larger than those of the active target electrons. We consider inelastic collisions of a proton with initial kinetic energy E and momentum p [(cp)² = E (E + 2 mc²)] with atoms of atomic number Z, characterized by the energy transfer W = E − E′ and the momentum transfer q = p − p′, where E′ and p′ are, respectively, the energy and momentum of the projectile after the collision. The corresponding DCS is most conveniently considered as a function of the energy transfer W and the recoil energy Q, defined as the kinetic energy of an electron with linear momentum equal to the momentum transfer [15],

$Q=\sqrt{{\left(cp\right)}^2+{\left(c{p}^{\prime }\right)}^2-2cpc{p}^{\prime }\cos \theta +{\mathrm{m}}_e^2{c}^4}-{\mathrm{m}}_e{c}^2.(42)$

The DCS obtained from the PWBA for ionizing collisions with electrons of a subshell a with binding energy E_a can be expressed as [17].

$\begin{array}{ccc}\hfill \frac{d^2{\sigma }_a}{dWdQ}& =\hfill & \frac{2\pi z_0^2{e}^4}{{\mathrm{m}}_e{v}^2}\left[\frac{2{\mathrm{m}}_e{c}^2}{WQ\left(Q+2{\mathrm{m}}_e{c}^2\right)}\frac{d{f}_a\left(Q,W\right)}{dW}\right.\hfill \\ \hfill & \hfill & +\left.\frac{2{\mathrm{m}}_e{c}^{2}W}{{\left[Q\left(Q+2{\mathrm{m}}_e{c}^2\right)-W^2\right]}^2}\left({\beta }^2-\frac{W^2}{Q\left(Q+2{\mathrm{m}}_e{c}^2\right)}\right)\frac{d{g}_a\left(Q,W\right)}{dW}\right]\hfill \end{array}(43)$

where z₀ = + 1 is the proton charge in units of e, and the functions df (Q, W)/dW and dg (Q, W)/dW are, respectively, the longitudinal and transverse generalized oscillator strengths (GOS). Bote and Salvat [17] have calculated these GOS for all electron shells of atoms with Z = 1 to 99 by using an independent-electron model with the Dirac-Hartree-Fock-Slater self-consistent potential of free atoms. The energy-loss DCS is obtained by integration over the kinematically allowed interval of recoil energies, (Q₋, Q₊), with endpoints given by Eq. 42 with cos θ = + 1 and −1,

$\frac{\mathrm{d}{\sigma }_a}{\mathrm{d}W}={\int }_{Q_{-}}^{Q_{+}}\frac{{\mathrm{d}}^2{\sigma }_a}{\mathrm{d}WdQ}\mathrm{d}Q.(44)$

In penelope-penh proton inelastic collisions are described by means of the PWBA with a simplified model of the GOS [1, 2], which is modulated so as to reproduce the cross sections for ionization of inner electron subshells read from the database. The main limitation of the PWBA is due to the neglect of the distortion of the projectile wave functions caused by the field of the target atom. For electrons and positrons, this distortion can be largely accounted for by using the distorted-wave Born approximation (DWBA), in which the projectile states are represented as distorted plane waves (see, e.g. [18], and references therein). Because of the slow convergence of the partial-wave series, this kind of calculation is only possible for projectile electrons and positrons with kinetic energies up to about 30E_a. Bote and Salvat [17] used an optimized computation strategy, which combines the DWBA and the PWBA, to generate a database of electron-impact ionization cross sections for the K shell and the L and M subshells of all the elements from hydrogen to einsteinium (Z = 1–99) and for energies of the projectile from 50 eV up to 1 GeV. The results were found to agree well with available experimental data [19].

Unfortunately, the calculation of cross sections for inelastic collisions from the DWBA is not feasible for charged particles heavier than the electron, because the smallness of the de Broglie wavelength of the projectile renders the calculation of free spherical waves extremely difficult. Chen et al. [20], and Chen and Crasemann [21, 22] went beyond the PWBA by using the perturbed-stationary-state approximation of Brandt and Lapicki [23], which accounts for 1) alterations in the binding of the active electron due to the presence of the projectile near the nucleus of the target atom, and 2) the deflection of the projectile path caused by the Coulomb field of the nucleus. In our PWBA calculations of ionization cross sections for protons, these effects are introduced by means of semi-classical correcting factors, which are described in the following paragraphs.

• Binding effect

In collisions where the projectile proton penetrates deep into the target atom, the presence of the projectile modifies the binding energy of the active electron and, in the case of positively charged projectiles, leads to a reduction of the DCS. For the K shell and L subshells, Brandt and Lapicki [23] performed a first-order perturbation analysis, assuming that the projectile follows a straight trajectory and using hydrogenic wave functions. They obtained an ionization-energy shift of the active target electron given by

$\mathrm{\Delta }{E}_a=\frac{2z_0{E}_a}{Z_a{\mathrm{\Theta }}_a}\left[g_a\left(\xi \right)-h_a\left(\xi \right)\right],(45)$

where Z_a = Z − δ_a is the effective nuclear charge felt by the electrons in the unperturbed orbitals, with δ_K = 0.3 and δ_Li = 4.15. The quantity Θ_a is the reduced ionization energy,

${\mathrm{\Theta }}_a=2n_a^2{E}_a/\left(Z_a^2{E}_{\mathrm{h}}\right),(46)$

where E_h = m_ee⁴/ℏ² = 27.211 eV is the Hartree energy. The last factor in Eq. 45 is a function of the dimensionless parameter

$\xi \equiv \frac{Z_a{E}_{\mathrm{h}}}{n_a{E}_a}\sqrt{\frac{{\mathrm{m}}_e}{M}\frac{2E}{E_{\mathrm{h}}}}.(47)$

In the calculations of ionization of K and L electrons we used the parameterization of the g_a(ξ) and h_a(ξ) functions given by Chen and Crasemann [21].

For M and outer shells, Chen et al. [20] considered that the effective ionization energy is the one of the “united” atom (i.e., of the atom with atomic number z₀ + Z). We have adopted a similar approach, which avoids the need of considering ionization energies of other atomic species. Expressing the ionization energies of the unperturbed states as (screened hydrogenic levels)

$E_a=\frac{{\left(Z-{\delta }_a^{\prime }\right)}^2}{2n_a^2}{E}_{\mathrm{h}},(\mathrm{48a})$

and noting that the screening constant ${\delta }_a^{\prime }$ is nearly the same for neighbouring elements, we can approximate the effective ionization energy in the form

$E_a^{\prime }=\frac{{\left(z_0+Z-{\delta }_a^{\prime }\right)}^2}{2n_a^2}{E}_{\mathrm{h}}.(\mathrm{48b})$

This gives the following ionization-energy shift

$\mathrm{\Delta }{E}_a=E_a^{\prime }-E_a=\frac{z_0^2+2z_0\left(Z-{\delta }_a^{\prime }\right)}{2n_a^2}{E}_{\mathrm{h}}.(49)$

• Coulomb deflection

For projectiles with small speeds, the PWBA, and the equivalent straight-trajectory semi-classical approximation [see, e.g., Ref. [24], and references therein], overestimate the ionization cross sections because they neglect the effect of the Coulomb field of the nucleus on the trajectory of the projectile. In the semi-classical treatment, the energy-loss DCS for a projectile following a classical hyperbolic orbit in the Coulomb potential of the bare target nucleus can be obtained by multiplying the energy-loss DCS, calculated by assuming that the projectile follows a straight trajectory, by a correction factor. This Coulomb-deflection factor was approximated as [23].

$F_a^{\mathrm{C}\mathrm{o}\mathrm{u}\mathrm{l}}\left(E;W\right)=\left(1-\frac{1}{3}{x}^{1/3}+\frac{5}{3}{x}^{2/3}\right)\exp \left(-2\pi x\right),(50)$

where

$x=Z_{0}Z\sqrt{\frac{M^3}{8m_e{M}_{\mathrm{r}\mathrm{e}\mathrm{d}}^2}\frac{E_{\mathrm{h}}}{E^3}}W.(51)$

The ionization cross section, including the binding and Coulomb-deflection corrections, is given by

${\sigma }_a^{\mathrm{i}\mathrm{o}\mathrm{n}}={\int }_{E_a+\mathrm{\Delta }{E}_a}^{W_{\max }}{F}_a^{\mathrm{C}\mathrm{o}\mathrm{u}\mathrm{l}}\left(E;W\right)\frac{\mathrm{d}{\sigma }_a^{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}}}{\mathrm{d}W}dW.(52)$

We have generated a database of proton-impact ionization cross sections for the K shell and the L, M and N subshells of the elements with Z = 1 to 99, by numerical integration of the energy-loss DCS obtained from the longitudinal and transverse GOSs calculated by Bote and Salvat [17]. Figure 1 displays these ionization cross sections for electron subshells of the titanium and gold atoms. For comparison purposes, the plots include also values calculated by Chen and Crasemann [21, 22] for the DHFS potential but only with the longitudinal GOS. It is worth mentioning that our database includes relativistic effects in a more consistent way, and it covers the energy range up to 10¹¹ eV for all elements from hydrogen (Z = 1) to einsteinium (Z = 99).

FIGURE 1

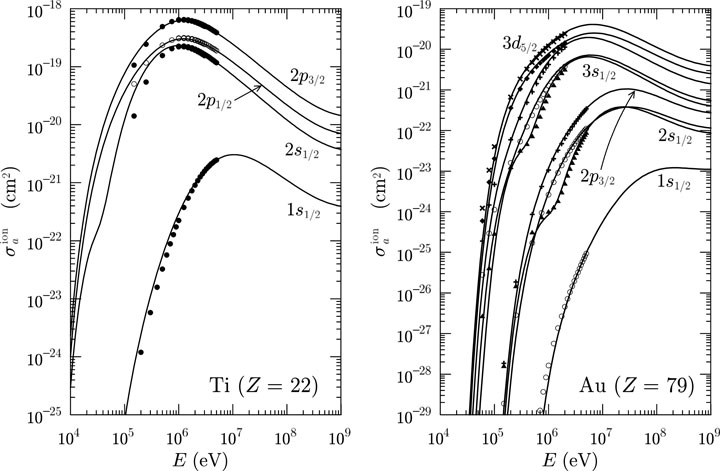
FIGURE 1. Cross sections for ionization of the K, L and M subshells of titanium and gold by impact of protons as functions of the kinetic energy of the projectile. Solid curves represent the values in the penh database. Symbols are results from equivalent PWBA calculations by Chen and Crasemann [21, 22], which also include the binding and Coulomb-deflection corrections.

In the simulation code, the ionization cross sections are multiplied by an energy-dependent factor (deduced from the Sternheimer-Liljequist GOS model) that accounts for the reduction of the cross section caused by the density-effect correction [3].

4 Neutron Contribution to the Dose Distribution

The databases presented in the previous Sections for elastic collisions and impact ionization of protons provide realistic models for electromagnetic interactions of protons, and the class II simulation scheme avoids the use of multiple scattering approximations and their associated uncertainties.

As mentioned above, the original penh code [3] gave a spatial dose distribution that was nearly correct near the proton beam axis, but the simulated dose was too small far from the beam axis. This was first noted by Verbeek et al. [25] and latter confirmed by the authors through comparison with results from the fluka and Geant4 codes, which include neutron transport. The main cause of this underestimation of the distant dose was attributed to the neglect of neutron transport, and this motivated the inclusion of the present simple approach for neutrons. Preliminary simulations with the parameter $\mathtt{F}\mathtt{N}\mathtt{A}\mathtt{B}\mathtt{S}=1$ gave depth-dose distributions from pencil beams of protons that were closer to, but slightly exceeded those from Geant4. The discrepancy can be readily corrected by using a smaller value of $\mathtt{F}\mathtt{N}\mathtt{A}\mathtt{B}\mathtt{S}$.

Figure 2 compares depth-dose distributions of proton beams incident normally on a water phantom with energies of 100 and 200 MeV simulated with the penh and Geant4 codes. The red histograms were produced by assuming that neutrons resulting from proton-induced nuclear reactions are absorbed at the reaction site. The blue histograms resulted from assuming that neutrons are transported as described in Section 2.4 with $\mathtt{F}\mathtt{N}\mathtt{A}\mathtt{B}\mathtt{S}=1$. It is seen that the transport and absorption of neutrons increases the depth-dose beyond the Bragg peak by nearly a factor of 10, slightly exceeding the depth-dose generated by the Geant4 code (green histograms). Reducing the value of $\mathtt{F}\mathtt{N}\mathtt{A}\mathtt{B}\mathtt{S}$ to 0.85 and to 0.8 for 100 and 200 MeV protons gives depth-dose distributions nearly coincident with those from Geant4. The latter are seen to agree closely with the penh result, except in the deep fall of the Bragg peak, probably because of differences in the proton transport physics of the two codes. Another relevant effect of neutron transport is a slight decrease of the depth-dose at shallow depths, which is visible in the plot for the 200 MeV beam; this effect is expected to increase in importance with the energy of incident protons because of the higher energies of the released neutrons.

FIGURE 2

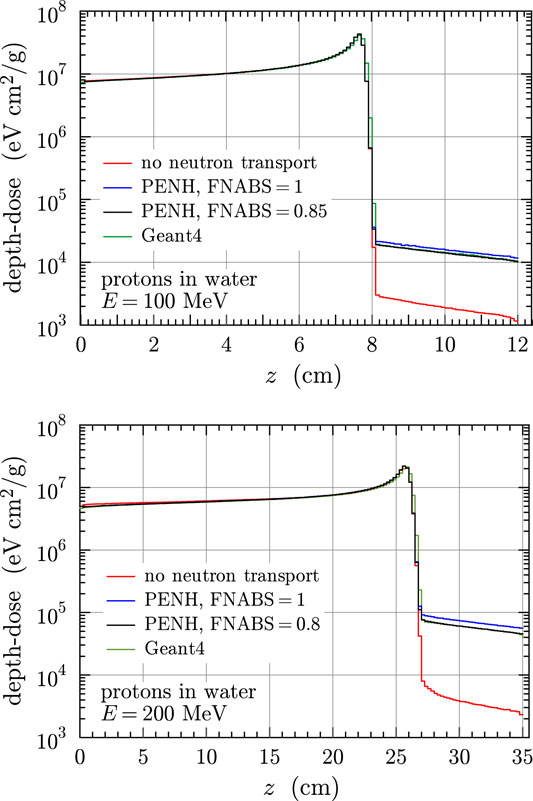
FIGURE 2. Depth-dose functions of 100 and 200 MeV proton beams impinging normally on a water phantom. The green histograms are results from the Geant4 code. Other histograms represent results from penh with neutrons absorbed at the reaction site (red), and neutrons transported as explained in Section 2.4 with the indicated values of $\mathtt{F}\mathtt{N}\mathtt{A}\mathtt{B}\mathtt{S}$ (blue and black).

5 Simulation of Proton-Induced X-Ray Emission

As penh uses fairly reliable cross sections for proton impact ionization, together with a careful modeling of electromagnetic interactions, it may be used to simulate proton-induced x-ray emission (PIXE) spectra [26]. The code describes the relaxation of ionized atoms by means of the penelope subroutines, which use transition probabilities from the Evaluated Atomic Data Library of Perkins et al. [27] and empirical values of the x-ray energies [1]. The simulation of PIXE spectra by penh is analogous to that of electron induced x-ray emission by the penelope code, which has been proved to be effective for quantification in electron-probe microanalysis [28]. It is worth noticing that penh accounts for both the attenuation and the generation of x-ray fluorescence within the target. It also follows the bremsstrahlung emitted by secondary electrons, which produces a smooth background of in the simulated PIXE spectra. Primary protons also contribute to the background through the emission of atomic bremsstrahlung (see [29] and references therein), however, this mechanism is not accounted for in penh. In its present form, our simulation code can be useful to determine the influence of the composition and local geometry of the irradiated target on the line intensities of the emitted x rays.

Figure 3 displays results from two simulations of x-ray spectra emitted from a silver target bombarded with 3 MeV protons impinging in a direction at an angle of 45° from the target surface. In those simulations neutrons were not followed, and the variance reduction techniques of interaction forcing and emission splitting of bremsstrahlung photons and x rays [1] were applied. The upper plot shows the energy spectrum of all photons that emerge from the target. The continuous background corresponds to bremsstrahlung emitted by secondary electrons. Since the maximum energy of secondary electrons released in inelastic collisions of 3 MeV photons is about 6.5 keV, the spectral background ends at this energy. A weak and noisy background component that extends to higher energies in the simulated spectrum (not shown in the upper plot of Figure 3) corresponds to gamma rays released in proton-induced nuclear reactions. The lower plot of Figure 3 shows the energy spectrum of photons that emerge in directions forming angles less than 30° with the normal to the target, restricted to the energy interval of L lines. The most prominent x-ray lines can be readily identified from their numerical values in the penelope database.

FIGURE 3

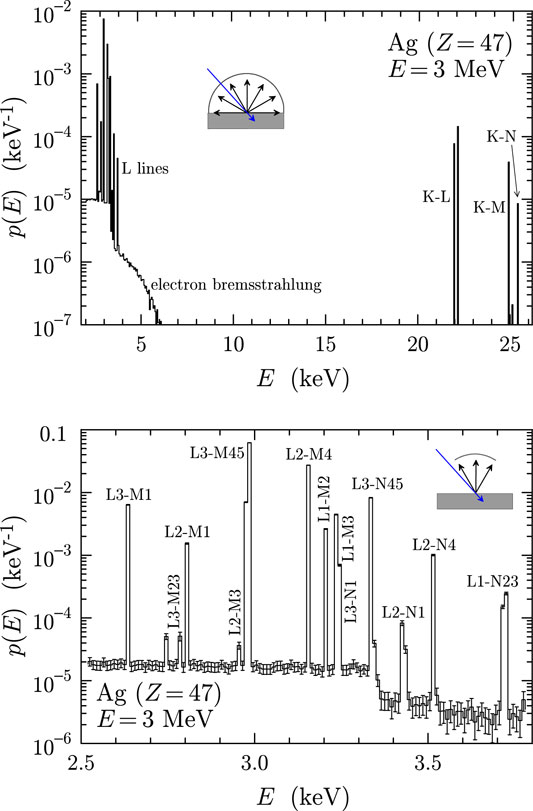
FIGURE 3. PIXE spectra from a silver plate irradiated with 3 MeV protons incident at an angle of 45° to the surface. The upper plot is the spectrum obtained by collecting all photons that emerge from the surface. The spectrum in the lower plot is restricted to the energy interval of L x-ray lines; it was recorded by assuming a detector that only collects photons that emerge at angles less the 30° from the normal to the target.

Simulated photon spectra correspond to an ideal detector with unit efficiency. They are output in the form of histograms with a fixed bin width, which implies a resolution in energy of the order of the bin width. To get results with an appearance closer to measurement data, the simulated spectrum should be convolved with the response function of the detector [28]. Comparison of spectra so obtained with measured spectra may help to identify features not evident from the experimental result.

6 Concluding Comments

In its present form, the penh code provides a consistent description of electromagnetic interactions of electrons, positrons and protons with matter for projectiles with energies up to 1 GeV. The use of nuclear data from ENDF-formatted files allows accounting for proton-induced nuclear reactions, and the release of gammas and secondary particles resulting from these interactions, in the energy range covered by available libraries, which usually extends up to about 200 MeV. For protons with somewhat higher energies, the code can extrapolate the nuclear data, with the risk of distorting the results.

Since the interaction models implemented in penh lose validity at low energies, the code should not be used for electrons, positrons and photons with E ≲ 1 keV, and for protons and neutrons with E < 100 keV.

The method adopted for tracking neutrons is intended only to correct for the effect of neutron transport on the simulated dose distributions, of interest mostly in proton therapy. Processes where neutrons may have more relevance cannot be dealt with penh.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

Financial support from the Spanish Ministerio de Ciencia, Innovación y Universidades /Agencia Estatal de Investigación /European Regional Development Fund, European Union, (projects nos. RTI2018-098117-B-C21 and RTI2018-098117-B-C22) is gratefully aknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Salvat F. PENELOPE 2018: A Code System for Monte Carlo Simulation of Electron and Photon Transport. Boulogne-Billancourt, France: OECD Nuclear Energy Agency (2019). document NEA/MBDAV/R(2019)1. doi:10.1787/32da5043-en

CrossRef Full Text | Google Scholar

2. Salvat F. A Generic Algorithm for Monte Carlo Simulation of Proton Transport. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2013) 316:144–59. doi:10.1016/j.nimb.2013.08.035

CrossRef Full Text | Google Scholar

3. Salvat F, Quesada JM. Nuclear Effects in Proton Transport and Dose Calculations. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2020) 475:49–62. doi:10.1016/j.nimb.2020.03.017

CrossRef Full Text | Google Scholar

4. Koning AJ, Delaroche JP. Local and Global Nucleon Optical Models from 1 keV to 200 MeV. Nucl Phys A (2003) 713:231–310. doi:10.1016/s0375-9474(02)01321-0

CrossRef Full Text | Google Scholar

5. Salvat F, Mart̆nez JD, Mayol R, Parellada J. Analytical Dirac-Hartree-Fock-Slater Screening Function for Atoms (Z=1-92). Phys Rev A (1987) 36:467–74. doi:10.1103/physreva.36.467

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Trkov A, Herman M. ENDF-6 Formats Manual: Data Formats and Procedures for the Evaluated Nuclear Data Files. Technical Report CSEWG Document ENDF-102. Upton, NY: Brookhaven National Laboratory (2018). Report BNL-90365-2009 Rev. 2. doi:10.2172/1425114

CrossRef Full Text | Google Scholar

7. Salvat F, Fernández-Varea JM. Radial: A Fortran Subroutine Package for the Solution of the Radial Schrödinger and Dirac Wave Equations. Comput Phys Commun (2019) 240:165–77. doi:10.1016/j.cpc.2019.02.011

CrossRef Full Text | Google Scholar

8. Olver F, Lozier D, Boisvert R, Clark C. NIST Handbook of Mathematical Functions. New York: Cambridge University Press (2010). Available from: http://dlmf.nist.gov/ (Accessed December 1, 2021).

Google Scholar

9. Coursey J. S., Schwab D. J., Tsai J. J., Dragoset R. A.. Atomic Weights and Isotopic Compositions with Relative Atomic Masses. [Dataset]. Gaithersburg, MD: National Institute of Standards and Technology (2015). Available from www.nist.gov/srd/chemistry (Accessed December 1, 2021).

Google Scholar

10. Su X-W, Han Y-L. Global Optical Model Potential for Alpha Projectile. Int J Mod Phys E (2015) 24:1550092. doi:10.1142/s0218301315500925

CrossRef Full Text | Google Scholar

11. Ferrari A, Sala PR, Fassò A, Ranft J. Fluka: a Multi-Particle Transport Code. Technical Report CERN-2005-00X. Geneva: CERN (2005). INFN TC 05/11, SLAC-R-773. doi:10.2172/877507

CrossRef Full Text | Google Scholar

12. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. Geant4—a Simulation Toolkit. Nucl Instrum Meth A (2003) 506:250–303. doi:10.1016/S0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

13. Allison J, Amako K, Apostolakis J, Araujo HM, Arce Dubois P, Asai M, et al. Geant4 Developments and Applications. IEEE Trans Nucl Sci (2006) 53:270–8. doi:10.1109/TNS.2006.869826

CrossRef Full Text | Google Scholar

14. Allison J, Amako K, Apostolakis J, Arce P, Asai M, Aso T, et al. Recent Developments in Geant4. Nucl Instrum Meth A (2016) 835:186–225. doi:10.1016/j.nima.2016.06.125

CrossRef Full Text | Google Scholar

15. Fano U. Penetration of Protons, Alpha Particles, and Mesons. Annu Rev Nucl Sci (1963) 13:1–66. doi:10.1146/annurev.ns.13.120163.000245

CrossRef Full Text | Google Scholar

16. Inokuti M. Inelastic Collisions of Fast Charged Particles with Atoms and Molecules-The Bethe Theory Revisited. Rev Mod Phys (1971) 43:297–347. doi:10.1103/revmodphys.43.297

CrossRef Full Text | Google Scholar

17. Bote D, Salvat F. Calculations of Inner-Shell Ionization by Electron Impact with the Distorted-Wave and Plane-Wave Born Approximations. Phys Rev A (2008) 77:042701. doi:10.1103/physreva.77.042701

CrossRef Full Text | Google Scholar

18. Segui S, Dingfelder M, Salvat F. Distorted-wave Calculation of Cross Sections for Inner-Shell Ionization by Electron and Positron Impact. Phys Rev A (2003) 67:062710. doi:10.1103/physreva.67.062710

CrossRef Full Text | Google Scholar

19. Llovet X, Powell CJ, Salvat F, Jablonski A. Cross Sections for Inner-Shell Ionization by Electron Impact. J Phys Chem Reference Data (2014) 43:013102. doi:10.1063/1.4832851

CrossRef Full Text | Google Scholar

20. Chen MH, Crasemann B, Mark H. Relativistic Calculation of atomicM-Shell Ionization by Protons. Phys Rev A (1983) 27:2358–64. doi:10.1103/physreva.27.2358

CrossRef Full Text | Google Scholar

21. Hsiung Chen M, Crasemann B. Relativistic Cross Sections for Atomic K- and L-Shell Ionization by Protons, Calculated from a Dirac-Hartree-Slater Model. At Data Nucl Data Tables (1985) 33:217–33. doi:10.1016/0092-640x(85)90002-6

CrossRef Full Text | Google Scholar

22. Chen MH, Crasemann B. Atomic K-, L-, and M-Shell Cross Sections for Ionization by Protons: A Relativistic Hartree-slater Calculation. At Data Nucl Data Tables (1989) 41:257–85. doi:10.1016/0092-640x(89)90020-x

CrossRef Full Text | Google Scholar

23. Brandt W, Lapicki G. L-shell Coulomb Ionization by Heavy Charged Particles. Phys Rev A (1979) 20:465–80. doi:10.1103/physreva.20.465

CrossRef Full Text | Google Scholar

24. Amundsen PA. Coulomb Deflection Effects in Ion-Induced K-Shell Ionisation. J Phys B: Mol Phys (1977) 10:2177–87. doi:10.1088/0022-3700/10/11/018

CrossRef Full Text | Google Scholar

25. Verbeek N, Wulff J, Bäumer C, Smyczek S, Timmermann B, Brualla L. Single Pencil Beam Benchmark of a Module for Monte Carlo Simulation of Proton Transport in the PENELOPE Code. Med Phys (2020) 48:456–76. doi:10.1002/mp.14598

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Ishii K. PIXE and its Applications to Elemental Analysis. QuBS (2019) 3:12. doi:10.3390/qubs3020012

CrossRef Full Text | Google Scholar

27. Perkins ST, Cullen DE, Chen MH, Hubbell JH, Rathkopf J, Scofield J. Tables and Graphs of Atomic Subshell and Relaxation Data Derived from the LLNL Evaluated Atomic Data Library (EADL), Z = 1–100. Technical Report UCRL-ID-50400. Livermore, California: Lawrence Livermore National Laboratory (1991).

Google Scholar

28. Llovet X, Salvat F. PENEPMA: A Monte Carlo Program for the Simulation of X-Ray Emission in Electron Probe Microanalysis. Microsc Microanal (2017) 23:634–46. doi:10.1017/s1431927617000526

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ishii K, Yamazaki H, Matsuyama S, Galster W, Satoh T, Budnar M. Contribution of Atomic Bremsstrahlung in PIXE Spectra and Screening Effect in Atomic Bremsstrahlung. X-ray Spectrom (2005) 34:363–5. doi:10.1002/xrs.838

CrossRef Full Text | Google Scholar