Network Reconstruction in Terms of the Priori Structure Information

In this paper, we investigate the reconstruction of networks based on priori structure information by the Element Elimination Method (EEM). We firstly generate four types of synthetic networks as small-world networks, random networks, regular networks and Apollonian networks. Then, we randomly delete a fraction of links in the original networks. Finally, we employ EEM, the resource allocation (RA) and the structural perturbation method (SPM) to reconstruct four types of synthetic networks with 90% priori structure information. The experimental results show that, comparing with RA and SPM, EEM has higher indices of reconstruction accuracy on four types of synthetic networks. We also compare the reconstruction performance of EEM with RA and SPM on four empirical networks. Higher reconstruction accuracy, measured by local indices of success rates, could be achieved by EEM, which are improved by 64.11 and 47.81%, respectively.

1 Introduction

Reconstructing a network based on priori structure information has attracted lots of attention for the network science [1]. Prior information about the connectivity patterns or potential interactions of the networks are accessible via public database [2, 3], high-throughput experiments [4], or data mining of interaction knowledge [5–7]. A wide diversity of methods based on priori structure information have been developed for the problem of network reconstruction [1, 8, 9]. Among various models, a few reconstruction models would provide a reliable estimate of a network’s structure with priori structure information. Link prediction is a typical method which uses accessible structure to estimate the likelihood of existence of unobserved links or identifies spurious links in a network [10, 11]. The unknown structure of a network is then reconstructed by link prediction. A few link prediction models are validated in both synthetic networks and empirical networks, which are local similarity indices [12–14], maximum likelihood methods [11, 15] and methods based on predictability [16, 17].

The other method uses accessible structure information to reconstruct a class of networks with evolutionary games [18, 19]. Such model, known as compressive sensing reconstruction model (CSR), is initially proposed to solve the problems of global network reconstruction [20–22]. The CSR method provides theoretical framework to dealing with networks purely from measured time-series information. To reconstruct a network with N nodes, the CSR method reconstructs the adjacent matrix column by column and each column is a vector with N elements [23, 24]. Contrary to the CSR method, the adjacent matrix is reconstructed by the Element Elimination Method (EEM) in a similar fashion, but the number of elements in different column might be N_i(N_i ≤ N, i = 1, 2, … , N) because EEM initially eliminates coupling nodes based on priori structure information. Exploiting the natural sparsity of the vectors, the pioneering work has applied EEM to achieve a successful reconstruction in scale-free networks with a small fraction of hubs [25]. However, in many cases, examples of real-world networks are not characterized by scale-free [26], i.e., the collaboration network of film actors [27, 28], the neural network of the worm Caenorhabditis elegans [26], the power grid of the western United States [29, 30], and drug trafficking network [31], et al. In addition, unique structure could be observed in world airline networks [32, 33] and Apollonian networks [34–36], which are characterized by scale-free and also satisfies basic features of small-world. EEM for reconstructing networks characterized by other features has not been fully explored. We are interested in, to achieve a successful reconstruction, the detailed amount of time-series information required for EEM in spite of the priori structure information. This motivates us to investigate the application of EEM to other networks characterized by different features.

In this paper, we investigate the reconstruction of general networks, which are characterized by four types of synthetic networks as small-world networks, random networks, regular networks and Apollonian networks. Typically, the reconstruction accuracy of EEM is evaluated on four types of networks. We will show the performance of EEM, characterized by low information requirements and high reconstruction accuracy. Experiments on four synthetic networks demonstrate that comparing with the resource allocation (RA) [12] and the structural perturbation method (SPM) [16], EEM can effectively enhance the reconstruction accuracy. Further, three local indices of success rates demonstrate that the reconstruction accuracy obtained by EEM when reconstructing three separately local structure in a network is close. In addition, experiments on four empirical networks demonstrate that EEM outperforms RA and SPM. Compared with RA and SPM, EEM has higher reconstruction accuracy, measured by local indices of success rates, which are improved by 64.11 and 47.81%, respectively.

2 Methods and Models

2.1 The Procedure of the Network Reconstruction

Uncovering a network’s structure has many potential applications so that we can assess the system’s resilience [37–39], understand the dynamical mechanisms [40], identify significant nodes in a network [41, 42], detect community structure [43], locate diffusion sources Hu et al. [44, 45], and analyze the networks’ properties [46–48]. In this paper, an Element Elimination Method (EEM) [25] is employed to reconstruct the structure of networks. We then give the illustration of the procedures of employing EEM to reconstruct synthetic networks: 1) Generate synthetic networks. 2) Extract time-series information from observed data. 3) Reconstruct the networks with EEM. Noting that the adjacent relationships between nodes in the network are sparse and would not change over time, we could explore the casual relationships between nodes’ time-series information. Consequently, we could uncover the unknown link set E^P of the networks by EEM based on priori link set E^T.

As illustrated in Figure 1, a procedure of network reconstruction is presented. Supposing the relationships between node 2 and other 5 nodes should be reconstructed, and only one adjacent relationship (a blue line in Figure 1A) is known. However, we are confused about which one is the original network from vastly different networks with possible connective relationships. Simultaneously, the network is evolving over the time, and a few time-series information of nodes’ strategies and payoffs could be obtained. We then build a model to bridge node 2’s strategies and its payoffs, as Figure 1B illustrated. Consequently, we can use EEM to reconstruct the network’s structure and obtain the adjacent relationships as shown in Figure 1C.

FIGURE 1

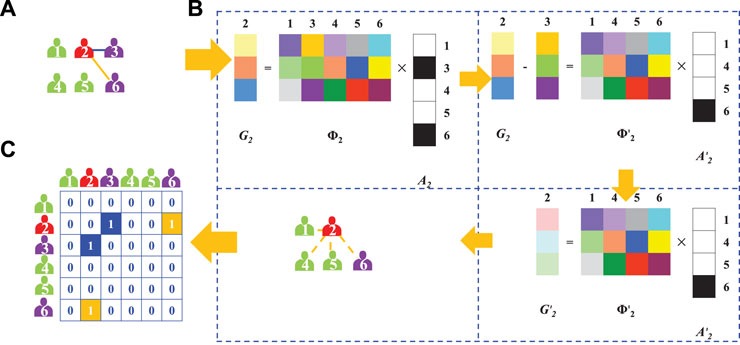
FIGURE 1. (Color Online) An illustration of reconstructing the hidden structure of a node based on priori structure information. (A) Original adjacent relationships of a node. For a node 2 in red with two neighbors, node 3 and node 6 in purple, we can observe a priori relationship, represented with a blue line, between node 2 and node 3. (B) EEM. We establish vector G₂ and matrix Φ₂ in the reconstruction form G₂ = Φ₂ ⋅A₂ from time-series information, where vector A₂ captures the adjacent relationships between node 2 and the other nodes. After subtracting time-series information determined by node 2 and priori neighbor, node 3, on the both sides of the equation, the unknown connections of node 2 can be reconstructed by optimizing the solution of the following equation ${\mathit{G}}_2^{\prime }={\mathbf{\Phi }}_2^{\prime }\cdot {\mathit{A}}_2^{\prime }$ using EEM. (C) A reconstructed adjacent matrix. The unknown neighbors of node 2 could be uncovered by EEM. The adjacent matrix is presented, in which golden blocks represent reconstructed link.

2.2 Generation of Synthetic Network

In order to evaluate the reconstruction performance of EEM in small-world networks and networks characterized by other features, we generate four types of synthetic networks. Noting that small-world network is a model of network that can be tuned between random network and regular network [26], we also consider the networks when their connection topology is assumed to be completely regular or completely random. Besides, the performance on the Apollonian networks by EEM has seldom been evaluated. Then, we generate four types of synthetic networks which are small-world networks, random networks, regular networks and Apollonian networks. The precedent findings indicate that the assortative coefficient has a direct influence on the accuracy of network reconstruction [49]. Therefore, some statistical properties have to be tuned when the networks are generated.

Supposing a network is composed of N nodes and |E| links. To minimize the influence from different network structure, we fix a default mean assortative coefficient $⟨r⟩$ for three types of synthetic networks, excluding Apollonian networks. Given wiring rules between nodes, we could generate vastly different networks with the given number of nodes N. Initially, the generated synthetic networks should have sufficient links that the total number of links of the network should exceed the number of links |E|. Then we randomly delete some of the links so that the number of the residual links is equal to |E|. In this way, the generated synthetic networks would have N nodes and |E| links. We select one network from the synthetic network set whose mean assortative coefficient is close to the value of default $⟨r⟩$ (the absolute error is less than 10^–3). The other types of synthetic networks are generated by another wiring rules in a similar way. Actually, synthetic networks generated whose statistical properties are close to default value are limited. On the other hand, the generation procedure of the regular network and the Apollonian network results in merely one realization of the synthetic networks. In this paper, each synthetic network has performed only one realization for the experiments.

Due to privacy or confidentiality issues, the complete structure of a network is not accessible. In addition, it is an impossible mission for us to record nodes’ complete time-series information. In spite of the difficulties, some priori information about the adjacent relationships between a few nodes, and discrete records of nodes’ time-series information might be available. Despite the limited information, the connective relationships between nodes has a direct effect on the individual node, which contributes to node’s attitude or selection in the next time. The dependence from the network’s structure on nodes’ interactions provide information for us to utilize the time-series information of nodes to describe the adjacent relationships behind them [24, 50].

2.3 The Model of the Evolutionary Game

The main challenge lies in that the structure of the network is inaccessible, also in that merely limited nodes’ time-series information is available. Since the time-series information is closely related to the connective relationships between nodes, we can reconstruct the unknown structure from the limited time-series information.

We use an evolutionary game model, the Prisoner Dilemma Game (PDG) model, to describe the nodes’ dynamics [51–53]. In each round of the game, the nodes usually weigh the benefits against the risks and selects a strategy. Here, we use SY_i(t) to define the strategy of node i. We denote vector SY_i(t) = (1,0)^T to represent a cooperation strategy, while we denote SY_i(t) = (0,1)^T to represent a defection strategy. Here, T stands for ‘transpose’.

When node i and node j trigger a game, the payoff of node i is dependent on both two nodes’ strategies and a uniform payoff matrix P, which is defined as:

$\mathbf{P}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill b\hfill & \hfill 0\hfill \end{array}\right)(1)$

where b (1 < b < 2) is a parameter characterizing the volume of payoff when node i select a defection strategy. In the t round, node i would play with all its different neighbors with the same strategy. When node i encounters a neighbor j, node i would gain payoff from node j as:

$F_{ij}(t)={\mathit{S}Y}_i^T(t)\cdot \mathbf{P}\cdot {\mathit{S}Y}_j(t).(2)$

In the same round, node i’s total payoffs G_i would be calculated, and it is the sum of the payoffs from all node i’s neighbors.

In a new round, node i would attempt to maximize its payoffs by updating its strategy. According to Fermi rule [54], node i randomly select a node j from its neighbors after t round. In t + 1 round, node i would then adopt node j’s strategy with the probability

$W({\mathit{S}Y}_i(t+1)\leftarrow {\mathit{S}Y}_j(t))=\frac{1}{1+exp[(T{G}_i(t)-T{G}_j(t))/\kappa ]},(3)$

where TG_i(t) is node i’s cumulative payoffs from 1 to t round. TG_j(t) is similarly defined. Parameter κ characterizes node’s rationality when it update strategies. Parameter κ = 0 corresponds to rational selection behavior of nodes.

Since game occurs among connected nodes, the information of the adjacent relationships between nodes are hidden in their dynamical records of strategies or payoffs in the game. Then we can utilize the information to uncover a networks’ structure when we collect the time-series information about the strategies and payoffs of nodes. When we reconstruct a certain network, the limited time-series information is usually presented in a random sample of sufficient time-series information.

2.4 Element Elimination Method

Given limited time-series information of nodes, an EEM could be applied to reconstruct a network based on priori structure information. EEM is a variant of the CSR method, which utilizes priori structure information to exclude the priori connective relationships before reconstruction. Suppose that the relationships between nodes in a certain network can be represented by an adjacency matrix A with dimensions N × N, where N is the number of nodes in the network. EEM decomposes the process of reconstructing the entire network into many subnetwork recovery problems, and the network structure, namely, the adjacency matrix A, is reconstructed column by column [55,56]. An adjacency vector A_i of a node is used to describe the adjacent relationships between node i (i = 1, 2, … , N) and the other N − 1 nodes in the network, which contains no loop. The adjacency vector ${\mathit{A}}_i={(a_{i1},a_{i2},\dots ,a_{i,i-1},a_{i,i+1},\dots ,a_{i,N})}^T$ with element a_ij = 1 when node i and node j are connected, and a_ij = 0 otherwise. Suppose that N_i (N_i ≤ N − 1) nodes in the adjacency vector A_i have undetermined relationships with node i. EEM is employed to find out node i’s (i = 1, 2, … , N) direct neighbors from N_i possible nodes, namely a shorter adjacency vector ${\mathit{A}}_i={(a_{i1}^{\prime },a_{i2}^{\prime },\dots ,a_{i,N_i}^{\prime })}^T$ of node i (i = 1, 2, … , N).

The training set E^T sheds light on the priori neighbor set ${\mathbf{\Gamma }}_i^K$ of node i, which contains (N − N_i − 1) nodes. Then we could calculate the sum of payoffs ${\mathit{G}}_{{\mathbf{\Gamma }}_i^K}^{\prime }$ of node i obtained from the priori neighbors in neighbor set ${\mathbf{\Gamma }}_i^K$ according to Eq. 2. Subtracting payoffs ${\mathit{G}}_{{\mathbf{\Gamma }}_i^K}^{\prime }$ from G_i, we obtain payoffs ${\mathit{G}}_i^{\prime }$ of node i. The payoffs ${\mathit{G}}_i^{\prime }$ implies the hidden adjacent relationships between node i and N_i other nodes because node i gains payoffs merely from its neighbors.

Most real-world networks are characterized by natural sparsity and the adjacency vector A_i of node i is sparse, which refers to vector A_i has only a few nonzero elements (i.e. a_ij = 1). Noting that the value of each element in node i’s priori adjacency vector ${\mathit{A}}_{{\mathbf{\Gamma }}_i^K}$ is 1, vector ${\mathit{A}}_i^{\prime }$ would still be sparse because the number of zero elements has not been changed but the number of nonzero elements has decreased when we remove the priori adjacency vector ${\mathit{A}}_{{\mathbf{\Gamma }}_i^K}$ from vector A_i. The sparsity of ${\mathit{A}}_i^{\prime }$ makes EEM applicable. Initially, the nodes’ strategies and payoffs are recorded in discrete round t₁, t₂, … , t_M. Since new payoffs are obtained from the game between node i and N_i nodes, we can build a model as Eq. 4. The sparse vector ${\mathit{A}}_i^{\prime }$ then can be reconstructed by solving the following convex optimization problem [57, 58]:

$\begin{array}{cc}\hfill & \mathrm{m}\mathrm{i}\mathrm{n}\Vert {\mathit{A}}_i^{\prime }{\Vert }_1\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\mathit{G}}_i^{\prime }={\mathbf{\Phi }}_i^{\prime }\cdot {\mathit{A}}_i^{\prime },\hfill \end{array}(4)$

where $\Vert {\mathit{A}}_i^{\prime }{\Vert }_1={\sum }_{j=1}^{N_i}|a_{ij}^{\prime }|$ is the L₁ norm of vector ${\mathit{A}}_i^{\prime }$. The available dynamical payoffs of node i can be expressed by ${\mathit{G}}_i^{\prime }={(G_i^{\prime }(t_1),G_i^{\prime }(t_2),\dots ,G_i^{\prime }(t_M))}^T$. The payoffs of node i obtained from the corresponding nodes in limited rounds can be expressed by an M × N_i sensing matrix ${\mathbf{\Phi }}_i^{\prime }$ (M ≪ N_i). In particular, we write ${\mathbf{\Phi }}_i^{\prime }=$

$\left(\begin{array}{cccc}\hfill F_{i1}(t_1)\hfill & \hfill F_{i,2}(t_1)\hfill & \hfill \dots \hfill & \hfill F_{i,N_i}(t_1)\hfill \\ \hfill F_{i1}(t_2)\hfill & \hfill F_{i,2}(t_2)\hfill & \hfill \dots \hfill & \hfill F_{i,N_i}(t_2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \dots \hfill & \hfill ⋮\hfill \\ \hfill F_{i1}(t_M)\hfill & \hfill F_{i,2}(t_M)\hfill & \hfill \dots \hfill & \hfill F_{i,N_i}(t_M)\hfill \end{array}\right).$

The elements in matrix ${\mathbf{\Phi }}_i^{\prime }$ could be calculated using the formula shown in Eq. 2. According to Eq. 4, we could obtain adjacency vector ${\mathit{A}}_i^{\prime }={(a_{i1}^{\prime },a_{i2}^{\prime },\dots ,a_{N_i}^{\prime })}^T$ by solving the convex optimization problem. We could obtain the complete adjacency vector ${\mathit{A}}_i={(a_{i1},a_{i2},\dots ,a_{iN})}^T$ by combining the reconstructed vector ${\mathit{A}}_i^{\prime }$ and the priori neighbor set ${\mathit{A}}_{{\mathbf{\Gamma }}_i^K}$ of node i. In a similar fashion, the neighbor-connection vectors of all the other nodes can be obtained, yielding the network’s adjacency matrix A = (A₁, A₂, … , A_N).

3 Experimental Results

3.1 Datasets

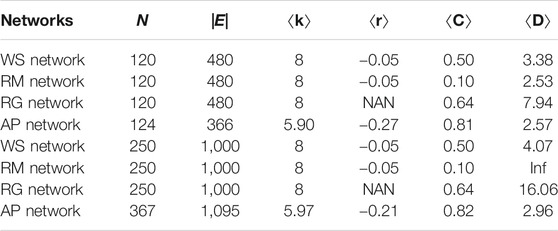
In order to understanding the performance of EEM in reconstructing the synthetic networks, the experiments are conducted in four types of networks. The basic statistical properties of the synthetic networks are presented in Table 1. N and |E| are the number of nodes and links. $⟨k⟩$ is the mean degree, $⟨r⟩$ is the mean assortative coefficient, $⟨C⟩$ is the mean clustering coefficient, and $⟨D⟩$ is the mean shortest distance. Here, we use abbreviation WS, RM, RG and AP to represent small-world networks, random networks, regular networks and Apollonian networks, respectively.

TABLE 1

TABLE 1. The statistical properties of four synthetic networks.

We assume that the strategies and payoffs of each node in a certain round t is one piece of time-series information. In the experiments, we use M pieces of accessible time-series information obtained from discrete round t₁ to round t_M to reconstruct different networks. In this paper, we set N, namely the number of nodes in the network, as the maximum value of M. Then we use an index of information sufficiency η(η ≡ M/N) to represent the size of the time-series information used in the network reconstruction. Intuitively, the time-series information is sufficient when the pieces of the accessible time-series information M = N, while the time-series information is insufficient when 0 < M < N. Correspondingly, the accessible time-series information is sufficient when the index of information sufficiency η = 1 and the accessible time-series information is insufficient when 0 < η < 1. The reconstruction models are also applied to reconstruct networks with different priori information of the structure, measured by a probability P_s(0 ≤ P_s ≤ 1).

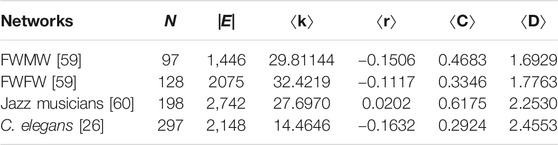
In addition, the performance of EEM is also evaluated in reconstructing the empirical networks. Table 2 shows the basic statistical properties of all four networks. These networks are chosen because they are characterized by large clustering coefficient and short distance.

TABLE 2

TABLE 2. The statistical properties of four empirical networks.

3.2 Metrics

To test the EEM’s accuracy, the original existent link set, E, are randomly divided into two parts: the priori set E^T, and the probe set E^P. Clearly, E = E^T ∪E^P and E^T ∩E^P = ∅. In this paper, the priori set always contains P_s of links, and the remaining 1 − P_s of links constitute the probe set. We apply four standard indices to quantify the reconstruction accuracy: the success rates of existent links SR, the success rates of nonexistent links SN [24], precision PRE [61, 62] and the area under the receiver operating characteristic curve AUC [63] are applied. In addition, we apply local indices of success rates in the experiments.

Both the success rates of existent links SR and the success rates of nonexistent links SN estimate the similarity of the reconstructed networks and the original networks. The success rates of existent links SR denotes the ratio of the number of links reconstructed by the reconstruction models to the number of real existent links in the network. The success rates of nonexistent links SN denotes the ratio of the number of nonexistent links distinguished by the reconstruction models to the number of real nonexistent links in the network. We obtain

$SR=\frac{1}{N}\sum _{i=1}^N\frac{|{\mathbf{\Gamma }}_{io}\cap {\mathbf{\Gamma }}_{ir}|}{|{\mathbf{\Gamma }}_{io}|}(5)$

$SN=\frac{1}{N}\sum _{i=1}^N\frac{|\overline{{\mathbf{\Gamma }}_{io}}\cap \overline{{\mathbf{\Gamma }}_{ir}}|}{|\overline{{\mathbf{\Gamma }}_{io}}|}(6)$

where Γ_io and Γ_ir denote real neighbor set of node i and neighbor set of node i reconstructed by the reconstruction models, respectively. |⋅| denotes the number of elements in a set ⋅. $\overline{{\mathbf{\Gamma }}_{io}}$ and $\overline{{\mathbf{\Gamma }}_{ir}}$ are the supplementary set of set Γ_io and Γ_ir. Each node in set $\overline{{\mathbf{\Gamma }}_{io}}$ is not adjacent to node i. Correspondingly, each node in reconstructed set $\overline{{\mathbf{\Gamma }}_{ir}}$ is not adjacent to node i. A successful reconstruction is achieved when the success rates of existent links SR (0 ≤ SR ≤ 1) and the success rates of nonexistent links SN(0 ≤ SN ≤ 1) are close to the value of 1.

Precision PRE is defined as the ratio of existent links reconstructed by models to the number of the whole unknown existent links. In our case, to calculate precision we need to rank all the unknown links in decreasing order according to existent possibilities computed by reconstruction models. Then we focus on the top-L (here L = |E^P|) links. If there are H links successfully reconstructed, then

$PRE=\frac{H}{L}(7)$

The area under the receiver operating characteristic curve AUC evaluates the reconstruction models’ performance according to the whole unknown link list. Provided the existent possibility of all unknown links, AUC can be interpreted as the probability that a randomly chosen unknown existent link is given a higher existent possibility than a randomly chosen nonexistent link. In the implementation, the value of AUC is calculated with a function perfcurve by Matlab.

Clearly, a higher value of the success rates of existent links SR, the success rates of nonexistent links SN, precision PRE or the area under the receiver operating characteristic curve AUC means a higher reconstruction accuracy. We conduct 50 times independent simulation for averaging the indices of reconstruction accuracy as the mean success rates of existent links $⟨SR⟩$, the mean success rates of nonexistent links $⟨SN⟩$, the mean precision $⟨PRE⟩$ and the mean area under the receiver operating characteristic curve $⟨AUC⟩$.

To understand the reconstruction performance of EEM when reconstructing local structure of the network divide the structure of each type of network into separately local structure. Supposing that the roles of nodes in the network are leaders, brokers and peripheral executors. We denote leaders are nodes with small degrees and the number of leaders in each type of network is 6. In addition, the subnetwork composed of leaders is a connected subgraph. Then brokers are nodes which are connected with leaders, and the residual nodes are peripheral executors. The sets of leaders, brokers and peripheral executors are not overlapped. We use letters L, B and P to represent the adjacent relationships between leaders, the adjacent relationships between leaders and brokers, and the adjacent relationships among peripheral executors and brokers, respectively. Then, we could obtain the success rates of existent links of each local structure normalized by the number of real existent links |Γ_io| of the network.

$S{R}_{Lr}=\frac{1}{N}\sum _{i=1}^N\frac{|{\mathbf{\Gamma }}_{Lio}\cap {\mathbf{\Gamma }}_{Lir}|}{|{\mathbf{\Gamma }}_{io}|}(8)$

$S{R}_{Br}=\frac{1}{N}\sum _{i=1}^N\frac{|{\mathbf{\Gamma }}_{Bio}\cap {\mathbf{\Gamma }}_{Bir}|}{|{\mathbf{\Gamma }}_{io}|}(9)$

$S{R}_{Pr}=\frac{1}{N}\sum _{i=1}^N\frac{|{\mathbf{\Gamma }}_{Pio}\cap {\mathbf{\Gamma }}_{Pir}|}{|{\mathbf{\Gamma }}_{io}|}(10)$

The sum of three local success rates of existent links is equal the global success rates of existent links.

$SR=S{R}_{Lr}+S{R}_{Br}+S{R}_{Pr}(11)$

Correspondingly, the maximum of three local success rates of existent links would be

$S{R}_{Lo}=\frac{1}{N}\sum _{i=1}^N\frac{|{\mathbf{\Gamma }}_{Lio}|}{|{\mathbf{\Gamma }}_{io}|}(12)$

$S{R}_{Bo}=\frac{1}{N}\sum _{i=1}^N\frac{|{\mathbf{\Gamma }}_{Bio}|}{|{\mathbf{\Gamma }}_{io}|}(13)$

$S{R}_{Po}=\frac{1}{N}\sum _{i=1}^N\frac{|{\mathbf{\Gamma }}_{Pio}|}{|{\mathbf{\Gamma }}_{io}|}(14)$

when the original network is successfully reconstructed. To quantify the success rates of three different local structure, we define local indices of success rates as follows:

$AP{P}_{SRL}=\frac{S{R}_{Lr}}{S{R}_{Lo}}(15)$

$AP{P}_{SRB}=\frac{S{R}_{Br}}{S{R}_{Bo}}(16)$

$AP{P}_{SRP}=\frac{S{R}_{Pr}}{S{R}_{Po}}(17)$

Similarly, a higher value of local index of success rates APP_SRL, APP_SRB, or APP_SRP means a higher reconstruction accuracy. We conduct 50 times independent simulation for averaging the indices of success rates $⟨AP{P}_{SRL}⟩$, $⟨AP{P}_{SRB}⟩$ and $⟨AP{P}_{SRP}⟩$.

3.3 Experimental Results on Synthetic and Empirical Networks

In order to understand the performance of EEM, four types of synthetic networks hosting a PDG dynamical process are considered in our paper. Figure 2A depicts the index of reconstruction accuracy for a synthetic small-world network, measured by the mean success rates of existent links $⟨SR⟩$, based on 90% priori structure information. The mean success rates of existent links $⟨SR⟩$ increases monotonously when the index of information sufficiency η is varying from 0.1 to 0.4. Especially the mean reconstruction accuracy $⟨SR⟩$ reaches the maximum value of 1 when the index of information sufficiency η = 0.4. The increment rate of the mean reconstruction accuracy $⟨SR⟩$ is 9.97%. Then the mean reconstruction accuracy $⟨SR⟩$ keeps the value of 1 when the index of information sufficiency η is larger than 0.4. As shown in Figures 2B–H, the mean reconstruction accuracy $⟨SR⟩$ increases monotonously when the index of information sufficiency η is less than 0.4. In addition, the mean reconstruction accuracy $⟨SR⟩$ reaches 1 for the different types of synthetic networks when the index of information sufficiency η exceeds 0.4.

FIGURE 2

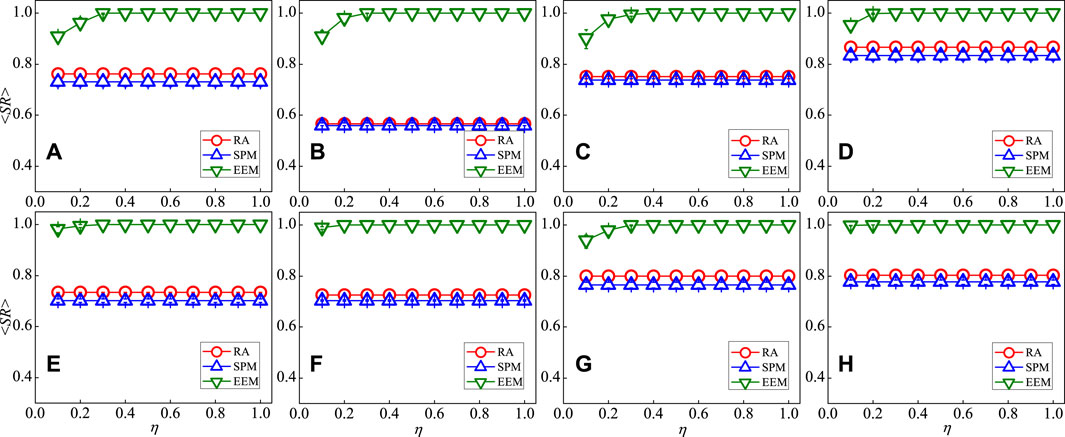
FIGURE 2. (Color Online) The mean success rates of existent links $⟨SR⟩$ of reconstructing four types of networks: (A) small-world network with 120 nodes, (B) random network with 120 nodes, (C) regular network with 120 nodes, (D) Apollonian network with 124 nodes, (E) small-world network with 250 nodes, (F) random network with 250 nodes, (G) regular network with 250 nodes, (H) Apollonian network with 367 nodes, hosting a PDG dynamical process. The lines with circle, triangle and inverted triangle symbols are the mean success rates of existent links $⟨SR⟩$ obtained by RA, SPM and EEM based on 90% priori structure information. The mean reconstruction accuracy indices are achieved by averaging over 50 independent experimental results. For each experiment, measurements are randomly picked from a time series of temporary evolution. The index of information sufficiency rate η indicates the amount of the available time-series information used in the reconstruction. The payoff parameter for the PDG is b = 1.2.

Moreover, we compare the experimental results between EEM and two link prediction models which are the resource allocation (RA) and the structural perturbation method (SPM). Figures 2A–H show that when the index of information sufficiency η is low (i.e., η = 0.1), the mean success rates of existent links $⟨SR⟩$ obtained by EEM on small-world networks, random networks, regular networks and Apollonian networks reaches 0.9093, 0.9085, 0.9021, 0.9361, 0.9823, 0.9897, 0.9402 and 0.9982, respectively. Compared with RA and SPM, EEM’s mean success rates of existent links $⟨SR⟩$ are higher, which is improved by at least 8.07 and 12.22% on the networks with 120–124 nodes, respectively. Compared with RA and SPM, EEM’s mean success rates of existent links $⟨SR⟩$ are higher, which is improved by at least 17.53 and 22.81% on the networks with 250–367 nodes, respectively. The experimental results of Figure 2 indicate that EEM has a well tradeoff that provides high quality reconstruction accuracy while requiring less time-series information.

Intuitively, a network’s structure would be accurately reconstructed when more priori information about the structure of the network are presented. Figure 3 shows the dependence of the values of $⟨SR⟩$ on probability P_s, the priori information of the structure, where we see that, in the cases of lower index of information sufficiency η (η ≤ 0.4), $⟨SR⟩$ increases monotonously when the probability P_s increases. On the other hand, the mean success rates of existent links $⟨SR⟩$ approaches the maximum value of 1 when the index of information sufficiency η is larger than 0.4. In terms of the probability P_s, the highest performance is achieved for the highest P_s. The intuitive reason for the relatively superior performance with the four synthetic networks lies in the sufficiency of the available information of the networks’ structure.

FIGURE 3

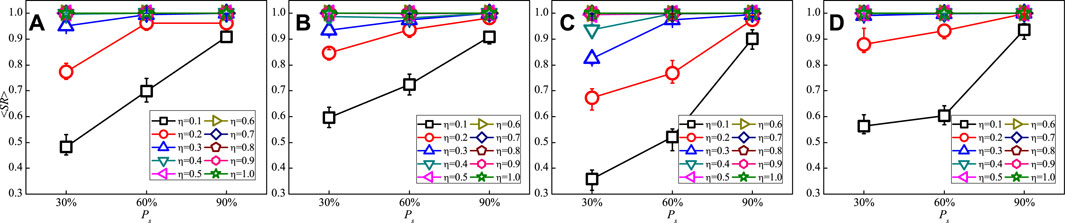
FIGURE 3. (Color Online) The mean success rates of existent links $⟨SR⟩$ of reconstructing four types of networks: (A) small-world network with 120 nodes, (B) random network with 120 nodes, (C) regular network with 120 nodes, (D) Apollonian network with 124 nodes, hosting a PDG dynamical process. The lines with different symbols are the mean success rates of existent links $⟨SR⟩$ obtained by EEM when the index of information sufficiency rate η catches different values. The mean reconstruction accuracy indices are achieved by averaging over 50 independent experimental results. For each experiment, measurements are randomly picked from a time series of temporary evolution. The priori information of the structure, measured by a probability P_s, indicates the amount of available priori information of the structure used in the reconstruction. The payoff parameter for the PDG is b = 1.2.

In the following, we verify the performance of EEM in local structure of the networks. We divide the structure of each type of network into three separately local structure with subscript L, B, P for them. Figure 4A depicts reconstruction success rate of a small-world network, measured by the mean local index of success rates $⟨AP{P}_{SRL}⟩$, $⟨AP{P}_{SRB}⟩$, and $⟨AP{P}_{SRP}⟩$, based on 90% priori structure information.

FIGURE 4

FIGURE 4. (Color Online) The mean local indices of success rates $⟨AP{P}_{SRL}⟩$, $⟨AP{P}_{SRB}⟩$, and $⟨AP{P}_{SRP}⟩$ of reconstructing four types of networks: (A) small-world network with 120 nodes, (B) random network with 120 nodes, (C) regular network with 120 nodes and (D) Apollonian network with 124 nodes, hosting a PDG dynamical process. The lines with circle, triangle and inverted triangle symbols are the mean local indices of success rates $⟨AP{P}_{SRL}⟩$, $⟨AP{P}_{SRB}⟩$, and $⟨AP{P}_{SRP}⟩$ obtained by RA, SPM and EEM based on 90% priori structure information. The mean reconstruction accuracy indices are achieved by averaging over 50 independent experimental results. For each experiment, measurements are randomly picked from a time series of temporary evolution. The index of information sufficiency rate η indicates the amount of the available time-series information used in the reconstruction. The payoff parameter for the PDG is b = 1.2.

As illustrated in the main graph in Figure 4A, the mean local index of success rates $⟨AP{P}_{SRL}⟩$ obtained by EEM is higher than RA or SPM. Especially the mean local index of success rates $⟨AP{P}_{SRL}⟩$ obtained by EEM reaches 96.41% when the index of information sufficiency η = 0.1, while the mean local index of success rates $⟨AP{P}_{SRL}⟩$ obtained by RA and SPM are both 88.95%. The mean local index of success rates $⟨AP{P}_{SRB}⟩$ and $⟨AP{P}_{SRP}⟩$ obtained by EEM are 93.95 and 86.68% when the index of information sufficiency η = 0.1, as shown in the subgraph (α)-(β) in Figure 4A. Correspondingly, the mean local index of success rates $⟨AP{P}_{SRB}⟩$ and $⟨AP{P}_{SRP}⟩$ obtained by RA are 62.67 and 79.51%, $⟨AP{P}_{SRB}⟩$ and $⟨AP{P}_{SRP}⟩$ obtained by SPM are 62.67 and 73.06%. The similar experimental results could also be found in the cases of random network, regular network and Apollonian network in Figures 4B–D, which indicate that EEM can achieve higher reconstruction accuracy with low time-series information than RA or SPM.

The underlying reason that EEM could obtain higher reconstruction accuracy than RA or SPM might be twofold. Firstly, EEM is applicable to reconstruct networks with sparse connective relationships because Wang et al. developed a paradigm [19, 24, 25] to address the network reconstruction problems and Candès et al. provided the theoretical framework for this paradigm [57, 58]. Both EEM and two link prediction models utilize the identical priori structure information of the network to obtain direct information of the unknown structure. In addition, EEM bridges the relationships between the nodes’ payoffs and strategies by virtue of time-series information because the payoffs can merely be obtained from each node’s neighbors. Then EEM could extract indirect information of the unknown structure from the above relationships which strengthens the reliability of the experimental results. RA and SPM could also extract valuable indirect information of the unknown structure, but the valuable information still originates from the priori structure information of the network due to lack of a universal theoretical framework.

Secondly, both the reconstruction accuracy of the local structure and the reconstruction accuracy of the global structure obtained by EEM highly consist. As illustrated in Figure 4, the absolute error between three mean local index of success rates $⟨AP{P}_{SRL}⟩$, $⟨AP{P}_{SRB}⟩$ and $⟨AP{P}_{SRP}⟩$ obtained by EEM on each network is less than 0.1, which indicates that the reconstruction accuracy on three separate local structure obtained by EEM is almost the same. Consequently, the global reconstruction accuracy and the local reconstruction accuracy highly consist because the global reconstruction accuracy is the linear combination of three mean local index of success rates as: $⟨SR⟩=S{R}_{Lo}\cdot ⟨AP{P}_{SRL}⟩+S{R}_{Bo}\cdot ⟨AP{P}_{SRB}⟩+S{R}_{Po}\cdot ⟨AP{P}_{SRP}⟩$, where SR_Lo, SR_Bo and SR_Po are constant for each network. The high reconstruction accuracy of three separately local structure contribute to a high reconstruction accuracy of the global structure. We also observe that the reconstruction accuracy on three separate local structure obtained by RA or SPM fluctuates. Especially in the reconstruction experiments on synthetic random networks, the maximum absolute error between three mean local index of success rates obtained by RA or SPM reaches 0.3837. The experimental results indicate that the reconstruction accuracy obtained by RA and SPM is largely dependent on the priori structure information of the network. The reconstruction accuracy of RA or SPM would be high when the local priori structure is consistent with the global structure, and the reconstruction accuracy would be low otherwise.

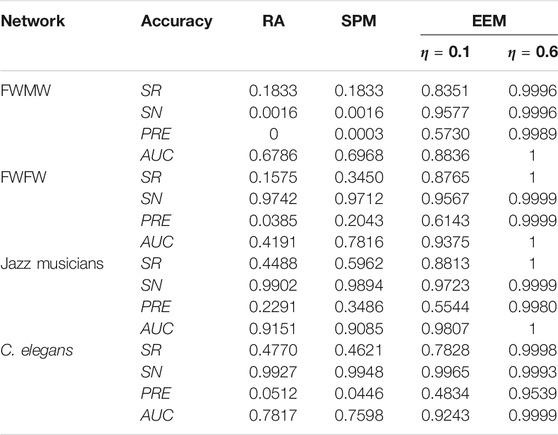
Finally, we test the results for four empirical networks. As shown in Table 3, we reconstruct the network structure by EEM, RA and SPM with 90% priori structure information. The empirical results indicate that four indices of reconstruction accuracy obtained by EEM are higher than RA and SPM for four empirical networks when the index of information sufficiency rate η = 0.1. Four indices of reconstruction accuracy obtained by EEM are higher than RA and SPM. Compared with RA, EEM’s reconstruction accuracy, measured by the mean success rates of existent links $⟨SR⟩$, which are improved by 355.54, 456.38, 96.37 and 64.11%, corresponding to FWMW, FWFW, Jazz musicians, Neural network of C. elegans. Compared with SPM, EEM’s reconstruction accuracy, measured by the mean success rates of existent links $⟨SR⟩$, which are improved by 355.54, 154.07, 47.81 and 69.38%,corresponding to FWMW, FWFW, Jazz musicians, Neural network of C. elegans. Empirical results indicate that the empirical networks reconstructed by EEM are closer to the original networks than those reconstructed by RA and SPM.

TABLE 3

TABLE 3. The value of four indices of reconstruction accuracy for four empirical networks.

3.4 Conclusion

In summary, we have investigated the performance of EEM for reconstructing synthetic networks, which are characterized by four types of networks as small-world networks, random networks, regular networks and Apollonian networks, based on priori structure information. The mean success rates of existent links $⟨SR⟩$ obtained by EEM could achieve at least 0.9021 when the index of information sufficiency η is 0.1. Compared with RA and SPM, EEM has higher mean success rates of existent links $⟨SR⟩$, which is improved by 8.07 and 12.22% on the networks with 120–124 nodes, respectively. Compared with RA and SPM, EEM has higher mean success rates of existent links $⟨SR⟩$, which is improved by 17.53 and 22.81% on the networks with 250–367 nodes, respectively. The experimental results also indicate that separately local structure in each type of network could be accurately reconstructed by EEM. In addition, EEM’s reconstruction accuracy is also evaluated on four empirical networks. Compared with RA and SPM, EEM has higher mean success rates of existent links $⟨SR⟩$, which is improved by 64.11 and 47.81%, respectively. The reason that EEM obtain higher reconstruction accuracy than RA or SPM might lie in that EEM could utilize time-series information to strengthen the reliability of the experimental results and EEM’s capability to reconstruct the local structure and the global structure highly consist. The evaluation of EEM on both synthetic networks and empirical networks suggest that EEM is applicable for networks with sparsely connective relationships and it has high reconstruction accuracy by low information requirements.

Although the efficiency of EEM has been measured in reconstructing network’s structure with both synthetic networks and empirical networks, there are still a lot of questions to be considered further. For example, the results show that EEM can give remarkably higher reconstruction accuracy on a network hosing a PDG dynamical process, but the performance of EEM has not been validated under another dynamical process. Although EEM could also be extended to cases with large-scale network, the computing time might increase exponentially. In addition, EEM’s capability to identify spurious links has not been explored. Noting that EEM can well capture the adjacent relationships from limited information and thus give more accurate reconstruction, such features make EEM appealing to reconstructing general networks with extremely low data requirement. Despite underlying challenges, we will make attempt to continue our research referring to the problems of network reconstruction.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

J-QF provided this topic and wrote the paper. QG, KY and J-GL guided, discussed and modified the manuscript. All authors contributed to manuscript and approved the submission version.

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos. 71771152 and 61773248), the National Social Science Fund of China (No.16BJY158), the Major Program of National Fund of Philosophy and Social Science of China (Nos. 20ZDA060 and 18ZDA088), and the Scientific Research Project of Shanghai Science and Technology Committee (Grant No. 19511102202).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors acknowledge the valuable discussion with Huan-Mei Qin, Guang Liang, Ren-De Li, Hong-Yi Ding, Shao-Yong Han.

References

1. Liao JC, Boscolo R, Yang Y-L, Tran LM, Sabatti C, Roychowdhury VP. Network Component Analysis: Reconstruction of Regulatory Signals in Biological Systems. Proc Natl Acad Sci (2003) 100:15522–7. doi:10.1073/pnas.2136632100

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Matys V, Fricke E, Geffers R, Göβling E, Haubrock M, Hehl R. TRANSFAC(R): Transcriptional Regulation, from Patterns to Profiles. Nucleic Acids Res (2003) 31:374–8. doi:10.1093/nar/gkg108

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Keseler IM, Collado-Vides J, Gama-Castro S, Ingraham J, Paley S, Paulsen IT. Ecocyc: A Comprehensive Database Resource for Escherichia Coli. Nucleic Acids Res (2004) 33:D334–D337. doi:10.1093/nar/gki108

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK. Transcriptional Regulatory Networks in Saccharomyces Cerevisiae. Science (2002) 298:799–804. doi:10.1126/science.1075090

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dong GG, Wang F, Shekhtmane LM, Danziger MM, Fan JF, Du RJ. Optimal Resilience of Modular Interacting Networks. Proc Natl Acad Sci USA. (2021) 118:e1922831118. doi:10.1073/pnas.1922831118

6. Bussemaker HJ, Li H, Siggia ED. Building a Dictionary for Genomes: Identification of Presumptive Regulatory Sites by Statistical Analysis. Proc Natl Acad Sci (2000) 97:10096–100. doi:10.1073/pnas.180265397

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bussemaker HJ, Li H, Siggia ED. Regulatory Element Detection Using Correlation With Expression. Nat Genet (2001) 27:167–71. doi:10.1038/84792

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Chang C, Ding Z, Hung YS, Fung PCW. Fast Network Component Analysis (Fastnca) for Gene Regulatory Network Reconstruction From Microarray Data. Bioinformatics (2008) 24:1349–58. doi:10.1093/bioinformatics/btn131

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Cugueró-Escofet MÀ, Quevedo J, Alippi C, Roveri M, Puig V, García D. Model- vs. Data-Based Approaches Applied to Fault Diagnosis in Potable Water Supply Networks. J Hydroinformatics (2016) 18:831–50. doi:10.2166/hydro.2016.218

CrossRef Full Text | Google Scholar

10. Lü L, Zhou T. Link Prediction in Complex Networks: A Survey. Physica A: Stat Mech Its Appl (2011) 390:1150–70. doi:10.1016/j.physa.2010.11.027

CrossRef Full Text | Google Scholar

11. Clauset A, Moore C, Newman MEJ. Hierarchical Structure and the Prediction of Missing Links in Networks. Nature (2008) 453:98–101. doi:10.1038/nature06830

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhou T, Lü L, Zhang Y-C. Predicting Missing Links via Local Information. Eur Phys J B (2009) 71:623–30. doi:10.1140/epjb/e2009-00335-8

CrossRef Full Text | Google Scholar

13. Lü L, Jin C-H, Zhou T. Similarity Index Based on Local Paths for Link Prediction of Complex Networks. Phys Rev E (2009) 80:046122. doi:10.1103/PhysRevE.80.046122

CrossRef Full Text | Google Scholar

14. Liben-Nowell D, Kleinberg J. The Link-Prediction Problem for Social Networks. J Am Soc Inf Sci (2007) 58:1019–31. doi:10.1002/asi.20591

CrossRef Full Text | Google Scholar

15. Guimerà R, Sales-Pardo M. Missing and Spurious Interactions and the Reconstruction of Complex Networks. Proc Natl Acad Sci (2009) 106:22073–8. doi:10.1073/pnas.0908366106

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lü L, Pan L, Zhou T, Zhang Y-C, Stanley HE. Toward Link Predictability of Complex Networks. Proc Natl Acad Sci USA (2015) 112:2325–30. doi:10.1073/pnas.1424644112

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Sun J, Feng L, Xie J, Ma X, Wang D, Hu Y. Revealing the Predictability of Intrinsic Structure in Complex Networks. Nat Commun (2020) 11:1–10. doi:10.1038/s41467-020-14418-6

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhang H-F, Wang W-X. Complex System Reconstruction. Acta Physica Sinica (2020) 69:088906. doi:10.7498/aps.69.20200001

CrossRef Full Text | Google Scholar

19. Wang W-X, Lai Y-C, Grebogi C. Data Based Identification and Prediction of Nonlinear and Complex Dynamical Systems. Phys Rep (2016) 644:1–76. doi:10.1016/j.physrep.2016.06.004

CrossRef Full Text | Google Scholar

20. Xu M, Xu C-Y, Wang H, Li Y-K, Hu J-B, Cao K-F. Global and Partitioned Reconstructions of Undirected Complex Networks. Eur Phys J B (2016) 89:1–6. doi:10.1140/epjb/e2016-60956-2

CrossRef Full Text | Google Scholar

21. Barranca VJ, Zhou D. Compressive Sensing Inference of Neuronal Network Connectivity in Balanced Neuronal Dynamics. Front Neurosci (2019) 13:1101. doi:10.3389/fnins.2019.01101

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Li R-D, Guo Q, Ma H-T, Liu J-G. Network Reconstruction of Social Networks Based on the Public Information. Chaos (2021) 31:033123. doi:10.1063/5.0038816

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Shen Z, Wang W-X, Fan Y, Di Z, Lai Y-C. Reconstructing Propagation Networks With Natural Diversity and Identifying Hidden Sources. Nat Commun (2014) 5:1–10. doi:10.1038/ncomms5323

CrossRef Full Text | Google Scholar

24. Wang W-X, Lai Y-C, Grebogi C, Ye J. Network Reconstruction Based on Evolutionary-Game Data via Compressive Sensing. Phys Rev X (2011) 1:021021. doi:10.1103/PhysRevX.1.021021

CrossRef Full Text | Google Scholar

25. Ma L, Han X, Shen Z, Wang W-X, Di Z. Efficient Reconstruction of Heterogeneous Networks From Time Series via Compressed Sensing. PLoS One (2015) 10:e0142837. doi:10.1371/journal.pone.0142837

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Watts DJ, Strogatz SH. Collective Dynamics of 'Small-World' Networks. Nature (1998) 393:440–2. doi:10.1038/30918

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Amaral LAN, Scala A, Barthélémy M, Stanley HE. Classes of Small-World Networks. Proc Natl Acad Sci (2000) 97:11149–52. doi:10.1073/pnas.200327197

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ravasz E, Barabási A-L. Hierarchical Organization in Complex Networks. Phys Rev E (2003) 67. doi:10.1103/PhysRevE.67.026112

CrossRef Full Text | Google Scholar

29. Albert R, Albert I, Nakarado GL. Structural Vulnerability of the North American Power Grid. Phys Rev E Stat Nonlin Soft Matter Phys (2004) 69:025103. doi:10.1103/PhysRevE.69.025103

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Crucitti P, Latora V, Marchiori M. A Topological Analysis of the Italian Electric Power Grid. Physica A: Stat Mech Its Appl (2004) 338:92–7. doi:10.1016/j.physa.2004.02.029

CrossRef Full Text | Google Scholar

31. Bright D, Koskinen J, Malm A. Illicit Network Dynamics: The Formation and Evolution of a Drug Trafficking Network. J Quant Criminol (2019) 35:237–58. doi:10.1007/s10940-018-9379-8

CrossRef Full Text | Google Scholar

32. Barrat A, Barthélemy M, Pastor-Satorras R, Vespignani A. The Architecture of Complex Weighted Networks. Proc Natl Acad Sci (2004) 101:3747–52. doi:10.1073/pnas.0400087101

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Verma T, Araújo NAM, Nagler J, Andrade JS, Herrmann HJ. Model for the Growth of the World Airline Network. Int J Mod Phys C (2016) 27:1650141. doi:10.1142/S0129183116501412

CrossRef Full Text | Google Scholar

34. Soares DJB, Andrade JS, Herrmann HJ, da Silva LR. Three-Dimensional Apollonian Networks. Int J Mod Phys C (2006) 17:1219–26. doi:10.1142/S0129183106009175

CrossRef Full Text | Google Scholar

35. Andrade RFS, Andrade JS, Herrmann HJ. Ising Model on the Apollonian Network With Node-Dependent Interactions. Phys Rev E (2009) 79:036105. doi:10.1103/PhysRevE.79.036105

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Araújo NA, Andrade RFS, Herrmann HJ. Q-State Potts Model on the Apollonian Network. Phys Rev E (2010) 82:046109. doi:10.1103/physreve.82.046109

CrossRef Full Text | Google Scholar

37. Dong G, Wang F, Shekhtman LM, Danziger MM, Fan J, Du R. Optimal Resilience of Modular Interacting Networks. Proc Natl Acad Sci USA (2021) 118:e1922831118. doi:10.1073/pnas.1922831118

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Dong G, Fan J, Shekhtman LM, Shai S, Du R, Tian L. Resilience of Networks With Community Structure Behaves as if Under an External Field. Proc Natl Acad Sci USA (2018) 115:6911–5. doi:10.1073/pnas.1801588115

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Gao J, Barzel B, Barabási A-L. Universal Resilience Patterns in Complex Networks. Nature (2016) 530:307–12. doi:10.1038/nature16948

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Xu X, Zhang J, Small M. Superfamily Phenomena and Motifs of Networks Induced From Time Series. Proc Natl Acad Sci (2008) 105:19601–5. doi:10.1073/pnas.0806082105

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Ren Z-M. Age Preference of Metrics for Identifying Significant Nodes in Growing Citation Networks. Physica A: Stat Mech its Appl (2019) 513:325–32. doi:10.1016/j.physa.2018.09.001

CrossRef Full Text | Google Scholar

42. Liu J-G, Ren Z-M, Guo Q. Ranking the Spreading Influence in Complex Networks. Physica A: Stat Mech its Appl (2013) 392:4154–9. doi:10.1016/j.physa.2013.04.037

CrossRef Full Text | Google Scholar

43. Pan Y, Li D-H, Liu J-G, Liang J-Z. Detecting Community Structure in Complex Networks via Node Similarity. Physica A: Stat Mech its Appl (2010) 389:2849–57. doi:10.1016/j.physa.2010.03.006

CrossRef Full Text | Google Scholar

44. Hu Z-L, Shen Z, Tang C-B, Xie B-B, Lu J-F. Localization of Diffusion Sources in Complex Networks With Sparse Observations. Phys Lett A (2018) 382:931–7. doi:10.1016/j.physleta.2018.01.037

CrossRef Full Text | Google Scholar

45. Hu Z-L, Han X, Lai Y-C, Wang W-X. Optimal Localization of Diffusion Sources in Complex Networks. R Soc Open Sci (2017) 4:170091. doi:10.1098/rsos.170091

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Wang X, Su J, Ma F, Yao B. Mean First-Passage Time on Scale-free Networks Based on Rectangle Operation. Front Phys (2021) 9:238. doi:10.3389/fphy.2021.675833

CrossRef Full Text | Google Scholar

47. Ren Z-M, Zeng A, Zhang Y-C. Bridging Nestedness and Economic Complexity in Multilayer World Trade Networks. Humanit Soc Sci Commun (2020) 7:1–8. doi:10.1057/s41599-020-00651-3

CrossRef Full Text | Google Scholar

48. Buldyrev SV, Parshani R, Paul G, Stanley HE, Havlin S. Catastrophic cascade of Failures in Interdependent Networks. Nature (2010) 464:1025–8. doi:10.1038/nature08932

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Guo Q, Liang G, Fu JQ, Han JT, Liu JG. Roles of Mixing Patterns in the Network Reconstruction. Phys Rev E (2016) 94:052303. doi:10.1103/PhysRevE.94.052303

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Han X, Shen Z, Wang W-X, Lai Y-C, Grebogi C. Reconstructing Direct and Indirect Interactions in Networked Public Goods Game. Sci Rep (2016) 6:1–12. doi:10.1038/srep30241

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Nowak MA, May RM. Evolutionary Games and Spatial Chaos. Nature (1992) 359:826–9. doi:10.1038/359826a0

CrossRef Full Text | Google Scholar

52. Rong Z, Yang H-X, Wang W-X. Feedback Reciprocity Mechanism Promotes the Cooperation of Highly Clustered Scale-free Networks. Phys Rev E (2010) 82:047101. doi:10.1103/PhysRevE.82.047101

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Tang Y, Jing M, Yu Y. Conditional Neutral Reward Promotes Cooperation in the Spatial Prisoner's Dilemma Game. Front Phys (2021) 9:79. doi:10.3389/fphy.2021.639252

CrossRef Full Text | Google Scholar

54. Szabó G, Tőke C. Evolutionary Prisoner's Dilemma Game on a Square Lattice. Phys Rev E (1998) 58:69–73. doi:10.1103/PhysRevE.58.69

CrossRef Full Text | Google Scholar

55. Wang W-X, Yang R, Lai Y-C, Kovanis V, Harrison MAF. Time-Series-Based Prediction of Complex Oscillator Networks via Compressive Sensing. Epl (Europhysics Letters) (2011) 94:48006. doi:10.1209/0295-5075/94/48006

CrossRef Full Text | Google Scholar

56. Han X, Shen Z, Wang WX, Di Z. Robust Reconstruction of Complex Networks From Sparse Data. Phys Rev Lett (2015) 114:028701. doi:10.1103/PhysRevLett.114.028701

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Candès EJ, Romberg J, Tao T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Trans Inform Theor (2006) 52:489–509. doi:10.1109/TIT.2005.862083

CrossRef Full Text | Google Scholar

58. Candès EJ, Wakin MB. An Introduction to Compressive Sampling. IEEE Signal Process Mag (2008) 25:21–30. doi:10.1109/msp.2007.914731

CrossRef Full Text | Google Scholar

59. Baird D, Luczkovich J, Christian RR. Assessment of Spatial and Temporal Variability in Ecosystem Attributes of the St marks National Wildlife Refuge, Apalachee bay, florida. Estuarine, Coastal Shelf Sci (1998) 47:329–49. doi:10.1006/ecss.1998.0360

CrossRef Full Text | Google Scholar

60. Gleiser PM, Danon L. Community Structure in Jazz. Advs Complex Syst (2003) 06:565–73. doi:10.1142/S0219525903001067

CrossRef Full Text | Google Scholar

61. Zhou T, Ren J, Medo M, Zhang YC. Bipartite Network Projection and Personal Recommendation. Phys Rev E Stat Nonlin Soft Matter Phys (2007) 76:046115. doi:10.1103/PhysRevE.76.046115

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Liu JG, Shi K, Guo Q. Solving the Accuracy-Diversity Dilemma via Directed Random Walks. Phys Rev E (2012) 85:016118. doi:10.1103/PhysRevE.85.016118

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Hanley JA, McNeil BJ. The Meaning and Use of the Area under a Receiver Operating Characteristic (Roc) Curve. Radiology (1982) 143:29–36. doi:10.1148/radiology.143.1.7063747

PubMed Abstract | CrossRef Full Text | Google Scholar