- College of Physics and Electromechanics, Fujian Longyan University, Longyan, China
We study theoretically the properties of local heat originated from energy exchange between electrons passing through a quantum dot (QD) coupled to a phonon bath. The dot is sandwiched between two normal metal leads and also side-coupled to Majorana bound states (MBSs) formed at opposite ends of a topological superconductor nanowire. We find that in addition to the negative differential of heat generation (NDHG) in the Coulomb blockade regime, another NDHG emerges near the leads’ Fermi level due to the dot-MBS coupling. This dual NDHG effect is robust against the variation of intradot Coulomb interaction strength, and disappears if the QD is coupled to regular Fermions. Direct hybridization between the MBSs reduces their impacts on the electronic transport processes, and eliminates the dual NDHG effect. Our results show that the dual NDHG effect is quite efficient for inferring the existence of MBSs, and may remedy some limitations of the detection schemes relying on tunneling spectroscopy technique.
1 Introduction
Majorana bound states (MBSs) are zero energy quasi-particles of Majorana fermions typically formed in low-dimensional topological superconductors [1, 2]. They obey non-Abelian statistics and can serve as anyons whose braiding can be used for constructing elementary logic gates for quantum computation [3–6]. Such a kind of logic gate depends only on the topology of the braiding path, and then small imperfections in the braiding are tolerable on the condition that the manipulations are topologically equivalent. Correspondingly, MBSs have been extensively investigated in the past decades as a prominent candidate for fault-tolerant topological quantum computation [7]. In addition, the MBSs are also promising in spintronics and thermoelectric effects. For example, the MBSs will strengthen the intrinsic π phase difference between spin-triplet pairings in Josephson junction [8]. Such a π-phase shift is demonstrated to induce a spin-dependent superconducting phase, i.e., spin-phase that is adjustable with the help of electric gates and the coupling energy between MBSs. This effect suggests an all-electrical spin control scheme and can also be used to manipulate and detect the MBSs [8]. If the electron-hole symmetry property of the MBSs is broken (e.g. by side-coupling one mode of the MBSs to a quantum dot (QD)) [9], the sign of the thermopower, which measures the generated bias voltage in response to a temperature difference applied at different ends of the system, can be reversed by changing the hybridization amplitude between the QD and the MBS [10, 11], or direct coupling between the MBSs [12, 13]. Moreover, the magnitude of the thermopower or thermoelectric efficiency can be significantly enhanced due to the existence of the MBSs [12, 13]. These results are useful in designing thermoelectric devices or detecting MBSs.
Experimentally, topological superconductors have been successfully realized in heterostructures comprised of a one-dimensional semiconductor nanowire having strong Rashba spin-orbit interaction and a proximitizing s-wave superconductor [1, 2, 14, 15]. With the help of a strong external magnetic field, the phase of the heterostructure can be driven into topological superconductor one and thus enable the formation of MBSs at opposite ends of the nanowire. As for the detection of MBSs, the most efficient scheme is the tunneling spectroscopy in Majorana nanowires sandwiched between normal metal leads. The MBSs will manifest itself by a zero-bias anomalous conductance peak [15]. Since this anomalous peak in the electric conductance may also originate from other reasons, such as the Kondo effect [16], anti-localization [17] and subgap states [18], some other detection schemes for the MBSs were then continuingly put forward. For example, signatures of MBSs can be inferred from the sign change or abnormal enhancement of the thermopower as was indicated above [9–13]. The existence of the MBSs can be deduced by measuring the Majorana entropy of an initial equilibrium state of the system [19]. Generally, the Majorana entropy will be ruined even when the transport amplitude of one mode of the MBSs is significantly blockaded, which can be directly measured in experiments. To avoid the above general issues, Smirnov very recently proposed to adjust the tunneling phases of one mode of the MBSs to bring out the universal Majorana plateau. Meanwhile, an experimental scheme that is realizable within present techniques was also proposed to measure entropy of the MBSs [19]. Signatures induced by MBSs may also be deduced from transport phenomena such as the abnormal changes of the shot noise [20–22], quantum noise [23, 24], thermoelectric noise [25], sign change of the tunnel magnetoresistance [26], splitting of the photon-assisted subbands [27], etc.
In fact, due to the unique charge neutral and zero energy properties, the above detection schemes still come with great difficulties and it is not sure if the existence of the MBSs can be completely determined. Recently, impacts of electron-phonon interaction on the MBSs-assisted transport have been studied [28, 29]. This is triggered by two motivations: one is that the electron-phonon interaction will induce significant decoherence effects that will change the transport behaviors and roles in quantum computation [30]; the other is that the phonons will play important roles in Majorana-induced Andreev reflection processes [28]. With continuing improvement of nanofabrication techniques, the length of the device becomes smaller than that of electron-phonon scattering, and thus the electron-phonon interaction is the main cause of heat generation by electrical current [30–34]. With increasing integration density on a chip, the issue of generated heat becomes more and more vital [35]. If the waste heat can not be removed as quickly as possible, the chips may not function properly. As was demonstrated by Sun et. al. [31, 32], the behaviors of the heat generation in nanodevices are quite different from those in the usual macroscopic ones. The Joule heating law Q = JV for the local heat power density, where J is current density and V is the bias voltage applied across the system, is violated. Electrons transporting through a QD may absorb energy from a phonon bath attached to it even at zero temperature [36]. In the presence of intradot Coulomb interaction, the magnitude of heat generation may be quite small even under a large current [32]. In the Coulomb blockade regime, the heat generation decreases although the current’s amplitude is monotonously enhanced for increasing bias voltage, a phenomenon was named as negative differential of the heat generation (NDHG) [32]. The NDHG is very similar to the negative differential conductance effect unique in nanodevices, and is expected to play an important role in phonon engineering subjects. In our previous work, MBSs-mediated heat generation by electrical current in a QD without Coulomb interaction was investigated [37]. It was found that the magnitude of the heat generation and electrical current is sensitive to the existence of MBSs. Under some conditions, the heat generation and electrical current can be individually suppressed and enhanced by changing the dot-MBSs or MBS-MBS couplings, which is ideal for energy-saving instruments. In the present manuscript, we revisit the problem of heat generation by taking the intradot Coulomb interaction into consideration. We find that the MBSs will induce another NDHG in addition to that in the absence of MBSs, which is named as dual NDHG that can be used for inferring the existence of the MBSs.
2 Model and Methods
The system under investigation can be described by the following Hamiltonian (ℏ = 1) [28, 29, 31, 32, 37].
where the first term in the right side of Eq. 1 describes the β-th (β = L/R) lead with
where the operator η1/2 denotes the two modes of the MBSs located at opposite ends of the nanowire. In the present paper, we consider that the QD is only coupled to one mode of the MBSs with coupling amplitude λ. The quantity ɛM is the overlap strength between the MBSs. The Majorana operators follow {ηα, ηβ} = 2δαβ and
To decouple the electron-phonon interaction in Eq. 1, we next perform a canonical transformation, [28, 29, 31, 32, 37],
where the dot level is
where
where
3 Results and Discussion
In the following numerical calculations, we choose the phonon frequency ωq ≡ 1 as energy unit (ℏ = 1), and consider the case of the dot is symmetrically coupled to the left and right leads with

FIGURE 1. Electrical current and heat generation varying with respective to the bias voltage when the QD is coupled to MBSs. (A) and (B) are for
The line-shape of the heat generation in Figure 1B resembles that of the current influenced by the Coulomb blockade effect, but has no small steps induced by the electron-phonon interaction. The reason is that the heat generation in Eq. 5 is calculated from the transformed Hamiltonian in which the electron and phonon is decoupled. Therefore, the plateaus in the heat generation are much flatter compared to those in the current. The heat generation has a delay of ωq as compared to the electric current in Figure 1A [32]. This is because the heat generation Jq is caused by the phonon absorption and emission processes occurred between energy states ɛ and ɛ ± ωq [31, 32]. When the bias voltage is small eV < ωq, the electrons can not absorb enough energy from the external electrical field to emit phonon having energy ℏωq, and therefore the magnitude of the heat generation is zero. It is worth pointing out that this delay effect is absent in macroscopic systems and is more distinct at low temperature regimes. It emerges regardless of the existence of intradot Coulomb interaction or some other fields [31–34, 36]. In the presence of interaction between the MBSs at the ends of a nanowire (
When the dot level is tuned by gate voltage to be
To show the novel dual NDHG effect induced by the MBSs, we present the results when the dot is side-coupled to another QD serving as regular fermion in Figure 2. For the sake of notational consistency, we use the same symbols δM and
in which
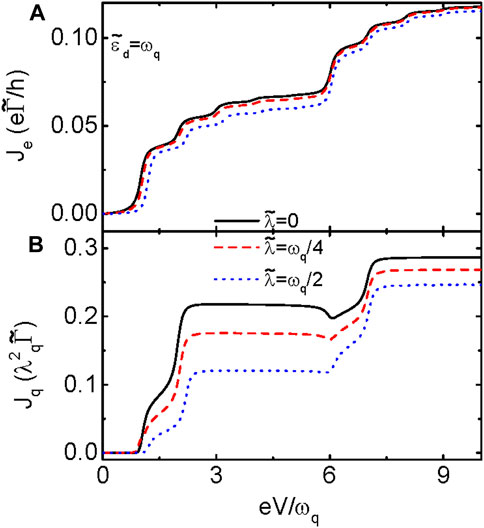
FIGURE 2. Je in (A) and Jq in (B) versus the bias voltage when the QD is coupled to regular fermions in another QD. As the present manuscript focuses on the NDHG occurred at non-zero dot level, here only the results of λq = ωq is presented. Other parameters are the same to those in Figure 2.
Figure 3 presents the impacts of different intradot Coulomb interaction on the electrical current and heat generation in both QD-MBS and QD-QD structures. The electrical current in Figure 3A when the dot is coupled to MBS shows small phonon-induced steps and plateaus. The intradot Coulomb interaction results in another plateau in higher voltage regimes and changes the strength of the current. The current in Figure 3C of QD-QD structure resembles that in Figure 3A and indicates the insufficiency of detecting MBS by transport means. The magnitude of the heat generation in Figure 3B for QD-MBS is decreased even for a weak
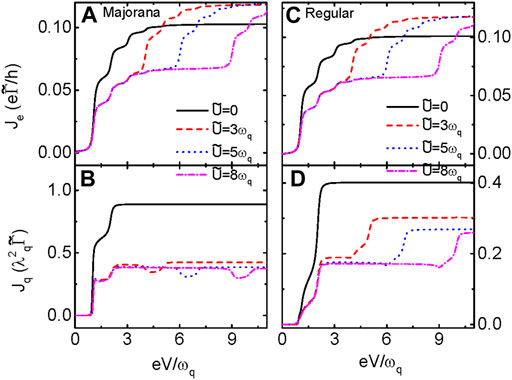
FIGURE 3. (A) and (B) are individually for Je and Jq in QD coupled to MBSs, and (C) and (D) are Je and Jq in QD connected to regular fermions, respectively. The Coulomb interaction is chosen at different values with fixed
Finally in Figure 4, we study the influences of direct hybridization between the MBSs δM, which is determined by the length and material properties of the nanowire, on the electrical current and heat generation when the QD is coupled to MBS. The case of the dot connected to another QD has been extensively studied [40], and we do not show it here. When the two modes of the MBSs are overlapped (δM ≠ 0), their impacts on the electrical current and heat generation is weakened. We find that the current in Figure 4A is slightly enhanced by increasing δM, with the positions of the steps and plateaus remaining unchanged. The magnitude of the heat generation, however, decreases in the presence of δM as shown in Figure 4B. The NDHG in the Coulomb blockade regime is almost unchanged by δM, whereas that near
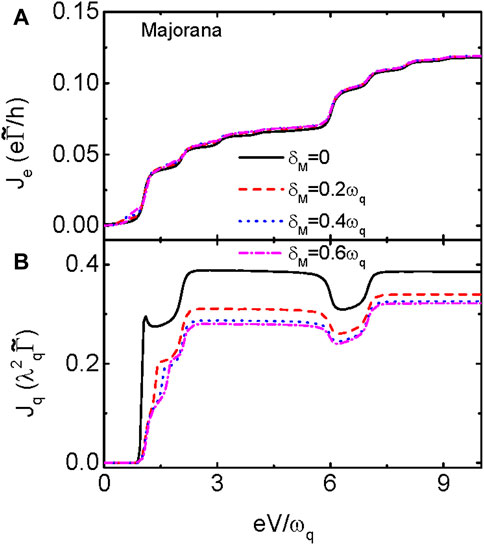
FIGURE 4. Je in (A) and Jq in (B) as functions of the bias voltage when the QD is coupled to MBSs for different values of δM and fixed. The Coulomb interaction is chosen at different values with fixed
4 Summary
In summary, we study properties of electric current and heat generation in a QD hybridized to one mode of MBSs prepared at the one end of a nanowire. Our results show that the properties of the electric current under the influence of MBS are quite similar to those when the dot is coupled to regular fermions. In the presence of intradot Coulomb interaction, the heat generation has a NDHG effect in the Coulomb blockade regime when there is no coupling between the QD and MBS. But another NDHG in lower bias voltage regime emerges, which is called the dual NDHG effect unique to the MBSs, when the dot interacts with the MBS. We find that the dual NDHG arises even for quite weak intradot Coulomb interaction and disappears if the MBS is replaced by regular fermions. The overlap between the two modes of the MBSs destroys the dual NDHG effect, and reduces the magnitude of the electrical current because now the MBSs resemble regular fermions. The present results indicate that the behaviors of the heat current may be rather efficient for detecting the MBSs as compared to the pure electrical method.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
Z-HW derived the formulae, performed partial numerical calculations, and wrote the original manuscipt. W-CH discussed the physical model, performed partial numerical calculations, and contributed in the paper writting.
Funding
This work was supported by Thirteenth five-year plan of educational science in Fujian province (Grant Nos. FJJKCG19-297 and 2019CG0707).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Fu L, Kane C. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys Rev Lett (2008) 100:096407. doi:10.1103/PhysRevLett.100.096407
2. Qi X, Zhang S. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057. doi:10.1103/RevModPhys.83.1057
3. Nayak C, Simon S, Stern A, Freedman M, Sarma S. Non-abelian Anyons and Topological Quantum Computation. Rev Mod Phys (2008) 80:1083. doi:10.1103/RevModPhys.80.1083
4. Alicea J, Oreg Y, Refael G, von Oppen F, Fisher M. Non-abelian Statistics and Topological Quantum Information Processing in 1d Wire Networks. Nat Phys (2011) 7:412. doi:10.1038/nphys1915
5. Karzig T, Knapp C, Lutchyn R, Bonderson P, Hastings M, Nayak C, et al. Scalable Designs for Quasiparticle-Poisoning-Protected Topological Quantum Computation with Majorana Zero Modes. Phys Rev B (2017) 95:235305. doi:10.1103/PhysRevB.95.235305
6. Huang H, Narozniak M, Liang F, Zhao Y, Castellano A, Gong M, et al. Emulating Quantum Teleportation of a Majorana Zero Mode Qubit. Phys Rev Lett (2021) 126:090502. doi:10.1103/PhysRevLett.126.090502
7. Karzig T, Cole W, Pikulin D. Quasiparticle Poisoning of Majorana Qubits. Phys Rev Lett (2021) 126:057702. doi:10.1103/PhysRevLett.126.057702
8. Liu X, Li X, Deng D, Liu X, Sarma S. Majorana Spintronics. Phys Rev B (2016) 94:014511. doi:10.1103/PhysRevB.94.014511
9. Hou C, Shtengel K, Refael G. Thermopower and mott Formula for a Majorana Edge State. Phys Rev B (2013) 88:075304. doi:10.1103/PhysRevB.88.075304
10. López R, Lee M, Serra L, Lim J. Thermoelectrical Detection of Majorana States. Phys Rev B (2014) 89:205418. doi:10.1103/PhysRevB.89.205418
11. Leijinse M. Thermoelectric Signatures of a Majorana Bound State Coupled to a Quantum Dot. New J Phys (2014) 16:015029. doi:10.1088/1367-2630/16/1/015029
12. Hong L, Chi F, Fu Z, Hou Y, Wang Z, Li K, et al. Large Enhancement of Thermoelectric Effect by Majorana Bound States Coupled to a Quantum Dot. J Appl Phys (2020) 127:124302. doi:10.1063/1.5125971
13. Chi F, Fu Z, Liu J, Li K, Wang Z, Zhang P. Thermoelectric Effect in a Quantum Dot Side-Coupled to Majorana Bound States. Nanoscale Res Lett (2020) 15:79. doi:10.1186/s11671-020-03307-y
14. Mourik V, Zuo K, Frolov S, Plissard S, Bakkers E, Kouwenhoven L. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science (2012) 336:1003. doi:10.1126/science.1222360
15. Liu D, Baranger H. Detecting a Majorana-Fermion Zero Mode Using a Quantum Dot. Phys Rev B (2011) 84:201308. doi:10.1103/PhysRevB.84.201308
16. Wang R, Su W, Zhu J, Ting C, Li H, Chen C, et al. Kondo Signatures of a Quantum Magnetic Impurity in Topological Superconductors. Phys Rev Lett (2019) 122:1–6. doi:10.1103/PhysRevLett.122.087001
17. Pikulin D, Dahlhaus J, Wimmer M, Schomerus H, Beenakker C. A Zero-Voltage Conductance Peak from Weak Antilocalization in a Majorana Nanowire. New J Phys (2012) 14:125011. doi:10.1088/1367-2630/14/12/125011
18. Kells G, Meidan D, Brouwer P. Low-energy Subgap States in Multichannel P-Wave Superconducting Wires. Phys Rev B (2012) 85:060507. doi:10.1103/PhysRevB.85.060507
19. Smirnov S. Majorana Entropy Revival via Tunneling Phases. Phys Rev B (2021) 103:075440. doi:10.1103/PhysRevB.103.075440
20. Liu D, Cheng M, Lutchyn R. Probing Majorana Physics in Quantum-Dot Shot-Noise Experiments. Phys Rev B (2015) 91:081405. doi:10.1103/PhysRevB.91.081405
21. Smirnov S. Non-equilibrium Majorana Fluctuations. New J Phys (2017) 19:063020. doi:10.1088/1367-2630/aa70a9
22. Bathellier D, Raymond L, Jonckheere T, Rech J, Zazunov A, Martin T. Finite Frequency Noise in a normal Metal-Topological Superconductor junction. Phys Rev B (2019) 99:104502. doi:10.1103/PhysRevB.99.104502
23. Smirnov S. Majorana Finite-Frequency Nonequilibrium Quantum Noise. Phys Rev B (2019) 99:165427. doi:10.1103/PhysRevB.99.165427
24. Smirnov S. Dynamic Majorana Resonances and Universal Symmetry of Nonequilibrium Thermoelectric Quantum Noise. Phys Rev B (2019) 100:245410. doi:10.1103/PhysRevB.100.245410
25. Smirnov S. Universal Majorana Thermoelectric Noise. Phys Rev B (2018) 97:165434. doi:10.1103/PhysRevB.97.165434
26. Tang L, Mao W. Detection of Majorana Bound States by Sign Change of the Tunnel Magnetoresistance in a Quantum Dot Coupled to Ferromagnetic Electrodes. Front Phys (2020) 8:147. doi:10.3389/fphy.2020.00147
27. Chi F, He T, Wang J, Fu Z, Liu L, Liu P, et al. Photon-assisted Transport through a Quantum Dot Side-Coupled to Majorana Bound States. Front Phys (2020) 8:254. doi:10.3389/fphy.2020.00254
28. Dai N, Sun Q. Phonon-assisted Andreev Reflection at a Majorana Zero Mode. Phys Rev B (2019) 99:085436. doi:10.1103/PhysRevB.99.085436
29. Wang X, Wu B, Zhang S, Wang Q, Gong W. Influences of Electron–Phonon Interaction on Quantum Transport through One Quantum-Dot System with Side-Coupled Majorana Zero Mode. Ann Phys (2020) 415:168127. doi:10.1016/j.aop.2020.168127
30. Li N, Ren J, Wang L, Zhang G, Hänggi P, Li B. Colloquium: Phononics: Manipulating Heat Flow with Electronic Analogs and beyond. Rev Mod Phys (2012) 84:1045. doi:10.1103/RevModPhys.84.1045
31. Sun Q, Xie X. Heat Generation by Electric Current in Mesoscopic Devices. Phys Rev B (2007) 75:155306. doi:10.1103/PhysRevB.75.155306
32. Liu J, Song J, Sun Q, Xie X. Electric-current-induced Heat Generation in a Strongly Interacting Quantum Dot in the Coulomb Blockade Regime. Phys Rev B (2009) 79:161309. doi:10.1103/PhysRevB.79.161309
33. Chi F, Zheng J, Liu Y, Guo Y. Refrigeration Effect in a Single-Level Quantum Dot with thermal Bias. Appl Phys Lett (2012) 100:233106. doi:10.1063/1.4720093
34. Chi F, Sun L. Photon-assisted Heat Generation by Electric Current in a Quantum Dot Attached to Ferromagnetic Leads. Chin Phys Lett (2016) 33:117201. doi:10.1088/0256-307X/33/11/117201
35. Lebedev A, Vinokur V. Heat Generation Due to the anderson Catastrophe in Mesoscopic Devices. Phys Rev B (2020) 102:195111. doi:10.1103/PhysRevB.102.195111
36. Pei W, Sun Q. Time-averaged Heat Generation in a Quantum Dot Driven by an Alternating Current Bias. J Appl Phys (2012) 112:124306. doi:10.1063/1.4769804
37. Wang Z. Heat Generation by Electrical Current in a Quantum Dot Hybridized to Majorana Nanowires. Front Phys (2021) 9:704493. doi:10.3389/fphy.2021.704493
38. Stefański P. Properties of the Majorana-State Tunneling Josephson junction Mediated by an Interacting Quantum Dot. J Phys Condens Matter (2019) 31:185301. doi:10.1088/1361-648X/ab052a
39. Ricco L, de Souza M, Figueria M, Shelykh I, Seridonio A. Spin-dependent Zero-Bias Peak in a Hybrid Nanowire-Quantum Dot System: Distinguishing Isolated Majorana Fermions from Andreev Bound States. Phys Rev B (2019) 99:155159. doi:10.1103/PhysRevB.99.155159
Keywords: heat current, electron-phonon interaction, majorana fermions, quantum dot, negative differential heat generation
Citation: Wang Z-H and Huang W-C (2021) Dual Negative Differential of Heat Generation in a Strongly Correlated Quantum Dot Side-Coupled to Majorana Bound States. Front. Phys. 9:727934. doi: 10.3389/fphy.2021.727934
Received: 20 June 2021; Accepted: 12 July 2021;
Published: 20 August 2021.
Edited by:
Feng Chi, Zhongshan Institute, ChinaReviewed by:
Yingjie Chen, Qufu Normal University, ChinaLian-Liang Sun, North China University of Technology, China
Copyright © 2021 Wang and Huang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhu-Hua Wang, bHl3emg2NjZAMTYzLmNvbQ==
 Zhu-Hua Wang
Zhu-Hua Wang Wen-Cheng Huang
Wen-Cheng Huang