Repeatability and Reproducibility of Microdosimetry With a Mini-TEPC

Experimental microdosimetry measures the energy deposited in a microscopic sensitive volume (SV) by single ionizing particles traversing the SV or passing by. The fundamental advantage of experimental microdosimetry over the computational approach is that the first allows to determine distributions of energy deposition when information on the energy and nature of the charged particles at the point of interest is incomplete or fragmentary. This is almost always the case in radiation protection applications, but discrepancies between the modelled and the actual scenarios should be considered also in radiation therapy. Models for physical reality are always imperfect and rely both on basic input data and on assumptions and simplifications that are necessarily implemented. Furthermore, unintended events due to human errors or machine/system failures can be minimized but cannot be completely avoided.

Though in proton radiation therapy (PRT) a constant relative biological effectiveness (RBE) of 1.1 is assumed, there is evidence of an increasing RBE towards the end of the proton penetration depth. Treatment Planning Systems (TPS) that take into account a variable linear energy transfer (LET) or RBE are already available and could be implemented in PRT in the near future. However, while the calculated dose distributions produced by the TPS are routinely verified with ionization chambers as part of the quality assurance program of every radiotherapy center, there is no commercial detector currently available to perform routine verification of the radiation quality, calculated by the TPS through LET or RBE distributions. Verification of calculated LET is required to make sure that a complex robustly optimized plan will be delivered as planned. The scientific community is coming to conclusion that a new domain of Quality Assurance additionally to the physical dose verification is required, and microdosimetry can be the right approach to address that. A first important prerequisite is the repeatability and reproducibility of microdosimetric measurements. This work aims at studying experimentally the repeatability and reproducibility of microdosimetric measurements performed with a miniaturized Tissue Equivalent Proportional Counter (mini-TEPC) in a 62 MeV proton beam. Experiments were carried out within 1 year and without propane gas recharging and by different operators. RBE was also calculated by applying the Loncol’s weighting function r(y) to microdosimetric distributions. Demonstration of reproducibility of measured microdosimetric quantities ${\overline{y}}_F$, ${\overline{y}}_D$ and RBE₁₀ in 62 MeV proton beam makes this TEPC a possible metrological tool for LET verification in proton therapy. Future characterization will be performed in higher energy proton beams.

Introduction

In current proton therapy a fixed RBE equal to 1.1 is used to weight the physical dose for all depths of the primary proton range [1]. However, an increase in RBE has been observed in several biological assays, in correspondence to the LET increase in the last few millimeters of the primary particle range [2–5]. In spite of this radiobiological evidence, there is no quantitative and widely accepted procedure for radiation quality specification in current proton therapy practice. Assuming a constant RBE of 1.1 can lead to an underestimation of the RBE-weighted dose to surrounding healthy tissues, which is thought to be one of the sources of unintended normal tissue toxicity [6].

The introduction of improved treatment planning that takes into account the variations of LET and RBE with depth could result in a higher therapeutic gain by restraining the dose delivered to surrounding healthy tissues and critical organs [7]. Treatment Planning Systems (TPS) that consider a variable LET or RBE as an optimization strategy are already available and could be implemented in PRT to improve the treatment outcome in the near future. In this context, experimental microdosimetry [8] can be used to validate simulated physical quantities that are descriptive of the radiation quality, in an analogous way as ionization chambers are used to validate the accuracy of Monte Carlo dose calculations, as part of the quality assurance program of every radiotherapy center [9]. Standard detectors should be made available to perform routine verification of the radiation quality calculated by the TPS through LET or RBE distributions.

The introduction of microdosimetric measurements as a verification of radiation quality in a clinical environment requires some important prerequisites. One important prerequisite is the reproducibility of the measurements.

The reference device in experimental microdosimetry is the Tissue Equivalent Proportional Counter (TEPC), which registers event by event the energy deposited in macroscopic volumes of gas with an inner pressure that allows to mimic the interaction in a micrometric volume of biological tissue. At the Legnaro National Laboratories of the Italian Institute for Nuclear Physics (LNL-INFN) miniaturized TEPCs have been developed and designed to cope with high intensity beams of clinical facilities. With respect to the commercial Farwest LET-½ counter, which has a cross sectional area of 127 mm², the smallest mini-TEPC has a cylindrical sensitive volume with an active cross-sectional area of only 0.8 mm². The original prototype of the mini-TEPC was designed to work with continuous gas flow to guarantee a constant refresh of the counting gas inside the sensitive volume [10]. However, safety and security regulations in radiotherapy centers generally prohibit access to clinical rooms with propane gas bottles. For this reason, a new prototype has been developed, to work without gas flow [11]. The microdosimetric characterization of the 62 MeV modulated proton beam line of CATANA (Centro di AdroTerapia ed Applicazioni Nucleari Avanzate), the Italian Eye Proton Therapy Facility in Catania, Italy [12] has been performed with this detector in different measurement runs. The measurements were repeated four times in separate measurement runs, at a distance of 4 months from each other, so that the last was carried out 1 year after the first without changing the gas in this period of time.

The detector response has been characterized both in terms of repeatability, the short term variation in measurements taken by a single person under the same experimental conditions, and in terms of reproducibility, the variation of the response in different measurement runs.

Bearing in mind the clinical potential of microdosimetry, the main aim of this paper is to study the repeatability and reproducibility of measurements carried out during four measurement runs at the 62 MeV therapeutic proton beam of CATANA with a miniaturized Tissue Equivalent Proportional Counter (mini-TEPC) used in sealed mode without flowing the filling gas and without changing it for 1 year.

Frequency and dose mean values of lineal energy were derived from microdosimetric distributions and compared with the track and dose‒mean LET calculated by means of Geant4 simulations. RBE was also assessed by microdosimetric measurements, using a biological weighting function, and then it was compared with biological measurements performed by other authors in the same radiation field. The standard deviation of repeated measurements is evaluated.

Materials and Methods

The Detector

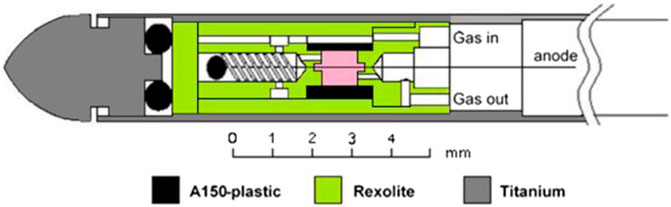
The new mini-TEPC is based on the design of an existing prototype described in [10]. Only the gas ducts have been enlarged to improve the vacuum cleaning and the gas filling procedures. More attention has been paid in the machining of the external case to guarantee the vacuum tightness [11]. The scheme of the detector is reported in Figure 1. The sensitive volume is a right cylinder of 0.9 mm in diameter and height, and it is indicated in pink in Figure 1. The anode is a 10 µm gold-plated tungsten wire and the cathode is a 0.35 mm thick cylindrical shell made of conductive A150 plastic. The sensor is embedded in an additional insulating cylindrical shell, made of Rexolite^®, of 0.35 mm of thickness. The detector is inserted in a 0.2 mm thick titanium sleeve which serves for vacuum sealing and electromagnetic shielding.

FIGURE 1

FIGURE 1. Simplified scheme of the detector.

After 3–4 days of vacuum and as many days of continuous flow with propane gas, the detector was sealed at a pressure of 454.0 mbar corresponding to a diameter of 75 μg/cm² in propane. The pressure was monitored in the various measurement runs, and after 1 year the registered pressure inside the mini-TEPC was 453.7 mbar. More details on the mini-TEPC are given in [11].

The CATANA Spread out Bragg Peak and Monte Carlo Simulations

The 62 MeV proton spread out Bragg peak (SOBP) of the LNS-INFN has a total range in water of 29.5 mm and a width of 11 mm. The energy modulation is obtained passively with a rotating wheel [12]. The detector was placed at several positions across the SOBP; Figure 2 shows the relative depth-dose profile in water, and the measuring positions at the different runs. Different depths were obtained interposing between the collimator and the mini-TEPC several layers of polymethyl methacrylate (PMMA), 0.35 mm in thickness. A total of about 25 positions were analyzed for each measurement run. The equivalent depth in water was obtained by multiplying the PMMA total thickness by a constant factor 1.16, which corresponds to the average ratio of the stopping powers of protons in PMMA and water in the energy range 0–62 MeV. The water-equivalent thickness of the detector, evaluated as 1.4 mm, was added to the phantom thickness. By comparing the microdosimetric distributions measured at several specific depths obtained with stacks of different (but nominally equal) PMMA layers, a maximum uncertainty of 0.2 mm was observed in the corresponding water depth. Conservatively, the uncertainty in positioning has been assessed as ± 0.2 mm at all depths.

FIGURE 2

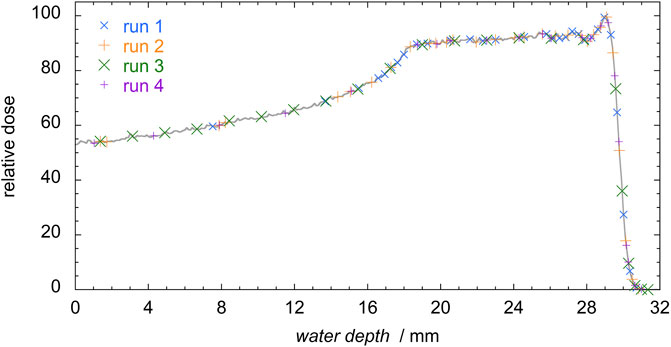
FIGURE 2. Simulated depth-dose profile (grey) and measurements positions in the four measurement runs. A total of 130 distributions were measured.

The CATANA beam line has been simulated with the HADRONTHERAPY [13] application of the Geant4 Monte Carlo code [14] to obtain the unrestricted total track-averaged LET, ${\overline{L}}_T^{tot}$, and the total dose-averaged LET, ${\overline{L}}_D^{tot}$, which include the contribution by both primary and secondary particles originating from nuclear interactions, as a function of the penetration depth in water, z. The calculation was performed on the basis of the implementation reported in [15], improved and updated to reduce the dependence on the transport parameters such as voxel size, production cut and step length [16, 17]. The formulation adopted to perform the calculation in a region is the following:

${\overline{L}}_T^{tot}\left(z\right)=\frac{{{\displaystyle \sum }}_{j=1}^n{\left({{\displaystyle \sum }}_{i=1}^N{L}_i{l}_i\right)}_j}{{{\displaystyle \sum }}_{j=1}^n{\left({{\displaystyle \sum }}_{i=1}^N{l}_i\right)}_j} (1)$

${\overline{L}}_D^{tot}\left(z\right)=\frac{{{\displaystyle \sum }}_{j=1}^n{\left({{\displaystyle \sum }}_{i=1}^N{L}_i{\epsilon }_i\right)}_j}{{{\displaystyle \sum }}_{j=1}^n{\left({{\displaystyle \sum }}_{i=1}^N{\epsilon }_i\right)}_j}(2)$

At each particle step $i$, the electronic stopping power, $L_i$ , extracted from the Geant4 look-up tables, is weighted with the particle track length $l_i$ and the energy loss ${\epsilon }_i$, respectively. The index j is referred to all n ions generated by the primary beam in hadronic interactions. This approach allows for a precise and simultaneous evaluation of absorbed dose and average LETs, for a voxel size of arbitrary dimensions, with negligible dependence with the cut variations [18]. Electromagnetic and hadronic interactions were simulated with the G4EmStandardPhysics-option4 and the QGSP-BIC-HP physics list, respectively [19, 20]. More details on the Monte Carlo simulations of absorbed dose and LET are given in [17].

The simulated ${\overline{L}}_T^{tot}\left(z\right)$ and ${\overline{L}}_D^{tot}\left(z\right)$ distributions are compared to the measured frequency-mean and dose-mean lineal energies.

Measurements and Data Analysis

Four measurement runs were carried out, at a time interval of about 4 months from each other, the last one exactly 1 year after the first. The mini-TEPC was kept sealed, without changing the filling gas, and the same operating conditions were used: the anode was kept grounded through the preamplifier and the cathode was biased at −700 V. A total of about 2∙10⁶ events were counted at each position. The signal of the detector was processed by a low-noise custom-made preamplifier, whose output was then fed in parallel to two spectroscopy amplifiers set at different gains, but with the same shaping time constant of 0.5 µs. Each output signal was then digitized separately by peak-sensing analog-to-digital converters (ADC) and then histogrammed. In the first three runs a data acquisition system (DAQ) based on CAMAC (computer-automated measurement and control) standard was used, with a 14 bit ADC module (model AD114 by EG and G ORTEC) for the high gain sub-spectrum, and a 13 bit ADC (model AD413 by EG and G ORTEC) for the low gain part. During the fourth measurement run a compact Multi Channel Analyzer (MCA) module (model ASPEC-MCA-927 by EG and G ORTEC) was used in place of the CAMAC system; data were also acquired in parallel with a digital FPGA (field-programmable gate array) based DAQ (model DT5780 by CAEN), which digitizes the complete waveforms directly from the preamplifier by means of flash-ADCs and then implements a trapezoidal filter for the pulse height analysis. Differences with the data acquired with the two systems are also discussed in this paper as a reproducibility test. Microdosimetric distributions from the different measurement runs have been analyzed with the same methodology by different operators.

Data from the four measurement runs were calibrated in lineal energy using the spectrum acquired beyond the Bragg peak, where the dose decreased by around 80% (in purple in Figure 4). The value of 143 keV/μm was assigned to the flex of the proton edge and the same factor was used for all the data of the same measurement run [21].

A detection threshold of about 0.4 keV/μm was registered due to environmental noise conditions, but all the frequency distributions of the lineal energy, f(y), have been linearly extrapolated down to 0.01 keV/μm.

The microdosimetric lineal energy distributions f(y) were processed to calculate the dose weighted distribution d(y), and then the frequency and dose-mean lineal energy, ${\overline{y}}_F$ and ${\overline{y}}_D$, according to the following equations:

$d\left(y\right)=\frac{yf\left(y\right)}{{{\displaystyle \int }}_0^{\infty }yf\left(y\right)\mathrm{d}y} (3)$

${\overline{y}}_F=\underset{0}{\overset{\infty }{{\displaystyle \int }}}yf\left(y\right)\mathrm{d}yand{\overline{y}}_D=\underset{0}{\overset{\infty }{{\displaystyle \int }}}yd\left(y\right)\mathrm{d}y(4)$

The RBE was assessed from the dose distributions of the lineal energy d(y), through the application of the Loncol’s biological weighting function r(y), shown in Figure 3 [22],

$RB{E}_{\mu }=\underset{0}{\overset{\infty }{{\displaystyle \int }}}r\left(y\right)d\left(y\right)\mathrm{d}y (5)$

FIGURE 3

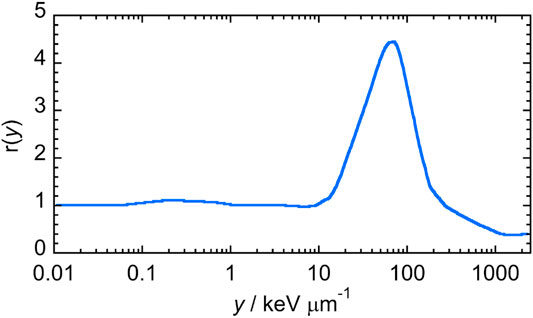
FIGURE 3. Loncol’s biological weighting function. Figure adapted from [22].

The microdosimetric $RB{E}_{\mu }$ calculated with Equation 5 was compared to the $RB{E}_{10}$ of human glioblastoma U87 cells that had been exposed to the same radiation field [3].

The repeatability of the measurements acquired with the mini-TEPC was studied by repeating nine times the same measurement at a water depth z = 23 mm, in the first measurement run; operating conditions and data analysis procedure were kept the same.

The reproducibility of the response of the detector is analyzed in terms of shape of the microdosimetric distributions in four positions of the SOBP (P1 at entrance, P3 at mid-SOBP, P4 at Bragg Peak and P5 at fall-off) measured 1 year apart. For all the other positions the reproducibility has been studied in terms of mean values of lineal energy, ${\overline{y}}_F$ and ${\overline{y}}_D$, calculating for each position the standard deviation of the five values with respect to the average. The same procedure was applied to evaluate the reproducibility of the microdosimetric RBE assessment,$RB{E}_{\mu }$

Results and Discussion

As an example of the measured microdosimetric distributions, a subset of yd(y) distributions measured at five specific positions across the SOBP is shown in Figure 4. As protons slowdown in the phantom, their LET increases and also the stochastic probability of large lineal energy events. In consequence, the yd(y) distributions shift to larger y values as the depth increases. The p-edge region is clearly recognizable in the last spectrum, beyond the Bragg peak.

FIGURE 4

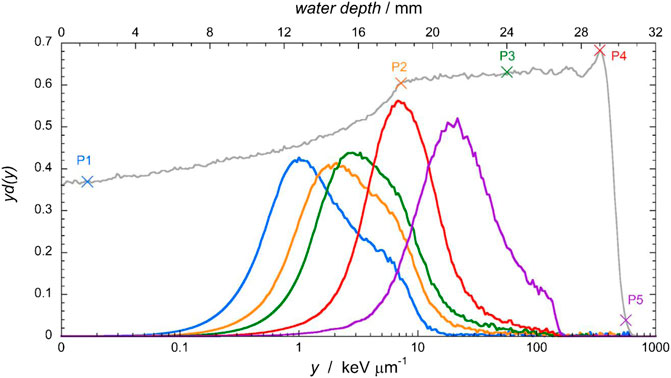
FIGURE 4. Microdosimetric yd(y) distributions measured at five different positions across the SOBP, indicated as P1, P2, P3 P4, and P5 in the depth-dose profile.

Repeatability

Repeatability tests (or test-retest reliability studies) aim to evaluate the precision of successive measurements of the same quantity, under the same experimental conditions, i.e., with the same method, the same radiation field, the same operator, and using the same equipment within short intervals of time.

To test this feature of the mini-TEPC, repeated measurements in the same position of the SOBP were performed in one measurement run. The chosen position is at around 23 mm in water equivalent depth that corresponds to the mid-SOBP position obtained with a calibrated PMMA range shifter. Nine microdosimetric distributions were consecutively gathered without changing any operational condition or parameters of the detector and acquisition set-up. Figure 5 shows the results of the nine consecutive measurements. The microdosimetric yd(y) distributions are very similar to each other, and to quantify the reproducibility it is more convenient to look at the frequency-mean and dose-mean values of the lineal energy, ${\overline{y}}_F$ and ${\overline{y}}_D$, which are summarized in Table 1.

FIGURE 5

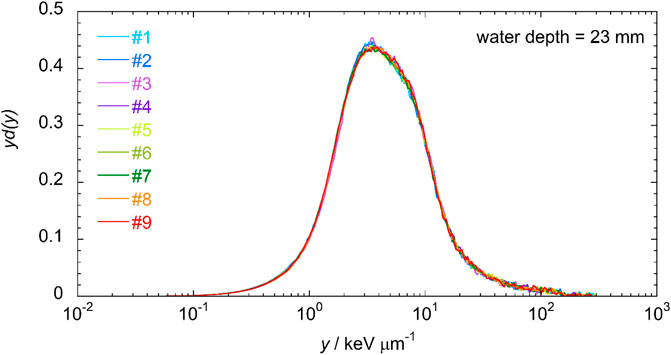
FIGURE 5. Nine microdosimetric distributions gathered in the same measurement run at a depth of 23 mm.

TABLE 1

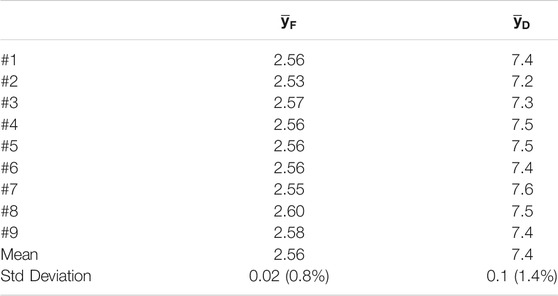
TABLE 1. Individual and average values of the frequency and dose mean lineal energies of the nine microdosimetric distributions reported in Figure 5, and the standard deviation of the measurements.

The ${\overline{y}}_F$values are distributed with a relative standard deviation from the average of 0.8%, while the standard deviation of ${\overline{y}}_D$ values from the average is 1.4%. Differences in ${\overline{y}}_D$ values are larger due to the contribution of rare large sized events, which only give a small contribution to ${\overline{y}}_F$. The observed differences are acceptable within the total uncertainties, which are 7% for the frequency-mean lineal energy and 5% for the dose-mean lineal energy [23].

Reproducibility

Reproducibility is the major principle of the scientific method. It means that to have a scientific result, what is produced as an outcome in one study should be obtained in an independent study when the same methodology is applied. In the case of the study of the reproducibility of the mini-TEPC response, four measurement runs covering 1 year of time were performed and considered as independent studies in which the conditions of measurement (electronic noise, environmental conditions, cabling, stack of PMMA layers, etc.) were changed together with the operators that gathered and analyzed the data, though using the same analysis methodology.

In the fourth measurement run, data were also acquired with a different data acquisition system. A fully digital DAQ that registers signals directly from the preamplifier performing a digital pulse processing (DPP) for the peak height was used, in parallel to the analog DAQ where the signal is processed through a Gaussian shaping amplifier and then the peak amplitude is converted into a digit by means of a peak sensing ADC. The post-processing of the peak-heights histograms was the same for both data sets. Ideally, the microdosimetric distributions and derived quantities should be independent of the DAQ, however small differences are expected due to the different processing of the raw signal at the output of the preamplifier: shaping amplifier and peak sensing ADC or digital solution. The microdosimetric distributions measured with the two DAQs in the five positions of Figure 4, are shown as a representative example in Figure 6. The results obtained in other positions are summarized in Table 2, through the frequency and dose mean lineal energy values, ${\overline{y}}_F$ and ${\overline{y}}_D$ obtained from the distributions.

FIGURE 6

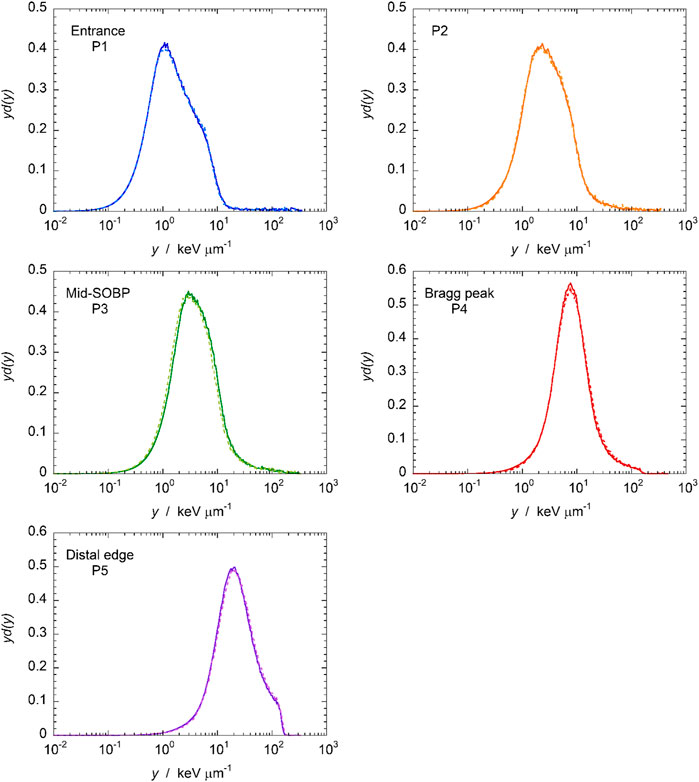
FIGURE 6. Microdosimetric distributions measured at five positions along the SOBP (see Figure 4). The solid line indicates the distribution acquired with shaping amplifier and peak sensing ADC, the dash line the one gathered with the digital solution.

TABLE 2

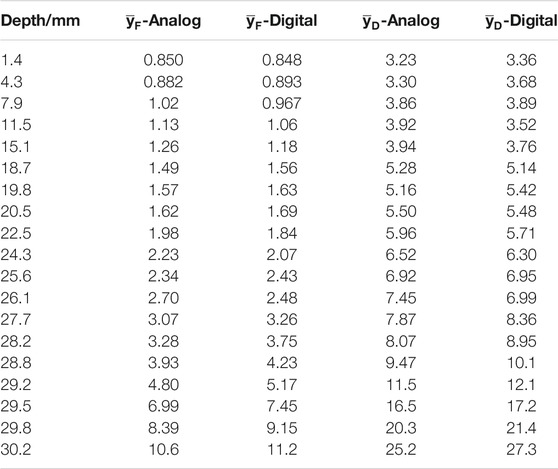
TABLE 2. The frequency and dose mean lineal energies obtained during the fourth measurement run at different positions, with the two DAQs: pulse shaping plus peak sensing ADC (analog) or fully digital (digital). See text for more details.

In order to check the reproducibility of data gathered with the mini-TEPC, the first comparison that is worth doing regards the shape of the microdosimetric distributions in the same positions 1 year apart. The microdosimetric distributions measured at the five positions of Figure 4 are shown in Figure 7, using the same colors: the line represents the spectrum of the first measurement run while the circles stand for the spectrum of the last measurement run 1 year apart both gathered with the same analog DAQ. Microdosimetric distributions measured in four positions are presented: entrance, mid-SOBP, Bragg peak and distal edge.

FIGURE 7

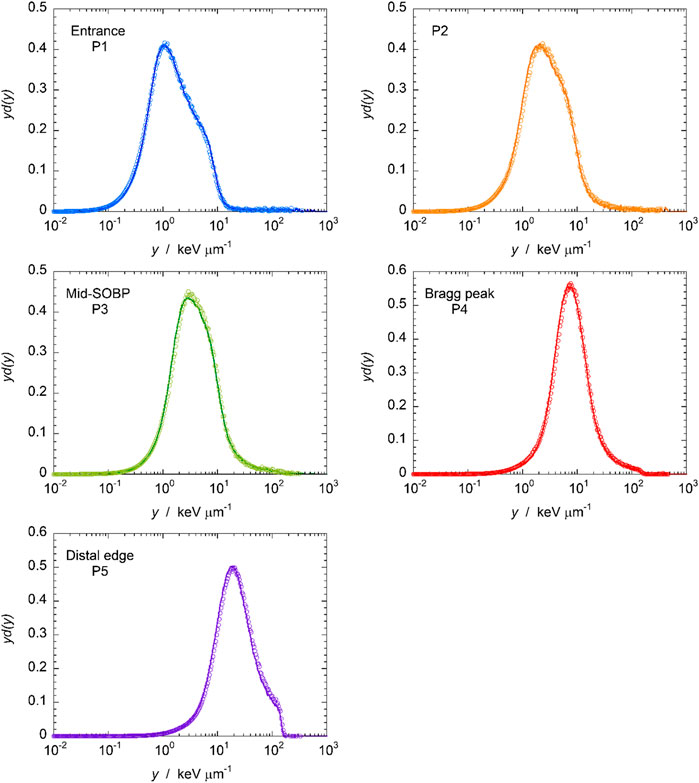
FIGURE 7. Five microdosimetric distributions measured at five positions along the SOBP (see Figure 4). The solid line indicates the spectrum of the first run, circles the one gathered in the fourth run.

From Figure 7 it is possible to observe that the shape of the microdosimetric distributions is consistent in all the shown positions 1 year apart indicating that the response of the detector is stable.

The frequency-mean lineal energy values, as a function of the water depth, were multiplied by a constant factor 1.5, because a systematic reduction the experimental values of ${\overline{y}}_F\left(z\right)$ was observed, as compared to the ${\overline{L}}_T^{tot}\left(z\right)$ [11]. The five sets of experimental $1.5{\overline{y}}_F\left(z\right)$ values and the simulated ${\overline{L}}_T^{tot}\left(z\right)$ are shown in Figure 8, as a function of the water depth z. The average value of the five sets of measurements is also shown in Figure 8 as a green line, while the light green band represents 1 standard deviation. It can be easily noticed that the dispersion of values obtained at different runs is small, and that the agreement between the experimental values of $1.5{\overline{y}}_F\left(z\right)$ and the simulated ${\overline{L}}_T^{tot}\left(z\right)$ is very good, at all depths.

FIGURE 8

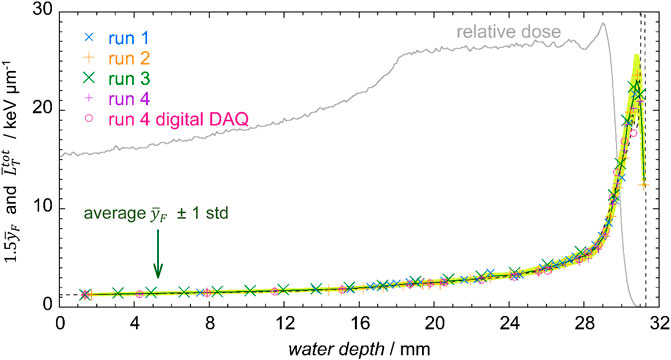
FIGURE 8. MC simulated ${\overline{L}}_T^{tot}\left(z\right)$ (dashed black line) and experimental ${\overline{y}}_F\left(z\right)$ (symbols) as a function of the water depth. The average values of five different experimental data are also represented (green line) with 1 standard deviation (light green band). The MC simulated depth-dose profile is also shown.

The differences in the frequency-mean lineal energy values for the five significant positions indicated in Figure 4, are reported in Table 3.

TABLE 3

TABLE 3. Average values and standard deviation of $1.5{\overline{y}}_F$ from microdosimetric distributions measured in five SOBP positions, as shown in Figure 4. Numbers in parenthesis indicate the corresponding measurement runs.

The standard deviation of the data is always less than 5%, except from the regions where the ${\overline{y}}_F\left(z\right)$ and the ${\overline{L}}_T^{tot}\left(z\right)$ vary more rapidly, at the beginning and above all, at the end of the SOBP. In these regions small shifts in the water depth result in large variations in the value. In the reported measurements we considered an uncertainty of 0.2 mm in the position of the detector, due to the fact that different sets of PMMA layers were used, which produces larger standard deviations in the ${\overline{y}}_F$ values measured beyond the Bragg peak. Apart from the last 1.5 mm of the proton depth, the standard deviations of the data seem to be independent of the depth. To confirm that the dispersion of measured ${\overline{y}}_F$ values is approximately the same at any position across the SOBP, the relative standard deviation values (RSD) are histogrammed in Figure 9. It can be noted that the values of the relative standard deviation of the frequency-mean lineal energies are approximately Gaussian, as expected for the probability distribution of a random error. The centroid of the Gaussian fit is at a relative standard deviation of 5% with a variance of 2%, meaning that, according to the Gaussian distribution confidence levels, 68% of the data are assessed with a standard deviation of 5 ± 2%. This means that for approximately the 84% of the data the standard deviation is smaller than the usual uncertainty of 7% assigned to ${\overline{y}}_F$, and about 98% of the data have a standard deviation smaller than 9%.

FIGURE 9

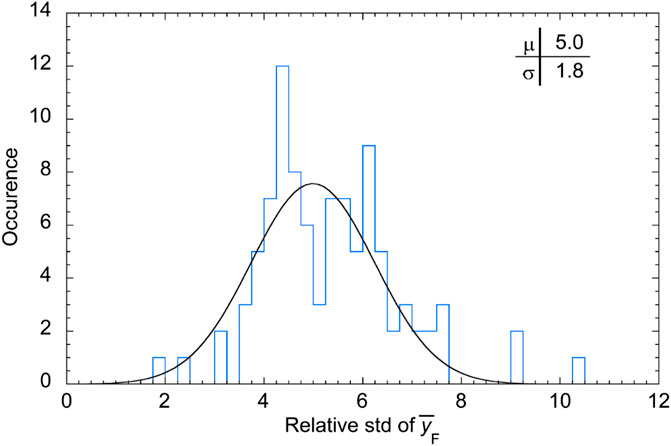
FIGURE 9. Occurrence of the relative standard deviation values for the frequency-mean lineal energy.

The analysis of the reproducibility was repeated for the dose mean lineal energy ${\overline{y}}_D$ , whose measured values are shown in Figure 10. The computed total dose-average LET, ${\overline{L}}_D^{tot}$, is also shown for comparison (black line). It is clear from the figure that the dispersion of ${\overline{y}}_D$ values derived in different measurement run is small, and that the correspondence to simulated ${\overline{L}}_D^{tot}$ is very good, even if in the entrance region the lineal energy is generally smaller than the LET, and beyond the Bragg peak it is generally larger. These small differences are to be expected.

FIGURE 10

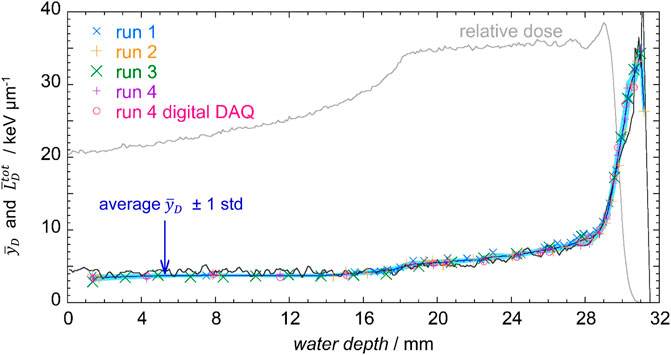
FIGURE 10. Total MC simulated ${\overline{L}}_D^{tot}$ (black line) and measured ${\overline{y}}_D$ (symbols), as a function of the water depth. The average ${\overline{y}}_D$ value of five measurements is also shown with 1 standard deviation (blue line with light blue band). The MC simulated depth-dose profile is also shown.

When comparing the mean values of the lineal energy and the corresponding average LET values, it is important to notice that LET and the lineal energy are analogous but different quantities. One of the relevant differences is that the LET describes the mean energy loss by a particle in a thin matter layer of infinite extension, therefore it is always centered on the core of the charged particle track. In contrast, the lineal energy is determined by the energy imparted to a volume of finite dimensions, arbitrarily positioned in the irradiated matter. When a large volume is irradiated with heavy ions, energy will be deposited by both the primary particle and the secondary electrons emerging from the primary track. If the volume is small, it is sometimes crossed by the core of the ion track but more often by the delta electrons. The energy deposited in the sensitive volume SV by delta electrons initiated outside SV produces small size events that contribute to the microdosimetric distributions, whereas they are not counted as independent events in LET calculations. In general, the size of the volume has a large impact on the overall microdosimetric spectrum, and the frequency and dose mean values of the lineal energy can be smaller or greater than the corresponding track- and dose-averaged LET [24].

Another factor that has to be taken into account is that measurements are performed in propane while simulations in water, which could results in some differences between the measured microdosimetric distributions and those that would be measured in water, in particular in the distal edge, where the ratio of the stopping powers in propane and water increases with respect to the average value [25].

In Table 4, data from five microdosimetric distributions for each of the five positions shown in Figure 4, are reported together with the corresponding standard deviation.

TABLE 4

TABLE 4. Average values and standard deviation of ${\overline{y}}_D$ obtained in five five positions along the SOBP, as indicated in Figure 4. Numbers in parenthesis indicate the corresponding measurement runs.

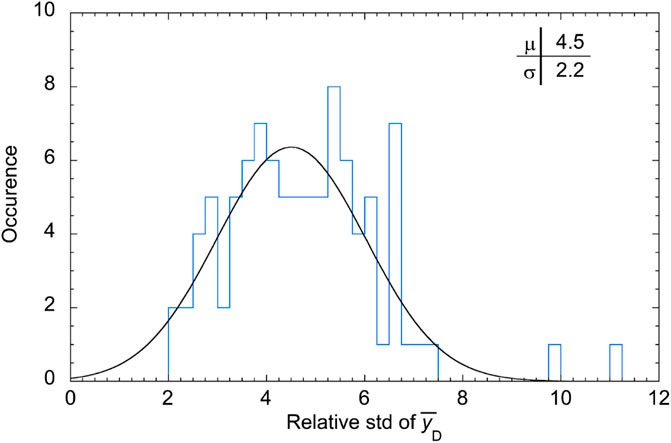
The relative standard deviation is 11% at P1, and in the entrance region of the SOBP before the dose plateau, where rare large-size events are most influential on the dose-mean lineal energy [11], while it is almost independent of the measuring position in the other regions of the SOBP. being randomly distributed about a mean value of 4.5%. The complete distribution of the relative standard deviation of the dose-mean lineal energy values is reported as a histogram in Figure 11.

FIGURE 11

FIGURE 11. Occurrence of the relative standard deviation values for the dose-mean lineal energy ${\overline{y}}_D$.

The distribution of the relative std is approximately a Gaussian function, as the probability distribution of a random error. The mean value is 4.5% and the variance 2.2%. This means that about 84% of the data have a standard deviation smaller than 7% and about 98% of the data have a relative standard deviation smaller than 9%.

The largest deviations are reached in the entrance part of the SOBP, where rare large y events caused by high LET target fragments produced in nuclear reactions contribute significantly to ${\overline{y}}_D$. All microdosimetric distributions have been acquired with a total number of 2·10⁶ events, for a measuring time of about 3 min. With this statistics, there is a small number of large y events (only about 20 events above 100 keV/μm, and less than 10 events above 250 keV/μm), which have therefore large statistical uncertainties, up to 100% if only one event has been counted. In Figure 12, two yd(y) distributions are shown, measured in the first position P1 during the second and the third measuring runs. The double logarithmic representation emphasizes the contribution of rare large y events to the dose-weighted distribution. The two distributions are very similar, and mainly differ for a few large size events at y > 260 keV/μm that are present in the first measurement run but not in the second one. It is this small fraction of events in the rightmost part of the first spectrum that increases the corresponding ${\overline{y}}_D$ value from 2.95 to 3.87 keV/μm, and this is mostly responsible for the high ${\overline{y}}_D$ standard deviation, up to 11%, in entrance region of the SOBP. However, the statistical uncertainty of this contribution is very large, close to 100%. The ${\overline{y}}_D$variation excluding events above 260 keV/μm is about 1% for these two microdosimetric distributions. In general, to reduce the statistical uncertainty a larger number of events should be measured, in particular in the entrance region, where the impact of rare large y events is maximum.

FIGURE 12

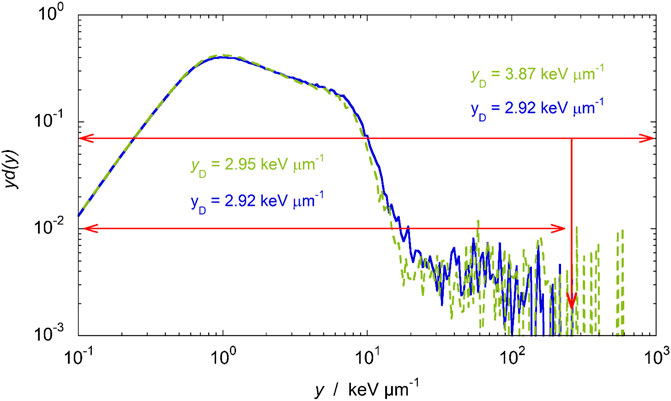
FIGURE 12. yd(y) distributions measured in two different measurement runs at water-depth = 1.4 mm. The double logarithmic scale points out the influence of rare high y events.

Finally, the dose distributions of the lineal energy can be weighted on empirical biological weighting functions, to assess the RBE variability as a function of the depth. The uncertainty on the evaluated microdosimetric RBEμ values derived from application of the Loncol’s function has been also studied.

The RBE_µ has been calculated for the whole set of data from the four measurement runs, using Equation 5. The results are shown in Figure 13, together with the average values.

FIGURE 13

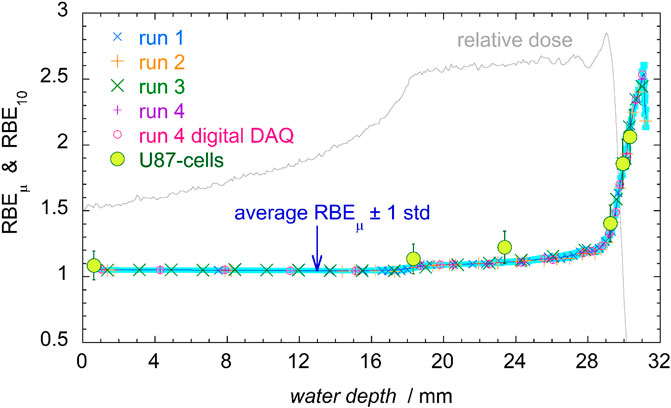
FIGURE 13. RBE_µ of the four measurement runs (see legend), with the average values (blue line) and its standard deviation (light blue band). The large green circles represent radiobiological data from in vitro cell survival experiment for glioblastoma U87 cells, with a 10% uncertainty [3].

The RBE₁₀ values for human glioblastoma U87 cells irradiated in the same radiation field [3] are also shown in Figure 13. At a first glance, it is noticeable that at all depths the RBE_μ values are all concentrated close to the mean, exhibiting little spread.

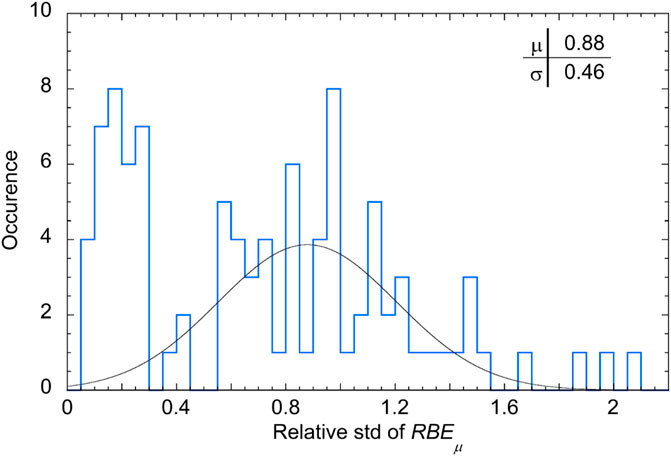
The distribution of the relative standard deviation is histogrammed in Figure 14. Two population groups can be individuated: a first group of samples with very small standard deviations from the mean (below 0.3%), on the left side of the plot, and a wider distribution of events with approximately Gaussian shape and mean value of 0.88. The first group is populated by measurements performed at the entrance region of the SOBP, in which most part of the d(y) distribution is in the range of y values less than 10 keV/μm, where the Loncol’s weighting function r(y) is approximately equal to 1 (see Figure 3). Following Eq. 5, the RBE_µ is then almost the same as the integral of d(y) which is equal to one by definition of d(y), independently of the spectral shape. Consequently, RBEμ values in the entrance region dominated by small y events are also almost equal to 1 with only small deviations.

FIGURE 14

FIGURE 14. Occurrence of the relative standard deviation values for the microdosimetric RBE_m.

Finally, it can also be observed that RBE_µ values are the same as the RBE₁₀ radiobiological data, within a 10% estimated uncertainty on RBE₁₀. This result encourages the use of microdosimetry as a tool for a fast and cheap assessment of the relative biological effectiveness.

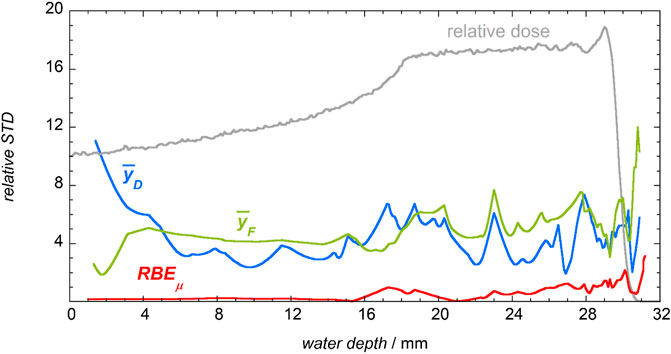
To summarize the results, Figure 15 shows the relative standard deviations of repeated measurements of ${\overline{y}}_F$, ${\overline{y}}_D$ and RBE_µ as a function of the measuring depth z across the SOBP. These relative standard deviations can be interpreted as the type A standard uncertainties, according to GUM definitions [26]. Based on the analysis of our results, the uncertainties in the entrance region at small depths can be reduced increasing the statistics of recorded events, while the uncertainties in the distal part of the SOBP, where the radiation quality changes rapidly, can be reduced increasing the precision in the detector positioning.

FIGURE 15

FIGURE 15. The relative standard deviation values for ${\overline{y}}_F$, ${\overline{y}}_D$ and RBE_µ as a function of the water depth.

Conclusion

Four consecutive measurement runs have been performed at the 62 MeV proton beam line of CATANA, which is used to treat ocular melanoma, with a mini-TEPC working without gas flow. The analysis of the results allowed to evaluate the repeatability and the reproducibility of microdosimetric measurements with this detector, with particular focus on the frequency-mean and dose mean values of the lineal energy, and on the microdosimetric assessment of the RBE with the Loncol’s weighting function. The response of this new mini-TEPC is repeatable when it measures in a short time span the same spectrum, showing only small fluctuations below 2% both in ${\overline{y}}_F$ and ${\overline{y}}_D$. Furthermore, measurements are reproducible and stable over 1 year within approximately a 5% uncertainty on ${\overline{y}}_F$ and ${\overline{y}}_D$. The differences are higher in the entrance part of the dose profile, due to the contribution of rare large events that are subject to large uncertainties, and in the distal part, where the sharp change in radiation quality makes the positioning uncertainties more influential.

Experimental ${\overline{y}}_F$ values have been compared to unrestricted total track-averaged LET values obtained by means of Monte Carlo simulations. The agreement is good within one standard deviation when a factor 1.5 is applied to experimental data.

Experimental ${\overline{y}}_D$ values have been compared to unrestricted total dose-averaged LET values obtained by means of Monte Carlo simulations. The two quantities are in good agreement, though small differences are observable, which are consistent with the different nature of lineal energy y and LET. The observed stability and reproducibility over time encourages the use of experimental microdosimetry as a tool for radiation quality assurance purposes. In addition, microdosimetric quantities could be included in new treatment planning systems meant to optimize innovative irradiation modalities that lead to higher therapeutic gains.

Finally, it has been shown that microdosimetric distributions can be used to assess the biological effectiveness using the Loncol’s biological weighting function (RBE_μ). The RBE_μ has been calculated for the five sets of microdosimetric distributions, and the resulting data show only minor fluctuations around the average, with a standard deviation that is less than 1% in most of the SOBP profile. This result suggests that experimental microdosimetry can provide a fast and cheap biological effectiveness assessment with high reproducibility and stability over time.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AB: performed the measurements, analyzed and discussed the results, and wrote the first draft of the paper. AS: performed the measurements, and analyzed and discussed the results. PCo: took part in the measurements and discussion. GP and PCi: performed the simulations and assisted the group during the measurement campaigns. BR, AP, and FV revised the manuscript. VC: coordinated the work, performed the measurements, analyzed the data, and wrote the final version of the manuscript.

Funding

The research is funded by the fifth commission of INFN.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with the authors PCo, GP, PCi, and VC.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Paganetti H, Niemierko A, Ancukiewicz M, Gerweck LE, Goitein M, Loeffler JS, et al. Relative Biological Effectiveness (RBE) Values for Proton Beam Therapy. Int J Radiat Oncology*Biology*Physics (2002) 53:407–21. doi:10.1016/s0360-3016(02)02754-2

CrossRef Full Text | Google Scholar

2. Britten RA, Nazaryan V, Davis LK, Klein SB, Nichiporov D, Mendonca MS, et al. Variations in the RBE for Cell Killing along the Depth-Dose Profile of a Modulated Proton Therapy Beam. Radiat Res (2013) 179:21–8. doi:10.1667/rr2737.1 |

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Chaudhary P, Marshall TI, Perozziello FM, Manti L, Currell FJ, Hanton F, et al. Relative Biological Effectiveness Variation along Monoenergetic and Modulated Bragg Peaks of a 62-MeV Therapeutic Proton Beam: a Preclinical Assessment. Int J Radiat Oncology*Biology*Physics (2014) 90:27–35. doi:10.1016/j.ijrobp.2014.05.010

CrossRef Full Text | Google Scholar

4. Paganetti H. Relative Biological Effectiveness (RBE) Values for Proton Beam Therapy. Variations as a Function of Biological Endpoint, Dose, and Linear Energy Transfer. Phys Med Biol (2014) 59:R419–R472. doi:10.1088/0031-9155/59/22/r419 |

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Paganetti H, Blakely E, Carabe-Fernandez A, Carlson DJ, Das IJ, Dong L, et al. Report of the AAPM TG-256 on the Relative Biological Effectiveness of Proton Beams in Radiation Therapy. Med Phys (2019) 46(3):e53–e78. doi:10.1002/mp.13390 |

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lühr A, von Neubeck C, Krause M, Troost EGC. Relative Biological Effectiveness in Proton Beam Therapy - Current Knowledge and Future Challenges. Clin translational Radiat Oncol (2018) 9:35–41. doi:10.1016/j.ctro.2018.01.006

CrossRef Full Text | Google Scholar

7. Unkelbach J, Paganetti H. Robust Proton Treatment Planning: Physical and Biological Optimization. Semin Radiat Oncol (2018) 28(2):88–96. doi:10.1016/j.semradonc.2017.11.005 |

PubMed Abstract | CrossRef Full Text | Google Scholar

8.International Commission on Radiation Units and Measurements (ICRU). Microdosimetry. Report 36 (1983).

Google Scholar

9. Wagenaar D, Tran LT, Meijers A, Marmitt GG, Souris K, Bolst D, et al. Validation of Linear Energy Transfer Computed in a Monte Carlo Dose Engine of a Commercial Treatment Planning System. Phys Med Biol (2020) 65:025006. doi:10.1088/1361-6560/ab5e97 |

PubMed Abstract | CrossRef Full Text | Google Scholar

10. De Nardo L, Cesari V, Donà G, Magrin G, Colautti P, Conte V, et al. Mini-TEPCs for Radiation Therapy. Radiat Prot Dosimetry (2004) 108(4):345–52. doi:10.1093/rpd/nch023 |

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Conte V, Bianchi A, Selva A, Petringa G, Cirrone GAP, Parisi A, et al. Microdosimetry at the CATANA 62 MeV Proton Beam with a Sealed Miniaturized TEPC. Physica Med (2019) 64:114–22. doi:10.1016/j.ejmp.2019.06.011 |

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Cirrone GAP, Cuttone G, Lojacono PA, Lo Nigro S, Mongelli V, Patti IV, et al. A 62-MeV proton beam for the treatment of ocular melanoma at Laboratori Nazionali del Sud-INFN. IEEE Trans Nucl Sci (2004) 51(3):860–5. doi:10.1109/tns.2004.829535

CrossRef Full Text | Google Scholar

13. Cirrone GAP, Cuttone G, Di Rosa F, Raffaele L, Russo G, Guatelli S, et al. The Geant4 Toolkit Capability in the Hadron Therapy Field: Simulation of a Transport Beam Line. Nucl Phys B (2005) 150:54–7. doi:10.1016/j.nuclphysbps.2005.04.061

CrossRef Full Text | Google Scholar

14. Allison J, Amako K, Apostolakis J, Arce P, Asai M, Aso T, et al. Recent Developments in GEANT4. Nucl Instrum Meth A (2016) 835:186–225. doi:10.1016/j.nima.2016.06.125

CrossRef Full Text | Google Scholar

15. Romano F, Cirrone GAP, Cuttone G, Rosa FD, Mazzaglia SE, Petrovic I, et al. A Monte Carlo Study for the Calculation of the Average Linear Energy Transfer (LET) Distributions for a Clinical Proton Beam Line and a Radiobiological Carbon Ion Beam Line. Phys Med Biol (2014) 59:2863–82. doi:10.1088/0031-9155/59/12/2863 |

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Petringa G, Cirrone GAP, Cuttone G, Pandola L, Milluzzo GG, Pisciotta P, et al. Development and Analysis of the Track-, Dose-LET and RBE Calculations with a Therapeutical Proton and Ion Beams Using Geant4 Monte Carlo Code. Physica Med (2017) 42(1):9. doi:10.1016/j.ejmp.2017.09.023

CrossRef Full Text | Google Scholar

17. Petringa G, Pandola L, Agosteo S, Catalano R, Colautti P, Conte V, et al. Monte Carlo Implementation of New Algorithms for the Evaluation of Averaged-Dose and -track Linear Energy Transfers in 62 MeV Clinical Proton Beams. Phys Med Biol (2020) 65(23):235043. doi:10.1088/1361-6560/abaeb9 |

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhu H, Chen Y, Sung W, McNamara AL, Tran LT, Burigo LN, et al. The Microdosimetric Extension in TOPAS: Development and Comparison with Published Data. Phys Med Biol (2019) 64:145004. doi:10.1088/1361-6560/ab23a3 |

PubMed Abstract | CrossRef Full Text | Google Scholar

19.Geant4. Geant4 Physics List Guide (2009). Available from: http://geant4-userdoc.web.cern.ch/geant4-userdoc/UsersGuides/PhysicsListGuide/html/index.html.

Google Scholar

20. Ivanchenko VN, Apostolakis J, Bagulya A, Bogdanov A, Grichine V, Incerti S, et al. Geant4 Electromagnetic Physics for LHC Upgrade. J Phys Conf Ser (2014) 513:022015. doi:10.1088/1742-6596/513/2/022015

CrossRef Full Text | Google Scholar

21. Bianchi A, Mazzucconi D, Selva A, Colautti P, Parisi A, Vanhavere F, et al. Lineal Energy Calibration of a Mini-TEPC via the Proton-Edge Technique. Radiat Measurements (2021) 141:106526. doi:10.1016/j.radmeas.2021.106526

CrossRef Full Text | Google Scholar

22. Loncol T, Cosgrove V, Denis JM, Gueulette J, Mazal A, Menzel HG, et al. Radiobiological Effectiveness of Radiation Beams with Broad LET Spectra: Microdosimetric Analysis Using Biological Weighting Functions. Rad Prot Dosim (1994) 52:347–52. doi:10.1093/oxfordjournals.rpd.a082212

CrossRef Full Text | Google Scholar

23. Moro D, Seravalli E, Colautti P. Statistical and Overall Uncertainties in Proton Therapy Microdosimetric Measurements. LNL Report 200/2003 (2003).

Google Scholar

24. Lindborg L, Hultqvist M, Carlsson Tedgren Å, Nikjoo H. Lineal Energy and Radiation Quality in Radiation Therapy: Model Calculations and Comparison with experiment. Phys Med Biol (2013) 58(10):3089–105. doi:10.1088/0031-9155/58/10/3089 |

PubMed Abstract | CrossRef Full Text | Google Scholar

25.PSTAR (2021). Htmlpping Power and Range Tables for Protons. Available from: https://physics.nist.gov/PhysRefData/Star/Text/PSTAR.html.

Google Scholar

26.BIPM. Guide to the Expression of Uncertainty in Measurement. JCGM 100:2008 (2008).