Competition Between Red Blood Cell Aggregation and Breakup: Depletion Force due to Filamentous Viruses vs. Shear Flow

Human blood is a shear-thinning fluid with a complex response that strongly depends on the red blood cell’s (RBC’s) ability to form aggregates, called rouleaux. Despite numerous investigations, microscopic understanding of the break up of RBC aggregates has not been fully elucidated. Here, we present a study of breaking up aggregates consisting of two RBCs (a doublet) during shear flow. We introduce the filamentous fd bacteriophage as a rod-like depletant agent with a very long-range interaction force, which can be tuned by the rod’s concentration. We visualize the structures while shearing by combining a home-build counter-rotating cone-plate shear cell with microscopy imaging. A diagram of dynamic states for shear rates versus depletant concentration shows regions of different flow responses and separation stages for the RBCs doublets. With increasing interaction forces, the full-contact flow states dominate, such as rolling and tumbling. We argue that the RBC doublets can only undergo separation during tumbling motion when the angle between the normal of the doublets with the flow direction is within a critical range. However, at sufficiently high shear rates, the time spent in the critical range becomes too short, such that the cells continue to tumble without separating.

1 Introduction

Blood is a shear-thinning fluid with a complex response that strongly depends on the red blood cells (RBCs) ability to form aggregates in the form of stacks, as has been shown by experiments [1–5] and simulations [6]. The RBCs tend to aggregate into ordered clusters when under low external forces (or in stasis), such as in the center of big vessels, at bifurcations, and behind valves (e.g., venous valves) [7]. Initially, two red blood cells stack face-to-face, resulting in a doublet which grows linearly as more cells aggregate onto the stack [8]. This initial process takes a couple of seconds. Over time some of the smaller stacks attach to the sides of bigger stacks, forming three-dimensional structures, which can finally form a percolated network that displays a yield stress. Although there are multiple factors for RBCs aggregation, fibrinogen has been identified as the key plasma component that contributes to formation of rouleaux [9, 10]. For instance, after an cardiac event [11], the concentration of fibrinogen is increased which can lead to an enhanced tendency of the RBCs to aggregate [10]. Furthermore, pathological conditions such as sickle cell anemia [12], diabetes [13] and others contribute to an increased RBCs aggregability.

Two mutually exclusive models have been proposed to describe the rouleaux formation [14]. In the bridging model, the free ends of the plasma proteins (i.e., fibrinogen) are absorbed onto the membrane of adjacent RBCs and consequently forming parallel cross-bridges between the cells [15–19]. The depletion model states that plasma proteins experience imbalance in conformational entropy in the vicinity of the RBCs surface, thus creating a layer of excluded volume, called the depletion layer. When the RBCs are close to each other, their excluded volumes start to overlap, and the difference in osmotic pressure between the excluded volume and bulk causes the RBCs to aggregate [14, 20–23].

The formation of rouleaux is a reversible process, and the aggregates disperse when exposed to external force, such as shear flow. The adhesion strength of the aggregates influences the perfusion in the cardiovascular system [24, 25]. Therefore, understanding the mechanism behind rouleaux formation leads to a better understanding of blood rheology.

Despite of numerous investigations, microscopic understanding of the formation and breakup of RBC’s aggregates has not been fully elucidated [26]. A possible explanation is that most studies were in bulk rheology and the model macromolecules used to induce an attractive force between the RBCs show contradicting evidence [27–29]. The studies performed at a cell-to-cell level show that tank-treading is essential in the disaggregation process [30, 31] and the minimal drag force during shearing is in the range 0.5–5 pN [6, 32]. Thus, in this work, we will study the breakup of aggregates of two RBCs (a doublet) in shear flow by combining a home-build counter-rotating cone-plate shear cell with transmission microscopy imaging to enable visualization of the structures while shearing. A similar experimental setup was used by Fischer et al. [33–35] to study single RBC under shear flow.

Moreover, we will introduce the rod-like fd-virus as a new interaction agent. The fd-virus is an intrinsically mono-disperse, very slender rod-like particle with a length of 880 nm, based on the length of the DNA strand, a bare diameter of 6.6 nm and a persistence length of 2.2 μm. At physiological pH, fd is negatively charged [36] and it is therefore to be expected that it will be repelled by the RBCs and no specific attractive interaction with the red blood cells will be present. Slender rods are far more effective depletant than the commonly used polymers, as also the orientational entropy is strongly reduced when rods are confined between two cells [37–39]. As such the rod-like virus is a pure depletant that induces long-ranged attraction at very low volume fractions, inducing a depletion force that can be tuned by varying the concentration of these rods [40–44].

The paper is organized as follows. We will first shortly introduce the concepts of Jeffrey orbits and the conditions to separate the cells. In the experimental section we introduce the fd-virus as a long-ranged pure depletant and the methodology to study doublets in shear flow. After discussing the stability of rod-RBC mixtures in equilibrium, we present the non-equilibrium diagram of dynamic states varying the shear rate versus the depletant’s concentration, showing regions for different flow responses and stages of separation of the RBCs doublets. We finish with a discussion of the results.

2 Theoretical Considerations of Jeffrey Orbits

Anisotropic particles in shear flow generally undergo a tumbling motion, the so-called Jeffrey orbits [45–47], where the angle of the rotation is described by

$\tan \phi \left(t\right)=r_e\tan \left(2\pi t/T\right),(1)$

where t is the time and r_e = 2 is the ratio of the major vs. minor axis [46]. The length of the period T depends on the shear rate $\dot{\gamma }$ as

$T=\frac{2\pi }{\dot{\gamma }}\left(r_e+\frac{1}{r_e}\right).(2)$

Figure 1 shows a tumbling doublet, where φ is the angle of the doublet’s normal vector $\widehat{n}$ in the v − ∇v plane. The gradient in the shear flow induces a drag force that leads to the separation of the cells. However, separation can only occur when the center of mass of one cell is higher in the gradient direction than the contact points on each side of the cell, see Figure 1. Thus, the angle of the normal with the flow direction has to be

${\phi }_{crit}|\pi /2-{\phi }_{con}\le {\phi }_{crit}\le \pi /2+{\phi }_{con},(3)$

where φ_con is the angle between the diagonal line of the RBC and the point where the cells make contact, along the flow direction, see Figure 1. Given the morphology of the RBC, φ_con ≈ arctan(1 µm/3 µm) = 0.1π. Figure 2 shows the angle φ of a doublet over time for different shear rates obtained by Eq. 1, where the filled circles represent the range of the critical angle φ_crit. Hence, the time-span when the doublet has the correct orientation to break up is strongly limited by the shear rate. The frequency of the tumbling depends on the shape of the object, and in the case of the RBCs doublets, this shape will change when they start to separate.

FIGURE 1

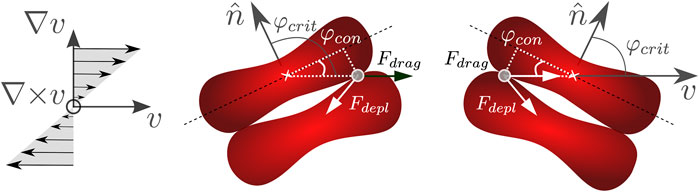
FIGURE 1. Schematic representation of a tumbling doublet, where the normal of the doublet rotates in the velocity-gradient plane.

FIGURE 2

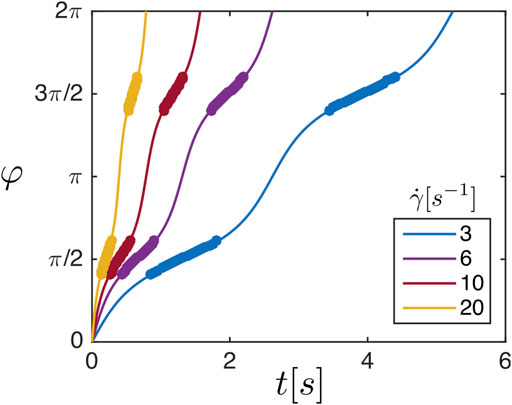
FIGURE 2. The angle φ that the normal of the doublet makes with the velocity direction over t for a single doublet at different shear rates. The filled circles represent the range of the angle, φ_crit, when the tumbling aggregates are in the orientation such that they can be broken-up.

3 Materials and Methods

3.1 Sample Preperation

The experiments were always performed with fresh blood obtained from healthy human adult donors by the finger pricking method. The blood droplets were collected in Ethylenediaminetetraacetic Acid (EDTA) coated tubes (450474, MiniTube K3EDTA, Labnet Supplies) to avoid coagulation. The RBCs were washed at least four times with phosphate-buffered saline buffer (PBS) and diluted in a buffer mixture consisting of PBS and OptiPrep (OP, D1556, Sigma-Aldrich, Germany) in order to density match the RBCs. The ratio of PBS to OP in the final buffer is 60:40%.

The fd-viruses (MW of 16.4 × 10⁶ g/mol [36, 48, 49]) is grown in large quantities in E. Coli (XL1-Blue) as the host bacteria using standard biochemical protocols [50]. At physiological pH, fd is highly negatively charged and has its isoelectric point at pH 4.2.

To determine the interaction between fd and RBC in equilbrium, fd has been fluorescently labeled with the Alexa Fluor 488 NHS-Ester (Succinimidyl ester) dye (A20000, ThermoFisher Scientific). In this way the fd could be visualized in a fluorescence microscope, as the fd-virus is very thin and thus not visible in a bright field light microscope. Every 1 in 700 viruses has been labeled, allowing for individual viruses to be resolved. The final sample contained 1vol% of RBCs and 4 mg/ml of fd-virus.

For the shear experiments, when choosing the RBC’s concentration, we have to compromise between good statistics and avoiding collisions, which favors high and low RBC’s concentration, respectively. Hence, the RBC’s concentration was fixed at 1vol%. The fd concentration range was 0.05–3 mg/ml. The choice of the lowest value is based on the onset of aggregation seen in Figure 4. Higher concentrations of fd than 3 mg/ml were not considered in this experiment as beyond this concentration, and at such a low volume fraction of RBCs, the cells do not achieve aggregation in the limited in − vitro time window of ∼ 1.5 h. Here, the viscosity at that concentration of fd is so high that the diffusion-limited aggregation of the cells is significantly slowed down.

The experiments were performed at room temperature.

3.2 Shear Cell

The experiments were conducted in a home built shear cell, which is the 3rd generation of its kind as used in Ref. [51]. We used a cone/plate geometry, with an angle of 1.5° and 50 µm truncated off the tip. The advantage of using the counter-rotating shear cell is that at a certain depth in the sample, there is a plane where the velocity is zero, i.e., the stagnation plane, which depends on the rotational velocity of the top vs. bottom part of the shear cell. The zero-velocity plane was set at r = 3 mm, 50 µm above the bottom plate to reduce wall effects. However, a perfect zero velocity plane is not always reached depending on the dynamic state. At increasing shear rate the gradient within the focal depth becomes too high, that it is increasingly difficult to maintain an object in the observation window.

About 100 µL of the sample is carefully pipetted on the bottom plate of the shear cell. The cone is lowered while observing simultaneously through the light microscope in transmission mode, such that the tip of the cone is brought to the desired position of 50 µm above the bottom plate. We let the sample rest to equilibrate for a couple of minutes, depending on the concentration of fd. Once we visually observe that doublets have formed, we start to shear the sample. The movies are acquired at steady shear state, approximately 5 s after the onset of shear.

3.3 Microscopy

The fluorescence experiments were performed on a microscope (Axioplan 2, Carl Zeiss Microscopy) equipped with a LED at 470 nm operated at 100% as an excitation light source (UHP-F-470, Prizmatix). We used the oil immersion objective (100 ×, N.A. 1.45, αPlan-Fluar, 000000-1084-514, Carl Zeiss). Here the samples were loaded in a rectangular capillary (0.1 × 1.00 mm, Vitrotube, 5010, VitroCom) for imaging.

The equilibrium and shear experiments were performed on an inverted microscope (Axiovert 200M, Carl Zeiss Microscopy). For the equilibrium fd-RBC experiments we loaded in μ-Slide channels (30 μL, 80606, ibidi). The samples were observed up to a maximum of one hour, until the RBCs start to display conformational changes.

For the shear experiment we used two objectives: an air objective (20 ×, N.A. 0.4, LD Epiplan, 422850-9900-0, Carl Zeiss) for bigger field of view and increasing statistics, or a water immersion objective (63 ×, N.A. 1.3, LCI Plan-Neofluar, 440872-9970-0, Carl Zeiss) for higher resolution movies, acquiring more frames for statistics. We took 3,000 images of 2560 × 2160 pix (813 × 686 μm²) or 5000 images of 717 × 717 pix (183 × 183 μm²) both at 15fps, respectively. For all experiments we used the Andor Neo 5.5 sCMOS camera for image acquisition.

A machine learning algorithm was not straight forward to implement due to the dynamic nature of our system. Therefore, the movies were manually analyzed by identifying and counting the dynamic states per image using Cell Counter plugin in Fiji [52].

4 Results

4.1 Fd-Virus as Ideal Depletant for RBCs Aggregation

At physiological pH, fd is highly negatively charged and therefore it is expected that it will not have any specific attractive interaction with the red blood cells. To establish that indeed fd does not interact with the red blood cells in a non-trivial manner, we observed the mixture of RBCs and fluorescently labeled fd to qualitatively access any interaction. Figure 3 presents images of red blood cells dispersed in mixtures of fluorescently labeled and non-labeled fd. Initially, both the LED and the halogen lamp were switched on, see Figure 3A–F, to visualize the RBCs and fd. Then the intensity of the halogen lamp was gradually lowered to zero, see Figure 3G–I, to visualize only fd. Although the fluorescent labels make fd hydrophobic, we did not observe any interaction between the red blood cells and the virus. No viruses were observed inside the cells or immobilized on the surface of the cells. At times the viruses can be seen bouncing on the surface of the RBCs. Upon contact, they move along the surface until, eventually, they diffuse away, see Supplementary Movie S1.

FIGURE 3

FIGURE 3. Fluorescently labeled rods in a sea of non-labeled rods at a 1:700 ratio and total rods concentration of 4 mg/ml, depleting two RBCs. In (A–F), the fluorescence LED and halogen lamp were used to visualize the rods and the none stained RBCs, respectively. (G–I) The intensity of the halogen lamp is gradually lowered to zero, so that only the rods are visible. The Brownian path of the rods sometimes intersects with the RBC. Upon impact, the rods change direction and diffuse away. No rods are seen inside the RBCs. See Supplementary Movie S1.

Having established that the fd-RBC interaction is purely repulsive, in Figure 4, we show the development of potential aggregates at 1vol% of RBCs dispersed in density matched PBS medium. For fd concentration bellow ∼ 0.05 mg/ml we do not observe formation of aggregates in the limited time window of observation. Whereas, in the same time but at higher fd concentration we initially see doublets as well as triplets or even longer rouleaux. Note that the weight fraction needed for aggregation is three orders of magnitude lower as observed with the commonly used dextran [53].

FIGURE 4

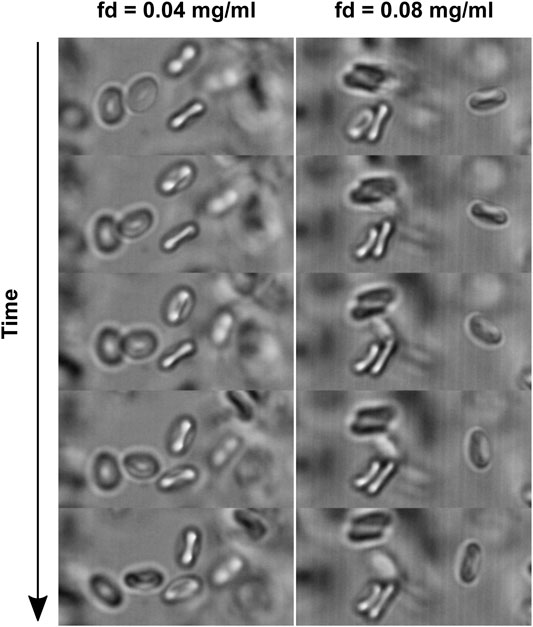
FIGURE 4. Red blood cells dispersed in a density matched medium at two fd concentrations, where aggregates are only observed at the higher concentration. The time difference between the frames is 20 s.

4.2 Diagram of Dynamic States

By applying shear to aggregated RBCs, we observe a rich dynamic response of the doublets behavior, depending on the applied shear rate and fd concentration. We identified four dynamic states, which we define as follows. There are two dynamic states where the cells stay attached face-to-face, maximizing the contact area. In the rolling state, the normal of the cells corresponds to the axis of rotation of the cells and points in the ∇ ×v direction. On the contrary, in the tumbling state, the normal undergoes full rotations in the v − ∇v plane. Furthermore, there are two states where the cells are still in contact with each other but not at maximum overlap area, the so-called intermediate states. In the hinge state, there is a contact between the face of one cell and the side of the other, and in the chain state the contact is between the sides of two cells. We also identified split events during the time of our observation, where the doublets fully separate. Figure 5 depicts the four states and the final event by representing them with three time snapshots from the movies.

FIGURE 5

FIGURE 5. The four identified dynamics states of red blood cell doublets during shear flow (A–D), and the final split event (E). For two dynamics states, the cells are attached face-to-face: rolling, where the normal corresponds to the axis of rotation and it points in the vorticity direction (A); tumbling, where the normal undergoes full rations in the velocity-gradient plane (B). There are two intermediate states: (C) hinge, where the side of one cell is attached to the face of the other cell; (D) chain, where cells are flowing side-to-side. See Supplementary Movie S2. Finally split, the cells separate (E). The time values in the picture insets are variable as it depends on the shear rate as shown in Figure 2, here the typical values are in the order of 0.2 s.

Already in the first frame, we can label the doublets according to these definitions, as each of them has a specific, well-defined morphology. The doublets are then followed in time until they leave the field of view. The projection of the rolling doublets does not change in time and, similarly, the chain state is also stable over time. The projections for the tumbling and hinge states do change, which we used to confirm the initial labeling. We rarely see any changes in the morphologies throughout the movies. However, we occasionally observed the splitting of doublets when it is originally in a tumbling state, especially for the lower shear rates and at the start of the movies.

To quantify the response of the system, we produce histograms of the relative occurrence of the dynamic states at two fd concentrations, varying the shear rate, and a plot of the number of doublets vs the shear rate for a few selected concentrations, see Figures 6, 7, respectively. The number of pairs counted in our field of view at each parameter space is given at the top of the histogram. At the lowest fd concentration, see Figure 6A, shearing at low shear rates facilitates shear-induced aggregation by aligning the cells and convecting them towards each other, as we observe that the number of pairs at full contact area, i.e., tumblers and rollers, increases with shear rate. However, this is counteracted at even higher shear rates, where the system disaggregates at this weak attraction force. Indeed, Figure 7 shows that at shear rates higher than 6s⁻¹ and such low fd concentration no doublets are observed anymore.

FIGURE 6

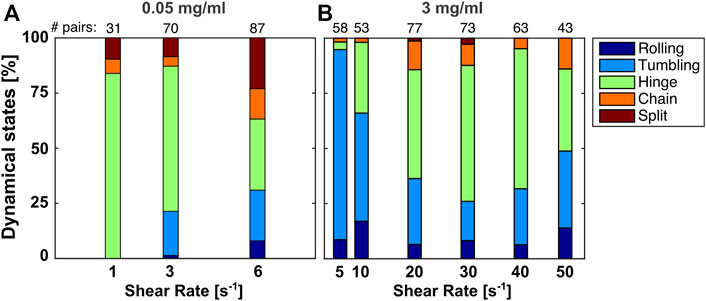
FIGURE 6. The fractions of the four dynamic states and the final split event plotted as histograms over different shear rates, for the lowest and highest measured concentration of fd.

FIGURE 7

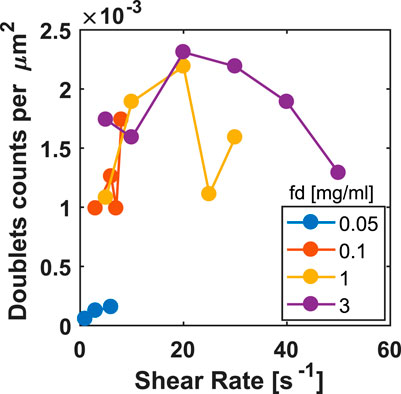
FIGURE 7. The total number of doublets counted over the shear rate for the indicated fd concentrations.

For the higher fd concentrations, see Figure 6B, there is no obvious effect of the shear rate on the number of dynamic states observed. The number of splits is small because we can only define them during the time window of observation. Although, the single cells are not counted here, they are likely a result of the doublets splitting. This can be seen in Figure 7, as we observe less doublets at the higher shear rates.

We also studied the dynamic states as a function of concentration for a low and high shear rate. Figure 8 shows the distribution of the dynamic states varying the fd concentration at two fixed shear rates 6 and 20 s⁻¹. Indeed, for a shear rate of 6 s⁻¹ the number of full face-to-face contact doublets increases with increasing concentration, which means that the attraction force defeats the separating drag force. On the contrary, for 20 s⁻¹ this concentration dependence is not obvious, even though the drag force is higher.

FIGURE 8

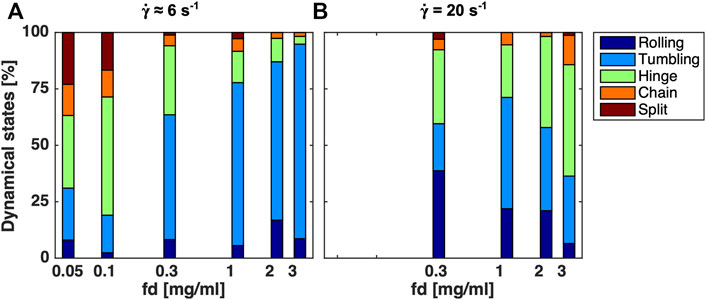
FIGURE 8. A histogram of dynamic states and the splitting events for increasing fd concentrations at a fixed (A) $\dot{\gamma }\approx$6 s⁻¹ and (B) $\dot{\gamma }=$ 20 s⁻¹.

5 Discussion

With the results presented above, we now need to answer the question what is needed to separate a doublet by shear flow to obtain single RBCs. In a shear flow the forces acting onto the doublets are a combination of extensional and rotational flow. As the force necessary to separate the RBCs when the director is pointing along the extensional stress direction is high, we believe it is more likely that the driving force behind separation is the gradient during rotational flow. In the rolling state, the normal of the RBCs points in the ∇×v direction. Thus, there is no gradient that acts as a force onto the individual cells and only the tumbling state can result in separation of the doublet. Even when a doublet is in the tumbling state, the functional dependence on the shear rate is not obvious. The reason is the competition between the residence time of the doublet’s normal pointing in the ∇v direction, which decreases with increasing shear rate as can be seen in Figure 2, and the drag force that increases with the shear rate. In addition, two factors need to be considered to unravel this competition. First, one should keep in mind that the doublet is only held together by depletion forces. This means that we also need to account for the effect that flow has on this interaction. Second, the single objects are not solid-like particles but can deform under flow. Hence, it is not trivial to understand the competition between the different dynamic states where the doublet conserves its structure, the in-between states, and the disaggregation of the doublet.

Comparing the fraction of tumblers to the fraction of rollers, we observe that the tumbling state is almost always more prominent than the rolling state also at high shear rates. This might be surprising as Dupire et al. [54] observed for non-fluidized cells, i.e., cells that do not undergo tank-treading, a transition from tumbling to rolling at elevated shear rates. They argue that the rolling state is the preferred dynamic state as cells deform less in that state, and therefore this state is less energetically costly. However, in a tumbling doublet, where the cells can deform less, the argument of Dupire et al. plays a lesser role, therefore the tumbling state might be more stable even at high shear rates because on average it reduces the stress. Depending on the orientation of the object, it experiences a higher torque as the velocity gradient over the object is larger.

Fischer et al. [33, 34] have shown experimentally that the RBCs can be fluid-like objects that undergo a tank-treading motion when subjected to shear flow $\dot{\gamma }=$ 28–575 s⁻¹, and the cells have shape memory to revert to after cessation of flow [35]. Dupire et al. [54] also found a hysteresis with the shear rate in the fluidized regime. The cells transition from tank-treading to tumbling intermittently while decreasing $\dot{\gamma }$, and the tumbling evolves to rolling, and then the transition to tank-treading occurs via a transient Frisbee-like spinning motion with increasing $\dot{\gamma }$. The tank-treading motion also plays an important roll in the disaggregation process of doublets [30, 31]. However, in our setup we were not able to observe the tank-treading motion, though we do not exclude its contribution as we are in the fluidized regime.

Concerning the effect of shear flow on the interaction force, we note that the depletion force F_depl has a shear rate dependence as depletion might be distorted by the shear flow [41, 55]. A shear rate of $\dot{\gamma }=$ 20 s⁻¹ already affects the orientation of infinite dilute rods as it corresponds to the rotational diffusion time of the rods at infinite dilution [55]. The diffusion time strongly decreases with concentration such that the effect of shear flow is also much stronger at high concentrations [56]. Thus, the depleting rods will be aligned, which will probably lower the depletion force. Further investigations are needed to study this effect. However, currently, we believe that this effect is small, and as such, we will not take it into consideration.

We now focus on the moment when the doublet resides with the orientation such that it can be separated, i.e., φ < |φ_crit|. Out of equilibrium, when subjected to shear flow, the RBCs are separated by a stokes drag force, which can only occur when the doublet is oriented such that there is a gradient in the velocity between the two cells. Thus, the RBC experiences the relative drag force of the surrounding fluid, as illustrated in Figure 1:

$F_{drag}=\mathrm{\Gamma }\mathrm{\Delta }{v}_{0\to 1},(4)$

where Γ is the friction with the fluid and Δv_0→1 is the relative velocity between the two RBCs given by the product of the shear rate $\dot{\gamma }$ and the thickness of the cell l = 2 µm,

$\mathrm{\Delta }{v}_{0\to 1}=\dot{\gamma }l.(5)$

The hydrodynamic friction is

$\mathrm{\Gamma }=6\pi \eta rs,(6)$

where η is the viscosity of the medium, r = 4 µm is the radius of the cell and s = 0.566 is the shape factor for a disk in an edgewise motion [57, 58]. The surrounding medium is shear-thinning [55, 59], thus for a fd-suspension at c = 4.6 mg/ml in PBS-OP and shear rates of $\dot{\gamma }=$ 3, 6, 10 and 20 s⁻¹, the viscosity is η = 20, 18, 15 and 12 mPa s, resulting in F_drag = 5.1, 9.1, 13.1 and 20.3 pN.

The force balance when the tumbling doublet is oriented with the normal in the gradient direction is given by

$\mathrm{\Delta }F=F_{drag}-F_{friction}-F_{interaction}.(7)$

Assuming that F_friction ≪ F_interaction for pure depletion interaction as induced by fd, then F_friction → 0. If ΔF > 0, then the cell’s displacement ΔS during the residence time t_res where the angle of the normal is smaller than φ_crit is defined as

$\mathrm{\Delta }S=\frac{1}{2}\left(\mathrm{\Delta }F/m_{RBC}\right)t_{res}^2,(8)$

where m_RBC = 27 pg is the mass of the cell. Using Eq. 1 with $\dot{\gamma }=$ 3, 6, 10 and 20 s ⁻¹ we obtain t_res = 0.95, 0.48, 0.29 and 0.14 s. Assuming that the RBCs split when ΔS ≥ø _RBC, then the minimum required force to separate the cells is ΔF = 0.0005, 0.0019, 0.0053 and 0.0212 fN, indicating that any drag force higher than the interaction force would cause separation.

Figure 8A shows the fraction of the dynamic states with increasing fd concentrations at a relatively low shear rate of $\dot{\gamma }\approx$6 s ⁻¹. We observe that the fully aggregated rolling and tumbling states increase with the concentration of fd, which means that now the aggregation force exceeds the drag force.

For the higher shear rate $\dot{\gamma }=$ 20 s⁻¹ in Figure 8B there is no obvious trend with the concentration, apart from the smaller number of rolling doublets. However, the effect of shear flow can be better appreciated by comparing Figures 8A,B, where the fraction of tumbling doublets decrease, while the fraction of the intermediate states such as hinge and chain increase with increasing shear rate. Indeed, this effect is most obvious in Figure 6B where the shear rate dependence is plotted for the highest fd concentration we measured. The fraction of the fully aggregated states drops initially, so that the drag force is now higher than the aggregation force. However, above a shear rate of $\dot{\gamma }=$ 20 s⁻¹ the fraction of the states becomes stable. Thus, from Figures 6B, 8 we infer that the doublets do not fully separate but are locked mostly in the hinge state. We can explain this, observing that actually $\mathrm{\Delta }S\propto 1/\dot{\gamma }$, which follows from Eq. 8. Thus the competition between the increase of F_drag and the decrease of t_res with increasing $\dot{\gamma }$, could leave the doublet not fully separated within the tumbling period and steer the doublet into the hinge state.

The chain dynamic state, is similar to that seen in Ref. [46], [60] for spheres, i.e., two cells are flowing together side-by-side, without a tether. Furthermore, in the movies, see Supplementary Movie S2, we see that the normal of the individual cells point in different directions, rotating in the ∇ ×v − ∇v plane, which means that there is no bridging between the cells. Chaining of beads could also be caused by strong shear-thinning, as was shown by Van Loon et al. [60].

From the discussion of our results, we infer that normal shear flow is not sufficient to break up a doublet into single cells. The shear rate dependence of disaggregation that has been observed in the past [61–63] in the rheoscopes experiments is most probably connected to the breakup of larger, percolating, clusters and higher shear rates ∼ 500 s ⁻¹. To obtain fully separated cells, one might need to take the full hydrodynamic peeling load onto the cells into account, as has been shown in Ref. [64] for exfoliation of layered 2D materials. More importantly, capillary flow is probably needed and potentially also encounters with the bifurcation of the blood vessels. In our study, we assume that the fd rods act as pure depletant and in order to separate the cells shear drag competes with the osmotic pressure pushing the cells together, i.e., we should be able to slide the cells away from each other. However, in the case of plasma proteins or dextran induced aggregation there is evidence that the aggregation contains also bridging contributions [27–29]. In fact, Chien et al. [30] have shown experimentally that tank-treading of the cells membrane plays an important role in disaggregation of doublets in dextran solution. This has been recently confirmed by simulations in Ref. [31]. Furthermore, Brust et al. [10] have shown that rouleaux induced by fibrinogen and dextran persist even at the microvascular circulation level. This is another aspect that requires further research, especially in connection with the aggregation force.

One could ask if it is relevant if clusters break up into single cells. From the rheological point of view, fully dispersed single RBCs have the same behavior at the same volume fraction. Brooks et al. [65] have shown that at low volume fractions, < 20vol%, there is no shear-thinning observed. Hence, the effect of clustering at a level of a couple of RBCs on the flow behavior is probably small.

6 Conclusion

Aggregates of two RBCs under shear flow were studied using fd virus as an ideal depletion agent to induce attraction. Four dynamic states were observed: rolling and tumbling, where the two cells are in full contact; hinge and chain which are two intermediate states; as well as the event of the cells separating, split. The occurrence of these dynamic states depends on the concentration of the depletion agent and the applied shear rate. We show that the drag force enforced by the shear flow is of the same order as the depletion force so that the cells should separate for sufficiently high shear rates and low fd concentrations. However, full separation of all doublets at the highest shear rates was not observed. We attribute this observation to the complex interplay of forces and dynamic interactions. As the tumbling rate increases with shear rate, the time-windows for separation is shortened, which is not compensated by the increased drag force. Intermediate states that form due to partial separation are not easily destroyed. Our results suggest that complex interactions, such as encounters with other doublets or bifurcations in the microvascular system, are required to fully separate the blood in single cells.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.

Author Contributions

OK and TK carried out the experiment and MPL supervised the project. OK and MPL wrote the manuscript with support from TK.

Conflict of Interest

All authors were employed by Forschungszentrum Jülich GmbH and declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.721368/full#supplementary-material

References

1. Merrill EW, Gilliland ER, Cokelet G, Shin H, Britten a., Wells RE. Rheology of Human Blood, Near and at Zero Flow. Biophysical J (1963) 3:199–213. doi:10.1016/s0006-3495(63)86816-2

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Chien S, Usami S, Taylor HM, Lundberg JL, Gregersen MI. Effects of Hematocrit and Plasma Proteins on Human Blood Rheology at Low Shear Rates. J Appl Physiol (1966) 21:81–7. doi:10.1152/jappl.1966.21.1.81

CrossRef Full Text | Google Scholar

3. Errill EW. Rheology of Blood. Physiol Rev (1969) 49:863–88. doi:10.1152/physrev.1969.49.4.863

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Skalak R, Keller SR, Secomb TW. ASME Centennial Historical Perspective Paper: Mechanics of Blood Flow. J Biomechanical Eng (1981) 103:102–15. doi:10.1115/1.3138253

CrossRef Full Text | Google Scholar

5. Jariwala S, Horner JS, Wagner NJ, Beris AN. Application of Population Balance-Based Thixotropic Model to Human Blood. J Non-Newtonian Fluid Mech (2020) 281:104294. doi:10.1016/j.jnnfm.2020.104294

CrossRef Full Text | Google Scholar

6. Fedosov DA, Pan W, Caswell B, Gompper G, Karniadakis GE. Predicting Human Blood Viscosity In Silico. Proc Natl Acad Sci (2011) 108:11772–7. doi:10.1073/pnas.1101210108

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Blanco P, Volpicelli G. Common Pitfalls in point-of-care Ultrasound: A Practical Guide for Emergency and Critical Care Physicians. Crit Ultrasound J (2016) 8:15. doi:10.1186/s13089-016-0052-x

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Bertoluzzo SM, Bollini A, Rasia M, Raynal A. Kinetic Model for Erythrocyte Aggregation. Blood Cell Mol Dis (1999) 25:339–49. doi:10.1006/bcmd.1999.0261

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Fåhraeus R. The Snspension Stability of the BIood. Physiol Rev (1929) 9:241–74. doi:10.1152/physrev.1929.9.2.241

CrossRef Full Text | Google Scholar

10. Brust M, Aouane O, Thiébaud M, Flormann D, Verdier C, Kaestner L, et al. The Plasma Protein Fibrinogen Stabilizes Clusters of Red Blood Cells in Microcapillary Flows. Sci Rep (2014) 4:4348. doi:10.1038/srep04348

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Potron G, Nguyên P, Pignon B. Fibrinogen, Arterial Risk Factor, in Clinical Practice. Clin Hemorheol Microcirc (1994) 14:739–67. doi:10.3233/ch-1994-14601

CrossRef Full Text | Google Scholar

12. Obiefuna PC, Photiades DP. Sickle Discocytes Form More Rouleaux In Vitro Than normal Erythrocytes. J Trop Med Hyg (1990) 93:210–4.

Google Scholar

13. Chong-Martinez B, Buchanan TA, Wenby RB, Meiselman HJ. Decreased Red Blood Cell Aggregation Subsequent to Improved Glycaemic Control in Type 2 Diabetes Mellitus. Diabet Med (2003) 20:301–6. doi:10.1046/j.1464-5491.2003.00926.x

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bäumler H, Neu B, Donath E, Kiesewetter H. Basic Phenomena of Red Blood Cell Rouleaux Formation. Biorheology (1999) 36:439–42.

PubMed Abstract | Google Scholar

15. Merrill EW, Gilliland ER, Lee TS, Salzman EW. Blood Rheology: Effect of Fibrinogen Deduced by Addition. Circ Res (1966) 18:437–46. doi:10.1161/01.res.18.4.437

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chien S, Jan K-M. Ultrastructural Basis of the Mechanism of Rouleaux Formation. Microvasc Res (1973) 5:155–66. doi:10.1016/0026-2862(73)90068-x

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chien S, Jan K-M. Red Cell Aggregation by Macromolecules: Roles of Surface Adsorption and Electrostatic Repulsion. J Supramol Struct (1973) 1:385–409. doi:10.1002/jss.400010418

CrossRef Full Text | Google Scholar

18. Brooks DE. The Effect of Neutral Polymers on the Electrokinetic Potential of Cells and Other Charged Particles. J Colloid Interf Sci (1973) 43:714–26. doi:10.1016/0021-9797(73)90416-5

CrossRef Full Text | Google Scholar

19. Skalak R, Zarda PR, Jan KM, Chien S. Mechanics of Rouleau Formation. Biophysical J (1981) 35:771–81. doi:10.1016/s0006-3495(81)84826-6

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Neu B, Wenby R, Meiselman HJ. Effects of Dextran Molecular Weight on Red Blood Cell Aggregation. Biophysical J (2008) 95:3059–65. doi:10.1529/biophysj.108.130328

CrossRef Full Text | Google Scholar

21. Lekkerkerker HN, Tuinier R. Colloids and the Depletion Interaction, Lecture Notes in Physics, Vol. 833. Dordrecht: Springer Netherlands (2011).

Google Scholar

22. Armstrong JK, Wenby RB, Meiselman HJ, Fisher TC. The Hydrodynamic Radii of Macromolecules and Their Effect on Red Blood Cell Aggregation. Biophysical J (2004) 87:4259–70. doi:10.1529/biophysj.104.047746

CrossRef Full Text | Google Scholar

23. Baskurt OK, Meiselman HJ. Erythrocyte Aggregation: Basic Aspects and Clinical Importance. Clin Hemorheol Microcirc (2013) 53:23–37. doi:10.3233/ch-2012-1573

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Baskurt OK, Meiselman HJ. Hemodynamic Effects of Red Blood Cell Aggregation. Indian J Exp Biol (2007) 45:25–31.

Google Scholar

25. Kirschkamp T, Schmid-Schönbein H, Weinberger A, Smeets R. Effects of Fibrinogen and α2-Macroglobulin and Their Apheretic Elimination on General Blood Rheology and Rheological Characteristics of Red Blood Cell Aggregates. Ther Apher Dial (2008) 12:360–7. doi:10.1111/j.1744-9987.2008.00610.x

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Meiselman HJ. Red Blood Cell Aggregation: 45 Years Being Curious. Biorheology (2009) 46:1–19. doi:10.3233/bir-2009-0522

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Bronkhorst PJH, Grimbergen J, Brakenhoff GJ, Heethaar RM, Sixma JJ. The Mechanism of Red Cell (Dis)aggregation Investigated by Means of Direct Cell Manipulation Using Multiple Optical Trapping. Br J Haematol (1997) 96:256–8. doi:10.1046/j.1365-2141.1997.d01-2036.x

CrossRef Full Text | Google Scholar

28. Lee K, Danilina AV, Kinnunen M, Priezzhev AV, Meglinski I. Probing the Red Blood Cells Aggregating Force with Optical Tweezers. IEEE J Select Top Quan Electron (2016) 22:365–70. doi:10.1109/jstqe.2015.2477396

CrossRef Full Text | Google Scholar

29. Lee K, Kinnunen M, Khokhlova MD, Lyubin EV, Priezzhev AV, Meglinski I, et al. Optical Tweezers Study of Red Blood Cell Aggregation and Disaggregation in Plasma and Protein Solutions. J Biomed Opt (2016) 21:035001. doi:10.1117/1.jbo.21.3.035001

CrossRef Full Text | Google Scholar

30. Chien S, Feng S-s., Vayo M, Sung LA, Usami S, Skalak R. The Dynamics of Shear Disaggregation of Red Blood Cells in a Flow Channel. BIR (1990) 27:135–47. doi:10.3233/bir-1990-27202

CrossRef Full Text | Google Scholar

31. Abbasi M, Farutin A, Ez-Zahraouy H, Benyoussef A, Misbah C. Erythrocyte-erythrocyte Aggregation Dynamics under Shear Flow. Phys Rev Fluids (2021) 6:023602. doi:10.1103/physrevfluids.6.023602

CrossRef Full Text | Google Scholar

32. Chien S, Sung LA, Kim S, Burke AM, Usami S. Determination of Aggregation Force in Rouleaux by Fluid Mechanical Technique. Microvasc Res (1977) 13:327–33. doi:10.1016/0026-2862(77)90098-x

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Fischer TM, Stöhr-Liesen M, Schmid-Schönbein H. The Red Cell as a Fluid Droplet: Tank Tread-like Motion of the Human Erythrocyte Membrane in Shear Flow. Science (1978) 202:894–6. doi:10.1126/science.715448

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Fischer TM. On the Energy Dissipation in a Tank-Treading Human Red Blood Cell. Biophysical J (1980) 32:863–8. doi:10.1016/s0006-3495(80)85022-3

CrossRef Full Text | Google Scholar

35. Fischer TM. Shape Memory of Human Red Blood Cells. Biophysical J (2004) 86:3304–13. doi:10.1016/s0006-3495(04)74378-7

CrossRef Full Text | Google Scholar

36. Fraden S. Phase Transitions in Colloidal Suspensions of Virus Particles. In: M Baus, LF Rull, and JP Ryckaert, editors. Observation, Prediction, and Simulation of Phase Transitions in Complex Fluids. Dordrecht: Kluwer Academic (1995). p. 113–64. doi:10.1007/978-94-011-0065-6_3

CrossRef Full Text | Google Scholar

37. Lekkerkerker HNW, Tuinier R. Depletion Interaction. In: Colloids and the Depletion Interaction, Lecture Notes in Physics, Vol. 833. Dordrecht: Springer Netherlands (2011). p. 57–108. doi:10.1007/978-94-007-1223-2_2

CrossRef Full Text | Google Scholar

38. Guu D, Dhont JKG, Lettinga MP. Dispersions and Mixtures of Particles with Complex Architectures in Shear Flow. Eur Phys J Spec Top (2013) 222:2739–55. doi:10.1140/epjst/e2013-02055-2

CrossRef Full Text | Google Scholar

39. García ÁG, Nagelkerke MMB, Tuinier R, Vis M. Polymer-mediated Colloidal Stability: On the Transition between Adsorption and Depletion. Adv Colloid Interf Sci (2019) 275:102077. doi:10.1016/j.cis.2019.102077

CrossRef Full Text | Google Scholar

40. Adams M, Dogic Z, Keller SL, Fraden S. Entropically Driven Microphase Transitions in Mixtures of Colloidal Rods and Spheres. Nature (1998) 393:349–52. doi:10.1038/30700

CrossRef Full Text | Google Scholar

41. July C, Lang PR. Depletion Interactions Effected by Different Variants of Fd Virus. Langmuir (2010) 26:18647–51. doi:10.1021/la104151u

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Guu D, Dhont JKG, Vliegenthart GA, Lettinga MP. Depletion Induced Clustering in Mixtures of Colloidal Spheres Andfd-Virus. J Phys Condens Matter (2012) 24:464101. doi:10.1088/0953-8984/24/46/464101

CrossRef Full Text | Google Scholar

43. De Sio S, Lang PR. Depletion Interaction Mediated by Fd-Virus: On the Limit of Low Density and Derjaguin Approximation. Z für Physikalische Chem (2015) 229:1161–75. doi:10.1515/zpch-2014-0553

CrossRef Full Text | Google Scholar

44. Opdam J, Guu D, Schelling MPM, Aarts DGAL, Tuinier R, Lettinga MP. Phase Stability of Colloidal Mixtures of Spheres and Rods. J Chem Phys (2021) 154:204906. doi:10.1063/5.0048809

CrossRef Full Text | Google Scholar

45. Jeffery GB, Filon LNG. The Motion of Ellipsoidal Particles Immersed in a Viscous Fluid. Proc R Soc Lond Ser A, Containing Pap a Math Phys Character (1922) 102:161–79.

Google Scholar

46. Zia IYZ, Cox RG, Mason SG, Taylor GI. Ordered Aggregates of Particles in Shear Flow. Proc R Soc Lond Ser A. Math Phys Sci (1967) 300:421–41.

Google Scholar

47. Rosén T, Do-Quang M, Aidun CK, Lundell F. Effect of Fluid and Particle Inertia on the Rotation of an Oblate Spheroidal Particle Suspended in Linear Shear Flow. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 91:053017. doi:10.1103/PhysRevE.91.053017

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Newman J, Swinney HL, Day LA. Hydrodynamic Properties and Structure of Fd Virus. J Mol Biol (1977) 116:593–603. doi:10.1016/0022-2836(77)90086-9

CrossRef Full Text | Google Scholar

49. Torbet J. Neutron Scattering Study of the Solution Structure of Bacteriophages Pf1 and Fd. FEBS Lett (1979) 108:61–5. doi:10.1016/0014-5793(79)81179-5

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Sambrook J, Russell DW. Molecular Cloning: A Laboratory Manual. 3rd ed. Cold Spring Harbor, N.Y: Cold Spring Harbor Laboratory Press (2001).

Google Scholar

51. Kirchenbuechler I, Guu D, Kurniawan NA, Koenderink GH, Lettinga MP. Direct Visualization of Flow-Induced Conformational Transitions of Single Actin Filaments in Entangled Solutions. Nat Commun (2014) 5:5060–8. doi:10.1038/ncomms6060

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, et al. Fiji: An Open-Source Platform for Biological-Image Analysis. Nat Methods (2012) 9:676–82. doi:10.1038/nmeth.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Neu B, Meiselman HJ. Depletion-mediated Red Blood Cell Aggregation in Polymer Solutions. Biophysical J (2002) 83:2482–90. doi:10.1016/s0006-3495(02)75259-4

CrossRef Full Text | Google Scholar

54. Dupire J, Socol M, Viallat A. Full Dynamics of a Red Blood Cell in Shear Flow. Proc Natl Acad Sci (2012) 109:20808–13. doi:10.1073/pnas.1210236109

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Lang C, Kohlbrecher J, Porcar L, Radulescu A, Sellinghoff K, Dhont JKG, et al. Microstructural Understanding of the Length- and Stiffness-dependent Shear Thinning in Semidilute Colloidal Rods. Macromolecules (2019) 52:9604–12. doi:10.1021/acs.macromol.9b01592

CrossRef Full Text | Google Scholar

56. Lang C, Lettinga MP. Shear Flow Behavior of Bidisperse Rodlike Colloids. Macromolecules (2020) 53:2662–8. doi:10.1021/acs.macromol.9b02239

CrossRef Full Text | Google Scholar

57. Lamb H. Hydrodynamics. New York: Dover publications (1945).

Google Scholar

58. Sewchand LS, Rowlands S, Lovlin RE. Resistance to the Brownian Movement of Red Blood Cells on Flat Horizontal Surfaces. Cel Biophys (1982) 4:41–6. doi:10.1007/bf02788554

CrossRef Full Text | Google Scholar

59. Lang C. Dynamics and Phase Behavior of ( Non- ) Ideal Liquid-Crystals under Shear. Leuven: KU Leuven (2019). Ph.D. thesis.

Google Scholar

60. Van Loon S, Fransaer J, Clasen C, Vermant J. String Formation in Sheared Suspensions in Rheologically Complex media: The Essential Role of Shear Thinning. J Rheology (2014) 58:237–54. doi:10.1122/1.4853455

CrossRef Full Text | Google Scholar

61. Schmid-Schoenbein H, Wells R, Schildkraut R. Microscopy and Viscometry of Blood Flowing under Uniform Shear Rate(rheoscopy). J Appl Physiol (1969) 26:674–8. doi:10.1152/jappl.1969.26.5.674

CrossRef Full Text | Google Scholar

62. Shiga T, Imaizumi K, Harada N, Sekiya M. Kinetics of Rouleaux Formation Using TV Image Analyzer. I. Human Erythrocytes. Am J Physiol (1983) 245:H252–8. doi:10.1152/ajpheart.1983.245.2.H252

CrossRef Full Text | Google Scholar

63. Baskurt OK, Meiselman HJ. Blood Rheology and Hemodynamics. Semin Thromb Hemost (2003) 29:435–50. doi:10.1055/s-2003-44551

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Salussolia G, Barbieri E, Pugno NM, Botto L. Micromechanics of Liquid-phase Exfoliation of a Layered 2D Material: A Hydrodynamic Peeling Model. J Mech Phys Sol (2020) 134:103764. doi:10.1016/j.jmps.2019.103764

CrossRef Full Text | Google Scholar

65. Brooks DE, Goodwin JW, Seaman GV. Interactions Among Erythrocytes under Shear. J Appl Physiol (1970) 28:172–7. doi:10.1152/jappl.1970.28.2.172

CrossRef Full Text | Google Scholar