A Network View of Portfolio Optimization Using Fundamental Information

This article proposes the use of a novel approach to portfolio optimization, referred to as “Fundamental Networks” (FN). FN is an effective and robust network-based fundamental-incorporated method, and can be served as an alternative to classical mean-variance framework models. As a proxy for a portfolio, a fundamental network is defined as a set of “interconnected” stocks, among which linkages are a measure of similarity of fundamental information and are referred to asset allocation directly. Two empirical models are provided in this paper as applications of Fundamental Networks. We find that Fundamental Networks efficient portfolios are in general more mean-variance efficient in out-of-sample performance than Markwotiz’s efficient portfolios. Specifically, portfolios set for profitability goals create excess return in a general/upward trending market; portfolios targeted for operating fitness perform better in a downward trending market, and can be considered as a defensive strategy in the event of a crisis.

1 Introduction

The problem of portfolio optimization is one of the most important issues in asset management [1]. Modern Portfolio Theory (MPT) has served as the foundation and industry standard for portfolio optimization, being capable of demonstrating the concepts of diversification and risk-return efficiency based on a mean-variance framework [2, 3]. However, within the last few decades, practitioners and academics have become aware of its drawbacks. First, the high sensitivity of the estimated mean-variance efficient portfolio to estimation errors in expected return may lead to non-robust results [4–12]. Second, the mean-variance optimization requires the inversion of a positive-definite co-variance matrix which would lead to large estimation errors and will further offset the benefits of diversification. Hence, the portfolio cannot be constructed for a large number of stocks [13]. Third, the lack of hierarchical structure in a correlation matrix allows weights to vary freely in unintended ways, which is a root cause to the mean-variance efficient portfolio’s instability [14]. Moreover, MPT only involves the analysis of prices and is not able to incorporate the fundamental analysis which has been deemed value-relevant to stock return by not only well-known investors mentioned earlier, but also multiple researchers in the past [15–19].

To our knowledge, substitution of mean-variance framework has not been well discussed in the area of portfolio optimization. Studies introduced fundamental analysis to mean-variance model are still confined by the drawbacks. The application of financial networks started a new branch in optimizing portfolios. However, few of them conveyed fundamental information. Therefore, the main purpose of our research is to bridge portfolio optimization to fundamental analysis with network structure.

In this paper, we propose a novel approach for portfolio optimization, referred to as “Fundamental Networks” (FN), an effective and robust network-based fundamental-incorporated method. It can be used as an alternative to the classical Markowitz’s model. Compare to it, FN avoids the estimation errors of expected return and standard deviation,and also removes the requirement of a positive definite co-variance matrix. As a proxy for a portfolio, a fundamental network is defined as a set of “interconnected” stocks, among which linkages are a measure of similarity of fundamental information among stocks. The capital allocated to a stock is proportionate to the concept of weighted degree in network theory.

The fundamental networks bridge portfolios to fundamental information with network theory. The process of portfolio optimization is decomposed into steps as asset selection and capital allocation [20]. iterature referred to this paper is classified as fundamental analysis and financial networks. However, few of them addressed the both steps.

Fundamental analysis is the most common way to assess firm value [19]. However, the application of fundamental analysis in portfolio optimization tends to focus on the stock selection rather than developing an effective and innovative weighting schema based on fundamental information [18, 20–24]. Attempts introduced an additional fundamental condition into Markowitz’s model for both optimal selection and allocation. Although these models are improved by selecting stocks of good economic condition for the portfolio, major limitations from Markowitz’s model have not been addressed [25–27]. Another area of studies which is related to our work is fundamental indexation, which assigns portfolio weights using metrics in financial statements instead of stock price and capitalization [28–30].

Pioneered by the remarkable work of [31]; network-based methods have found their way into finance literature, and Recent studies such as [32–35] explore their usefulness for optimal investment purposes. Indeed, as noted in [36]; many financial optimization problems including Markowitz’s, had an underlying network structure. The topology of network encodes the complex dependency structure of financial equities, extracts hierarchical and clustering properties, and reduces data complexity while preserving fundamental characteristics of information [34]. Because the functionality of complex networks relies on their underlying structure and structural stability, most empirical studies chose the minimum spanning tree (MST) as the base structure for their financial networks [37–41].

In network theory, information about the relative importance of nodes in a network can be obtained through centrality measures, which are the most fundamental and frequently used measures to reveal network structure [42–46]. Investment decisions are usually derived from choosing “central” or “non-central” assets from the network. “Non-central” investment strategy claims that a portfolio containing the outskirts of the network have greater diversification potential, and thus are exposed to less risk [32, 34, 35, 45]. However, these studies only select stocks, the allocation process is still under the Markowitz’s mean-variance framework, therefore its drawbacks inherited from the framework remain unsolved.

Our proposed FN can address both asset selection and capital allocation for portfolio investment. In the selection stage, a portfolio objective is set, such as maximizing changes of return on equity (ROE). In the allocation stage, we construct a fundamental network with proper network structure. To start with, we define each selected stock as a node in the network, and each node is described using its fundamental information set which may include changes in net profit, asset turnover and leverage ratio. Next, we define potential links in the network using similarity measure of information sets among stocks, similarity measure can be Euclidean distance or other common distance measures. Finally, a network structure such as the minimum spanning tree (MST) is applied to form connections among stocks, and weighted degrees are derived for capital allocation. Network efficiency is considered to be a measure of network instability and error tolerance [47].

Two empirical models are provided in this paper as applications of the FN. Model 1 is based on DuPont framework where the objective of selecting stocks with high ROE, changes in net profit, asset turnover and leverage ratio serve as fundamental information set to describe a node. Model 2 is focused on operating income, where stock nodes are presented as changes of gross profit. Both of these models use Euclidean distance to construct a MST to be used as the desired network structure. We evaluate model performance using Sharpe Ratio from year 2006 to 2018. Model 1 outperforms the mean-variance efficient portfolios for all risk cases, and Model 2 outperforms the mean-variance efficient portfolios in the low-risk cases. In other words, FN efficient portfolios are more mean-variance efficient in out-of-sample performance than Markwotiz’s efficient portfolios. In addition, the annual return of Model 1 is positively correlated to the annual return of the S&P 500 Index, while Model 2 is negatively correlated to that of the S&P 500 Index. Unlike the one fixed optimization goal of mean-variance framework, FN provide solutions to complex market conditions. In our study, Model 1 is suggested for general market condition, while Model 2 serves as a defensive strategy in the event of a crisis.

The major contributions of our proposed FN are:

• Proposing a Novel Framework for Portfolio Optimization: creating an network-based fundamental-incorporated method for portfolio optimization, completely different from the classical Markowitz’s model. Empirically, the out-of-sample performance is suggested that network efficient portfolios reached higher mean-variance efficiency than Markowitz’s solutions.

• Expanding Source of Information: incorporating fundamental information and providing flexibility in selecting portfolio objective. It can be any fundamental variable or financial ratio representing profitability, liquidity, solvency, operating efficiency etc.

• Lifting Restriction: removing portfolio size constraint in mean-variance framework, referred to the positive-definite requirement of co-variance matrix, so that enable large-scale portfolio optimization.

• Enhancing Robustness of Asset Allocation: increasing stability and robustness of optimal capital allocation on stocks by adopting optimal network structure.

The remainder of the paper is organized as follows: section 2 introduces the general mathematical model of fundamental networks. In section 3, two empirical studies are provided and evaluated. Section 4 presents our conclusions and avenues of future research.

2 Methodology

2.1 Stock Portfolio as a Network

In our FN model, the asset selection rule is determined by the chosen fundamental objective. The asset allocation process is to minimize stock similarity under an optimal network structure. For example, ROE is an indicator of corporate profitability. To maximize profitability of a portfolio, we choose the changes of ROE as the fundamental objective and filter a set of high performance companies out of the entire market. We then construct a network based on fundamental information set, using the same example as in Model 1. Elements in the set include changes in net profit, asset turnover and leverage ratio among others. The allocation result is expected to be positively correlated to the weighted degree of each node in the network.

The main novelty of this paper lies in the flexibility choosing objective, information sets and risk measures based on fundamentals. Objectives and information sets can be any fundamental variable or financial ratio representing profitability, liquidity, solvency, operating efficiency etc. Common network structures can refer to, but are not limited to minimum spanning trees, planar maximally filtered graphs, market graphs [48]. Variations in node representation, network structure and distance definition allow a variety of potential risk measures to be applied. Such risk measures can be derived as centrality, assortativity, and network efficiency among others. Since, centrality, assortativity and network efficiency are measures of similarity and stability in graph theory, these can be considered as diversification and robustness of allocation in portfolio theory [33, 34].

2.2 Fundamental Network Framework

In this paper, we introduce the concept of “Fundamental Network Framework” as a general process equating portfolio optimization with finding optimal network topology features (Figure 1). The framework is consisted of three stages: asset selection, fundamental network construction and asset allocation.

FIGURE 1

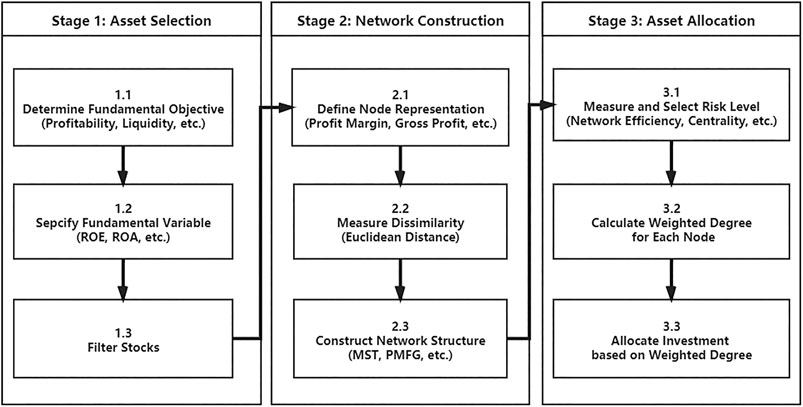
FIGURE 1. Flowchart for Portfolio Optimization under Fundamental Network Framework. Two empirical examples are specified in Table 2.

2.3 Fundamental Network Construction

According to Figure 1, Stage 1 and 2 is to define and construct fundamental networks by modeling a portfolio with topological features. A fundamental network is referred to a connected, undirected and weighted graph G(V, E, W).

Definition 1 (Fundamental Network) Define a connected, undirected and weighted graph

$G(V,E,W)(1)$

whereV = {v₁, …, v_n} denotes a set of stocks. Every stock and its fundamental/financial ratio information is represented as a node.E = {e₁, …, e_n} is the edge set.Wis the weighted adjacency matrix andw_i,j ∈ W, w_i,jrepresents the edge weight between nodesv_iandv_j.

In stage 1 (Figure 1), we need to define the fundamental objective such as profitability, and then refer a specific variable for the objective. In this paper, we only allow one dimension objective. Definition 2 is to mapping a stock to the fundamental variable. For instance, ROE is selected to describe profitability noted as the utility U = u(V) = ROE.

Definition 2 (Utility)Define a utility as

$U=u(V)(2)$

whereu() is a utility function.

Then filter stocks with the variable selected to establish a stock pool for later optimization. Notice that V_U are the selected stocks based on U and U_threshold. It can represent any predetermined objective such as profitability, liquidity, solvency, or operating efficiency.

Definition 3 (Stock Pool) Select a subset of stocks satisfying

$V_U\in V,\forall v\in V_U,u(v)\ge U_{threshold}(3)$

whereU_thresholdis a threshold level ofU.

Stage 2 is mainly to construct fundamental networks based on selected stock pool. Specifically, each node represents the fundamental(s) of a stock. A linkage between two nodes represents the dissimilarity of the corresponding stocks. In this paper, dissimilarity measure is referred to Euclidean distance.

Definition 4 (Fundamental Node)DefineV = {v₁, …, v_n}, a node is

$v_i=\{I_{(i,q)}|q=\mathrm{1,2},\dots ,m\}(4)$

wherev_iis the fundamental information set ofstock_iandI_(i,q)is referred to qth fundamental variable representing a stock.I_(i,q)ranges from financial ratios to the variables in the financial statements such as leverage ratio, net income,Δgrossprofit, etc. Note that m is noted as the number of variables to define a node.

Definition 5 (Dissimilarity) Define Euclidean distance as the measure of dissimilarity between two nodes i, j, D = {d(i, j), ∀i, j ∈ [1, n]}.

$d(i,j)=\sqrt{I_{(i,q)}-I_{(j,q)}},q=\mathrm{1,2},\dots ,m;(5)$

A network with the set V_U can be constructed by Definition 1–3. Given node set V_U, network structure E is derived from network generation algorithms such as small-world networks, scale-free networks and minimum spanning tree etc. The topology features of G(V_U, E, W) vary when choosing different network models. It is found a more complex topology often comes with a greater systemic risk [37, 49, 50] and a structural optimized network structure will also lead to an optimized portfolio [35, 51].

Fundamental network structural stability and dissimilarity in graph theory is defined in our model as portfolio risk in portfolio theory. Network efficiency is considered to be a risk tolerance measure in graph theory [47]. By bridging stock portfolios to networks, we are able to use network efficiency as a risk measure of a portfolio.

In this paper, we use minimum spanning tree (MST) as the base network structure. A minimum spanning tree (MST) is a tree T(V_U, E_T, W_T) ∈ G(V, E, W) with minimum total edge weight.

Definition 6 (Minimum Spanning Tree) Given a connected, undirected weighted graph G(V_U, E, W), the minimum spanning tree (MST) is a tree T(V_U, E_MST, W_MST) ⊆ G with minimum total edge weight defined as:

$w_{MST}=\sum _{e_{i,j}\in E_{MST}}{w}_{i,j},\forall \mathcal{G}\subseteq G(6)$

where$\mathcal{G}$is subgraph ofGandE_MST ⊆ E,W_MST ⊆ W.

2.4 Risk Measurement and Asset Allocation

In stage 3 (Figure 1), after the network is constructed, we introduce total network efficiency (TNE), which is a measure of systemic attack and error tolerance, as the risk measure in our model. A network with higher network efficiency has a higher tolerance to errors and attacks [47].

Definition 7 Total Network Efficiency (TNE)

$TNE(G)=\sum _{i\ne j\in G}\frac{1}{d_{i,j}}(7)$

whered_i,jis the distance of all paths from nodev_itov_j ∈ G(V_U, E, W),∀i ≠ j. Note thatG(V_U, E, W) is a undirected graph, sod_i,j=d_j,i.

TNE is positively related to the number of nodes and edges since it is defined as the sum of reciprocal of all edges in a network. Therefore, increasing size of an FN will increase its TNE, indicating a reduction of instability and an increase in diversification.

In addition, given a certain number of nodes, a minimum spanning tree has the maximum of TNE $\forall \mathcal{G}\in G$. Mathematically, according to Definition 7, a minimum spanning tree T minimizes ∑_i,jd_i,j, ∀i, j ∈ G such that $TN{E}_T\ge TN{E}_{\mathcal{G}},\forall \mathcal{G}\in G$, where $\mathcal{G}$ is arbitrary subgraph of G. Given a total number of n stocks where $V_{U_i}=\{v_1,\dots ,v_n\}$, u(v_i) ≥ U_threshold, the minimum spanning tree set $T=\{T_i(V_{U_i},E_i,W)\}$, i = 1, …, n are the portfolios with maximized.

Finally, investment allocation is calculated from the weighted degree of the nodes in the network. From a network perspective, a stock with high weighted degree is systemically important as it is assigned a large portion of investment.

Definition 8 (Investment Allocation)Given a connected weighted graph.

G(V_U, E, W), V_U = {v₁, …, v_n} is a n-stocks portfolio satisfying∀v_i ∈ V_U, U(v_i) ≥ U_threshold, wherev_irepresents the fundamental information set of a stockI_i.

DefineX = (x₁, x₂, …, x_n) as the vector of investment allocation,x_ias the proportion of investment in stocki, and${\sum }_{i=1}^n{x}_i=1$.

$x_i=\frac{{\sum }_{j\in N(v_i)}{w}_{i,j}}{{\sum }_{i,j\in V}{w}_{i,j}},(8)$

whereN(v_i) is the neighbor set ofv_i,w_i,jrepresents the edge weight between two stocks’ fundamentalsv_iandv_j.

3 Empirical Analysis and Results

In this section, we present two empirical solutions in portfolio optimization as applications of Fundamental Networks. While minimizing fundamental network structural instability, the models are distinct from their fundamental objectives and node variables to adapt to different market scenarios. Our optimized portfolios outperforms Markwotiz’s under certain market conditions.

3.1 Data and Models

Financial statement data are from the Compustat database,the sampled stocks are S&P 1,500 index members from 2006–2018. There are around 550 to 580 stocks each year after excluding those missing necessary data. The backtest started from 04/15/2007 and the positions are adjusted at the first trading day right after each April 15th when all companies had released their financial statements. Risk free rate refers to 1-year t-bill rate. Price returns are calculated annually between each April 15th. Fundamental variables are selected from annual financial statements. A detailed description of fundamental variable settings is shown in Table 2. All fundamental values can be found in the supplementary data set.

To illustrate the flexibility of FN framework in selecting portfolio objectives and fundamental information, we introduce two models in the empirical analysis Table 2. Model 1 maximizes company profitability described by changes of Return on Common Equity (ROE). In accordance with DuPont Analysis, each node is defined by changes in net profit, asset turnover and leverage ratio. Model 2 is focused on operating fitness, fundamental objective is defined as changes of operating income, and stock nodes are presented as changes of gross profit.

In the FN models, Euclidean distance is referred to the measure of diversification. Therefore, instead of restricted by the positive-definite requirement of co-variance matrix in mean-variance framework, portfolio size in FN models can be as large as the stock Universe. In our examples, the portfolio size ranges up to around 550 stocks.

The FN networks displayed in Figures 2, 3 are portfolios selected from efficient frontiers of Model 1 and 2 in 2009, each consisted of 200 stocks. Each node represents a stock while linkages measure similarity of their fundamental information. Size of node is positively correlated to weighted degree and investment allocation.

FIGURE 2

FIGURE 2. Fundamental Network: Model 1, 200 stocks in 2009. Size of node is positively correlated to weighted degree and investment allocation.

FIGURE 3

FIGURE 3. Fundamental Network: Model 2, 200 stocks in 2009. Weighted degree is higher for the nodes (larger) near the end points than those in the middle since no hierarchical structure is detected.

Apparently, the structural complexity of the two networks varies significantly that Model 1 has a hierarchical structure and higher interconnectedness than Model 2. This outcome is related to the complexity-stability debate [52] that whether a positive correlation exists between them. Interconnectedness is a key feature in measuring network complexity. In finance, many studies suggested that interconnectedness conveys higher systemic risk in bank networks [53]. According to [54]; there is no economic theory at hand that can be used to answer the question of the optimal level of interconnectedness for a financial system from a general equilibrium perspective. However, our empirical results suggest that the portfolios with high interconnectedness have higher volatility in out-of-sample performance (Table 1).

TABLE 1

TABLE 1. Performance Comparison.

TABLE 2

TABLE 2. Model Specifications.

3.2 Empirical Results

The assessment of the performance is based on out-of-sample statistics in the holding period which is 252 trading days. In stead of individual portfolios, this paper is to compare all the portfolios on the efficient frontiers. Therefore, we investigate the performance from both risk and time perspectives.

Specifically, we note Sharpe Ratio as Sharpe(q, t), where t is the time and q represents qth percentile of the risk distribution, q = {0, 5%, 10%, …, 1}. To compare models with different risk measures, we normalize risk into [0, 1]. Then Sharpe ratio can be represented at intervals of 5% from 0 to 1, for a total number of 21 risk levels.

$Sharp{e}_q=\frac{1}{n}\sum _{t=\mathrm{1,2},\dots ,n}Sharpe(q,t)(9)$

where Sharpe_q is the average Sharpe ratio of qth percentile portfolios over time t.

For example, efficient frontiers are constructed for each year. Sharpe(5%, 2008) is referred to Sharpe ratio of the portfolio on the frontier with the lowest 5% risk at the year 2008. $Sharp{e}_{5_{\%}}$ is the average of all the portfolios with lowest 5% risk from the years between 2007–2019 Figure 4.

FIGURE 4

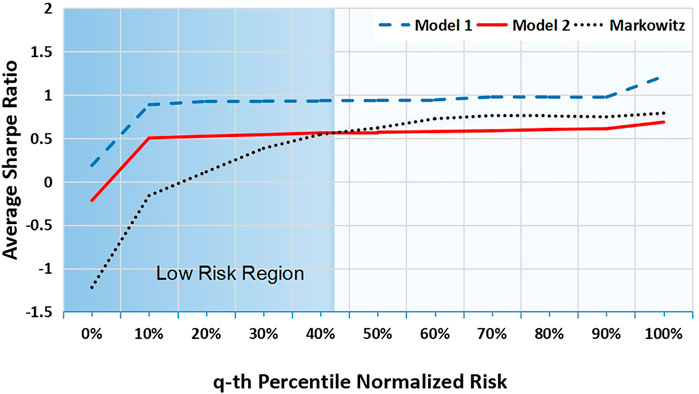
FIGURE 4. Fundamental Network Efficient Frontiers Model Out-of-Sample Performance. Model 1 (blue) is generally more mean-variance efficient than the benchmark while Model 2 (red) only outperforms in the low risk region (q ≤ 45%). Mean-variance efficient frontier is the benchmark (black).

In addition, we introduce ${\widehat{Sharpe}}_t$ as the average of Sharpe ratios for all portfolios on the efficient frontier at time t. Similarly, $\widehat{R}$ and $\hat{\sigma }$ represent average return and volatility of the efficient frontier at time t.

In Table 1, the Model 1 significantly outperforms Markwotiz’s in the year of 2012–2014, 2016, and 2017. These years are often considered to be “good” years where the market earnings growth are positive. The model 2 maximizes operating income and outperforms Markowitz’s in “bad” years (2007, 2008, 2015, 2018). The result is consistent with [55] who suggested that high operating performance companies have low volatility and outperforms high volatility stocks.

Define R = R(q, t), ∀q, t to be the actual return of the efficient frontier for all time t; R₀ = R₀(q, t), ∀q, t is the actual return of mean-variance efficient frontier for all time t; R_Market is the annual return of the stock market which is represented by the annual return of the S&P 500 Index in this paper.

Let the premium between fundamental network frontier and mean-variance frontier to be:

$R(q,t)-R_0(q,t)=\beta R_{Market}(q,t)+\alpha ,\forall q,t(10)$

As a result, Model 1 creates excess return when market grows but may suffer loss when market drops. Meanwhile, Model 2 has a negative β which means it outperforms Markowitz’s when market goes down. Model 1 refers to an aggressive strategy by optimizing company profitability. Model 2 is a defensive strategy with emphasis on operating income (Table 3).

TABLE 3

TABLE 3. Regressions Analysis and Diagnostics.

4 Conclusion and Discussion

We propose a novel approach, named Fundamental Networks (FN), for asset allocation under a network framework, which allows network stability measures to become applicable for portfolio optimization. FN avoids confrontation of estimation errors and the positive definite requirement of the covariance matrix in mean-variance framework. Our FN model provides robust and well-diversified solutions for investment.

Two examples with different fundamental objectives and variables are demonstrated in the paper. We conclude that network efficient portfolios, when properly defined with fundamental variables, are also mean-variance efficient in out-of-sample performance under certain market conditions. Moreover, our approach is adaptive to different market conditions. Portfolios set for profitability goals create excess return in an upward trending market, and outperform Markowitz’s benchmark when averaged across years. On the other hand, portfolios targeted for operating fitness produce better returns in the down trending market, and can be used as a defensive strategy in times of crisis. This empirical result also suggests that fundamental networks with lower interconnectedness are less volatile than those with higher complexity.

In conclusion, FN takes into consideration all filtered stocks and their interconnections, including some stocks which are insignificant but indispensable for the diversification of portfolios. The fundamentals-integrated network reveals both interesting known structures (similarity among stocks) and other structural patterns that are typically lost in the mean-variance framework. When combined with fundamentals and financial ratio information, such patterns can be developed as strategies under different market conditions. This coherent and principled network approach should prove useful for various forms of portfolio construction not limited to fundamental information. More generally, the proposed model is expected to be applied to other complex systems, because of its ability to generalize and connect networks from arbitrary data sets.

There are several avenues for future work. Firstly, a theoretical interpretation of fundamental networks is desired. Secondly, we can investigate, compare, discover patterns for optimal solutions with various fundamental objectives and variables. Thirdly, we can test and analyze more network structures (e.g., planar maximally filtered graph, market graph, maximum cliques among others), and network topological features (e.g., density, assortativity and community structure and others). Finally, fundamental networks open the door for multi-layer stock networks modeling fundamental-price dynamics, a potential interpretation for market efficiency.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XY and HY contributed to conception and design of the study. XY organized the database. HY performed the statistical analysis. XY, HY, ZY and SZ wrote sections of the manuscript. XY, HY, and ZY wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Elton EJ, Gruber MJ, Brown SJ, Goetzmann WN. Modern Portfolio Theory and Investment Analysis. New York: John Wiley & Sons (2009).

2. Markowitz H. Portfolio Selection. J Finance (1952) 7:77. doi:10.2307/2975974

CrossRef Full Text | Google Scholar

3. Markowitz HM. Portfolio Selection: E cient Diversification of Investments. Cowles Foundation Monograph 16 (1959). Diversification, 1959.

4. Mainik G, Mitov G, Rüschendorf L. Portfolio Optimization for Heavy-Tailed Assets: Extreme Risk index vs. Markowitz. J Empirical Finance (2015) 32:115–34. doi:10.1016/j.jempfin.2015.03.003

CrossRef Full Text | Google Scholar

5. Kolm PN, Tütüncü R, Fabozzi FJ. 60 Years of Portfolio Optimization: Practical Challenges and Current Trends. Eur J Oper Res (2014) 234:356–71. doi:10.1016/j.ejor.2013.10.060

CrossRef Full Text | Google Scholar

6. Chopra VK, Ziemba WT. The Effect of Errors in Means, Variances, and Covariances on Optimal Portfolio Choice. In: Handbook of the Fundamentals of Financial Decision Making: Part I (World Scientific) (2013). p. 365–73. (Singapore: World Scientific). doi:10.1142/9789814417358_0021

CrossRef Full Text | Google Scholar

7. Jagannathan R, Ma T. Risk Reduction in Large Portfolios: Why Imposing the Wrong Constraints Helps. J Finance (2003) 58:1651–83. doi:10.1111/1540-6261.00580

CrossRef Full Text | Google Scholar

8. Jorion P. Bayesian and Capm Estimators of the Means: Implications for Portfolio Selection. J Banking Finance (1991) 15:717–27. doi:10.1016/0378-4266(91)90094-3

CrossRef Full Text | Google Scholar

9. Michaud RO. The Markowitz Optimization Enigma: Is 'Optimized' Optimal? Financial Analysts J (1989) 45:31–42. doi:10.2469/faj.v45.n1.31

CrossRef Full Text | Google Scholar

10. Jorion P. Bayes-stein Estimation for Portfolio Analysis. J Financial Quant Anal (1986) 21:279–92. doi:10.2307/2331042

CrossRef Full Text | Google Scholar

11. Jorion P. International Portfolio Diversification with Estimation Risk. J Bus (1985) 58:259–78. doi:10.1086/296296

CrossRef Full Text | Google Scholar

12. Barry CB. Portfolio Analysis under Uncertain Means, Variances, and Covariances. J Finance (1974) 29:515–22. doi:10.1111/j.1540-6261.1974.tb03064.x

CrossRef Full Text | Google Scholar

13. López de Prado M. Building Diversified Portfolios that Outperform Out of Sample. Jpm (2016) 42:59–69. doi:10.3905/jpm.2016.42.4.059

CrossRef Full Text | Google Scholar

14. Raffinot T. Hierarchical Clustering-Based Asset Allocation. Jpm (2017) 44:89–99. doi:10.3905/jpm.2018.44.2.089

CrossRef Full Text | Google Scholar

15. Nissim D, Penman SH. Ratio Analysis and Equity Valuation: From Research to Practice. Rev Account Stud (2001) 6:109–54. doi:10.1023/a:1011338221623

CrossRef Full Text | Google Scholar

16. Sloan RG. Do stock Prices Fully Reflect Information in Accruals and Cash Flows about Future Earnings? Account Rev (1996) 289–315.

Google Scholar

17. Lev B, Thiagarajan SR. Fundamental Information Analysis. J Account Res (1993) 31:190–215. doi:10.2307/2491270

CrossRef Full Text | Google Scholar

18. Ou JA, Penman SH. Financial Statement Analysis and the Prediction of Stock Returns. J Account Econ (1989) 11:295–329. doi:10.1016/0165-4101(89)90017-7

CrossRef Full Text | Google Scholar

19. Ball R, Brown P. An Empirical Evaluation of Accounting Income Numbers. J Account Res (1968) 6:159–78. doi:10.2307/2490232

CrossRef Full Text | Google Scholar

20. Edirisinghe NCP, Zhang X. Generalized Dea Model of Fundamental Analysis and its Application to Portfolio Optimization. J Banking Finance (2007) 31:3311–35. doi:10.1016/j.jbankfin.2007.04.008

CrossRef Full Text | Google Scholar

21. Ho CTB. Performance Measurement Using Data Envelopment Analysis and Financial Statement Analysis. Ijor (2007) 2:26–38. doi:10.1504/ijor.2007.011441

CrossRef Full Text | Google Scholar

22. Küçükşahin H, Coşkun E. The Performance of Fundamental Indexes: An Application on Istanbul. Ege Acade Rev (2020) 20:1-18. doi:10.21121/eab.595407

CrossRef Full Text | Google Scholar

23. Xidonas P, Mavrotas G, Psarras J. A Multicriteria Methodology for Equity Selection Using Financial Analysis. Comput Operations Res (2009) 36:3187–203. doi:10.1016/j.cor.2009.02.009

CrossRef Full Text | Google Scholar

24. Yu Z, Serban N, Rouse WB. The Demographics of Change: Enterprise Characteristics and Behaviors that Influence Transformation. J Enterprise Transformation (2013) 3:285–306. doi:10.1080/19488289.2013.860346

CrossRef Full Text | Google Scholar

25. Tarczyński W. Different Variants of Fundamental Portfolio. Folia Oeconomica Stetinensia (2014) 14:47–62.

Google Scholar

26. Lyle MR, Yohn TL. Fundamental Analysis and Mean-Variance Optimal Portfolios. Forthcoming, The Accounting Review (2019). Lakewood Ranch: American Accounting Association.

Google Scholar

27. Zhang H, Yan C. Modelling Fundamental Analysis in Portfolio Selection. Quantitative Finance (2018) 18:1315–26. doi:10.1080/14697688.2017.1418520

CrossRef Full Text | Google Scholar

28. Blitz D, Swinkels L. Fundamental Indexation: An Active Value Strategy in Disguise. J Asset Manag (2008) 9:264–9. doi:10.1057/jam.2008.23

CrossRef Full Text | Google Scholar

29. Arnott RD, Hsu J, Moore P. Fundamental Indexation. Financial Analysts J (2005) 61:83–99. doi:10.2469/faj.v61.n2.2718

CrossRef Full Text | Google Scholar

30. Hsu JC. Cap-weighted Portfolios Are Sub-optimal Portfolios. J investment Manage (2004) 4.

Google Scholar

31. Mantegna RN. Hierarchical Structure in Financial Markets. Eur Phys J B (1999) 11:193–7. doi:10.1007/s100510050929

CrossRef Full Text | Google Scholar

32. Peralta G, Zareei A. A Network Approach to Portfolio Selection. J empirical Finance (2016) 38:157–80. doi:10.1016/j.jempfin.2016.06.003

CrossRef Full Text | Google Scholar

33. Kaya H. Eccentricity in Asset Management. Jntf (2015) 1:1–32. doi:10.21314/jntf.2015.003

CrossRef Full Text | Google Scholar

34. Pozzi F, Di Matteo T, Aste T. Spread of Risk across Financial Markets: Better to Invest in the Peripheries. Sci Rep (2013) 3:1665. doi:10.1038/srep01665

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Onnela JP, Chakraborti A, Kaski K, Kertész J, Kanto A. Dynamics of Market Correlations: Taxonomy and Portfolio Analysis. Phys Rev E Stat Nonlin Soft Matter Phys (2003) 68:056110. doi:10.1103/PhysRevE.68.056110

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Nagurney A. Networks in Economics and Finance in Networks and beyond: A Half century Retrospective. Networks (2019) 77 (1), 50–65. (New York: Wiley Online Library).

37. Khashanah K, Yang H. Evolutionary Systemic Risk: Fisher Information Flow Metric in Financial Network Dynamics. Physica A: Stat Mech its Appl (2016) 445:318–27. doi:10.1016/j.physa.2015.10.012

CrossRef Full Text | Google Scholar

38. Heiberger RH. Stock Network Stability in Times of Crisis. Physica A: Stat Mech its Appl (2014) 393:376–81. doi:10.1016/j.physa.2013.08.053

CrossRef Full Text | Google Scholar

39. Eom C, Kwon O, Jung W-S, Kim S. The Effect of a Market Factor on Information Flow between Stocks Using the Minimal Spanning Tree. Physica A: Stat Mech its Appl (2010) 389:1643–52. doi:10.1016/j.physa.2009.12.044

CrossRef Full Text | Google Scholar

40. Coelho R, Gilmore CG, Lucey B, Richmond P, Hutzler S. The Evolution of Interdependence in World Equity Markets-Evidence from Minimum Spanning Trees. Physica A: Stat Mech its Appl (2007) 376:455–66. doi:10.1016/j.physa.2006.10.045

CrossRef Full Text | Google Scholar

41. Situngkir H, Surya Y. On Stock Market Dynamics Through Ultrametricity Of Minimum Spanning Tree. Tech. Rep. Bandung: Bandung Fe Institute (2005).

42. Zhu S, Kou M, Lai F, Feng Q, Du G. The Connectedness of the Coronavirus Disease Pandemic in the World: A Study Based on Complex Network Analysis. Front Phys (2021) 8:642. doi:10.3389/fphy.2020.602075

CrossRef Full Text | Google Scholar

43. Gao C, Su Z, Liu J, Kurths J. Even central Users Do Not Always Drive Information Diffusion. Commun ACM (2019) 62:61–7. doi:10.1145/3224203

CrossRef Full Text | Google Scholar

44. Newman MEJ. Mathematics of Networks. New palgrave encyclopedia Econ (2008) 2:1–8. doi:10.1057/978-1-349-95121-5_2565-1

CrossRef Full Text | Google Scholar

45. Chi KT, Liu J, Lau FC. A Network Perspective of the Stock Market. J Empirical Finance (2010) 17:659–67.

Google Scholar

46. Hu J, Chengyi X, Huijia L, Peican Z, Wenjun X. Properties and structural analyses of USA's regional electricity market: A visibility graph network approach. Applied Mathematics and Computation (2010) (Elsevier) 385, 125434.

47. Latora V, Marchiori M. Efficient Behavior of Small-World Networks. Phys Rev Lett (2001) 87:198701. doi:10.1103/physrevlett.87.198701

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Kalyagin VA, Koldanov AP, Koldanov PA, Pardalos PM, Zamaraev VA. Measures of Uncertainty in Market Network Analysis. Physica A: Stat Mech its Appl (2014) 413:59–70. doi:10.1016/j.physa.2014.06.054

CrossRef Full Text | Google Scholar

49. Yalamova R, McKelvey B. Explaining what Leads up to Stock Market Crashes: A Phase Transition Model and Scalability Dynamics. J Behav Finance (2011) 12:169–82. doi:10.1080/15427560.2011.602484

CrossRef Full Text | Google Scholar

50. He J, Deem MW. Structure and Response in the World Trade Network. Phys Rev Lett (2010) 105:198701. doi:10.1103/physrevlett.105.198701

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Shi Y, Zheng Y, Guo K, Jin Z, Huang Z. The Evolution Characteristics of Systemic Risk in China's Stock Market Based on a Dynamic Complex Network. Entropy (2020) 22:614. doi:10.3390/e22060614

PubMed Abstract | CrossRef Full Text | Google Scholar

52. McCann KS. The Diversity-Stability Debate. Nature (2000) 405:228–33. doi:10.1038/35012234

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Battiston S, Martinez-Jaramillo S. Financial Networks and Stress Testing: Challenges and New Research Avenues for Systemic Risk Analysis and Financial Stability Implications (2018). Amsterdam: Elsevier.

54. Martinez-Jaramillo S, Carmona CU, Kenett DY. Interconnectedness and Financial Stability. J Risk Manage Financial Institutions (2019) 12 (2), 168–83. Henry Stewart Publications.

Google Scholar

55. Dutt T, Humphery-Jenner M. Stock Return Volatility, Operating Performance and Stock Returns: International Evidence on Drivers of the 'low Volatility' Anomaly. J Banking Finance (2013) 37:999–1017. doi:10.1016/j.jbankfin.2012.11.001

CrossRef Full Text | Google Scholar