Impact of Cation Stoichiometry on the Crystalline Structure and Superconductivity in Nickelates

The recent discovery of superconductivity in infinite-layer nickelate films has aroused great interest since it provides a new platform to explore the mechanism of high-temperature superconductivity. However, superconductivity only appears in the thin film form and synthesizing superconducting nickelate films is extremely challenging, limiting the in-depth studies on this compound. Here, we explore the critical parameters in the growth of high-quality nickelate films using molecular beam epitaxy. We found that stoichiometry is crucial in optimizing the crystalline structure and realizing superconductivity in nickelate films. In precursor NdNiO₃ films, optimal stoichiometry of cations yields the most compact lattice while off-stoichiometry of cations causes obvious lattice expansion, influencing the subsequent topotactic reduction and the emergence of superconductivity in infinite-layer nickelates. Surprisingly, in-situ reflection high energy electron diffraction indicates that some impurity phases always appear once Sr ions are doped into NdNiO₃ although the X-ray diffraction data are of high quality. While these impurity phases do not seem to suppress the superconductivity, their impacts on the electronic and magnetic structure deserve further studies. Our work demonstrates and highlights the significance of cation stoichiometry in the superconducting nickelate family.

Introduction

Over the past decades, there have been a great number of investigations on the superconductivity in nickelates, as they are natural analogs of high-T_c cuprates [1–8]. More recently, superconductivity was eventually found in the hole-doped infinite-layer nickelates [9], which have a layered structure and 3d^9−x electronic configuration similar to those of cuprate superconductors. This significant discovery provides a new platform to explore the mechanism of high-temperature superconductivity and triggers intense research interests [10–16]. Comprehensive theoretical studies have been reported [17–25], whereas experimental progress is still limited and several key issues remain unsolved. First, nickelates display some properties distinct from cuprates despite similar structures [13, 22, 26]. Second, superconductivity has only been observed in nickelate thin films, while bulk samples show an insulating behavior [27, 28]. These puzzles cast shadow on the understanding of underlying physics of high-T_c superconductivity. Therefore, more experimental progress is undoubtedly required.

However, the difficulty in reproducing the superconductivity in infinite-layer nickelates is obvious in light of only a few precedents for successful synthesis of superconducting nickelates [9, 12, 29, 30]. Recent reports of the observation on the superconductivity in hole-doped LaNiO₂, which was not superconducting previously, also emphasize the importance of the film quality [31, 32]. Some influential factors are reported, for instance, the increasing target ablation, different laser fluences in the pulsed laser deposition (PLD), and (002) peak positions in X-ray diffraction (XRD) scans, offering meaningful guidance for the Nd_1-xSr_xNiO₃ growth [33]. Some indirect evidence hints their relevance to the stoichiometry [34, 35], which deserves, but still lacks, a thorough investigation.

In this work, we employed molecular beam epitaxy (MBE) to grow perovskite neodymium nickelate films with different cation stoichiometries which are of significance in optimization and reproduction of superconductivity in nickelate films. We found that off-stoichiometry in both nickel-rich and nickel-poor films leads to obvious lattice expansion, which is shown to hinder the subsequent topotactic reduction and the emergence of superconductivity in infinite-layer nickelates. In addition, based on the stoichiometry effect, the out-of-plane (OOP) lattice constant is found to be helpful in the MBE growth calibration. Finally, an impurity phase in the Sr-doped samples was always shown in reflection high energy electron diffraction (RHEED) patterns, which can coexist with superconductivity.

Methods

The NdNiO₃ and Nd_1-xSr_xNiO₃ films were epitaxially grown on TiO₂-terminated (001)-oriented SrTiO₃ single-crystalline substrates using a DCA R450 MBE system. Before the growth, we used the quartz crystal microbalance (QCM) to measure a rough beam flux. The value of flux is for reference only, for it depends strongly on the background pressure, installation angle of the crucibles of sources, and the shape of the source materials. During the growth, RHEED was employed to monitor the growth process and surface quality. The films were grown at 550—650°C (measured by a thermocouple thermometer) and under an oxidant (distilled ozone) background pressure of ∼4.0 × 10^–6 Torr. A residual gas analyzer (RGA) was utilized to real-time monitor the ozone partial pressure, which is essential for the stabilization of the oxidation state of Ni^3+x. SrTiO₃ substrates were etched in buffered HF acid for about 70 s and annealed in flowing pure oxygen at 1,000°C for 80 min before growth to obtain a TiO₂-terminated step-and-terrace surface [36]. The film crystalline structure was examined by XRD using a Bruker D8 Discover diffractometer. The resolution of our 2θ-ω scans is 0.0071°. And the step length of 2θ in the XRD measurements is 0.04°. The terraced micromorphology of films was revealed by Asylum Research MFP-3D atomic force microscopy (AFM). Specimens for cross-sectional scanning transmission electron microscopy (STEM) were prepared by focused ion beam (FIB) techniques. Atomic-resolution annular dark-field (ADF) images were acquired on JEOL JEM ARM 200F outfitted with an ASCOR fifth-order probe corrector. In order to attain an infinite-layer phase, Nd_0.8Sr_0.2NiO₃ was sealed in a vacuum chamber together with ∼0.1 g CaH₂ powder and then heated to 280°C for 4 h, with a warming (cooling) rate of 10–15°C/min [9]. Temperature-dependent resistivity was measured via the standard van der Pauw geometry in a homemade transport property measurement system.

Results and Discussion

Effect of Cation Stoichiometry on NdNiO₃ Films

Taking the advantage of MBE technique, a series of NdNiO₃ films with different Nd:Ni flux ratios were grown. For many perovskite oxides ABO₃, the deposition time for each source can be extracted precisely using a shuttered mode [37, 38] because the alternative growth of AO and BO₂ monolayers leads to RHEED intensity oscillations with intensity reaching a maximum (or minimum) value at the end of depositing one full atomic monolayer. However, the intensity at the end of growing an atomic monolayer for NdNiO₃ is not the maximum (or minimum) value. Hence, the co-deposition method where AO and BO₂ layers are deposited simultaneously is adopted. The period of RHEED oscillations in the co-deposition corresponds to the growth of one unit cell [37, 38]. The nominal ratio of Nd and Ni was roughly calibrated to 1:1 based on QCM measurements. Then, we adjust the relative Nd:Ni flux ratio precisely by successively changing the deposition time for Ni, which effectively alters the cation stoichiometry.

XRD patterns shown in Figure 1A demonstrate clear (00l) reflections, indicating the reasonable crystalline quality in these samples. Figure 1B shows a plot of the OOP lattice constants calculated from the (002) peak position as a function of the nominal Nd:Ni flux ratio (represented by the blue triangles), as well as the corresponding Gaussian fit (yellow dashed line). An increment of the OOP lattice constant is observed in both sides of the flux ratio deviated from the optimal value. Given that the in-plane lattice is fully strained to the substrates as revealed by the reciprocal space mapping (RSM) shown in Figure 1C, it is clear that off-stoichiometry gives rise to a lattice expansion, similar with the situation in SrTiO₃ [39]. Since the (002) peak position over 48° was deemed to be indispensable for superconductivity [33], we note the sensitivity of the OOP lattice constant to cation stoichiometry should attract more attention.

FIGURE 1

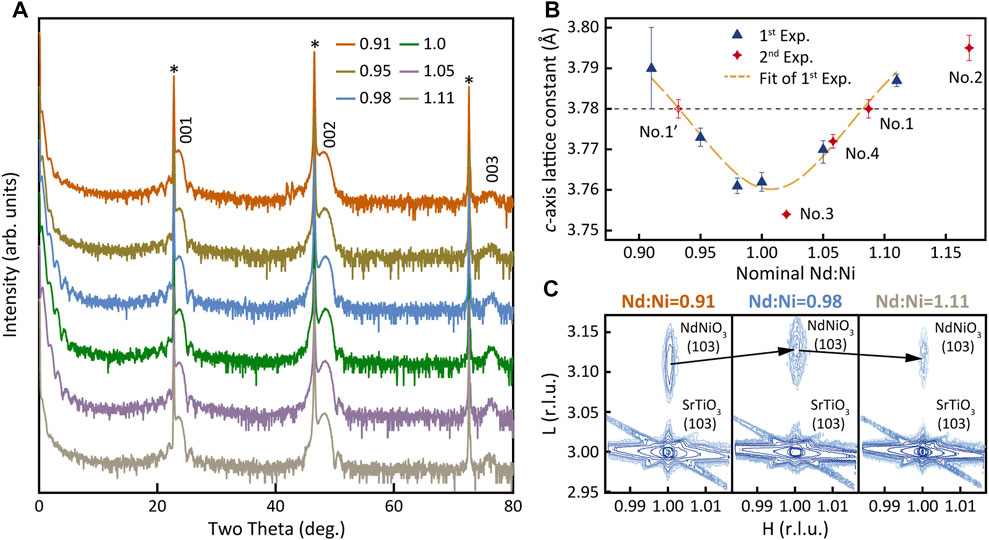
FIGURE 1. Effect of cation stoichiometry on NdNiO₃ films. (A) XRD 2θ-ω scans of NdNiO₃ films with different nominal Nd:Ni flux ratios. The curves are vertically offset for clarity. (B) Pseudo-cubic lattice constant along the (00l) direction as a function of the nominal Nd:Ni flux ratio. The blue triangles and yellow dashed line represent the experimental data and the corresponding Gaussian fit result, respectively. The red closed stars denote the data points obtained in another set of experiment, according to the numerical order marked in the figure, while the open star is another possible position for the No. 1 sample. The black dashed line denotes the c-axis lattice constant of the No. 1 sample. The error bars come from the fitting error of diffraction peaks. (C) Reciprocal space mappings around SrTiO₃ (103) peak for NdNiO₃ films with different flux ratios.

Based on this finding, the OOP lattice constant can be employed in turn as a unique indicator of stoichiometry and aided in the calibration of beam flux ratio which is essential in MBE growth. As mentioned above, the precise deposition time of each source is not available using the shuttered mode. In the co-deposition, although the oscillations are observed, the overall intensity shows little dependence on the variation of the Nd:Ni flux ratio, which is commonly employed in the growth of other systems [40, 41]. Hence, another specific way is demanded to conduct the calibration. Using the OOP lattice constant as an indicator is proved to be feasible and reliable. As shown in Figure 1B, the c-lattice constants as a function of stoichiometry can be nicely fitted with the Gaussian function shown below:

$\text{y}=3.797-0.037\times {\text{e}}^{-{\left(\frac{\text{x}-1.006}{0.083}\right)}^2}.(1)$

The deviation of the flux ratio from the optimum can be estimated from the fitted parabolic function. A real practice of the calibration process is specifically shown in Figure 1B denoted by the red stars. The NdNiO₃ samples were grown in the order shown by the numbers in the figure. The OOP lattice constant of the first sample is indicated by the black dashed line. Thus, the deviation of the beam flux ratio away from the optimum can be determined. Note that both No. 1 and No. 1′ positions are possible for this sample with only the lattice constant known. Hence, No. 2 and No. 3 samples were both grown, in which the dosage of nickel was reduced and increased, respectively, according to the deviation. The values of the OOP lattice constant of the two samples are within expectations, and the Nd:Ni flux ratio for No. 3 is nearly the optimum. The No. 4 sample was also grown to further prove the validity of this method and the result was consistent. It should be noted that other factors such as anion concentration also affects the lattice [42], which could explain the slight changes in exact OOP lattice constants of our films.

Then, a series of NdNiO₃ films were grown using the calibration process mentioned above. The persistent RHEED oscillations confirm the layer-by-layer growth mode, the period of which marked in Figure 2A is exactly the time required to deposit a layer of one unit cell NdNiO₃. The thickness obtained from the RHEED oscillation curve is 27 u.c., which is in good agreement with the fit of Kiessig fringes [43] shown in Figure 2B. The rocking curve measurement (Figure 2C) shows a full width at half-maximum (FWHM) value of 0.017°, indicating a high degree of crystalline perfection. The RHEED patterns taken along [110] and [100] directions are shown as insets of Figure 2A. The half-order diffractions can be observed, manifesting the existence of NiO₆ octahedral rotation [44]. In the atomic-resolution ADF-STEM images shown in Figures 2D,E, an abrupt and straight interface between the SrTiO₃ substrates and the NdNiO₃ film is observed. The film shows a high crystalline quality with well-ordered Nd and Ni atoms (denoted by orange and green circles, respectively) forming the perovskite lattice, and no defects such as atomic intermixing and stacking faults are observed. The smooth surface with a terraced morphology is achieved and revealed by AFM imaging (Figure 2F).

FIGURE 2

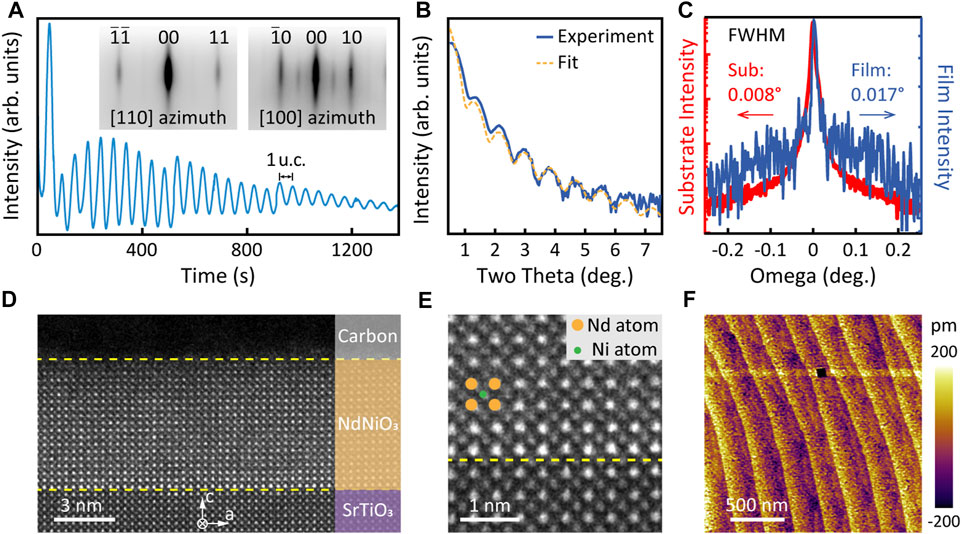
FIGURE 2. Structural characterizations of optimal NdNiO₃ films. (A) RHEED intensity oscillations taken along the (110) direction and RHEED patterns (inset) of a 27 u.c. thick NdNiO₃ film grown on SrTiO₃ substrates. The period of the oscillations denoted by the arrow indicates the time needed for the growth of one-unit-cell-thick NdNiO₃ by the co-deposition mode. (B) Magnification of the high-resolution XRD 2θ-ω scan of the 27 u.c. NdNiO₃ film at a low incident angle with clear Kiessig fringes, and the corresponding fit of film thickness is shown as the yellow dashed line. (C) Rocking curves of the NdNiO₃ film and SrTiO₃ substrate. The values of FWHM are both obtained in a linear scale. (D, E) Cross-sectional STEM-ADF images of an 18 u.c. thick NdNiO₃ film on SrTiO₃ substrates under different magnifications. (F) A representative AFM image of the surface morphology showing clear terraces of the NdNiO₃ film.

Effect of Cation Stoichiometry on the Emergence of Superconductivity

The growth of Sr-doped NdNiO₃ is conducted using a similar co-deposition method based on both optimal and off-stoichiometric NdNiO₃. Shutter times (deposition time per unit cell) for Nd and Ni are corresponding to a single period of RHEED intensity oscillations during the NdNiO₃ co-deposition growth. The period of SrTiO₃ film is also calibrated in advance to obtain the precise shutter time of Sr. Taking Nd_0.8Sr_0.2NiO₃ for instance, in the one-unit-cell growth, the shutters of Sr, Nd, and Ni opened together and Sr closed at 20% shutter time, Nd at 80%, and Ni at 100%.

The RHEED intensity oscillations of 18 u.c. thick Nd_0.8Sr_0.2NiO₃ under the optimal flux ratio are shown in Figure 3A. The oscillations are not perfectly smooth but still sustained for a long time. The variation in the shape of RHEED oscillations across the growth is due to the interface effect because the growth of NdNiO₃ on SrTiO₃ is heteroepitaxial, which is commonly seen in the growth of other materials [45, 46]. The disparity in the crystalline quality originating from stoichiometry is obvious from the comparison of 2θ-ω diffraction patterns of Nd_0.8Sr_0.2NiO₃ films under different flux ratios (Figures 3B,D). The deviation from stoichiometry in our experiment is 10 and 15% nominally. In both Nd-rich and Ni-rich cases, the (002) diffraction peaks of off-stoichiometric Nd_0.8Sr_0.2NiO₃ films are relatively weaker and broader and the peak positions are below 48°, marked by the yellow dashed line. The corresponding temperature-dependent resistivities exhibit metal–insulator transitions or show an insulating behavior (Figure 4A). After topotactic reduction, some diffraction peaks corresponding to the reduced phase are observed in 10% off-stoichiometric samples, which are relatively weaker than the optimal sample. Few obvious infinite-layer phase is detected when the deviation is up to 15%, though the perovskite phase is still clear before reduction (Figures 3C,D). As expected, the insulating behaviors are revealed in all off-stoichiometric samples after reduction, as shown in Figure 4B. As such, our results demonstrate the significance of stoichiometry, which could impede the complete transformation of perovskite phase to infinite-layer phase and hinder the superconductivity when the deviation is more than 10%.

FIGURE 3

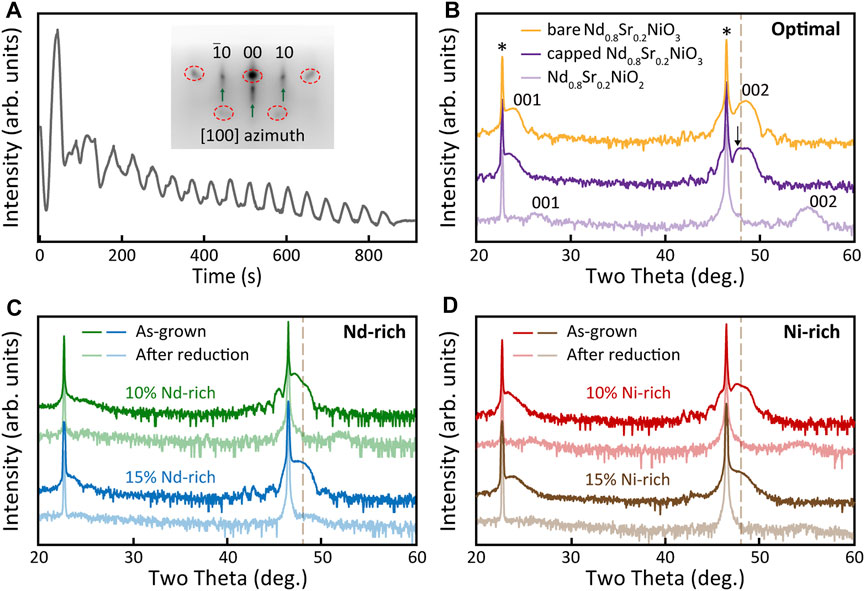
FIGURE 3. Effect of cation stoichiometry on the reduction of Nd_1-xSr_xNiO₃. (A) RHEED intensity oscillations and pattern (inset) of an 18 u.c. thick optimal Nd_0.8Sr_0.2NiO₃ film grown on SrTiO₃ substrates. The red open dashed circles and green arrows indicate the diffractions of the impurity phases and the perovskite phase of the film, respectively. (B) High-resolution XRD 2θ-ω scans of the nickelate films grown under an optimal flux ratio. The Nd_0.8Sr_0.2NiO₃ film before and after capping the SrTiO₃ layer is called bare and capped Nd_0.8Sr_0.2NiO₃, respectively. The dashed line represents the critical two theta values of 48°. (C) High-resolution XRD 2θ-ω scans of as-grown and reduced Nd-rich Nd_0.8Sr_0.2NiO₃ films. (D) High-resolution XRD 2θ-ω scans of as-grown and reduced Ni-rich Nd_0.8Sr_0.2NiO₃ films.

FIGURE 4

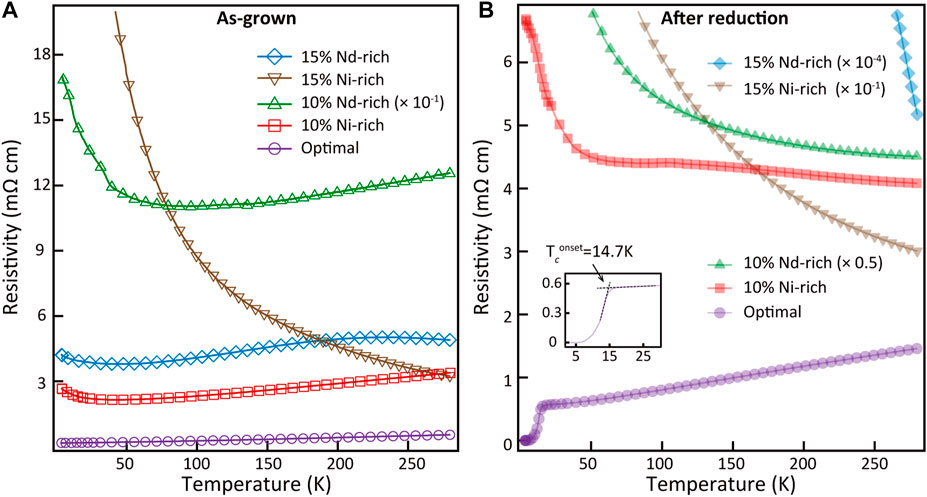
FIGURE 4. Effect of cation stoichiometry on the transport properties of Nd_1-xSr_xNiO₃ and Nd_1-xSr_xNiO₂. Temperature-dependent resistivity for reduced nickelate films grown under optimal and off-stoichiometric flux ratios before (A) and after (B) reduction. The resistivities of several samples were scaled for clarity, as denoted in the legends. Inset of B shows the zoom-in view at low temperatures from 3 to 30 K of optimal Nd_0.8Sr_0.2NiO₂ sample. The onset transition temperature is about 14.7 K, and zero resistivity is achieved at about 4.7 K.

Furthermore, for the optimal Nd_0.8Sr_0.2NiO₃ (inset of Figure 3A), though the diffraction pattern of Nd_0.8Sr_0.2NiO₃ is clear and sharp as shown by the green arrows, there exists impurity phases as indicated by the red dashed open circles, so do most of our Sr-doped samples. It should be noted that no corresponding diffraction peak was detected in XRD scans, suggesting a possible short-range order of the impurity phases, but its chemical composition is not clear up to now. Even so, these impurity phases do not seem to suppress the superconductivity in Nd_1-xSr_xNiO₂ (Figure 4B). As shown in Figure 3B, after topotactic reduction, the OOP lattice constant shrinks to ∼3.38 Å (calculated from the (001) peak position). According to the documented doping level dependence of the OOP lattice constant [12, 15], the actual Sr concentration in our film is consistent with the nominal value determined in the growth process. We also employed the Scherrer equation (2) to estimate the thickness of the nickelate film in the infinite-layer phase [33, 47]:

${\text{d}}_{\text{Scherrer}}=\frac{k\lambda }{b\cos \theta }(2)$

where d_Scherrer is the Scherrer thickness; K is the Scherrer constant, which is 1.091 in our case [33]; λ is the wavelength of X-ray which is 1.5418 Å; and θ and b are the Bragg angle and the full width at half maximum intensity of the corresponding diffraction peak, respectively. The calculated Scherrer thickness (58.07 Å) basically matches with the situation where the precursor perovskite has been fully converted into the infinite-layer structure (60.84 Å). Moreover, XRD patterns of the Nd_1-xSr_xNiO₃ film usually show a double-peak-like feature after capping with SrTiO₃ layers, which is reminiscent of the stacking faults in previous reports [33, 48]. However, we measured the same sample before and after capping and found the peak only appearing in the latter (Figure 3B), implying that the peak at ∼48^o is more corresponding to the first-order thickness fringe of the SrTiO₃ capping layer, the intensity of which is enhanced by both the film and substrate.

Conclusion

In summary, optimization of the quality of nickelate films was investigated in this work using MBE. The crystalline lattice and topotactic reduction of nickelates are both susceptible to off-stoichiometry. Obvious lattice expansion caused by off-stoichiometry was observed in NdNiO₃ films, and the crystalline structure and transport properties are both influenced after subsequent topotactic reduction. Our finding is consistent with a previous report, where the (002) peak position over 48^o in the precursor phase nickelate is deemed as the requisite for superconductivity [33]. In addition, we introduced a new practical method using the OOP lattice constant to calibrate the Nd:Ni flux ratio in NdNiO₃ growth. Moreover, we found the repetitive appearance of some impurity phases in RHEED patterns for most of our Sr-doped samples, which appear to be unavoidable but do not seem to suppress the superconductivity.

Given the sensitivity of the structure of nickelate films to the variation of cation stoichiometry, any growth parameters that may affect the final stoichiometry in the films should be controlled carefully. For MBE, PLD, and many other growth techniques, lots of parameters have an impact on the stoichiometry, including beam flux ratio, chemical composition of targets, growth temperature, laser plume, laser fluence, and target ablation [34, 35, 49–53]. These growth parameters can be adjusted by referring to our findings about the stoichiometry dependence on the OOP lattice constant. Finally, although the superconductivity is not obviously affected by the impurity phases in Sr-doped nickelates, further investigation on their potential impacts on the electronic and magnetic structure is demanded.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

YN conceived the project. YL, WS, and WG grew the nickelate films. YL, WS, WG, and JY conducted the materials and structural characterization. XC and YZ conducted the STEM measurements. JY, YL, and WS conducted the reduction experiments. YL and WS performed the transport measurements. YL and YN prepared the manuscript with contribution from all authors. YL acknowledges discussions with JW and HS.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11774153, 11861161004, and 51772143), the Fundamental Research Funds for the Central Universities (Grant Nos. 0213-14380198 and 0213-14380167), the Research Grants Council of Hong Kong (N_PolyU531/18), and the Hong Kong Polytechnic University grant (No. ZVRP).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chen CH, Cheong S-W, Cooper AS. Charge Modulations in La_2−xSr_xNiO_4+y: Ordering of Polarons. Phys Rev Lett (1993) 71(15):2461–4. doi:10.1103/PhysRevLett.71.2461

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Anisimov VI, Bukhvalov D, Rice TM. Electronic Structure of Possible Nickelate Analogs to the Cuprates. Phys Rev B (1999) 59(12):7901–6. doi:10.1103/PhysRevB.59.7901

CrossRef Full Text | Google Scholar

3. Lee K-W, Pickett WE. Infinite-layer LaNiO₂: Ni¹⁺ is not Cu²⁺. Phys Rev B (2004) 70(16). doi:10.1103/PhysRevB.70.165109

CrossRef Full Text | Google Scholar

4. Chaloupka J, Khaliullin G. Orbital Order and Possible Superconductivity in LaNiO₃/LaMO₃ Superlattices. Phys Rev Lett (2008) 100(1):016404. doi:10.1103/PhysRevLett.100.016404

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Hansmann P, Yang X, Toschi A, Khaliullin G, Andersen OK, Held K. Turning a Nickelate Fermi Surface into a Cupratelike One through Heterostructuring. Phys Rev Lett (2009) 103(1):016401. doi:10.1103/PhysRevLett.103.016401

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Poltavets VV, Lokshin KA, Nevidomskyy AH, Croft M, Tyson TA, Hadermann J, et al. Bulk Magnetic Order in a Two-Dimensional Ni¹⁺/Ni²⁺(d⁹/d⁸) Nickelate, Isoelectronic with Superconducting Cuprates. Phys Rev Lett (2010) 104(20):206403. doi:10.1103/PhysRevLett.104.206403

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Han MJ, Wang X, Marianetti CA, Millis AJ. Dynamical Mean-Field Theory of Nickelate Superlattices. Phys Rev Lett (2011) 107(20):206804. doi:10.1103/PhysRevLett.107.206804

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhang J, Botana AS, Freeland JW, Phelan D, Zheng H, Pardo V, et al. Large Orbital Polarization in a Metallic Square-Planar Nickelate. Nat Phys (2017) 13(9):864–9. doi:10.1038/Nphys4149

CrossRef Full Text | Google Scholar

9. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572(7771):624–7. doi:10.1038/s41586-019-1496-5

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hepting M, Li D, Jia CJ, Lu H, Paris E, Tseng Y, et al. Electronic Structure of the Parent Compound of Superconducting Infinite-Layer Nickelates. Nat Mater (2020) 19(4):381–5. doi:10.1038/s41563-019-0585-z

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Rossi M, Lu H, Nag A, Li D, Osada M, Lee K, et al. Orbital and Spin Character of Doped Carriers in Infinite-Layer Nickelates (2020). ArXiv [Preprint]Available at: https://arxiv.org/abs/2011.00595v1 (Accessed November 1, 2020).

Google Scholar

12. Zeng S, Tang CS, Yin X, Li C, Li M, Huang Z, et al. Phase Diagram and Superconducting Dome of Infinite-Layer Nd_1−xSr_xNiO₂ Thin Films. Phys Rev Lett (2020) 125(14):147003. doi:10.1103/PhysRevLett.125.147003

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Goodge BH, Li D, Lee K, Osada M, Wang BY, Sawatzky GA, et al. Doping Evolution of the Mott-Hubbard Landscape in Infinite-Layer Nickelates. Proc Natl Acad Sci U.S.A (2021) 118(2):e2007683118. doi:10.1073/pnas.2007683118

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang BY, Li D, Goodge BH, Lee K, Osada M, Harvey SP, et al. Isotropic Pauli-Limited Superconductivity in the Infinite-Layer Nickelate Nd_0.775Sr_0.225NiO₂. Nat Phys (2021) 17(4):473–7. doi:10.1038/s41567-020-01128-5

CrossRef Full Text | Google Scholar

15. Li D, Wang BY, Lee K, Harvey SP, Osada M, Goodge BH, et al. Superconducting Dome in Nd_1−xSr_xNiO₂ Infinite Layer Films. Phys Rev Lett (2020) 125(2):027001. doi:10.1103/PhysRevLett.125.027001

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Gu Q, Li Y, Wan S, Li H, Guo W, Yang H, et al. Single Particle Tunneling Spectrum of Superconducting Nd_1-xSr_xNiO₂ Thin Films. Nat Commun (2020) 11(1):6027. doi:10.1038/s41467-020-19908-1

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Nomura Y, Hirayama M, Tadano T, Yoshimoto Y, Nakamura K, Arita R. Formation of a Two-Dimensional Single-Component Correlated Electron System and Band Engineering in the Nickelate Superconductor NdNiO₂. Phys Rev B (2019) 100(20):100. doi:10.1103/PhysRevB.100.205138

CrossRef Full Text | Google Scholar

18. Jiang M, Berciu M, Sawatzky GA. Critical Nature of the Ni Spin State in Doped NdNiO₂. Phys Rev Lett (2020) 124(20):207004. doi:10.1103/PhysRevLett.124.207004

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Katukuri VM, Bogdanov NA, Weser O, van den Brink J, Alavi A. Electronic Correlations and Magnetic Interactions in Infinite-Layer NdNiO₂. Phys Rev B (2020) 102(24):102. doi:10.1103/PhysRevB.102.241112

CrossRef Full Text | Google Scholar

20. Leonov I, Skornyakov SL, Savrasov SY. Lifshitz Transition and Frustration of Magnetic Moments in Infinite-Layer NdNiO₂ upon Hole Doping. Phys Rev B (2020) 101(24):101. doi:10.1103/PhysRevB.101.241108

CrossRef Full Text | Google Scholar

21. Wu X, Di Sante D, Schwemmer T, Hanke W, Hwang HY, Raghu S, et al. Robust D_x2−y2 -wave Superconductivity of Infinite-Layer Nickelates. Phys Rev B (2020) 101(6):101. doi:10.1103/PhysRevB.101.060504

CrossRef Full Text | Google Scholar

22. Botana AS, Norman MR. Similarities and Differences between LaNiO₂ and CaCuO₂ and Implications for Superconductivity. Phys Rev X (2020) 10(1):10. doi:10.1103/PhysRevX.10.011024

CrossRef Full Text | Google Scholar

23. Zhang Y, Lin L-F, Hu W, Moreo A, Dong S, Dagotto E. Similarities and Differences between Nickelate and Cuprate Films Grown on a SrTiO₃ Substrate. Phys Rev B (2020) 102(19):102. doi:10.1103/PhysRevB.102.195117

CrossRef Full Text | Google Scholar

24. Sakakibara H, Usui H, Suzuki K, Kotani T, Aoki H, Kuroki K. Model Construction and a Possibility of Cupratelike Pairing in a New D₉ Nickelate Superconductor (Nd,Sr)NiO₂. Phys Rev Lett (2020) 125(7):077003. doi:10.1103/PhysRevLett.125.077003

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Been E, Lee W-S, Hwang HY, Cui Y, Zaanen J, Devereaux T, et al. Electronic Structure Trends across the Rare-Earth Series in Superconducting Infinite-Layer Nickelates. Phys Rev X (2021) 11(1):11. doi:10.1103/PhysRevX.11.011050

CrossRef Full Text | Google Scholar

26. Zhao D, Zhou YB, Fu Y, Wang L, Zhou XF, Cheng H, et al. Intrinsic Spin Susceptibility and Pseudogaplike Behavior in Infinite-Layer LaNiO₂. Phys Rev Lett (2021) 126(19):197001. doi:10.1103/PhysRevLett.126.197001

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wang B-X, Zheng H, Krivyakina E, Chmaissem O, Lopes PP, Lynn JW, et al. Synthesis and Characterization of Bulk Nd_1−xSr_xNiO₂ and Nd_1−xSr_xNiO₃. Phys Rev Mater (2020) 4(8):4. doi:10.1103/PhysRevMaterials.4.084409

CrossRef Full Text | Google Scholar

28. Li Q, He C, Si J, Zhu X, Zhang Y, Wen H-H. Absence of Superconductivity in Bulk Nd_1−xSr_xNiO₂. Commun Mater (2020) 1(1):1. doi:10.1038/s43246-020-0018-1

CrossRef Full Text | Google Scholar

29. Gao Q, Zhao Y, Zhou X, Zhu Z. Preparation of Superconducting Thin Film of Infinite-Layer Nickelate Nd_0.8Sr_0.2NiO₂. Chin Phys Lett (2021) 38(7):077401. doi:10.1088/0256-307X/38/7/077401

Google Scholar

30. Zhou X-R, Feng Z-X, Qin P-X, Yan H, Wang X-N, Nie P, et al. Negligible Oxygen Vacancies, Low Critical Current Density, Electric-Field Modulation, In-Plane Anisotropic and High-Field Transport of a Superconducting Nd_0.8Sr_0.2NiO₂/SrTiO₃ Heterostructure. Rare Met (2021) 40(10):2847–54. doi:10.1007/s12598-021-01768-3

CrossRef Full Text | Google Scholar

31. Osada M, Wang BY, Goodge BH, Harvey SP, Lee K, Li D, et al. Nickelate Superconductivity without Rare-Earth Magnetism: (La,Sr)NiO₂. (2021). Available at: https://arxiv.org/abs/2105.13494 (Accessed May 27, 2021).

Google Scholar

32. Zeng SW, Li CJ, Chow LE, Cao Y, Zhang ZT, Tang CS, et al. Superconductivity in Infinite-Layer Lanthanide Nickelates. (2021). Available at: https://arxiv.org/abs/2105.13492 (Accessed May 27, 2021). doi:10.21203/rs.3.rs-576278/v1

CrossRef Full Text | Google Scholar

33. Lee K, Goodge BH, Li D, Osada M, Wang BY, Cui Y, et al. Aspects of the Synthesis of Thin Film Superconducting Infinite-Layer Nickelates. APL Mater (2020) 8(4):041107. doi:10.1063/5.0005103

CrossRef Full Text | Google Scholar

34. Preziosi D, Sander A, Barthélémy A, Bibes M. Reproducibility and Off-Stoichiometry Issues in Nickelate Thin Films Grown by Pulsed Laser Deposition. AIP Adv (2017) 7(1):015210. doi:10.1063/1.4975307

CrossRef Full Text | Google Scholar

35. Breckenfeld E, Chen Z, Damodaran AR, Martin LW. Effects of Nonequilibrium Growth, Nonstoichiometry, and Film Orientation on the Metal-To-Insulator Transition in NdNiO₃ Thin Films. ACS Appl Mater Inter (2014) 6(24):22436–44. doi:10.1021/am506436s

CrossRef Full Text | Google Scholar

36. Kawasaki M, Takahashi K, Maeda T, Tsuchiya R, Shinohara M, Ishiyama O, et al. Atomic Control of the SrTiO₃ Crystal Surface. Science (1994) 266(5190):1540–2. doi:10.1126/science.266.5190.1540

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Britze K, Meyer-Ehmsen G. High Energy Electron Diffraction at Si(001) Surfaces. Surf Sci (1978) 77(1):131–41. doi:10.1016/0039-6028(78)90166-8

CrossRef Full Text | Google Scholar

38. Clarke S, Vvedensky DD. Origin of Reflection High-Energy Electron-Diffraction Intensity Oscillations during Molecular-Beam Epitaxy: A Computational Modeling Approach. Phys Rev Lett (1987) 58(21):2235–8. doi:10.1103/PhysRevLett.58.2235

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Brooks CM, Kourkoutis LF, Heeg T, Schubert J, Muller DA, Schlom DG. Growth of Homoepitaxial SrTiO₃ Thin Films by Molecular-Beam Epitaxy. Appl Phys Lett (2009) 94(16):162905. doi:10.1063/1.3117365

CrossRef Full Text | Google Scholar

40. Zhang TW, Mao ZW, Gu ZB, Nie YF, Pan XQ. An Efficient and Reliable Growth Method for Epitaxial Complex Oxide Films by Molecular Beam Epitaxy. Appl Phys Lett (2017) 111(1):011601. doi:10.1063/1.4990663

CrossRef Full Text | Google Scholar

41. Sun HY, Zhang CC, Song JM, Gu JH, Zhang TW, Zang YP, et al. Epitaxial Optimization of Atomically Smooth Sr₃Al₂O₆ for Freestanding Perovskite Films by Molecular Beam Epitaxy. Thin Solid Films (2020) 697:137815. doi:10.1016/j.tsf.2020.137815

CrossRef Full Text | Google Scholar

42. Heo S, Oh C, Son J, Jang HM. Influence of Tensile-Strain-Induced Oxygen Deficiency on Metal-Insulator Transitions in NdNiO_3−δ Epitaxial Thin Films. Sci Rep (2017) 7(1):4681. doi:10.1038/s41598-017-04884-2

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Björck M, Andersson G. GenX: an Extensible X-ray Reflectivity Refinement Program Utilizing Differential Evolution. J Appl Cryst (2007) 40(6):1174–8. doi:10.1107/S0021889807045086

CrossRef Full Text | Google Scholar

44. Catalano S, Gibert M, Fowlie J, Íñiguez J, Triscone J-M, Kreisel J. Rare-earth nickelates RNiO₃: Thin Films and Heterostructures. Rep Prog Phys (2018) 81(4):046501. doi:10.1088/1361-6633/aaa37a

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Schöffmann P, Pütter S, Schubert J, Zander W, Barthel J, Zakalek P, et al. Tuning the Co/Sr Stoichiometry of SrCoO_2.5 Thin Films by RHEED Assisted MBEgrowth. Mater Res Express (2020) 7(11):116404. doi:10.1088/2053-1591/abc58b

CrossRef Full Text | Google Scholar

46. Paik H, Chen Z, Lochocki E, Seidner H. A, Verma A, Tanen N, et al. Adsorption-controlled Growth of La-Doped BaSnO₃ by Molecular-Beam Epitaxy. APL Mater (2017) 5(11):116107. doi:10.1063/1.5001839

CrossRef Full Text | Google Scholar

47. Klug JHP, Alexander LE: X-ray Diffraction Procedures for Polycrystalline and Amorphous Materials In: Ben Post, editors Berichte der Bunsengesellschaft für physikalische Chem. New York-Sydney-Toronto: John Wiley & Sons (1975). 79(6):553 1974, 966 Seiten, Preis: £ 18.55. doi:10.1002/bbpc.19750790622

CrossRef Full Text | Google Scholar

48. Zeng SW, Yin XM, Li CJ, Tang CS, Han K, Huang Z, et al. Observation of Perfect Diamagnetism and Interfacial Effect on the Electronic Structures in Nd_0.8Sr_0.2NiO₂ Superconducting Infinite Layers (2021). ArXiv [Preprint]Available at: https://arxiv.org/abs/2104.14195 (Accessed April 29, 2021).

Google Scholar

49. Seo SSA, Nichols J, Hwang J, Terzic J, Gruenewald JH, Souri M, et al. Selective Growth of Epitaxial Sr₂IrO₄ by Controlling Plume Dimensions in Pulsed Laser Deposition. Appl Phys Lett (2016) 109(20):201901. doi:10.1063/1.4967450

CrossRef Full Text | Google Scholar

50. Kobayashi K, Kamata N, Fujimoto I, Okada M, Suzuki T. Effect of Growth Conditions on Stoichiometry in MBE-Grown GaAs. J Vac Sci Technol B (1985) 3(2):753–5. doi:10.1116/1.583135

CrossRef Full Text | Google Scholar

51. Schiller S, Beister G, Sieber W. Reactive High Rate D.C. Sputtering: Deposition Rate, Stoichiometry and Features of TiO_x and TiN_x Films with Respect to the Target Mode. Thin Solid Films (1984) 111(3):259–68. doi:10.1016/0040-6090(84)90147-0

CrossRef Full Text | Google Scholar

52. Selinder TI, Larsson G, Helmersson U, Olsson P, Sundgren JE, Rudner S. Target Presputtering Effects on Stoichiometry and Deposition Rate of Y‐Ba‐Cu‐O Thin Films Grown by Dc Magnetron Sputtering. Appl Phys Lett (1988) 52(22):1907–9. doi:10.1063/1.99740

CrossRef Full Text | Google Scholar

53. Nilsen O, Lie M, Fjellvåg HF, Kjekshus A. Rare Earth Oxide Thin FilmsGrowth of Oxides with Complex Stoichiometry by the ALD Technique, Exemplified by Growth of La_1–xCa_xMnO₃. Rare Earth Oxide Thin Films. In: M Fanciulli, and G Scarel, Editors.Topics in Applied Physics. Berlin, Heidelberg): Springer Berlin Heidelberg (2006). p. 87–100.