
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 20 August 2021
Sec. Interdisciplinary Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.715791
Flows with chemical reactions in porous media are fundamental phenomena encountered in many natural, industrial, and scientific areas. For such flows, most existing studies use continuum assumptions and focus on volume-averaged properties on macroscopic scales. Considering the complex porous structures and fluid–solid interactions in realistic situations, this study develops a sophisticated lattice Boltzmann (LB) model for simulating reactive flows in porous media on the pore scale. In the present model, separate LB equations are built for multicomponent flows and chemical species evolutions, source terms are derived for heat and mass transfer, boundary schemes are formulated for surface reaction, and correction terms are introduced for temperature-dependent density. Thus, the present LB model offers a capability to capture pore-scale information of compressible/incompressible fluid motions, homogeneous reaction between miscible fluids, and heterogeneous reaction at the fluid–solid interface in porous media. Different scenarios of density fingering with homogeneous reaction are investigated, with effects of viscosity contrast being clarified. Furthermore, by introducing thermal flows, the solid coke combustion is modeled in porous media. During coke combustion, fluid viscosity is affected by heat and mass transfer, which results in unstable combustion fronts.
Flows of miscible fluids in porous media are frequently encountered in natural and industrial processes, like underground water movement [1], geologic carbon sequestration [2], enhanced oil recovery [3], and blood transport [4]. Dynamics of such flows are complex due to the unsteady flow, heat and mass transfer, and porous structure involved [5]. This situation becomes more complicated when chemical reactions are introduced.
In a porous medium, two fluids containing chemical solutes are put into contact along an interface. Chemical solutes are transported through the interface to react and thereby modify fluid properties, like density and viscosity. Meanwhile, if density or viscosity gradients exist across the interface, density or viscosity fingering may develop during the fluid transport [6]. Thus, interplay between interface instability and chemical reaction ensues. Such phenomena have been studied, for example, in systems containing ester-alkaline or CO2-alkaline miscible solutions. Experiments were carried out to show that changes in chemical solutes modified the reaction type and intensity, leading to either enhanced or suppressed density fingering [7–10]. In parallel, theoretical analyses were conducted to predict viscous or density fingering scenarios with the reaction A + B → C [11–13]. In a porous medium with a partially miscible interface between the two fluids, Loodts et al. [11] suggested that different density contributions and diffusion rates of the three chemical species (A, B, and C) could introduce eight types of density profiles. Trevelyan et al. [12] theoretically showed that such a problem with a miscible interface could yield up to sixty-two types of density profiles. Each profile potentially represented a unique type of density fingering. As for viscous fingering with the reaction A + B → C, a linear stability analysis predicted and classified various fingering scenarios in a parameter plane spanned by viscosity ratios [13]. Under the guidance of theoretical predictions, efforts have been devoted to numerical simulations of interface instabilities with chemical reactions in porous media. For instance, Loodts et al. [14] numerically showed that the reaction A + B → C could accelerate, inhibit, or introduce the development of density fingering. They further demonstrated that different species diffusion rates could introduce four fingering types [15]. Numerical simulations were also performed to model viscous fingering dynamics with the reaction A + B → C [16]. Results suggested that the reaction could introduce a non-monotonic viscosity profile and thereby trigger the development of fingering. These simulations provided spatial and temporal properties of interface instabilities with chemical reactions, thus enriching experimental and theoretical findings.
The above studies focused on porous media flows with a homogeneous reaction between miscible fluids. On the other hand, a heterogeneous reaction can take place between fluid and solid phases. Explicitly, such a type of reaction consumes chemical solutes from the fluid phase and solid matrices to yield dissolved (dissolution reaction) or solid (precipitation reaction) products, which subsequently modifies medium structures and flow motions [17]. Until now, porous media flows with heterogeneous reactions have been extensively investigated. For example, acid dissolution experiments showed that the dissolution reaction increased medium porosity behind the moving fluid interface and thereby triggered fingering phenomena (or infiltration instability) [6, 18]. Fredd and Fogler were among the first to experimentally identify different fingering channels under various flow and dissolution rates [19]. The fingering phenomena induced by the dissolution reaction were observed to be destabilized by medium heterogeneity and brine pH [20]. In parallel, experiments on porous media flows with precipitation reactions showed that the reaction could generate a locally adverse mobility gradient to cause the onset of fingering [21]. The interplay between viscous fingering and precipitation reaction was experimentally studied, with the influencing factors and fingering shapes being clarified [22]. In the meantime, numerical simulations of porous media flows with heterogeneous reactions were conducted. For instance, fingering dynamics induced by dissolution reactions were tracked and compared on different simulation length scales [23]. Continuum models were built to describe fingering properties and classify different fingering regimes under the effects of chemical dissolution [24, 25]. In the presence of precipitation reactions, viscous fingering was modeled and found to be intensified [26, 27]. In some applications, like in situ combustion for heavy oil recovery, the combustion between hot air and solid fuels, as a typical form of heterogeneous reaction, releases heat to change fluid properties [28]. Thus, thermal flows were included in numerical studies on porous media flows with heterogeneous reaction. Field-scale modeling of solid coke combustion suggested the important role of heat conduction in stabilizing the combustion front [29] and identified key factors influencing the coke combustion rate and the front sweep efficiency [30, 31].
Overall, for porous media flows with chemical reactions, existing works focus on using empirical correlations and volume-averaged techniques to determine effective flow and reaction properties on microscopic scales. However, pore-scale information is necessary to provide further understanding of the microscopic phenomena involved [32]. In the past 3 decades, the lattice Boltzmann (LB) method has been developed and has become a powerful solver for porous media flows on the pore scale. This is attributed to its attractive advantages, like its general kinetic foundation, high parallelism, and ability to handle multiphysics and complex boundaries [33, 34]. Recently, LB models have been proposed to simulate flows of reactive fluids in porous media, like methane hydrate dissolution [35], solid coke combustion [32], and reactive mixing with viscous fingering [36]. Although these works showed the superior ability of the LB method in modeling porous media flows, some limitations should be noted. For example, changes in fluid density or viscosity with temperature are usually not accounted for, models for multicomponent reactions (like A + B → C) are underdeveloped, and iterative boundary schemes for conjugate heat transfer are complex and time-consuming. We have developed a series of LB models to overcome these shortcomings separately [37–40]. Nevertheless, a uniform LB model is still needed. This work thus proposes an LB model to simulate pore-scale reactive flows in porous media, with homogeneous and heterogeneous reactions and compressible and incompressible fluid densities being considered.
In a porous medium with porosity ϕ, a fluid 2 of solute B initially fills the pore spaces between solid matrices. Another fluid 1 of solute A is put into contact with fluid 2 along an interface. The two fluids are assumed to be miscible and have their own species concentration, viscosity, temperature, and density, which are noted by subscripts 1 and 2, respectively. As an example, a schematic of the fluid distribution with a vertical interface is shown in Figure 1. Once fluid transport starts, the two solutes A and B come into contact and react in the mixing zone as follows:
The reaction product C is in the dissolved form, Q is the reaction heat, and the reaction rate of this homogeneous reaction is Ro. Meanwhile, the nonreactive solid matrices can be coated with a reactive solid Bs to react with A as follows:
The product P is in either the dissolved or the solid form, representing the dissolution or the precipitation reaction, respectively. It should be noted that fluid 2 does not contain solute A, and thus, this heterogeneous reaction only takes place at the interface I between fluid 1 and solid Bs. With this heterogeneous reaction, solid Bs is dissolved gradually, and the update of the porous structure is tracked as follows [41]:
where VB and VBm are the volume and the molar volume of solid Bs, respectively, and SB is the reactive surface area. The reaction rate of this heterogeneous reaction is noted as Re.
The above homogeneous and heterogeneous reactions usually cause variations in fluid properties (like concentration, temperature, density, and viscosity) and medium structures, which subsequently alter flow motions in porous media. We seek to study the fluid transport properties of such a system, focusing on effects of chemical reactions. Evolutions of fluid flow and species concentrations in pore spaces are described by the following conservation equations:
where
Here T, cp, α, and ρ are the local temperature, specific heat at constant pressure, thermal diffusivity, and density, respectively. In addition, at the interface I between solute A and solid Bs, the heterogeneous reaction Eq. 2 is described as follows [32, 41]:
where n is the interface normal pointing to the fluid phase, + and − denote parameters on either side of I, k = αρcp is the local thermal conductivity, q is the reaction heat flux, and ar is the stoichiometric coefficient of species r.
By introducing the characteristic length L, velocity U, temperature Tch, concentration Cch, and density ρch, dimensionless parameters marked by asterisks are derived as follows:
Key characteristic numbers are as follows: the Reynolds number Re, the Peclet number Pe, the Prandtl number Pr, and the Schmidt number Sc.
It is emphasized that the above equations consider homogeneous and heterogeneous reactions via the source term Sr and boundary conditions Eqs. 8–10, respectively. Evolutions of chemical species are described using Eq. 6 separately, thus allowing for homogeneous reactions between multiple solutes. Furthermore, both compressible and incompressible fluid flows can be taken into account, by setting the fluid density as a constant and a variable, respectively. On one hand, for compressible flows, the inclusion of heat transfer brings in the temperature-dependent fluid density. On the other hand, for incompressible flows, the thermophysical properties in Eq. 7 are fixed as constants in the fluid phase ϑl = ϑ0 (ϑ = cp, α, ρ), which can be different from those in the solid phase, namely, ϑs ≠ ϑl.
An LB model is now developed to solve the above governing equations for porous media flows with chemical reactions. For pore-scale simulations, the multiple-relaxation-time (MRT) scheme was shown to be able to correctly capture the no-slip velocity condition at the fluid–solid boundary and avoid the unphysical dependence of permeability on viscosity [42–44]. The MRT collision operator is thus employed in our model development. Considering that this work focuses on reactive fluid flows in two-dimensional (2D) porous media, the most popular two-dimensional nine-velocity (D2Q9) scheme is applied, with the discrete velocities ei and weight coefficients wi being as follows [34]:
Here, e = δx/δt is the lattice speed, with δx and δt denoting the lattice spacing and the time step, respectively. In this work, e is given as the velocity unit, that is, e = 1. The transformation matrix M corresponding to the D2Q9 scheme is as follows [34]:
This matrix maps the distribution functions from the physical space
Due to the temperature-dependent density and different thermophysical properties between the solid and fluid phases, Eqs. 6, 7 are rewritten as follows [45]:
Source terms in the derived species and energy conservation equations are as follows [39]:
More details about the derivation can be found in our recent work [39]. It should be noted that that for compressible fluids with fixed ρl = ρ0, the terms Fr2 and
An MRT LB model is developed to solve Eqs 4, 5, 15, 16 for describing reactive fluid flows in porous media. The LB evolution equations are as follows [34, 37, 46]:
for i, j = 0, 1, … , 8, where fi(x, t), gr,i(x, t), and hi(x, t) are distribution functions for the fluid density, mass fraction of species r, and local temperature, respectively. The corresponding equilibrium distribution functions
Here, ρp is a variable related to the fluid pressure as
with D and θ being the model dimension and the dimensionless temperature of a fluid mixture, respectively. The other correction term
In evolution Eqs. 18–20, S, Sr, and ST are diagonal relaxation matrices of the relaxation rates si, sr,i, and sT,i in the moment space, respectively. To avoid discrete lattice effects, distribution functions for the force and source terms are defined as follows [34, 36]:
Time derivative terms in Eqs 19, 20 are treated using the backward-difference scheme as follows [5]:
Based on the transformation equation (14), evolution equations (18–20) are implemented in the moment space as follows:
The equilibrium moments
and the corresponding moments for the force and source terms are as follows:
Finally, macroscopic variables are obtained from the distribution functions as follows:
Through the Chapman–Enskog analysis on the present LB equations, the governing equations can be recovered with the relaxation times τ, τr, and τT being as follows [46, 47]:
Furthermore, for compressible fluid flows, the constraints on the correction term in the moment space (
with
The other gradient terms in Eq. 17 are calculated using the isotropic central scheme as follows [48]:
Finally, the heterogeneous reaction at interface I between fluid 1 and solid Bs is modeled by resolving the interface conditions in Eqs. 8–10. On one hand, with the derived thermal source term FT, conjugate heat transfer conditions (Eq. 10) are realized by solving the energy Eq. 7. On the other hand, to solve Eqs 8, 9, the interface mass fraction gradient
where
where
Compared with recent LB models for porous media flows [32, 35], the present MRT LB model offers several advances. First, by introducing correction terms, both incompressible fluid flows with a fixed fluid density and compressible flows with a temperature-dependent one can be modeled. Second, separate LB equations with reactive source terms are developed to account for homogeneous reactions between multiple solutes, like A + B → C. Third, for heterogeneous reaction at the solid–fluid interface, additional source terms and the bounce-back scheme are built to realize the conjugate heat transfer and species conservation conditions, without iterative calculations. In addition, different from our recent LB models [37–40], the present one offers a capacity to achieve these advances simultaneously.
In the above section, a multicomponent MRT LB model has been presented for studying porous media flows with chemical reactions on the pore scale. Advances of this model over existing ones are introduced. This section conducts simulations of reactive fluid flows in porous media. The obtained results will show the ability of the present LB model in predicting hydrodynamic instabilities at the fluid interface, thermal flows in both pores and solid matrices, and effects of chemical reactions on fluid transport.
This section aims to investigate density fingering with the reaction A+ B → C between two miscible solutions 1 and 2 in porous media. As depicted in Figure 2, a 2D homogeneous structure is constructed, with the geometric parameters lx = 1, ly = 2/3, rx = 27δx, ry = 27δx, d = 12δx, lp = 15δx, and ϕ = 0.69 (in lattice units). Initially, the porous medium is saturated with a host fluid 2 of solute B. Another fluid 1 of solute A is placed upon the medium and in contact with fluid 2 along the top boundary (y = 0). The two solutions are assumed to be incompressible and isothermal. Then, across the partially miscible top boundary, A dissolves into fluid 2, and no mass transfers in the reverse direction. Dissolved A reacts with B to generate a solute C as in Eq. 1, with the reaction rate being as follows [14]:
Here, k is the kinetic reaction constant. All three chemical species contribute to fluid density and viscosity changes as follows [13, 14]:
where βr is the concentration expansion coefficient of species r.
Here, g is the acceleration vector of gravity. With such effects, different density stratifications develop, and density fingering may be triggered.
In this incompressible system, the thermal flow is not considered. Thus, fluid motion and species evolutions in pore spaces are described using Eqs 4–6. In addition, fluid density is fixed as ρl = ρ0, the reaction source term is defined as Sr = arRo, the heterogeneous reaction at the fluid–solid interface is not considered, and the three species are assumed to diffuse at the same rate Dr = D. For dimensionless parameters in Eq. 11, the characteristic length L, velocity U, concentration Cch, and density ρch are as follows:
The Rayleigh numbers Rar and the Damköhler number Da are defined as follows:
For such a problem, our recent works have studied fingering dynamics with effects of the reaction A + B → C and differential diffusion [37, 38]. Thus, in the following simulations, we introduce the impact of the three chemical species on fluid viscosity (Eq. 48) and seek to understand how the development of density fingering is affected. The Schmidt number and the Damköhler number are fixed as Sc = 100 and Da = 5, respectively, and different values of RaAB, RaCB, RA, and RC are selected to change test conditions. During LB simulations, the no-slip and no-flux bottom wall and matrix interface are realized using the halfway bounce-back scheme, periodic conditions are set at the two lateral boundaries, and the partially miscible top boundary is implemented using the non-equilibrium extrapolation scheme. The relaxation rates in this simulation case are set as follows: s0 = s3 = s5 = 0, s1 = 1.1, s2 = 1.2, s4 = s6 = (16τ − 8)/(8τ − 1), s7 = s8 = 1/τ, sr,0 = 1, sr,1 = sr,2 = 1.1, sr,3 = sr,4 = sr,5 = sr,6 = 1/τr, and sr,7 = sr,8 = 0.9. A mesh of Nx × Ny = 1,500 × 1,000 lattice size is used after grid convergence validations.
We focus on density fingering phenomena with fluid viscosity variations caused by chemical species. Simulations with RaAB = 1, RaCB = 1, RA = 0, and different values of RC are first performed. From our calculated results, different types of density fingering are identified, and fingering is found to be stabilized as C decreases the fluid viscosity (RC < 0). To illustrate such effects, the results of three cases with RC = −3, 0, 3 are provided and discussed. It should be noted that the three values of RC represent the three different scenarios where the reaction product C decreases, cannot change, or increases the fluid viscosity, respectively. For each of the three cases, Figure 3 depicts density distributions at six time instants, with the dimensionless density being calculated as ρ* = (ρ − ρ0)/(ρ0βBCB,0). From the constant-viscosity case (RC = 0) in Figures 3A,B, a classical density fingering development pattern is observed, that is, fluid diffusion, individual fingering growth, fingering merge, and new fingering reinitiation [37]. It should be noted that during the initial diffusion stage, dense fluid accumulates near the top boundary to overcome the viscous shear force blow. Fingering develops when the driving force introduced by the accumulated dense fluid is large enough.
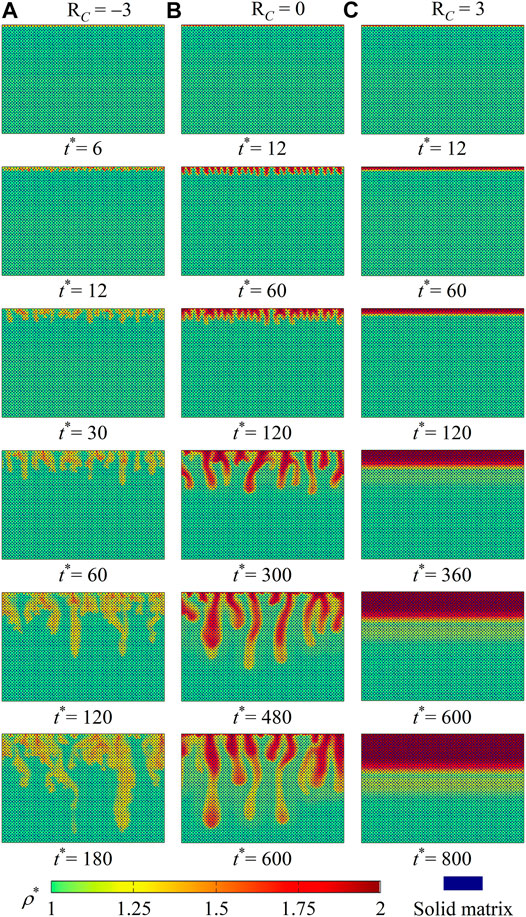
FIGURE 3. Density contours ρ* at six time instants for cases with RaAB = 1, RaCB = 1, and RA = 0 and (A) RC = −3, (B) RC = 0, and (C) RC = 3.
Compared with this constant-viscosity case, the introduction of viscosity variations in Figures 3A,C yields different density fingering dynamics. On one hand, when chemical product C decreases the fluid viscosity (Figure 3A with RC = −3), the classical fingering development pattern is observed. However, fingering starts earlier and grows faster than in the constant-viscosity case (Figure 3B). Such an accelerated fingering propagation finally leads to diluted fingers. On the other hand, in the case with solute C increasing the fluid viscosity (Figure 3C with RC = 3), even though the dissolution of A and the reaction A+ B → C can introduce a buoyantly unstable stratification, the fluid interface remains flat at each time instant, and no density fingering occurs.
In order to explain such influence of fluid viscosity variations, distributions of species concentrations (
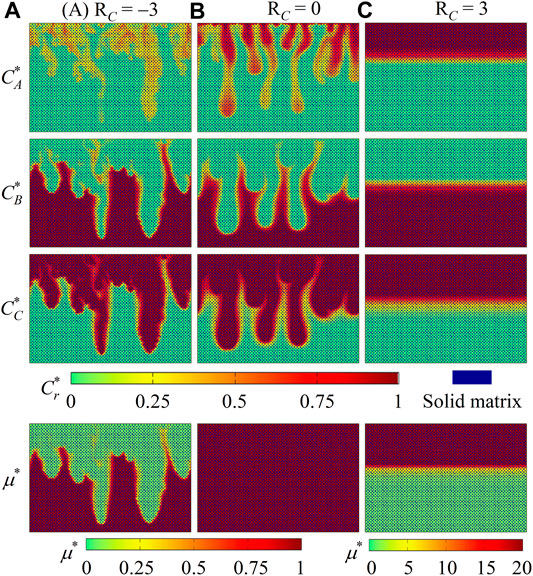
FIGURE 4. Contours of species concentrations
To quantitatively compare fingering dynamics in the three cases, Figure 5 plots temporal evolutions of the front position lm/ly, volume-averaged storage of A in the host fluid
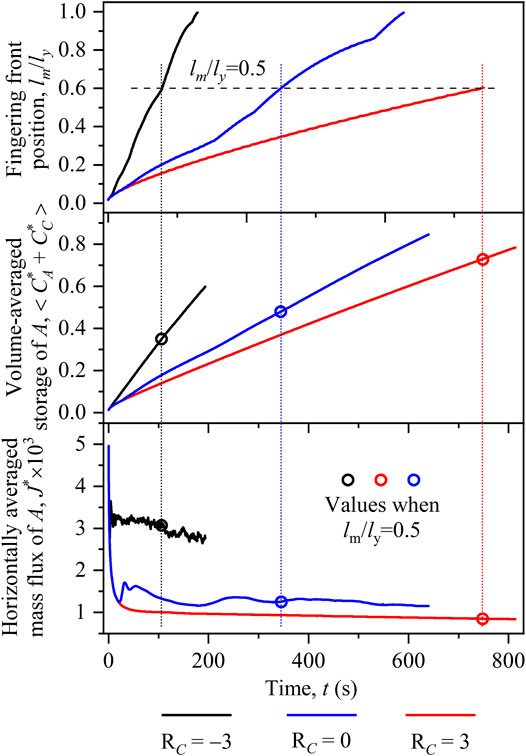
FIGURE 5. Temporal evolutions of (A) front position lm/lx, (B) volume-averaged storage of A in the host fluid
In general, when solute C decreases the fluid viscosity (RC < 0), density fingering is destabilized, and the destabilizing intensity ascends with descending RC. To further illustrate this impact, three cases with RaAB = 0.1 are conducted. Different from the above cases with RaAB = 1, the contribution to fluid density of A is smaller than that of B. Thus, in nonreactive cases, the unstable density contrast introduced by the dissolution of A from the top boundary is not large enough to bring in density fingering phenomena. As conducted in cases with RaAB = 1, Figures 6, 7 provide distributions of fluid density, species concentrations, and fluid viscosity. In the constant-viscosity case with RaCB = 1 and RC = 0 (Figures 6B, 7B), the uniform fluid viscosity distribution and the flat fluid interface are observed. This indicates that the reaction A + B → C, without viscosity variations, cannot trigger the onset of density fingering. On the contrary, once the unstable viscosity contrast (RC = −3) comes into play in the other two cases, density fingering appears and experiences the classical fingering development stages. First, in the case with RaCB = 1 and RC = −3 (Figures 6A, 7A), the density contrast remains the same as in the constant-viscosity case (Figures 6B, 7B), but fluid viscosity in the top layer drops down with the generation of C. As a result, viscous force decreases and fluid mobility increases in the top area, which makes dissolved A grow in a finger-like shape and thus induces the development of density fingering. Second, in the case with RaCB = 0.1 and RC = −3 (Figures 6C, 7C), a buoyantly stable density stratification develops with chemical reaction. Nevertheless, as illustrated in the zoom-in view, the fluid interface is distorted with time and finally becomes fingered. It is because the chemical product C decreases fluid viscosity in the top area and thus helps dissolved A develop into density fingering. These cases with a small density contrast suggest that decreased fluid viscosity with the chemical product C can destabilize or even trigger the development of density fingering.

FIGURE 6. Density contours ρ* at six time instants for cases with RaAB = 0.1 and RA = 0 and (A) RaCB = 1, RC = −3, (B) RaCB = 1, RC = 0, and (C) RaCB = 0.1, RC = −3.
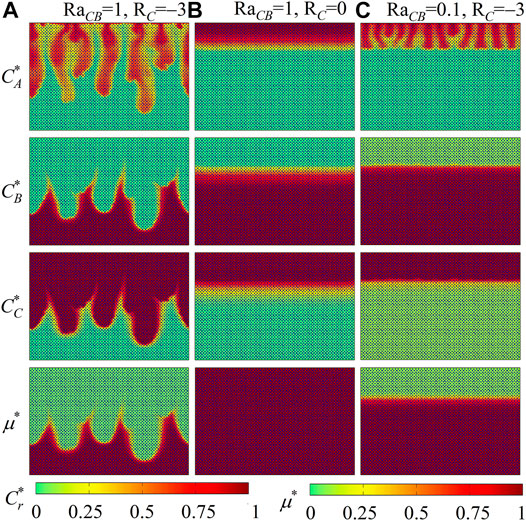
FIGURE 7. Contours of species concentrations
The developed LB model is then applied to explore the solid coke combustion dynamics in porous media, which is a typical heterogeneous reaction at the interface between hot air and coke. As displayed in Figure 8, a 2D homogeneous structure with porosity ϕ = 0.406 is considered. The geometric parameters are set as lx = 900 μm, ly = 760 μm, d = 18 μm, δ = 3 μm, rx = 42 μm, and ry = 33 μm, respectively. Initially, solid coke is homogeneously deposited on unreactive solid matrices, and the pore spaces are filled with hot nitrogen at the temperature T0 = 773 K. Then, hot air at the temperature T0 and with the oxygen (O2) mass fraction
where A, E, and R are the pre-exponential factor, the activation energy, and the ideal gas constant, respectively. As for boundary conditions, zero-gradient conditions are applied for all the scalars at the outlet, and the top and the bottom are periodic. The impact of reaction heat and mass transfer on fluid viscosity is considered as follows [51]:
Here,
For this case, fluid flow and species evolutions in pore spaces, as well as heat transfer in both pores and solid phases are described using Eqs 4–7. The reaction source term is set as Sr = 0 because homogeneous reaction is not involved. On the other hand, coke combustion is described using Eqs 8–10 and implemented using the bounce-back scheme in Eqs 44, 45. The conversion between physical and lattice units is based on dimensionless parameters in Eq. 11 and the characteristic parameters are selected as L = 0.5rx, U = αl/L, ρch = ρl,0, and Tch = 3,000 K [39]. In the subsequent simulations, the required parameters are set as A = 9.717 × 106 m/s, E = 131.09 kJ/mol, hr = 388.5 kJ/mol, ρscp,s/ρlcp,l = 368, and αs/αg = 0.119, respectively. The Reynolds, Prandtl, and Peclet numbers are fixed as Re = 1.4, Pr = 0.7, and Pe = 1.5, the driving force is
Our recent work has investigated the general coke combustion dynamics and evaluated the key influencing conditions, with the fluid viscosity being assumed to be a constant [39]. In practical applications, however, fluid viscosity varies with heat and mass transfer. Therefore, this work extends to studying the impact of viscosity variations on the combustion front stability. A base case with Ry = 0 and Rt = 0 is simulated at first. Figure 9 illustrates the distributions of residual coke, O2 mass fraction
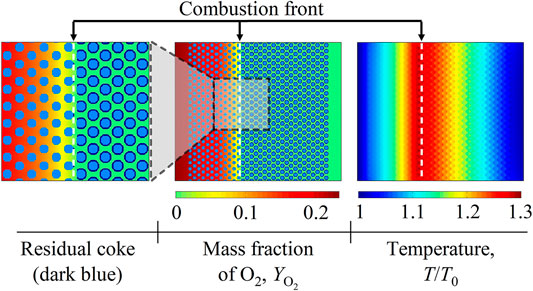
FIGURE 9. Contours of residual coke, the O2 mass fraction
The fluid viscosity remains uniform in the above base case. Thus, two cases with Ry = −4, Rt = 0 and Ry = −4, Rt = −3 are then considered. Other simulation parameters are set to be the same as in the base case, except for the Peclet number Pe = 10. Spatial distributions of residual coke, the O2 mass fraction
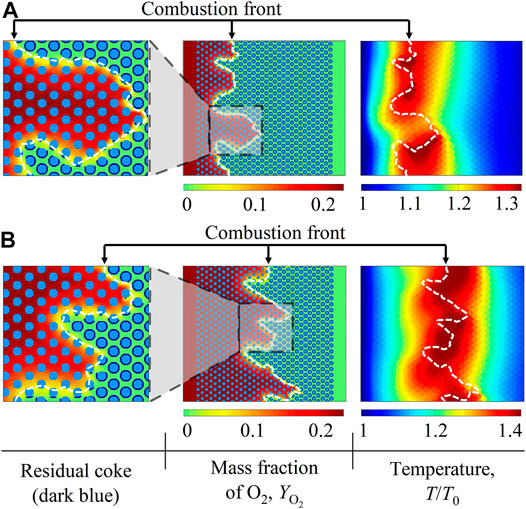
FIGURE 10. Contours of residual coke, the O2 mass fraction
In the case with Rt = −3, the fluid viscosity decreases with the increasing temperature. By comparing results in Figures 10A,B, such temperature-induced viscosity variations are found to influence coke combustion properties. On one hand, the fluid prorogation along the x direction is accelerated and more fingers at the combustion front are triggered. This destabilizing impact is attributed to the fact that combustion heat is released to increase the local temperature and decrease the fluid viscosity at the combustion front. Subsequently, the unstable viscosity contrast between fluids at the combustion front and on the downstream side is enlarged, which enhances viscous fingering phenomena. On the other hand, the combustion front temperature increases. It is explained by the fact that in the combustion front area, the high temperature induces the low fluid viscosity and the accelerated fluid flow velocity. Subsequently, the injected O2 can easily expand to react with coke and release heat, which leads to the increased combustion front temperature.
To further quantify differences between the two cases with viscosity variations, temporal evolutions of the volume-averaged temperature Tv/T0 and the residual coke ratio Vrc are calculated and illustrated in Figure 11. As can be seen, each line of Vrc decreases with time because coke burns out gradually, while every temperature curve shows an increasing pattern due to the released combustion heat. In addition, the inclusion of temperature-induced viscosity variations is found to bring in high burning temperature and fast coke consumption. It is due to the fact that the increased front temperature brings in the decreased fluid viscosity and, hence, the enhanced coke combustion intensity. This quantitatively verifies the above observations in Figure 10. It should be emphasized that these two cases feature finger-like combustion fronts. They are thus undesirable in practical applications because the downstream fluid cannot be efficiently displaced.
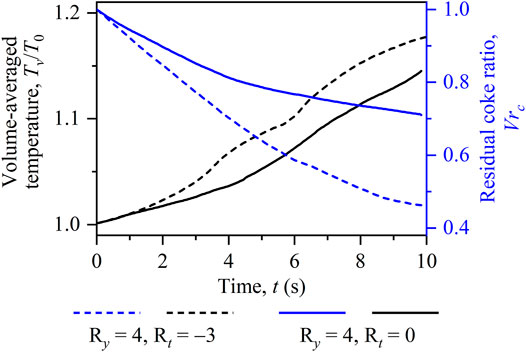
FIGURE 11. Temporal evolutions of the volume-averaged temperature Tv/T0 and the residual coke ratio Vrc for the two cases with Ry = 4, Rt = 0 and Ry = 4, Rt = −3.
Flows of reactive fluids in porous media have been studied on the pore scale. A multicomponent multiple-relaxation-time lattice Boltzmann (LB) model is developed to describe fluid motions and species evolutions in pore spaces, as well as heat transfer in both void pores and the solid phase. In the present model, separate LB equations are built to describe fluids and species evolutions during homogeneous reaction between miscible fluids; source terms and boundary schemes are derived to account for heterogeneous reaction at the fluid–solid interface; and additional correlation terms are introduced to model both incompressible and compressible (with temperature-dependent fluid density) fluid flows. Based on this model, two types of physical problems are simulated. One is density fingering with the homogeneous reaction A + B → C. Results show that depending on variations in the fluid viscosity caused by the chemical product C, the development of density fingering can be enhanced, suppressed, or even triggered. To further study effects of thermal flows, solid coke combustion in porous media is carried out. Simulation results successfully capture coke combustion dynamics and the evolution of the porous structure. Furthermore, the viscosity contrast caused by heat and mass transfer is found to change the coke combustion stability considerably. These two cases verify the capability of the proposed LB model in resolving flows of reactive fluids and the coupled viscosity and density instabilities on the pore scale. Extension to 3D porous media flows with chemical reaction is currently underway. The results are expected to clarify the differences and similarities between 2D and 3D simulations.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
TL has conducted the research while KL has supervised the project, with regular discussions with each other. Both authors have contributed to the writing of the manuscript.
This work was supported by the UK Engineering and Physical Sciences Research Council under grant nos. EP/R029598/1 and EP/S012559/1 and the China Scholarship Council (CSC) under grant no. 201706160161.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co‐authorship with one of the authors KL.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The PhD scholarship for TL from the UCL Mechanical Engineering Department is gratefully acknowledged.
1. Stevens JD, Sharp JM, Simmons CT, Fenstemaker TR. Evidence of Free Convection in Groundwater: Field-Based Measurements Beneath Wind-Tidal Flats. J Hydrol (2009) 375:394–409. doi:10.1016/j.jhydrol.2009.06.035
2. Cardoso SS, Andres JT. Geochemistry of Silicate-Rich Rocks Can Curtail Spreading of Carbon Dioxide in Subsurface Aquifers. Nat Commun (2014) 5:5743–6. doi:10.1038/ncomms6743
3. Rongy L, Haugen KB, Firoozabadi A. Mixing from Fickian Diffusion and Natural Convection in Binary Non-Equilibrium Fluid Phases. Aiche J (2012) 58:1336–45. doi:10.1002/aic.12685
4. Jiang XZ, Luo KH, Ventikos Y. Principal Mode of Syndecan-4 Mechanotransduction for the Endothelial Glycocalyx Is a Scissor-Like Dimer Motion. Acta Physiol (Oxf) (2020) 228:e13376. doi:10.1111/apha.13376
5. He Y-L, Liu Q, Li Q, Tao W-Q. Lattice Boltzmann Methods for Single-Phase and Solid-Liquid Phase-Change Heat Transfer in Porous Media: A Review. Int J Heat Mass Transf (2019) 129:160–97. doi:10.1016/j.ijheatmasstransfer.2018.08.135
6. De Wit A. Chemo-Hydrodynamic Patterns and Instabilities. Annu Rev Fluid Mech (2020) 52:531–55. doi:10.1146/annurev-fluid-010719-060349
7. Budroni MA, Riolfo LA, Lemaigre L, Rossi F, Rustici M, De Wit A. Chemical Control of Hydrodynamic Instabilities in Partially Miscible Two-Layer Systems. J Phys Chem Lett (2014) 5:875–81. doi:10.1021/jz5000403
8. Thomas C, Loodts V, Rongy L, De Wit A. Convective Dissolution of CO 2 in Reactive Alkaline Solutions: Active Role of Spectator Ions. Int J Greenh Gas Control (2016) 53:230–42. doi:10.1016/j.ijggc.2016.07.034
9. Cherezov I, Cardoso SSS. Acceleration of Convective Dissolution by Chemical Reaction in a Hele-Shaw Cell. Phys Chem Chem Phys (2016) 18:23727–36. doi:10.1039/c6cp03327j
10. Wylock C, Rednikov A, Colinet P, Haut B. Experimental and Numerical Analysis of Buoyancy-Induced Instability During CO2 Absorption in NaHCO3-Na2CO3 Aqueous Solutions. Chem Eng Sci (2017) 157:232–46. doi:10.1016/j.ces.2016.04.061
11. Loodts V, Trevelyan PM, Rongy L, De Wit A. Density Profiles Around A+B→C Reaction-Diffusion Fronts in Partially Miscible Systems: A General Classification. Phys Rev E (2016) 94:043115. doi:10.1103/PhysRevE.94.043115
12. Trevelyan PM, Almarcha C, De Wit A. Buoyancy-Driven Instabilities Around Miscible A+B→C Reaction Fronts: a General Classification. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 91:023001. doi:10.1103/PhysRevE.91.023001
13. Hejazi SH, Trevelyan PMJ, Azaiez J, De Wit A. Viscous Fingering of a Miscible Reactive A + B → C Interface: a Linear Stability Analysis. J Fluid Mech (2010) 652:501–28. doi:10.1017/s0022112010000327
14. Loodts V, Knaepen B, Rongy L, De Wit A. Enhanced Steady-State Dissolution Flux in Reactive Convective Dissolution. Phys Chem Chem Phys (2017) 19:18565–79. doi:10.1039/c7cp01372h
15. Loodts V, Saghou H, Knaepen B, Rongy L, De Wit A. Differential Diffusivity Effects in Reactive Convective Dissolution. Fluids (2018) 3:83. doi:10.3390/fluids3040083
16. Nagatsu Y, De Wit A. Viscous Fingering of a Miscible Reactive A+B→C Interface for an Infinitely Fast Chemical Reaction: Nonlinear Simulations. Phys Fluids (2011) 23:043103. doi:10.1063/1.3567176
17. Szymczak P, Ladd AJC. Reactive-infiltration Instabilities in Rocks. Part 2. Dissolution of a Porous Matrix. J Fluid Mech (2014) 738:591–630. doi:10.1017/jfm.2013.586
18. Szymczak P, Ladd AJC. Reactive-infiltration Instabilities in Rocks. Fracture Dissolution. J Fluid Mech (2012) 702:239–64. doi:10.1017/jfm.2012.174
19. Fredd CN, Fogler HS. Influence of Transport and Reaction on Wormhole Formation in Porous Media. Aiche J (1998) 44:1933–49. doi:10.1002/aic.690440902
20. Menke HP, Bijeljic B, Blunt MJ. Dynamic Reservoir-Condition Microtomography of Reactive Transport in Complex Carbonates: Effect of Initial Pore Structure and Initial Brine Ph. Geochim Cosmochim Acta (2017) 204:267–85. doi:10.1016/j.gca.2017.01.053
21. Nagatsu Y, Ishii Y, Tada Y, De Wit A. Hydrodynamic Fingering Instability Induced by a Precipitation Reaction. Phys Rev Lett (2014) 113:024502. doi:10.1103/PhysRevLett.113.024502
22. Haudin F, De Wit A. Patterns Due to an Interplay Between Viscous and Precipitation-Driven Fingering. Phys Fluids (2015) 27:113101. doi:10.1063/1.4934669
23. Hao Y, Smith MM, Carroll SA. Multiscale Modeling of CO2-Induced Carbonate Dissolution: From Core to Meter Scale. Int J Greenh Gas Control (2019) 88:272–89. doi:10.1016/j.ijggc.2019.06.007
24. Golfier F, Zarcone C, Bazin B, Lenormand R, Lasseux D, Quintard M. On the Ability of a Darcy-Scale Model to Capture Wormhole Formation during the Dissolution of a Porous Medium. J Fluid Mech (2002) 457:213–54. doi:10.1017/s0022112002007735
25. Panga MKR, Ziauddin M, Balakotaiah V. Two-scale Continuum Model for Simulation of Wormholes in Carbonate Acidization. Aiche J (2005) 51:3231–48. doi:10.1002/aic.10574
26. Sabet N, Mohammadi M, Zirahi A, Zirrahi M, Hassanzadeh H, Abedi J. Numerical Modeling of Viscous Fingering During Miscible Displacement of Oil by a Paraffinic Solvent in the Presence of Asphaltene Precipitation and Deposition. Int J Heat Mass Transf (2020) 154:119688. doi:10.1016/j.ijheatmasstransfer.2020.119688
27. Sabet N, Hassanzadeh H, Abedi J. Dynamics of Viscous Fingering in Porous Mdia in the Presence of In Situ Formed Precipitates and Their Subsequent Deposition. Water Resour Res (2020) 56:e2019WR027042. doi:10.1029/2019wr027042
28. Guo K, Li H, Yu Z. In-Situ Heavy and Extra-Heavy Oil Recovery: A Review. Fuel (2016) 185:886–902. doi:10.1016/j.fuel.2016.08.047
29. Zhu ZY. Efficient Simulation of thermal Enhanced Oil Recovery Processes. Stanford, California, USA: Ph.D. thesis, Stanford University (2011).
30. Srinivasareddy D, Kumar GS. A Numerical Study on Phase Behavior Effects in Enhanced Oil Recovery by In Situ Combustion. Pet Sci Technology (2015) 33:353–62. doi:10.1080/10916466.2014.979999
31. Zheng H, Shi WP, Ding DL, Zhang CY. Numerical Simulation of In Situ Combustion of Oil Shale. Geofluids (2017) 2017. doi:10.1155/2017/3028974
32. Xu Q, Long W, Jiang H, Zan C, Huang J, Chen X, et al. Pore-Scale Modelling of the Coupled Thermal and Reactive Flow at the Combustion Front During Crude Oil In-Situ Combustion. Chem Eng J (2018) 350:776–90. doi:10.1016/j.cej.2018.04.114
33. Li Q, Luo KH, Kang QJ, He YL, Chen Q, Liu Q. Lattice Boltzmann Methods for Multiphase Flow and Phase-Change Heat Transfer. Prog Energ Combust Sci (2016) 52:62–105. doi:10.1016/j.pecs.2015.10.001
34. Guo Z, Shu C. Lattice Boltzmann Method and its Applications in Engineering. Singapore, Singapore: World Scientific Publisher (2013). Vol. 3, p. 25–8.
35. Zhang L, Zhang C, Zhang K, Zhang L, Yao J, Sun H, et al. Pore‐Scale Investigation of Methane Hydrate Dissociation Using the Lattice Boltzmann Method. Water Resour Res (2019) 55:8422–44. doi:10.1029/2019wr025195
36. Lei T, Meng X, Guo Z. Pore-scale Study on Reactive Mixing of Miscible Solutions With Viscous Fingering in Porous media. Comput Fluids (2017) 155:146–60. doi:10.1016/j.compfluid.2016.09.015
37. Lei T, Luo KH. Pore-Scale Study of Dissolution-Driven Density Instability With Reaction A + B → C in Porous media. Phys Rev Fluids (2019) 4:063907. doi:10.1103/physrevfluids.4.063907
38. Lei TM, Luo KH. Differential Diffusion Effects on Density-Driven Instability of Reactive Flows in Porous Media. Phys Rev Fluids (2020) 5:033903. doi:10.1103/physrevfluids.5.033903
39. Lei T, Wang Z, Luo KH. Study of Pore-Scale Coke Combustion in Porous Media Using Lattice Boltzmann Method. Combust Flame (2021) 225:104–19. doi:10.1016/j.combustflame.2020.10.036
40. Lei T, Luo KH. Pore-Scale Simulation of Miscible Viscous Fingering With Dissolution Reaction in Porous Media. Phys Fluids (2021) 33:034134. doi:10.1063/5.0045051
41. Kang Q, Chen L, Valocchi AJ, Viswanathan HS. Pore-Scale Study of Dissolution-Induced Changes in Permeability and Porosity of Porous media. J Hydrol (2014) 517:1049–55. doi:10.1016/j.jhydrol.2014.06.045
42. d’Humieres D. Multiple-Relaxation-Time Lattice Boltzmann Models in Three Dimensions. Philosophical Trans R Soc Lond Ser A: Math Phys Eng Sci (2002) 360:437–51. doi:10.1098/rsta.2001.0955
43. Guo Z, Zheng C. Analysis of Lattice Boltzmann Equation for Microscale Gas Flows: Relaxation Times, Boundary Conditions and the Knudsen Layer. Int J Comput Fluid Dyn (2008) 22:465–73. doi:10.1080/10618560802253100
44. Lallemand P, Luo L-S. Theory of the Lattice Boltzmann Method: Dispersion, Dissipation, Isotropy, Galilean Invariance, and Stability. Phys Rev E (2000) 61:6546–62. doi:10.1103/physreve.61.6546
45. Karani H, Huber C. Lattice Boltzmann Formulation for Conjugate Heat Transfer in Heterogeneous media. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 91:023304. doi:10.1103/PhysRevE.91.023304
46. Li Q, Luo KH, He YL, Gao YJ, Tao WQ. Coupling Lattice Boltzmann Model for Simulation of Thermal Flows on Standard Lattices. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85:016710. doi:10.1103/PhysRevE.85.016710
47. Feng Y, Tayyab M, Boivin P. A Lattice-Boltzmann Model for Low-Mach Reactive Flows. Combust Flame (2018) 196:249–54. doi:10.1016/j.combustflame.2018.06.027
48. Guo Z, Zheng C, Shi B. Force Imbalance in Lattice Boltzmann Equation for Two-phase Flows. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 83:036707. doi:10.1103/PhysRevE.83.036707
49. Zhang T, Shi B, Guo Z, Chai Z, Lu J. General Bounce-Back Scheme for Concentration Boundary Condition in the Lattice-Boltzmann Method. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85:016701. doi:10.1103/PhysRevE.85.016701
50. Mailybaev AA, Bruining J, Marchesin D. Analysis of In Situ Combustion of Oil With Pyrolysis and Vaporization. Combust Flame (2011) 158:1097–108. doi:10.1016/j.combustflame.2010.10.025
Keywords: lattice Boltzmann method, pore scale, porous media, chemical reaction, interface instability
Citation: Lei T and Luo KH (2021) Lattice Boltzmann Simulation of Multicomponent Porous Media Flows With Chemical Reaction. Front. Phys. 9:715791. doi: 10.3389/fphy.2021.715791
Received: 27 May 2021; Accepted: 29 July 2021;
Published: 20 August 2021.
Edited by:
Sauro Succi, Italian Institute of Technology (IIT), ItalyReviewed by:
Francisco Welington Lima, Federal University of Piauí, BrazilCopyright © 2021 Lei and Luo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kai H. Luo, ay5sdW9AdWNsLmFjLnVr
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.