Learning-Based Image Transport Through Disordered Optical Fibers With Transverse Anderson Localization

Fiber-optic imaging systems play a unique role in biomedical imaging and clinical practice due to their flexibilities of performing imaging deep into tissues and organs with minimized penetration damage. Their imaging performance is often limited by the waveguide mode properties of conventional optical fibers and the image reconstruction method, which restrains the enhancement of imaging quality, transport robustness, system size, and illumination compatibility. The emerging disordered Anderson localizing optical fibers circumvent these difficulties by their intriguing properties of the transverse Anderson localization of light, such as single-mode-like behavior, wavelength independence, and high mode density. To go beyond the performance limit of conventional system, there is a growing interest in integrating the disordered Anderson localizing optical fiber with deep learning algorithms. Novel imaging platforms based on this concept have been explored recently to make the best of Anderson localization fibers. Here, we review recent developments of Anderson localizing optical fibers and focus on the latest progress in deep-learning-based imaging applications using these fibers.

Introduction

The integration of optical fiber devices and imaging processing algorithms enables the fiber-optic imaging system (FOIS) to perform imaging deep into organs or tissues in a minimally invasive way, which is a formidable task for other imaging techniques, such as the conventional microscopy. The general layout (Figure 1A) of a FOIS consists of the following components: an optical fiber, a proximal-end illumination unit, a distal-end collection unit, and a data processing unit. Depending on the application and the optical fiber type used, the outer diameter and the optical fiber length can range from ∼125 to ∼1,000 µm and from a few centimeters to a few meters, respectively [1]. The miniature size, high flexibility, and long light delivery distance lay the foundation of FOIS’s uniqueness, opening new horizons and creating numerous opportunities for both basic biomedical research and clinical practices. In fundamental research, such as deep brain imaging, an FOIS can be easily implanted in freely moving animal skulls for long-term imaging studies [2–6]. For clinical practices, a handheld FOIS can go deep into human organs or tissues with minimized penetration damages, which significantly benefits clinical diagnostics and surgical procedures [7–9].

FIGURE 1

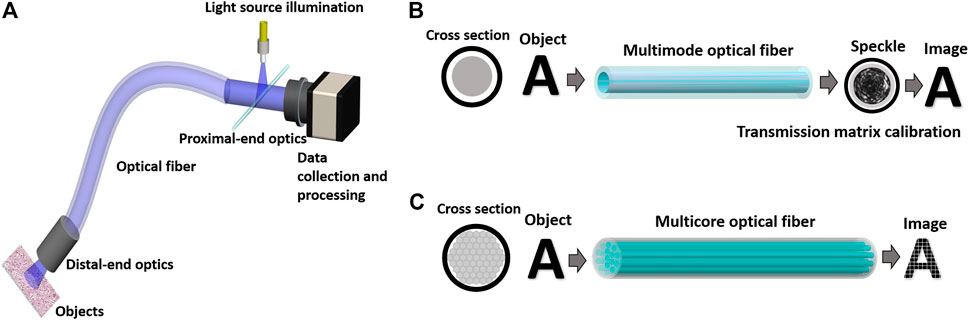
FIGURE 1. (A) General layout of a FOIS, (B) Schematic of image transport through a multimode optical fiber, (C) Schematic of image transport through a multicore optical fiber.

Different types of optical fibers have been explored to develop the FOIS utilizing various mechanisms of image transport and recovery [1, 4, 10–29]. Among FOIS solutions, multicore optical fibers (MCFs) and multimode optical fibers (MMFs) are two widely deployed fiber types. Several state-of-the-art systems using MMFs or MCFs have demonstrated excellent imaging performance and made tremendous progress in different application scenarios [3–6, 11, 23, 25, 26, 29–31]. Despite these conventional optical fibers’ success, some challenges remain, hindering further enhancement of FOIS imaging capabilities. The main issues are the high sensitivity to environmental perturbations, low imaging quality and speed, complex and expensive systems, and poor compatibility with incoherent spectrally broad illumination. These challenges originate from restrictions related to both the optical fiber device and the image reconstruction technique. For MMFs, its single large core supports thousands of orthogonal modes. The imaging information is encoded in the multimode interference speckle patterns (Figure 1B). Benefiting from its small diameter (∼200 µm), MMF-based FOISs are reported to be the least invasive endoscopic imaging method, especially for deep brain imaging [3]. Unfortunately, the multimode interference of MMFs is extremely sensitive to any tiny variations, such as mechanical bending or thermal perturbations, that effects the fiber refractive index distribution [4, 12]. Some attempts have been made to tackle this difficulty, such as an insightful complex theoretical framework and the application of graded-index MMFs [11, 12, 32–34]. Nevertheless, this issue is far from truly resolved. For most demonstrated biomedical imaging applications, the MMF still has to be kept stringently in its shape and the length is limited to a few centimeters, which severely limits the implementation of MMF-based FOIS in many scenarios [3–6, 33]. While faced with robustness issues, powerful techniques have been developed to unscramble imaging information embedded in the speckle patterns recorded with MMF-based FOISs [11, 12, 32, 35]. As indicated in Figure 1B, the wave propagation behavior through the MMF is calibrated by measuring the transmission matrix (TM) with interferometry and a wavefront shaping device, such as a spatial light modulator (SLM) or a digital micromirror device (DMD) [3, 35]. The TM method has been successfully demonstrated in practical biomedical imaging [3, 4, 6]. Yet, due to the restrictions of the MMF multimode interference, the TM-based imaging process is also vulnerable to external perturbations. Minor thermal fluctuations (a few degrees Celsius) or tiny mechanical twisting (a few hundred micrometers) can change mode coupling and scramble the pre-calibrated TM [4]. In addition, the experimental realization and the imaging algorithm of the TM-based method require relatively complex and high-cost systems while being limited by imaging speed and illumination coherence [17, 35–37]. Meanwhile, the imaging quality is often impaired by evident artifacts, such as defective background and ghost images [3, 4].

MCFs have a much larger diameter than the MMFs, ranging from a few hundred micrometers up to 1 mm. MCFs are widely utilized imaging fibers and have been applied with great success in practical applications [1, 2, 13, 14, 20, 22, 23, 26, 30]. They consist of thousands of individual cores, which are often referred to as “coherent fiber bundles” [1]. Each core in MCFs can work as a pixel to sample and transport the intensity image (Figure 1C). Although the image sampling is straightforward, the densely compacted core patterns featured in MCFs produce pixelated artifacts in transported images (Figure 1C) [14, 38–40]. The compact structure even further limits the imaging robustness, imaging quality, and illumination choice. For example, the coherent core-to-core coupling is sensitive to wavelength tuning and perturbations [15–17, 38, 39, 41]. Severely blurred images are obtained away from the optimal wavelength or under fiber deformations. Especially for techniques using a wavefront-shaping method to mitigate pixelated artifacts, the strong core-to-core coupling in MCFs makes the imaging rather intolerant to perturbations. To mitigate the influence of the core-to-core coupling, MCF-based FOISs resort to narrowband illumination and deploy a low mode density design. Besides the cross-talk issue, conventional MCF-based FOISs usually require bulky and complex distal optics or mechanical actuators, which limit the extent of miniaturization and can induce severe penetration damage [10, 13].

The physical properties of the optical fiber fundamentally restrain the system performance, whereas the image reconstruction algorithm deployed in the FOIS is equally important to 1) recover the object from raw data and 2) simplify the hardware realization. In practice, the raw imaging data from the proximal end of the optical fiber are not readily interpretable; they are either speckle patterns or feature severe artifacts. The imaging information is most likely hidden or incomplete with these sparse and noisy patterns. To reconstruct the object from the raw fiber-delivered data is an ill-posed inverse imaging problem that lacks a unique solution or is unstable with raw data. There are different approaches to obtain the estimation of the object. The process of transforming the object into the raw image through the imaging system can be modeled by a forward operator. Based on the forward model as well as prior knowledge about the objects, most conventional methods tackle this issue through solving the regularized optimization problem by carefully designed regularizers and minimization algorithms. Such model-based methods have been widely implemented and achieved great success. Yet, some difficulties remain to be overcome 1): significant artifacts arise with more noisy or low-quality raw imaging data 2): the handcrafted model limits the universality and might be unavailable for some complex physical systems. On the other hand, the choice of the image reconstruction method also affects the complexity of the experimental system. For methods requiring wavefront shaping process, the configurations and workflow tend to be complicated and induce high costs.

Instead of relying on conventional optical fibers and algorithms, another avenue to go beyond the barrier would be exploring new waveguiding physics as well as resort to a learning-based approach to tackle the inverse imaging problem. Recently, the emerging transverse Anderson localizing optical fiber (ALOF) provided a lot of evidence that transversely random fiber structures can be utilized as astonishing robust and high-quality imaging carriers [42–45]. ALOFs can potentially supersede conventional optical fibers based on their counterintuitive but intriguing properties: highly multimode systems with single-mode-like behaviors and wavelength-independent point spread functions [46–49]. They enable imaging encoding through densely distributed localized fiber modes that are highly robust to perturbations. They can also transport images under broadband illumination without wavelength-dependent blurry problems suffered by the MCFs. The underlying physics originates from the transverse Anderson localization effects, which guarantees robust, broadband, and high-quality image transport [42, 43]. While the novel waveguiding physics can relieve the device restrictions, it still requires a well-designed imaging reconstruction algorithm to make the utmost of the fiber. Due to their outstanding performance on image classifications, segmentations, and reconstructions, deep-learning (DL) methods have motivated researchers to deploy these algorithms in the fiber optical imaging area [18, 19, 27, 50–54]. DL-based research in optics and photonics is fast-growing. It has gained great success in various applications, and proved to outperform conventional model-based algorithms in many imaging problems [55, 56]. In particular, DL methods can be well adapted for the inverse problem of the FOISs. One important reason is that accurate physics modeling of the complex wave propagations through special optical fibers is often a formidable task. For example, due to the absence of analytical solutions, numerical simulations require substantial computational resources even for simplified wave propagation within a ALOF [57]. On the other hand, DL-based solutions boosted by big data stand for a universal approach without the need for a handcrafting forward model [58–60]. They are able to directly “learn” the underlying physics of a complex waveguiding system merely relying on a set of training data without any prior knowledge [19]. Boosted by the new-generation graphics processing units (GPUs), many DL-based tasks can be processed with a personal computer and reach milliseconds per frame imaging speed for a trained DL neural network. Unlike conventional solutions, DL-based methods directly utilize raw intensity images and claim no particular requirements on the coherence or polarization properties of the illumination. They can, therefore, bypass the constraints of complex and high-cost optical systems, such as interferometry and wavefront shaping devices, leading to cost-effective configurations with low complexity.

In this review, we focus on the learning-based ALOF imaging systems. Anderson localization related research is an active and extremely broad area. We mainly focus on the discoveries of ALOF that are related to imaging applications. We will present recent progress of the Anderson localization of light in waveguide-like structures in the first section. Following the discussion of ALOFs, we will give a brief introduction to the basics of the DL and convolutional neural network (CNN). Finally, we will give a summary of recent progress in imaging through integrating ALOF with CNNs. Due to the fiber-optic imaging oriented applications, the discussion of the algorithm will be limited to the deep convolutional neural network (DCNN).

Anderson Localizing Disordered Optical Fiber

Historical Review on the Origin of ALOF

We summarize the historical development of ALOFs in Figure 2. We mainly select those which made important impacts on the imaging applications of ALOFs. As shown in Figure 2, Anderson localization was first introduced by P.W. Anderson to describe electron’s motion in a highly disordered medium within the quantum mechanic’s framework [61]. In his seminal paper, disordered defects in the potential landscape cause multiple scattering of electron waves, resulting in spatially localized electronic states. Since it is a consequence of the wave nature, Anderson localization is broadly applicable to both quantum mechanical waves defined by the Schrödinger equation and classical wave systems, such as acoustics, elastics, electromagnetics, and optics [62–68]. Among various classical wave realizations, Anderson localization of light has attracted tremendous attention due to mature experimental tools to probe the localization phenomena and diverse possibilities to construct disordered “optical potentials” using disordered refractive index distributions [69–72]. Many efforts have been made to observe and apply Anderson localization of light in various systems [44–46, 73–82]. For Anderson localization of light to occur, the wave scattering must be strong enough so that the wavelength in the medium is comparable to the scattering mean free path, the so-called Ioffe-Regel criterion [83]. In 3D system, it remains quite challenging to satisfy this criterion. Even if large refractive index variations meet the needs for observing 3D localization of light, the optical system usually introduces considerable losses, making it difficult to differentiate Anderson localization-induced exponential decay from optical loss-induced exponential decay. But this restriction is considerably relieved in quasi-2D optical systems [84, 85]. One realization of such a system is a waveguide-like structure (Figure 3A₁) where the refractive index distribution is disordered in the transverse plane but uniform along the optical wave propagation direction [42, 84]. To require the optical waves to be localized in the 2D transverse plane, merely the wavevector’s transverse components need to be taken into consideration. The transverse component can be 10 to 100 times smaller than the full wavevector [85, 86]. Even if the mean free path is much larger than the wavelength, localization of light could still occur transversely in quasi-2D optical systems. As the simulation demonstrated in Figure 3A₂, by coupling a Gaussian beam into the disordered waveguide, the beam first goes through an initial expansion and eventually localizes to a stable state fluctuating around with a stable beam radius [42]. The above optical wave behavior in the quasi-2D system is often cited as transverse Anderson localization (TAL). The 2D TAL was proposed by Abdullaeav et al. and De Raedt et al. independently based on different mechanisms [84, 87]. Abdullaeav’s scheme is to impose the disorder on top of an existing ordered lattice with periodic potential. Without the imposed randomness, the wave behavior would be the Bloch-periodic solutions that extend over the whole lattice. By introducing sufficient disorder into effective index or coupling coefficients, the wave propagation would collapse into localized states in certain regions of the lattice. For De Raedt’s scheme, instead of introducing disorder to an existing lattice, a completely random underlying potential (e.g., 2D refractive index distribution in an optical fiber) is created. De Raedt proposed an optical-fiber-like waveguide structure as shown in Figure 3A₁. The pixels in the transverse plane have a randomly chosen refractive index of n₁ or n₂ with equal probabilities. The longitudinal refractive index distribution is uniform. The size of the pixel is assumed to be comparable to the wavelength. Based on intensive numerical simulations, De Raedt demonstrated that optical waves decay exponentially in the transverse plane and remain localized transversely with longitudinal beam propagation. Such TAL behavior is caused by multiple scattering in the transverse plane and similar to the simulation results shown in Figure 3A₂. Abdullaeav’s and De Raedt’s results were purely theoretical investigations. The first experimental observation of TAL of light was demonstrated by Segev’s team in 2007 [85]. Their optical system is based on a scheme similar to Abdullaeav’s proposition: disorder is imposed on an existing ordered triangular lattice of waveguides using photorefractive crystals. In this pioneering work, they use an intense laser to write a transversely disordered but longitudinally uniform refractive index distribution into the photorefractive crystal and probe the TAL of light with another laser beam. The photoinduced refractive index variation is on the order of 10⁻⁴. The small variations of the refractive index result in large localization beam radii with significant standard deviations among different realizations of the random refractive index profiles. In this case, the beam radius of TAL is meaningful in a statistically averaging sense. Yet, by introducing sufficiently large refractive index variations, the sample-to-sample variations of TAL beam radius can be significantly suppressed so that the localized beam radius of one realization can resemble the ensemble average [57, 86, 88–90]. This self-averaging behavior would guarantee similar localization lengths for different disordered refractive index profile realizations, highly desired for pushing TAL optical waveguides into practical applications. After Segev team’s pioneering work, many efforts have been made to explore TAL phenomena, which finally led to the development of ALOFs [91–94].

FIGURE 2

FIGURE 2. Historical overview of ALOF developments.

FIGURE 3

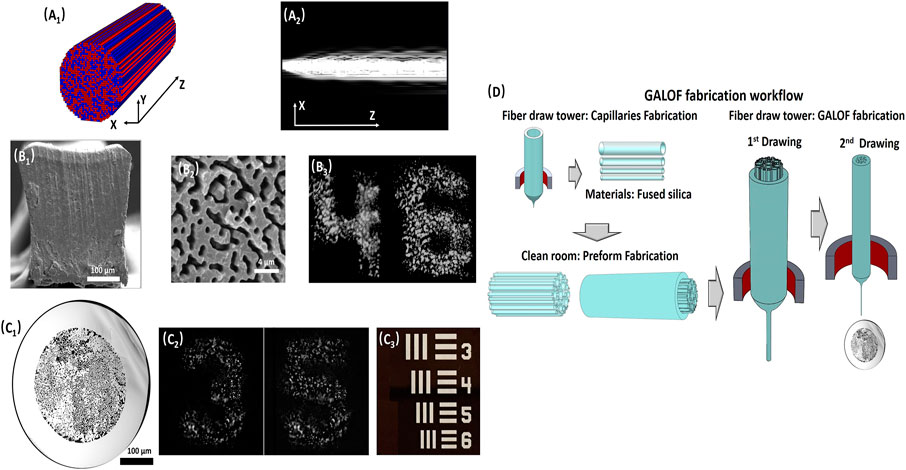
FIGURE 3. (A₁) Schematic of a quasi-2D disordered waveguide structure for observation of transverse Anderson localization; each pixel is randomly assigned by a refractive index of n₁ or n₂ (red or blue color) with equal probabilities. (A₂) Cross section of a Gaussian beam propagation process in the disordered waveguide. (B₁) SEM image of PALOF cross section. (B₂) SEM image of a zoomed-in area of the PALOF cross section. The sample is exposed to a solvent to differentiate between polymethyl methacrylate (PMMA) and polystyrene (PS) polymer. The darker regions are PMMA; the Material filling fraction is ∼50%; The feature size is ∼0.9 µm. (B₃) Transported images of numbers “4” and “6” through a 5-cm-long PALOF sample. The numbers are elements from group 3 in the 1951 USAF resolution test chart. (C₁) SEM image of GALOF cross section: white areas are fused silica and black areas are air holes; the material filling fraction is ∼28.5%; The feature size is ∼1.6 µm. (C₂) Transported images of numbers “3” and “5” through a 4.5-cm-long GALOF sample. The numbers are elements from group 3 in the 1951 USAF resolution test chart. (C₃) Elements in the 1951 USAF resolution test chart. (D) GALOF fabrication process. (A_1,A₂), (B₁,B₂), and (C₁–C₃) are adapted with permission from [42, 86], and [103] ^© The Optical Society, respectively. (B₃) is adapted with permission [98] ^© IEEE.

Design Parameters of ALOF Related to TAL Modes

Experimentally demonstrated ALOFs are waveguide-like binary disordered structures (similar to Figure 3A₁) and are in line with De Raedt proposed design. Depending on the optical fiber materials, there are mainly two types of ALOFs that were developed by different teams: 1) all-solid-state ALOFs, such as polymer ALOFs (PALOFs, Figure 3B₁) and tellurite glass ALOFs; 2) the glass-air ALOFs (GALOFs, Figure 3C₁) [79, 86, 95–100]. In the following discussions, we mainly take the PALOFs and GALOFs as examples. For device-level applications, one would expect that the beam’s localization radius is sufficiently stable based on self-averaging behavior. Otherwise, the transported beam radius could vary with the transverse location in the disordered structure unpredictably. Stable localized beam radii require a proper ALOF design with enhanced TAL. Previous studies in the ALOF design suggest the following most relevant transverse structure parameters: the transverse size of cross-section, the feature size (width of each refractive index pixel), the material filling fraction (ratio of low-index materials to the high-index host medium), and the refractive index contrast [42, 57, 90, 98]. First, the transverse size of the ALOF should be large enough so that the localized modes in the interior area would not be affected by boundary effects and are merely decided by the TAL mechanism. For example, the diameters of most recently reported ALOFs range from ∼125 to ∼400 µm. Second, the optimum feature size was speculated to be around half of the free-space wavelength for fiber materials with a refractive index around 1.5. The above design is just an educated guess, whereas the truly optimal feature size relative to the wavelength is still in dispute [98]. Recent observation of localization radius being independent of the wavelength within a rather wide spectral range has cast more shadows on the optimal feature size speculation [47, 48]. While this issue needs more investigation to provide more experimental evidence, our empirical observations based on GALOF fabrications and tests show that strong TAL requires a feature sizes on the order of the free-space wavelength [44]. Third, the optimal material filling fraction suggested by intense numerical simulation shows that 50% should be the ideal design [42, 57]. This parameter is from the observation that a higher material filling fraction results in a smaller localized beam radius. It should be noted that the above conclusions apply to refractive index contrasts below 0.5. For even larger refractive index contrasts, it is still an open question [98]. While a 50% material-filling fraction is relatively easier to achieve for PALOFs, a similar material-filling fraction is still quite challenging for GALOF fabrication. The reported highest material filling fraction of the GALOF is still below 30%. Finally, increasing the refractive index contrast between the two filling materials can generally enhance TAL and reduce the localized beam radius. Previous investigations have confirmed that an index difference of ∼0.5 for GALOF can considerably reduce the localized beam radius compared to the index difference of ∼0.1 for PALOF. Nevertheless, one should be cautious with the finding that the dependence of localization length’s reduction on index difference enhancement tends to saturate asymptotically [42]. Therefore, further reductions in localization length may be quite small by increasing index difference beyond the threshold value.

Besides the discussed design parameters, the optical losses of the fiber materials need to be taken into consideration for specific applications. For imaging applications, PALOF fibers suffer from huge signal attenuations in the visible band, limiting their image transportation distance to less than 20 cm [74]. In comparison, the fused silica based GALOFs have much smaller material losses, which is shown to support image transport distance, at least, to 1-m level [44]. Fused silica is also the mature and widely deployed optical fiber industrial-grade material, making it cost-effective and easy-to-implement. Based on the above roadmap of ALOF design, both PALOFs and GALOFs have demonstrated superior imaging capabilities. As shown in Figures 2B,C, they can directly transport high-quality intensity images from a resolution test chart. Different observations have further confirmed that the quality of the images transported by ALOFs are comparable to or even higher than some of the best commercially available coherent fiber bundles. As a special case of MCFs, the core-to-core coupling in fiber bundles degrades the point spread function with increasing transmission distance [101]. In order to suppress the cross talk between individual cores, the MCFs usually have to randomize the core size and control the core density, which results in low mode density. But low mode density brings in more severe pixelated artifacts. ALOFs resolve the contradiction by strongly coupling all the neighboring sites but preventing the cross talk through extreme randomness. Therefore, ALOFs feature about two orders higher mode densities than MCFs and can outperform them in terms of transmitted image quality. Especially, the point spread function of ALOFs is determined by the localization length that is independent of the transmission distance.

Fabrication Techniques of ALOF

Finally, the fabrication of ALOFs is also an important topic to explore. PALOF’s fabrication has been reported by Mafi’s team [99, 102]. To fabricate the PALOF, 40,000 polymethyl methacrylate (PMMA) strands are randomly mixed with 40,000 polystyrene (PS) strands first. Then the randomly mixed strands are assembled into a preform with a square cross section, the side length of which is ∼2.5 inches. The preform is further drawn into the final PALOF with a diameter of ∼250 µm. The optimal GALOF fabrication recipe is still under investigation. The first GALOF was reported by Karbasi et al. in 2012, which is drawn from “satin quartz” (Heraeus Quartz) at Clemson University [95, 99]. The “satin quartz” is a type of porous artisan glass. This type of GALOF has a diameter of 250 μm, which is drawn from a rod preform with a diameter of 8 mm. The average air-filling fraction is about ∼5%. The feature size of air holes varies from 0.2 to 5.5 µm. Chen and Li at Corning Inc. also reported their random air-line GALOFs that were fabricated using the outside vapor deposition process [96, 99]. They first create a silica soot blank by soot deposition in the laydown process. The silica soot is chlorine dried in a consolidation furnace, then further consolidated in the presence of 100% N₂. The N₂ was trapped in the blank to form glass with randomly distributed air bubbles. Finally, the preform with random air bubbles are drawn into fibers with random airlines. The air-filling fraction of the air-line GALOFs is lower than 2%. The air hole size is being around 0.2–0.4 µm. Being limited by the low air-filling fractions, these early reported GALOFs can only support TAL in some local areas of the transverse plane and are not suited for the image transport. In 2017, Zhao et al. developed GALOFs with ∼28.5% air-filling fraction using the well-established stack-and-draw fabrication technique [44, 79]. The feature sizes are around 1.6 µm. Due to the high air-filling fraction, TALs can be observed across the whole disordered area. A high-quality image transport process has been demonstrated through a meter-long GALOF sample [44]. The fabrication workflow of Zhao’s GALOF is shown in Figure 3D. In the preform fabrication phase, hundreds of silica capillary tubes are first drawn with various outer diameters (ODs) and inner diameters (IDs). The ODs of the capillaries vary from ∼100 to 180 µm. The ratio of ID to OD ranges from 0.5 to 0.8. These capillaries are cut into the same 1-m-long length and randomly mixed. Then they are assembled and fed into a silica jacket with an inner diameter of ∼15 mm to create the preform. In the fiber fabrication phase, the first step is to draw the preform into a cane with ∼3 mm OD. The second step is to draw the cane to the desired fiber size (OD: ∼400 μm, ID: ∼280 µm). During the fiber fabrication process, it is important to monitor the variations of the cross section with a bright-field microscope. The finished GALOF samples feature characteristic distributions of air-hole areas that typically range from 0.64 µm² to over 100 μm². Statistically, air holes with an area of 2.5 µm² cover the largest disordered area.

Wavelength Dependence and Wavefront Qualities of TAL in ALOF

ALOFs’ intriguing mode properties lay the foundation for developing robust FOIS with high imaging quality. Different types of ALOFs share similar properties regardless of the specific materials. Previous investigations focus more on PALOF-based platforms since PALOFs appeared earlier than GALOFs. The early investigations on ALOF’s beam multiplexing properties proved that multiple-beam propagations are feasible for PALOFs [42, 88]. The spatially multiplexed beams are also highly robust: the TAL beam propagation channels can withstand substantial bending, the degree of which goes beyond the limit of conventional optical fiber [88]. In later research, Giancarlo et al. discovered that the TAL transmission channels in the PALOF demonstrate a high degree of resilience to mechanical perturbations and variations of beam coupling positions, which are strong evidence of single-mode channels [46]. This explains the high stability of PALOF’s beam multiplexing against macro bending. The emerging GALOFs further confirm the ALOFs’ high robustness against strong mechanical fiber bending through image transport tests [18, 44]. As shown in Figure 4A, for the same meter-long GALOF sample, the transmitted pattern under a 180-degree mechanical bending is almost the same as the one delivered through the straight fiber [44]. Recent research also showed that a considerable number of transmission localized modes in GALOFs have low M² values (close to ∼1) based on both numerical simulations and experimental measurements (Figure 4B–D) [49]. Here, M² value is a widely used metric to evaluate laser beam quality, which is equal to one for an ideal diffraction-limited beam. More details regarding the calculations of M² values refer to Ref. [104]. A double-slit interference experiment in this research proves the high spatial coherence of these localized GALOF modes. The above observations demonstrate that the localized modes in GALOF exhibit nearly-diffraction-limited wavefront quality, making the localized transmission channels comparable to single-mode optical fibers. Significantly, these high-quality modes can be excited easily without any expensive and sophisticated devices, such as spatial light modulators. What further distinguishes the ALOFs from other imaging fibers is the wavelength independence of the localization lengths over a reasonably broad spectral range (∼1 µm bandwidth). Since the width of the point spread function of the ALOFs is determined by the localization lengths, the imaging capabilities of the ALOFs should not be degraded with broadband illumination. This phenomenon has been observed experimentally for both PALOFs and GALOFs by different research groups [47, 48]. Referring to Figure 4F, two different localized spots at the GALOF are picked up to investigate the dependence of localization length on wavelength tuning. It appears that the localization length fluctuates around a stable averaging value for wavelengths varying from 540 to 1,600 nm. With the same GALOF sample, the colorful light-emitting array from the smartphone screen pixels is coupled into the input facet of the GALOF sample. Due to the wavelength independence properties, after transmitting through 27 cm long fiber, the individual smartphone pixels are clearly visible and separable with different colors (Figure 4E). All above-mentioned unique properties guarantee the device foundations for robust high-quality colorful image transport through ALOFs, which breaks the bottlenecks imposed by the conventional MMFs or MCFs and opens more possibilities for fiber-optic imaging. We summarize some of the important imaging-related parameters of three different types of fiber (MMF, MCF and GALOF) in Table 1. Since the GALOF developed at CREOL is the first glass-air ALOF that supports high-quality long-distance imaging, in the following discussions, we mainly focus on this type of ALOF.

FIGURE 4

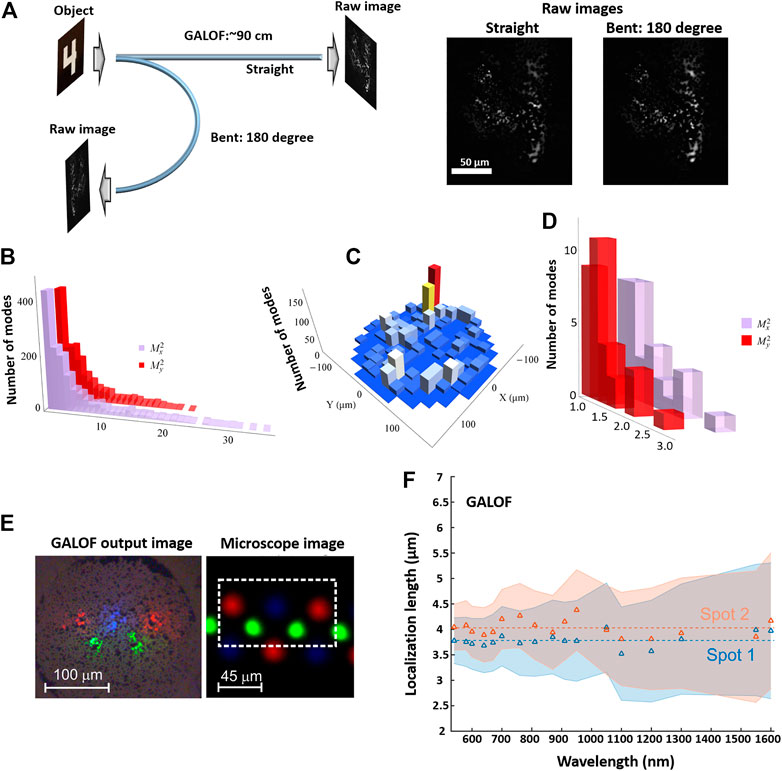
FIGURE 4. (A) Images of digit “4” from group 3 on the 1951 USAF resolution test chart are transported through a 90-cm-long GALOF sample for both straight and bent status, (B) Histogram of numerically calculated M² values for 1,500 localized modes in a real GALOF sample. The vertical axis represents the total number of modes for different M² values, (C) Numerically calculated density histogram of the positions of the modes in (B) in the GALOF cross-section. The value of each pixel corresponds to the number of localized modes, (D) Histogram of M² values for 30 localized modes measured in the experiment, (E) Nearfield image of the smartphone screen pixels after being transported through a 27 cm-long GALOF. The microscope image shows the pixel arrangement that is imaged onto the input facet of the GALOF. (F) Localization length obtained from the transmitted beam at the GALOF output facet vs. wavelength for two different spots. The shaded areas indicate the uncertainty. The two dashed lines correspond to the averaging values of the measurements for each output spot, (A–D) are adapted with permission from [103] ^© The Optical Society. (E,F) are adapted with permission from [48].

TABLE 1

TABLE 1. Comparison of imaging-related parameters for MMF, MCF and GALOF.

Learning-Based Approach for Fiber-Optic Imaging

Fundamentals of CNN

The learning-based approach has attracted lots of attention recently, mainly focusing on the DCNNs to tackle the inverse imaging problem of the fiber-optic system [18, 19, 27, 50–52, 105]. DCNN is a specific class of machine learning techniques. Nowadays, the deep neural network is often praised by mass media as one of the most fascinated techniques. From a historical perspective, the neural network has been more than 50 years old since Frank Rosenblatt first developed the perceptron in 1957 [106, 107]. The concept of CNNs is also well known for more than 30 years. The neural network with the backpropagation was proposed and deployed to solve imaging problems as early as the 1980s [108–110]. In the past half century, the research of neural networks experienced a few degressions and progressions. The resurgence is spurred by the rise of the graphic processing unit (GPU), the breakthrough in the algorithms for large-scale deep neural networks, and the huge amount of data for various applications brought by the digital era [58, 111–116]. In the following discussions, we focus on some basics of neural networks [117]. Neural network architectures are mostly based on multiple-layer computational geometry. The latter layer receives output from the previous layer. Every single layer consists of many processing units, which can be called “neurons”. We can take a simple two-layer fully-connected neural network as an example to illustrate the above framework (Figure 5A). In this two-layer neural network, neurons in each layer are connected to all the previous layer outputs (or the input data), which is the so-called fully-connected or densely-connected architecture. The neurons can take numerous inputs and generate a new output. The output of the neurons further serves as the input for the neurons in the next layers. The processing of each neuron consists of a linear operation and a nonlinear operation. As shown in Figure 5B, the linear operation includes weighted averaging plus an additional bias. In this process, the weighted parameters and bias parameters are introduced into the neural network. These parameters are trainable, the values of which are iterated and updated in the training process. Following the linear operations, the activation function acts on the output of the linear operation to impose nonlinearity. There are several widely used activation functions, such as sigmoid, tanh, or ReLU. Among these different options, ReLU is the most popular activation function in practice and plays a central role in DCNNs (Figure 5C).

FIGURE 5

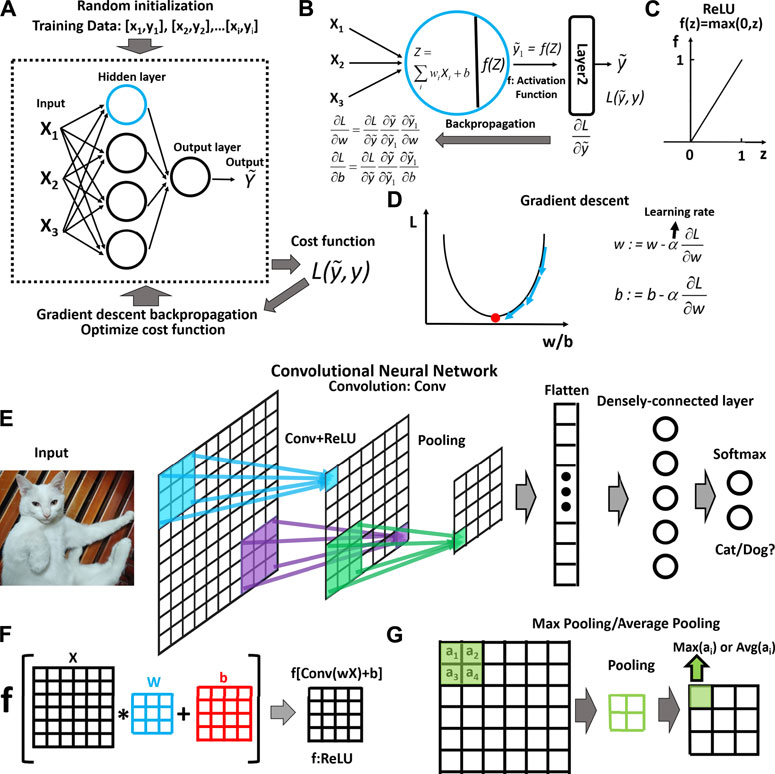
FIGURE 5. (A) Schematic of a neural network with two fully-connected layers and its training workflow, (B) Schematic of the key mathematical operations for a node (highlighted by blue circle): 1) linear operations by introducing weights parameters “w” and bias parameters “b”; 2) nonlinear operations by activation functions: such as ReLU, sigmoid, tanh, (B) also shows the backpropagation through chain rule during the training process, (C) An example of the activation function: ReLU is the most popular nonlinear operation. (D) Illustration of optimization process using gradient descent: iterated updated parameters to look for the local minimum, (E) Schematic of a classification convolutional neural network: 1) the convolutional operation and pooling operation extract the imaging features; 2) fully-connected layers classify the learned high-level feature, (F) Illustration of the convolutional layer and the nonlinear operation. A small kernel with 3$\times$3 size is often deployed in this process, (G) Illustration of pooling operations. 2$\times$2 is a common choice of pooling patch size.

The first step to solve a specific problem is to “teach” the neural networks using the data. In this training process, the parameters are iteratively adjusted by optimizing the cost function so that the neural network “learns” the underlying model from the data. The training process can be supervised or unsupervised. We mainly take supervised learning as an example here. Generally, the data would be divided into three datasets, the training dataset, the validation dataset, and the test dataset. The training dataset is what the neural network sees and learns from. The validation dataset accompanies the dynamic training process to generate temporal test errors for real-time evaluation. The neural network merely evaluates the training and tunes the parameters based on the validation data but never learns from the validation dataset. Different from the validation dataset, the test dataset is only be used once after the training process. It serves to evaluate the trained model’s capability to what extent it could accurately generalize problem. A schematic of the training workflow is shown in Figure 5A. The training data are loaded into the network after a randomized initialization. The optimization of the parameters is then evaluated by calculating the loss through the cost function based on a certain metric. For imaging problems, mean squared error (MSE), mean absolute error (MAE), and structural similarity index measure (SSIM) are widely accepted metrics [118, 119]. The training process aims to minimize the cost function using these metrics by iteratively updating each trainable layer’s parameters. In Figure 5D, we visualize the basic concept of the gradient descent process and exemplify the equations to update the weights and the bias. In practice, popular optimization methods, such as the Adam optimization algorithm, are mainly based on the variants of gradient descent, for example, the stochastic gradient descent (SGD) [58, 120]. The SGD can use a subset of the data to update the model iteratively, while gradience descent requires running through all the data during the training phase. In order to apply the SGD to train the network, the backpropagation procedure was developed (Figures 5A,B,D) [108, 109]. The procedure computes the gradient of the cost function relative to each layer’s weights based on the chain rules. The gradient propagates backward from the output to the input such that the gradients relative to the weights of each layer can be calculated.

The above neural network basics can be directly applied to the understanding of CNNs. A CNN is designed to handle multiple array data, which fits the imaging data, such as 3D array color imaging data or 2D array gray-scale imaging data [58]. The general purpose of the CNN is to extract feature maps from the imaging data through convolutional layers and pooling layers. It usually applies many alternating layers of the convolutional operation and pooling operation to gradually extract high-level features from the low-level features. As shown in Figures 5E,F, each unit of the feature maps is connected to the previous feature maps’ local area through a kernel (or a filter) that carries the weight parameters and is shared by the same feature map. Specifically speaking, the kernel moves in the feature maps with a certain stride to calculate the weighted sum. The weighted sum is added with the bias map (Figure 5F). Then, the above linear operation results are passed to a nonlinear activation operation, such as the ReLU. It should be noted that different feature maps are using different kernels. The choice of the kernel size depends on the specific applications (3 × 3 kernel in Figure 5). The above operation’s primary purpose is to detect the local conjunctions of imaging features of each layer. The reason is that the local group values of imaging data are often highly correlated, and the local statistics of imaging data are invariant to locations [58]. For a regular CNN, the pooling layer follows the above convolutional layer. The pooling operation is to extract the maximum or average local patch in the feature maps (Figure 5G). The pooling layer manages to merge semantically similar imaging features into one. It extracts dominant features that are invariant to locations [58]. After going through the convolutional layers and pooling layers, the feature maps are flattened into a vector. This vector is subsequently fully connected to other densely connected layers. The final layer outputs a vector containing the probability distribution for a classification problem with a size matching the desired parameters, such as shown in Figure 5E. The sample architecture shown in Figure 5E is an oversimplified model. In practice, very deep architecture containing dozens or even hundreds of layers can be deployed to tackle various imaging problems. In particular, the DCNN model to solve the inverse imaging problem is mostly based on an encoder-decoder architecture in which the input imaging data are down-sampled first (similar to Figure 5E) and then up-sampled to output a 2D or 3D array data with the same size as the image of the object. More details about a few popular DCNN architectures are shown in the next section.

The Advantages of the Learning-Based Approach

The DCNN-based learning approach has great advantages over model-based approaches. As we can see from Figures 6A,B, a general fiber-optic imaging problem can be formulated as recovering the image of the object from noisy and distorted raw imaging data. In real-world imaging configurations, this inverse imaging problem is ill-posed. Some conventional methods aiming to develop a direct inverse operator of the forward operator H would suffer from significant artifacts for the ill-posed inverse problems. Model-based conventional methods develop the regularized formulation to overcome these difficulties. Assuming that Y=HX (Y: raw image, H: forward operator, X: Object), the estimation of the object $\tilde{X}$ can be reconstructed through solving a regularized optimization problem:

$\tilde{\mathit{X}}\mathrm{=}\underset{\mathrm{X}}{\mathrm{argmin}}\mathit{f}\mathrm{(}\mathit{HX}\mathrm{,}\mathit{Y}\mathrm{)+}\mathit{\gamma \phi }\mathrm{(}\mathit{X}\mathrm{)}(1)$

In Eq. 1, f is the cost function to measure the error between HX and Y. φ is the regularizer that encodes the prior knowledge of the object. It promotes the solutions matching with the prior knowledge and reduces ill-posedness. γ is the regularization parameter that tunes the relative strength of the two terms. Although the model-based approach plays an undisputed central role in dealing with the inverse problem, it imposes some demanding requirements that limit its application and performance. From Eq. 1, the model-based methods required modeling the forward operator accurately and handcrafting the cost function, the regularizer as well as the optimization algorithm for each new application. However, it is challenging to develop a general design that can handle a large class of problems. For some complex physics systems, such as the wave propagation in the ALOF, even accurate modeling of the forward operator is not readily available. Besides, the optimization procedure has to be performed for each imaging operation, which may take a few minutes up to a few hours per frame for a typical optimization process [60]. The DCNN-based learning approach can overcome these limitations faced by the conventional model-based approach. As a data-driven solution, the DCNN “learns” the parametric function for the inverse problem [59] from the training data directly. There is no need to handcraft the forward model, the regularizer, the cost function, and the optimization algorithm. This unique feature circumvents the unavailability of the physics model for complicated multimode fiber-optic imaging systems. More than that, a data-driven learning capability simultaneously contributes to simplifications of the experimental hardware. For previous imaging FOIS solutions, the experimental configurations often feature a complicated design in that cracking the underlying physics model requires multi-dimensional measurements [3, 4, 34]. In contrast, digital camera processed intensity images can be directly deployed to uncover any complex underlying models through the neural networks’ self-learning. DCNN stands for a more general framework that includes the model-based approach as one of its special cases. It is, therefore, not surprising that the DCNN architecture can be decoupled from a specific problem and transferred between various applications. Moreover, the DCNN is much more computationally efficient than the model-based approach: trained DCNN merely needs calculation times of milliseconds per frame. In addition to generality and speed, recent research has also demonstrated that the DCNN yields high-quality solutions to inverse imaging problems [19, 121–129]. In general, the deployment of the DCNN in the fiber-optic imaging opens a new avenue for high-quality and high-speed FOISs with simple hardware realizations. Meanwhile, it should be noted that the DCNNs mostly work as black boxes in fiber imaging tasks. In other words, it is still quite challenging to understand how the predictions are made through the DCNNs. Despite the black-box nature, various approaches have been developed aiming at interpreting the deep learning model. Interested readers can refer to [130–132]. In the following sections, we mainly show our recent progress for this type of FOIS by integrating the ALOF-based FOIS with DCNN.

FIGURE 6

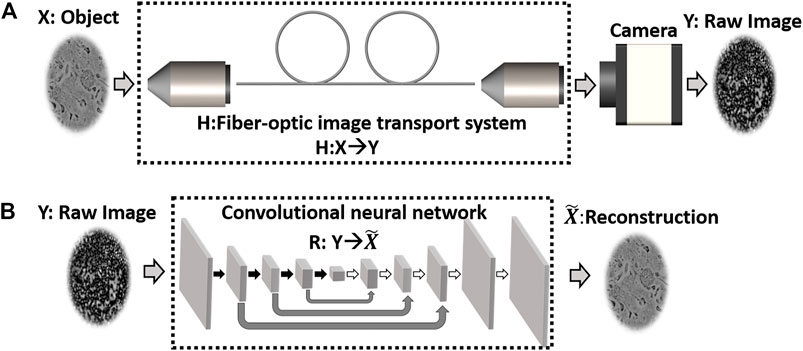
FIGURE 6. (A) A general fiber-optic imaging system. The physics model of the fiber-optic imaging system can be treated as a forward operator H. H acts on the object X to generate the raw image. A digital camera collects the raw image Y, (B) Learning-based approach (convolutional encoder-decoder architecture) to solve the inverse problem of reconstructing X from the raw image. R stands the inverse operator that maps the raw image into $\tilde{X}$, the estimation of the object.

Recent Progress of Learning-Based Fiber-Optic Imaging With GALOFs

Based on the previous discussions of ALOFs and the DCNN, we proceed to review our recent progress based on the integration of GALOFs and DCNNs. In the introduction section, we listed the issues encountered by conventional FOISs: the high sensitivity to perturbations, low imaging quality and speed, complex and expensive systems, and poor compatibility with incoherent broadband illumination. Our lab recently focuses on developing the GALOF-DCNN solution to mitigate these barriers and enhance the FOIS’s performance to the next level [18, 19, 52, 133, 134]. Our systems can be divided into two categories: image recovery and image recognition. For image recovery, the GALOF-DCNN system achieves highly robust image transport and nearly artifact-free imaging quality as well as the capability of imaging objects with varying depths. For image recognition, the GALOF-DCNN system demonstrates highly accurate and very robust (up to ∼74 bending degree) classifications without imaging reconstruction.

The image reconstruction system designs are illustrated in Figures 7A–C. The learning approach for GALOF-DCNN systems is based on supervised learning. Therefore, the experimental systems have to collect the raw images and the reference images for the same area of interest simultaneously. The setup (Figure 7A) contains two beamlines: one is for ground truth data; the other is for raw imaging data. Meanwhile, the setup also incorporates a temperature control module and a mechanical bending function, aiming to investigate the robustness of the GALOF-DCNN system under various thermal and mechanical perturbations. Depending on the light source’s properties, there are two different DCNN architectures adapted for the image reconstructions. Referring to Figures 7B,C, the U-Net model is utilized for gray-scale image reconstruction [135], while the inception model is applied to color image reconstruction [136]. The U-Net model or the inception model merely defines the general framework. Each sampling block’s specific layer design is carefully customized to fit the GALOF-DCNN system and a particular illumination. For example, within the U-Net model, the ResNet framework [137] is applied in each individual down-sampling block as well as in the up-sampling blocks (Figure 7B), which dramatically improves the quality of image reconstruction (more details can be found in Ref. [19]). Despite that the U-Net model works well for gray-scale fiber imaging, the inception model proves to be more effective for color fiber imaging based on imaging performance evaluation. This is a consequence of the inception network’s ability to extract image features at varying scales through simultaneous utilization of different kernel sizes. It should be noted that the inception model is also optimized to fit the GALOF-DCNN system: each parallel branch contains a customized U-Net module (more details are given in Ref. [134]).

FIGURE 7

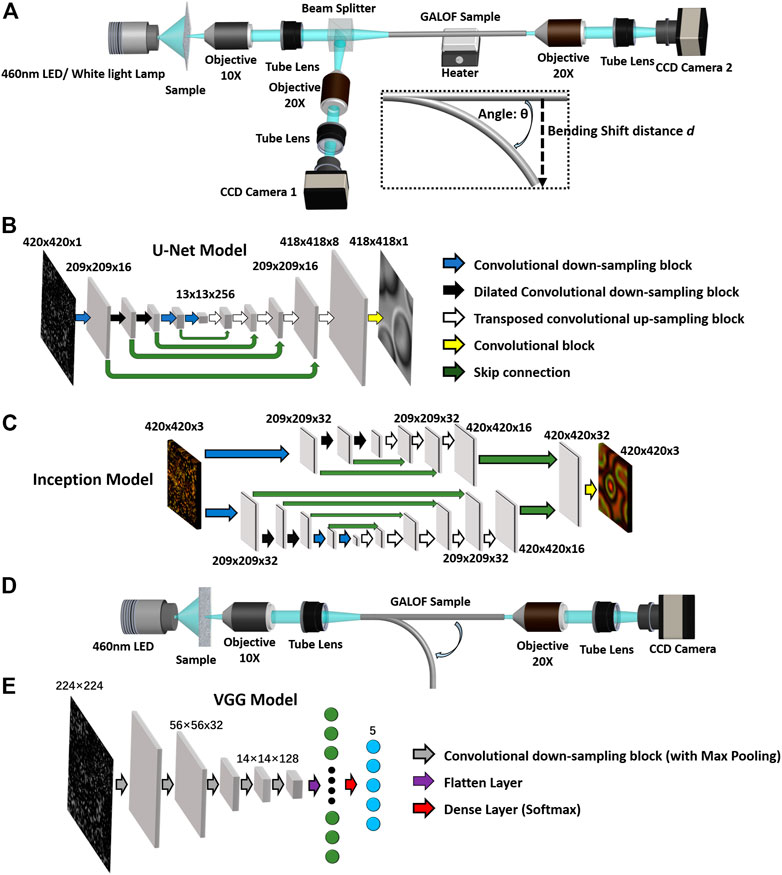
FIGURE 7. (A) Schematic of the cell imaging setup. The light source can be either a 460-nm LED or a white light lamp. The LED serves for gray-scale imaging. The white light lamp is used for color imaging. The sample is illuminated under transmission mode. The image of the sample is relayed through the 4f system consisting of a 10× objective and a tube lens. The relayed image is split into two copies: one is recorded by camera 1, working as the reference image (ground truth); the GALOF samples the other one for generating raw image purpose. The fiber-sampled image is transported through a meter-long GALOF sample (∼80 cm) and finally recorded by camera 2. The data collected by camera two is the raw images. A heater is attached at the center of the GALOF sample to increase the fiber temperature. The imaging process is tested under both straight and bent fiber status. As shown in the inset, the input end of the GALOF is fixed while the output end is bent by a bending shift distance d. The relation between the bending angle θ and the bending shift distance d is given by d = L[1-cos(θ)]/θ, (B) The architecture of the DCNN for gray-scale cell image reconstruction based on a U-Net framework. The image is adapted with permission from [19]. More details refer to [19], (C) The architecture of the DCNN for color cell image reconstruction is based on an inception CNN framework. The image is adapted with permission from [134] ^© The Optical Society, (D) Schematic of the cell recognition setup. The design of the setup (D) is similar to the setup in (A), except that the beamline for reference image collection is removed due to its imaging-free capabilities. The setup just collects the raw speckle images for classification purposes. Similar to the inset shown in (A), the imaging recognition process is also tested under bent fiber status with the same bending mechanism. More details refer to [52]. (E) The architecture of the DCNN for cell recognition is based on a VGG framework. More details refer to [52].

The image reconstruction results are demonstrated in Figures 8A–D. First, the GALOF-DCNN system is able to deliver nearly artifact-free single-color or full-color cell images in real-time through a meter-long fiber (Figure 8A), which is a very difficult task for conventional FOIS. The GALOF’s unique properties, such as high-quality wavefront, high mode density, and wavelength-independent localization length, remove the device-level limitations for high-quality imaging. On the basis of the GALOF transport, the DCNN accurately simulate the underlying inverse operator of the imaging system, which finally recovers the fine features of the cell sample with high accuracy. The training time for the GALOF-DCNN system is ∼6.4 h for 15,000 imaging pairs. Once trained, the reconstruction speed is 0.05 s per frame with nearly artifact-free quality (more details in Ref. [19]). Second, the GALOF-DCNN demonstrates superior imaging robustness compared to existing FOISs using other types of optical fibers. Referring to Figure 8B, the quality of cell imaging is almost not affected even under a 2-cm bending shift and a 30°C temperature increase. The high robustness is mainly attributed to the single-mode-like behavior of the localized modes embedded in GALOF’s disordered structure. Similar behaviors can hardly be observed in other multimode waveguide systems, which distinguishes the GALOF-DCNN system from FOISs based on conventional fibers. It should be noted that the DCNN model deployed in these robustness tests is only trained one time using the data obtained from straight fiber operating at room temperature. The test time for any bent fiber or fiber being heated is just tens of milliseconds. This one-time-only training method is fundamentally different from other learning-based FOISs that perform several time-consuming re-trainings for each individual bending angle or thermal status. The GALOF-DCNN truly provides a practical one-shot solution for high-speed, robust and artifact-free cell imaging based on its superior robustness. Third, the GALOF-DCNN is highly adaptable for variations of object depth. For objects located at various distances from the fiber input facet (0–4 mm), the system successfully transports high-quality cell images without the assistance of extra distal-end optics (Figure 8C). It shows that the GALOF-DCNN system can tolerate the defocus up to a few millimeters. This capability enables a simplified distal-end design that could minimize the penetration damage to the living object. Fourth, the GALOF-DCNN is proved to be a general system by a transfer-learning test, which is also strong evidence of capturing the underlying physics model well. As shown in Figure 8D, the DCNN is trained using a mixture of different objects: human red blood cells, frog blood cells, and polymer microspheres. Then, the trained model is directly deployed to test the object of bird blood cells which represent a different cell type. It still maps the raw image into cell image reconstruction with reasonably high imaging quality. It should be noted that the learning-based research in the area of optics and photonics often train and test the DCNN using the same type of objects that shares similar image features. It is not trivial to train and test the DCNN using objects carrying significantly different image features.

FIGURE 8

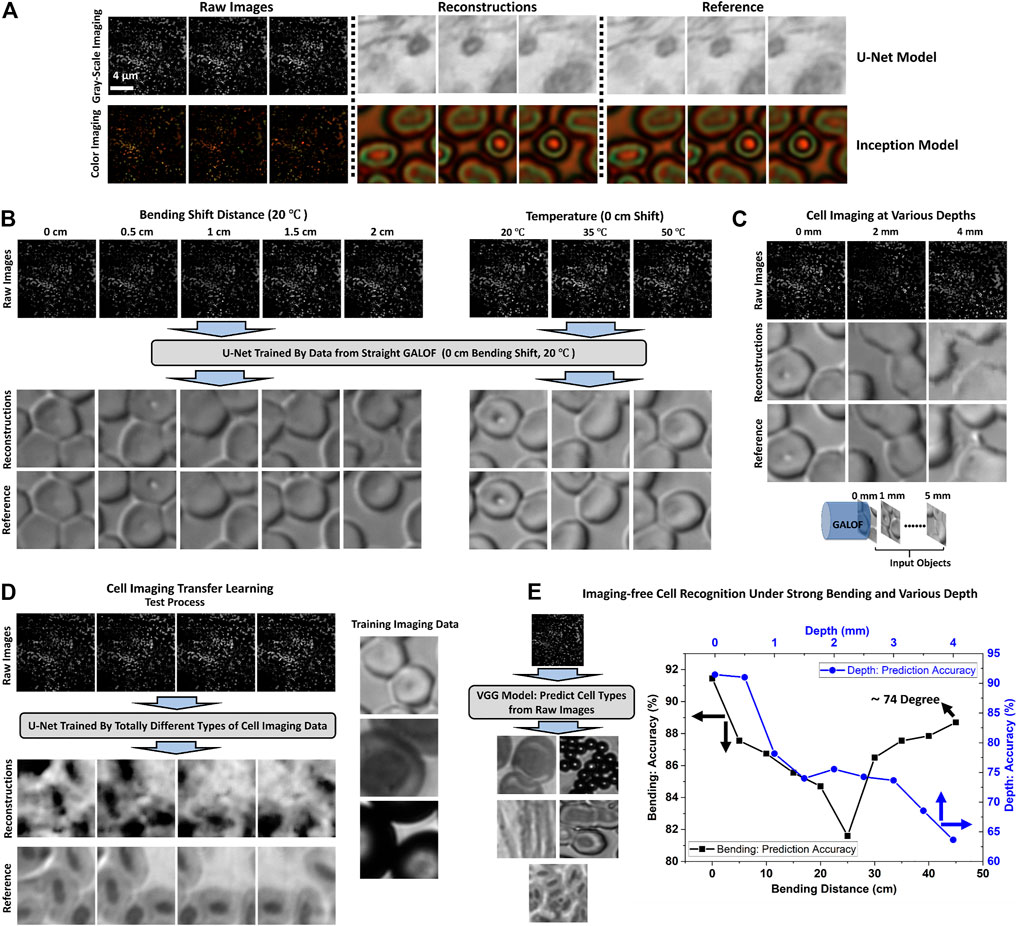
FIGURE 8. (A–D) Cell image reconstruction results based on GALOF-DCNN systems. (A) Top row: gray-scale cell imaging for cancerous human stomach cells. Images in the top row are adapted with permission from [19]. Bottom row: color cell imaging for human red blood cells. Images in the bottom rows are adapted with permission from [134] ^© The Optical Society. Both gray-scale and color images are obtained under 0 mm object depth, (B) Cell imaging robustness tests under both mechanical bending and thermal variations at 0 mm object depth, (C) Cell image transport under various object depths for straight fiber status. (A–C) The DCNN is trained and tested using the same type of cell breed. More details refer to [19], (D) Transfer learning test for cell image transport under straight fiber status and 0 mm object depth. The DCNN model is trained (human red blood cells, frog blood cells and polymer microspheres) and tested (bird blood cells) using different types of cell breeds. More details refer to [19]. Images in (B–D) are adapted with permission from [19], (E) Cell recognition test results under different bending (0 mm object depth) and object depth (straight fiber) status. The images are adapted with permission from [52]. More details refer to [52] ^© IEEE.

It is well-known that a high-quality image is vitally important for recognizing cell types. However, we recently prove that high-quality image recovery is not always necessary for the cell recognition. We develop the system shown in Figures 7D,E to realize imaging-free object recognition for various cell types. The configuration shares a similar layout for the image reconstruction task except that the beamline for the reference data is removed. The reason is that the raw data label switches from ground-truth images to cell type identification numbers. The cell type identification is the prior knowledge so that it can be separately processed using the computer. Correspondingly, the DCNN model is based on a VGG architecture (Figure 7E) [138] which is designed for image classification tasks (more details are given in Ref. [52]). Based on the above design, the raw speckle image data are loaded into the trained VGG model. The VGG model outputs the probability distributions to identify the specific cell type (Figure 7E). Similar to the image reconstruction system, the robustness and the depth variation adaptability of the object recognition system are also evaluated based on the prediction accuracy. Related results are demonstrated in Figure 8E. The accuracy of the cell recognition is about ∼92% for straight GALOF sample with a 0 mm object depth. When fixing the object depth at 0 mm, a nearly bending-independent classification accuracy is observed for strong mechanical deformation up to ∼74° (corresponding to a 45 cm bending shift distance). The error tolerance of the cell classification is apparently much larger than the image reconstruction task (∼3°). The mechanism may be attributed to the fault tolerance of VGG-based designs in conjunction with the localized mode’s single-mode nature. It should be noted that the current GALOF is far from being perfect in that many extending modes co-exist with the localized modes. Such extending modes do not share the stability with respect to perturbations. Despite that, the 74-degree bending angle with a meter-long fiber sample would be sufficient to enable most practical medical endoscopy applications. In addition to the high robustness, the depth variation adaptability tests also show that the GALOF-DCNN system has a superior capability of handling the defocusing issue. For an object depth of 0.5 mm, the accuracy is as high as ∼92%, while for depths smaller than 1 mm, the accuracy remains higher than 80%.

Outlook

The disordered structure of the current GALOF is far from the optimal design. To fully exploit the potential of transverse Anderson localization, further investigations on the fabrication technique are required to improve the fiber quality and its random structure parameters, such as air-filling fraction and the air-hole uniformity. The current stack-and-draw technique for GALOF faces some challenges. It requires hundreds of manually assembled capillaries to create the preform and a recursive manufacturing process to obtain the final product, which is time-consuming and labor-intensive. More importantly, the random structures’ parameters are hard to approach the optimal design due to the limitation of the packed tube geometry. Due to similar reasons, it is also difficult to maintain a high degree of repeatability and accuracy of the random structure. The potential solutions to these challenges might be in additive manufacturing or 3D printing technique. It has been proved that 3D printing can be applied to create complex cross-sections for optical fiber preform with high accuracy and repeatability [139–142]. Especially, single-step fiber fabrication can be realized by printing the preform in just a few hours. A similar 3D printing technique could be deployed to make the preform for GALOF fabrication and simplify the recursive manufacturing process. In addition to the fabrication techniques, the glass material is another important factor that determines the imaging performance of GALOFs. The current GALOF mainly works at the visible band. For biomedical applications, it is desired to extend the spectral range from the visible band to ∼1,500 nm. This spectral range is the therapeutic window that enables optical detection and treatment in a living body [1]. Being limited by the transmission window of silica, it is difficult to go beyond ∼3 µm. Instead of silica, tellurite glass has a broad transmission window up to 7 μm, a larger refractive index, and high thermal and chemical stabilities [143, 144]. It could be the ideal candidate to develop a novel GALOF reaching the near-infrared range. Recently reported all-solid-state ALOF has already shown the great potential of tellurite glasses by transporting near-infrared (∼1.55 µm) images [100]. For the algorithms, the current learning approach is based on supervised learning, which requires a large amount of high-quality labeled imaging data. However, it is often quite challenging to meet this requirement in practice. For example, one important application scenario of a fiber-imaging system is the endoscopic imaging of organs or tissues. Limited by the unique imaging objects and environments, it is quite challenging to access the distal end of the imaging unit and acquire labeled training data. To resolve these issues, unsupervised or semi-supervised learning approaches might be able to provide a new avenue for future systems in that they do not need strictly labeled data [127, 145–147]. This would release the demanding requirements on the amount of necessary training data and time as well as reduce the heavy burden on system calibrations. To implement unsupervised or semi-supervised learning, integrating the physics modeling with the DCNN architecture is shown to be a wise choice [127, 146]. Besides, recently fast-growing generative adversarial networks would be able to provide another potential solution to fiber imaging systems as well [148]. Overall, learning-based GALOF FIOSs appear to make the best use of both the GALOF’s unique properties based on TAL and the learning approach’s high performance in solving imaging problems. With more improvements to come, the interplay between the GALOF and the deep learning algorithms have great potential to dramatically enhance the performances of future FOISs. We are very optimistic that our findings contribute to the development of next generation high-fidelity fiber optic imaging systems for basic biomedical research and clinical practice.

Author Contributions

JZ conceived the review topic, prepared the data, made the figures, and wrote the first draft. XH, SG, JA-L, RC, and AS provided assistance in data and figure preparations. All authors discussed, revised, and approved the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge Professor Arash Mafi’s assistance in preparing the figures.

References

1. Keiser G, Xiong F, Cui Y, Shum PP. Review of Diverse Optical Fibers Used in Biomedical Research and Clinical Practice. J Biomed Opt (2014) 19(8):080902. doi:10.1117/1.jbo.19.8.080902

CrossRef Full Text | Google Scholar

2. Szabo V, Ventalon C, De Sars V, Bradley J, Emiliani V. Spatially Selective Holographic Photoactivation and Functional Fluorescence Imaging in Freely Behaving Mice with a Fiberscope. Neuron (2014) 84(6):1157–69. doi:10.1016/j.neuron.2014.11.005

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Turtaev S, Leite IT, Altwegg-Boussac T, Pakan JMP, Rochefort NL, Čižmár T. High-fidelity Multimode Fibre-Based Endoscopy for Deep Brain In Vivo Imaging. Light Sci Appl (2018) 7(1):92. doi:10.1038/s41377-018-0094-x

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ohayon S, Caravaca-Aguirre A, Piestun R, DiCarlo JJ. Minimally Invasive Multimode Optical Fiber Microendoscope for Deep Brain Fluorescence Imaging. Biomed Opt Express (2018) 9(4):1492–509. doi:10.1364/BOE.9.001492

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Turcotte R, Schmidt CC, Booth MJ, Emptage NJ. Volumetric Two-Photon Fluorescence Imaging of Live Neurons Using a Multimode Optical Fiber. Opt Lett (2020) 45(24):6599–602. doi:10.1364/OL.409464

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Vasquez-Lopez SA, Turcotte R, Koren V, Plöschner M, Padamsey Z, Booth MJ, et al. Subcellular Spatial Resolution Achieved for Deep-Brain Imaging In Vivo Using a Minimally Invasive Multimode Fiber. Light Sci Appl (2018) 7(1):110. doi:10.1038/s41377-018-0111-0

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Coda S, Siersema P, Stamp G, Thillainayagam A. Biophotonic Endoscopy: a Review of Clinical Research Techniques for Optical Imaging and Sensing of Early Gastrointestinal Cancer. Endosc Int Open (2015) 03(5):E380–E392. doi:10.1055/s-0034-1392513

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ho S-H, Uedo N, Aso A, Shimizu S, Saito Y, Yao K, et al. Development of Image-Enhanced Endoscopy of the Gastrointestinal Tract. J Clin Gastroenterol (2018) 52(4):295–306. doi:10.1097/mcg.0000000000000960

PubMed Abstract | CrossRef Full Text | Google Scholar

9. McGoran JJ, McAlindon ME, Iyer PG, Seibel EJ, Haidry R, Lovat LB, et al. Miniature Gastrointestinal Endoscopy: Now and the Future. Wjg (2019) 25(30):4051–60. doi:10.3748/wjg.v25.i30.4051

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Flusberg BA, Cocker ED, Piyawattanametha W, Jung JC, Cheung ELM, Schnitzer MJ. Fiber-optic Fluorescence Imaging. Nat Methods (2005) 2(12):941–50. doi:10.1038/nmeth820

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Choi Y, Yoon C, Kim M, Yang TD, Fang-Yen C, Dasari RR, et al. Scanner-Free and Wide-Field Endoscopic Imaging by Using a Single Multimode Optical Fiber. Phys Rev Lett (2012) 109(20):203901. doi:10.1103/physrevlett.109.203901

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Čižmár T, Dholakia K. Exploiting Multimode Waveguides for Pure Fibre-Based Imaging. Nat Commun (2012) 3:1027. doi:10.1038/ncomms2024

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hughes M, Chang TP, Yang G-Z. Fiber Bundle Endocytoscopy. Biomed Opt Express (2013) 4(12):2781–94. doi:10.1364/BOE.4.002781

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chang Y, Lin W, Cheng J, Chen SC. Compact High-Resolution Endomicroscopy Based on Fiber Bundles and Image Stitching. Opt Lett (2018) 43(17):4168–71. doi:10.1364/OL.43.004168

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Tsvirkun V, Sivankutty S, Bouwmans G, Katz O, Andresen ER, Rigneault H. Widefield Lensless Endoscopy with a Multicore Fiber. Opt Lett (2016) 41(20):4771–4. doi:10.1364/OL.41.004771

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Weiss U, Katz O. Two-photon Lensless Micro-endoscopy with In-Situ Wavefront Correction. Opt Express (2018) 26(22):28808–17. doi:10.1364/OE.26.028808

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Andresen ER, Sivankutty S, Tsvirkun V, Bouwmans G, Rigneault H. Ultrathin Endoscopes Based on Multicore Fibers and Adaptive Optics: A Status Review and Perspectives. J. of Biomedical Optics (2016) 21(12):121506. doi:10.1117/1.JBO.21.12.121506

CrossRef Full Text | Google Scholar

18. Zhao J, Sun Y, Zhu Z, Antonio-Lopez JE, Correa RA, Pang S, et al. Deep Learning Imaging through Fully-Flexible Glass-Air Disordered Fiber. ACS Photon (2018) 5(10):3930–5. doi:10.1021/acsphotonics.8b00832

CrossRef Full Text | Google Scholar

19. Zhao J, Sun Y, Zhu H, Zhu Z, Antonio-Lopez JE, Correa RA, et al. Deep-learning Cell Imaging through Anderson Localizing Optical Fiber. Adv Photon (2019) 1(6):1–12. doi:10.1117/1.ap.1.6.066001

CrossRef Full Text | Google Scholar

20. Grant-Jacob JA, Jain S, Xie Y, Mackay BS, McDonnell MDT, Praeger M, et al. Fibre-optic Based Particle Sensing via Deep Learning. J Phys Photon (2019) 1(4):044004. doi:10.1088/2515-7647/ab437b

CrossRef Full Text | Google Scholar

21. Caravaca-Aguirre AM, Piestun R. Single Multimode Fiber Endoscope. Opt Express (2017) 25(3):1656–65. doi:10.1364/OE.25.001656

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Gordon GSD, Joseph J, Sawyer T, Macfaden AJ, Williams C, Wilkinson TD, et al. Full-field Quantitative Phase and Polarisation-Resolved Imaging through an Optical Fibre Bundle. Opt Express (2019) 27(17):23929–47. doi:10.1364/OE.27.023929

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Gordon GSD, Mouthaan R, Wilkinson TD, Bohndiek SE. Coherent Imaging through Multicore Fibres with Applications in Endoscopy. J Lightwave Technol (2019) 37(22):5733–45. doi:10.1109/jlt.2019.2932901

CrossRef Full Text | Google Scholar

24. Zhao T, Ourselin S, Vercauteren T, Xia W. Seeing through Multimode Fibers with Real-Valued Intensity Transmission Matrices. Opt Express (2020) 28(14):20978–91. doi:10.1364/OE.396734

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Caramazza P, Moran O, Murray-Smith R, Faccio D. Transmission of Natural Scene Images through a Multimode Fibre. Nat Commun (2019) 10(1):2029. doi:10.1038/s41467-019-10057-8

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Orth A, Ploschner M, Wilson ER, Maksymov IS, Gibson BC. Optical Fiber Bundles: Ultra-slim Light Field Imaging Probes. Sci Adv (2019) 5(4):eaav1555. doi:10.1126/sciadv.aav1555

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Shao J, Zhang J, Huang X, Liang R, Barnard K. Fiber Bundle Image Restoration Using Deep Learning. Opt Lett (2019) 44(5):1080–3. doi:10.1364/OL.44.001080

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Choudhury D, McNicholl DK, Repetti A, Li S, Phillips DB, Whyte G, et al. Computational Optical Imaging with a Photonic Lantern. Nat Commun (2020) 11(1):5217. doi:10.1038/s41467-020-18818-6

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Guan H, Liang W, Li A, Gau Y-TA, Chen D, Li M-J, et al. Multicolor Fiber-Optic Two-Photon Endomicroscopy for Brain Imaging. Opt Lett (2021) 46(5):1093–6. doi:10.1364/OL.412760

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Hughes MR. Inline Holographic Microscopy through Fiber Imaging Bundles. Appl Opt (2021) 60(4):A1–A7. doi:10.1364/AO.403805

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Leite IT, Turtaev S, Čižmár DE, Čižmár T. Observing Distant Objects with a Multimode Fiber-Based Holographic Endoscope. APL Photon (2021) 6(3):036112. doi:10.1063/5.0038367

CrossRef Full Text | Google Scholar

32. Plöschner M, Tyc T, Čižmár T. Seeing through Chaos in Multimode Fibres. Nat Photon (2015) 9(8):529–35. doi:10.1038/nphoton.2015.112

CrossRef Full Text | Google Scholar

33. Boonzajer Flaes DE, Stopka J, Turtaev S, de Boer JF, Tyc T, Čižmár T. Robustness of Light-Transport Processes to Bending Deformations in Graded-Index Multimode Waveguides. Phys Rev Lett (2018) 120(23):233901. doi:10.1103/PhysRevLett.120.233901

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Lee S-Y, Parot VJ, Bouma BE, Villiger M. Reciprocity-induced Symmetry in the Round-Trip Transmission through Complex Systems. APL Photon (2020) 5(10):106104. doi:10.1063/5.0021285

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Popoff SM, Lerosey G, Fink M, Boccara AC, Gigan S. Controlling Light through Optical Disordered media: Transmission Matrix Approach. New J Phys (2011) 13(12):123021. doi:10.1088/1367-2630/13/12/123021

CrossRef Full Text | Google Scholar

36. Popoff SM, Lerosey G, Carminati R, Fink M, Boccara AC, Gigan S. Measuring the Transmission Matrix in Optics: An Approach to the Study and Control of Light Propagation in Disordered Media. Phys Rev Lett (2010) 104(10):100601. doi:10.1103/physrevlett.104.100601

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Yu H, Park J, Lee K, Yoon J, Kim K, Lee S, et al. Recent Advances in Wavefront Shaping Techniques for Biomedical Applications. Curr Appl Phys (2015) 15(5):632–41. doi:10.1016/j.cap.2015.02.015

CrossRef Full Text | Google Scholar

38. Reichenbach KL, Xu C. Numerical Analysis of Light Propagation in Image Fibers or Coherent Fiber Bundles. Opt Express (2007) 15(5):2151–65. doi:10.1364/OE.15.002151

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Chen X, Reichenbach KL, Xu C. Experimental and Theoretical Analysis of Core-To-Core Coupling on Fiber Bundle Imaging. Opt Express (2008) 16(26):21598–607. doi:10.1364/OE.16.021598

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Stone JM, Wood HAC, Harrington K, Birks TA. Low index Contrast Imaging Fibers. Opt Lett (2017) 42(8):1484–7. doi:10.1364/OL.42.001484

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Kim D, Moon J, Kim M, Yang TD, Kim J, Chung E, et al. Toward a Miniature Endomicroscope: Pixelation-free and Diffraction-Limited Imaging through a Fiber Bundle. Opt Lett (2014) 39(7):1921–4. doi:10.1364/OL.39.001921

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Mafi A. Transverse Anderson Localization of Light: a Tutorial. Adv Opt Photon (2015) 7(3):459–515. doi:10.1364/AOP.7.000459

CrossRef Full Text | Google Scholar

43. Mafi A, Ballato J, Koch KW, Schulzgen A. Disordered Anderson Localization Optical Fibers for Image Transport-A Review. J Lightwave Technol (2019) 37:5652–9. doi:10.1109/JLT.2019.2916020

CrossRef Full Text | Google Scholar

44. Zhao J, Lopez JEA, Zhu Z, Zheng D, Pang S, Correa RA, et al. Image Transport through Meter-Long Randomly Disordered Silica-Air Optical Fiber. Sci Rep (2018) 8(1):3065. doi:10.1038/s41598-018-21480-0

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Tuggle M, Bassett C, Hawkins TW, Stolen R, Mafi A, Ballato J. Observation of Optical Nonlinearities in an All-Solid Transverse Anderson Localizing Optical Fiber. Opt Lett (2020) 45(3):599–602. doi:10.1364/OL.385438

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ruocco G, Abaie B, Schirmacher W, Mafi A, Leonetti M. Disorder-induced Single-Mode Transmission. Nat Commun (2017) 8:14571. doi:10.1038/ncomms14571

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Schirmacher W, Abaie B, Mafi A, Ruocco G, Leonetti M. What Is the Right Theory for Anderson Localization of Light? an Experimental Test. Phys Rev Lett (2018) 120(6):067401. doi:10.1103/PhysRevLett.120.067401

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Roth P, Wong GKL, Zhao J, Antonio-Lopez JE, Amezcua-Correa R, Frosz MH, Russell PSJ, Schülzgen A. Sixth International Workshop on Specialty Optical Fibers and Their Applications (WSOF 2019): Conference Digest. In: Sixth International Workshop on Specialty Optical Fibers and Their Applications (WSOF 2019) Conference Diges; 5 November 2019; Charleston, South Carolina. Bellingham, Washington: SPIE (2019). doi:10.1117/12.2557110

CrossRef Full Text | Google Scholar

49. Abaie B, Peysokhan M, Zhao J, Antonio-Lopez JE, Amezcua-Correa R, Schülzgen A, et al. Disorder-induced High-Quality Wavefront in an Anderson Localizing Optical Fiber. Optica (2018) 5(8):984–7. doi:10.1364/OPTICA.5.000984

CrossRef Full Text | Google Scholar

50. Borhani N, Kakkava E, Moser C, Psaltis D. Learning to See through Multimode Fibers. Optica (2018) 5(8):960–6. doi:10.1364/OPTICA.5.000960

CrossRef Full Text | Google Scholar

51. Rahmani B, Loterie D, Konstantinou G, Psaltis D, Moser C. Multimode Optical Fiber Transmission with a Deep Learning Network. Light Sci Appl (2018) 7(1):69. doi:10.1038/s41377-018-0074-1

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Hu X, Zhao J, Antonio-Lopez JE, Fan S, Correa RA, Schulzgen A. Robust Imaging-free Object Recognition through Anderson Localizing Optical Fiber. J Lightwave Technol (2021) 39:920–6. doi:10.1109/JLT.2020.3029416

CrossRef Full Text | Google Scholar

53. Rahmani B, Loterie D, Kakkava E, Borhani N, Teğin U, Psaltis D, et al. Actor Neural Networks for the Robust Control of Partially Measured Nonlinear Systems Showcased for Image Propagation through Diffuse media. Nat Mach Intell (2020) 2(7):403–10. doi:10.1038/s42256-020-0199-9

CrossRef Full Text | Google Scholar

54. Kürüm U, Wiecha PR, French R, Muskens OL. Deep Learning Enabled Real Time Speckle Recognition and Hyperspectral Imaging Using a Multimode Fiber Array. Opt Express (2019) 27(15):20965–79. doi:10.1364/OE.27.020965

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Wetzstein G, Ozcan A, Gigan S, Fan S, Englund D, Soljačić M, et al. Inference in Artificial Intelligence with Deep Optics and Photonics. Nature (2020) 588(7836):39–47. doi:10.1038/s41586-020-2973-6

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Ma W, Liu Z, Kudyshev ZA, Boltasseva A, Cai W, Liu Y. Deep Learning for the Design of Photonic Structures. Nat Photon (2021) 15(2):77–90. doi:10.1038/s41566-020-0685-y

CrossRef Full Text | Google Scholar

57. Karbasi S, Mirr CR, Frazier RJ, Yarandi PG, Koch KW, Mafi A. Detailed Investigation of the Impact of the Fiber Design Parameters on the Transverse Anderson Localization of Light in Disordered Optical Fibers. Opt Express (2012) 20(17):18692–706. doi:10.1364/OE.20.018692

PubMed Abstract | CrossRef Full Text | Google Scholar

58. LeCun Y, Bengio Y, Hinton G. Deep Learning. Nature (2015) 521(7553):436–44. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

59. McCann MT, Jin KH, Unser M. Convolutional Neural Networks for Inverse Problems in Imaging: A Review. IEEE Signal Process Mag (2017) 34(6):85–95. doi:10.1109/MSP.2017.2739299

CrossRef Full Text | Google Scholar

60. Barbastathis G, Ozcan A, Situ G. On the Use of Deep Learning for Computational Imaging. Optica (2019) 6(8):921–43. doi:10.1364/OPTICA.6.000921

CrossRef Full Text | Google Scholar

61. Anderson PW. Absence of Diffusion in Certain Random Lattices. Phys Rev (1958) 109(5):1492–505. doi:10.1103/physrev.109.1492

CrossRef Full Text | Google Scholar

62. John S. Localization of Light. Phys Today (1991) 44(5):32–40. doi:10.1063/1.881300

CrossRef Full Text | Google Scholar

63. Graham IS, Piché L, Grant M. Experimental Evidence for Localization of Acoustic Waves in Three Dimensions. Phys Rev Lett (1990) 64(26):3135–8. doi:10.1103/PhysRevLett.64.3135

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Hu H, Strybulevych A, Page JH, Skipetrov SE, van Tiggelen BA. Localization of Ultrasound in a Three-Dimensional Elastic Network. Nat Phys (2008) 4:945–8. doi:10.1038/nphys1101

CrossRef Full Text | Google Scholar

65. Chabanov AA, Stoytchev M, Genack AZ. Statistical Signatures of Photon Localization. Nature (2000) 404(6780):850–3. doi:10.1038/35009055

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Hu R, Tian Z. Direct Observation of Phonon Anderson Localization in Si/Ge Aperiodic Superlattices. Phys Rev B (2021) 103(4):045304. doi:10.1103/PhysRevB.103.045304

CrossRef Full Text | Google Scholar

67. Abouraddy AF, Di Giuseppe G, Christodoulides DN, Saleh BEA. Anderson Localization and Colocalization of Spatially Entangled Photons. Phys Rev A (2012) 86(4):040302. doi:10.1103/PhysRevA.86.040302

CrossRef Full Text | Google Scholar

68. Thompson C, Vemuri G, Agarwal GS. Anderson Localization with Second Quantized fields in a Coupled Array of Waveguides. Phys Rev A (2010) 82(5):053805. doi:10.1103/PhysRevA.82.053805

CrossRef Full Text | Google Scholar

69. Wiersma DS, Bartolini P, Lagendijk A, Righini R. Localization of Light in a Disordered Medium. Nature (1997) 390(6661):671–3. doi:10.1038/37757

CrossRef Full Text | Google Scholar

70. Störzer M, Gross P, Aegerter CM, Maret G. Observation of the Critical Regime Near Anderson Localization of Light. Phys Rev Lett (2006) 96(6):063904. doi:10.1103/PhysRevLett.96.063904

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Aegerter CM, Störzer M, Fiebig S, Bührer W, Maret G. Observation of Anderson Localization of Light in Three Dimensions. J Opt Soc Am A (2007) 24(10):A23–A27. doi:10.1364/JOSAA.24.000A23

CrossRef Full Text | Google Scholar

72. Hsieh P, Chung C, McMillan JF, Tsai M, Lu M, Panoiu NC, et al. Photon Transport Enhanced by Transverse Anderson Localization in Disordered Superlattices. Nat Phys (2015) 11(3):268–74. doi:10.1038/nphys3211

CrossRef Full Text | Google Scholar

73. Cao H, Zhao YG, Ho ST, Seelig EW, Wang QH, Chang RPH. Random Laser Action in Semiconductor Powder. Phys Rev Lett (1999) 82(11):2278–81. doi:10.1103/physrevlett.82.2278

CrossRef Full Text | Google Scholar

74. Karbasi S, Frazier RJ, Koch KW, Hawkins T, Ballato J, Mafi A. Image Transport through a Disordered Optical Fibre Mediated by Transverse Anderson Localization. Nat Commun (2014) 5:3362. doi:10.1038/ncomms4362

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Abaie B, Mobini E, Karbasi S, Hawkins T, Ballato J, Mafi A. Random Lasing in an Anderson Localizing Optical Fiber. Light Sci Appl (2017) 6–e17041. doi:10.1038/lsa.2017.41

CrossRef Full Text | Google Scholar

76. Crane T, Trojak OJ, Vasco JP, Hughes S, Sapienza L. Anderson Localization of Visible Light on a Nanophotonic Chip. ACS Photon (2017) 4(9):2274–80. doi:10.1021/acsphotonics.7b00517

CrossRef Full Text | Google Scholar

77. Trojak OJ, Crane T, Sapienza L. Optical Sensing with Anderson-localised Light. Appl Phys Lett (2017) 111(14):141103. doi:10.1063/1.4999936

CrossRef Full Text | Google Scholar

78. Choi SH, Kim S-W, Ku Z, Visbal-Onufrak MA, Kim S-R, Choi K-H, et al. Anderson Light Localization in Biological Nanostructures of Native Silk. Nat Commun (2018) 9(1):452. doi:10.1038/s41467-017-02500-5

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Zhao J, Antonio-Lopez JE, Correa RA, Mafi A, Windeck M, Schülzgen A. Image Transport through Silica-Air Random Core Optical Fiber. In: Conference on Lasers and Electro-Optics; 14-19 May 2017; San Jose, California. San Jose, California: Optical Society of America (2017). doi:10.1364/cleo_at.2017.jtu5a.91

CrossRef Full Text | Google Scholar

80. Tuan TH, Kuroyanagi S, Nagasaka K, Suzuki T, Ohishi Y. Near-infrared Optical Image Transport through an All-Solid Tellurite Optical Glass Rod with Transversely-Disordered Refractive index Profile. Opt Express (2018) 26(13):16054–62. doi:10.1364/OE.26.016054

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Shi NN, Tsai C-C, Carter MJ, Mandal J, Overvig AC, Sfeir MY, et al. Nanostructured Fibers as a Versatile Photonic Platform: Radiative Cooling and Waveguiding through Transverse Anderson Localization. Light Sci Appl (2018) 7(1):37. doi:10.1038/s41377-018-0033-x

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Gianfrate A, Dominici L, Ballarini D, Sanvitto D, Leonetti M. Transverse Localization of Light in Laser Written Designed Disorder. Appl Phys Lett (2020) 116(7):071101. doi:10.1063/1.5142161

CrossRef Full Text | Google Scholar

83. Ioffe AF, Regel AR. Non-crystalline, Amorphous and Liquid Electronic Semiconductors. Prog Semiconductors (1960) 4:237–91.

Google Scholar

84. De Raedt H, Lagendijk A, de Vries P. Transverse Localization of Light. Phys Rev Lett (1989) 62(1):47–50. doi:10.1103/physrevlett.62.47

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Schwartz T, Bartal G, Fishman S, Segev M. Transport and Anderson Localization in Disordered Two-Dimensional Photonic Lattices. Nature (2007) 446(7131):52–5. doi:10.1038/nature05623

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Karbasi S, Mirr CR, Yarandi PG, Frazier RJ, Koch KW, Mafi A. Observation of Transverse Anderson Localization in an Optical Fiber. Opt Lett (2012) 37(12):2304–6. doi:10.1364/OL.37.002304

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Abdullaev SS, Abdullaev FK. On Propagation of Light in Fiber Bundles with Random Parameters. Radiofizika (1980) 23:766–7.

Google Scholar

88. Karbasi S, Koch KW, Mafi A. Multiple-beam Propagation in an Anderson Localized Optical Fiber. Opt Express (2013) 21(1):305–13. doi:10.1364/OE.21.000305

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Karbasi S, Koch KW, Mafi A. Modal Perspective on the Transverse Anderson Localization of Light in Disordered Optical Lattices. J Opt Soc Am B (2013) 30(6):1452–61. doi:10.1364/JOSAB.30.001452

CrossRef Full Text | Google Scholar

90. Abaie B, Mafi A. Scaling Analysis of Transverse Anderson Localization in a Disordered Optical Waveguide. Phys Rev B (2016) 94(6):064201. doi:10.1103/physrevb.94.064201

CrossRef Full Text | Google Scholar

91. Lahini Y, Avidan A, Pozzi F, Sorel M, Morandotti R, Christodoulides DN, et al. Anderson Localization and Nonlinearity in One-Dimensional Disordered Photonic Lattices. Phys Rev Lett (2008) 100(1):013906. doi:10.1103/PhysRevLett.100.013906

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Szameit A, Kartashov YV, Zeil P, Dreisow F, Heinrich M, Keil R, et al. Wave Localization at the Boundary of Disordered Photonic Lattices. Opt Lett (2010) 35(8):1172–4. doi:10.1364/OL.35.001172

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Martin L, Di Giuseppe G, Perez-Leija A, Keil R, Dreisow F, Heinrich M, et al. Anderson Localization in Optical Waveguide Arrays with off-diagonal Coupling Disorder. Opt Express (2011) 19(14):13636–46. doi:10.1364/OE.19.013636

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Kartashov YV, Konotop VV, Vysloukh VA, Torner L. Light Localization in Nonuniformly Randomized Lattices. Opt Lett (2012) 37(3):286–8. doi:10.1364/OL.37.000286

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Karbasi S, Hawkins T, Ballato J, Koch KW, Mafi A. Transverse Anderson Localization in a Disordered Glass Optical Fiber. Opt Mater Express (2012) 2(11):1496–503. doi:10.1364/OME.2.001496

CrossRef Full Text | Google Scholar

96. Chen M, Li M-J. Observing Transverse Anderson Localization in Random Air Line Based Fiber. In: Proceedings Volume 8994, Photonic and Phononic Properties of Engineered Nanostructures IV; 19 February 2014; San Francisco, California, United States. San Francisco, California: SPIE (2014). doi:10.1117/12.2036573

CrossRef Full Text | Google Scholar

97. Tong HT, Cheng T, Kuroyanagi s, Tanaka S, Nagasaka K, Suzuki T, et al. Fabrication of an All-Solid Tellurite Disordered Optical Rod for Transverse Localization of Light. In: Lasers Congress 2016 (ASSL, LSC, LAC). Boston, Massachusetts: Optical Society of America (2016).

Google Scholar

98. Mafi A, Ballato J, Koch KW, Schülzgen A. Disordered Anderson Localization Optical Fibers for Image Transport-A Review. Published in: Journal of Lightwave Technology (2019) 37(22):5652–5659. doi:10.1109/JLT.2019.2916020

CrossRef Full Text | Google Scholar

99. Mafi A, Tuggle M, Bassett C, Mobini E, Ballato J. Advances in the Fabrication of Disordered Transverse Anderson Localizing Optical Fibers [Invited]. Opt Mater Express (2019) 9(7):2769–74. doi:10.1364/Ome.9.002769

CrossRef Full Text | Google Scholar

100. Hoang Tuan T, Kuroyanagi S, Nagasaka K, Suzuki T, Ohishi Y. Characterization of an All-Solid Disordered Tellurite Glass Optical Fiber and its NIR Optical Image Transport. Jpn J Appl Phys (2019) 58(3):032005. doi:10.7567/1347-4065/aaf926

CrossRef Full Text | Google Scholar

101. Karbasi S, Koch KW, Mafi A. Image Transport Quality Can Be Improved in Disordered Waveguides. Opt Commun (2013) 311:72–6. doi:10.1016/j.optcom.2013.08.042

CrossRef Full Text | Google Scholar

102. Karbasi S, Frazier RJ, Mirr CR, Koch KW, Mafi A. Fabrication and Characterization of Disordered Polymer Optical Fibers for Transverse Anderson Localization of Light. JoVE (2013) 102 (77) 50679. doi:10.3791/50679

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Zhao J, Peysokhan M, Antonio-Lopez JE, Sun Y, Abaie B, Mafi AA Path to High-Quality Imaging through Disordered Optical Fibers: a Review. Appl Opt (2019) 58(13):D50–D60. doi:10.1364/AO.58.000D50

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Svelto O. Properties of Laser Beams. In: Principles of Lasers. Boston, MA: Springer US (2010). p. 475–504. doi:10.1007/978-1-4419-1302-9_11

CrossRef Full Text | Google Scholar

105. Zhang J, Zhao J, Lin H, Tan Y, Cheng J-X. High-Speed Chemical Imaging by Dense-Net Learning of Femtosecond Stimulated Raman Scattering. J Phys Chem Lett (2020) 11(20):8573–8. doi:10.1021/acs.jpclett.0c01598

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Rosenblatt F. The Perceptron, a Perceiving and Recognizing Automaton Project Para. Cornell Aeronautical Laboratory (1957).

Google Scholar

107. Minsky M, Papert SA. Perceptrons: An Introduction to Computational Geometry. The MIT Press (2017). doi:10.7551/mitpress/11301.001.0001

CrossRef Full Text | Google Scholar

108. Rumelhart DE, Hinton GE, Williams RJ. Learning Representations by Back-Propagating Errors. Nature (1986) 323(6088):533–6. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

109. David ER, James LM. Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations. MIT Press (1987).

Google Scholar

110. Zhou Y-T, Chellappa R, Vaid A, Jenkins BK. Image Restoration Using a Neural Network. IEEE Trans Acoust Speech, Signal Process. (1988) 36(7):1141–51. doi:10.1109/29.1641

CrossRef Full Text | Google Scholar

111. Schmidhuber J. Deep Learning in Neural Networks: An Overview. Neural Networks (2015) 61:85–117. doi:10.1016/j.neunet.2014.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Widrow B, Lehr MA. 30 Years of Adaptive Neural Networks: Perceptron, Madaline, and Backpropagation. Proc IEEE (1990) 78(9):1415–42. doi:10.1109/5.58323

CrossRef Full Text | Google Scholar

113. Krizhevsky A, Sutskever I, Hinton GE. ImageNet Classification with Deep Convolutional Neural Networks. Commun ACM (2017) 60(6):84–90. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

114. Deng J, Dong W, Socher R, Li L-J, Li Fei-Fei L, Li F-F. ImageNet: A Large-Scale Hierarchical Image Database. In: 2009 IEEE Conference on Computer Vision and Pattern Recognition; 20-25 June 2009; Miami, FL, USA. IEEE (2009). doi:10.1109/CVPR.2009.5206848

CrossRef Full Text | Google Scholar

115. Silver D, Huang A, Maddison CJ, Guez A, Sifre L, van den Driessche G, et al. Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature (2016) 529(7587):484–9. doi:10.1038/nature16961

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Silver D, Schrittwieser J, Simonyan K, Antonoglou I, Huang A, Guez A, et al. Mastering the Game of Go without Human Knowledge. Nature (2017) 550(7676):354–9. doi:10.1038/nature24270

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Mitchell TM. Machine Learning. McGraw-Hill (1997).

Google Scholar

118. Zhou Wang Z, Bovik AC. Mean Squared Error: Love it or Leave it? A New Look at Signal Fidelity Measures. IEEE Signal Process Mag (2009) 26(1):98–117. doi:10.1109/MSP.2008.930649

CrossRef Full Text | Google Scholar

119. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image Quality Assessment: from Error Visibility to Structural Similarity. IEEE Trans Image Process (2004) 13(4):600–12. doi:10.1109/TIP.2003.819861

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Kingma DP, Ba J. arXiv:1412.6980 (2014). Adam: A Method for Stochastic Optimization.

Google Scholar

121. Wang H, Rivenson Y, Jin Y, Wei Z, Gao R, Günaydın H, et al. Deep Learning Enables Cross-Modality Super-resolution in Fluorescence Microscopy. Nat Methods (2019) 16(1):103–10. doi:10.1038/s41592-018-0239-0

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Rivenson Y, Wang H, Wei Z, de Haan K, Zhang Y, Wu Y, et al. Virtual Histological Staining of Unlabelled Tissue-Autofluorescence Images via Deep Learning. Nat Biomed Eng (2019) 3:466–77. doi:10.1038/s41551-019-0362-y

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Rivenson Y, Göröcs Z, Günaydin H, Zhang Y, Wang H, Ozcan A. Deep Learning Microscopy. Optica (2017) 4(11):1437–43. doi:10.1364/OPTICA.4.001437

CrossRef Full Text | Google Scholar

124. Sinha A, Lee J, Li S, Barbastathis G. Lensless Computational Imaging through Deep Learning. Optica (2017) 4(9):1117–25. doi:10.1364/OPTICA.4.001117

CrossRef Full Text | Google Scholar

125. Goy A, Arthur K, Li S, Barbastathis G. Low Photon Count Phase Retrieval Using Deep Learning. Phys Rev Lett (2018) 121(24):243902. doi:10.1103/PhysRevLett.121.243902

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Pinkard H, Phillips Z, Babakhani A, Fletcher DA, Waller L. Deep Learning for Single-Shot Autofocus Microscopy. Optica (2019) 6(6):794–7. doi:10.1364/OPTICA.6.000794

CrossRef Full Text | Google Scholar

127. Bostan E, Heckel R, Chen M, Kellman M, Waller L. Deep Phase Decoder: Self-Calibrating Phase Microscopy with an Untrained Deep Neural Network. Optica (2020) 7(6):559–62. doi:10.1364/OPTICA.389314

CrossRef Full Text | Google Scholar

128. Wang Y, Pinkard H, Zhou S, Waller L, Huang B. Image Denoising for Fluorescence Microscopy by Self-Supervised Transfer Learning. bioRxiv, 2021.02.01.429188 (2021). doi:10.1101/2021.02.01.429188

CrossRef Full Text | Google Scholar

129. Cheng S, Fu S, Kim YM, Song W, Li Y, Xue Y, et al. Single-cell Cytometry via Multiplexed Fluorescence Prediction by Label-free Reflectance Microscopy. Sci Adv (2021) 7(3):eabe0431. doi:10.1126/sciadv.abe0431

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Kohoutová L, Heo J, Cha S, Lee S, Moon T, Wager TD, et al. Toward a Unified Framework for Interpreting Machine-Learning Models in Neuroimaging. Nat Protoc (2020) 15(4):1399–435. doi:10.1038/s41596-019-0289-5

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Huff DT, Weisman AJ, Jeraj R. Interpretation and Visualization Techniques for Deep Learning Models in Medical Imaging. Phys Med Biol (2021) 66(4):04TR01. doi:10.1088/1361-6560/abcd17

PubMed Abstract | CrossRef Full Text | Google Scholar

132. Sheu Y-h. Illuminating the Black Box: Interpreting Deep Neural Network Models for Psychiatric Research. Front Psychiatry (2020) 11(1091). doi:10.3389/fpsyt.2020.551299

PubMed Abstract | CrossRef Full Text | Google Scholar

133. Zhao J, Fan S, Antonio-Lopez JE, Schülzgen A. Deep Learning Imaging through Specialty Multi-Mode Fibers. In: Optical Fiber Communication Conference (OFC) 2020; San Diego, California. Optical Society of America (2020). doi:10.1364/OFC.2020.W1B.1

CrossRef Full Text | Google Scholar

134. Hu X, Zhao J, Fan S, Antonio-Lopez JE, Correa RA, Schülzgen A. Learning-Supported Full-Color Cell Imaging through Disordered Optical Fiber. In: Conference on Lasers and Electro-Optics; Washington, DC. Washington, DC United States: Optical Society of America (2020). doi:10.1364/CLEO_SI.2020.SM2L.5

CrossRef Full Text | Google Scholar

135. Ronneberger O, Fischer P, Brox T. U-net: Convolutional Networks for Biomedical Image Segmentation. In: N Navab, J Hornegger, WM Wells&A, and F Frangi, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Cham: Springer International Publishing (2015). doi:10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

136. Szegedy C, Wei Liu L, Yangqing Jia J, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going Deeper with Convolutions. In: 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 7-12 June 2015; Boston, MA, USA. IEEE (2015). doi:10.1109/CVPR.2015.7298594

CrossRef Full Text | Google Scholar

137. He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 27-30 June 2016; Las Vegas, NV, USA. IEEE (2016). doi:10.1109/CVPR.2016.90

CrossRef Full Text | Google Scholar

138. Simonyan K, Zisserman A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv:1409.1556 (2014).

Google Scholar

139. Cook K, Canning J, Leon-Saval S, Reid Z, Hossain MA, Comatti J-E, et al. Air-structured Optical Fiber Drawn from a 3D-Printed Preform. Opt Lett (2015) 40(17):3966–9. doi:10.1364/OL.40.003966

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Chu Y, Fu X, Luo Y, Canning J, Tian Y, Cook K, et al. Silica Optical Fiber Drawn from 3D Printed Preforms. Opt Lett (2019) 44(21):5358–61. doi:10.1364/OL.44.005358

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Carcreff J, Cheviré F, Galdo E, Lebullenger R, Gautier A, Adam JL, et al. Mid-infrared Hollow Core Fiber Drawn from a 3D Printed Chalcogenide Glass Preform. Opt Mater Express (2021) 11(1):198–209. doi:10.1364/OME.415090

CrossRef Full Text | Google Scholar

142. van der Elst L, Faccini de Lima C, Gokce Kurtoglu M, Koraganji VN, Zheng M, Gumennik A. 3D Printing in Fiber-Device Technology. Adv Fiber Mater (2021) 3(2):59–75. doi:10.1007/s42765-020-00056-6

CrossRef Full Text | Google Scholar

143. El-Mallawany R. Tellurite Glass Smart Materials: Applications in Optics and beyond. Springer International Publishing (2018).

Google Scholar

144. Jha A, Richards BDO, Jose G, Toney Fernandez T, Hill CJ, Lousteau J, et al. Review on Structural, thermal, Optical and Spectroscopic Properties of Tellurium Oxide Based Glasses for Fibre Optic and Waveguide Applications. Int Mater Rev (2012) 57(6):357–82. doi:10.1179/1743280412Y.0000000005

CrossRef Full Text | Google Scholar

145. Creswell A, White T, Dumoulin V, Arulkumaran K, Sengupta B, Bharath AA. Generative Adversarial Networks: An Overview. IEEE Signal Process Mag (2018) 35(1):53–65. doi:10.1109/MSP.2017.2765202

CrossRef Full Text | Google Scholar

146. Monakhova K, Tran V, Kuo G, Waller L. Untrained Networks for Compressive Lensless Photography. Opt Express (2021) 29(13):20913–29. doi:10.1364/OE.424075

PubMed Abstract | CrossRef Full Text | Google Scholar

147. van Engelen JE, Hoos HH. A Survey on Semi-supervised Learning. Mach Learn (2020) 109(2):373–440. doi:10.1007/s10994-019-05855-6

CrossRef Full Text | Google Scholar

148. Bansal A, Ma S, Ramanan D, Sheikh Y. Recycle-GAN: Unsupervised Video Retargeting. In: ECCV (2018). doi:10.1007/978-3-030-01228-1_8

CrossRef Full Text | Google Scholar