Heat Generation by Electrical Current in a Quantum Dot Hybridized to Majorana Nanowires

Heat current generated by electronic transport through a quantum dot (QD) coupled to both a phonon bath and a Majorana nanowire hosting Majorana bound states (MBSs) is theoretically studied in the framework of non-equilibrium Green’s function technique. The calculated numerical results show that electrical current can be either enhanced or suppressed by the combined influences of the phonon bath and the MBSs at certain bias voltage regimes. The enhancement and suppression of the current’s magnitude for a fixed bias voltage will be reversed due to the direct hybridization between the MBSs. The simultaneous coupling between both MBSs will amplify the function of the MBSs on the current, with the same unchanged and essential qualitative impacts. Heat generation by the electrical current can be fully adjusted by the dot–MBS coupling, direct hybridization between the MBSs, and positions of the dot level. By properly choosing the above parameters, heat generation can be suppressed even for increased electrical current, which is favorable in removing waste heat generated by electrical current flowing through low-dimensional circuits.

1 Introduction

With continuing decreased size and increased density of electronic devices integrated in circuits, the issue of heat generation by electrical current becomes progressively vital. In mesoscopic and nanoscale systems, heat is mainly generated from electron–phonon interaction (EPI), by which the energy accompanying the electric current flowing through the scattering region is transferred to the phonon bath as heat. In fact, recent progresses in nano-fabrication and characterization have brought about a new subject of phononics, which is interested in carrying heat current and information by phonons in addition to electrons or photons [1, 2]. Similar to the case in the usual electronics, the elementary unit in phononics is the preparation, detection, and manipulation of the thermal diode and memory devices. The thermal diode is to switch on–off or to amplify heat current [3, 4], and the thermal memory devices are building blocks for a quantum computer in terms of phonons [5, 6]. Up to now, phononics is still in its primary stage in that the movement of phonons is quite difficult to be controlled, which is contrary to the case of electrons. This is mainly because those phonons are quasiparticles behaving as energy elements without either bare mass or charge [1, 2], which is totally different from the characteristics of electrons. In addition, there are no interactions between single phonon modes. Thus, understanding the nature and controlling the movement of phonons with the help of EPI has become a much interesting research subject, and many theoretical and experimental works about phonon-assisted tunneling through low-dimensional systems have been performed [2–10].

Very similar to the characteristics of phonons, another quasiparticle known as Majorana bound states (MBSs) with zero mass and charge has recently been extensively studied both theoretically and experimentally [11]. The MBSs are of their own antiparticles having no energy and have been successfully formed in various platforms, including superconductors with a non-centrosymmetric center [12, 13], topological insulators in proximity to superconductors [14], defects located in topological superconductors [15], and p-wave superconductors [16]. They are also realizable even in the semiconductor [17] or ferromagnetic [18] nanowires having strong spin–orbit interaction or Josephson junctions [19]. They are very promising in both fault-tolerant quantum computation and energy conservation electronic setups. In line with the preparation of MBSs, their detection is also an important task due to the unique zero-energy, chargeless, and massless nature. Motivated by this, many detection schemes for the existence of MBSs have been proposed, among which the most important one is the electrical transport spectroscopy which applies an electric field on the setup having MBSs and then detects the associated electrical current. The MBS induces an abnormal zero-bias peak in the differential conductance, by which the existence of MBSs can be deduced [20, 21]. This zero-bias peak in the differential conductance, however, can also be induced by other mechanisms, such as the Kondo effect [16] and Andreev bound states [20]. Some other schemes, for example, the unusual sign change or enhancement of thermopower by MBSs, were proposed recently [22–24]. Moreover, a semiconductor quantum dot (QD) side-coupled to MBSs and sandwiched between leads was also introduced to break electron–hole symmetry to avoid null thermoelectric signatures. A previous work shows that the sign change induced by changes in the dot level, dot–MBS coupling strength, and direct MBS–MBS coupling are an efficient demonstration of MBSs. The thermoelectric effect assisted by MBSs was studied in structures composed of a QD connected to more than one lead. Moreover, universal Majorana thermoelectric noise in such similar systems was proposed as a non-invasive electrical detection scheme for the MBSs [24]. Optical detection schemes were also put forward in recent years [25–28]. For example, Liu et al. demonstrated that MBSs will absorb and emit photons and then induce photon-assisted side band in the conductance, which can split the MBSs and result in a novel non-zero MBS mode. This provides a new detection means for the MBSs which are very different from the previously proposed ones [25]. All-optical detecting plans for the MBSs were put forward by Zhu et al. [26] relying on a QD coupled to nanomechanical resonators, and they found that the optical signatures are enhanced by MBSs. Tang et al. [29] have proved that the existence of MBSs will induce a sign change of the tunnel magnetic resistance, which measures the relative change in the electronic currents when the magnetic moments of two leads are changing from parallel to antiparallel configurations.

Heat generation by electrical current in universal nanostructures was theoretically investigated by Sun et al. by the non-equilibrium Keldysh Green’s function method [30], in which the heat originates from the EPI. The authors proved that the behaviors of the heat current in low-dimensional systems are quite different from Joule’s law valid in macroscopic structures. This issue then arouse many investigations [31–33], and it was found that phonon emission processes occur if the Coulomb repulsion equals the phonon energy and induces a high peak in heat generation at even a small electric current [32]. By changing the energy levels in the QD, the heat current decreases regardless of increased electrical bias voltage as the electrons emit phonons in this process. This may induce a negative differential of heat generation [32]. If the scattering region is under a temperature difference between its two ends, it was found that the electrons tunneling through the dot will absorb heat current from the phonon bath to the scattering region and then serve as a nano-refrigerator [32, 33]. In view of the similarities between phonons and MBSs, here we study electrical current and heat exchanged between electrons passing through a QD and a phonon bath interacting with the QD under the influence of a Majorana nanowire hosting MBSs (see Figure 1). Our results show that both the electrical current and heat generation can be fully adjusted by the existence of MBSs. Under some conditions, the electrical current can be enhanced with small heat generation, which is useful in energy-saving devices.

FIGURE 1

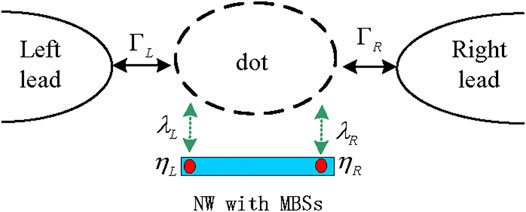
FIGURE 1. Plot of a quantum dot connected to MBSs prepared at the ends of a topological superconductor nanowire. The dot is coupled to the left and right leads and to a phonon bath with phonon frequency ${\omega }_q$.

2 Model and Methods

The Hamiltonian of the considered system composed of a semiconductor QD coupled to two leads and a Majorana nanowire is written as follows ($\hslash =1$) [30, 34–37]:

$H={\displaystyle \sum }_{k,\beta }{\epsilon }_{k\beta }{c}_{k\beta }^{†}{c}_{k\beta }+\left[{\epsilon }_d+{\lambda }_q\left(a^{†}+a\right)\right]d^{†}d+{\omega }_q{a}^{†}a+{\displaystyle \sum }_{k,\beta }\left(t_{k\beta }{c}_{k\beta }^{†}d+H.c\right)+H_{MBSs},(1)$

where the first term is for the left ($\beta =L$) and the right ($\beta =R$) electron lead with $c_{k\beta }^{†}$$\left(c_{k\beta }\right)$ being the electron creation (annihilation) operator having momentum k and energy ${\epsilon }_{k\beta }$. The second term denotes the electron on the QD, and $d_{\sigma }^{†}$$\left(d_{\sigma }\right)$ creates (annihilates) an electron with a quantized energy level ${\epsilon }_d$. $a^{†}\left(a\right)$ accounts for the creation (annihilation) operator of a phonon with frequency ${\omega }_q$, and the quantity ${\lambda }_q$ is the electron–phonon coupling magnitude. The third term denotes the single phonon mode, and the fourth term describes hopping between the QD and the leads with $t_{k\beta }$ being the matrix element. The last term in Eq. 1 is for the MBSs and their coupling to the QD [34–37], given as follows:

$H_{MBSs}=i{\delta }_M{\eta }_L{\eta }_R+\left({\lambda }_{L}d-{\lambda }_L^{\text{*}}{d}^{†}\right){\eta }_L+\left({\lambda }_{R}d+{\lambda }_R^{\text{*}}{d}^{†}\right){\eta }_R,(2)$

where the operator ${\eta }_{L/R}$ stands for the mode located on the left/right end of the nanowire and is coupled to the QD with the strength of ${\lambda }_{L/R}$, with ${\epsilon }_M$ being the overlap strength bewteen them. The Majorana operators satisfy $\left\{{\eta }_{\alpha },{\eta }_{\beta }\right\}=2{\delta }_{\alpha \beta }$ and ${\eta }_{\alpha }={\eta }_{\alpha }^{†}$. We follow the previous work to switch from the Majorana fermion representation to the equivalent regular fermion one by defining [34] ${\eta }_L=\left(1/\sqrt{2}\right)\left(f+f^{†}\right)$ and ${\eta }_R=\left(-i/\sqrt{2}\right)\left(f-f^{†}\right)$; the Hamiltonian $H_{MBSs}$ is rewritten as follows:

$H_{MBSs}={\epsilon }_M\left(f^{†}f-\frac{1}{2}\right)+\frac{1}{\sqrt{2}}\left({\lambda }_{L}d-{\lambda }_L^{\text{*}}{d}^{†}\right)\left(f+f^{†}\right)-\frac{1}{\sqrt{2}}\left({\lambda }_{R}d+{\lambda }_R^{\text{*}}{d}^{†}\right)\left(f-f^{†}\right).(3)$

We then perform a canonical transformation to eliminate the electron–phonon coupling, that is, [30–32] $\tilde{H}=XH{X}^{†}$ with $X=\text{exp}\left[\left({\lambda }_q/{\omega }_q\right)\left(a_q^{†}-a_q\right)d^{†}d\right]$. The transformed Hamiltonian reads as follows:

$\tilde{H}={\displaystyle \sum }_{k,\beta }{\epsilon }_{k\beta }{c}_{k\beta }^{†}{c}_{k\beta }+{\tilde{\epsilon }}_d{d}^{†}d+{\displaystyle \sum }_{k,\alpha }\left({\tilde{t}}_{k\beta }{c}_{k\alpha }^{†}d+H.c\right)+{\tilde{H}}_{MBSs},(4)$

where the dot level is transformed into ${\tilde{\epsilon }}_d={\epsilon }_d-g{\omega }_q$ with $g={\left({\lambda }_q/{\omega }_q\right)}^2$. The tunneling matrix element $t_{k\beta }$ and the dot–MBS coupling strengths ${\lambda }_{L/R}$ are individually transformed into ${\tilde{t}}_{k\alpha }=t_{k\alpha }X$ and ${\tilde{\lambda }}_{L/R}={\lambda }_{L/R}X$ with $X=\text{exp}\left[-g\left(a^{†}-a\right)\right]$. When $t_{k\alpha }$ is small compared to ${\lambda }_q$, X can be replaced by its expectation value $\langle X\rangle =\text{exp}\left[-g\left(N_{ph}+1/2\right)\right]$, in which $N_{ph}=1/\left[\text{exp}\left({\omega }_q/k_B{T}_p\right)-1\right]$ describes the phonon distribution function with $T_p$ being the phonon temperature [12, 13]. The Fourier transform of heat generation $Q\left(t\right)={\omega }_q\langle d{a}_q^{†}\left(t\right)a_q\left(t\right)/dt\rangle$ can be calculated from the above Hamiltonian and is as follows [30]:

$Q=\text{Re}{\omega }_q{\lambda }_q^2{{\displaystyle {\displaystyle \int \frac{d\epsilon }{2\pi }}}}^{\text{}}\left\{{\tilde{G}}^{<}\left(\epsilon \right){\tilde{G}}^{>}\left(\overline{\epsilon }\right)-2N_{ph}\left[{\tilde{G}}^{>}\left(\epsilon \right){\tilde{G}}^a\left(\overline{\epsilon }\right)+{\tilde{G}}^r\left(\epsilon \right){\tilde{G}}^{>}\left(\overline{\epsilon }\right)\right]\right\},(5)$

where $\overline{\epsilon }=\epsilon -{\omega }_q$ and ${\tilde{G}}^{r,a,\langle ,\rangle }\left(\epsilon \right)$ are the electron single-particle Green’s function. By using the equation of motion method, the retarded Green’s function is given by [30, 34–37]

${\tilde{G}}^r\left(\epsilon \right)=\frac{1}{\epsilon -{\tilde{\epsilon }}_d+i\widetilde{\text{Γ}}-K_1-|{\tilde{\lambda }}_L^2-{\tilde{\lambda }}_R^2{|}^{2}K\tilde{K}},(6)$

where $\widetilde{\text{Γ}}=\left({\widetilde{\text{Γ}}}_L+{\widetilde{\text{Γ}}}_R\right)/2$, with ${\widetilde{\text{Γ}}}_{\beta }=\text{exp}\left[-g\left(2N_{ph}+1\right)\right]{\text{Γ}}_{\beta }$ and ${\text{Γ}}_{\beta }=2\pi |t_{k\beta }{|}^2{\rho }_{\beta }$ (${\rho }_{\beta }$ is the local density of states in the lead β). The advanced Green’s function in the above equation is ${\tilde{G}}^a\left(\epsilon \right)={\left[{\tilde{G}}^r\left(\epsilon \right)\right]}^{\text{*}}$, and the lesser (greater) one is ${\tilde{G}}^{<(>)}\left(\epsilon \right)={\tilde{G}}^r\left(\epsilon \right){\widetilde{\text{Σ}}}^{<(>)}{\tilde{G}}^a\left(\epsilon \right)$, in which the self-energies are individually given by ${\widetilde{\text{Σ}}}^{<}=i\left[{\widetilde{\text{Γ}}}_L{f}_L\left(\epsilon \right)+{\widetilde{\text{Γ}}}_R{f}_R\left(\epsilon \right)\right]$ and ${\widetilde{\text{Σ}}}^{>}=-i\left\{{\widetilde{\text{Γ}}}_L\left[1-f_L\left(\epsilon \right)\right]+{\widetilde{\text{Γ}}}_R\left[1-f_R\left(\epsilon \right)\right]\right\}$ [15]. The Fermi distribution function is $f_{\beta }\left(\epsilon \right)=1/\left\{\text{exp}\left[\left(\epsilon -{\mu }_{\beta }\right)/k_B{T}_e\right]+1\right\}$, with chemical potential ${\mu }_{\beta }$. The quantities K, $K_1$, and $\tilde{K}$ in the above equation are given as $K=\epsilon /\left({\epsilon }^2-{\delta }_M^2\right),K_1=\left|{\tilde{\lambda }}_L-{\tilde{\lambda }}_R{|}^2\right|/2\left(\epsilon -{\delta }_M\right)+{\left|{\tilde{\lambda }}_L+{\tilde{\lambda }}_R\right|}^2/2\left(\epsilon +{\delta }_M\right)\tilde{K}=1/\left(\epsilon -{\tilde{\epsilon }}_d+i\widetilde{\text{Γ}}-K_2\right)$, and $K_2={\left|{\tilde{\lambda }}_L+{\tilde{\lambda }}_R\right|}^2/2\left(\epsilon -{\delta }_M\right)+{\left|{\tilde{\lambda }}_L-{\tilde{\lambda }}_R\right|}^2/2\left(\epsilon +{\delta }_M\right)$. In terms of the above canonical transformation, $G^r\left(\epsilon \right)$ is related to ${\tilde{G}}^r\left(\epsilon \right)$ by [7, 30] $G^r\left(\epsilon \right)={\displaystyle {\sum }_{n=-\infty }^{n=\infty }{L}_n\left\{{\tilde{G}}^r\left(\epsilon -n{\omega }_q\right)+\left[{\tilde{G}}^{<}\left(\epsilon -n{\omega }_q\right)-{\tilde{G}}^{<}\left(\epsilon +n{\omega }_q\right)\right]/2\right\}},$ and ${\tilde{G}}^{<}\left(\epsilon \right)=-2i({\text{Γ}}_L{f}_L\left(\epsilon \right)+{\text{Γ}}_R{f}_R\left(\epsilon \right)/\left({\text{Γ}}_L+{\text{Γ}}_R\right)\text{Im}{\tilde{G}}^r\left(\epsilon \right),$ and $L_n$ is given by $L_n=\text{exp}\left[-g\left(2N_{ph}+1\right)\right]\text{exp}\left(n{\omega }_q/2k_{B}T\right)I_n\left[2g\sqrt{2N_{ph}\left(N_{ph}+1\right)}\right]$, with $I_n\left(x\right)$ being the modified nth Bessel function. Finally, the electric current through the system reads as [7, 30]

$J=-\frac{e}{h}{{\displaystyle \int }}^{\text{}}\frac{d\epsilon }{2\pi }\left[f_L\left(\epsilon \right)-f_R\left(\epsilon \right)\right]\frac{{\text{Γ}}_L{\text{Γ}}_R}{{\text{Γ}}_L+{\text{Γ}}_R}\text{Im}{G}^r\left(\epsilon \right).(7)$

3 Results and Discussion

In this section, we present our numerical results of heat generation Q and electrical current J versus either the bias voltage $eV$ or the renormalized dot level ${\tilde{\epsilon }}_d$. We assume identical coupling between the dot and the two leads, that is, ${\text{Γ}}_L={\text{Γ}}_R=\text{Γ,}$ and choose $\widetilde{\text{Γ}}=1$ as the energy unit. To compare our results with those in the absence of MBSs given in Ref. 10, we set ${\omega }_q={\lambda }_q=3\widetilde{\text{Γ}}$ and symmetrical bias ${\mu }_L=-{\mu }_R=eV/2$. Usually, the QD and the phonon bath are at the same temperature $T_{ph}=T_e$, which is fixed at a rather low value of $0.00025\widetilde{\text{Γ}}$ favorable in experiments concerning the MBSs. When the dot is decoupled from the Majorana ${\tilde{\lambda }}_L={\tilde{\lambda }}_R=0$, the electrical current in Figure 2A increases with the increasing bias voltage and shows several small steps due to the phonon-assisted transport processes [7, 30–33]. The reason is that the dot’s level shifts to ${\tilde{\epsilon }}_d={\epsilon }_d-g{\omega }_q$ in the presence of EPI [7, 30–33], and then electrons transport through the dot whenever ${\mu }_L={\tilde{\epsilon }}_d+n{\omega }_q$ or ${\mu }_R={\tilde{\epsilon }}_d-n{\omega }_q$ for the present case of $V\ge 0$. The electric differential conductance $G_{dif}=\partial J/\partial V$ then will develop sharp peaks at the above leads’ chemical potentials [7], which is not illustrated here. Heat generation in Figure 2B also increases with the increasing bias voltage, but with a delay of ${\omega }_q$ as compared to the case in electric current [30]. The reason is that the heat Q is generated by the phonon emission processes from the state of ε to an empty state of $\epsilon -{\omega }_q$ [30]. Under the condition of $eV<{\omega }_q$, the energy provided by the external electric field is smaller than the phonon energy $\hslash {\omega }_q$, and then electrons cannot tunnel through the state and heat generation is zero. As shown in previous studies, such a delay effect of heat generation with respect to the current is more distinct at lower temperatures [30, 31]. It is worth pointing out that the steps in heat generation emerge at a different value of bias voltage in the electric current. It is well known that the current plateau is induced as the dot level ${\tilde{\epsilon }}_d$ and is in between the bias window, but that of heat generation emerges at$eV=2{\omega }_q$.

FIGURE 2

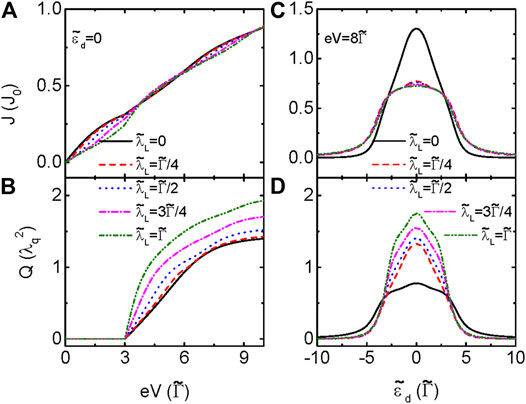
FIGURE 2. Electrical current (A) and heat generation (B) as functions of the bias voltage for ${\tilde{\epsilon }}_d=0$ at different ${\tilde{\lambda }}_L$. (C, D) Electrical current and heat generation vs the dot level for $eV=8\widetilde{\text{Γ}}$ and different ${\tilde{\lambda }}_L$. Other parameters are ${\omega }_q={\lambda }_q=3\tilde{\Gamma },$${\delta }_M={\tilde{\lambda }}_R$ = 0, and $T_e=T_p=0.00025\widetilde{\text{Γ}}$.

When the dot is hybridized to the MBSs formed at the left side of the nanowire (${\tilde{\lambda }}_L\ne 0$, ${\tilde{\lambda }}_R=0$), the magnitude of the electrical current in Figure 2A can be either enhanced or suppressed depending on the value of the bias voltage. More specifically, the current is suppressed in the bias regimes of $0\le eV\le {\omega }_q$ and $2{\omega }_q\le eV\le 3{\omega }_q$, whereas it is enhanced in the bias regime of ${\omega }_q\le eV\le 2{\omega }_q$. The reason is that, in these two regimes, the electrons emit and absorb phonons and the energy is lost and gained, respectively. As a consequence of it, the differential conductance will develop peaks at $eV=n{\omega }_q$ (not illustrated in the present manuscript), which is qualitatively consistent with the results found in Ref. [30]. Moreover, the peaks in the differential conductance may be positive corresponding to current’s increment or negative due to current’s decrement. The variation of the current or the differential conductance also indicates the phonon emission and absorption processes. The reason of the above results is that, in the presence of side-coupled MBSs [34], the jumps in the current are consistent with the eigenstates of the QD, which are at $\epsilon =\pm \sqrt{{\tilde{\epsilon }}_d^2+{\tilde{\lambda }}_L^2}$ and 0 [34–36]. From this, one can see that the electric current depends on EPI and hybridization between electrons in the dot and the MBSs. Heat generation in Figure 2B, however, is monotonously enhanced in the bias regimes of $eV\ge {\omega }_q$ in the presence of dot–MBS coupling. Such a behavior of heat generation proves that the relationship between the electrical current and the heat does not follow Joule’s law of $Q=JV$ valid in mesoscopic systems [30]. The enhancement of heat generation can be explained as follows [30]: heat generation arises from the phonon emission processes as an electron located at an energy state of ε transmitting to an empty state of $\epsilon -{\omega }_q$. On the condition of $eV<{\omega }_q$, the electric field cannot supply enough energy for electrons to fulfill such a process, and then the heat current is zero, which is the delay effect as shown in Figure 2. When the bias voltage $eV\ge {\omega }_q$, electrons will absorb enough energy to emit phonons and the magnitude of heat generation is increased accordingly. In the presence of coupling between the dot and MBSs, additional molecular states $\epsilon =\pm \sqrt{{\tilde{\epsilon }}_d^2+{\tilde{\lambda }}_L^2}$ are induced as discussed above, and then the phonon emission processes will become easier and heat generation is then increased. As the value of ${\tilde{\lambda }}_L$ is increased, heat generation is further enhanced as indicated in Figure 2B because the roles of the molecular states induced by dot–MBS coupling become more and more important. Figures 2B,C present the electrical current and heat generation versus the dot level ${\tilde{\epsilon }}_d$ for fixed $eV=8\widetilde{\text{Γ}}$ and different values of ${\tilde{\lambda }}_L$. The current is suppressed by the dot–MBS coupling when the dot level locates within $-\left({\omega }_q-\widetilde{\text{Γ}}\right)\le {\tilde{\epsilon }}_d\le {\omega }_q-\widetilde{\text{Γ}}$, which is qualitatively in agreement with the results obtained in Ref. [30] and Figure 2A. As ${\tilde{\epsilon }}_d\ge \left|{\omega }_q-\widetilde{\text{Γ}}\right|$, it is found that the current is increased by hybridization between the dot and the MBSs. This is induced by the newly emerged molecular state from the MBSs. The change in heat generation in Figure 2D is essentially opposite to the electrical current in Figure 2C. When the dot level is within $-\left({\omega }_q-\widetilde{\text{Γ}}\right)\le {\tilde{\epsilon }}_d\le {\omega }_q-\widetilde{\text{Γ}}$, the magnitude of heat generation is obviously enhanced due to the molecular states arisen from the coupling between the dot and the MBSs, which makes the phonon-emitting processes to become easier [30]. Out of this regime, heat generation is slightly enhanced by the increasing value of ${\tilde{\lambda }}_L$. The reason is that the zero-energy MBSs only play dominant roles near around ${\tilde{\epsilon }}_d=0$. When the dot level is much higher or lower than zero, the phonon-emitting processes due to the MBS-induced molecular states become difficult, and then heat generation is decreased. From Figure 2, it can be seen that, by tuning the dot level and the bias voltage, one can effectively adjust the magnitude of either the electrical current or heat generation, which is favorable in device design [30].

In real experiments, the two modes of the MBSs formed at different ends of a nanowire interact with each other with an amplitude of ${\delta }_M\propto e^{-\xi /L}$, where L is the length of the nanowire and ξ is the electrons’ coherence length [34–37]. Some previous works have demonstrated that this hybridization between the MBSs results in a sharp peak in the conductance when the dot level is aligned to the leads’ chemical potential and another two side peaks at about $\epsilon =\pm \sqrt{{\tilde{\epsilon }}_d^2+{\tilde{\lambda }}_L^2+{\delta }_M^2}$[34]. If the MBS–MBS coupling is strong enough, the central peak in the conductance reduces to the case of resonant level. Under the condition of ${\delta }_M\ne 0$ as shown in Figure 3A, the magnitude of the electrical current J increases when the bias voltage locates within $2n{\omega }_q\le eV\le \left(2n+1\right){\omega }_q$ and decreases as the bias voltage is $\left(2n+1\right){\omega }_q\le eV\le 2\left(n+1\right){\omega }_q$ with $n=\mathrm{0,1,2......}$. Such a change in the current induced by the MBS–MBS coupling is totally different from that in Figure 2A, where ${\delta }_M=0$. The reason is that the impact of hybridization between the MBSs will be suppressed due to their overlapping. The magnitude of heat generation in Figure 3B, however, is monotonously suppressed in the whole bias voltage regime except when $eV\le {\omega }_q$. For large enough MBS–MBS coupling strength (${\delta }_M={\tilde{\lambda }}_L=\widetilde{\text{Γ}}$), the magnitude of heat generation reduces almost to the case of the single dot decoupled from the MBSs (${\tilde{\lambda }}_L=0$). This can be seen by comparing the yellow dotted line in Figure 3B and the black solid one in Figure 2B. The reduction of heat generation by the inter-MBS coupling is because that the impact of each isolated mode of the MBSs is weakened if the MBSs at the two ends of the nanowire overlap with each other. In other words, the phonon absorbed by one MBS formed at one end of the nanowire will be subsequently emitted by the other MBS at the other end of the nanowire. As a result of it, the MBS-assisted heat generation is reduced as shown in Figure 3B. By comparing the curves in Figure 3B of ${\delta }_M=0$ (black solid line) with those of ${\delta }_M\ne 0$, one can find that the direct hybridization between the MBSs ${\delta }_M$ will strengthen the jumps in heat generation. As indicated above, the phonon absorbed (emitted) by one mode of the MBSs will be subsequently emitted (absorbed) by the other mode. Such phonon absorption and emission processes will change the behaviors of heat generation and induce additional jumps. We emphasize that even the impacts of the MBSs on the heat generation processes are weakened in the presence of hybridization between the MBSs, and the behavior of heat generation is quite different from the case of no MBSs because there are more phonon absorption and emission processes by interaction between the QD and the MBSs.

FIGURE 3

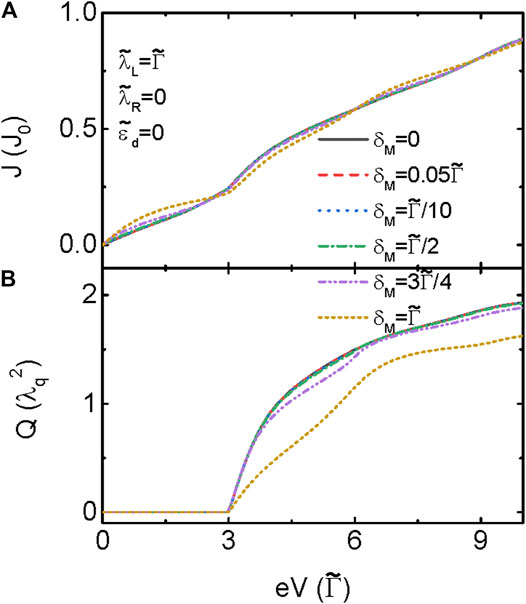
FIGURE 3. (A) Electrical current and (B) heat generation as functions of the bias voltage at different ${\delta }_M$. Other parameters are the same as in Figure 2.

If both ends of the nanowire are close to the QD [34, 35], the MBSs prepared may couple to the dot simultaneously. In 2011, Flensberg proposed a scheme composed of a QD that couples to both modes of the MBSs to implement a $\pi /8$ phase gate. The author proved that, by adding or removing one electron, non-Abelian rotations at the ground state with Majorana fermions are realizable and also proposed a scheme based on a QD with intradot Coulomb interaction. Moreover, the state of the system with Majorana fermions can also be read out with the help of the QD by a charge measurement. We present the electrical current J and heat generation Q in Figure 4 with finite values of ${\widetilde{\text{Γ}}}_L$ and ${\widetilde{\text{Γ}}}_R$. The behavior of the current in Figure 4A resembles that in Figure 2A, is further enhanced when the bias voltage is $2n{\omega }_q\le eV\le \left(2n+1\right){\omega }_q$, and decreases as $\left(2n+1\right){\omega }_q\le eV\le 2\left(n+1\right){\omega }_q$ by the increasing value of ${\tilde{\lambda }}_R$. The reason is that, for ${\delta }_M=0$, the dot is coupled to both isolated MBSs, which contribute to the tunneling processes almost independently. Heat generation in Figure 4B also resembles that in Figure 2B and is monotonously enhanced due to the presence of ${\tilde{\lambda }}_R$ as long as $eV\ge {\omega }_q$. The jumps in Figure 4A are more obvious if both modes of the MBSs are coupled to the dot than those in Figure 2A in which only the left mode of the MBSs is coupled to the dot. Figures 4C,D show the electrical current and heat generation on the condition of the dot are symmetrically coupled to the two modes of the MBSs with ${\widetilde{\text{Γ}}}_L={\widetilde{\text{Γ}}}_R=\widetilde{\text{Γ}}$. Similar to the results in Figure 3B, the current’s magnitude in Figure 4C is enhanced (suppressed) by MBS–MBS coupling ${\delta }_M$ when the bias voltage is within $\left(2n+1\right){\omega }_q\le eV\le 2\left(n+1\right){\omega }_q$ ($2n{\omega }_q\le eV\le \left(2n+1\right){\omega }_q$). Again, the amplitude of heat generation in Figure 4D is monotonously suppressed with the increasing value of ${\delta }_M$ for $eV\ge {\omega }_q$. Interestingly, the current can be enhanced when the bias voltage is within $6{\omega }_q\le eV\le 9{\omega }_q$, whereas heat generation is suppressed in the presence of direct hybridization between the MBSs, a phenomenon favorable in designing energy conservation devices.

FIGURE 4

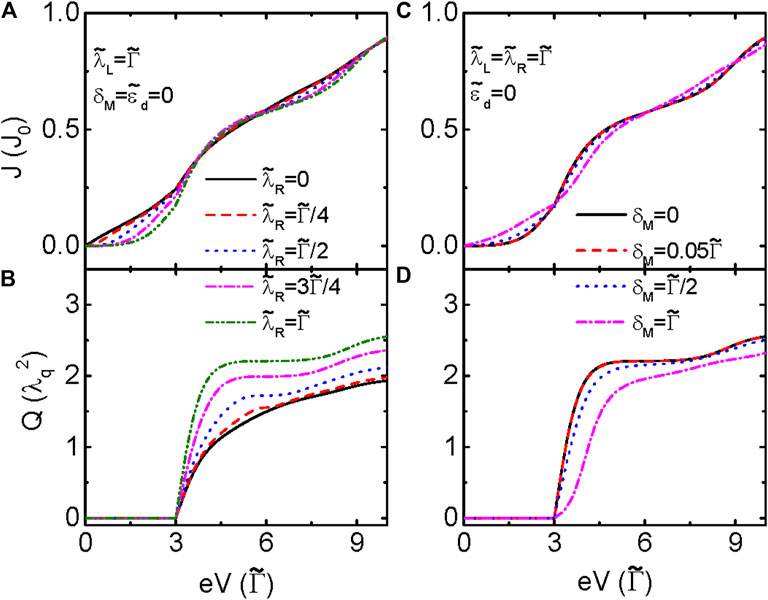
FIGURE 4. Electrical current and heat generation (A, B) as functions of the bias voltage and (C, D) vs the dot level at different values of ${\tilde{\lambda }}_R$. Other parameters are given in the figure and the same as in Figure 2.

4 Summary

In summary, the present paper studies electric transport and heat generation in a QD side-coupled to MBSs formed at opposite ends of a topological nanowire. It is found that the amplitude of the phonon-assisted current can be either enhanced or suppressed depending on the value of bias voltage compared to the phonon energy. If the dot is simultaneously coupled to the two isolated modes of the MBSs, the change in the current becomes more obvious, but it essentially resembles the case when it is coupled to only one mode of the MBSs. The direct overlap between the MBSs will totally reverse the functions of the MBSs on the current’s magnitude, which is individually enhanced and suppressed by hybridization between the MBSs in the bias regimes between which the current is suppressed and enhanced when the dot is only coupled to one isolated mode of the MBSs. The magnitude of heat generation is monotonously enhanced when the dot is coupled to either one or both of the isolated MBSs, whereas it is monotonously suppressed in the presence of direct overlap between the two MBSs. The variation of the electrical current and heat generation due to the MBSs enables the possibility of simultaneously enhancing the current while suppressing the generated heat and is ideal in designing energy conservation devices.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.

Author Contributions

ZW derived the formulae, performed the numerical calculations, and wrote the original manuscipt.

Funding

This work was supported by the thirteenth five-year plan of educational science in Fujian Province (Grant No. 2019CG0707).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Li NB, Ren J, Wang L, Zhang G, Hanggi P, Li BW. Colloquium: Phononics: Manipulating Heat Flow with Electronic Analogs and Beyond. Rev Mod Phys (2012) 84:1045–66. doi:10.1103/RevModPhys.84.1045

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Balandin AA. Nanophononics: Phonon Engineering in Nanostructures and Nanodevices. J Nanosci Nanotech (2005) 5:1015–22. doi:10.1166/jnn.2005.175

CrossRef Full Text | Google Scholar

3. Liang B, Yuan B, Cheng J-c. Acoustic Diode: Rectification of Acoustic Energy Flux in One-Dimensional Systems. Phys Rev Lett (2009) 103:104301. doi:10.1103/PhysRevLett.103.104301

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Li B, Wang L, Casati G. Thermal Diode: Rectification of Heat Flux. Phys Rev Lett (2004) 93:184301. doi:10.1103/PhysRevLett.93.184301

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Xie R, Bui CT, Varghese B, Zhang Q, Sow CH, Li B, et al. An Electrically Tuned Solid-State Thermal Memory Based on Metal-Insulator Transition of Single-Crystalline VO2 Nanobeams. Adv Funct Mater (2011) 21:1602–7. doi:10.1002/adfm.201002436

CrossRef Full Text | Google Scholar

6. Dubi Y, Di Ventra M. Colloquium: Heat Flow and Thermoelectricity in Atomic and Molecular Junctions. Rev Mod Phys (2011) 83:131–55. doi:10.1103/RevModPhys.83.131

CrossRef Full Text | Google Scholar

7. Chen Z-Z, Lü R, Zhu B-f. Effects of Electron-Phonon Interaction on Nonequilibrium Transport through a Single-Molecule Transistor. Phys Rev B (2005) 71:165324. doi:10.1103/PhysRevB.71.165324

CrossRef Full Text | Google Scholar

8. Balandin A, Wang KL. Significant Decrease of the Lattice thermal Conductivity Due to Phonon Confinement in a Free-Standing Semiconductor Quantum Well. Phys Rev B (1998) 58:1544–9. doi:10.1103/PhysRevB.58.1544

CrossRef Full Text | Google Scholar

9. Shamsa M, Liu W, Balandin AA, Liu J. Phonon-hopping thermal Conduction in Quantum Dot Superlattices. Appl Phys Lett (2005) 87:202105. doi:10.1063/1.2130711

CrossRef Full Text | Google Scholar

10. Rego LGC, Kirczenow G. Quantized thermal Conductance of Dielectric Quantum Wires. Phys Rev Lett (1998) 81:232–5. doi:10.1103/PhysRevLett.81.232

CrossRef Full Text | Google Scholar

11. Fu L, Kane CL. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys Rev Lett (2008) 100:096407. doi:10.1103/PhysRevLett.100.096407

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Alicea J, Oreg Y, Refael G, von Oppen F, Fisher MPA. Non-abelian Statistics and Topological Quantum Information Processing in 1d Wire Networks. Nat Phys (2011) 7:412–7. doi:10.1038/nphys1915

CrossRef Full Text | Google Scholar

13. Karzig T, Knapp C, Lutchyn RM, Bonderson P, Hastings MB, Nayak C, et al. Scalable Designs for Quasiparticle-Poisoning-Protected Topological Quantum Computation with Majorana Zero Modes. Phys Rev B (2017) 95:1–32. doi:10.1103/PhysRevB.95.235305

CrossRef Full Text | Google Scholar

14. Sato M, Fujimoto S. Topological Phases of Noncentrosymmetric Superconductors: Edge States, Majorana Fermions, and Non-abelian Statistics. Phys Rev B (2009) 79:1–16. doi:10.1103/PhysRevB.79.09450410.1103/physrevb.79.094504

CrossRef Full Text | Google Scholar

15. Qi X-L, Zhang S-C. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

16. Wang R, Su W, Zhu J-X, Ting CS, Li H, Chen C, et al. Kondo Signatures of a Quantum Magnetic Impurity in Topological Superconductors. Phys Rev Lett (2019) 122:1–6. doi:10.1103/PhysRevLett.122.087001

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Mourik V, Zuo K, Frolov SM, Plissard SR, Bakkers EPAM, Kouwenhoven LP. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science (2012) 336:1003–7. doi:10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Choy T-P, Edge JM, Akhmerov AR, Beenakker CWJ. Majorana Fermions Emerging from Magnetic Nanoparticles on a Superconductor without Spin-Orbit Coupling. Phys Rev B (2011) 84:1–6. doi:10.1103/PhysRevB.84.195442

CrossRef Full Text | Google Scholar

19. San-Jose P, Prada E, Aguado R. Ac Josephson Effect in Finite-Length Nanowire Junctions with Majorana Modes. Phys Rev Lett (2012) 108:1–5. doi:10.1103/PhysRevLett.108.257001

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ricco LS, de Souza M, Figueira MS, Shelykh IA, Seridonio AC. Spin-dependent Zero-Bias Peak in a Hybrid Nanowire-Quantum Dot System: Distinguishing Isolated Majorana Fermions from Andreev Bound States. Phys Rev B (2019) 99:1–9. doi:10.1103/PhysRevB.99.155159

CrossRef Full Text | Google Scholar

21. Liu C-X, van Heck B, Wimmer M. Josephson Current via an Isolated Majorana Zero Mode. Phys Rev B (2021) 103:1014510. doi:10.1103/PhysRevB.103.014510

CrossRef Full Text | Google Scholar

22. López R., Lee M., Serra L., Lim J. S. Thermoelectrical detection of majorana states. Phys Rev B (2014) 89:1–7. doi:10.1103/PhysRevB.89.205418

CrossRef Full Text | Google Scholar

23. Ricco LS, Dessotti FA, Shelykh IA, Figueira MS, Seridonio AC. Tuning of Heat and Charge Transport by Majorana Fermions. Sci Rep (2018) 8:2790–7. doi:10.1038/s41598-018-21180-9

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Smirnov S. Universal Majorana Thermoelectric Noise. Phys Rev B (2018) 97:1–14. doi:10.1103/PhysRevB.97.165434

CrossRef Full Text | Google Scholar

25. Tang H-Z, Zhang Y-T, Liu J-J. Photon-assisted Tunneling through a Topological Superconductor with Majorana Bound States. AIP ADVANCES (2015) 5:1–8. doi:10.1063/1.4939096

CrossRef Full Text | Google Scholar

26. Chen H, Zhu K. All-optical Scheme for Detecting the Possible Majorana Signature Based on Qd and Nanomechanical Resonator Systems. Sci China Phys Mech Astron (2015) 58:1–14. doi:10.1007/s11433-014-5637-4

CrossRef Full Text | Google Scholar

27. Väyrynen JI, Rastelli G, Belzig W, Glazman LI. Microwave Signatures of Majorana States in a Topological Josephson junction. Phys Rev B (2015) 92:1345081–5. doi:10.1103/PhysRevB.92.134508

CrossRef Full Text | Google Scholar

28. Chi F, He T-Y, Wang J, Fu Z-G, Liu L-M, Liu P, et al. Photon-assisted Transport through a Quantum Dot Side-Coupled to Majorana Bound States. Front Phys (2020) 8:2541–7. doi:10.3389/fphy.2020.00254

CrossRef Full Text | Google Scholar

29. Tang L-W, Mao W-G. Detection of Majorana Bound States by Sign Change of the Tunnel Magnetoresistance in a Quantum Dot Coupled to Ferromagnetic Electrodes. Front Phys (2020) 8:1471–8. doi:10.3389/fphy.2020.00147

CrossRef Full Text | Google Scholar

30. Sun Q-f., Xie XC. Heat Generation by Electric Current in Mesoscopic Devices. Phys Rev B (2007) 75:155306. doi:10.1103/PhysRevB.75.155306

CrossRef Full Text | Google Scholar

31. Liu J, Song J, Sun Q-f., Xie XC. Electric-current-induced Heat Generation in a Strongly Interacting Quantum Dot in the Coulomb Blockade Regime. Phys Rev B (2009) 79:161309. doi:10.1103/PhysRevB.79.161309

CrossRef Full Text | Google Scholar

32. Chi F, Zheng J, Liu Y-S, Guo Y. Refrigeration Effect in a Single-Level Quantum Dot with thermal Bias. Appl Phys Lett (2012) 100:233106. doi:10.1063/1.4720093

CrossRef Full Text | Google Scholar

33. Chi F, Sun L-L. Photon-assisted Heat Generation by Electric Current in a Quantum Dot Attached to Ferromagnetic Leads. Chin Phys. Lett. (2016) 33:1–6. doi:10.1088/0256-307X/33/11/117201

CrossRef Full Text | Google Scholar

34. Liu DE, Baranger HU. Detecting a Majorana-Fermion Zero Mode Using a Quantum Dot. Phys Rev B (2011) 84:201308R. doi:10.1103/PhysRevB.84.201308

CrossRef Full Text | Google Scholar

35. Prada E, Aguado R, San-Jose P. Measuring Majorana Nonlocality and Spin Structure with a Quantum Dot. Phys Rev B (2017) 96:085418. doi:10.1103/PhysRevB.96.085418

CrossRef Full Text | Google Scholar

36. Deng MT, Vaitiekenas S, Prada E, San-Jose P, Nygard J, Krogstrup P, et al. Nonlocality of Majorana Modes in Hybrid Nanowires. Phys Rev B (2018) 98:085125. doi:10.1103/physrevb.98.085125

CrossRef Full Text | Google Scholar

37. Stefański P. Properties of the Majorana-State Tunneling Josephson junction Mediated by an Interacting Quantum Dot. J Phys Condens Matter (2019) 31:1–18. doi:10.1088/1361-648X/ab052a

CrossRef Full Text | Google Scholar