The Superluminal Phenomenon of Light Near the Kerr–Newman Black Hole or Super-Gravitational Source

We use the Kerr–Newman metric based on the theory of general relativity to discuss the observed superluminal phenomenon of light near the black hole and whether it is observable astronomically at infinity or a weak gravitational place such as on Earth. The black hole has the rotation term a and the charge term R_Q as well as the Schwarzschild radius R_S. The geodesic of light in the spacetime structure is ds² = 0, and the equation for three velocity components (dr/dt, rd$\theta$/dt, rsin$\theta$d$\varphi$/dt) is obtained in the Boyer-Lindquist coordinates (r, θ$,$and $\varphi$) with the coordinate time t. Then, three cases of the velocity of light (dr/dt, 0, and 0), (0, rd$\theta$/dt, and 0), and (0, 0, and rsin$\theta$d$\varphi$/dt) are discussed in this research. According to our discussion, only the case of (dr/dt, 0, and 0) gives the possibility of the observations of the superluminal phenomenon and an example is shown at r between R_S and $(R_Q^2+a^2{\text{sin}}^2\theta /2)/R_S$at sin$\theta$>0, when R_Q ∼ R_S. The results reveal that the maximum speed of light and the range of the superluminal phenomenon are much related to the rotational term a and the charged term R_Q. It is at least reasonable at two poles and in the equatorial plane, when light propagates along the radial direction. Although the superluminal phenomenon is discussed in the Boyer-Lindquist coordinates, all the results are easy to be transformed or discussed in the Cartesian coordinates (x, y, z, t) by setting R² = x²+y²+z² = r²+a²sin²θ and rdr = RdR in the velocity of light. The conclusions of the superluminal phenomenon about the three velocity components (dR/dt, Rdθ/dt, Rsinθdϕ/dt) are different from them in the Boyer-Lindquist coordinates. Generally speaking, the superluminal phenomena for light can possibly occur in these cases where the radial velocity dr/dt is dominant, and the other two velocity components are comparably small. When the relative velocity between the observer coordinate frame and the black hole is not large, the superluminal phenomenon is possibly observable at infinity or in a weak gravitational frame such as on Earth. The results can also be applied on the super-gravitational sources.

Introduction

The so-called superluminal phenomenon [1] is an observation from a frame of reference that the speed of particle exceeds the speed of light c in free space. It is also called the faster-than-light (FTL) phenomenon, and some laboratory experiments [2] have been reported to demonstrate this. Some astronomical observations [1, 3–6] about this phenomenon have been revealed from relativistically massive sources near supermassive gravitational sources such as the black hole. Traditionally, the speed of light is limited in the theory of special relativity with a maximal value of c in free space. As we know, the free space is the flat spacetime structure and this maximal speed of light is a well certified phenomenon in special relativity. In this theory, as an electron in the synchrotron accelerator needs a lot of energy to reach its speed that is very close to c but does not always exceed c. It is the relativistic effect that the mass– energy equivalence principle exists, and the equivalent mass of the electron depends on its speed. Exceeding the speed of light seems unable to be observed macroscopically on Earth. Nowadays, it continuously attracts the attention of some scientists to investigate this FTL phenomenon. While some reports reveal this phenomenon, one always wants to explain it by the present theorem or try to break some concept such as the limitation of the speed of light to fit the phenomenon.

As early as in 1983, seven superluminal motions observed in the nuclei of some radio sources had been reported in a conference [7]. It pointed out that NRAO 140, 3C120, 3C273, 3C279, 3C345, 3C179, and BL Lac appear to separate with speeds greater than that of light [8]. The occurrences of superluminality are shown at the time when the axis of emission rotates or processes into the line of sight of the observer [8]. This conclusion supports our research on the rotating black hole, and it makes our study meaningful. The observations of the superluminal motion have been widely studied and are paid much attention, and some important reports continuously reveal new observations on this topic [8–23]. Especially, the superluminal motion often lasts several years but not merely within a very short period [11, 18]. Until 1988, the number of the radio sources which showed superluminal motion reached up to 23 [15]. The research even affects the Hubble constant measurement [21, 22]. Traditionally speaking, the explanation is based on the theory of special relativity [14]. However, as we know, the space-time structure near a super-gravitational source such as a black hole is very different from the flat space-time structure described by the Minkowski metric. It has been pointed out in the conclusions of Ref. [15] that the problem of exceeding large linear size of superluminal sources seems to require modifications of the most naïve beaming theories. Such explanations based on the theory of special relativity have not been enough to convince, and we shall not use the theory of special relativity to explain the phenomena in the general relativity region. It needs us to develop a more complete and reliable explanation for super-gravitational sources. Thus, we propose a new way to enhance the astronomical explanation.

Gravitational time delay is another astronomical phenomenon that has attracted attention. It implies that the observed speed of light would slow down when light passes through a giant star [24–28]. This reveals that the observation about the speed of light is affected by gravity, and the measured speed of light is not constant for an observer in a reference frame such as on Earth. Because the theory of special relativity is based on the Minkowski metric describing a flat space–time structure, it is not suitable for us to explain some astronomical phenomena. Gravitational time delay is a well-known fact predicted by the theory of general relativity, and the place nearby the supermassive star with strong gravity is good for observation. This phenomenon motivates us to think about a question whether it is possible on Earth to directly or indirectly observe the speed of light exceeding c near the super-gravitational sources such as the black hole. It is the astronomical phenomenon and some astronomical observations show possibilities to investigate this kind of superluminal phenomenon for massive particles [1, 3–6] which may be essentially explained by the speed of light exceeding c.

In this research, we study this observable phenomenon for light based on the theory of general relativity with the Kerr–Newman metric in the Boyer-Lindquist coordinates [29–31] where the constant speed of light exists in a local frame with proper time. Our discussions focus on the black hole and give some special results for the possible occurrence of this superluminal phenomenon of light.

The Kerr–Newman Metric and the Speed of Light

When we discuss the geodesic of light at the black hole, an appropriate and sufficient choice is using the Kerr–Newman metric [29–31] because it considers the angular momentum J and charges Q of a black hole simultaneously. The rotation of a black hole is inherited from the previous star, and it may be charged because the black hole absorbs charged plasma from the high-temperature accretion clouds or neighboring stars. The line– element expression of the Kerr–Newman metric in a particular set of spherical coordinates, also called Boyer–Lindquist coordinates (r, $\theta$, and $\varphi$), is

$\text{d}{s}^2=-c^2\text{d}{\tau }^2=\left(\frac{\text{d}{r}^2}{\text{Δ}}+\text{d}{\theta }^2\right){\rho }^2-{\left(c\text{d}t-a{\text{sin}}^2\theta \text{d}\varphi \right)}^2\frac{\text{Δ}}{{\rho }^2}+{\left(\left(r^2+a^2\right)\text{d}\varphi -ac\text{d}t\right)}^2\frac{{\text{sin}}^2\theta }{{\rho }^2}, (1)$

where ds is the invariant interval, $\tau$ is the proper time, t is the coordinate time, and a = J/Mc, with mass M of the black hole is the term about the angular momentum per mass,

${\rho }^2=r^2+a^2{\text{cos}}^2\theta ,(2)$

and

$\text{Δ}=r^2-r{R}_S+a^2+R_Q^2.(3)$

The Schwarzschild radius is $R_S=2GM/c^2$and G is the gravitational constant. $R_Q^2=$KQ²G/c⁴ is the term related to charge Q, and K is Coulomb’s constant. In addition, coordinate time is the time shown by the clock stationed at infinity where the proper time and coordinate time becomes identical [32]. The geodesic of light is ds² = 0, then through deductions, we have the velocity of light obeying the following equation:

$\frac{{\rho }^4}{\text{Δ}\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}{\left(\frac{\text{d}r}{dt}\right)}^2+\frac{{\rho }^4 }{r^2\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}{\left(r\frac{\text{d}\theta }{\text{d}t}\right)}^2-\frac{(\text{Δ}{a}^2{\text{sin}}^2\theta -{(r^2+a^2)}^2) }{r^2\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}{\left(r\text{sin}\theta \frac{\text{d}\varphi }{dt}\right)}^2-\frac{2ac(-\text{Δ}+(r^2+a^2))\text{sin}\theta }{r\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}\left(r\text{sin}\theta \frac{\text{d}\varphi }{dt}\right)=c^2.(4)$

In Eq. 4, $\left(\frac{\text{d}r}{\text{d}t}\right)$, $\left(r\frac{\text{d}\theta }{\text{d}t}\right)$, and $\left(r\text{sin}\theta \frac{\text{d}\varphi }{dt}\right)$are the three velocity components of light in the Boyer-Lindquist (r, θ, Φ, and t) coordinates, respectively. Equation 4 is also the geodesic of light in space. This way to obtain the velocity of light from ds² = 0 has been used to get the velocity of light in the Schwarzschild metric [33–36]. It reveals that the velocity of light at the black hole is much different from the Minkowski space–time structure, and the formula given in Eq. 4 is much complicated and dependent on the mass, the angular momentum, as well as the charge of a black hole. In the next section, we discuss the possibility of the superluminal phenomenon for each velocity component individually. Although the superluminal phenomenon is discussed in the Boyer-Lindquist coordinates, all the results in the following discussions are easy to be transformed or discussed in the Cartesian coordinates (x, y, z, t) as long as we set R² = x²+y²+z² = r²+a²sin²θ and rdr = RdR in the velocity of light.

Because we discuss the rotating black hole, we check the gravitational dragging [35] or the frame-dragging effect [33] to make sure the reasonability of our results. The black hole has the angular velocity ω. We consider the instantaneously local reference frame rotating with angular velocity ω and tangential velocity v with respect to the black hole. Then, a light beam in the equatorial plane (θ = π/2) propagates in the radial direction toward the center of the Kerr–Newman black hole. According to the equivalence principle, the gravitational acceleration of the black hole and the induced acceleration of the curved movement are both along the radial direction. Two persons at different instantaneous reference frames observe different trajectories of light. One observer A is in this instantaneously dragging reference frame moving with the velocity v the same as the tangentially rotating velocity with respect to the black hole, and the other observer B is in the non-rotating reference frame which is freely falling or has equivalent acceleration in the radial direction. It is alike a situation that a man, observer A, stays on a transparent train with a velocity v moving toward the right, and the other man, observer B, stands at rest on the platform on Earth. From the viewpoint of observer B, a light beam perpendicular to the movement of the train passes through it directly as the light trajectory L₁ shown in Figure 1. However, due to the dragging-frame effect, the observer A will see the same light beam propagating along the light trajectory L₂. It means that the non-rotating reference frame has the same viewpoint as that of observer B when light propagates in the equatorial plane from the place far away from the Kerr–Newman black hole along the radial direction to its center. The dragging-frame effect does not exist in this situation. It is also true when light propagates toward two poles.

FIGURE 1

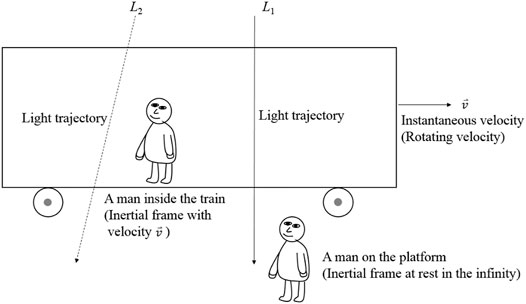
FIGURE 1. Observations of the light trajectory from different inertial frames. An inertial frame, the transparent train, has the tangential velocity v the same as the rotating velocity of the Kerr–Newman black hole. An observer stays on the train, and the other one is at rest on the platform. This observer on the platform is in the inertial frame far away from the black hole. A light beam observed by the observer on the platform is perpendicular to the movement of the train as the light trajectory L₁ where no dragging-frame effect exists. The same light beam observed by the observer moving with the train is the light trajectory L₂.

On the other hand, if light has no orbital angular momentum relative to the black hole at infinity, then the conservation of the orbital angular momentum has to be held even if light is very close to the black hole. Otherwise, the conservation of the orbital angular momentum is broken, and we have to ask where the additional orbital angular momentum comes from?

Before discussing, there is a basic requirement that the time is real at any reference frame. When we consider the geodesic along the radial direction without including the d$\varphi$term, then it requires the dt² term in Eq. 1 satisfying

${\rho }^2>0(5)$

and

$\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)>0.(6)$

From Eq. 6, it can be expanded as

$r^2-r{R}_S+R_Q^2+a^2{\text{cos}}^2\theta >0.(7)$

For any real r, Eq. 7 further requires the condition at r = R_S/2

$R_S^2\le 4\left(a^2{\text{cos}}^2\theta +R_Q^2\right).(8)$

It is the condition for the black hole at r = R_S/2, but at other place where r > 0 exists different condition. Such as at r = R_S, it requires

$R_Q^2+a^2{\text{cos}}^2\theta >0,(9)$

and at any r > R_S, Eq. 7 automatically satisfies till the place far away from the black hole. Although the event horizon depends on $\theta$, it is convenient to discuss the phenomenon using R_S as a reference position, and the event horizon approximates to a spherical surface while a << R_S and R_Q << R_S. Because the conditions of Eq. 8 holds true for all $\theta$, then it gives the lowest requirement

$R_S^2\le 4R_Q^2(10)$

at r = R_S/2 and $\theta$ = $\pi$/2, and Eq. 9 gives another requirement

$R_Q^2>0,(11)$

at r = R_S. Combining Eqs. 10, 11, it gives the $R_Q^2$ condition for the charged black hole. The other requirement for the dr² term in Eq. 1 is

$\text{Δ}>0.(12)$

It also gives the other condition at r = R_S/2 and θ = π/2

$R_S^2\le 4\left(a^2+R_Q^2\right).(13)$

From Eqs. 10, 13, the minimum rotated condition can be obtained

$0\le \left|a\right|(14)$

However, at r = R_S similar to Eq. 10, the requirement is

$R_Q^2+a^2>0,(15)$

which automatically satisfies the requirement. The other factor worth mentioning is ${\rho }^2$ when it is at the denominator. It raises a mathematical singularity at r = 0 and $\theta$ = $\pi$/2. If the black hole has a finite-sized nucleus, this singularity will automatically be removed because J = 0, Q = 0 as well as zero gravity at r = 0. According to Eqs. 10, 14, it means that even the massive star is very heavy, and in the formation of a charged and rotating black hole, there exists some basic conditions.

We may ask whether it is possible for a finite-sized nucleus to exist inside the black hole and remove the curvature singularity at r = 0? If so, it can solve the singularity problem at r = 0 from the black hole. Significant research in analyzing the radiating Schwarzschild black hole first introduces a coordinate coherent state approach to noncommutative effects in the weak field limit [37]. The absence of any curvature singularity at the terminal stage of the black hole evaporation is concluded. The physical meaning of noncommutativity is the concept of the point-like particles which no longer is meaningful, and it is replaced by the Gaussian mass density

${\rho }_{l_1}\left(\overrightarrow{r}\right)=\frac{M}{{\left(4\pi l_1^2\right)}^{3/2}}exp\left(-\frac{r^2}{4l_1^2}\right),(16)$

where l₁ is the noncommutative parameter with dimension of length and also the minimal width of the Gaussian function [37–41], and M is the total particle mass or mass-energy of the source. Noncommutativity is thought as an intrinsic property of the space–time manifold and does not depend on the curvature [37, 38]. It can be introduced in the theory of general relativity by modifying the source of matter [38]. It also concludes three situations to judge the existence of the black hole where black holes with mass M < M₀ = 0.5π^1/2θ do not exist [37]. It is further improved by substituting Gaussian mass density into Einstein’s equation to obtain the minimal mass M₀ = 1.9θ/G, and one conclusion gives the existence of black holes with two event horizons where M > M₀ for the Schwarzschild black hole [38]. The other conclusion is that there is no curvature singularity at the origin, and a regular de Sitter core is obtained at a short distance [38]. No curvature singularity at the origin, neither ‘naked’ nor ‘shielded’ by the event horizons, is also pointed out in the research of the charged black hole by using noncommutative geometry and Gaussian mass density [39]. The smearing effect is also used to turn a point-like charge e into a “charge droplet” with the Gaussian profile whose mathematic form is the Gaussian charge cloud with a minimal width l₂ [39]

${\rho }_{el}\left(\overrightarrow{r}\right)=\frac{e}{{\left(4\pi l_2^2\right)}^{3/2}}exp\left(-\frac{r^2}{4l_2^2}\right).(17)$

Then, the Reissner–Nordstrӧm-like metric is obtained. The resulting metric describing curvature singularity free in the origin can smoothly interpolate between the ordinary Reissner–Nordstrӧm metric at a large distance and the de Sitter space–time structure at a short distance [39].

This approach is further used to obtain a new exact solution of Einstein’s equation describing the rotating black hole [40]. The Kerr-like metric is obtained to make sure no curvature ring singularity and no anti-gravity Universe with causality violation due to the existence of closed time-like world-lines is encountered [40]. For the rotating charged black hole, following the Newman–Janis algorithm and writing the metric in the Boyer–Lindquist coordinates, we can obtain the line element of a Kerr–Newman-like metric [41].

$d{s}^2=\frac{\Sigma -a^2{\text{sin}}^2\theta }{{\rho }^2}{c}^{2}d{t}^2-\frac{{\rho }^2}{\Sigma }d{r}^2-{\rho }^{2}d{\theta }^2+2ac{\text{sin}}^2\theta \left(1-\frac{\Sigma -a^2{\text{sin}}^2\theta }{{\rho }^2}\right)dtd\varphi -\left[{\rho }^2+a^2{\text{sin}}^2\theta \left(2-\frac{\Sigma -a^2{\text{sin}}^2\theta }{{\rho }^2}\right)\right]{\text{sin}}^2\theta d{\varphi }^2, (18)$

in which ${\rho }^2$ has the same definition as given in Eq. 2, and $\Sigma$ is similar to $\text{Δ}$ in Eq. 3 but r-dependent on R_S and R_Q, that is,

$\Sigma =r^2-r\frac{2Gm\left(r\right)}{c^2}+a^2+\frac{KG}{c^4}q{\left(r\right)}^2.(19)$

Two r-dependent terms in $\Sigma$ are

$m\left(r\right)=M\frac{\gamma \left(\frac{3}{2};\frac{r^2}{4l_1^2}\right)}{\text{Γ}\left(\frac{3}{2}\right)},(20)$

and

$q{\left(r\right)}^2=\frac{Q^2}{\pi }\left[{\gamma }^2\left(\frac{1}{2};\frac{r^2}{4l_2^2}\right)-\frac{r}{\sqrt{2}{l}_2}\gamma \left(\frac{1}{2};\frac{r^2}{2l_2^2}\right)+\frac{\sqrt{2}r}{l_2}\gamma \left(\frac{3}{2};\frac{r^2}{4l_2^2}\right)\right],(21)$

here the lower incomplete Gamma function is

$\gamma \left(n;\frac{r^2}{4l^2}\right)=\underset{0}{\overset{\frac{r^2}{4l^2}}{{\displaystyle \int }}}{t}^{n-1}{e}^{-t}dt,(22)$

and Γ is the complete Gamma function giving the following equation Γ (3/2) = $\sqrt{\pi }/2$. The place of the event horizons r_H = r_H (M, Q, a) is determined by 1/g_rr = 0 or Σ(r_H) = 0. If we focus on the gravitational effect and ignore the tiny mass outside the black hole, then the original Kerr–Newman metric can be used to discuss the problem of the speed of light we are interested here. This metric naturally changes to the ordinary Kerr–Newman metric at r > =r_H. According to Eq. 16, the mass of the black hole must be less than M

$4\pi \underset{0}{\overset{r_H}{{\displaystyle \int }}}dr{r}^2{\rho }_{l_1}\left(r\right)<M.(23)$

It means there is some part of the black hole outside the event horizon which is

$4\pi M\underset{r_H}{\overset{\infty }{{\displaystyle \int }}}dr{r}^2\frac{1}{{\left(4\pi l_1^2\right)}^{3/2}}exp\left(-\frac{r^2}{4l_1^2}\right)>0.(24)$

This kind of black hole connects with the space outside of the event horizon. One possible way to cure this problem is to adopt the mass of the black hole totally within the event horizon or the outer one if there are two event horizons. In this metric, by calculating the Ricci scalar and Kretschmann invariant, it shows that the noncommutative effect erases the singularity at the origin.

All above mentioned research studies [37–41] are deduced from the mathematical viewpoint to solve unreasonable features such as the curvature singularity. They are mathematical deductions without any physical assumptions of material structures. This mass distribution is an ideal distribution and, in reality, most stellar bodies show deviations of the mass density distribution from spherically symmetric distributions. It may still work in some situations. However, the real material structure shall also be considered for discussing the possibility of the black hole formation. Recently, experiments [42] showed that the pressure inside the proton is as high as 10³⁵ Pa, which is 10 times greater than the core pressure of a neutron star. Such a strong pressure inside the proton indicates that the proton has a great ability to withstand the squeeze of gravity, so gravity collapse becomes a questionable problem. Thus, we must reconsider the internal structure of the black hole. According to the estimated mass of the observable Universe [43], the average mass–energy equivalence of the observable Universe is about 1.3 × 10⁷⁰ J. From the viewpoint of Coulomb’s interaction, to form a charged sphere, a lot of work needs to be done. The self-energy and the work done to move 2 × 10³⁰ C electrons into a 1-m-radius spherical region from an infinite far place, can be approximated as

$E_{self}=\frac{3}{5}\frac{\left(8.987\times {10}^9\right){\left(2\times {10}^{30}\right)}^2}{1}=2.16\times {10}^{70} J.(25)$

In theory, we cannot shrink 2 × 10³⁰ C electrons into a spherical region with a radius less than 1 m, even if we use all the observable energy of the Universe. The effect of quantum electrodynamics holds Coulomb’s law still useful in this case, and some corrections of the many-particle effect can be ignored here. As we know, a black hole cannot get so much energy to shrink electrons into a very small space, therefore, in this case, the inside of the charged black hole is a finite-sized nucleus.

Actually, the brief summary mentioned above from some references gives a reliable precondition to study our problem. Especially, Eqs. 18, 19 are much close to the ideas we introduce here, although they are based on the Gaussian distributions of mass and charge. The difference is that we directly determine the ranges of mass and charge at each radial position inside the black hole by confirming the absence of mathematical divergence everywhere. In the following section, we introduce the finite-sized nucleus inside the black hole to provide some conditions for the mass and charge distributions inside the black hole.

The Judgment of the Superluminal Requirements From the Velocity Component dr/dt of Light

According to Eq. 4, when we discuss the speed of light in the radial direction, the other velocity components are found to be zero. This choice is a convenient way to discuss the superluminal conditions. The rule used here is also applied to discuss other velocity components individually. We first focus on the dr/dt velocity component to check whether the superluminal phenomenon of light exists or not. The radial motion confined to the equatorial plane has been considered in the rotating black hole [46]. When an observer rests in a reference frame such as on Earth or the place with very weak gravitation, Eq. 1 provides the time relationship between proper time and coordinate time

$\text{d}{\tau }^2=\frac{\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}{{\rho }^2}\text{d}{t}^2.(26)$

According to the equivalence principle in the theory of general relativity, the time dilation requires the coefficient of the dt² less than one which gives rise to the following condition

$r>R_Q^2/R_S.(27)$

The range for this requirement also exists between 0 and R_S, and considering Eq. 11 at r = R_S it requires

$R_S^2>R_Q^2>0.(28)$

When r > R_S, the time dilation automatically satisfies Eq. 28 because it gives the maximum of R_Q less than R_S. However, it seems that Eq. 27 is not well-defined for the region $R_Q^2/R_S>$r ≥ 0. It is for this reason that we adopt a singularity at the center of the black hole where all mass and charges gather. When we use the model of a finite-sized nucleus in the black hole, Coulomb’s repulsive force as well as the strong interaction makes all particles non-shrinkable to a singularity, and the problem can be solved by establishing the charge distribution between 0 and R_S. Then, R_Q is a function of r and $\theta$ related to the totally enclosed charges at (r,$\theta$), that is,

$R_Q=R_Q\left(r,\theta \right).(29)$

This assumption is the same as the concept of the Gaussian charge cloud given in Eqs. 17, 21. Except for the previous discussions that the Gaussian charge cloud as given in Eq. 17 inside the charged black holes is used in some research [39, 41], in this article, Eqs. 8, 9 also support this assumption. It also means that a is a function of (r,$\theta$) between 0 and R_S which might be due to the distribution of its mass M. From the viewpoint of the rotational movement, Eq. 29 is reasonable for a rotationally charged black hole. It means that the charge distributions in Eq. 29 have to ensure Eq. 27 between 0 and R_S correctly and the time dilation is still correct for r ≥ 0. Using r = $\alpha$R_S with 0<$\alpha$<1, then Eq. 7 becomes

$\left(R_Q^2+a^2{\text{cos}}^2\theta \right)/\left(\alpha -{\alpha }^2\right)>R_S^2.(30)$

This inequality holds true for all $\theta$. For very small a, combing Eq. 27 with Eq. 30 gives

$\alpha >R_Q^2/R_S^2>\left(\alpha -{\alpha }^2\right).(31)$

According to Eq. 31, it reveals the minimum and maximum of the charge distribution varying with the radial distance r form r = 0 to r = Rs as shown in Figures 2A,B. Equation 31 extends the Gaussian profile of the charge clouds to more general cases which satisfies more distribution possibilities inside the charged black holes, not only the choice of the Gaussian charge cloud [39, 41].

FIGURE 2

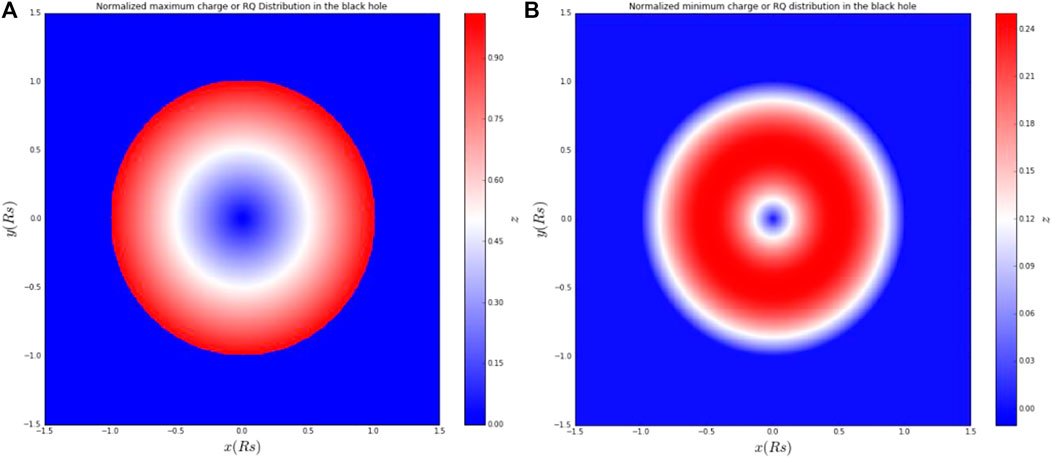
FIGURE 2. (A) Minimal distribution of R_Q and (B) the maximal distribution of R_Q varying with the radial distance r for very small a. The color bar is in units of R_S.

If the superluminal phenomenon occurs, it means $\left(\frac{\text{d}r}{\text{d}t}\right)>c$. Then according to the dr/dt term in Eq. 4, it gives the following requirement

$\frac{\text{Δ}\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}{{\rho }^4}>1.(32)$

Because ${\rho }^4>0$, it becomes

$\left({\text{Δ}}^2-\text{Δ}{a}^2{\text{sin}}^2\theta -{\rho }^4\right)>0.(33)$

Substituting Eqs. 2, 3 into Eq. 33 gives the following relation

$\begin{array}{l}0<2r^2(-r{R}_S+R_Q^2)+r^2{a}^2{\text{sin}}^2\theta +r^2{R}_S^2-2r{R}_S{R}_Q^2+R_Q^4\\ +(a^2+a^2{\text{cos}}^2\theta )(-r{R}_S+R_Q^2)+a^4{\text{cos}}^2\theta {\text{sin}}^2\theta .\end{array}(34)$

Further rearranging Eq. 34, we have

$\left(-r{R}_S+R_Q^2+a^2{\text{sin}}^2\theta /2\right)\left(2r^2-r{R}_S+R_Q^2+a^2/2+3a^2{\text{cos}}^2\theta /2\right)>a^4{\text{sin}}^4\theta /4,(\mathrm{35a})$

or

$\left(r{R}_S-R_Q^2-a^2{\text{sin}}^2\theta /2\right)\left(2r^2-r{R}_S+R_Q^2+a^2/2+3a^2{\text{cos}}^2\theta /2\right)<-a^4{\text{sin}}^4\theta /4.(\mathrm{35b})$

This inequality allows us to discuss the range for the occurrence of the superluminal phenomenon. First, the case at $\theta$ = 0 or $\pi$ is discussed, then Eq. 33 becomes

$(-r{R}_S+R_Q^2)(2r^2-r{R}_S+2a^2+R_Q^2)>0.(36)$

The solutions of Eq. 36 are

$-r{R}_S+R_Q^2>0(\mathrm{37a})$

and

$2r^2-r{R}_S+2a^2+R_Q^2>0.(\mathrm{37b})$

or

$-r{R}_S+R_Q^2<0(\mathrm{38a})$

and

$2r^2-r{R}_S+2a^2+R_Q^2<0.(\mathrm{38b})$

From Eqs. 37a, 37b, it gives the ranges of r that

$R_Q^2/R_S>r,(\mathrm{39a})$

$r<\frac{R_S-{\left[R_S^2-8\left(2a^2+R_Q^2\right)\right]}^{1/2}}{4},(\mathrm{39b})$

$r>\frac{R_S+{\left[R_S^2-8\left(2a^2+R_Q^2\right)\right]}^{1/2}}{4},(\mathrm{39c})$

accompanied with the condition in the square root due to the real r

$R_S^2\ge 8\left(R_Q^2+2a^2\right).(40)$

However, Eq. 39a does not satisfy the requirement in Eq. 27, and Eq. 40 obviously violates Eq. 13 at r = R_S/2 so we have to look for the other solution. Then, Eqs. 38a, 38b give other ranges for the superluminal phenomenon

$R_Q^2/R_S<r,(\mathrm{41a})$

and

$\frac{R_S-{[R_S^2-8\left(2a^2+R_Q^2\right)]}^{1/2}}{4}<r<\frac{R_S+{\left[R_S^2-8\left(2a^2+R_Q^2\right)\right]}^{1/2}}{4},(\mathrm{41b})$

with the same condition shown in Eq. 40. Both the abovementioned solutions for r cannot give satisfied ranges simultaneously. To sum up, the discussions from Eqs. 32–40, 41a, 41b are for the requirements and solutions of v_r², not v_r.

Then we discuss this phenomenon directly from the expression of the only velocity component (dr/dt) term obtained from Eq. 4. This term is as follows

$v_{r,pole}={\frac{\text{d}r}{\text{d}t}|}_{\theta =0,\pi }=\pm c\frac{r^2-r{R}_S+a^2+R_Q^2}{r^2+a^2}.(42)$

There are two expressions for (dr/dt), “+” One means light leaving away from the center of the black hole, and the symbol “−” means light propagating toward the center of the black hole. Therefore, the superluminal solution leaving away the center satisfies the condition $R_Q^2/R_S>r$. However, it still violates the requirement given in Eqs. 27, 28, gives r < R_S in Eq. 42. It means that the superluminal phenomenon does not take place when light leaves away from the center of the black hole at $\theta$ = 0 or $\pi$. The other superluminal solution toward the center has the same r condition that the superluminal phenomenon also does not take place when light propagates toward the center of the black hole at $\theta$ = 0 or $\pi$.

Next, Eq. 34 is discussed for any $\theta$situations. A tricky way to discuss Eq. 34 is to define

$a^4{\text{sin}}^4\theta /4=\left(\alpha a^2\right)\left(\beta a^2\right).(43)$

Then Eq. 34 can be directly divided into two terms

$\left(-r{R}_S+R_Q^2+a^2{\text{sin}}^2\theta /2\right)\ge \alpha a^2,(44)$

and

$\left(2r^2-r{R}_S+R_Q^2+a^2/2+3a^2{\text{cos}}^2\theta /2\right)\ge \beta a^2.(45)$

Equation 44 Gives the Range for the Superluminal Phenomenon

$r<\left[R_Q^2+a^2\left({\text{sin}}^2\theta /2-\alpha \right)\right]/R_S.(46)$

When Eq. 46 combines with Eq. 27, the range of r for the superluminal phenomenon is given as follows

$R_Q^2/R_S\le r<\left[R_Q^2+a^2\left({\text{sin}}^2\theta /2-\alpha \right)\right]/R_S.(47)$

It means that the superluminal phenomenon possibly occurs when this condition given in Eq. 47 is satisfied. Then, Eq. 47 further gives

${\text{sin}}^2\theta /2-\alpha >0,(\mathrm{48a})$

or

${\text{sin}}^2\theta /2>\alpha >0.(\mathrm{48b})$

In Eq. 48b, the first condition of α is defined. Meanwhile, the first condition of β is given by

$\beta >{\text{sin}}^2\theta /2.(49)$

In Eq. 45, it gives the second condition of β between R_Q, a, and R_S for the superluminal phenomenon

$\left[8\left(a^2/2+3a^2{\text{cos}}^2\theta /2+R_Q^2\right)-R_S^2\right]/8>\beta a^2.(50)$

Meanwhile, it also gives the second condition of $\alpha$ using Eqs. 43, 49, that is,

$2a^4{\text{sin}}^4\theta /[8(a^2/2+3a^2{\text{cos}}^2\theta /2+R_Q^2)-R_S^2]<\alpha a^2.(51)$

Combining 49 with 50, and 48b with 51, they give limited conditions for $\alpha$ and $\beta$, respectively

$\left[8\left(a^2/2+3a^2{\text{cos}}^2\theta /2+R_Q^2\right)-R_S^2\right]/8a^2>\beta >{\text{sin}}^2\theta /2,(52)$

and

${\text{sin}}^2\theta /2>\alpha >2a^2{\text{sin}}^4\theta /\left[8\left(a^2/2+3a^2{\text{cos}}^2\theta /2+R_Q^2\right) -R_S^2\right].(53)$

Furthermore, comparing the upper limitation with the lower limitation in Eq. 52 gives another condition for the other requirement of $R_Q^2$

$8\left(2a^2{\text{cos}}^2\theta +R_Q^2\right)>R_S^2.(54)$

This requirement is necessary to consider the superluminal phenomenon. After discussing the abovementioned conditions, the upper limitation of r can be obtained. Considering R_S ∼ R_Q, Eq. 47 reveals that the superluminal phenomena can be observed in the range

$R_S<r<R_S+a^2{\text{sin}}^2\theta /2R_S,(55)$

which is dependent on $\theta$. An example of the region where the superluminal phenomenon occurs for a black hole with a = 2R_S and R_Q = 0.999R_S is given in Figure 3A, where the deep blue region is a spherical region with a radius of R_S and the yellow region means the region for the occurrence of the superluminal phenomena. It means that the region of r ≥ R_S is discussed, and R_S is the boundary because it exists in the case of which the event horizon is close to a spherical surface when both a << R_S and R_Q << R_S. The furthest distance from the center of the black hole is given in Figure 3A is about 3R_S at the equator of $\theta$ = $\pi$/2. All the rotating axes as given in Figures 3A–D are parallel to the y-axis. According to Eq. 4, the speed distribution of light in the case of (dr/dt, 0, 0) is shown in Figure 3B where the unit of the color bar is c. The velocity distribution matches the region of the superluminal occurrence as given in Figure 3A and the maximum is about 2.20c at r = R_S and $\theta$ = $\pi$/2. When a is increased to 8R_S and R_Q is held at 0.999R_S, the speed distribution of light is as shown in Figure 3C. The maximum velocity of light is about 8c at r = R_S and $\theta$ = $\pi$/2, and the furthest distance of the superluminal phenomenon is 33R_S from the center of the black hole as shown in Figure 3C. For the case of a = 20R_S and R_Q = 0.999R_S, the speed distribution of light is as shown in Figure 3D. The maximum speed of light is about 20c at r = R_S and $\theta$ = $\pi$/2, and the farthest distance of the superluminal phenomenon is 201R_S from the center of the black hole in Figure 3D. From Figures 3C,D, the occurrences of the high speed of light is centered more and more toward the region near $\theta$ = $\pi$/2.

FIGURE 3

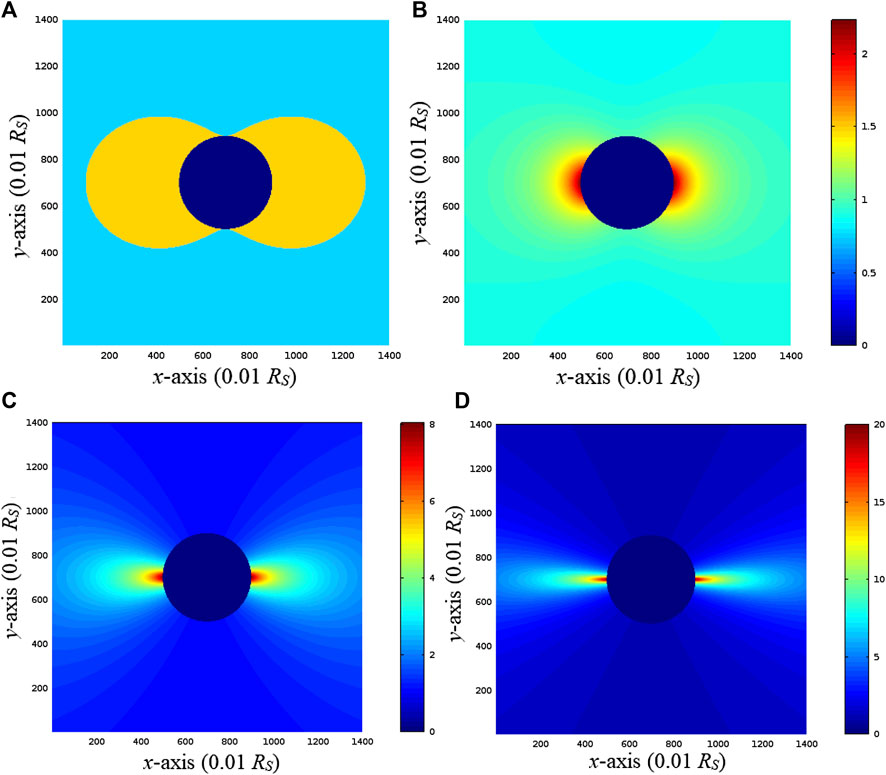
FIGURE 3. (A) Superluminal region is denoted by yellow. The center of the picture is a spherical region with a radius of R_S (deep blue color). In this case, a = 2R_S and R_Q = 0.999R_S. The maximum distance for the superluminal phenomenon from the center of the black hole is 3R_S at $\theta$ = $\pi$/2. (B) Speed distribution of light at a = 2R_S and R_Q = 0.999R_S. (C) Speed distribution of light at a = 8R_S and R_Q = 0.999R_S. The maximum distance of the superluminal phenomenon is 33R_S from the center of the black hole in this case. (D) Speed distribution at a = 20R_S and R_Q = 0.999R_S. The maximum distance of the superluminal phenomenon is 201R_S from the center of the black hole in this case. In all these cases, the rotational axes are parallel to the y-axis, and the color bars show in units of c.

Our discussion is using the Kerr–Newman metric that is a space–time solution in the theory of general relativity. So, considering light bending near the high-speed rotational supermassive black holes, it possibly explains some astronomical observations about the superluminal phenomena from the relativistically massive jet [1, 3–6]. This result can be also extended to some supermassive stars with very high density, large a, and R_Q.

The Judgment of the Superluminal Requirements for the Velocity Component r(d$\mathit{\theta }$/dt) of Light

The second study case is the velocity component rd$\theta$/dt term given in Eq. 4. All other velocity components are zero. This term is easy to check whether the superluminal phenomenon exists or not. Assuming that it happens, then

$\frac{r^2\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}{{\rho }^4}>1.(56)$

Expanding the abovementioned equation, we have

$r^2\left(-r{R}_S+R_Q^2\right)-r^2{a}^2{\text{cos}}^2\theta -a^4{\text{cos}}^4\theta >0.(57)$

It can be further rearranged as follows

$\left(-r{R}_S+R_Q^2-a^2{\text{cos}}^2\theta \right)r^2>a^4{\text{cos}}^4\theta .(58)$

Similar to the discussions of the velocity component dr/dt, a tricky way is to assume that

${\alpha }^2\beta ={\text{cos}}^4\theta .(59)$

Then, Eq. 58 gives the requirements of r as follows

$r^2>{\alpha }^2{a}^2,(60)$

$-r{R}_S+R_Q^2-a^2{\text{cos}}^2\theta >\beta a^2.(61)$

Combining Eq. 61 with 27, and considering the condition of Eq. 8, the range of r for the occurrence of the superluminal phenomenon is given by the following equation

$R_Q^2/R_S<r<\left(R_Q^2-a^2{\text{cos}}^2\theta -\beta a^2\right)/R_S..(62)$

Because $\beta \ge 0$, this requirement does not satisfy. Eq. 62 means that in this case of the velocity component $rd\theta /dt$ the superluminal phenomenon does not exist shown in the Boyer-Lindquist coordinates. However, this velocity component is possibly superluminal in the Cartesian coordinates at the condition in Eq. 27.

The Judgment of the Superluminal Requirements for the Velocity Component rsin$\mathit{\theta }$(d$\varphi$/dt) of Light

The velocity component rsin $\theta$(d$\varphi$/dt) term is the third case for discussing the possibility of the superluminal phenomenon. All other velocity components are zero. From Eq. 4, the velocity equation for this case is given as follows

$-\frac{(\text{Δ}{a}^2{\text{sin}}^2\theta -{(r^2+a^2)}^2) }{r^2\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}{\left(r\text{sin}\theta \frac{\text{d}\varphi }{dt}\right)}^2 -\frac{2ac\left(-\text{Δ}+\left(r^2+a^2\right)\right)\text{sin}\theta }{r\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}\left(r\text{sin}\theta \frac{\text{d}\varphi }{dt}\right)=c^2.(63)$

Next, we replace rsin $\theta$(d$\varphi$/dt) with hc, where h is a real value. Then the equation becomes

$-\frac{\left(\text{Δ}{a}^2{\text{sin}}^2\theta -{(r^2+a^2)}^2\right) }{r^2\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}{h}^2 -\frac{2a\left(-\text{Δ}+\left(r^2+a^2\right)\right)\text{sin}\theta }{r\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}h=1.(64)$

If the superluminal phenomenon takes place, it means h > 1. Eq. 64 is the second-order equation in the general form $A{h}^2+Bh+C=0.$It requires 0$\le B^2-4AC$to make sure the real solutions exists. According to this, we have the following equation

$0\le \frac{{\left\{2a\left[-\text{Δ}+\left(r^2+a^2\right)\right]\text{sin}\theta \right\}}^2-4\left[\text{Δ}{a}^2{\text{sin}}^2\theta -{(r^2+a^2)}^2\right]\left(\text{Δ}-a^2{\text{sin}}^2\theta \right) }{r^2{\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}^2}(65)$

After rearrangement, it gives

$0\le \frac{4\left({\text{r}}^2+a^2-r{R}_S+R_Q^2\right){\left(r^2+a^2{\text{cos}}^2\theta \right)}^2 }{r^2{\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}^2},(\mathrm{66a})$

or

$0\le \frac{4\text{Δ}{\rho }^4 }{r^2{\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}^2}.(\mathrm{66b})$

Because ${\rho }^4\ge$0 as well as the denominator $r^2{(\text{Δ}-a^2{\text{sin}}^2\theta )}^2\ge 0$, it requires $\text{Δ}\ge$0 and r > 0. The former condition has been shown in Eq. 8. Equation 66b makes sure that Eq. 64 has real solutions, and then we can further discuss whether the superluminal phenomenon exists or not in this case.

In the following equation, we solve Eq. 64 directly to obtain two solutions of h, that is,

$h_{\mp }=\frac{-\frac{2a(-\text{Δ}+(r^2+a^2))\text{sin}\theta }{r\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}\pm \frac{2{(r^2+a^2-r{R}_S+R_Q^2)}^{1/2}(r^2+a^2{\text{cos}}^2\theta ) }{r(\text{Δ}-a^2{\text{sin}}^2\theta )} }{2\frac{(\text{Δ}{a}^2{\text{sin}}^2\theta -{(r^2+a^2)}^2) }{r^2\left(\text{Δ}-a^2{\text{sin}}^2\theta \right)}}=\frac{-ra(-\text{Δ}+(r^2+a^2))\text{sin}\theta \pm r {(r^2+a^2-r{R}_S+R_Q^2)}^{1/2}(r^2+a^2{\text{cos}}^2\theta )}{(\text{Δ}{a}^2{\text{sin}}^2\theta -{(r^2+a^2)}^2)}=\frac{ra(r{R}_S-R_Q^2)\text{sin}\theta \mp r {(r^2+a^2-r{R}_S+R_Q^2)}^{1/2}(r^2+a^2{\text{cos}}^2\theta )}{(r^2+a^2)(r^2+a^2{\text{cos}}^2\theta )+(r{R}_S-R_Q^2)a^2{\text{sin}}^2\theta }.(67)$

It can be further expressed as

$h_{\pm }=\pm \frac{r{\left(r^2+a^2-r{R}_S+R_Q^2\right)}^{1/2}}{r^2+a^2}+r\left(r{R}_S-R_Q^2\right)a\sin \theta \frac{1\mp {\left(r^2+a^2-r{R}_S+R_Q^2\right)}^{1/2}a\sin \theta /\left(r^2+a^2\right)}{\left(r^2+a^2\right)\left(r^2+a^2{\text{cos}}^2\theta \right)+\left(r{R}_S-R_Q^2\right)a^2{\text{sin}}^2\theta },(68)$

The other two expressions of $h_{\pm }$ are

$h_{\pm }=\frac{r}{a\sin \theta }+\frac{r\left(r^2+a^2\right)\left(r^2+a^2{\text{cos}}^2\theta \right)}{a\sin \theta }\frac{\pm {\left(r^2+a^2-r{R}_S+R_Q^2\right)}^{1/2}a\sin \theta /\left(r^2+a^2\right)-1}{\left(r^2+a^2\right)\left(r^2+a^2{\text{cos}}^2\theta \right)+\left(r{R}_S-R_Q^2\right)a^2{\text{sin}}^2\theta }.(69)$

Then, the original problem is changed to whether h can be greater than one or not. Eq. 69 reveals a possible situation for

$\frac{r}{a\sin \theta }>1.(70)$

However, we have to discuss it with the second-long term on the right-hand side. Especially, this velocity component at sin$\theta$ = 0 in Eq. 69 is the same as the velocity component r (dθ/dt). The problem is not easy to deal with so we use the expression given in Eq. 68 to judge the occurrence of the superluminal phenomenon. When considering the solution for h₊ >1, the requirement from Eq. 68 is given as follows

$r^2{(r^2+a^2{\text{cos}}^2\theta )}^2\left(r^2+a^2-r{R}_S+R_Q^2\right)$

$-{[(r^2+a^2)(r^2+a^2{\text{cos}}^2\theta )-(-r{R}_S+R_Q^2)a\text{sin}\theta (r-a\text{sin}\theta )]}^2>0.(71)$

When sinθ∼0, this requirement becomes

$-a^2{\left(r^2+a^2\right)}^3+\left(-r{R}_S+R_Q^2\right)r^2{\left(r^2+a^2\right)}^2>0.(72)$

However, both terms on the left-hand side are negative when r > R_S, so the superluminal phenomenon does not occur at r > R_S when sinθ∼0. Next, we discuss all other cases of $\sin \theta$. Through expanding and rearranging Eq. 71, it gives the requirement

$\text{sin}\theta >\frac{1}{a(r-a\text{sin}\theta )}\left[\frac{a^2\left(r^2+a^2{\text{cos}}^2\theta \right)}{2(r{R}_S-R_Q^2)}+\frac{r^2(r^2+a^2{\text{cos}}^2\theta )}{2(r^2+a^2)}+\frac{(r{R}_S-R_Q^2)a^2{\text{sin}}^2\theta {(r-a\text{sin}\theta )}^2}{2(r^2+a^2)(r^2+a^2{\text{cos}}^2\theta )}\right]. (73)$

The three terms on the right-hand side of Eq. 73 are all positive. According to the geometric inequality in which the first term is equal to the third term, Eq. 73 can further simplify to the strict condition

$\text{sin}\theta >\frac{1}{a(r-a\text{sin}\theta )}\left[\frac{a^2\left(r^2+a^2{\text{cos}}^2\theta \right)}{2(r{R}_S-R_Q^2)}+\frac{r^2(r^2+a^2{\text{cos}}^2\theta )}{2(r^2+a^2)}+\frac{(r{R}_S-R_Q^2)a^2{\text{sin}}^2\theta {(r-a\text{sin}\theta )}^2}{2(r^2+a^2)(r^2+a^2{\text{cos}}^2\theta )}\right]$

$\ge \frac{1}{a(r-a\text{sin}\theta )}\left[\frac{a^2\text{sin}\theta (r-a\text{sin}\theta )}{{\left(r^2+a^2\right)}^{\frac{1}{2}}}+\frac{r^2\left(r^2+a^2{\text{cos}}^2\theta \right)}{2\left(r^2+a^2\right)}\right].(74)$

It means the most possible place for the superluminal phenomenon in this case is at sin$\theta =$1. It also requires r > asin$\theta$ in Eq. 74. This requirement needs three terms on the right-hand side to be small enough. When we look at the pre-factor on the right-hand side of Eq. 74, it gives the minimum value when

$a=\frac{r}{2\sin \theta }.(75)$

Using sin$\theta =$1 and combing the pre-factor, it gives the minimum

$\frac{a\text{sin}\theta }{{(r^2+a^2)}^{1/2}}+\frac{1}{a(r-a\text{sin}\theta )}\frac{r^2(r^2+a^2{\text{cos}}^2\theta )}{2(r^2+a^2)} \ge \frac{1}{\sqrt{5}}+\frac{8}{5}>1.(76)$

It means that Eq. 76 does not satisfy Eq. 73 because sinθ ≤ 1 and the superluminal phenomenon does not occur in this case of the velocity component rsin $\theta$(d$\varphi$/dt) at r > 0. But this conclusion may be corrected when we consider this velocity component Rsinθ(dϕdt) in the Cartesian coordinates.

The Meaning of the Superluminal Light

The faster-than-light photons have been discussed more than four decades [44–52]. The photon effective action, from one-loop vacuum polarization on a general curved space–time structure, has been calculated according to its contribution in QED. The quantum corrections to the local propagation of photons by introducing tidal gravitational forces on the photons has been investigated. This tidal gravitational effect depends explicitly on the local curvature and different observers will see different tidal effects according to their motion by the usual Lorentz transformations on the Riemann curvature tensor [44, 45]. Such quantum corrections in the curved space–time structure modify the characteristics of the photon propagation so as to make photons travel at speeds greater than unity in some cases. A superluminal low-frequency phase velocity for photons [46, 49] is a result of vacuum polarization in QED inducing interactions between the electromagnetic field and a non-dynamical curved space–time structure [44–49]. Theoretically speaking, this effect is non-dispersive and gauge invariant [44]. In quantum field theory, the pole in the photon propagator in the local Lorentz frame is shifted from k² = 0 to k²+ασ_abk^ak^b = 0 which depends explicitly on the local curvature as mentioned previously [45, 50].

Then, the equation of motion for the electromagnetic field or photon is determined by [44, 45].

$\frac{\delta W}{\delta A_{\mu }\left(x\right)}=0, (77)$

here the effective action W is given by

$W=W_0+W_1(78)$

with

$W_0=-\frac{1}{4}{\displaystyle \int d^{4}x}\sqrt{-g}{F}_{\mu \nu }{F}^{\mu \nu }(79)$

and

$F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }.(80)$

The lowest term in the expansion for W₁ is O (m⁻²) [44–51], that is,

$W_1=\frac{1}{m_e^2}{\displaystyle \int d^{4}x}\sqrt{-g}\left(aR{F}_{\mu \nu }{F}^{\mu \nu }+b{R}_{\mu \nu }{F}^{\mu \sigma }{F}_{\sigma }^{\nu }+c{R}_{\mu \nu \sigma \tau }{F}^{\mu \nu }{F}^{\sigma \tau }+d{D}_{\mu }{F}^{\mu \nu }{D}_{\sigma }{F}_{\nu }^{\sigma }\right),(81)$

here $g^{\mu \nu }=diag\left(1,-1,-1,-1\right)$, $R_{\nu \sigma \tau }^{\mu }={\Gamma }_{\nu \tau ,\sigma }^{\mu }-{\Gamma }_{\nu \sigma ,\tau }^{\mu }+{\Gamma }_{\lambda \sigma }^{\mu }{\Gamma }_{\nu \tau }^{\lambda }$ −Γ_λτ^μΓ_νσ^μ and m_e is the electron mass. The coefficients a, b, and c may be obtained from the coupling of a graviton to two on-mass shell photons in the flat space limit [44]. After redundant calculations in the weak gravitational field limit, we obtain a = −5α/720π, b = 26α/720π, and c = −2α/720π in terms of the fine structure constant α as well as the modified equation of motion for electromagnetic fields in gravity [44–51].

$D_{\mu }{F}^{\mu \nu }+\frac{\delta W_1}{\delta A_{\nu }\left(x\right)}=0.(82)$

The term involving the coefficient d influences W₁ in a very small way, so it can be omitted. Therefore, we obtain the modified equation of motion for the electromagnetic field [44–47, 50, 51].

$D_{\mu }{F}^{\mu \nu }+D_{\mu }\left[4aR{F}^{\mu \nu }+2b\left(R_{\sigma }^{\mu }{F}^{\sigma \nu }-R_{\sigma }^{\nu }{F}^{\sigma \mu }\right)+4c{R}_{\sigma \tau }^{\mu \nu }{F}^{\sigma \tau }\right]=0.(83)$

Generally speaking, the curvature is not isotropic so the modified equation of motion given in Eq. 83 provides the photon propagation differently in different directions [44]. By using the geometrical-optics plane-wave approximation in a gauge-invariant manner, F_μν = f_μνe^iθ is assumed in the derivations of the photon propagation where f_μν is a slowly varying amplitude and θ the rapidly varying phase with k_μ = D_μθ corresponding to the photon momentum [45–51]. The electromagnetic Bianchi identity further gives $f_{\mu \nu }=k_{\mu }{a}_{\nu }-k_{\nu }{a}_{\mu }$ [44–48, 50, 51] where a_μ specifies the direction of the polarization of the photon [45–48, 50, 51]. After another redundant calculation, it leads to a result that within the weak-field approximation, a photon propagating parallel to the gravitational wave has speed the same as c but the one propagating in an antiparallel direction to the gravitational wave has speed greater than c at certain situations [44]. Such a propagation is non-dispersive, so the phase and group velocities are the same [44]. It is also found out that the transverse photon motion in the Schwarzschild metric, say k_r = k_θ = 0, gives

$\left|\frac{k_t}{k_{\varnothing }}\right|=\left\{1+\frac{1}{2}\left[\frac{\frac{3R_s}{r^3}\left(\frac{\alpha }{90\pi m_e^2}\right)}{1+\frac{R_s}{r^3}\left(\frac{\alpha }{90\pi m_e^2}\right)}\right]\right\}c.(84)$

It means that the photon with radial polarization can travel with a velocity greater than c. Therefore, at least one type of photon has a speed greater than that of light in free space. The quantum correction due to vacuum polarization in gravity acts as a medium for the propagation of light [48]. However, such gravitational birefringence in the plane-wave and Schwarzschild metrics should be detectable or measurable on Earth. Another similar result is obtained from the Reissner–Nordstrӧm metric for characterizing a charged black hole [45]. According to the anisotropy of the background gravitational field and electromagnetic field, the vacuum polarization effect changes the photon propagation in the Reissner–Nordstrӧm space–time structure. The gravitational field may increase or decrease the photon velocity from c depending on its direction and polarization. For a black hole charging approximately equal to the accretion limit, superluminal occurrence is possible for photons propagating in the orbital direction at or beyond the horizon [45].

The light cone for radially directed photons in both the Schwarzschild and Reissner–Nordstrӧm geometries remains unperturbed [44–46]. For the Kerr space–time structure near a rotating black hole, this is no longer true and photons traveling on radial trajectories may have velocities differing from unity, either greater or smaller than the usual velocity of light c depending on the transverse polarization [46]. The orbital motions of photons have similar results that photons may have velocity shifts depending on their motions with or against the direction of spin [46]. Furthermore, the velocity shifts of photons may exist in the radial motion for any direction except along the polar axis [46]. In the dilation black hole, the dilatory effect is crucial in determining this ‘‘faster-than-light’’ phenomenon when the photon is near the event horizon in the extreme or near-extreme cases [47]. The light-cone condition can be also modified regardless of the spherically symmetric spacetimes [47]. Both results of the Kerr and dilation black holes are different from the cases of Schwarzschild and Reissner–Nordstrӧm black holes in which the light-cone conditions for the radial photons are unchanged [46, 47].

In summary, all superluminal phenomena discussed in [Refs. 44–52] exist in the local Lorentz frame. Vacuum polarization in QED can induce a superluminal low-frequency phase velocity for photons propagating in a non-dynamical, curved space–time structure [46, 49]. However, the most serious question we have to ask is whether the space-like photon momentum given by the light cone condition necessarily involves the problem of causal paradox [45]. Another key question is whether this superluminal propagation is observable in principle [45]. About the first question, it has even been mentioned that the tidal effects seem to strangely alter the causality structure of the manifold [44]. Because of the quantum corrections on photons in the curved space–time structure, it even gives an amazing result that in certain reference frames, photons could return to their source of origin before they were produced there based on the possibility of the closed time-like trajectories [51]. Therefore, the authors proposed that either the time machine is possible in principle or something is wrong in the superluminal propagation of photons due to quantum corrections of one-loop vacuum polarization [52]. When we calculate the quantum corrections in the curved space–time structure, it is clearly pointed out that one-loop vacuum polarization in QED is an effect in which the photon exists for part of the time as a virtual e⁻-e⁺ pair [44, 47, 51]. Two schematic pictures also clearly describe this idea of a virtual e⁻-e⁺ pair occurring in the curved space–time structure as given in Figures 1, 3 [49]. Due to this, we have to face a really serious problem whether the vacuum polarization in the curved space–time structure always takes place or just exists at certain time by random. In fact, even the speed modification of light exists; this randomness of the occurring virtual e⁻-e⁺ pair causes the faster-than-light phenomenon to take place randomly. Thus, the superluminal light based on quantum corrections due to vacuum polarization in the curved space–time structure becomes unexpected and occasionally so as to not be observed anytime. Especially, these faster-than-light photons show explicit effect in the local reference frame when they are very close to the black hole. This is exactly the second question we must ask whether such faster-than-light phenomena or gravitational birefringence are observable?

Therefore, our contributions are to derive the superluminal phenomena of light observed in the reference frame far away from the supergravitational sources such as black holes, such as on Earth, not the same as the abovementioned discussions in the local Lorentz frame. As we know, when light propagates in a strong gravitational field, the speed of light is different from that in the free space if the measurement time is the coordinate time t, and not the local proper time τ. We have seen the expression in the Schwarzschild metric [33–36, 53, 54] where the radial speed of light v_r at the black hole is [33–36].

$v_r=\frac{dr}{dt}=\left(1-\frac{R_s}{r}\right)c(85)$

observed by the far-away observer in the no-gravitational field in which the Schwarzschild radius is R_S = 2GM/c². Then, the experiencing time t for light along the radial direction from the initial place r₀ to the final place r (r₀>r), described by an observer far away the black hole, is [53].

$t\left(r\right)=\underset{r_0}{\overset{r}{{\displaystyle \int }}}\frac{1}{c\left(1-\frac{2GM}{c^{2}r}\right)}dr=\frac{r_0-r}{c}+\frac{2GM}{c^3}\ln \left(\frac{r_0-\frac{2GM}{c^2}}{r-\frac{2GM}{c^2}}\right).(86)$

It means that the time taken for light to reach the event horizon from any place r₀ is infinite observing far away from the black hole. However, this time interval described by total proper time in the local reference frames near the black hole is [54].

$\tau \left(r\right)=\underset{r_0}{\overset{r}{{\displaystyle \int }}}\frac{1}{c{\left(1-\frac{2GM}{c^{2}r}\right)}^{1/2}}d\tau =\left[\frac{r_0}{c}{\left(1-\frac{2GM}{c^2{r}_0}\right)}^{1/2}-\frac{r}{c}{\left(1-\frac{2GM}{c^{2}r}\right)}^{1/2}\right]+\left(\frac{2GM}{c^3}\right)\ln \left[\frac{r_0^{1/2}+{\left(r_0-\frac{2GM}{c^2}\right)}^{1/2}}{r^{1/2}+{\left(r-\frac{2GM}{c^2}\right)}^{1/2}}\right](87)$

Total proper time τ is surprisingly finite and much different from the time t observed or measured at a place far away the black hole, such as on Earth. These two different calculation results reveal the observations which are not the same from different observers, and they have been calculated almost one hundred years ago. It is a common truth that different observers have different observations no matter in the theory of special relativity or general relativity. When we want to discuss the propagation of light, we have to choose the appropriate observer in which kind of reference frame. All the superluminal phenomena reported before were observed from Earth [1, 3–6], so we have to use Earth’s viewpoints to explain why we can observe the superluminal phenomena near some super-gravitational sources such as black holes. According to our discussions, the speed of light may be larger than c if we use the coordinate time t and not the local proper time τ, to define its radial speed v_r = dr/dt, not dr/dτ. Based on this definition, we call the superluminal phenomenon of light when the speed of light like v_r is more than c in the supergravity such as a Kerr–Newman black hole. Actually, the speed of light in the local Lorentz frame is still v_r = dr/dτ = c, so the Lorentz invariance still holds true in our discussions. Therefore, causality is not broken, and we do not need to worry about the time machine issue.

Speaking more clearly, all observations on Earth or the satellites around the Earth use Earth’s time to record the propagation of light near the super-gravitational sources such as the calculation in Eq. 85, not Eq. 86 calculating in the local frames. Therefore, we have to deduce the propagation of light near the super-gravitational sources such as some black holes but observing on Earth to explain the observations of the superluminal phenomena. Our discussion is using the Kerr–Newman metric that is a space–time solution in the theory of general relativity. Considering the light propagation near the rotational and charged super-gravitational sources, it can explain some astronomical observations about the superluminal phenomena of the relativistically massive jets [1, 3–6]. The explanation is that the radial speeds of light or the main parts along the radial direction are superluminal near the super-gravitational sources such as black holes when we use Earth’s time to describe its propagation. For example, we can setup an imaginary experiment to measure the speed of light. When one light signal is emitted, after propagating a distance, it is received by a detector. Suppose this distance to be ten light years and the detecting Earth time is 1 year, according to these two data, the speed of light during this period is averagely 10 c. Due to such superluminal light, the relativistically massive jets can exhibit superluminal phenomena observed on Earth because the light signal larger than c reveals the relativistically massive jets moving faster than light. This result can be applicable on some super-gravitational sources with very high density, large rotation a, and large charges R_Q. All mathematical derivations still obey the Lorentz invariance in the local instantaneous frame, and we prove that the speed of light along the radial direction is superluminal at some conditions. The superluminal phenomenon is the observed truth in astronomy and its physics needs us to clarify and explain carefully. One thing necessarily mentioned again is that all observations were finished on Earth or the satellites around Earth, so the measured time is Earth’s time where we define 1 s is the period for light traveling 299,792,458 m in vacuum on Earth.

Our discussions show that only the case of the velocity of (dr/dt, 0, and 0) for light can possibly occur the superluminal phenomenon at $\theta$>0. The maximum speed of light is much related to the rotational term a and the charged term R_Q of a black hole. The results are at least reasonable at two poles and in the equatorial plane. The other two cases of the velocities of (0, rd$\theta$/dt, and 0) and (0, 0, and rsin$\theta$d$\varphi$/dt) for light do not have the possibility of the superluminal phenomenon. However, light can have at least one velocity component in the vicinity of a black hole. Generally speaking, the superluminal phenomenon also possibly occurs in these cases of (dr/dt, rd$\theta$/dt, and 0), (dr/dt, 0, and rsin$\theta$d$\varphi$/dt), or (dr/dt, rd$\theta$/dt, and rsin$\theta$d$\varphi$/dt). In those cases, the radial velocity component is dominant for the occurrences of the superluminal phenomena.

Conclusion

The superluminal phenomenon is an attracted research, and this phenomenon can be discussed based on the theory of general relativity with a given space–time structure. In this research, the Kerr–Newman metric is chosen for describing the space–time structure at the rotating and charged black hole and its vicinity. The results are also applicable for the super-gravitational sources. Our way is much close to the previous ideas [41] shown in Eqs. 18, 19, although they are based on the Gaussian distributions of mass and charge. The difference is that we directly determine the ranges of mass and charge at each radial position inside the black hole by confirming the absence of mathematical divergence everywhere. Our results extend to more general cases, not only the Gaussian distributions of mass and charge inside the black hole. Especially, the region we are interested in is outside the event horizon where the Kerr–Newman-like metric [41] changes to the ordinary Kerr–Newman metric what we use here. Therefore, no singularity appears in our discussions. The Kerr–Newman metric considers both a and R_Q terms that all kinds of the black hole at present knowledge are included. Because the black hole possesses strong gravity, it is a good astronomical example for studying the superluminal phenomenon in the Boyer-Lindquist coordinates. According to the Kerr–Newman metric, the geodesic as well as the velocity components of light can be established. In order to study this phenomenon, three velocity components are independently discussed, and they are (dr/dt, 0, and 0), (0, rd$\theta$/dt, and 0), and (0, 0, and rsin$\theta$d$\varphi$/dt). From our analysis, only the case of (dr/dt, 0, and 0) has the possibility of the occurrence of the superluminal phenomenon and an example is shown between R_S and $[R_Q^2+\left(a^2{\text{sin}}^2\theta \right)/2]/R_S$at sin$\theta$ > 0 when R_S ∼ R_Q. The result reveals that the superluminal phenomenon can possibly happen outside the black hole from the observer at infinity or in a reference frame with very weak gravity. The maximum speed of light and the range of the superluminal phenomenon are much related to the rotational term a and the charged term R_Q of a black hole, respectively. The results are at least reasonable at two poles and in the equatorial plane when light propagates in the radial direction. Although the superluminal phenomenon is discussed in the Boyer-Lindquist coordinates, all the results are easy to be transformed or discussed in the Cartesian coordinates (x, y, z, t) by setting R² = x²+y²+z² = r²+a²sin²θ and rdr = RdR in the velocity of light. The conclusions of the superluminal phenomenon about the three velocity components (dR/dt, Rdθ/dt, Rsinθdϕ/dt) are different from them in the Boyer-Lindquist coordinates. Generally speaking, the superluminal phenomena for light can possibly occur in these cases that the radial velocity dr/dt is dominant and the other two velocity components are comparably small or zero. Furthermore, the superluminal phenomenon here just means the results of the measurements from an observer in a reference frame such as on Earth. This conclusion can also be applied on some stars with very high density, large a, and big R_Q. The result can be also applied on the super-gravitational sources. According to the above results, it is also applicable to the massive particles. Once the massive particles fully or most partly moving along the radial direction near some quasars or black holes [1,3-6], it is possibly to observe their superluminal phenomena on the Earth, as long as their speeds in the spontaneously local reference frames are very close to c.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

The author confirms being the sole contributor of this study and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author thanks Institute of Astronomy and Astrophysics at Academia Sinica in Taiwan for the payment of this article. The author is also grateful to the reviewers for their comments to strengthen the statements in this article, and thankful to Dr. Ming-Jye Wang for his encouragement.

Abbreviations

PACS 04.20.Cv, fundamental problems and general formalism; PACS 95.30.-k, fundamental aspects of astrophysics; PACS 98.80.JK, mathematical and relativistic aspects of cosmology.

References

1. Mirabel IF, Rodríguez LF. A Superluminal Source in the Galaxy. Nature (1994) 371:46–8. doi:10.1038/371046a0

CrossRef Full Text | Google Scholar

2. Wang LJ, Kuzmich A, Dogariu A. Gain-Assisted Superluminal Light Propagation. Nature (2000) 406:277–9. doi:10.1038/35018520

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Blandford RD, Mckee CF, Rees MJ. Super-luminal Expansion in Extragalactic Radio Sources. Nature (1977) 267:211–6. doi:10.1038/267211a0

CrossRef Full Text | Google Scholar

4. Rodríguez LF, Mirabel IF. Grs 1915+105: a Superluminal Source in the Galaxy. Proc Natl Acad Sci (1995) 92:11390–2. doi:10.1073/pnas.92.25.11390

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Belloni T, Méndez M, King AR, Van Der Klis M, Van Paradijs J. An Unstable Central Disk in the Superluminal Black Hole X-Ray Binary GRS 1915+105. Astrophysical J (1997) 479:L145–L148. doi:10.1086/310595

CrossRef Full Text | Google Scholar

6. Jorstad SG, Marscher AP, Mattox JR, Aller MF, Aller HD, Wehrle AE, et al. Multiepoch Very Long Baseline Array Observations of‐EGRET Detected Quasars and BL Lacertae Objects: Connection between Superluminal‐Ejections and Gamma Ray Flares in Blazars. ApJ (2001) 556:738–48. doi:10.1086/321605

CrossRef Full Text | Google Scholar

7. Porcas R. Superluminal Motions: Astronomers Still Puzzled. Nature (1983) 302:753–4. doi:10.1038/302753a0

CrossRef Full Text | Google Scholar

8. Schilizzi RT, De Bruyn AG. Large-Scale Radio Structures of Superluminal Sources. Nature (1983) 303:26–31. doi:10.1038/303026a0

CrossRef Full Text | Google Scholar

9. Stockton A. A Galaxy Associated with 3C273. Nature (1978) 274:342–3. doi:10.1038/274342a0

CrossRef Full Text | Google Scholar

10. MarscherMarscher AP, Scott JS. Superluminal Motion in Compact Radio Sources. Pasp (1980) 92:127–33. doi:10.1086/130633

CrossRef Full Text | Google Scholar

11. Pearson TJ, Unwin SC, Cohen MH, Linfield RP, Readhead ACS, Seielstad GA, et al. Superluminal Expansion of Quasar 3C273. Nature (1981) 290:365–8. doi:10.1038/290365a0

CrossRef Full Text | Google Scholar

12. Conway RG, Davis RJ, Foley AR, Ray TP. Radio Jet of 3C273. Nature (1981) 294:540–2. doi:10.1038/294540a0

CrossRef Full Text | Google Scholar

13. Flatters C, Conway RG. The Radio Jet of the Quasar 3C273. Nature (1985) 314:425–6. doi:10.1038/314425a0

CrossRef Full Text | Google Scholar

14. Davis RJ, Muxlow TWB, Conway RG. Radio Emission from the Jet and Lobe of 3C273. Nature (1985) 318:343–5. doi:10.1038/318343a0

CrossRef Full Text | Google Scholar

15. Zensus JA, Pearson TJ. Superluminal Radio Sources. In: M. J. Reid, and J. M. Moran, editors. The Impact Of VLBI on Astrophysics And Geophysics. Cambridge, MA, USA: IAU (1988). p. 7–16.

CrossRef Full Text | Google Scholar

16. Davis RJ, Unwin SC, Muxlow TWB. Large-scale Superluminal Motion in the Quasar 3C273. Nature (1991) 354:374–6. doi:10.1038/354374a0

CrossRef Full Text | Google Scholar

17. Abraham Z, Romeno GE. Beaming and Precession in the Inner Jet of 3C 273. Astron Astrophysics (1999) 344:61–7.

Google Scholar

18. Biretta JA, Sparks WB, Macchetto F. Hubble Space TelescopeObservations of Superluminal Motion in the M87 Jet. ApJ (1999) 520:621–6. doi:10.1086/307499

CrossRef Full Text | Google Scholar

19. Romero GE, Chajet L, Abraham Z, Fan JH. Beaming and Precession in the Inner Jet of 3C 273 II. The Central Engine. Astron Astrophysics (2000) 360:57–64.

Google Scholar

20. Qian S-J, Zhang X-Z, Krichbaum TP, Zensus JA, Witzel A, Kraus A, et al. Periodic Variations of the Jet Flow Lorentz Factor in 3C 273. Chin J Astron Astrophys (2001) 1:236–44. doi:10.1088/1009-9271/1/3/236

CrossRef Full Text | Google Scholar

21. Mooley KP, Deller AT, Gottlieb O, Nakar E, Hallinan G, Bourke S, et al. Superluminal Motion of a Relativistic Jet in the Neutron-star Merger GW170817. Nature (2018) 561:355–9. doi:10.1038/s41586-018-0486-3

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hotokezaka K, Nakar E, Gottlieb O, Nissanke S, Masuda K, Hallinan G, et al. A Hubble Constant Measurement from Superluminal Motion of the Jet in GW170817. Nat Astron (2019) 3:940–4. doi:10.1038/s41550-019-0820-1

CrossRef Full Text | Google Scholar

23. Snios B, Nulsen PEJ, Kraft RP, Cheung CC, Meyer ET, Forman WR, et al. Detection of Superluminal Motion in the X-Ray Jet of M87. ApJ (2019) 879:8. doi:10.3847/1538-4357/ab2119

CrossRef Full Text | Google Scholar

24. Shapiro II. Fourth Test of General Relativity. Phys Rev Lett (1964) 13:789–91. doi:10.1103/physrevlett.13.789

CrossRef Full Text | Google Scholar

25. Kundi'c T, Turner EL, Colley WN, Gott JR, Rhoads JE, Wang Y, et al. A Robust Determination of the Time Delay in 0957+561 A, B and a Measurement of the Global Value of Hubble’s Constant. Astrophysical J (1997) 482:75–82.

Google Scholar

26. Lovell JEJ, Jauncey DL, Reynolds JE, Wieringa MH, King EA, Tzioumis AK, et al. The Time Delay in the Gravitational Lens PKS 1830−211. Astrophysical J (1998) 508:L51–L54. doi:10.1086/311723

CrossRef Full Text | Google Scholar

27. Biggs AD, Browne IWA, Helbig P, Koopmans LVE, Wilkinson PN, Perley RA. Time Delay for the Gravitational Lens System B0218+357. Monthly Notices R Astronomical Soc (1999) 304:349–58. doi:10.1046/j.1365-8711.1999.02309.x

CrossRef Full Text | Google Scholar

28. Demorest PB, Pennucci T, Ransom SM, Hessel JWT, Roberts MSE, Hessels JWT. A Two-Solar-Mass Neutron star Measured Using Shapiro Delay. Nature (2010) 467:1081–3. doi:10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Newman ET, Couch E, Chinnapared K, Exton A, Prakash A, Torrence R. Metric of a Rotating, Charged Mass. J Math Phys (1965) 6:918–9. doi:10.1063/1.1704351

CrossRef Full Text | Google Scholar

30. Virbhadra KS. Energy Associated with A Kerr-Newman Black Hole. Phys Rev D (1990) 41:1086–90. doi:10.1103/physrevd.41.1086

CrossRef Full Text | Google Scholar

31. Xulu SS. Møller Energy for the Kerr-newman Metric. Mod Phys Lett A (2000) 15:1511–7. doi:10.1142/s0217732300001651

CrossRef Full Text | Google Scholar

32. Mould RA. Basic Relativity. New York: Springer (2002). 324.

Google Scholar

33. Schutz BF. A First Course in General Relativity. Cambridge: Cambridge University Press (1985). 291–8.

Google Scholar

34. HansOhanian C, Ruffini R. Gravitation and Spacetime. 2nd ed.. New York: Norton & Company (1994). 225–445.

Google Scholar

35. De Felice F, Clarke CJS. Relativity on Curved Manifolds. Cambridge: Cambridge University Press (1990). p. 355–62.

Google Scholar

36. Stephani H. Relativity-An Introduction to Special and General Relativity. 3rd ed. Cambridge: Cambridge (2004). 303.

Google Scholar

37. Nicolini P. A Model of Radiating Black Hole in Noncommutative Geometry. J Phys A: Math Gen (2005) 38:L631–L638. doi:10.1088/0305-4470/38/39/l02

CrossRef Full Text | Google Scholar

38. Nicolini P, Smailagic A, Spallucci E. Noncommutative Geometry Inspired Schwarzschild Black Hole. Phys Lett B (2006) 632:547–51. doi:10.1016/j.physletb.2005.11.004

CrossRef Full Text | Google Scholar

39. Arsodi S, Nicolini P, Smailagic A, Spallucci E. Non-Commutative Geometry Inspired Charged Black Hole. Phys Lett B (2007) 645:261–6.

Google Scholar

40. Smailagic A, Spallucci E. "Kerrr" Black Hole: The Lord of the String. Phys Lett B (2010) 688:82–7. doi:10.1016/j.physletb.2010.03.075

CrossRef Full Text | Google Scholar

41. Modesto L, Nicolini P. Charged Rotating Noncommutative Black Holes. Phys Rev D (2010) 82:104035–14. doi:10.1103/physrevd.82.104035

CrossRef Full Text | Google Scholar

42. Burkert VD, Elouadrhiri L, Girod FX. The Pressure Distribution inside the Proton. Nature (2018) 557:396–9. doi:10.1038/s41586-018-0060-z

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Fukugita M, Peebles PJE. The Cosmic Energy Inventory. Astrophysics J (2004) 616:643–68.

CrossRef Full Text | Google Scholar

44. Drummond IT, Hathrell SJ. QED Vacuum Polarization in a Background Gravitational Field and its Effect on the Velocity of Photons. Phys Rev D (1980) 22:343–55. doi:10.1103/physrevd.22.343

CrossRef Full Text | Google Scholar

45. Daneils RD, Shore GM. “Faster Than Light Photons and Charged Black Holes,”. Nucl Phys (1994) 425:634–50.

Google Scholar

46. Daneils RD, Shore GM. “Faster Than Light Photons and Rotating Black Holes,”. Phys Lett B (1996) 367:75–83.

Google Scholar

47. Cho HT. "Faster Than Light" Photons in Dilaton Black Hole Spacetimes. Phys Rev D (1997) 56:6416–24. doi:10.1103/physrevd.56.6416

CrossRef Full Text | Google Scholar

48. Shore GM. “Causality and Superluminal Light,”. Time and Matt. (2006) 45-66.

Google Scholar

49. Hallowood TJ, Shore GM. “The Refractive Index of Curved Spacetime: The Fate of Causality in QED,”. Nucl Phys B (2008) 795:138–71.

Google Scholar

50. Shore GM. 'Faster Than Light' Photons in Gravitational fields - Causality, Anomalies and Horizons”. Nucl Phys B (1996) 460:379–94. doi:10.1016/0550-3213(95)00646-x

CrossRef Full Text | Google Scholar

51. Cai R-G. Propagation of Vacuum Polarized Photons in Topological Black Hole Spacetimes. Nucl Phys B (1998) 524:639–57. doi:10.1016/s0550-3213(98)00274-0

CrossRef Full Text | Google Scholar

52. Dogov AD, Novigov ID. “Superluminal Propagation of Light in Gravitational Field and Non-causality Signals,”. Phys Lett B (1998) 442:82–9.

Google Scholar

53. Landau LD, Lifshitz EM. The Classical Theory of Fields (1975). 309. Pergamon Press LTD., Fourth Revised English Edition.

Google Scholar

54. CharlesMisner W, KipThorne S, Wheeler JA. Sec. 31.2, 31.3, 31.4, & 33.2. Gravitation (1970).

Google Scholar