A Novel Meshfree Strategy for a Viscous Wave Equation With Variable Coefficients

A one-step new general mesh free scheme, which is based on radial basis functions, is presented for a viscous wave equation with variable coefficients. By constructing a simple extended radial basis function, it can be directly applied to wave propagation by using the strong form-based mesh free collocation method. There is no need to deal with the time-dependent variable particularly. Numerical results for a viscous wave equation with variable coefficients show that the proposed mesh free collocation method is simple with accurate solutions.

1 Introduction

The wave propagation exists in an interesting class of problems, such as the micro-scale heat transfer, seismic data acquisition and processing, etc. Acoustic wave modeling is an essential part of the technique of acoustic imaging [1]. Such problems have been widely investigated because of their realistic physical background. Related works can be found in [2] and references therein.

Since the governing equation of the problem considered is complex, and the corresponding physical domain or the boundary conditions are tangle some, the analytical solutions are almost inaccessible for most practical engineering problems [3–7]. The development of accurate and efficient numerical methods becomes an important research topic in computational physics.

The earliest numerical methods for wave equations include the finite difference method [8], the finite element method [9], the boundary element method [10] and the finite volume method [11]. It should be noted that most of the existed numerical methods are still based on the finite difference method (FDM) [12, 13], which lead to two-step finite difference approximations. More specifically, the finite difference method is used to deal with the time variable, and the rest procedures are finished by the other numerical methods. Coupled with the FDM, the radial basis function (RBF) collocation methods are widely-used to many problems thanks to their mesh free features. Akers et al. [14] investigated a radial basis function-finite differencing (RBF-FD) scheme which is applied to the initial value problem of the Benjamin-Ono equation. Bhardwaj and Kumar [15] used the FDM-based mesh less approach for the numerical solution of the nonlinear diffusion-wave equation. Based on the integrated radial basis functions and a finite difference scheme, the regularized long-wave equations are investigated in [16, 17]. Oruc [18] examined numerical solutions of Zakharov-Rubenchik system by using radial basis function finite difference (RBF-FD) mesh less method and an explicit Runge-Kutta method. The time discretization is accomplished by means of an implicit method based on the theta-weighted and finite difference methods, while the spatial discretization is described with the help of the finite difference scheme derived from the local radial basis function method. Recently, Lu et al [19] used the radial basis function mesh less method to solve the irregular region interface problem. Ranocha et al [20] created new classes of fully-discrete conservative methods for several nonlinear dispersive wave equations.

In order to simplify the conventional two-step solution process, Netuzhylov and Zilian [21] proposed a space-time mesh free collocation method for solving partial differential equations by a consistent discretization in both space and time. Motivated by this work, we aim to provide a truly mesh free method with one-step approximation, which is based on the RBFs, for a viscous wave equation with variable coefficients. Compared with the traditional FDM-based two-step methods, the newly-proposed one-step direct mesh free method is truly mesh free with easy implementation. The computational efficiency is excellent and the computational accuracy is mainly determined by numerical methods for wave field simulation.

The paper is organized as follows. In Section 2, formulation of the direct radial basis function with space-time Euclidean distance is briefly introduced. This is realized by considering time-dependent variable as normal time-independent variable. Thus, the time-dependent variable can be treated easily during the whole solution process. Section 3 presents the methodology for a viscous wave equation with variable coefficients under initial condition and boundary conditions. Numerical results with detailed discussions are presented for the accuracy of the proposed mesh free method in Section 4. Section 5 concludes this paper with some additional remarks.

2 Problem Description

Let’s consider a viscous wave equation on a bounded two-dimensional domain $\text{Ω}\subset R^2$

$Lu\equiv \frac{{\partial }^{2}u}{\partial t^2}+\alpha \frac{\partial u}{\partial t}-\frac{\partial }{\partial t}\nabla \cdot \left(Q\nabla u\right)-\nabla \cdot \left(A\nabla u\right)=f\left(x,y,t\right),t>0(1)$

where α is a nonnegative coefficient, f is a source term, $Q=\text{diag}\left(q_1,q_2\right)$ and $A=\text{diag}\left(a_1,a_2\right)$ are diagonal, nonnegative diffusion tensors with $q_1,q_2,a_1,a_2$ constant or variable coefficients. Solution to Eq. 1 requires the extra initial conditions

$u\left(x,y,0\right)=f_1\left(x,y\right),\left(x,y\right)\in \text{Ω}(2)$

$u_t\left(x,y,0\right)=f_2\left(x,y\right),\left(x,y\right)\in \text{Ω}(3)$

and boundary conditions

$Bu\left(x,y,t\right)=f_3\left(x,y,t\right),\left(x,y\right)\in \partial \text{Ω},t>0(4)$

with $f_1\left(x,y\right)$, $f_2\left(x,y\right)$ and $f_3\left(x,y,t\right)$ the given functions. B is a boundary operator. One should seek for the numerical solution of unknown function $u\left(x,y,t\right)$.

A variety of numerical methods have been investigated for Eqs. 1–4. Most of them are based on the finite difference method, which lead to two-step methods. More specifically, the finite difference method is used to deal with the time domain, which will lead to elliptic-type problems. Then the rest work is done by the other numerical methods. In order to improve the perplexing two-step methods, we propose a direct one-step collocation method by using an extended RBFs in the following section.

3 Formulation of the Extended Radial Basis Functions

The radial basis functions (RBFs) are extremely powerful tool for solving partial differential equations. It is “isotropic” for Euclidean spaces. The Kansa’s method [22, 23] is one of the most famous RBFs. It is also called the multi-quadrics RBF with the expression [24].

${\varphi }_{mq}\left(r_j\right)=\sqrt{1+{\left(\epsilon r_j\right)}^2}(5)$

where $r_j$ is the Euclidean distance between two points. ε is the RBF shape parameter which can balance the solution accuracy.

As is known to all, a linear combination of RBFs can provide the numerical solutions for boundary value problems governed by elliptic partial differential equations. In literatures, this can be not directly used to solve boundary value problems governed by parabolic or hyperbolic partial differential equations.

To make the direct applications possible, the time variable is treated equally with the space variables. More specifically, we construct a simple direct radial basis function by combining the two-dimensional point $\left(x,y\right)$ and the one-dimensional time variable t as a three-dimensional point $\left(x,y,t\right)$ for the space-time domain $\text{Ω}\times t$. For collocation points generation, the time variable is treated equally to the space variables x and y. For a simple example, the collocation points in the $x-$ and $y-$directions are evenly chosen with fineness $h_x=h_y=1/n$. The time-step for the rest $t-$direction is chosen as $\text{Δ}t=1/n$.

Similar to the traditional multi-quadric RBF, the extended radial basis function (ERBF) has the form

${\phi }_{mq}\left(r_j\right)=\sqrt{1+{\epsilon }^2{r}_j^2}=\sqrt{1+{\epsilon }^2{\left(x-x_j\right)}^2+{\epsilon }^2{\left(y-y_j\right)}^2+{\epsilon }^2{\left(t-t_j\right)}^2}(6)$

where $r_j=\Vert P-P_j\Vert$ represents the distance between two space-time coordinates $P=\left(x,y,t\right)$ and $P_j=\left(x_j,y_j,t_j\right)$.

In literatures [25–27], the other researchers have proposed some space-time radial basis functions with different types. We have done many investigations and found that they are not suitable to deal with the wave equations.

4 Implementation of the Extended Radial Basis Function

4.1 The Extended Radial Basis Function Solution Procedure

To solve the problem described by Eqs. 1–4, we use the ERBF to present the detailed procedure. Based on the definition of ERBF, Eqs 1–4 can be simulated by a one-step numerical method. The unknown function $u\left(x,y,t\right)$ can be approximated by the following expression

$\overline{u}(\cdot )\approx {\displaystyle \sum }_{j=1}^N{\lambda }_j{\phi }_{mq}\left({\cdot }_j\right),(7)$

where the unknown coefficients ${\left\{{\lambda }_j\right\}}_{j=1}^n$ should be solved.

To illustrate the ERBF solution procedure, the internal points ${\{P_i=(x_i,y_i,t_i)\}}_{i=1}^{N_I}$ are located inside the physical domain and initial boundary points ${\{P_i=(x_i,y_i,t_i)\}}_{i=N_I+1}^{N_I+N_t}$ and boundary points ${\{P_i=(x_i,y_i,t_i)\}}_{i=N_I+N_t+1}^N$ are located on the physical boundary. By substituting Eq. 7 into Eqs. 1–3, we have

${\displaystyle \sum }_{j=1}^N{\lambda }_{j}L{\phi }_{mq}\left(P_i,P_j\right)=f\left(P_i\right),i=1,\dots ,N_I,(8)$

${\displaystyle \sum }_{j=1}^N{\lambda }_j{\phi }_{mq}\left(P_i,P_j\right)=f_1\left(P_i\right),i=N_I+1,\dots ,N_I+N_t,(9)$

${\displaystyle \sum }_{j=1}^N{\lambda }_j\frac{\partial {\phi }_{mq}\left(P_i,P_j\right)}{\partial t}=f_2\left(P_i\right),i=N_I+N_t+1,\dots ,N_I+2N_t,(10)$

${\displaystyle \sum }_{j=1}^N{\lambda }_{j}B{\phi }_{mq}\left(P_i,P_j\right)=f_3\left(P_i\right),i=N_I+2N_t+1,\dots ,N,(11)$

where

$L{\phi }_{mq}=\frac{{\partial }^2{\phi }_{mq}}{\partial t^2}+\alpha \frac{\partial {\phi }_{mq}}{\partial t}--\frac{\partial }{\partial t}\nabla \cdot (Q\nabla {\phi }_{mq})-\nabla \cdot (A\nabla {\phi }_{mq}).(12)$

This is similar with the traditional strong-form collocation approach. We note that the two initial conditions require double initial boundary points, so the total collocation point number is $N=N_I+2N_t+N_b$.

Eqs. 8–11 has the following matrix form

$\mathbf{M\Lambda }=\mathbf{F},(13)$

where

$\mathbf{M}=\left[\begin{array}{cccc}{M}_{11}& M_{12}& M_{13}& M_{14}\\ M_{21}& M_{22}& M_{23}& M_{24}\\ M_{31}& M_{32}& M_{33}& M_{34}\\ M_{41}& M_{42}& M_{43}& M_{44}\end{array}\right](14)$

are $N\times N$ known matrix. $\mathbf{\Lambda }$ and $\mathbf{F}$ are $N\times 1$ vectors.

The unknown vector $\mathbf{\Lambda }$ in Eq. 13 can be solved by the direct solver in any software codes. Substitute the coefficients into Eq. 7, we get the numerical solution for any points in the whole physical domain.

4.2 Algorithms of the Extended Radial Basis Function

For the solution procedure of the ERBF, we summarize the corresponding simple algorithm steps as below.

Step 1. Enter the prescribed functions $f\left(x,y,t\right)$, $f_1\left(x,y\right)$, $f_2\left(x,y\right)$, $f_3\left(x,y,t\right)$, and the coefficients $q_1$, $q_1$, $a_1$, $a_2$.

Step 2. Select the point parameter n which is connected with the total collocation number N.

Step 3. Generate the collocation points $(x_i,y_i,t_i),I=\mathrm{1,2},\dots ,,N$ with internal points ${\left\{\left(x_i,y_i,t_i\right)\right\}}_{i=1}^{N_I}$, initial boundary points ${\left\{\left(x_i,y_i,t_i\right)\right\}}_{i=N_I+1}^{N_I+N_t}$ and boundary points ${\left\{\left(x_i,y_i,t_i\right)\right\}}_{i=N_I+N_t+1}^N$.

Step 4. Compute the interpolation matrix $\mathbf{M}$ and the right-hand vector $\mathbf{F}$.

Step 5. Solve $\mathbf{M\Lambda }=\mathbf{F}$.

Step 6. Substitute $\mathbf{\Lambda }$ into (Eq. 7) to construct the numerical solution $\overline{u}\left(x,y,t\right)$.

In this paper, the MATLAB is used to realize the algorithms of ERBF.

5 Numerical Experiments

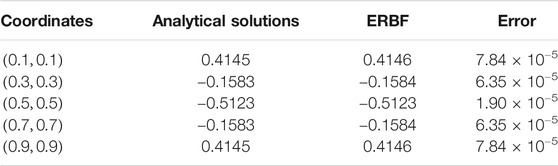
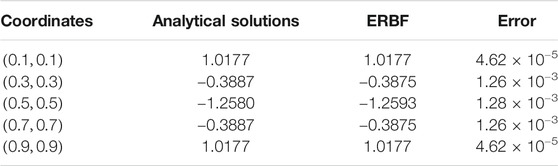
In order to study the convergence of ERBF, the relative errors between ERBF and analytical solutions are calculated. It should be noted that the parameter ε in the ERBF should be chosen first. The optimal choice is similar with the traditional RBFs. For more details about this topic, we refer readers to [24, 28, 29] and references therein. In this paper the parameter is determined with an prior determination. More specifically, the collocation points are fixed first to find the quasi-optimal parameter, after which it will be used for the rest computations.

We consider the problem with $\alpha =1$, $Q=A=I$, the corresponding exact solution is

$u\left(x,y,t\right)=\left[1+\frac{1}{2}\mathtt{sin}\left({\pi }^{2}t\right)\right]\mathtt{sin}\left(5\pi x\right)\mathtt{sin}\left(3\pi y\right).(15)$

The source function $f\left(x,y,t\right)$ can be deduced from the governing Eq. 1

$\begin{array}{c}u\left(x,y,t\right)={\pi }^2\mathtt{sin}\left(5\pi x\right)\mathtt{sin}\left(3\pi y\right)[34+\dots \\ \left(\frac{1}{2}+17{\pi }^2\right)\mathtt{cos}\left({\pi }^{2}t\right)+\left(17-\frac{1}{2}{\pi }^2\right)\mathtt{sin}\left({\pi }^{2}t\right)]\text{.}\end{array}(16)$

For fixed collocation point number parameter $n=8$, the total collocation point is 729, and the number of points in each dimension is $9\times 9\times 9$ in x, y and t dimensions, respectively. To reveal the numerical solution accuracy of the proposed method, the wave propagation of nodes is calculated by theoretical formula at $t=0.5s$ and $t=0.9s$, respectively. From Table 1 and Table 2, we find that numerical solutions of the proposed ERBF are very close with the analytical solutions for different points. The corresponding absolute errors remain the same at $t=0.5s$. And the corresponding absolute errors is a little large for some points, but it is still accurate enough for practical problems.

TABLE 1

TABLE 1. The comparison of the absolute errors at t = 0.5 s.

TABLE 2

TABLE 2. The comparison of the absolute errors at t = 0.9 s.

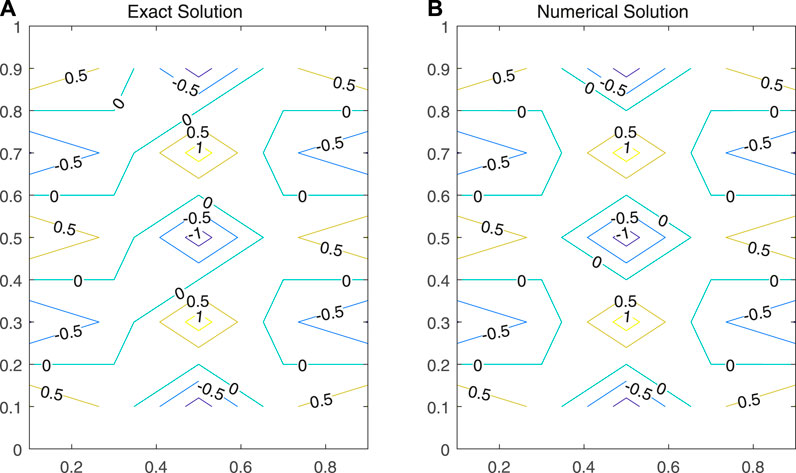
Figure 1 describes the contour plots of the numerical solutions and analytical solutions at time $t=0.5$. We find that the numerical solutions agree very well with the analytical solutions. It should be noted that the results for the other times have the same accurate results as shown in Figure 1.

FIGURE 1

FIGURE 1. Contour plot of exact solutions (A) and numerical solutions (B).

Tables 1, 2 show that the numerical results coincide very well with the analytical solutions for both $t=0.5s$ and $t=0.9s$. For time $t=0.5s$, the absolute errors for different points are almost the same. For the time $t=0.9s$, the absolute errors for points $\left(0.1,0.1\right)$ and $\left(0.9,0.9\right)$ are more accurate than the other points. Also, it should be pointed out that the ERBF results are more accurate than the other numerical methods [30, 31]. The corresponding comparison is revealed in Table 3 by using the maximum absolute error $L^{\infty }$. From which we can see that the time step of the proposed ERBF $1/9$ is larger than the other two methods 0.02, but the corresponding absolute error of the ERBF is smaller than the other two methods. And the computational time of the ERBF (CPU = 0.92 s) is less than the method (CPU = 15.70 s) used in [30].

TABLE 3

TABLE 3. Maximum absolute error $L^{\infty }$.

6 Conclusion

A one-step new general mesh free scheme for solving a viscous wave equation with variable coefficients is proposed. It is based on the strong form-based mesh free collocation method in conjunction with the radial basis functions. Numerical results show that the mesh free method is more simple than the other numerical methods with solution accuracy maintained. The proposed method with the localized technique can be extended to large-scale problems easily.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

FW designed the whole paper; JZ and IA wrote the manuscript; AF and HA analyzed experimental results.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

The work was supported by the Natural Science Foundation of Anhui Province (Project No. 1908085QA09) and the University Natural Science Research Project of Anhui Province (Project No. KJ2019A0591).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.701512/full#supplementary-material

References

1. Chen H, Zhou H, Jiang S, Rao Y. Fractional Laplacian Viscoacoustic Wave Equation Low-Rank Temporal Extrapolation. IEEE Access (2019) 99:1–11. doi:10.1109/ACCESS.2019.2927760

CrossRef Full Text | Google Scholar

2. Young DL, Gu MH, Fan CM. The Time-Marching Method of Fundamental Solutions for Wave Equations. Eng Anal Bound Elem (2009) 33:1411–25. doi:10.1016/j.enganabound.2009.05.008

CrossRef Full Text | Google Scholar

3. Wang LH, Qian ZH. A Meshfree Stabilized Collocation Method (SCM) Based on Reproducing Kernel Approximation November. Comput Method Appl M (2020) 371:113303. doi:10.1016/j.cma.2020.113303

CrossRef Full Text | Google Scholar

4. Mellouli H, Jrad H, Wali M, Fakhreddine D. Geometrically Nonlinear Meshfree Analysis of 3D-Shell Structures Based on the Double Directors Shell Theory with Finite Rotations. Steel Compos Struct (2019) 31(4):397–408. doi:10.12989/scs.2019.31.4.397

CrossRef Full Text | Google Scholar

5. Mellouli H, Jrad H, Wali M, Dammak F. Meshfree Implementation of the Double Director Shell Model for FGM Shell Structures Analysis. Eng Anal Bound Elem (2019) 99:111–21. doi:10.1016/j.enganabound.2018.10.013

CrossRef Full Text | Google Scholar

6. Mellouli H, Jrad H, Wali M, Dammak F. Free Vibration Analysis of FG-CNTRC Shell Structures Using the Meshfree Radial point Interpolation Method. Comput Math Appl (2020) 79(11):3160–78. doi:10.1016/j.camwa.2020.01.015

CrossRef Full Text | Google Scholar

7. Wang LH, Liu YJ, Zhou YT, Yang F. Static and Dynamic Analysis of Thin Functionally Graded Shell with In-Plane Material Inhomogeneity. Int J Mech Sci (2021) 193:106165. doi:10.1016/j.ijmecsci.2020.106165

CrossRef Full Text | Google Scholar

8. Li PW, Fan CM. Generalized Finite Difference Method for Two-Dimensional Shallow Water Equations. Eng Anal Bound Elem (2017) 80:58–71. doi:10.1016/j.enganabound.2017.03.012

CrossRef Full Text | Google Scholar

9. Baccouch M, Temimi H. A High-Order Space-Time Ultra-weak Discontinuous Galerkin Method for the Second-Order Wave Equation in One Space Dimension. J Comput Appl Math (2021) 389:113331. doi:10.1016/j.cam.2020.113331

CrossRef Full Text | Google Scholar

10. Xie X, Liu YJ. An Adaptive Model Order Reduction Method for Boundary Element-Based Multi-Frequency Acoustic Wave Problems. Comput Method Appl M (2021) 373:113532. doi:10.1016/j.cma.2020.113532

CrossRef Full Text | Google Scholar

11. Yang SP, Liu FW, Feng LB, Turner I. A Novel Finite Volume Method for the Nonlinear Two-Sided Space Distributed-Order Diffusion Equation with Variable Coefficients. J Comput Appl Math (2021) 388:113337. doi:10.1016/j.cam.2020.113337

CrossRef Full Text | Google Scholar

12. Takekawa J, Mikada H, A Mesh-free Finite-Difference Method for Elastic Wave Propagation in the Frequency-Domain. Comput Geosci-uk 118. (2018) p. 65–78. doi:10.1016/j.cageo.2018.05.011

CrossRef Full Text | Google Scholar

13. Gao LF, Keyes D. Combining Finite Element and Finite Difference Methods for Iso-Tropic Elastic Wave Simulations in an Energy-Conserving Manner. J Comput Phys (2019) 378:665–85. doi:10.1016/j.jcp.2018.11.031

CrossRef Full Text | Google Scholar

14. Akers B, Liu T, Reeger J. A Radial Basis Function Finite Difference Scheme for the Benjamin-Ono Equation. Math (2021) 9(1):65. doi:10.3390/math9010065

CrossRef Full Text | Google Scholar

15. Bhardwaj A, Kumar A. A Meshless Method for Time Fractional Nonlinear Mixed Diffusion and Diffusion-Wave Equation. Appl Numer Math (2021) 160:146–65. doi:10.1016/j.apnum.2020.09.019

CrossRef Full Text | Google Scholar

16. Ebrahimijahan A, Dehghan M. The Numerical Solution of Nonlinear Generalized Benjamin-Bona-Mahony-Burgers and Regularized Long-Wave Equations via the Meshless Method of Integrated Radial Basis Functions. Eng Comput-germany (2021) 37:93–122. doi:10.1007/s00366-019-00811-3

CrossRef Full Text | Google Scholar

17. Rasoulizadeh MN, Nikan O, Avazzadeh Z. The Impact of LRBF-FD on the Solutions of the Nonlinear Regularized Long Wave Equation. Math Sci (2021) doi:10.1007/s40096-021-00375-8

CrossRef Full Text | Google Scholar

18. Oruc O. A Radial Basis Function Finite Difference (RBF-FD) Method for Numerical Simulation of Interaction of High and Low Frequency Waves: Zakharov-Rubenchik Equations. Appl Math Comput (2021) 394:125787. doi:10.1016/j.amc.2020.125787

CrossRef Full Text | Google Scholar

19. Lu X, Zhang P, Shi LW, Hou SM, Kuang Y. A Radial Basis Function Meshless Numerical Method for Solving Interface Problems in Irregular Domains. Adv Appl Math Mech (2021) 13:645–70. doi:10.4208/aamm.OA-2020-0004

CrossRef Full Text | Google Scholar

20. Ranocha H, Mitsotakis D, Ketcheson DI. A Broad Class of Conservative Numerical Methods for Dispersive Wave Equations. Commun Comput Phys (2021) 29:979–1029. doi:10.4208/cicp.OA-2020-0119

CrossRef Full Text | Google Scholar

21. Netuzhylov H, Zilian A. Space-time Meshfree Collocation Method: Methodology and Application to Initial-Boundary Value Problems. Int J Numer Meth Eng (2009) 80(3):355–80.

CrossRef Full Text | Google Scholar

22. Kansa EJ. Multiquadrics-A Scattered Data Approximation Scheme with Applications to Computational Fluid-Dynamics-I. Comput Math Appl (1990) 19(8/9):127–45. doi:10.1016/0898-1221(90)90270-T

CrossRef Full Text | Google Scholar

23. Karageorghis A, Tappoura D, Chen CS. The Kansa RBF Method with Auxiliary Boundary Centres for Fourth Order Boundary Value Problems. Math Comput Simulat (2021) 181:581–97. doi:10.1016/j.matcom.2020.10.010

CrossRef Full Text | Google Scholar

24. Wang FZ, Hou ER. A Direct Meshless Method for Solving Two-Dimensional Second-Order Hyperbolic Telegraph Equations. J Math-uk (2020) 8832197. doi:10.1155/2020/8832197

CrossRef Full Text | Google Scholar

25. Myers DE, Iaco SD, Posa D, Cesare LD. Space-time Radial Basis Functions. Comput Math Appl (2002) 43:539–49. doi:10.1016/S0898-1221(01)00304-2

CrossRef Full Text | Google Scholar

26. Wang FZ, Hou ER, Ahmad I, Ahmad H. An Efficient Meshelss Method for Hyperbolic Telegraph Equations. Cmes-comput Model Eng (2021) doi:10.32604/cmes.2021.014739

CrossRef Full Text | Google Scholar

27. Wang FZ, Zheng KH, Ahmad I, Ahmad H. Gaussian Radial Basis Functions for Linear and Nonlinear Convection-Diffusion Problems. Open Phys (2021) 19:69–76. doi:10.1515/phys-2021-0011

CrossRef Full Text | Google Scholar

28. Rippa S. An Algorithm for Selecting a Good Value for the Parameter C in Radial Basis Function Interpolation. Adv Comput Math (1999) 19:193–210. doi:10.1023/A:1018975909870

CrossRef Full Text | Google Scholar

29. Fasshauer GE, Zhang JG. On Choosing Optimal Shape Parameters for RBF Approximation. Numer Algorithms (2007) 45:345–68. doi:10.1007/s11075-007-9072-8

CrossRef Full Text | Google Scholar

30. Su MY, Ren ZH, Zhang ZY. An ADI Finite Volume Element Method for a Viscous Wave Equation with Variable Coefficients. Cmes-comp Model Eng (2020) 123(2):739–76. doi:10.32604/cmes.2020.08563

CrossRef Full Text | Google Scholar

31. Zampieri E, Pavarino LF. Implicit Spectral Element Methods and Neumann-Neumann Preconditioners for Acoustic Waves. Comput Method Appl M (2006) 195(19-22):2649–73. doi:10.1016/j.cma.2005.06.005

CrossRef Full Text | Google Scholar