Percolation Analysis of Brain Structural Network

The brain network is one specific type of critical infrastructure networks, which supports the cognitive function of biological systems. With the importance of network reliability in system design, evaluation, operation, and maintenance, we use the percolation methods of network reliability on brain networks and study the network resistance to disturbances and relevant failure modes. In this paper, we compare the brain networks of different species, including cat, fly, human, mouse, and macaque. The differences in structural features reflect the requirements for varying levels of functional specialization and integration, which determine the reliability of brain networks. In the percolation process, we apply different forms of disturbances to the brain networks based on metrics that characterize the network structure. Our findings suggest that the brain networks are mostly reliable against random or k-core-based percolation with their structure design, yet becomes vulnerable under betweenness or degree-based percolation. Our results might be useful to identify and distinguish brain connectivity failures that have been shown to be related to brain disorders, as well as the reliability design of other technological networks.

Introduction

Network reliability measures the ability of a network to perform prescribed functions against disturbance. Whether it is a power grid, a transportation network, a brain network, or other functional networks, the losses caused by network failures are huge. The northeast blackout of 2003 in North America, with an estimated 50 million people affected [1], was a large-scale power grid paralysis due to a line trip. And traffic congestions due to network failure usually generate substantial costs every year, together with traffic accidents and disasters [2]. Recent studies have demonstrated that the structural properties of the network largely determine system reliability and resilience under various damage [3–5]. This is also true for brain networks, which are the critical infrastructure for complex biological systems. Many brain disorders, such as Alzheimer disease (AD), amyotrophic lateral sclerosis (ALS), and schizophrenia, etc., have been found related to network connectivity alterations [6], causing physical or psychological pain to patients and their families. Network reliability is of great significance to understand the design principle and failure mechanism of these complex systems.

Accordingly, the network reliability of technological networks is mainly focused on, such as transportation networks, communication networks, and power grids [7]. The study of network reliability involves two-terminal [8], k-terminal [9, 10], and all-terminal [11, 12] network connectivity, which are defined as the probability that a subset of nodes are able to communicate with each other, and measured as integrity for many networks without distinguishing specific function. In addition, dedicated evaluation methods of reliability are proposed to address specific characteristics of the network. In the transportation network, network reliability mainly considers road destination reachability and commuter travel time. For example, connectivity reliability (CR) refers to the probability of network nodes staying connected, which is a static evaluation of the road network structure [13]. Travel time reliability (TTR), or congestion delay index (CDI), considers the probability of travel time from origin to a destination within a specified interval. And capacity related reliability (CRR) measures the probability that the traffic capacity can support a certain level of traffic demand [14]. In communication networks, note that CRR is also used in evaluating network reliability, with heterogeneous link capacities [15], to sustain the transmission requirements. Diameter-constrained reliability (DCR) is another probability metric about the maximum delay requirements after random failures, which limits the terminal set and path length [16]. In power grids, indicators for measuring network reliability proposed by the European Network of Transmission System Operators for Electricity (ENTSOE) [3] include energy not supplied (ENS), which is an estimation of the supply of energy that final consumers cannot obtain due to incidents. Total loss of power (TLP) is a measure of generation shortfall. And restoration time (RT) refers to the time it takes for the system to recover from the disturbance. The aforementioned research methods of network reliability have similarity to some extent: based on probability tools, they concern the state or efficiency of operative path “connectivity.”

In this paper, we focus on the reliability of the brain network. The anatomic connections between the cerebral cortex regions form the structural network on which the neural activities unfold. Functional networks are formed by the dynamical interaction of neural activities among cortical areas [17]. At present, many studies aim at the structural and functional characteristics of brain networks [18], which establish anatomical or functional correlations, calculate features with neurological significance, and reveal the organization principles or operating rules of the brain from the unique perspective of complex networks. The organization of a structure and function network is interdependent. The topology, synchronization, and other dynamic properties of functional networks are strongly influenced by small world and other structural connectivity indicators. On the contrary, the dynamics can adjust the structure network topology in a slower timescale [19]. The coupling of the brain structure and functional network may lead to cascading failure between the two networks, which can be summarized by a universal model [20]. For example, in human brain networks [6], densely connected modules are formed by geometrically close neural elements, promoting the specific function of the local area. And the formation of long-range connections between these modules promotes the scheduling and integration of global function. It is suggested that this “modularity” or “integration” nature changes in the brain connectome with neuropsychiatric disorder. Functional separation refers to the processing of neurons between functional related areas in a community. There are two kinds of integration processes in the network, one is based on the efficiency of global communication, the other is based on the ability of network integration of distributed information [21]. For example, AD patients appear to have modular reorganization in the resting state networks [22], and patients with schizophrenia appear to have reduced density of rich club connections [23], which play a significant role in brain integrative processes, etc. These studies reflect that fact that brain disorders are also strongly related to network structural reliability.

Here, we introduce the methods of engineering network reliability into brain network analysis and provide information on how the structural features affect the reliability, aiming at the failure mode of the brain network through the percolation method [24]. The percolation theory [25, 26] is originally used for the diffusion of forest fires or the distribution of oil and gas in porous stones. It has successfully been applied to describe a large variety of natural systems, such as the complex Earth system [27]. It is generalized for the shift of the network state between connected and disconnected at a critical point. We suppose that the critical state represents some inherent properties of the brain network, including the vulnerability of the brain network to varying degrees of external damage. Our study of the percolation process guides us to locate the vulnerable point that causes brain disorder, determine the stage of brain disease, and identify possible common characteristics of different brain disease manifestations.

Structure of the Brain Network

To decompose the structure of the network intuitively, we show community topology of structural brain networks of different species in Figure 1, including fly, cat, mouse, macaque, and human. This community structural feature is shared by all of these brain networks. Comparatively, the cat and macaque networks belong to small-scale networks (dozens of nodes, hundreds of edges), the human network belongs to medium-scale networks (hundreds of nodes, thousands of edges), and the fly and mouse networks belong to large networks (∼tens of thousands of edges). The number of network nodes and edges is shown in Table 1. This may be due to the different anatomical resolution of different species. Note that the mouse network is densely connected, while the human network shows a clearer modular pattern with a few connections between different communities. These structural properties can determine the reliability and failure mode of the brain network to some extent.

FIGURE 1

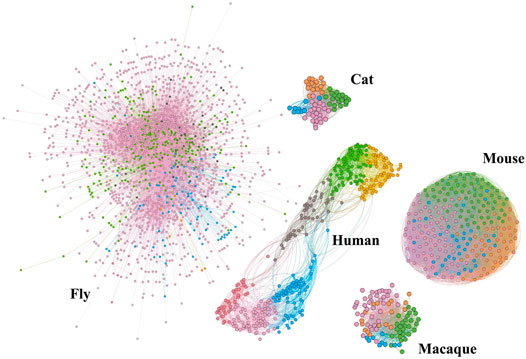
FIGURE 1. Community topology of brain structural networks for different species, including cat, fly, human, mouse, and macaque. Among them, the networks of cat, fly, mouse, and macaque are from the Network Repository [28] http://networkrepository.com.

TABLE 1

TABLE 1. Overview of brain structure networks in different species.

Next, we calculate the distributions of topological features to compare different species networks, from micro and macro perspectives (shown in Figure 2), as well as the meso perspective (shown in Figure 3). Degree defines the number of adjacent edges belonging to a given node from a micro perspective. The degree $k_i$ of node $i$ can be calculated according to the adjacency matrix of the network (see Eq. 1).

$\begin{array}{c}{k}_i={\displaystyle \sum }_{j=1}^n{A}_{ij}\end{array}(1)$

FIGURE 2

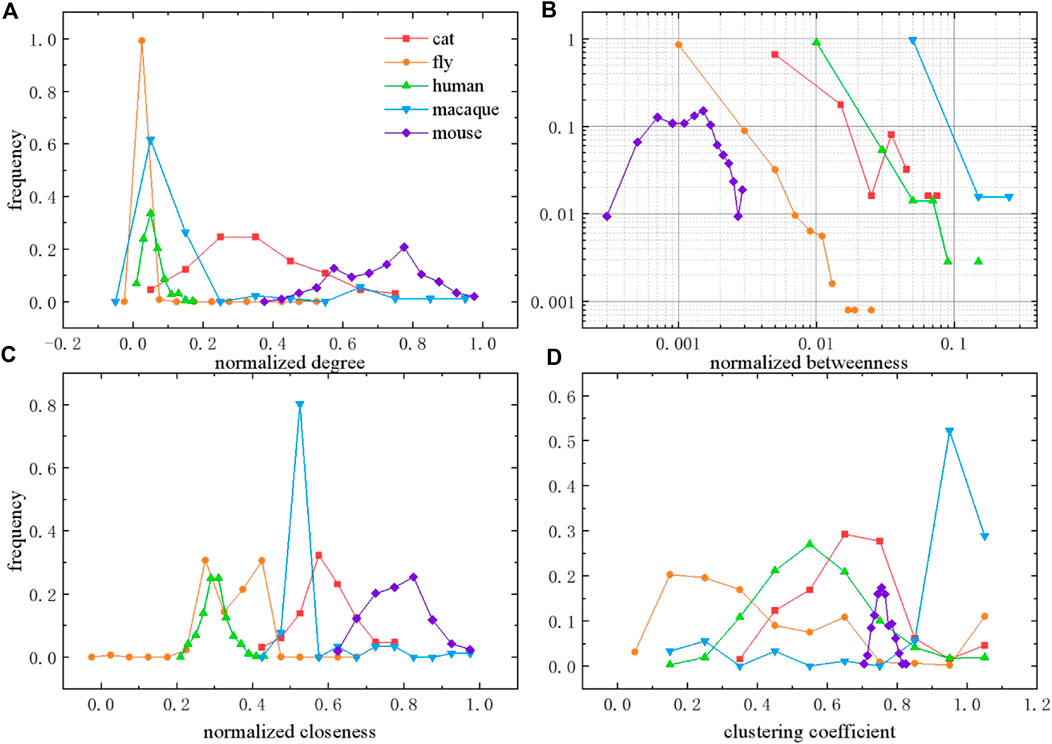
FIGURE 2. Distributions of topological features in different species brain networks. (A) Degree distribution normalized by $N-1$. (B) Betweenness distribution normalized by $N\ast (N-1)/2$. (C) Closeness distribution normalized by $1/(N-1)$. (D) Clustering coefficient distribution.

FIGURE 3

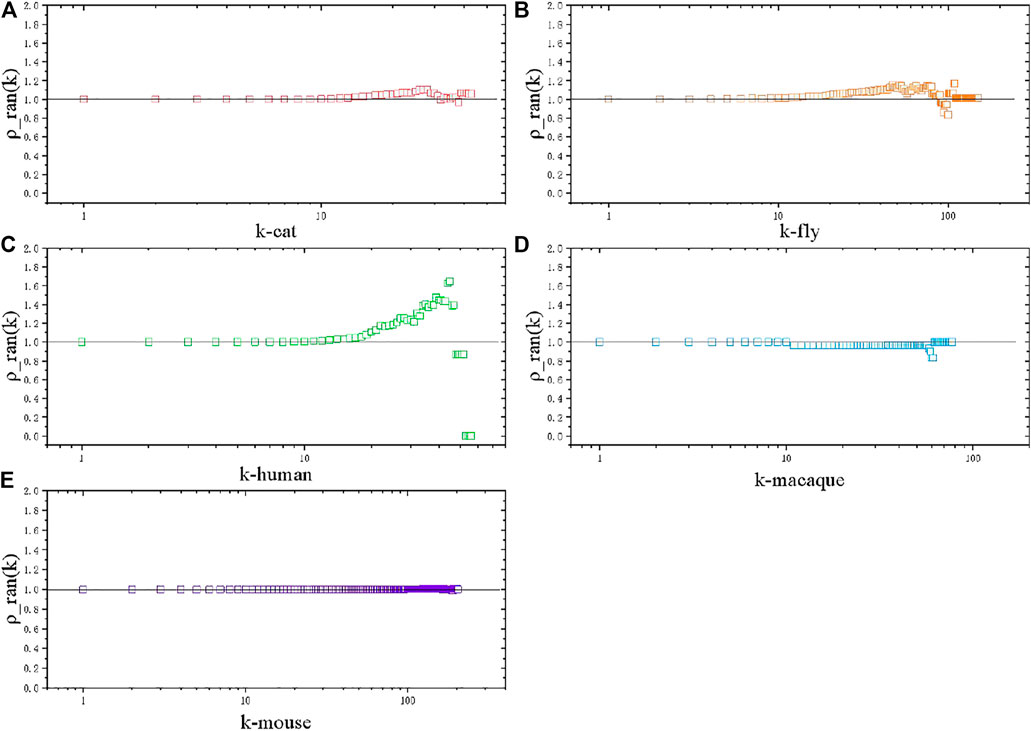
FIGURE 3. Rich club coefficient, normalized by the null model. (A) Cat brain network. (B) Fly brain network. (C) Human brain network. (D) Macaque brain network. (E) Mouse brain network.

As shown in Figure 2A, degree is normalized by $N-1$ to facilitate comparisons between species brain networks of different scales, where $N$ is the number of nodes in the network. For degree distribution, most nodes in fly, human, and macaque networks have a low degree. For mouse and cat networks, degrees in the mouse network are generally high. Betweenness centrality $c_B$ measures the extent to which all-pairs shortest paths pass through a given node $i$ (see Eq. 2) from a macro perspective.

$\begin{array}{c}{c}_B\left(i\right)={\displaystyle \sum }_{st}\frac{g_{st}\left(i\right)}{g_{st}}\end{array}(2)$

where $g_{st}$ is the number of shortest paths between $s, t$ and $g_{st}\left(i\right)$ is the number of those path passing through node $i$. The betweenness is normalized by $N\ast (N-1)/2$, as shown in Figure 2B. It is suggested that the distributions of different species networks seem to follow a scale free distribution, with the mouse network showing certain deviation. The macaque network has the largest betweenness due to its heterogeneous structure, given its relatively small degree and a few large degree nodes. And the betweenness of the mouse network is the smallest, due to its dense connections. Closeness centrality is another important topological metric from a macro perspective, which is defined as the inverse of the average distance from a given node to others (see Eq. 3).

$\begin{array}{c}{c}_i=\frac{n-1}{{{\displaystyle \sum }}_{j=1}^{n-1}{d}_{ij}}\end{array}(3)$

where $d_{ij}$ is the shortest path length between $i$ and $j$. The closeness distributions of all species networks, normalized by $1/(N-1)$, are shown in Figure 2C. It is shown that the nodes in the mouse network have the highest closeness, and the lowest closeness is in the fly network. The clustering coefficient measures the fraction of two neighbors of a given node that are also connected (see Eq. 4).

$\begin{array}{c}{C}_i=\frac{2E_i}{k_i(k_i-1)}\end{array}(4)$

where node $i$ has degree $k_i$, and $E_i$ are edges that actually exist between those $k_i$ neighboring nodes. As shown in Figure 2D, the distribution of the human network is symmetrical with a characteristic value around $0.6$. The macaque network has the largest mean value compared with other distributions, showing strong local connections. Therefore, the structural properties of the network are not completely measured by a single metric, and need comprehensive consideration from different angles.

In the case of the meso perspective, we calculate the rich club coefficient of these species networks with normalization to the null model [29]. The rich club phenomenon, existing in scientific collaboration networks and air transportation networks, is also studied to understand global efficiency in both unweighted and weighted structural brain networks of the human connectome [30], while brain network comparison with other species are rarely involved. Rich club coefficient $\Phi \left(k\right)$ (see Eq. 5), which quantifies the proximity between nodes with high degrees, is defined as the ratio of the actual number of edges between nodes with degree $>k$ to the total edges.

$\begin{array}{c}\Phi \left(k\right)= \frac{2E_{>k}}{N_{>k}(N_{>k}-1)}\end{array}(5)$

Considering that nodes with high degrees have higher probability of interconnection with each other by definition, we usually need a null model to obtain normalized rich club coefficient ${\rho }_{ran}\left(k\right)$ (see Eq. 6) by comparing original rich club coefficient $\text{Φ}\left(k\right)$ with rich club coefficient ${\text{Φ}}_{ran}\left(k\right)$ of the random network (null model) [23, 31].

$\begin{array}{c}{\rho }_{ran}\left(k\right)= \frac{\text{Φ}\left(k\right)}{{\text{Φ}}_{ran}\left(k\right)}\end{array}(6)$

The null model is created by performing a link shuffle to randomize the original network, keeping the same degree distribution. ${\rho }_{ran}\left(k\right)$ greater than 1 reflects the rich club phenomenon of a network. As shown in Figure 3, the rich club phenomenon is significant in the human network (Figure 3C), indicating that nodes with high degrees tend to connect with each other, which may enable global functional communication and integration of distributed brain regions. Our results suggest also that brain networks of other species do not show significantly similar routing principles of integration. It is found that cat and fly networks display a very weak rich club effect (Figures 3A,B), and rich club coefficients in macaque and mouse networks are almost close to 1 (Figures 3D,E). We suppose that the human brain network, compared to other species, has more complicated and diverse functions with higher integration requirements, leading to a much higher rich club coefficient. Meanwhile, the structural properties may affect the reliability of the brain network, which will be discussed in the next section. Actually, networks with rich clubs are usually more vulnerable [32], because the removal of a few rich club members can destroy the overall global connectivity. Here we focus on the connectivity performance of the brain network under different disturbances, through percolation analysis.

Percolation on the Brain Network

In this section, we perform different types of percolation analysis, including degree-based percolation, betweenness-based percolation, $k$-core-based percolation, and random percolation. Percolation of different types may represent different external disturbances [33]. We remove nodes from the network with a fraction $q$ according to the network structural features concerning degree, betweenness, and $k$-core. When the removal fraction is tuned increasingly from zero to unit, at a certain critical probability $q_c$, the state of the network shifts from connected to disconnected, and this critical phenomenon is called percolation. In the percolation case, we have no giant cluster for $q>q_c$ and one giant cluster at least for $q<q_c$. The critical probability $q_c$ for networks with different topological properties may be different, determined by the structure of the network. We analyze the performance of networks during the percolation process, to reveal how the brain networks of different species respond to disturbance. When different external types of disturbances are applied to the network, the reliability and failure modes of the network could be uncovered.

The giant component $G$ (size of the largest connected component) of the network decreases with the removal fraction in Figure 4. As the nodes are removed gradually with a certain order, it will generate various damages to the original network. Figure 4A is the betweenness-based percolation, we remove nodes in descending order of betweenness. It is notable that $G$, for the macaque brain network, drops comparatively fast with a certain critical removed fraction around $0.1$, which is because the macaque network has the largest betweenness. When approaching the critical point, we can observe a sharp decline in the giant component, which may be accompanied by a substantial or complete loss of network function. Other brain networks also decrease quickly at their critical point, except for the mouse brain network. For the strong robustness of the mouse network against disturbances, where the giant component is decreasing almost linearly, we can see from Figure 2A that the connections in the mouse network are particular dense, meaning that the network is highly connected globally. When one of the nodes is removed, other nodes can still maintain connections, which constitutes the high reliability of the mouse brain network. Figure 4B is the degree-based percolation, we remove nodes in descending order of degree. As the betweenness-based percolation, we can observe a similar trend for different species. The cat brain network decreases faster than the human brain network for degree-based percolation.

FIGURE 4

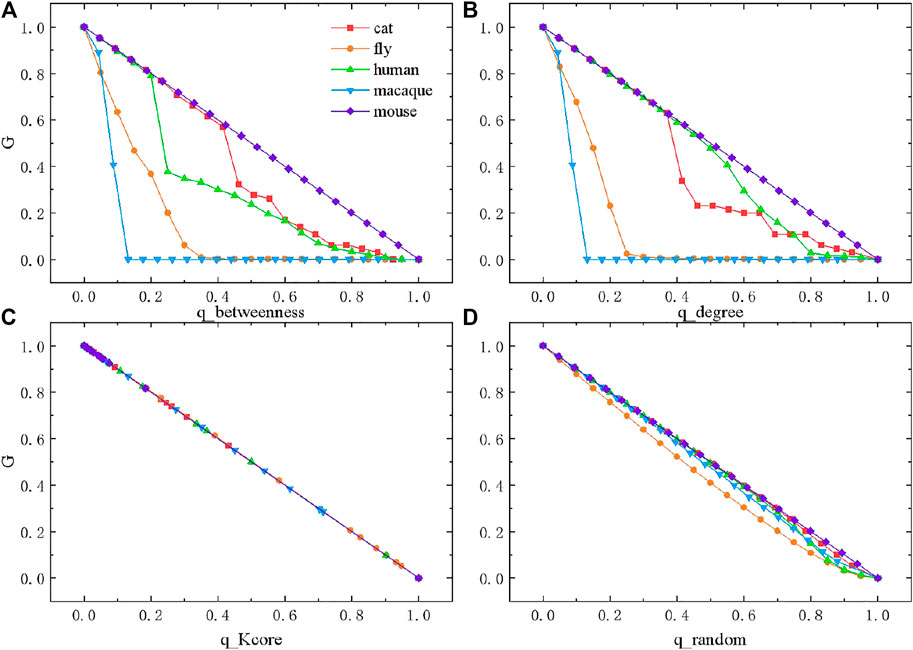
FIGURE 4. Percolation on species brain networks under four forms of disturbances. (A) Percolation based on betweenness. (B) Percolation based on degree. (C) Percolation based on $k$-core. (D) Random percolation.

Next, we perform $k$-core-based percolation in Figure 4C. $k$-core decomposition is a method to decompose and analyze the hierarchy structure of the network [34]. When we remove nodes with a degree less or equal to $(k-1)$ from the network, all the remaining nodes with an updated degree larger or equal to $k$ in the remaining graph are called $k$-core. Nodes belonging to k-core, yet not belonging to $(k+1)$-core, are defined as $k$-shell. In $k$-core-based percolation, we start with the smallest $k$-shell and remove the nodes from the network at each step. Differing from the above two percolation modes, the percolation based on $k$-core shows a distinct failure mode. All species brain networks follow a linear decrease pattern. This is due to the fact that a higher $k$-shell of networks will not become disconnected when small layers are removed.

In contrast to the above three percolation methods based on the network structural features, we also perform random percolation (Figure 4D). Without considering network topology, we randomly remove a fraction of nodes from the network at each step. Surprisingly, the change of $G$ in the network during the random percolation process is almost uniform throughout, where every decrement is similar for each removal fraction. This is possibly because a few highly connected nodes in each network behave like a backbone and maintain the whole network.

Conclusion

We perform network reliability analysis on a brain network, which is the critical infrastructure for biological intelligence. Network reliability pursues the ability to meet the functional requirements in a specific operating environment. Therefore, the fragility of the network under disturbance is particularly important, that a network with high-reliability has the ability to offset the impact of disturbances and strives to maintain connectivity. Here, we pay attention to the global and local connectivity of the brain network, whose loss may cause biological dysfunction as brain disorders. We analyze the brain networks of different species, including cat, fly, human, mouse, and macaque, and explore similarities and differences in structural features and percolation patterns, which may reflect the causality from varying levels of functional specialization and integration.

While the properties of species brain networks are formed during evolution, one of the core tasks is to ensure high reliability, against various disturbances. High reliability of the network suggests balance between global connectivity and local connectivity. We find that brain networks are mostly reliable against random or $k$-core-based percolation with their structure design, yet they become vulnerable under betweenness or degree-based percolation. Furthermore, our study may be useful for building models for the inherent reliability of the brain network, and help to discover the operating rules and disease mechanisms that may exist during the process of operation. Although for the brain or other biological networks, it may be difficult to artificially revise the wiring rules of the network, we hope that an identified relation between the brain organization principles and external disturbances can help guide the avoidance of brain disorders, as reference for other technological networks.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://networkrepository.com/bn.php.

Ethics Statement

Ethical review and approval was not required for the animal study because our data comes from a public data set.

Author Contributions

SG, XQC, and YML performed the analysis. XQC validated the analysis and drafted the manuscript. RK and TL reviewed the manuscript. DQL designed the research. All authors have read and approved the content of the manuscript.

Funding

We acknowledge support from National Natural Science Foundation of China Grants 71822101, 71890973/71890970, 61961146005, and 71771009.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Minkel JR. The 2003 Northeast Blackout–Five Years Later[J]. Scientific American (2008) 13.

Google Scholar

2. Iida Y. Basic Concepts and future directions of road network reliability analysis. Atr (1999) 33(2):125–34. doi:10.1002/atr.5670330203

CrossRef Full Text | Google Scholar

3. Martinez-Anido CB, Bolado R, De Vries L, Fulli G, Vandenbergh M, Masera M. European power grid reliability indicators, what do they really tell? Electric Power Syst Res (2012) 90:79–84.

Google Scholar

4. Moreno Y, Nekovee M, Vespignani A. Efficiency and reliability of epidemic data dissemination in Complex networks. Phys Rev E (2004) 69(5):055101. doi:10.1103/physreve.69.055101

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zeng G, Li D, Guo S, Gao L, Gao Z, Stanley HE, et al. Switch between Critical percolation modes in City traffic dynamics. Proc Natl Acad Sci USA (2019) 116(1):23–8. doi:10.1073/pnas.1801545116

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Van den Heuvel MP, Sporns O. A Cross-disorder Connectome landscape of brain dysconnectivity. Nat Rev Neurosci (2019) 1.

CrossRef Full Text | Google Scholar

7. Duan D-L, Ling X-D, Wu X-Y, Zhong B. Reconfiguration of distribution network for loss reduction and reliability improvement based on an enhanced genetic algorithm. Int J Electr Power Energ Syst (2015) 64:88–95. doi:10.1016/j.ijepes.2014.07.036

CrossRef Full Text | Google Scholar

8. Ramirez-Marquez JE, Coit DW. A Monte-Carlo simulation approach for approximating multi-state two-terminal reliability. Reliability Eng Syst Saf (2005) 87(2):253–64. doi:10.1016/j.ress.2004.05.002

CrossRef Full Text | Google Scholar

9. Hardy G, Lucet C, Limnios N. K-terminal network reliability measures with binary decision diagrams. IEEE Trans Rel (2007) 56(3):506–15. doi:10.1109/tr.2007.898572

CrossRef Full Text | Google Scholar

10. Yeh F-M, Lu S-K, Kuo S-Y. OBDD-based evaluation of k-terminal network reliability. IEEE Trans Reliability (2002) 51(4):443–51.

Google Scholar

11. Sharafat AR, Ma'rouzi OR. All-terminal network reliability using recursive truncation algorithm. IEEE Trans Rel (2009) 58(2):338–47. doi:10.1109/tr.2009.2020120

CrossRef Full Text | Google Scholar

12. Srivaree-Ratana C, Konak A, Smith AE. Estimation of all-terminal network reliability using an artificial neural network. Comput Operations Res (2002) 29(7):849–68. doi:10.1016/s0305-0548(00)00088-5

CrossRef Full Text | Google Scholar

13. Bell MG, Iida Y. Transportation Network analysis. New York: Chichester (1997). doi:10.1002/9781118903032

CrossRef Full Text

14. Chen A, Yang H, Lo HK, Tang WH. A Capacity related reliability for transportation networks. Atr (1999) 33(2):183–200. doi:10.1002/atr.5670330207

CrossRef Full Text | Google Scholar

15. Soh S, Rai S. An efficient Cutset approach for evaluating Communication-network reliability with heterogeneous link-Capacities. IEEE Trans Rel (2005) 54(1):133–44. doi:10.1109/tr.2004.842530

CrossRef Full Text | Google Scholar

16. Cancela H, Petingui L. Diameter Constrained network reliability: exact evaluation by factorization and bounds. Reportes Técnicos (2001) 01-03.

Google Scholar

17. Honey CJ, Kötter R, Breakspear M, Sporns O. Network structure of Cerebral Cortex shapes functional Connectivity on multiple time scales. Proc Natl Acad Sci (2007) 104(24):10240–5. doi:10.1073/pnas.0701519104

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Rubinov M, Sporns O. Complex network measures of brain Connectivity: uses and interpretations. Neuroimage (2010) 52(3):1059–69. doi:10.1016/j.neuroimage.2009.10.003

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bullmore E, Ed, and O Sporns. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci (2009) 10(3):186–98. doi:10.1038/nrn2575

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Duan D, Lv C, Si S, Wang Z, Li D, Gao J, et al. Universal behavior of Cascading failures in interdependent networks. Proc Natl Acad Sci USA (2019) 116(45):22452–7. doi:10.1073/pnas.1904421116

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Sporns O. Network attributes for segregation and integration in the human brain. Curr Opin Neurobiol (2013) 23(2):162–71. doi:10.1016/j.conb.2012.11.015

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen G, et al. Modular reorganization of brain resting state networks and its independent validation in Alzheimer's disease patients. Front Hum Neurosci (2013) 7:456. doi:10.3389/fnhum.2013.00456

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Van den Heuvel MP, Sporns O, Collin G, Scheewe T, Mandl RCW, Cahn W, et al. Abnormal rich Club organization and functional brain dynamics in schizophrenia. JAMA psychiatry (2013) 70(8):783–92. doi:10.1001/jamapsychiatry.2013.1328

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Li D, Zhang Q, Zio E, Havlin S, Kang R. Network reliability analysis based on percolation theory. Reliability Eng Syst Saf (2015) 142:556–62. doi:10.1016/j.ress.2015.05.021

CrossRef Full Text | Google Scholar

25. Stauffer D, Aharony A. Introduction to percolation theory. United Kingdom: Taylor & Francis (2018). doi:10.1201/9781315274386

CrossRef Full Text

26.A Bunde, and S Havlin, editors. Fractals and Disordered Systems. Germany: Springer Science & Business Media (2012).

27. Fan J, Meng J, Ludescher J, Chen X, Ashkenazy Y, Kurths J, et al. Statistical physics approaches to the Complex Earth system. Phys Rep (2020) 8:961–84. doi:10.1016/j.physrep.2020.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Rossi R, Ahmed N. The network data repository with interactive graph analytics and visualization. in Twenty-Ninth AAAI Conference on Artificial Intelligence; Austin, TX, United StatesAAAI Press (2015).

Google Scholar

29. Colizza V, Flammini A, Serrano MA, Vespignani A. Detecting rich-Club ordering in Complex networks. Nat Phys (2006) 2(2):110–5. doi:10.1038/nphys209

CrossRef Full Text | Google Scholar

30. Van den Heuvel MP, Sporns O. Rich-club organization of the human Connectome. J Neurosci (2011) 31(44):15775–86. doi:10.1523/jneurosci.3539-11.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

31. McAuley JJ, da Fontoura Costa L, Caetano TS. Rich-club phenomenon across Complex network hierarchies. Appl Phys Lett (2007) 91(8):084103. doi:10.1063/1.2773951

CrossRef Full Text | Google Scholar

32. Zhou S, Mondragón RJ. The rich-Club phenomenon in the Internet topology. IEEE Commun Lett (2004) 8(3):180–2. doi:10.1109/lcomm.2004.823426

CrossRef Full Text | Google Scholar

33. Fornito A, Zalesky A, Breakspear M. The Connectomics of brain disorders. Nat Rev Neurosci (2015) 16(3):159–72. doi:10.1038/nrn3901

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Carmi S, Havlin S, Kirkpatrick S, Shavitt Y, Shir E. A model of Internet topology using k-shell decomposition. Proc Natl Acad Sci (2007) 104(27):11150–4. doi:10.1073/pnas.0701175104

PubMed Abstract | CrossRef Full Text | Google Scholar