Spontaneous Formations of Dynamical Steady States in Polariton Condensates

We present a numerical analysis on dynamical steady states of polariton Bose–Einstein condensates (BECs) in an incoherent exciton reservoir driven by a ring-shaped optical pump. The balance between the loss and gain of polariton BEC induces a variety of steady states with different configurations, including approximate Gaussian distribution and topological defects, such as vortex–antivortex pairs, vortices with a winding number, and solitons. Besides, the system becomes unstable under fast decay rates and small pumping ring, where BECs can no longer exist in the long-time limit. We also confirm the soliton is dynamically stable in this system, with a steady polariton current induced by the repulsive polariton–polariton and polariton–exciton interactions.

1 Introduction

Polariton is a strong light–matter–coupled quasiparticle formed in semiconductor microcavities. Sufficiently strong optical pump can stimulate a spontaneous transition of bosonic polaritons to Bose–Einstein condensates (BECs) [1, 2]. Many features of atomic BEC have been successfully demonstrated in polariton BEC, such as long-rang coherence [3, 4], superfluid flow [4–6], and quantized vortices [7–10]. The combination of photon component with an extremely light effective mass and exciton component with strong interaction is essential for the high transition temperature [11–13] and fast thermalization in polariton BECs. Recent experiments have shown that polariton interactions can be enhanced by orders of magnitude through injecting an itinerant electron gas into a monolayer transition metal dichalcogenides [14, 15]. Moreover, the nonlinear interaction between polaritons and reservoir excitons causes a variety of reconfigurable potential barrier for polariton BECs [16], such as parabolic potential [17], chiral polaritonic lenses [18], and ring-shaped potential [19, 20]. Besides, rich vortex multistability [21–23] and Thomas–Fermi regime [24] revealed in the ring-shaped pumping potential provide opportunities to explore topological defects in nonequilibrium systems.

The polariton BEC is a dynamical steady state instead of a thermal equilibrium due to the rapid radiative decay of polariton and optical pump maintaining excitons. It provides a platform to study nonequilibrium quantum system with a macroscopic coherence. The leakage of photons from cavity and the decay of excitons via radiative and nonradiative processes set a finite lifetime of polaritons. The development of new structures can extend the cavity photon lifetime from 20 to 30 ps [25] to 200 ps or more [26, 27]. Since the leaking photons carry the density, momentum, energy, spin, and phase information of polaritons, it is possible to characterize the nonequilibrium dynamics of polariton BECs via photon luminescence of the escaped photons [28, 29].

The aim of this study was to investigate dynamical steady states of polariton BECs in incoherent exciton reservoir driven by a ring-shaped optical pump. Owing to the nonequilibrium nature of polariton BEC, the ring-shaped pump and decay can induce considerable effect on the steady states. First, the phase diagram of the steady states of polariton BEC by varying pumping and decay rates is depicted. The phase diagram consists of regions where the polariton BEC acquires an approximate Gaussian distribution, a vortex ring structure, a soliton structure, and a ring mode configuration. Second, different types of steady states in the phase diagram are, respectively, investigated by the density and phase distributions. Some exotic topological defects, such as higher order vortices and vortex–antivortex pairs, are then characterized and distinguished. And the effects of noise of initial condition and particle number on the dynamical evolution processes are discussed. Finally, the stability of solitons in the two-dimensional nonequilibrium system is analyzed. We find that several steady states can form spontaneously inside the pumping ring due to particle current induced by the nonlinear polariton–polariton and polariton–exciton interaction.

The remainder of this article is organized as follows. In Section 2, we present the mean-field formalism to incorporate the reservoir exciton. The phase diagram of steady states of polariton BEC is depicted and analyzed in Section 3. The features of different phases in the phase diagram are investigated in Section 4. Finally, we summarize the main results in Section 5.

2 Theoretical Model

At the mean-field level, the condensate dynamics can be described in terms of the Gross–Pitaevskii equation (GPE), which can be generalized to nonequilibrium systems by considering pumping and loss of polaritons with stimulated scattering [30, 31]. As a result, an open-dissipative GPE (ODGPE) with complex terms for condensate wave function $\phi \left(\mathbf{r},t\right)$ can be introduced, together with a dynamical equation for the density $n\left(\mathbf{r},t\right)$ of exciton reservoir. A coupled equation set is used to describe the complex coupling system of polariton BEC and exciton reservoir [32] as follows:

$i\frac{\partial \phi \left(\mathbf{r},t\right)}{\partial t}=\left[-\frac{{\nabla }^2}{2}+g_c{\left|\phi \left(\mathbf{r},t\right)\right|}^2+g_{R}n\left(\mathbf{r},t\right)+GP\left(\mathbf{r}\right)-\frac{i}{2}\left({\gamma }_c-R_{R}n\left(\mathbf{r},t\right)\right)\right]\phi \left(\mathbf{r},t\right),$

$\frac{\partial n\left(\mathbf{r},t\right)}{\partial t}=P\left(\mathbf{r}\right)-\left({\gamma }_R+R_R{\left|\phi \left(\mathbf{r},t\right)\right|}^2\right)n\left(\mathbf{r},t\right).(1)$

Here, $\mathbf{r}=\left(x,y\right)$ denotes the spatial coordinate and $P\left(\mathbf{r}\right)$ represents the pumping rate of exciton reservoir. In the following discussion, we choose a ring-shaped pump which can be written as follows:

$P\left(\mathbf{r}\right)=\{\begin{array}{cc}100J_6\left(\alpha \mathbf{r}\right),& \left|\mathbf{r}\right|<R\\ 0,& \left|\mathbf{r}\right|>R\end{array},(2)$

where $J_6$ is the first-kind Bessel function of the 6th order and the maximal pumping rate is fixed at $P_{max}=35.57$ by the pre-factor. The first node of $J_6$ is located at radius R by tuning the parameter α. A small α corresponds to a large radius R of the pumping ring. In an experiment, the pumping ring can be achieved by shaping the pulsed laser beam into a ring [24].

The exciton reservoir provides a source for creating condensed polaritons via stimulated scattering processes. The dynamics of polariton BEC is controlled by the following parameters: the decay rates of coherent polaritons ${\gamma }_c$ and incoherent exciton reservoir ${\gamma }_R$, the stimulated scattering rate $R_R$ from the exciton reservoir into the polariton BEC, the nonlinear polariton–polariton interaction $g_c$ and polariton–exciton interaction $g_R$, and an additionally pump-induced shift G [33]. In Eq. 1, the variables and coefficients are dimensionless by using the time scale $\tau =1/{\Gamma }_c$ and the length scale of the diffraction length of polariton matter wave $L=\sqrt{\hslash /\left(m_p{\Gamma }_c\right)}$, where $m_p$ is the effective mass of polariton and ${\Gamma }_c$ is the decay rate of coherent polaritons in physical units [22]. According to the typical parameters of a GaAs-based microcavity, we use the dimensionless parameters ${\gamma }_R=2,$$R_R=0.1,$$g_c=0.001,$$g_R=0.01,$ and $G=0.01$ [32, 34] in Eq. 1 to numerically simulate the dynamics of polariton BEC by a time-splitting Fourier pseudospectral method. Such an algorithm is unconditionally stable, and of spectral accuracy in space and second-order accuracy in time [35], and has been widely used to study dynamics of vortices and solitons in BECs [36–38]. In the following discussion, all results are tested for convergence and stability.

3 Phase Diagram

Previous investigations on polariton BEC have revealed various types of spontaneous formations of steady states [39, 40]. However, the boundaries between different steady states are ambiguous in the presence of balance between polariton loss and gain from reservoir. In this section, we discuss the steady-state solutions of polariton BEC by numerically evolving Eq. 1 with a different pumping radius R and the ratio between polaritons and reservoir decays ${\gamma }_c/{\gamma }_R$. In the seeds of the numerical evolution, we keep the ratio between initial numbers of excitons and polaritons more than ${10}^4:1$ and induce random noises in both the exciton reservoir and polariton to simulate fluctuations. In the presence of a nonresonant ring-shaped pumping laser, more polaritons condense in this two-dimensional system through stimulated scattering of excitons. In the long-time limit, the total numbers of polaritons and reservoir excitons become constants upon time evolution, and their corresponding distributions are considered as the dynamical steady state.

In Figure 1, we show the phase diagram of steady states with tuning the pumping radius R and decay rate ratio ${\gamma }_c/{\gamma }_R$. According to the structures of density and phase distributions, the phase diagram can be separated into different regions, including approximate Gaussian distribution (AGD, red), vortices (yellow), solitons (green), ring mode (blue), and unstable region (gray). Here, the red circles label the phase transition points obtained by numerical simulation and the blue dotted lines are drawn by connecting neighboring circles to show the phase boundaries approximately.

FIGURE 1

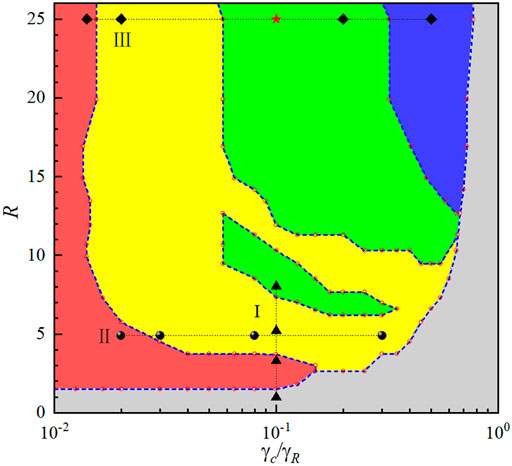
FIGURE 1. (Color online) Phase diagram described by Eq. 1 for the pumping radius R and the decay ratio ${\gamma }_c/{\gamma }_R$. Different colors represent different types of steady states of polaritons: approximate Gaussian distribution (red), vortices (yellow), solitons (green), ring mode (blue), and unstable region (gray). The blue dotted lines show approximate phase boundaries.

We find that faster loss of polaritons (large ${\gamma }_c/{\gamma }_R$) and slower replenishment from reservoir excitons (small pumping radius R) drive the system into an unstable region where no BEC can exist in the long-time limit. When the loss of polaritons is slow (${\gamma }_c/{\gamma }_R\mathrm{\lesssim }0.6$), steady states of BEC can form with increasing pumping radius. Specifically, the combination between loss and gain of polariton in the system induces a special region of vortex formation (yellow). Such a vortex state is under a subtle competition with the soliton phase (green) since the energies of the two states are very close in a broad region around the phase boundary, and the time evolution results are highly sensitive on the initial noise introduced to polaritons and reservoir excitons.

4 Dynamical Evolution

The density and phase distributions of polariton BEC in different steady states are investigated, respectively, in Figures 2, 3, 5. For polariton BECs with fixed decay ratio ${\gamma }_c/{\gamma }_R=0.1$, different steady states appear with increasing pumping ring radius R as in Figures 2A–D, corresponding to the black triangles in the phase diagram Figure 1. When pumping radius R is very small ($R=1$ in Figure 2A), the system presents no BEC in the long-time limit since the polariton experiences more severe loss than creation. As the pumping radius increases, more reservoir excitons supplement polaritons due to stimulated scattering, and a steady state of BEC starts to emerge as shown in Figure 2B. The density distribution inside the pumping ring tends to an approximated Gaussian profile as in the Thomas–Fermi regime. Similar phenomena have been used to measure polariton–polariton interaction strength [24]. By further increasing R, the systems transform to a vortex ring structure (Figure 2C). A remarkable finding is that in this rotationally symmetric system, the vortex ring acquires a winding number $\left|m\right|=2$ as shown by the phase distribution of Figure 2C. Such a vortex solution spontaneously breaks rotation symmetry, where polaritons are squeezed to the edge of pumping ring, and phase singularity is at the ring center. When the pumping radius is increased to $R=8$ (Figure 2D), the steady state is a soliton solution, where most density are localized in the center of pumping ring. Soliton and vortex are spatially localized solutions in nonlinear system, which can also present in nonequilibrium system.

FIGURE 2

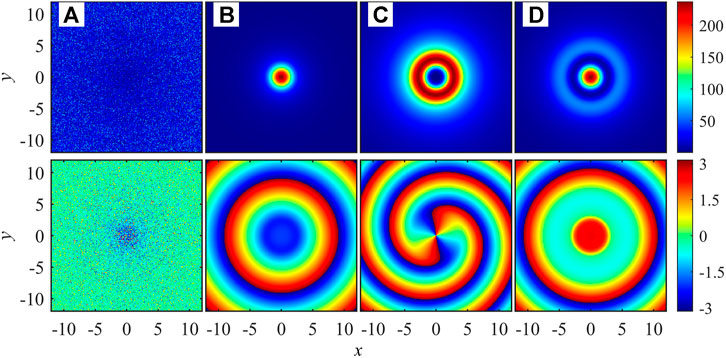
FIGURE 2. (Color online) Polaritons density $|\phi \left(x,y\right){|}^2$(upper panels) and phase distributions $\theta \left(x,y\right)$(lower panels) of steady states simulated by Eq. 1 at $t=400$ with the decay ratio ${\gamma }_c/{\gamma }_R=0.1$. (A–D): Pumping radius $R=\mathrm{1,3,5.2},8$, corresponding to locations marked by triangles of I from bottom to up in Figure 1, respectively.

FIGURE 3

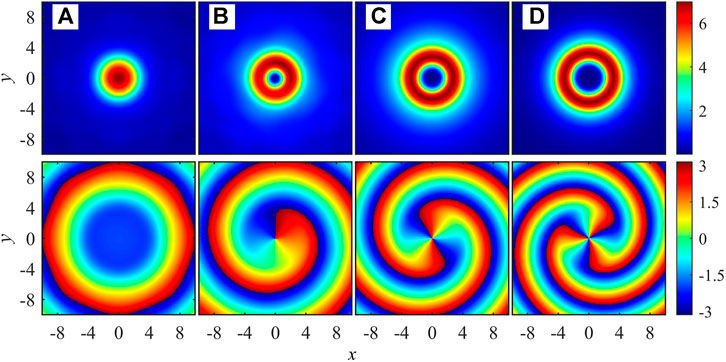
FIGURE 3. (Color online) Steady-state distributions of polaritons density $|\phi \left(x,y\right){|}^2$(upper panels) and phase $\theta \left(x,y\right)$(lower panels) described by Eq. 1 at $t=400$ with the pumping radius $R=5$. (A–D): the decay ratios ${\gamma }_c/{\gamma }_R=0.02,0.03,0.08,0.3$, corresponding to locations marked by spheres of II from left to right in Figure 1, respectively.

High-order vortices are unstable in conservative systems, which will evolve into vortices with winding numbers $m=\pm 1.$ However, it is possible to stabilize high-order vortices in a nonequilibrium system since the reservoir excitons continuously replenish polaritons [23]. To characterize such exotic topological defects in detail, we fix the pumping radius at a relatively small value of $R=5$ in Figure 3 and choose four typical values of decay rate ratio ${\gamma }_c/{\gamma }_R$ to obtain the density and phase distributions of steady states. The choices are labeled by black dots in the phase diagram in Figure 1. By increasing the decay rate ratio ${\gamma }_c/{\gamma }_R$, the polariton BEC transforms from AGD (Figure 3A) to vortex ring structures with winding number up to $\left|m\right|=3$ (Figures 3B–D). In the high-density region of vortex, the phase forms a spiral geometry. We also find that the vortex with larger winding number has a larger vortex core. Besides, notice that the winding numbers in Figures 3B,C are positive and the vortices rotate counterclockwise, while the winding number in Figure 3D is negative with clockwise rotating vortex. This parity symmetry is broken by the fluctuation of initial noises of the polariton and reservoir excitons. We also note that high-order vortex can be easily found in numerical simulations when the decay rate ratio ${\gamma }_c/{\gamma }_R$ is large and the pumping radius R is relative small in the vortex region (yellow area) of Figure 1, and the maximal winding number we have found is $\left|m\right|=5$ for the parameters chosen in this study.

To further characterize the effect of fluctuations in the initial condition, we study the time evolution of the total number of polaritons $N_p\left(t\right)={\displaystyle \int |\phi \left(\mathbf{r},t\right){|}^{2}dr}$ (solid lines), and reservoir excitons $N_R\left(t\right)={\displaystyle \int n\left(\mathbf{r},t\right)dr}$ (dash lines) are shown in Figure 4, using the same parameters as in Figures 3B–D. We find that the initial state only influences the transient dynamics of the system but has no effect on the steady states in the long-time limit. In fact, the dynamical steady state is quite robust against the initial conditions of the polaritons and reservoir excitons, and it is solely determined by the pumping radius and decay rates. Comparing the results with different decay ratios ${\gamma }_c/{\gamma }_R=0.03,0.08,0.3$ in Figure 4, polariton population $N_P$ first decreases very rapidly and gradually accumulate because of the stimulated scattering process from the exciton reservoir. By contrast, the overall behavior of the number of reservoir excitons $N_R$ is to decrease upon evolution. When dynamical steady states have been achieved with the balance between gain and loss of polariton BECs, a larger decay rate ratio ${\gamma }_c/{\gamma }_R$ leads to a smaller polariton population and a lower density distribution $|\phi \left(\mathbf{r},t\right){|}^2$ around the border of the pumping ring. As a result, the stimulated scattering process is reduced and more reservoir excitons are retained in the long-time limit.

FIGURE 4

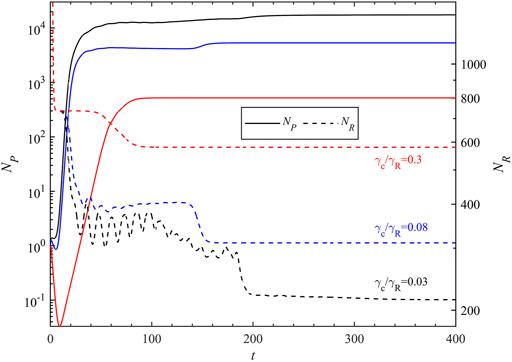
FIGURE 4. (Color online) Evolutions of total number of polaritons $N_p$ (solid lines) and reservoir excitons $N_R$ (dash lines) with time t for the decay ratios ${\gamma }_c/{\gamma }_R=0.03,0.08,0.3$, corresponding to the cases of Figures 3B–D, respectively.

If the exciton reservoir is pumped by a large ring-shaped laser with radius $R=25$, the steady states show quite distinct structures by varying the decay rate ratio ${\gamma }_c/{\gamma }_R$ as illustrated in Figures 5A–D, which correspond to the solid squares marked in Figure 1. For the case of small decay rate ratio ${\gamma }_c/{\gamma }_R=0.014$ in Figure 5A, a polariton BEC with AGD appears within the pumping ring. A random distribution of polariton exists outside of the pumping ring, owing to the low decay rate of polariton and the outward particle flow induced by repulsive polariton–polariton and polariton–exciton interactions. By increasing the polariton decay rate, vortex–antivortex pairs start to emerge as shown in Figure 5B. In two dimensions, the spontaneous formation of vortex pairs is usually the result of interaction of the condensed particles with thermal phase fluctuations [41]. We notice that thermal effects are not strong enough to excite vortex pairs in this mean-field system. But the interplay between disorder potential induced by polariton–exciton interaction and the nonequilibrium nature can excite vortex–antivortex pairs [8]. The number of vortex–antivortex pairs varies with decay rates, and the pairs can move instead of having a pinned position with evolution. As the polariton decay rate further increases, the soliton solution spontaneously appears with ${\gamma }_c/{\gamma }_R=0.1$ as in Figure 5C. In this case, a ring mode structure is present in the density profile, located at the exact position of the phase jump. At even higher ${\gamma }_c/{\gamma }_R$ as in Figure 5D, a ring mode structure is present.

FIGURE 5

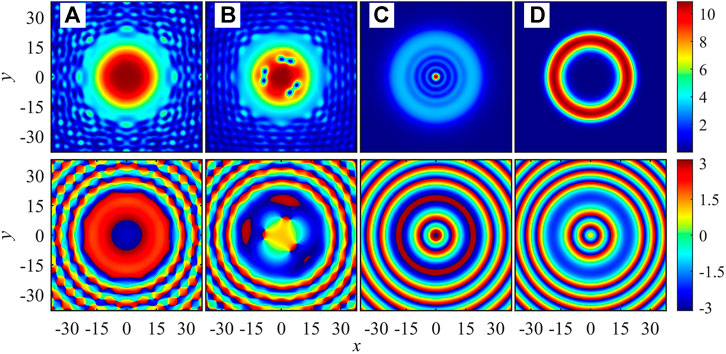
FIGURE 5. (Color online) Steady-state distributions of polaritons density $|\phi \left(x,y\right){|}^2$ (upper panels) and phase $\theta \left(x,y\right)$ (lower panels) described by Eq. 1 at $t=400$ with the pump radius $R=25$. (A–D): Decay ratios ${\gamma }_c/{\gamma }_R=0.014,0.02,0.1,0.5$, corresponding to locations marked by squares of III from left to right in Figure 1, respectively.

Soliton is a self-localized, shape-preserving solution of nonlinear partial differential equations. Solitons in polariton BEC are inherently dissipative and different from the ones in closed systems. To confirm the stability of solitons, we investigate the radial density evolution of soliton as shown in Figure 6A, with $R=25$ and ${\gamma }_c/{\gamma }_R=0.1$. This choice of parameters corresponds to the red star labeled in the phase diagram in Figure 1. We can find that a soliton establishes very rapidly from an initial random distribution of polariton BEC and survives for a very long time. This indicates that a dynamical steady soliton can be excited in the nonequilibrium system. In Figure 6B, we choose a typical time of $t=1000$ and plot the radial density $\rho \left(r\right)=|\phi \left(r\right){|}^2$ (black solid line) and phase $\theta \left(r\right)$ (red dotted line) distributions of polariton BEC. Notice that the phase distribution displays sharp gradient at the exact positions of density minima indicated by arrows. The fast variation of phase implies the existence of a large superfluid velocity along the radial direction. In Figure 6C, we show the distribution of superfluid velocity $v_s\left(r\right)=\partial \theta \left(r\right)/\partial r$ (blue solid line) and the polariton current $j\left(r\right)=\rho \left(r\right)v_s\left(r\right)$ (magenta dotted line). Notice that for $r<R$, both the superfluid velocity and the polariton current is negative, indicating a current flow toward the center inside the pumping ring. For $r>R$, both $v_s\left(r\right)$ and $j\left(r\right)$ are positive and the polaritons are flowing to the exterior of the pumping ring. This observation is a direct consequence of the steady solution of soliton, which is induced by the nonlinear repulsive interaction of polariton–polariton $g_c$ and polariton–exciton $g_R$.

FIGURE 6

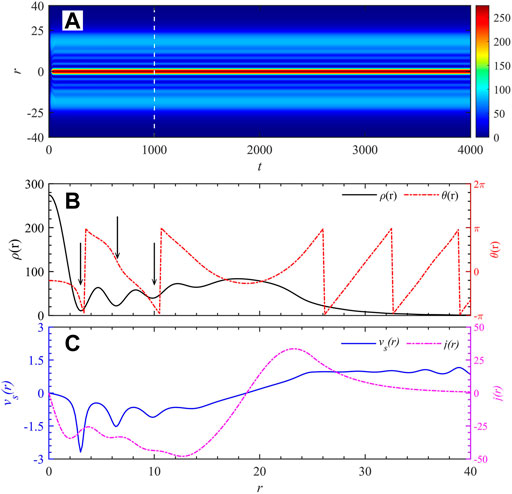
FIGURE 6. (Color online) (A) Radial evolution of polaritons density $|\phi \left(r,t\right){|}^2$ described by Eq. 1 with pumping radius $R=25$ and decay ratio ${\gamma }_c/{\gamma }_R=0.1$, corresponding to location marked by pentangle in Figure 1. (B) Radial distribution of polaritons density $\rho \left(r\right)$ and phase $\theta \left(r\right)$ at $t=1000$. (C) Radial superfluid velocity $v_s\left(r\right)$ and polaritons current $j\left(r\right)$.

5 Conclusion

In this work, we investigate the spontaneous formation of steady states of polariton BEC described by ODGPE under ring-shaped pump and incoherent exciton reservoir. By varying the pump radius and decay rates, we systematically map out the phase diagram via the density and phase distributions of polariton BEC and investigate the features of different phases. Specifically, we distinguish the regions of approximate Gaussian distribution (AGD), spontaneous formed vortices, solitons, and ring mode phases. We also find a region where the polariton BEC is unstable in the long-time limit. We also verify the soliton to be dynamically stable in this two-dimensional nonequilibrium system, where a balance is established in the long-time limit between excited polaritons around the ring-shaped laser and the polariton current flowing away from the boundary.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by Department of Education of Zhejiang Province (Grant No. KYZ04Y20182), the Beijing Natural Science Foundation (Z180013), the National Natural Science Foundation of China (Grant Nos. 11522436, 11774425, 12074428), the National Postdoctoral Program for Innovative Talents (Grant No. BX201601908), the China Postdoctoral Science Foundation (Grant No. 2017M620991), and the Research Funds of Renmin University of China (Grant Nos. 16XNLQ03 and 18XNLQ15).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Deng H, Weihs G, Santori C, Bloch J, Yamamoto Y. Condensation of Semiconductor Microcavity Exciton Polaritons. Science (2002) 298:199–202. doi:10.1126/science.1074464

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Carusotto I, Ciuti C. Quantum Fluids of Light. Rev Mod Phys (2013) 85:299–366. doi:10.1103/RevModPhys.85.299

CrossRef Full Text | Google Scholar

3. Nardin G, Lagoudakis KG, Wouters M, Richard M, Baas A, André R, et al. Dynamics of Long-Range Ordering in an Exciton-Polariton Condensate. Phys Rev Lett (2009) 103:256402. doi:10.1103/PhysRevLett.103.256402

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Fischer J, Savenko IG, Fraser MD, Holzinger S, Brodbeck S, Kamp M, et al. Spatial Coherence Properties of One Dimensional Exciton-Polariton Condensates. Phys Rev Lett (2014) 113:203902. doi:10.1103/PhysRevLett.113.203902

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Amo A, Sanvitto D, Laussy FP, Ballarini D, Valle ED, Martin MD, et al. Collective Fluid Dynamics of a Polariton Condensate in a Semiconductor Microcavity. Nature (2009) 457:291–5. doi:10.1038/nature07640

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Chestnov IY, Rubo YG, Kavokin AV. Pseudodrag of a Polariton Superfluid. Phys Rev B (2019) 100:085302. doi:10.1103/PhysRevB.100.085302

CrossRef Full Text | Google Scholar

7. Lagoudakis KG, Wouters M, Richard M, Baas A, Carusotto I, André R, et al. Quantized Vortices in an Exciton–Polariton Condensate. Nat Phys (2008) 4:706–10. doi:10.1038/nphys1051

CrossRef Full Text | Google Scholar

8. Roumpos G, Fraser MD, Löffler A, Höfling S, Forchel A, Yamamoto Y. Single Vortex-Antivortex Pair in an Exciton-Polariton Condensate. Nat Phys (2011) 7:129. doi:10.1038/nphys1841

CrossRef Full Text | Google Scholar

9. Kwon MS, Oh BY, Gong SH, Kim JH, Kang HK, Kang S, et al. Direct Transfer of Light’s Orbital Angular Momentum onto a Nonresonantly Excited Polariton Superfluid. Phys Rev Lett (2019) 122:045302. doi:10.1103/PhysRevLett.122.045302

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Sun FX, Niu ZX, Gong QH, He QY, Zhang W. Emergence and Stability of Spontaneous Vortex Lattices in Exciton-Polariton Condensates. Phys Rev B (2019) 100:014517. doi:10.1103/PhysRevB.100.014517

CrossRef Full Text | Google Scholar

11. Christopoulos S, von Högersthal GBH, Grundy AJD, Lagoudakis PG, Kavokin AV, Baumberg JJ, et al. Room-temperature Polariton Lasing in Semiconductor Microcavities. Phys Rev Lett (2007) 98:126405. doi:10.1103/PhysRevLett.98.126405

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Plumhof JD, Stöferle T, Mai L, Scherf U, Mahrt RF. Room-temperature Bose-Einstein Condensation of Cavity Exciton-Polaritons in a Polymer. Nat Mater (2014) 13:247–52. doi:10.1038/nmat3825

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Gu J, Chakraborty B, Khatoniar M, Menon VM. A Room-Temperature Polariton Light-Emitting Diode Based on Monolayer Ws 2. Nat Nanotechnol (2019) 14:1024–8. doi:10.1038/s41565-019-0543-6

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Tan LB, Cotlet O, Bergschneider A, Schmidt R, Back P, Shimazaki Y, et al. Interacting Polaron-Polaritons. Phys Rev X (2020) 10:021011. doi:10.1103/PhysRevX.10.021011

CrossRef Full Text | Google Scholar

15. Emmanuele R, Sich M, Kyriienko O, Shahnazaryan V, Withers F, Catanzaro A, et al. Highly Nonlinear trion-polaritons in a Monolayer Semiconductor. Nat Commun (2020) 11:1–7. doi:10.1038/s41467-020-17340-z

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Pieczarka M, Boozarjmehr M, Estrecho E, Yoon Y, Steger M, West K, et al. Effect of Optically Induced Potential on the Energy of Trapped Exciton Polaritons below the Condensation Threshold. Phys Rev B (2019) 100:085301. doi:10.1103/PhysRevB.100.085301

CrossRef Full Text | Google Scholar

17. Tosi G, Christmann G, Berloff N, Tsotsis P, Gao T, Hatzopoulos Z, et al. Sculpting Oscillators with Light within a Nonlinear Quantum Fluid. Nat Phys (2012) 8:190–4. doi:10.1038/nphys2182

CrossRef Full Text | Google Scholar

18. Dall R, Fraser MD, Desyatnikov AS, Li GY, Brodbeck S, Kamp M, et al. Creation of Orbital Angular Momentum States with Chiral Polaritonic Lenses. Phys Rev Lett (2014) 113:200404. doi:10.1103/PhysRevLett.113.200404

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sun YB, Yoon Y, Khan S, Ge L, Steger M, Pfeiffer LN, et al. Stable Switching Among High-Order Modes in Polariton Condensates. Phys Rev B (2018) 97:045303. doi:10.1103/PhysRevB.97.045303

CrossRef Full Text | Google Scholar

20. Mukherjee S, Myers DM, Lena RG, Ozden B, Beaumariage J, Sun Z, et al. Observation of Nonequilibrium Motion and Equilibration in Polariton Rings. Phys Rev B (2019) 100:245304. doi:10.1103/PhysRevB.100.245304

CrossRef Full Text | Google Scholar

21. Ma XK, Peschel U, Egorov OA. Incoherent Control of Topological Charges in Nonequilibrium Polariton Condensates. Phys Rev B (2016) 93:035315. doi:10.1103/PhysRevB.93.035315

CrossRef Full Text | Google Scholar

22. Yulin AV, Desyatnikov AS, Ostrovskaya EA. Spontaneous Formation and Synchronization of Vortex Modes in Optically Induced Traps for Exciton-Polariton Condensates. Phys Rev B (2016) 94:134310. doi:10.1103/PhysRevB.94.134310

CrossRef Full Text | Google Scholar

23. Ma XK, Schumacher S. Vortex Multistability and Bessel Vortices in Polariton Condensates. Phys Rev Lett (2018) 121:227404. doi:10.1103/PhysRevLett.121.227404

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Estrecho E, Gao T, Bobrovska N, Comber-Todd D, Fraser MD, Steger M, et al. Direct Measurement of Polariton-Polariton Interaction Strength in the thomas-fermi Regime of Exciton-Polariton Condensation. Phys Rev B (2019) 100:035306. doi:10.1103/PhysRevB.100.035306

CrossRef Full Text | Google Scholar

25. Wertz E, Ferrier L, Solnyshkov D, Johne R, Sanvitto D, Lemaître A, et al. Spontaneous Formation and Optical Manipulation of Extended Polariton Condensates. Nat Phys (2010) 6:860–4. doi:10.1038/nphys1750

CrossRef Full Text | Google Scholar

26. Steger M, Liu GQ, Nelsen B, Gautham C, Snoke DW, Balili R, et al. Long-range Ballistic Motion and Coherent Flow of Long-Lifetime Polaritons. Phys Rev B (2013) 88:235314. doi:10.1103/PhysRevB.88.235314

CrossRef Full Text | Google Scholar

27. Steger M, Gautham C, Snoke DW, Pfeiffer L, West K. Slow Reflection and Two-Photon Generation of Microcavity Exciton–Polaritons. Optica (2015) 2:1–5. doi:10.1364/OPTICA.2.000001

CrossRef Full Text | Google Scholar

28. Sanvitto D, Marchetti F, Szymańska M, Tosi G, Baudisch M, Laussy FP, et al. Persistent Currents and Quantized Vortices in a Polariton Superfluid. Nat Phys (2010) 6:527–33. doi:10.1038/nphys1668

CrossRef Full Text | Google Scholar

29. Lagoudakis KG, Manni F, Pietka B, Wouters M, Liew TCH, Savona V, et al. Probing the Dynamics of Spontaneous Quantum Vortices in Polariton Superfluids. Phys Rev Lett (2011) 106:115301. doi:10.1103/PhysRevLett.106.115301

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wouters M, Carusotto I. Excitations in a Nonequilibrium Bose-Einstein Condensate of Exciton Polaritons. Phys Rev Lett (2007) 99:140402. doi:10.1103/PhysRevLett.99.140402

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Keeling J, Berloff NG. Spontaneous Rotating Vortex Lattices in a Pumped Decaying Condensate. Phys Rev Lett (2008) 100:250401. doi:10.1103/PhysRevLett.100.250401

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Manni F, Lagoudakis KG, Liew TCH, André R, Deveaud-Plédran B. Spontaneous Pattern Formation in a Polariton Condensate. Phys Rev Lett (2011) 107:106401. doi:10.1103/PhysRevLett.107.106401

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wouters M, Carusotto I, Ciuti C. Spatial and Spectral Shape of Inhomogeneous Nonequilibrium Exciton-Polariton Condensates. Phys Rev B (2008) 77:115340. doi:10.1103/PhysRevB.77.115340

CrossRef Full Text | Google Scholar

34. Navadeh-Toupchi M, Takemura N, Anderson MD, Oberli DY, Portella-Oberli MT. Polaritonic Cross Feshbach Resonance. Phys Rev Lett (2019) 122:047402. doi:10.1103/PhysRevLett.122.047402

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Bao W, Wang H. An Efficient and Spectrally Accurate Numerical Method for Computing Dynamics of Rotating Bose–Einstein Condensates. J Comput Phys (2006) 217:612–26. doi:10.1016/j.jcp.2006.01.020

CrossRef Full Text | Google Scholar

36. Prasad SB, Bland T, Mulkerin BC, Parker NG, Martin AM. Vortex Lattice Formation in Dipolar Bose-Einstein Condensates via Rotation of the Polarization. Phys Rev A (2019) 100:023625. doi:10.1103/PhysRevA.100.023625

CrossRef Full Text | Google Scholar

37. Liu YK, Liu Y, Yang SJ. Stable Knotted Structure in Spin-1 Bose-Einstein Condensates with Spin-Orbit Coupling. Phys Rev A (2019) 99:063626. doi:10.1103/PhysRevA.99.063626

CrossRef Full Text | Google Scholar

38. Prasad SB, Mulkerin BC, Martin AM. Stationary States, Dynamical Stability, and Vorticity of Bose-Einstein Condensates in Tilted Rotating Harmonic Traps. Phys Rev A (2020) 101:063608. doi:10.1103/PhysRevA.101.063608

CrossRef Full Text | Google Scholar

39. Saito H, Kanamoto R. Self-rotation and Synchronization in Exciton-Polariton Condensates. Phys Rev B (2016) 94:165306. doi:10.1103/PhysRevB.94.165306

CrossRef Full Text | Google Scholar

40. Gladilin VN, Wouters M. Noise-induced Transition from Superfluid to Vortex State in Two-Dimensional Nonequilibrium Polariton Condensates. Phys Rev B (2019) 100:214506. doi:10.1103/PhysRevB.100.214506

CrossRef Full Text | Google Scholar

41. Pitaevskii L, Stringari S. Bose-Einstein Condensation and Superfluidity. NewYork: Oxford University Press (2016).