
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 30 June 2021
Sec. Chemical Physics and Physical Chemistry
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.691727
This article is part of the Research Topic Coherent Phenomena in Molecular Physics View all 15 articles
 Tiana Townsend1
Tiana Townsend1 Charles J. Schwartz1
Charles J. Schwartz1 Bethany Jochim2
Bethany Jochim2 Kanaka Raju P.2,3
Kanaka Raju P.2,3 T. Severt2
T. Severt2 Naoki Iwamoto1
Naoki Iwamoto1 J. L. Napierala1
J. L. Napierala1 Peyman Feizollah2
Peyman Feizollah2 S. N. Tegegn1
S. N. Tegegn1 A. Solomon1
A. Solomon1 S. Zhao1
S. Zhao1 K. D. Carnes2
K. D. Carnes2 I. Ben-Itzhak2
I. Ben-Itzhak2 E. Wells1*
E. Wells1*An adaptive learning algorithm coupled with 3D momentum-based feedback is used to identify intense laser pulse shapes that control
The intramolecular migration of hydrogen continues to be an active area of investigation in ultrafast science [1–11] with implications for topics ranging from combustion [12] to peptide dissociation [13] and characterizing conformational differences in molecules [14, 15]. In some cases the migration of hydrogen leads to the formation of new molecular ions, such as
The formation of
Ethane (C2H6) is composed of two back-to-back methyl groups, and thus it is an excellent baseline system for examining hydrogen-related bond rearrangement.
Motivated by significant
The experimental techniques applied in this study have recently been discussed elsewhere [21, 36], and in this section we will only highlight a few key points. Two different approaches are used to examine the interactions of intense laser pulses with ethane gas: First, the laser pulses are shaped using an acousto-optic programmable dispersive filter (AOPDF) [37] and the ethane reaction products are measured using velocity map imaging (VMI) [38, 39]. Second, COLd Target Recoil Ion Momentum Spectroscopy (COLTRIMS) [40, 41] characterizes the dissociation dynamics of the ethane molecule following strong-field ionization.
In the shaped pulse/VMI portion of the experiment linearly polarized pulses with a duration of 35 fs full-width at half-maximum (FWHM) in intensity and a center wavelength of 785 nm are generated at 1 kHz by a Ti:Sapphire laser system named KLS. In this laser system, the compressor grating pair is in the Treacy configuration [42] while the stretcher gratings are in the Martinez configuration [43]. The amplified pulse energy of about 1.5 mJ was attenuated to the levels needed in the experiment. These near-Fourier-transform limited pulses will be denoted as TL pulses in this article. The acousto-optic programmable dispersive filter [37] was placed between the laser oscillator and multi-pass amplifier. In this experiment, we controlled only the spectral phase of the laser pulse. Pulse characteristics were determined using a second-harmonic-generation frequency-resolved-optical-grating (SHG-FROG) [44] device. Our version of VMI [45–47] integrates the momentum image of a given
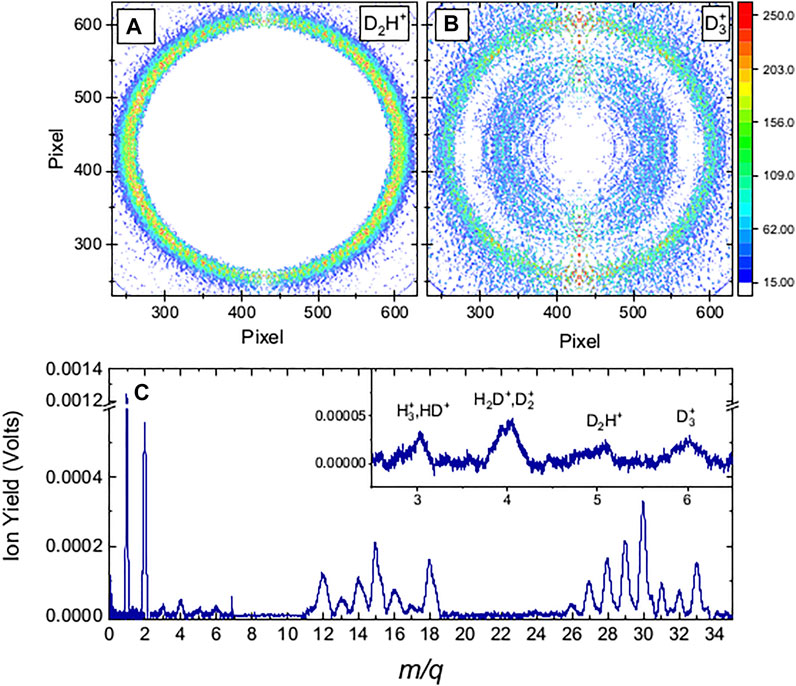
FIGURE 1. Molecular fragmentation data obtained with 35 fs FWHM, 1.3
In the closed-loop adaptive control approach, ion-specific three-dimensional momentum information provides the feedback to drive a genetic algorithm that optimizes the pulse shapes to a control objective [46, 47]. The raw VMI data is inverted on-the-fly to recover a slice through the center of the three-dimensional momentum distribution using a modified “onion-peeling” algorithm as described by Rallis et al. [47]. The yield within user-defined regions of interest on the momentum plot is then evaluated, resulting in a numerical value that defines the “fitness” of the laser pulse being examined. The adaptive search parameterizes the pulse characteristics in terms of the spectral phase, which is broken into 16 evenly spaced segments between 734 and 830 nm. Since a portion of this range is beyond the pulse bandwidth, the effective number of search parameters is somewhat smaller than 16. Linear interpolation fills in the values between the adjacent phases. The algorithm is allowed to adjust each phase value between 0 and 2π.
To complement the closed-loop studies, systematic scans of the second- and third-order pulse dispersion were made for a few values of fourth-order dispersion. In this pulse-parameterization scheme [21, 50, 51], we describe the spectral phase,
In the COLTRIMS [40, 41] measurement, the laser pulses are produced by the PULSAR laser [53] at 10 kHz, with 25-fs (FWHM in intensity) pulse duration, a central wavelength of 790 nm, and maximum pulse energy of 2 mJ. The laser pulses were again characterized with SHG-FROG. The pulses are focused by a
The experiments on D3C-CH3 (1,1,1-d3 ethane, 98% pure) with shaped pulses and VMI detection used both an adaptive search strategy and a systematic search of pulse parameters. With this target,
As the intensity was increased, the VMI of the
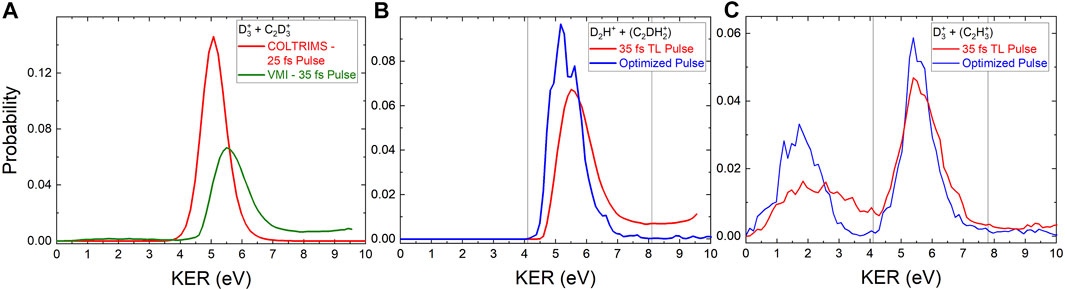
FIGURE 2. (A) The red line shows the probability for two-body
We were able to increase the D2H+:
Figure 2 shows the KER distributions obtained for the D2H+ and
Notably, the D2H+ KER distribution obtained with the pulse optimized to increase the D2H+:
The characteristics of the optimized pulse are shown in Figure 3. While there is indeed a trailing secondary pulse around 125 fs after the main pulse, there are other features of the pulse shape that could be significant. To try and determine which pulse parameters are important for the manipulation of the control objective, we systematically scanned the linear chirp and third-order dispersion for three values of fourth-order dispersion. During these systematic scans we recorded the D2H+ and
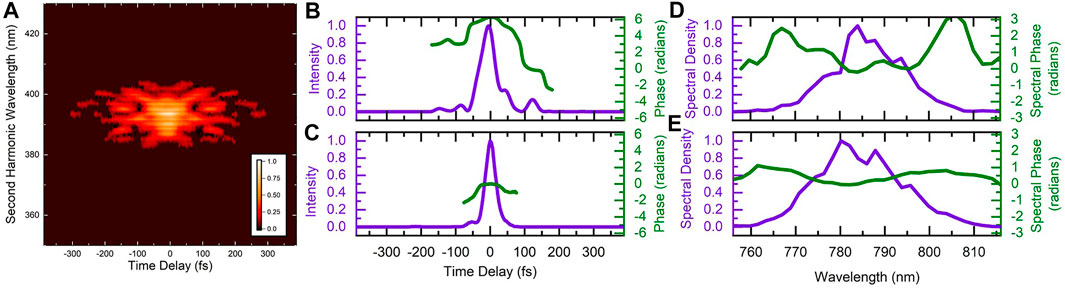
FIGURE 3. (A) Measured frequency-resolved-optical-grating trace of the laser pulse optimized to increase the D2H+:
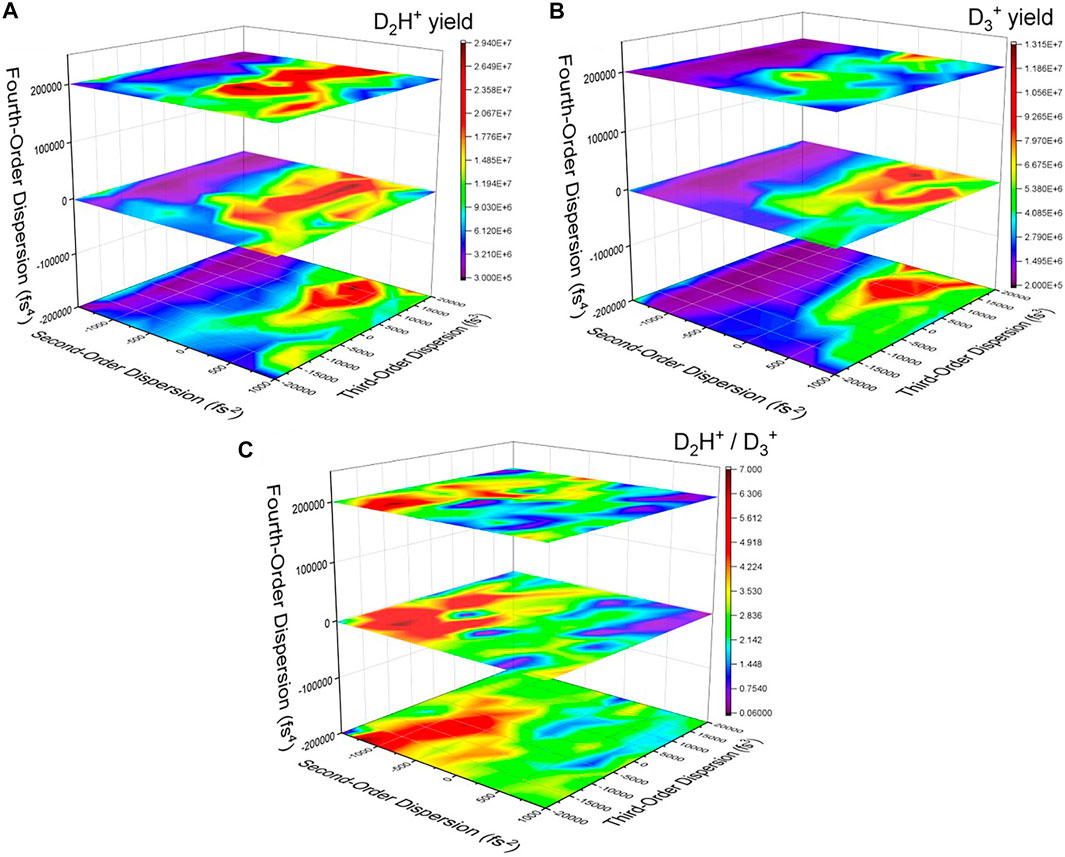
FIGURE 4. The yield of (A) D2H+ and (B)
From a time-domain perspective, the second–and fourth-order dispersions lengthen the pulse symmetrically, while the third-order dispersion adds a pedestal either before or after the main pulse (see, e.g., Ref. 50). Thus, some of the temporal characteristics of the optimized pulse (Figure 3) can be reproduced, but the secondary pulse would be more difficult to construct using dispersive pulse parameters. As shown in Figure 4C, there are a number of combinations of pulse parameters that reach nearly the same level of effectiveness at manipulating the D2H+:
One curious element of the dispersion scan is the comparison to the previous work of Schirmel et al., who also examined
One possible explanation for the seemingly conflicting results is that different intensities lead to different dissociation dynamics. The TL intensity of 1.3
Another factor potentially confounding our understanding of how the production of
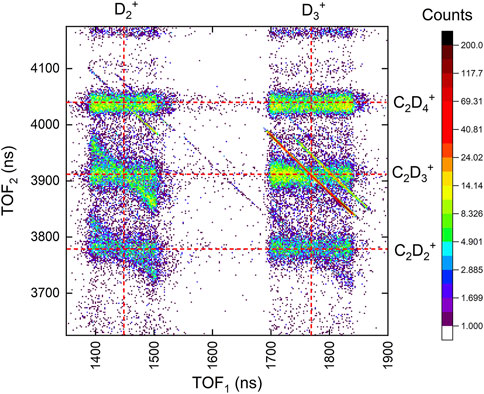
FIGURE 5. The portion of the coincidence-time-of-flight map of two-body channels including

TABLE 1. Ethane (C2D6) branching ratios for two-body double ionization by 25-fs, 1.5
We also analyzed the three-body D +
Using momentum conservation to deduce the contribution from the deuterium atom gives a KER distribution for this three-body channel, shown in Figure 6. The KER distribution is similar to the
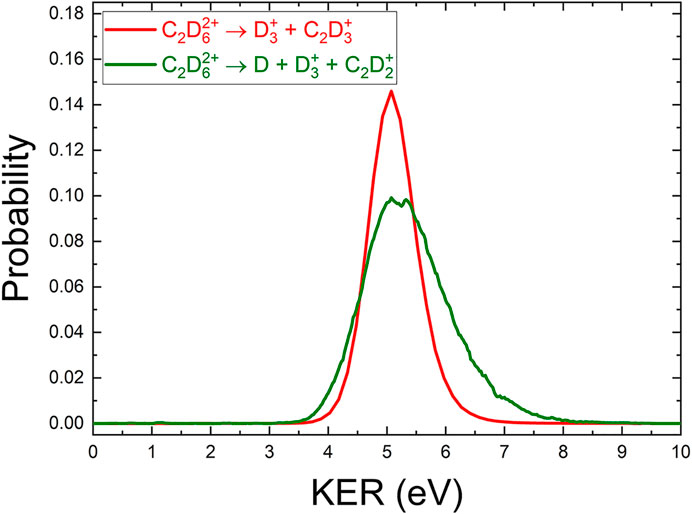
FIGURE 6. A comparison of the (COLTRIMS-derived) KER spectrum of
In addition, we did not find any significant evidence for
Since the control experiments with the D3C-CH3 isotopologue of ethane are designed to distinguish between the involvement of the hydrogen atoms on one or both sides of the molecule, the angular distributions from the VMI data might provide information about the dissociation dynamics beyond the KER shift shown in Figure 2B. Since the angular COLTRIMS data can be readily corrected using available experimental symmetries [36], we compared the COLTRIMS-measured
The angular distributions of the D2H+ and
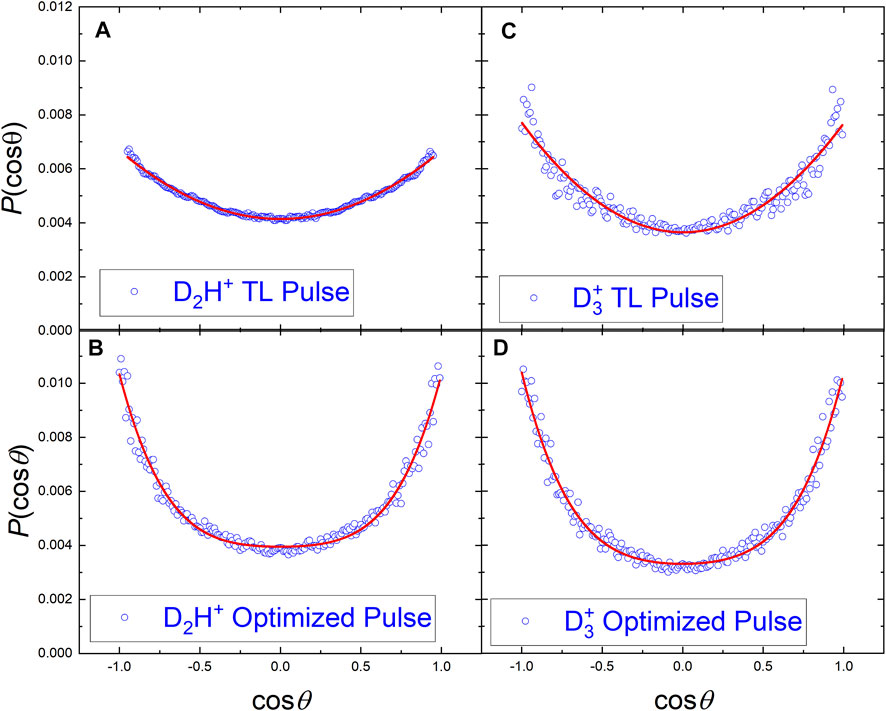
FIGURE 7. The angular distributions of D2H+ and
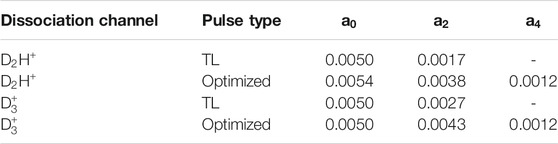
TABLE 2. Legendre polynomial coefficients,
The optimized pulse, therefore, is observed to have a significant impact on the yield, KER, and angular distribution of the D2H+ ions. In contrast, the
By using the D3C-CH3 isotopologue of ethane we were able to separate two different types of dissociation processes leading to the formation of trihydrogen cations:
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
TT and TS led the analysis of the COLTRIMS measurements, while CS led the VMI analysis with assistance from TT, NI, and ST. BJ led the adaptive control experiments and KP led the dispersion scan experiments with assistance from NI, CS, JN, AS, TS, PF, ST, and EW. TS, BJ, SZ, KC, IB-I, and EW carried out the COLTRIMS experiment. IB-I and EW mentored the students and postdocs. EW wrote the manuscript with assistance from TT, TS, BJ, KP, KC, and IB-I. All authors reviewed the manuscript prior to submission.
Augustana University personnel and equipment are supported by the National Science Foundation grant PHYS-2011864. JR Macdonald Laboratory personnel and equipment are supported by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Science, Office of Science, United States Department of Energy under award #DE-FG02-86ER1349.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank Charles Fehrenbach for assistance with the PULSAR laser and the members of Vinod Kumarappan’s group for assistance with the KLS laser.
1. Endo T, Neville SP, Wanie V, Beaulieu S, Qu C, Deschamps J, et al. Capturing Roaming Molecular Fragments in Real Time. Science 370 (2020) 1072–7. doi:10.1126/science.abc2960
2. Kling NG, Díaz-Tendero S, Obaid R, Disla MR, Xiong H, Sundberg M, et al. Time-resolved Molecular Dynamics of Single and Double Hydrogen Migration in Ethanol. Nat Commun 10 (2019). doi:10.1038/s41467-019-10571-9
3. Ando T, Shimamoto A, Miura S, Iwasaki A, Nakai K, Yamanouchi K. Coherent Vibrations in Methanol Cation Probed by Periodic H3+ Ejection after Double Ionization. Commun Chem 1 (2018). doi:10.1038/s42004-017-0006-7
4. Kübel M, Siemering R, Burger C, Kling NG, Li H, Alnaser AS, et al. Steering Proton Migration in Hydrocarbons Using Intense Few-Cycle Laser fields. Phys Rev Lett 116 (2016) 193001. doi:10.1103/physrevlett.116.193001
5. Livshits E, Luzon I, Gope K, Baer R, Strasser D. Time-resolving the Ultrafast H2 Roaming Chemistry and H3+ Formation Using Extreme-Ultraviolet Pulses. Commun Chem 3 (2020). doi:10.1038/s42004-020-0294-1
6. Ma P, Wang C, Li X, Yu X, Tian X, Hu W, et al. Ultrafast Proton Migration and Coulomb Explosion of Methyl Chloride in Intense Laser fields. J Chem Phys 146 (2017) 244305. doi:10.1063/1.4989565
7. Xu S, Zhao H, Zhu X, Guo D, Feng W, Lau K-C, et al. Dissociation of [HCCH]2+ to H2+ and C2+: a Benchmark Reaction Involving H Migration, H-H Combination, and C-H Bond Cleavage. Phys Chem Chem Phys 20 (2018) 27725–9. doi:10.1039/c8cp05780j
8. Michie MJ, Ekanayake N, Weingartz NP, Stamm J, Dantus M. Quantum Coherent Control of H3+ Formation in strong fields. J Chem Phys 150 (2019) 044303. doi:10.1063/1.5070067
9. Jochim B, Berry B, Severt T, Feizollah P, Zohrabi M, P KR, Dependence on the Initial Configuration of strong Field-Driven Isomerization of C2H2 Cations and Anions. J Phys Chem Lett 10 (2019) 2320–7. doi:10.1021/acs.jpclett.9b00520
10. McDonnell M, LaForge AC, Reino-González J, Disla M, Kling NG, Mishra D, et al. Ultrafast Laser-Induced Isomerization Dynamics in Acetonitrile. J Phys Chem Lett 11 (2020) 6724–9. doi:10.1021/acs.jpclett.0c01344
11. Wang E, Shan X, Chen L, Pfeifer T, Chen X, Ren X, et al. Ultrafast Proton Transfer Dynamics on the Repulsive Potential of the Ethanol Dication: Roaming-Mediated Isomerization versus Coulomb Explosion. The J Phys Chem A 124 (2020) 2785–91. doi:10.1021/acs.jpca.0c02074
12. Sharma S, Raman S, Green WH. Intramolecular Hydrogen Migration in Alkylperoxy and Hydroperoxyalkylperoxy Radicals: Accurate Treatment of Hindered Rotors. J Phys Chem A 114 (2010) 5689–701. doi:10.1021/jp9098792
13. Zhao J, Song T, Xu M, Quan Q, Siu KWM, Hopkinson AC, et al. Intramolecular Hydrogen Atom Migration along the Backbone of Cationic and Neutral Radical Tripeptides and Subsequent Radical-Induced Dissociations. Phys Chem Chem Phys 14 (2012) 8723. doi:10.1039/c2cp40708f
14. Hoerner JK, Xiao H, Dobo A, Kaltashov IA. Is There Hydrogen Scrambling in the Gas Phase? Energetic and Structural Determinants of Proton Mobility within Protein Ions. J Am Chem Soc 126 (2004) 7709–17. doi:10.1021/ja049513m
15. Shen Y, Zhao X, Wang G, Chen DDY. Differential Hydrogen/deuterium Exchange during Proteoform Separation Enables Characterization of Conformational Differences between Coexisting Protein States. Anal Chem 91 (2019) 3805–9. doi:10.1021/acs.analchem.9b00558
16. Hoshina K, Furukawa Y, Okino T, Yamanouchi K. Efficient Ejection of
17. Ando T, Iwasaki A, Yamanouchi K. Strong-field Fourier Transform Vibrational Spectroscopy of Methanol Cation and its Isotopologues Using Few-Cycle Near-Infrared Laser Pulses. Mol Phys 117 (2019) 1732–40. doi:10.1080/00268976.2019.1572244
18. Ekanayake N, Nairat M, Kaderiya B, Feizollah P, Jochim B, Severt T, et al. Mechanisms and Time-Resolved Dynamics for Trihydrogen Cation (
19. Ekanayake N, Severt T, Nairat M, Weingartz NP, Farris BM, Kaderiya B, et al. H2 Roaming Chemistry and the Formation of
20. Ekanayake N, Nairat M, Weingartz NP, Michie MJ, Levine BG, Dantus M. Substituent Effects on
21. Iwamoto N, Schwartz CJ, Jochim B, PK R, Feizollah P, Napierala JL, et al. Strong-field Control of
22. Townsend D, Lahankar SA, Lee SK, Chambreau SD, Suits AG, Zhang X, et al. The Roaming Atom: Straying from the Reaction Path in Formaldehyde Decomposition. Science 306 (2004) 1158–61. doi:10.1126/science.1104386
23. Luzon I, Livshits E, Gope K, Baer R, Strasser D. Making Sense of Coulomb Explosion Imaging. J Phys Chem Lett 10 (2019) 1361–7. doi:10.1021/acs.jpclett.9b00576
24. Mebel AM, Bandrauk AD. Theoretical Study of Unimolecular Decomposition of Allene Cations. J Chem Phys 129 (2008) 224311. doi:10.1063/1.3037204
25. Xu H, Okino T, Yamanouchi K. Tracing Ultrafast Hydrogen Migration in Allene in Intense Laser fields by Triple-Ion Coincidence Momentum Imaging. J Chem Phys 131 (2009) 151102. doi:10.1063/1.3251032
26. Furukawa Y, Hoshina K, Yamanouchi K, Nakano H. Ejection of Triatomic Hydrogen Molecular Ion from Methanol in Intense Laser fields. Chem Phys Lett 414 (2005) 117–21. doi:10.1016/j.cplett.2005.07.108
27. Kotsina N, Kaziannis S, Kosmidis C. Phase Dependence of OD+, HOD+, and
28. Nakai K, Kato T, Kono H, Yamanouchi K. Communication: Long-Lived Neutral H2 in Hydrogen Migration within Methanol Dication. J Chem Phys 139 (2013) 181103. doi:10.1063/1.4830397
29. Kotsina N, Kaziannis S, Kosmidis C. Hydrogen Migration in Methanol Studied under Asymmetric Fs Laser Irradiation. Chem Phys Lett 604 (2014) 27–32. doi:10.1016/j.cplett.2014.04.040
30. Hoshina K, Kawamura H, Tsuge M, Tamiya M, Ishiguro M. Metastable Decomposition and Hydrogen Migration of Ethane Dication Produced in an Intense Femtosecond Near-Infrared Laser Field. J Chem Phys 134 (2011) 064324. doi:10.1063/1.3549137
31. Kraus PM, Schwarzer MC, Schirmel N, Urbasch G, Frenking G, Weitzel KM. Unusual Mechanism for
32. Kanya R, Kudou T, Schirmel N, Miura S, Weitzel KM, Hoshina K, et al. Hydrogen Scrambling in Ethane Induced by Intense Laser fields: Statistical Analysis of Coincidence Events. J Chem Phys 136 (2012) 204309. doi:10.1063/1.4720503
33. Schirmel N, Reusch N, Horsch P, Weitzel KM. Formation of Fragment Ions (H+,
34. Boran Y, Gutsev GL, Kolomenskii AA, Zhu F, Schuessler A, Strohaber J. Dissociative Ionization of Ethane with Femtosecond Pulses of Radiation. J Phys B: At Mol Opt Phys 51 (2018) 035003. doi:10.1088/1361-6455/aa98d4
35. Zhang Y, Ren B, Yang CL, Wei L, Wang B, Han J, et al. Formation of
36. Zhao S, Jochim B, Feizollah P, Rajput J, Ziaee F, P KR, et al. Strong-field-induced Bond Rearrangement in Triatomic Molecules. Phys Rev A 99 (2019). doi:10.1103/physreva.99.053412
37. Verluise F, Laude V, Cheng Z, Spielmann C, Tournois P. Amplitude and Phase Control of Ultrashort Pulses by Use of an Acousto-Optic Programmable Dispersive Filter: Pulse Compression and Shaping. Opt Lett 25 (2000) 575. doi:10.1364/ol.25.000575
38. Chandler DW, Houston PL. Two-dimensional Imaging of State-Selected Photodissociation Products Detected by Multiphoton Ionization. J Chem Phys 87 (1987) 1445–7. doi:10.1063/1.453276
39. Eppink ATJB, Parker DH. Velocity Map Imaging of Ions and Electrons Using Electrostatic Lenses: Application in Photoelectron and Photofragment Ion Imaging of Molecular Oxygen. Rev Scientific Instr 68 (1997) 3477–84. doi:10.1063/1.1148310
40. Dörner R, Mergel V, Jagutzki O, Spielberger L, Ullrich J, Moshammer R, et al. Cold Target Recoil Ion Momentum Spectroscopy: a ‘momentum Microscope’ to View Atomic Collision Dynamics. Phys Rep 330 (2000) 95–192. doi:10.1016/s0370-1573(99)00109-x
41. Ullrich J, Moshammer R, Dorn A, Dörner R, Schmidt LPH, Schmidt-Böcking H. Recoil-ion and Electron Momentum Spectroscopy: Reaction-Microscopes. Rep Prog Phys 66 (2003) 1463. doi:10.1088/0034-4885/66/9/203
42. Treacy E. Optical Pulse Compression with Diffraction Gratings. IEEE J Quan Electronics 5 (1969) 454–8. doi:10.1109/jqe.1969.1076303
43. Martinez O. Design of High-Power Ultrashort Pulse Amplifiers by Expansion and Recompression. IEEE J Quan Electronics 23 (1987) 1385–7. doi:10.1109/jqe.1987.1073518
45. Kling NG, Paul D, Gura A, Laurent G, De S, Li H, et al. Thick-lens Velocity-Map Imaging Spectrometer with High Resolution for High-Energy Charged Particles. J Instrumentation 9 (2014) P05005. doi:10.1088/1748-0221/9/05/P05005
46. Wells E, Rallis C, Zohrabi M, Siemering R, Jochim B, Andrews P, et al. Adaptive strong-field Control of Chemical Dynamics Guided by Three-Dimensional Momentum Imaging. Nat Commun 4 (2013) 2895. doi:10.1038/ncomms3895
47. Rallis CE, Burwitz TG, Andrews PR, Zohrabi M, Averin R, De S, et al. Incorporating Real Time Velocity Map Image Reconstruction into Closed-Loop Coherent Control. Rev Scientific Instr 85 (2014) 113105. doi:10.1063/1.4899267
48. Judson RS, Rabitz H. Teaching Lasers to Control Molecules. Phys Rev Lett 68 (1992) 1500–3. doi:10.1103/PhysRevLett.68.1500
49. Brif C, Chakrabarti R, Rabitz H. Control of Quantum Phenomena: Past, Present and Future. New J Phys 12 (2010) 075008. doi:10.1088/1367-2630/12/7/075008
50. Lev U, Graham L, Madsen CB, Ben-Itzhak I, Bruner BD, Esry BD, et al. Quantum Control of Photodissociation Using Intense, Femtosecond Pulses Shaped with Third Order Dispersion. J Phys B: At Mol Opt Phys 48 (2015) 201001. doi:10.1088/0953-4075/48/20/201001
51. Nairat M, Lozovoy VV, Dantus M. Order of Magnitude Dissociative Ionization Enhancement Observed for Pulses with High Order Dispersion. J Phys Chem A 120 (2016) 8529–36. doi:10.1021/acs.jpca.6b08659
53. Ren X, Summers AM, P KR, Vajdi A, Makhija V, Fehrenbach CW, et al. Single-shot Carrier-envelope-phase Tagging Using an F–2f Interferometer and a Phase Meter: a Comparison. J Opt 19 (2017) 124017. doi:10.1088/2040-8986/aa9865
54. Lozovoy VV, Zhu X, Gunaratne TC, Harris DA, Shane JC, Dantus M. Control of Molecular Fragmentation Using Shaped Femtosecond Pulses. J Phys Chem A 112 (2008) 3789–812. doi:10.1021/jp071691p
55. Joachain CJ, Kylstra NJ, Potvliege RM. Atoms in Intense Laser Fields (Cambridge University Press) (2011).
Keywords: coherent control, molecular dynamics, bond rearrangement, laser physics, imaging, ultrafast science
Citation: Townsend T, Schwartz CJ, Jochim B, P. KR, Severt T, Iwamoto N, Napierala JL, Feizollah P, Tegegn SN, Solomon A, Zhao S, Carnes KD, Ben-Itzhak I and Wells E (2021) Controlling
Received: 06 April 2021; Accepted: 10 June 2021;
Published: 30 June 2021.
Edited by:
Tamar Seideman, Northwestern University, United StatesReviewed by:
Arkaprabha Konar, Kent State University, United StatesCopyright © 2021 Townsend, Schwartz, Jochim, P., Severt, Iwamoto, Napierala, Feizollah, Tegegn, Solomon, Zhao, Carnes, Ben-Itzhak and Wells. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: E. Wells, ZXJpYy53ZWxsc0BhdWdpZS5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.