- 1School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an, China
- 2School of Computer Science and Engineering, Northwestern Polytechnical University, Xi’an, China
Inference of the gene regulation mechanism from gene expression patterns has become increasingly popular, in recent years, with the advent of microarray technology. Obtaining the states of genes and their regulatory relationships would greatly enable the scientists to investigate and understand the mechanisms of the diseases. However, it is still a big challenge to determine relationships from several thousands of genes. Here, we simplify the above complex gene state determination problem as an inference of the distribution of the ensemble Boolean networks (BNs). In order to investigate and calculate the distribution of the BNs’ states, we first compute the probabilities of the different BNs’ states and obtain the number of states
1 Introduction
Gene network is an important tool to study the biological system from the molecular level. Gene network is an interaction network formed by DNA, RNA, protein, and metabolic intermediates involved in gene regulation. Gene network research is expected to reveal the function and behavior of genome from a systematic perspective. It is helpful in explaining the life process in detail from the genomic level, so as to achieve the goal of systematically explaining cell activity, life activity, disease, and treatment. Therefore, gene network has attracted great attention in the study of biological growth, development, and diseases. The research results of gene network have important theoretical significance and application value.
Genetic regulatory network (GRN) has aroused lots of interests over the past years [1–3]. There exists a large proportion of genes regulating or interacting with the other genes through proteins, which can be modeled by the GRN. Various types of GRNs, such as Boolean networks (BNs) and extended probabilistic Boolean networks, stochastic Boolean networks, and multiple-valued networks [4–6], have been developed for different applications. For example, BNs were first proposed by Kauffpman [7, 8] to model the complex and nonlinear biological systems. Furthermore, various factors, such as gene perturbation, context-sensitive, and asynchronous, are also thoroughly investigated [9, 10].
However, the research results of BNs are relatively limited, due to the difficulties for solving logical dynamic systems with a systematic tool [11]. In the viewpoint of biology, considering there are a huge number of genes expression states at the same time, this incurs the difficulties of inferring the states of the gene expression at a given time stamp.
Recently, Cheng et al. [11] proposed the semi-tensor product (STP) of matrices, which can only represent the logical equation as an algebraic equation, but also convert the dynamics of a BCN into a linear discrete-time control system. Based on such reformation, many interesting properties have been obtained for BCN [12–16]. The optimal control is an interesting topic in system control theory. Other than the STP technique, they developed statistical methods for solving problems in BNs. A Mayer-type optimal control problem for BCNs with multi-input and single-input has been well studied in Refs. [17] and [18], respectively. The states of biological networks and electronic networks are often influenced by instantaneous disturbances. In addition, they may still experience abrupt changes at certain points, because of the switching phenomenon and sudden noise, that is, impulsive effects. Impulsive dynamical networks have attracted the interests of many researchers for their various applications in information science, bioinformatics, and automated control systems.
There are many cells with the same function in an organ. However, it is hard to get the states of every single cell. Here in this study, we find that the states of a proportion of cells share one particular distribution. Thus, it is useful for biologists to conclude whether the illness is caused by the changes of the cell state distribution or not.
From a biological standpoint, inference of gene regulation mechanism from expression patterns is becoming increasingly important, along with the invent of DNA microarray technology. Thus, we need to get the ensemble distribution of the BNs and determine the states of genes, which is the key for further exploration of the expression profiles of thousands of genes. Specifically, in this study, we proposed an algorithm for inferring the distribution states of the BNs. First, we compute the probability of different BNs’ states and get the value of
2 The Finite Number of Boolean Networks
2.1 The States of Boolean Networks
This section provides a base knowledge for Section 2.1.
First, we suppose that there are many Boolean networks in one group, and the probability of different BNs’ states is P.
where
We assume that
and the value of the cells
Although we know the number of cells, it is difficult to determine, even if a distribution
Theorem 1 We know the number of BNs in the ensemble is M and the value of the ensemble
Proof: The system consists of M number of identical transforms, which have
Two specific examples are given to illustrate Theorem 1, while there is an ensemble with 5 BNs. Thus,
(1) We assume that there are three Boolean networks in state
(2) We assume that there are four Boolean networks in state
We can easily find that even if the number of M is very large, the conclusion still holds.
2.2 The Maximum Probabilistic Distribution of Boolean Networks
In this section, we study and prove the maximum probabilistic distribution of the Boolean network. The maximum probabilistic distribution is a Gaussian distribution, and then the cells’ states distribution can be determined as shown in Figure 1.
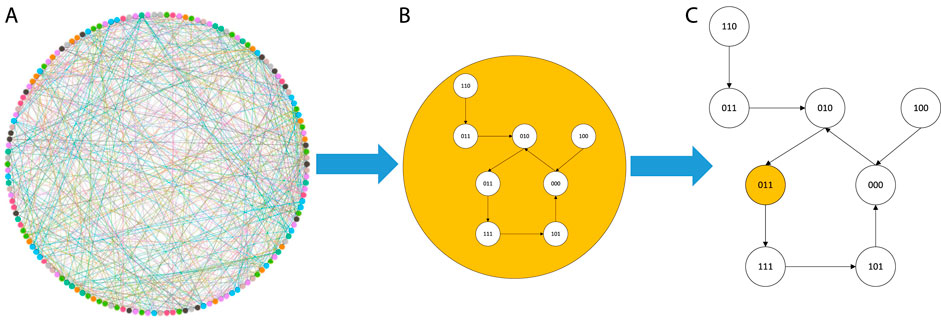
FIGURE 1. State change in a system: (A) all nodes’ state change, (B) one node of these nodes, and (C) the state change rule for one node, and there are eight states in these nodes.
Although given
To determine the probability, we need to assume that the number of M is relatively large. In contrast, the data of BNs do not need be large. When M goes to infinite,
Using Eq. 8 (the specific calculation process is shown in the Appendix), we can get the following equation:
When we compute the partial derivative of
Substituting Eqs 10–12 into Eq. 7, we can get the following equations:
So there is
When given the number of BN M, represented as the scale, we can get the distribution
Definition II1 When
Definition II 2 Partition function [19] is
where Q indicates the sum of the probability of all the states. The partition of Eq. 17 plays an important role as a normalization constant.
After the computation of
From Eq. 3, it can be rewritten as
Replacing Eq. 19 with Eq. 17, we can get
From the result, we can get the information about that in a canonical ensemble. When E is given, M tends to infinite,
Theorem 2 When H and E are given and M tends to infinite, the best of the distribution M is the true distribution. In other words, the fluctuation is equal to 0.
Proof We need to talk about a function,
However,
Since the second term and the third term of f are the linear functions, the second derivative of
Using the Taylor series which starts
The peak of f is as follows:
Substituting Eqs 21 and 24 into Eq. 23, we can get
Ignoring the term
So there is
Thus, we complete the proof of this theorem.
2.3 The Fluctuation of the Distribution
This section is aiming to prove that cells are impossible in the same states, when the number of cells goes to infinity.
It is easy to find that Eq. 27 is a Gaussian distribution. Now, we need to prove the function Eq. 7 is a δ function. We need to prove the fluctuation would be eliminated when
Theorem 3 When
Proof: There is a distribution that
Obviously, there is
and
Then Eq. 29 can be rewritten as
Comparing Eq. 27 with Eq. 30, we can get
and substituting it into Eq. 28, there is
where
Until now, the proof of Theorem three is finished. When H and E are fixed and
3 Experiments
In this section, we perform analysis of the cells’ states distribution model, that is, Eq 26. We establish that two experiments are conducted in order to illustrate the distribution of the BNs’ states, which can be used to verify our conclusions. Since there are no practical data for the state changes of the same type of cells, we can only simulate the transformation process of these cells through Boolean network, and then we also perform extensive analyses of the data of the state changes of these cells.
3.1 A Boolean Network with 100 Cells
In this example, we choose the state change function [17]. While the number of cells is 100, the number of the same Boolean is 1,000. And the Boolean network’s state change rule is illustrated as follows:
where
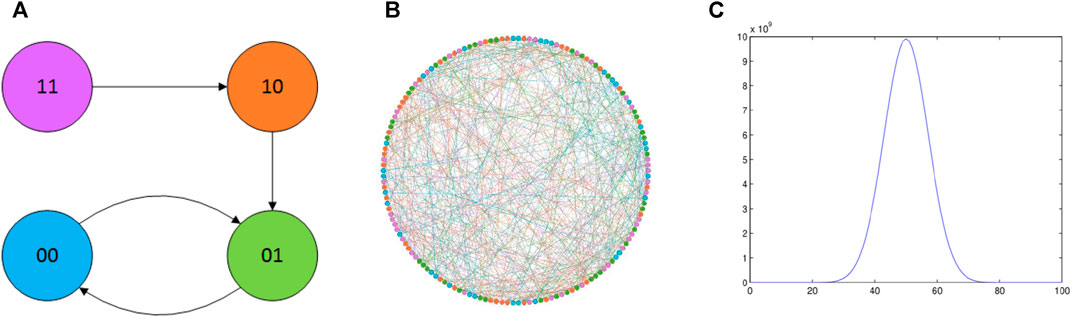
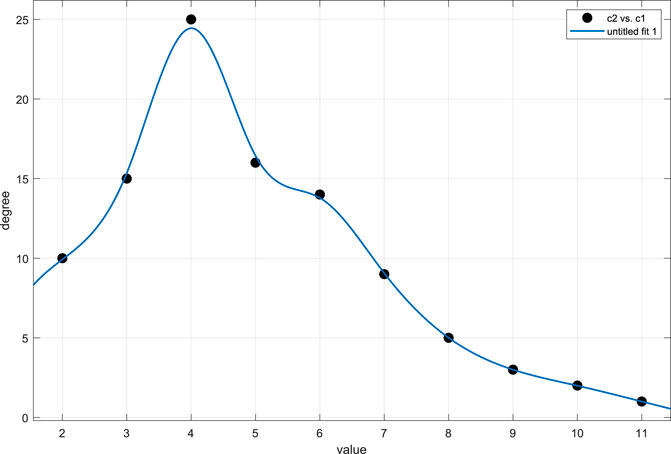
FIGURE 2. Cells of the system (31). The state change in the system (31), and the distribution of these states of combination. (A) Node’s states change, and there are four states in these cells; (B) the relation of 100 cells, and these cells were randomly generated; (C) main result of the system (31): the distribution of these states of combination.
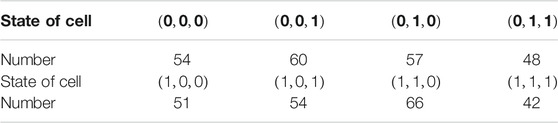
Assume that the number of four initial states in the cells is shown in Table 1.
From Theorem 1, we can obtain the k combinations.
We generate the particular network relationship between cells in a random manner, where each node represents a cell, and the edge indicates a connection between two cells. The probability of connecting the two cells is initialized as 0.05. The indicators of the association network between the cells are shown in the following table.
Through Figure 3; Table 2, we get the basic characteristics of this cellular network; there are 1,000 nodes, 2,781 edges, and so on. The visualization of the network is shown in Figure 2B. In this figure, different colors of the nodes are expressed as different states of the cells.
When the cell states change, they will be initialized with a random state, and the influence of states by other states is modeled as well. Assuming that the number of identical states between the connected cells is greater than 10, the other cells directly skip the changed state, and switch directly to the next state. Thus, the function
where
The state change rule as shown in Figure 2A demonstrates the end state is
3.2 A Boolean Network with 150 Cells
In this example, we choose the state change function similar to the previous reported one [12]. Here, the number of cells is 500, meaning the number of the same Boolean is 500. Along with the Boolean network’s state change, the mathematical rules can be formatted as
where
Assume that the number of four initial states in the cells is as shown in Table 3.
Form Theorem 1, we can get there are about k combinations.
We generate a network relationship among cells in a random manner, where each node represents the cell, and the edge indicates that there is a connection between the two cells, and the probability of connecting the two cells is 0.05. The indicators of the association network between the cells are shown in the following Table 4.
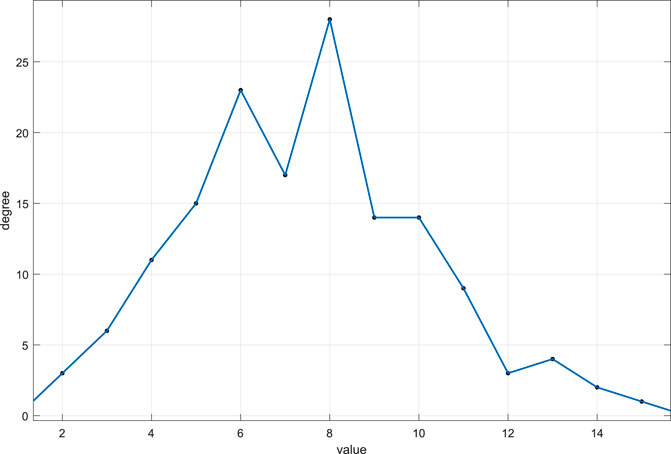
Through Figure 4; Table 3, we get the basic characteristics of this cellular network; there are 450 nodes, 1890 edges, and so on. The visualization of the network is shown in Figure 5B. Here, different colors of the nodes are expressed as different states of the cells.
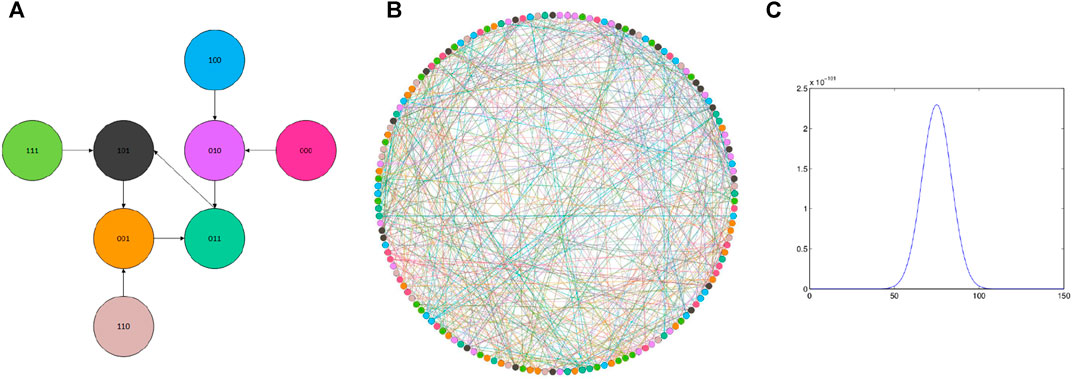
FIGURE 5. Cells of the system (33). State change in the system (33), and the distribution of these states of combination: (A) node’s state change, and there are eight states in these cells; (B) relation of 150 cells, and these cells were randomly generated; (C) result of the system (33): the distribution of these states of combination.
The state change rule as shown in Figure 5A, and the end state is
From these two experiments, we verify that the distribution of these states is a Gaussian distribution, and these cells cannot be in the same state when the number of cells approaches to the infinity. Thus, the above theorems are right.
4 Conclusion
In this article, we study and calculate the distribution of the Boolean networks’ states. First, we compute the probability of different BNs’ states and get the value of
5 Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
6 Author Contributions
XC drafted the idea. ZL did the derivation, while BR drafted the manuscript. All authors have read through the manuscript.
7 Funding
This work was supported in part by National Natural Science Foundation of China (Grant Nos. 62003273, 62073263), Natural Science Foundation of Shaanxi Province (Grant No. 2020JQ-217), Fundamental Research Funds for the Central Universities (Grant No. 3102019HHZY03002).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Ideker T, Galitski T, Hood L. A NEWAPPROACH TODECODINGLIFE: Systems Biology. Annu Rev Genom Hum Genet (2001) 2:343–72. doi:10.1146/annurev.genom.2.1.343
2. Kim J, Park S-M, Cho K-H. Discovery of a Kernel for Controlling Biomolecular Regulatory Networks. Sci Rep (2013) 3:2223. doi:10.1038/srep02223
3. Zhang Z, Xia C, Chen Z. On the Stabilization of Nondeterministic Finite Automata via Static Output Feedback. Appl Math Comput (2020) 365:124687. doi:10.1016/j.amc.2019.124687
4. Shmulevich I, Dougherty ER, Kim S, Zhang W. Probabilistic Boolean Networks: a Rule-Based Uncertainty Model for Gene Regulatory Networks. Bioinformatics (2002) 18(2):261–74. doi:10.1093/bioinformatics/18.2.261
5. Liang J, Han J. Stochastic Boolean Networks: An Efficient Approach to Modeling Gene Regulatory NetworksBMC Syst Biol (2012) 6:113. doi:10.1186/1752-0509-6-113
6. Peican Zhu P, Jie Han J. Stochastic Multiple-Valued Gene Networks. IEEE Trans Biomed Circuits Syst (2014) 8(1):42–53. doi:10.1109/tbcas.2013.2291398
7. Kauffman SA. Metabolic Stability and Epigenesis in Randomly Constructed Genetic Nets. J Theor Biol (1969) 22:437–67. doi:10.1016/0022-5193(69)90015-0
8. Kauffman SA. The Origins of Order. Self-Organization and Selection in Evolution. Oxford University Press (1993).
9. Zhu P, Liang J, Han J. Gene Perturbation and Intervention in Context-Sensitive Stochastic Boolean Networks. BMC Syst Biol (2014) 8–60. doi:10.1186/1752-0509-8-60
10. Zhu P, Han J. Asynchronous Stochastic Boolean Networks as Gene Network Models[J]. J Compu. Biol. (2014) 21(10):771–83. doi:10.1089/cmb.2014.0057
11. Cheng D. Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach[M]. Berlin: Springer (2010).
12. Cheng D, Qi H. A Linear Representation of Dynamics of Boolean Networks. IEEE Trans Automat Contr (2010) 55:2251–8. doi:10.1109/tac.2010.2043294
13. Li R, Yang M, Chu T. State Feedback Stabilization for Boolean Control Networks. IEEE Trans Automat Contr (2013) 58:1853–7. doi:10.1109/tac.2013.2238092
14. Li B, Lu J, Liu Y, Wu Z-G. The Outputs Robustness of Boolean Control Networks via Pinning Control. IEEE Trans Control Netw Syst (2020) 7(1):201–9. doi:10.1109/tcns.2019.2913543
15. Liu A, Li H. On Feedback Invariant Subspace of Boolean Control Networks. Sciece China Inf Sci (2020) 63(12):229201. doi:10.1007/s11432-019-9869-6
16. Zhang Z, Xia C, Chen S, Yang T, Chen Z. Reachability Analysis of Networked Finite State Machine with Communication Losses: A Switched Perspective. IEEE J Select Areas Commun (2020) 38(5):845–53. doi:10.1109/jsac.2020.2980920
17. Laschov D, Margaliot M. Observability of Boolean Networks: A Graph-Theoretic Approach. Cambridge, U.K.: Cambridge Scientific Publishers, Cambridge (2013).
18. Laschov D, Margaliot M. A Maximum Principle for Single-Input Boolean Control Networks. IEEE Trans Automat Contr (2011) 56:913–7. doi:10.1109/tac.2010.2101430
19. Baxter RJ. Partition Function of the Eight-Vertex Lattice Model. Ann Phys (2000) 281(1-2):187–222. doi:10.1006/aphy.2000.6010
Appendix
Logarithm Eq. 4, we can get
Replacing Eq. A2 with Eq. 8, we can get
Keywords: network, Gaussian distribution, state pattern, gene expression, Boolean
Citation: Cui X, Ren B and Li Z (2021) Determining the Maximum States of the Ensemble Distribution of Boolean Networks. Front. Phys. 9:690748. doi: 10.3389/fphy.2021.690748
Received: 04 April 2021; Accepted: 28 May 2021;
Published: 12 November 2021.
Edited by:
Chengyi Xia, Tianjin University of Technology, ChinaReviewed by:
Jinling Liang, Southeast University, ChinaZhipeng Zhang, Tianjin University of Technology, China
Copyright © 2021 Cui, Ren and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaodong Cui, eGRjaG9pQGdtYWlsLmNvbQ==
 Xiaodong Cui
Xiaodong Cui Binghao Ren2
Binghao Ren2