Generation of High-Order Vortex States From Two-Mode Squeezed States

We report a scheme for generation of high-order quadrature vortex states using two-mode photon-number squeezed states, generated via the non-linear process of Spontaneous Parametric Down Conversion. By applying a parametric rotation in the quadratures $\left(\widehat{X},\widehat{Y}\right)$, using a ϕ converter, the Gaussian profile of the photon-number squeezed input state can be mapped into a superposition of Laguerre-Gauss modes in the quadratures with N vortices or singularities, for an input state containing $2N$ photons, thus mapping photon-number fluctuations to interference effects in the quadratures. Our scheme has the potential to improve measurement sensitivity beyond the Standard uantum Limit (SQL $\propto \sqrt{N}$), by exploiting the advantages of optical vortices, such as high dimensionality or topological properties, for applications requiring reduced uncertainty, such as quantum cryptography, quantum metrology and sensing.

1 Introduction

In quantum optics, a beam of light is in a squeezed state if its electric field amplitude has a reduced uncertainty, in relation to that of a coherent state. Thus, the term squeezing refers to squeezed uncertainty. In general, for a classical coherent state with N particles, the sensitivity of a measurement is limited by shot noise to the Standard Quantum Limit (SQL $\propto \sqrt{N}$). On the other hand, quantum states, such as photon-number squeezed states, hold the promise of improving measurement precision beyond the SQL. Squeezed states of light find a myriad of applications, such as in precision measurements, radiometry, calibration of quantum efficiencies, or entanglement-based quantum cryptography, to mention only a few [1–10].

An optical vortex is a singularity or zero point intensity of an optical field. More specific, a generic Laguerre-Gauss beam of order m of the form $\psi \propto e^{im\varphi }{e}^{-r^2}$, with ϕ its azymuthal phase and $r=\sqrt{x^2+y^2}$ its radial coordinate, has an optical vortex in its center for $m>0$. The phase in the field circulates around such singularity giving rise to vortices. Integrating around a path enclosing a vortex yields an integer number, multiple of π. This integer is known as the topological charge. There is a broad range of applications of optical vortices in diverse areas, such as in astronomy for detection of extra-solar planets, in optical tweezers for manipulation of cells and micro-particles, in optical communication to improve the spectral efficiency, in Orbital Angular Momentum (OAM) multiplexing, and in quantum cryptography to increase communication bandwidth [11–20].

In this article, we report a scheme for generation of high-order quadrature vortex states using two-mode photon-number squeezed states generated via the non-linear process of Spontaneous Parametric Down Conversion (SPDC). By applying a parametric rotation in the quadratures $\left(\widehat{X},\widehat{Y}\right)$ using a ϕ converter, the quadrature representation of the photon-number squeezed input state can be mapped into a vortex state in the quadratures containing N vortices or singularities, for an input state containing $2N$ photons, thus mapping photon-number fluctuations to interference effects in the quadrature, giving rise to the emergence of a state with a well-defined number of vortices. Our scheme has the potential of exploiting the advantages of optical vortices, such as high dimensionality or topological properties, for applications requiring precision beyond the SQL $\propto \sqrt{N}$, such as quantum cryptography, quantum metrology and sensing.

A ϕ converter, also called mode converter, is customarily used in classical optics to convert two orthogonal Hermite-Gauss modes into a Laguerre-Gauss mode. The main motivation of the present work is to explore if an equivalent operation exists that can transform a Hermite-Gauss quadrature representation into a Laguerre-Gauss representation. We found such operation indeed exists. A remarkable feature of this operation is that it can be experimentally realized by using a balanced 50:50 beam splitter. A key application of the scheme reported here is in generation of photon-number squeezed states from quadrature vortex states, by implementation of the inverse protocol.

The article is structured as follows: First, in Section 2 we review the properties of two-mode photon-number squeezed states such as their quadrature representation and photon-number distribution, second in Section 3 we introduce the concept of quadrature rotation. Next, in Section 4, we present the quadrature representation of the rotated states in terms of Laguerre-Gauss modes. In Section 5, we present numerical simulations confirming the creation of N vortices for a squeezed input state containing $2N$ photons. In Section 6, we present analytical and numerical derivations for the photon-number distribution of the resulting quadrature vortex states, revealing super-Poissonian photon statistics. Finally, in Section 7, we present our conclusions.

2 2-Mode Photon-Number Squeezed State

Consider a truncated two-mode photon-number squeezed state, produced by SPDC, in the Fock state representation of the form [21]:

$|\psi \rangle =\frac{D}{\text{cosh}r}{\displaystyle \sum }_{j=0}^N{\left(\text{tanh}r\right)}^j|j{\rangle }_a|j{\rangle }_b(1)$

where $\left(a,b\right)$ are modes labels, D is a normalization factor and r is the squeezing parameter. In what follows, we consider $\left|j{\rangle }_a\right|j{\rangle }_b=|j,j\rangle$. The wave-vector and polarization for each mode will be determined by the specific type of SPDC process and configuration being used. For example, in the case of non-collinear type-I SPDC, the two modes would correspond to distinct directions governed by the wave-vectors of signal and idler photons. In order to keep our description as general as possible, we do not limit to a particular SPDC process.

To obtain a quadrature representation of the wavefunction for the state in Eq. 1, we use the standard representation of Fock states ($\left\{|n\rangle \right\}$) in the position basis ($\left\{|x\rangle \right\}$) which, up to a scaling factor, is equivalent to the Hermite-Gauss polynomial of order n, of the form $\langle x|n\rangle =\sqrt{\frac{1}{\pi 2^{n}n!}}{H}_n\left(x\right)e^{-\left(x^2\right)/2}$ [24]. A 2D representation can be obtained by ascribing orthogonal bases ($\left\{|x,y\rangle \right\}$) to each mode, where $|x,y\rangle =|x\rangle |y\rangle$ are the eigenvectors of the quadrature operators $\widehat{X}=\frac{\widehat{a}+{\widehat{a}}^{†}}{\sqrt{2}}$ and $\widehat{Y}=\frac{\widehat{b}+{\widehat{b}}^{†}}{\sqrt{2}}$, with eigenvalues x and y, respectively. Here ($\widehat{a},\widehat{b}$) are annihilation operators for the two modes $\left(a,b\right)$ [24]. In this notation, the two-mode photon-number states $|n_x,n_y\rangle$ can be written in the quadrature representation as $\langle x,y|n_x,n_y\rangle =\sqrt{\frac{1}{\pi 2^{\left(n_x+n_y\right)}{n}_x!n_y!}}{H}_{n_x}\left(x\right)H_{n_y}\left(y\right)e^{-\left(x^2+y^2\right)/2}$ [22–25]. Using these expressions, the two-mode photon-number squeezed input state $|\psi \rangle$ has a quadrature representation of the form $\langle x,y|\psi \rangle =\psi \left(x,y\right)$:

$\begin{array}{l}\psi \left(x,y\right)=\frac{D}{\text{cosh}r}\stackrel{N}{{\displaystyle \sum }_{j=0}}{\left(\text{tanh}r\right)}^j\times \\ \sqrt{\frac{1}{\pi 4^j{\left(j!\right)}^2}}{H}_j\left(x\right)H_j\left(y\right)e^{-\left(x^2+y^2\right)/2}.\end{array}(2)$

The quadrature representation of the input state $|\psi \rangle$ is depicted in Figure 1B and Figure 1C. Such quadrature representation reveals a Gaussian profile, with no vortices or singularities for squeezing parameter $r=1$. Note that the quadrature profile is not equivalent to the transverse profile of the beam, since $\widehat{X}$ and $\widehat{Y}$ are quadrature operators, not transvese coordinates. Moreover, the plots in Figures 1B,C correspond to the quadrature representation of the wavefunction of the input state $\psi \left(x,y\right)$, which is not equivalent to the Wigner function in phase space. The photon-number distribution for the input state $P\left(n,n\right)=|\langle n,n|\psi \rangle {|}^2$ can be calculated obtaining the well known sub-Poissonian quantum statistics. Tracing over one mode we obtain $P\left(n\right)={\left|\frac{\text{tanh}{r}^n}{\text{cosh}r}\right|}^2$. Photon-number distributions for different values of the squeezing parameter $r=\mathrm{1,0.5},0.1$ are displayed in Figure 1D, revealing thermal statistics when tracing over one mode, while the overall photon-number statistics for the 2-mode squeezed states is sub-Poissonian.

FIGURE 1

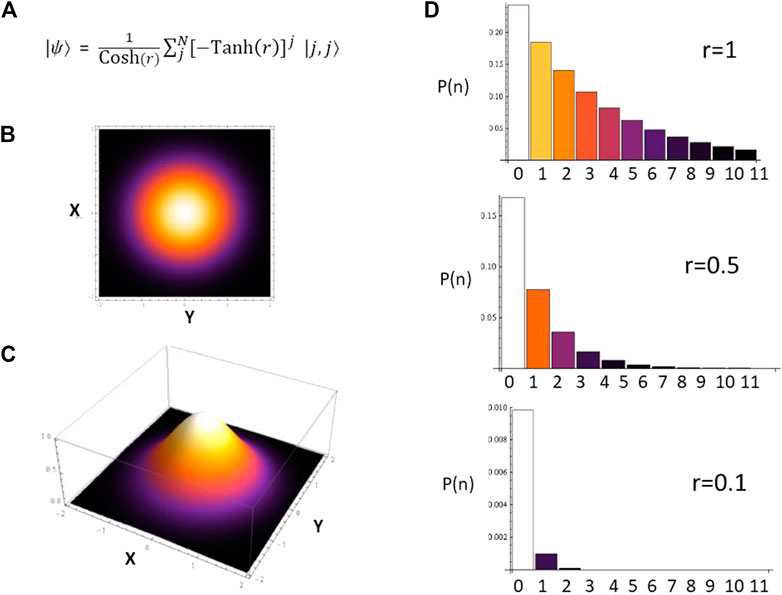
FIGURE 1. (A) Two-mode photon-number squeezed input state $|\psi \rangle$. (B,C) Quadrature representation of input state (not Wigner function) displaying a Gaussian profile with no vortices or singularities, for squeezing parameter $r=1$. (D) Photon-number distribution for different values of squeezing parameter $r=\mathrm{1,0.5},0.1$, revealing thermal statistics by tracing over one mode (see text for details).

3 Quadrature Rotation

The photon-number squeezed state depicted in Figure 1 displays a standard Gaussian profile in the quadratures $\left(\widehat{X},\widehat{Y}\right)$, with no topological charges or phase singularities. In order to imprint a vortex in the quadratures $\left(\widehat{X},\widehat{Y}\right)$, we introduce a rotation $\widehat{C}$ by an angle ϕ, represented by a unitary operator of the form:

$\widehat{C}=e^{i2\varphi \left[{\widehat{a}}^{†}\widehat{b}+{\widehat{b}}^{†}\widehat{a}\right]},(3)$

where $\left({\widehat{a}}^{†},\widehat{a}\right)$ and $\left({\widehat{b}}^{†},\widehat{b}\right)$ are creation and destruction operators for modes $\left(a,b\right)$, which satisfy the standard commutation rules $\left[{\widehat{a}}^{†},\widehat{a}\right]=1$ and $\left[{\widehat{b}}^{†},\widehat{b}\right]=1$. Interestingly, $\widehat{C}$ is mathematically equivalent to the unitary operator describing the action of a beam splitter in Fock space [1], therefore it can be easily implemented in the laboratory.

The input state transformed under the unitary operator $\widehat{C}$ becomes $|{\psi }^{\prime }\rangle$ :

$|{\psi }^{\prime }\rangle =\widehat{C}|\psi \rangle ,(4)$

which represents a rotation of the quadrature by an angle ϕ. In the Heisenberg picture, considering standard commutation rules for creation and annhiliation operators, we obtain the following expression (see Appendix A):

$\begin{array}{l}|{\psi }^{\prime }\rangle =\frac{D}{\text{cosh}r}\stackrel{N}{{\displaystyle \sum }_{j=0}}{\left(\text{tanh}r\right)}^j\times \\ {\left(\frac{{\widehat{a}}^{†}}{\sqrt{2}}+i\frac{{\widehat{b}}^{†}}{\sqrt{2}}\right)}^j{\left(\frac{{\widehat{b}}^{†}}{\sqrt{2}}+i\frac{{\widehat{a}}^{†}}{\sqrt{2}}\right)}^j|\mathrm{0,0}\rangle .\end{array}(5)$

By a binomial expansion in Eq. 5 we obtain:

$\begin{array}{l}|{\psi }^{\prime }\rangle =\frac{D}{\text{cosh}r}\stackrel{N}{{\displaystyle \sum }_{j=0}}{A}_j^{r,N}\times \\ \stackrel{j}{{\displaystyle \sum }_{k=0}}\stackrel{j}{{\displaystyle \sum }_{l=0}}{B}_{k,l}^{\varphi }{C}_{kl}^{Nj}|j-\left(l-k\right),j+\left(l-k\right)\rangle .\end{array}(6)$

where D is the normalization factor. The coefficients in the sums are of the form $A_j^{r,N}={\left(\text{tanh}r\right)}^j\sqrt{\frac{\left(j\right)!\left(j\right)!}{2^N}}$, $B_{k,l}^{\varphi }={\left(i2\varphi \right)}^{l+k}$, while $C_{k,l}^{Nj}$ takes the form (see Appendix A):

$C_{lk}^{Nj}=\frac{\sqrt{\left(j-l+k\right)!\left(j+l-k\right)!}}{k!\left(j-k\right)!l!\left(j-l\right)!}.(7)$

In order to observe the action of the rotation $\widehat{C}$ in the quadratures we turn to the quadrature representation of the transformed ket $\langle x,y|{\psi }^{\prime }\rangle ={\psi }^{\prime }\left(x,y\right)$.

4 Laguerre-Gauss Mode Expansion

The quadrature representation of the rotated state ${\psi }^{\prime }\left(x,y\right)$ results in:

$\begin{array}{l}{\psi }^{\prime }\left(x,y\right)=\frac{D}{\text{cosh}r}\stackrel{N}{{\displaystyle \sum }_{j=0}}{A}_j^{r,N}\times \\ \stackrel{j}{{\displaystyle \sum }_{k=0}}\stackrel{j}{{\displaystyle \sum }_{l=0}}{B}_{k,l}^{\varphi }{C}_{lk}^{Nj}{H}_{j-\left(l-k\right)}\left(x\right)H_{j+\left(l-k\right)}\left(y\right)e^{-\left(x^2+y^2\right)/2},\end{array}(8)$

where $H_{j-\left(l-k\right)}\left(x\right)=\langle x|j-l+k\rangle$ and $H_{j+\left(l-k\right)}\left(y\right)=\langle y|j+l-k\rangle$ are Hermite-Gauss polynomials of order $\left(j-l+k\right)$ and $\left(j+l-k\right)$, respectively.

It is well known that Hermite-Gauss (HG) modes with spatial dependence $H_p\left(x\right)H_q\left(y\right)$ may become a single Laguerre-Gauss (LG) mode of order $L_q^{p-q}\left(x^2+y^2\right)$ provided a phase change of $\pi /2$ in the mode profile is achieved [11]. Such Laguerre-Gauss mode is associated with a quadrature vortex number of $\left(p-q\right)$ [16, 21–24, 26–34].

By choosing the rotation parameter $\varphi =\pi /4$, we may obtain the required phase change to convert the Hermite-Gauss modes into a single Laguerre-Gauss mode. By relabeling the indices $\left(l-k\right)=m$, with $m=0,\dots ,N/2$, we note the quadrature profile can be written as a sum of products of HG modes of the form $H_{j-m}\left(x\right)H_{j+m}\left(y\right)$. Selecting $\varphi =\pi /4$, the quadrature profile can be written in terms of LG modes of the form $L_{j-m}^{2m}\left(r^2\right)$, thus resulting in a superposition of LG modes of order $2m$ in the quadrature representation.

5 Numerical Results

To explore the resulting mode-profile in the quadrature $\left(\widehat{X},\widehat{Y}\right)$, we performed numerical simulations for a superposition of LG modes of the form:

$\begin{array}{l}{\psi }_{LG}\left(x,y\right)=\frac{1}{\text{cosh}r}\stackrel{N}{{\displaystyle \sum }_{j=0}}\stackrel{j}{{\displaystyle \sum }_{m=0}}{A}_j^{r,N}{C}_{kl}^{Nj}\times \\ L_{j-m}^{2m}\left(x^2+y^2\right)e^{-\left(x^2+y^2\right)/2},\end{array}(9)$

where r is the squeezing parameter and the coefficients take the form $A_j^{r,N}={\left(\text{tanh}r\right)}^j\sqrt{\frac{\left(j\right)!\left(j\right)!}{2^N}}$, $C_{lk}^{Nj}=\frac{\sqrt{\left(j-l+k\right)!\left(j+l-k\right)!}}{k!\left(j-k\right)!l!\left(j-l\right)!}$.

We performed numerical simulations in the quadrature for different values of squeezing parameter r, and different values of photon-number N. The results are depicted in Figure 2 and Figure 3. The main result we observe is that, for a sufficiently small squeezing parameter r, the resulting quadrature profile exhibits $N/2$ vortices for an input state with $N/2$ photons per mode. In this way, we have mapped the reduced uncertainty in photon-number in Fock space, to a reduced uncertainty in vortex-number in the quadrature.

FIGURE 2

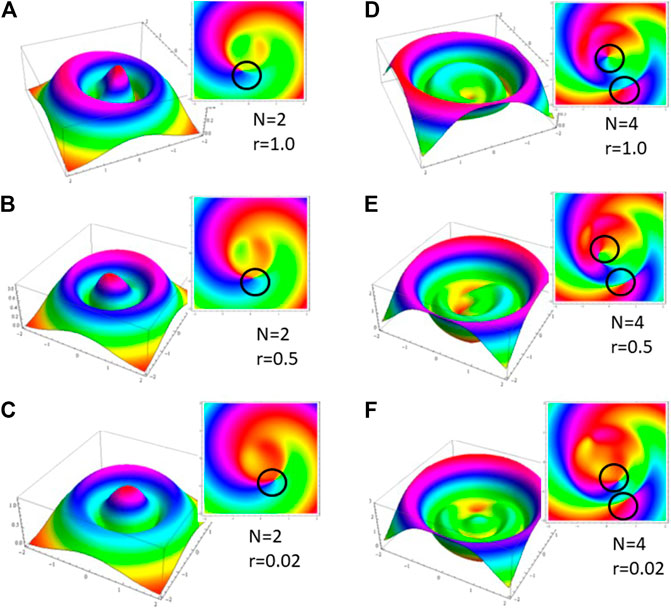
FIGURE 2. 3D plots of amplitude $\left|{\psi }_{LG}\left(x,y\right)\right|$ for resulting Laguerre-Gauss mode in the quadrature representation, depicting the impact of the squeezing parameter r on the formation of vortices, for different values of squeezing parameter r and total photon-number N. Insets correspond to phase profiles $\left|{\varphi }_{LG}\left(x,y\right)\right|$ for resulting Laguerre-Gauss mode revealing vortices or singularities in the quadratures (not in the transverse profile of the beam). (A)$N=2$, $r=1$, (B)$N=2$, $r=0.5$, (C)$N=2$, $r=0.02$, (D)$N=4$, $r=1$, (E)$N=4$, $r=0.5$, (F)$N=4$, $r=0.02$. As the squeezing parameter decreases, the formation of $N/2$ vortices in the quadratures becomes apparent (see text for details).

FIGURE 3

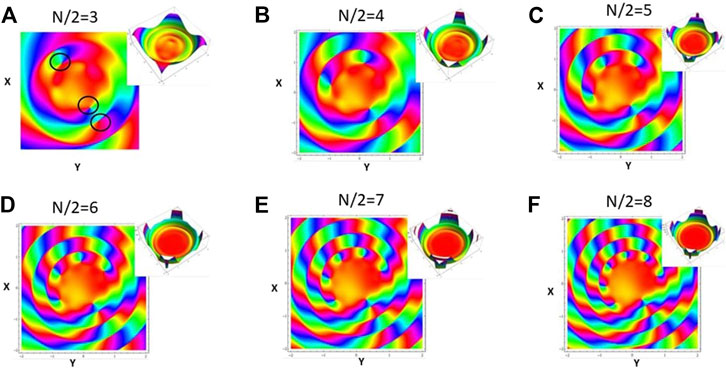
FIGURE 3. Phase profile $\left|{\varphi }_{LG}\left(x,y\right)\right|$ of resulting Laguerre-Gauss quadrature representation for a squeezing parameter $r=0.02$, exploring the impact of the photon-number ($N/2$ per mode) in the formation of vortices. Insets correspond to amplitude plots $\left|{\psi }_{LG}\left(x,y\right)\right|$. The numerical results confirm creation of $N/2$ vortices for N total input photons. (A)$N/2=3$, (B)$N/2=4$, (C)$N/2=5$, (D)$N/2=6$, (E)$N/2=7$, (F)$N/2=8$, with $N/2$ input photons per mode (see text for details).

5.1 Dependence on Squeezing Parameter r

In order to better understand the impact of the squeezing parameter r in the formation of vortices in the quadrature, we performed numerical simulations for different squeezing parameters, and for different total number of photons N. This is displayed in Figures 2A–F. Figure 2 left column corresponds to $N=2$ total photon number and right column corresponds to $N=4$ total number of photons. Different rows in decreasing order correspond to squeezing parameters $r=\mathrm{1,0.5},0.02$. Numerical simulations clearly reveal that vortices are formed as r decreases, thus as the uncertainty in photon-number decreases, as expected. Thus confirming that the reduced uncertainty in Fock space is mapped to reduced uncertainty in vortex number, in the quadrature.

5.2 Dependence on Photon-Number N

To confirm the viability of generation of high-order vortex states in the quadratures we performed numerical simulations for larger total number of photons ($N>2$). This is depicted in Figure 3, for a squeezing parameter $r=0.02$. Figures 3A–F display plots of phase profile associated with ${\psi }_{LG}\left(x,y\right)$, calculated via${\varphi }_{LG}\left(x,y\right)={\text{tan}}^{-1}\left[\frac{\mathrm{\Im }\left[{\psi }_{LG}\left(x,y\right)\right]}{\mathrm{\Re }\left[{\psi }_{LG}\left(x,y\right)\right]}\right]$, for $N/2=\mathrm{3,4,5,6,7,8}$ input photons per mode, further confirming the azymuthal charge and vorticity in quadrture space increases with the number of photons. Insets display 3D plots of mode amplitude $\left|{\psi }_{LG}\left(x,y\right)\right|$. As predicted, in all cases the number of vortices is equal to thel number of photons per mode $N/2$ in the initial 2-mode photon-number squeezed state containing N photons, thus confirming the mapping of photon-number in Fock space to quadrature vortex-number in quadrature.

6 Photon-Number Distribution of Quadrature Vortex States

The generation of vortices in the quadrature can be considered an interference effect arising from photon-number fluctuations, therefore it is expected that the photon-number distribution should be modified for quadrature vortex states. To further confirm that photon-number fluctuations are mapped into interference effects in the quadratures, resulting in the emergence of vortices, for a two-mode photon-number squeezed input state, we calculated the photon-number distribution for the resulting vortex states $P\left(n_1,n_2\right)=|\langle n_1,n_2|{\psi }^{\prime }\rangle {|}^2$. Using orthogonality of Fock states, the sums in Eq. 6 collapse into a single sum, of the form:

$P\left(n_1,n_2\right)=|\frac{D}{\text{cosh}r}{\displaystyle \sum }_{k=0}^{n_1+n_2}{A}_{n_1,n_2}^{N,r}{B}_{n_1,n_2}^{\varphi ,k}{C}_{n_1,n_2}^{N,k}{|}^2,(10)$

where $A_{n_1,n_2}^{N,r}=\text{tanh}{\left(r\right)}^{\frac{n_1+n_2}{2}}\sqrt{\frac{\left(n_1+n_2\right)!\left(n_1+n_2\right)!}{2^N}}$, $B_{n_1,n_2}^{\varphi ,k}={\left(i2\varphi \right)}^{2k+\frac{n_2-n_1}{2}}$, and $C_{n_1,n_2}^{N,k}$ results in:

$C_{n_1,n_2}^{N,k}=\frac{\sqrt{\left(n_1\right)!\left(n_2\right)!}}{\sqrt{k!\left(\frac{n_1+n_2}{2}-k\right)!(k+\frac{(n_2-n_1)}{2})!(n_1-k)!}}.(11)$

Equation 11 reveals the photon-number fluctuations which give rise to the emergence of vortices. Numerical results for the photon-number distributions of quadrature vortex states are presented in Figure 4 and Figure 5, confirming the predicted photon-number fluctuations and super-Poissonian statistics.

FIGURE 4

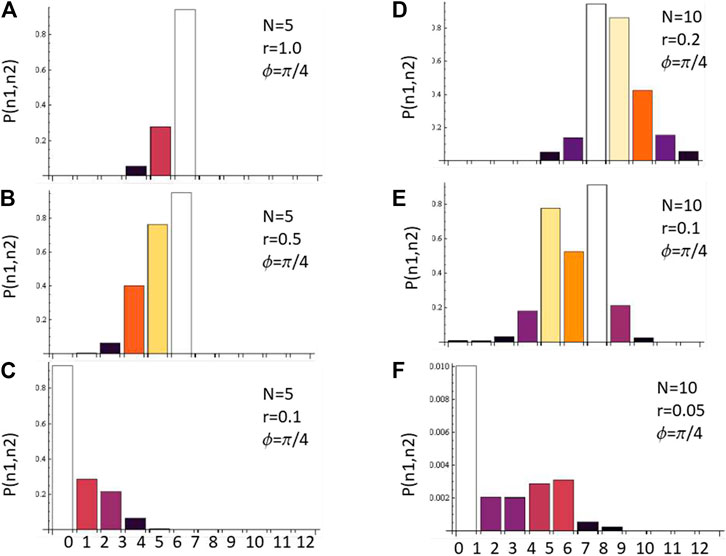
FIGURE 4. Photon-number statistics $P\left(n_1,n_2\right)$ for quadrature vortex states considering $n_1=n_2$ and a truncation parameter given by N photons per mode. Left column $N=5$ and $\varphi =\pi /4$, right column $N=10$ and $\varphi =\pi /4$. Different rows correspond to squeezing parameters (A)$r=1.0$, (B)$r=0.5$, (C)$r=0.1$, (D)$r=0.2$, (E)$r=0.1$, (F)$r=0.05$. The photon-number fluctuations due to quadrature vortex formation is revealed (see text for details).

FIGURE 5

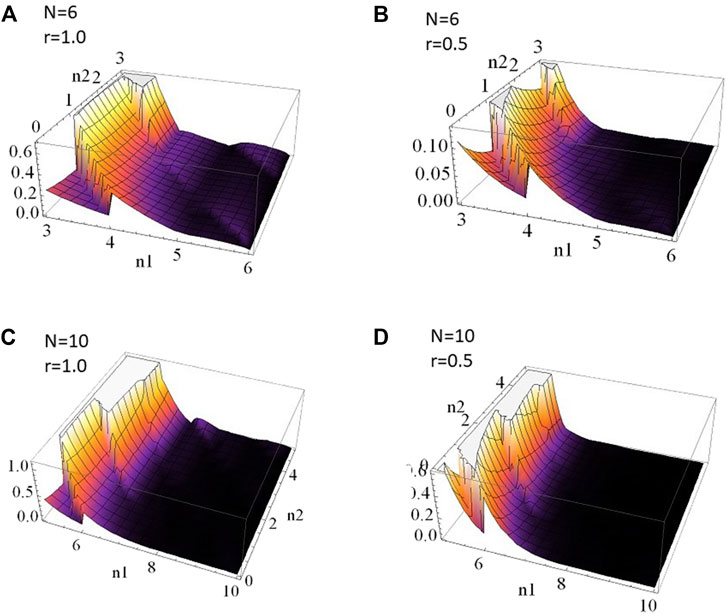
FIGURE 5. Numerical simulations of photon-number statistics $P\left(n_1,n_2\right)$ for quadrature vortex states, taking $n_1\ge n_2$, and a truncation parameter given by N total photons in the two-mode state, for a rotation parameter $\varphi =\pi /4$. Numerical results are displayed in Panel 5 for: (A)$N=6$ and $r=1$, (B)$N=6$ and $r=0.5$, (C)$N=10$ and $r=1$, (D)$N=10$ and $r=0.5$. The photon-number distribution peaks at $n_1=n_2\approx N/2$.

In order to further illustrate the photon-number imbalance between the two modes, introduced by the rotation in the quadratures, we performed numerical simulations for the two-mode photon number distribution $P\left(n_1,n_2\right)$ for vortex states, taking $n_1\ge n_2$ and a truncation parameter of N total photons in the two-mode state, for a rotation parameter $\varphi =\pi /4$. Numerical results for different squeezing parameter values are displayed in Figure 5: (a) $N=6$ and $r=1.0$, (b) $N=6$ and $r=0.5$, (c) $N=10$ and $r=1.0$, (d) $N=10$ and $r=0.5$. For a sufficiently large squeezing parameter, the photon-number distribution peaks for $n_1=n_2\approx N/2$.

7 Discussion

We presented a scheme for generation of high-order quadrature vortex states starting from a two-mode photon-number squeezed state generated via the non-linear process of Spontaneous Parametric Down Conversion (SPDC). By applying a parametric rotation in the quadratures $\left(\widehat{X},\widehat{Y}\right)$ using a ϕ converter, the quadrature representation of the photon-number squeezed input state is transformed into a high-order quadrature vortex state, with N vortices, for an input state containing $2N$ photons, thus mapping the fluctuations in photon-number to interference effects in the quadrature as depicted by optical singularities with zero-point intensity and singular phase. Furthermore, we obtained analytical and numerical expressions for the super-Poissonian photon-number statistics and fluctuations, giving rise to vortex formation in the quadratures.

Vortex states are customarily generated using various tools, such as Dove prisms, spiral plates, fork holograms, or astigmatic mode converters such as a cylindrical lenses. The important distinction is that these operations act on the transverse profile of the input beam. In the context of the present article, the rotation is performed on the quadrature representation of the state, which can be readily implemented in the lab by a balanced beam splitter. A key application of our scheme is in generation of two-mode photon-number squeezed states from two-mode quadrature vortex states, by implementing the inverse protocol.

Our scheme has the potential of exploiting the advantages of optical vortices, such as high dimensionality and topological properties, for quantum applications requiring squeezed uncertainty beyond the SQL limit ($\sqrt{N}$), such as quantum cryptography, quantum metrology and quantum sensing [35–42].

Data Availability Statement

The data and numerical codes are available upon request.

Author Contributions

GP and AB conceived the idea and performed analytical derivations. GP and AB performed numerical simulations. GP wrote the manuscript. All authors provided critical feedback and helped shape the research, analysis and manuscript.

Funding

GP acknowledges financial support via grants PICT Startup 2015 0710 and UBACyT PDE 2017.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Loudon R. The Quantum Theory of Light. 3rd ed. Oxford, United Kingdom: Oxford University Press (2000).

2. Xiao M, Wu L-A, Kimble HJ. Precision Measurement beyond the Shot-Noise Limit. Phys Rev Lett (1987) 59:278–81. doi:10.1103/physrevlett.59.278

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Walther P, Pan J-W, Aspelmeyer M, Ursin R, Gasparoni S, Zeilinger A. De Broglie Wavelength of a Non-local Four-Photon State. Nature (2004) 429:158–61. doi:10.1038/nature02552

PubMed Abstract | CrossRef Full Text | Google Scholar

4. McKenzie K, Shaddock DA, McClelland DE, Buchler BC, Lam PK. Experimental Demonstration of a Squeezing-Enhanced Power-Recycled Michelson Interferometer for Gravitational Wave Detection. Phys Rev Lett (2002) 88:231102. doi:10.1103/physrevlett.88.231102

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Goda K, Miyakawa O, Mikhailov EE, Saraf S, Adhikari R, McKenzie K, et al. A Quantum-Enhanced Prototype Gravitational-Wave Detector. Nat Phys (2008) 4:472–6. doi:10.1038/nphys920

CrossRef Full Text | Google Scholar

6. Ourjoumtsev A, Tualle-Brouri R, Laurat J, Grangier P. Generating Optical Schrödinger Kittens for Quantum Information Processing. Science (2006) 312:83. doi:10.1126/science.1122858

PubMed Abstract | CrossRef Full Text

7. Vahlbruch H, Chelkowski S, Hage B, Franzen A, Danzmann K, Schnabel R. Demonstration of a Squeezed-Light-Enhanced Power- and Signal-Recycled Michelson Interferometer. Phys Rev Lett (2005) 95:211102. doi:10.1103/physrevlett.95.211102

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wagner K, Janousek J, Delaubert V, Zou H, Harb C, Treps N, et al. Entangling the Spatial Properties of Laser Beams. Science (2008) 321:541–3. doi:10.1126/science.1159663

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Jain N, Huisman SR, Bimbard E, Lvovsky AI. A Bridge between the Single-Photon and Squeezed-Vacuum States. Opt Express (2010) 18:18254–9. doi:10.1364/oe.18.018254

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Neergaard-Nielsen S, Melholt Nielsen B, Hettich C, Molmer K, Polzik ES. Phys Rev Lett (2006) 97:083604. doi:10.1103/physrevlett.97.083604

PubMed Abstract | CrossRef Full Text

11. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Krenn M, Handsteiner J, Fink M, Fickler R, Ursin R, Malik M, et al. Twisted Light Transmission over 143 Km. Proc Natl Acad Sci USA (2016) 113:13648–53. doi:10.1073/pnas.1612023113

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Paterson L, MacDonald MP, Arlt J, Sibbett W, Bryant PE, Dholakia K. Controlled Rotation of Optically Trapped Microscopic Particles. Science (2001) 292:912. doi:10.1126/science.1058591

PubMed Abstract | CrossRef Full Text

14. Wang J, Yang J-Y, Fazal IM, Ahmed N, Yan Y, Huang H, et al. Terabit Free-Space Data Transmission Employing Orbital Angular Momentum Multiplexing. Nat Photon (2012) 6:488–96. doi:10.1038/nphoton.2012.138

CrossRef Full Text | Google Scholar

15. Tian N, Fu L, Gu M. Resolution and Contrast Enhancement of Subtractive Second Harmonic Generation Microscopy with a Circularly Polarized Vortex Beam. Sci Rep (2015) 5:13580. doi:10.1038/srep13580

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Fickler R, Lapkiewicz R, Plick WN, Krenn M, Schaeff C, Ramelow S, et al. Quantum Entanglement of High Angular Momenta. Science (2012) 338:640–3. doi:10.1126/science.1227193

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Korobchevskaya K, Peres C, Li Z, Antipov A, Sheppard CJR, Diaspro A, et al. Intensity Weighted Subtraction Microscopy Approach for Image Contrast and Resolution Enhancement. Sci Rep (2016) 6:25816. doi:10.1038/srep25816

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Emile O, Emile J. Naked Eye Picometer Resolution in a Michelson Interferometer Using Conjugated Twisted Beams. Opt Lett (2017) 42:354. doi:10.1364/ol.42.000354

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Fickler R, Campbell G, Buchler B, Lam PK, Zeilinger A. Quantum Entanglement of Angular Momentum States with Quantum Numbers up to 10,010. Proc Natl Acad Sci USA (2016) 113:13642–7. doi:10.1073/pnas.1616889113

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Padgett MJ. Orbital Angular Momentum 25 Years on [Invited]. Opt Express (2017) 25:11265. doi:10.1364/oe.25.011265

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Caves CM, Zhu C, Milburn GJ, Schleich W. Photon Statistics of Two-Mode Squeezed States and Interference in Four-Dimensional Phase Space. Phys Rev A (1991) 43:3854–61. doi:10.1103/physreva.43.3854

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Karimi E, Boyd RW, de la Hoz P, de Guise H, Řeháček J, Hradi Z, et al. Radial Quantum Number of Laguerre-Gauss Modes. Phys Rev A (2014) 89:8185. doi:10.1103/PhysRevA.89.063813

23. Nienhuis G, Visser J. Angular Momentum and Vortices in Paraxial Beams. J Opt A: Pure Appl Opt (2004) 6:S248–S250. doi:10.1088/1464-4258/6/5/020

CrossRef Full Text | Google Scholar

24. Agarwal GS, Puri RR, Singh RP. Vortex States for the Quantized Radiation Field. Phys Rev A (1997) 56:4207–15. doi:10.1103/physreva.56.4207

CrossRef Full Text | Google Scholar

25. Nienhuis G, Visser J. Angular Momentum and Vortices in Paraxial Beams. J Opt A: Pure Appl Opt (2004) 6:S248–S250. doi:10.1088/1464-4258/6/5/020

CrossRef Full Text | Google Scholar

26. Sanchez-Soto L, Klimov AB, de la Hoz P, Rigas I, Řeháček J, Hradil Z, et al. Phys Rev A (2013) 88:053839. doi:10.1103/physreva.88.053839

CrossRef Full Text

27. Hemsing E, Knyazik A, Dunning M, Xiang D, Marinelli A, Hast C, et al. Coherent Optical Vortices from Relativistic Electron Beams. Nat Phys (2013) 9:549–53. doi:10.1038/nphys2712

CrossRef Full Text | Google Scholar

28. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the Orbital Angular Momentum States of Photons. Nature (2001) 412:313–6. doi:10.1038/35085529

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Oemrawsingh SSR, Aiello A, Eliel ER, Nienhuis G, Woerdman JP. How to Observe High-Dimensional Two-Photon Entanglement with Only Two Detectors. Phys Rev Lett (2004) 92:217901. doi:10.1103/physrevlett.92.217901

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Marrucci L, Karimi E, Slussarenko S, Piccirillo B, Santamato E, Nagali E, et al. Spin-to-orbital Conversion of the Angular Momentum of Light and its Classical and Quantum Applications. J Opt (2011) 13:064001. doi:10.1088/2040-8978/13/6/064001

CrossRef Full Text | Google Scholar

31. Molina-Terriza G, Rebane L, Torres JP, Torner L, Carrasco S. J Eur Opt Soc (2007) 2:07014. doi:10.2971/jeos.2007.07014

CrossRef Full Text

33. Karimi E, Santamato E. Radial Coherent and Intelligent States of Paraxial Wave Equation. Opt Lett (2012) 37:2484. doi:10.1364/ol.37.002484

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Plick WN, Lapkiewicz R, Ramelow S, Zeilinger A. The Forgotten Quantum Number: A Short Note on the Radial Modes of Laguerre-Gauss Beams. arXiv:1306.6517.

35. Salomaa MM, Volovik GE. Quantized Vortices in superfluidHe3. Rev Mod Phys (1987) 59:533–613. doi:10.1103/revmodphys.59.533

CrossRef Full Text | Google Scholar

36. Puentes G, LundeenBranderhorst JSM, Coldesstrodt-Ronge H, Smith B, Walmsley IA. Phys Rev Lett (2009) 102:080404. doi:10.1103/physrevlett.102.080404

PubMed Abstract | CrossRef Full Text

37. Puentes G, Datta A, Feito A, Eisert J, Plenio MB, Walmsley IA. Entanglement Quantification from Incomplete Measurements: Applications Using Photon-Number-Resolving Weak Homodyne Detectors. New J Phys (2010) 12:033042. doi:10.1088/1367-2630/12/3/033042

CrossRef Full Text | Google Scholar

38. Puentes G, Waldherr G, Neumann P, Balasubramanian G, Wrachtrup J. Scientific Rep (2014) 4:1–6. doi:10.1038/srep04677

CrossRef Full Text

39. Puentes G, Aiello A, Voigt D, Woerdman JP. Phys Rev A (2007) 75:032319. doi:10.1103/physreva.75.032319

CrossRef Full Text

40. Puentes G, Colangelo G, Sewell RJ, Mitchell MW. Planar Squeezing by Quantum Non-demolition Measurement in Cold Atomic Ensembles. New J Phys (2013) 15:103031. doi:10.1088/1367-2630/15/10/103031

CrossRef Full Text | Google Scholar

41. Moulieras S, Lewenstein M, Puentes G. Entanglement Engineering and Topological protection by Discrete-Time Quantum Walks. J Phys B: Mol Opt Phys (2013) 46:104005. doi:10.1088/0953-4075/46/10/104005

CrossRef Full Text | Google Scholar

42. Takayama O, Puentes G. Enhanced Spin Hall Effect of Light by Transmission in a Polymer. Opt Lett (2018) 43:1343–6. doi:10.1364/ol.43.001343

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix a

The starting point of the derivation is Eq. 5, which defines a $\pi /4$ mode converter:

$\widehat{C}=\frac{1}{2}\left({\widehat{a}}^{†}{\widehat{b}}^{†}+{\widehat{a}}^{†}{\widehat{b}}^{†}\right)(12)$

where ${\widehat{a}}^{†}\left({\widehat{b}}^{†}\right)$ are the bosonic mode operators acting on orthogonal modes and follow regular bosonic commutation relations. Also, let us consider the initial state of the two mode system to be the following

$|\psi \rangle ={\displaystyle \sum }_j{A}_j|j{\rangle }_a|j{\rangle }_b(13)$

The above describes a general two-mode state in the Fock basis with total number of particles N distributed between the two modes. Now Eq. 13 can be written in terms of the mode operators as follows

$|\psi \rangle ={\displaystyle \sum }_j{A}_j{\left({\widehat{a}}^{†}\right)}^j{\left({\widehat{b}}^{†}\right)}^j|0{\rangle }_a|0{\rangle }_b(14)$

where it is understood that the operator ${\widehat{a}}^{†}\left({\widehat{b}}^{†}\right)$ acts on mode $|0{\rangle }_a\left(|0{\rangle }_b\right)$. We want to find how the state $|\psi \rangle$ transforms under the action of $\widehat{C}$. Moving to the Heisenberg picture, the mode operators ${\widehat{a}}^{†}\left({\widehat{b}}^{†}\right)$ evolve under $\widehat{C}$ as

${\widehat{a}}^{†}\to \text{exp}\left(i2\varphi \widehat{C}\right){\widehat{a}}^{†}\text{exp}\left(-i2\varphi {\widehat{C}}^{†}\right)(15)$

Using the Baker-Hausdorff lemma, we can write Eq. 15 as follows

$\text{exp}\left(i2\varphi \widehat{C}\right){\widehat{a}}^{†}\text{exp}\left(-i2\varphi {\widehat{C}}^{†}\right)={\widehat{a}}^{†}+i2\varphi \left[\widehat{C},{\widehat{a}}^{†}\right]+(16)$

$\frac{{\left(i2\varphi \right)}^2}{2!}\left[\widehat{C},\left[\widehat{C},{\widehat{a}}^{†}\right]\right]+\dots (17)$

Solving for the commutators, we see that $\left[\widehat{C},\widehat{a}\right]=-{\widehat{b}}^{†}/2$ and. Plugging these values back into Eq. 16, we see that we can group the terms as

$\begin{array}{l}{\widehat{a}}^{†}\left(1-\frac{{\left(\varphi \right)}^2}{2!}+\dots \right)-i{\widehat{b}}^{†}\left(\varphi -\frac{{\varphi }^3}{3!}+\dots \right)\\ ={\widehat{a}}^{†}\text{cos}\varphi -i{\widehat{b}}^{†}\text{sin}\varphi \end{array}(18)$

Now for a $\pi /4$ mode converter, we put $\varphi =\pi /4$ resulting in the transformation

${\widehat{a}}^{†}\to \frac{1}{\sqrt{2}}\left({\widehat{a}}^{†}-i{\widehat{b}}^{†}\right)(19)$

and similarly for ${\widehat{b}}^{†}$. Therefore, Eq. 14 is transformed to

$|\psi {\rangle }_v={\displaystyle \sum }_j{A}_j{\left({\widehat{a}}^{†}+i{\widehat{b}}^{†}\right)}^j{\left({\widehat{b}}^{†}+i{\widehat{a}}^{†}\right)}^j|0{\rangle }_a|0{\rangle }_b$

under the effect of the $\pi /4$ mode converter. It is understood in Eq. 20 that factors $1/\sqrt{2}$ have been absorbed into $A_j$. Equation 6 follows from here by a binomial expansion of the terms.