The Field-Frequency Lock for Fast Field Cycling Magnetic Resonance: From NMR to MRI

Magnetic field stability plays a fundamental role in Nuclear Magnetic Resonance (NMR) and Magnetic Resonance Imaging (MRI) experiments, guaranteeing accuracy and reproducibility of results. While high levels of stabilization can be achieved for standard NMR techniques, this task becomes particularly challenging for Fast Field Cycling (FFC) NMR and MRI, where the main magnetic field is switched to higher or lower levels during the pulse sequence, and field stabilization must be guaranteed within a very short time after switching. Recent works have addressed the problem with rigorous tools from control system theory, proposing a model based approach for the synthesis of magnetic field controllers for FFC-NMR. While an experimental proof of concept has underlined the correctness of the approach for a complete FFC-NMR setup, the application of the novel, model based Field-Frequency Lock (FFL) system to a FFC-MRI scanner requires proper handling of field encoding gradients. Furthermore, the proof of concept work has also stressed how further advances in the hardware and firmware could improve the overall performances of the magnetic field control loop. The main aim of this perspective paper is then discussing the key challenges that arise in the development of the FFL system suitable for a complete MRI scanner, as well as defining possible research directions by means of preliminary, simulated experiments, with the final goal of favoring the development of a novel, model based FFL system for FFC-MRI.

1 Introduction

Fast Field Cycling (FFC) Nuclear Magnetic resonance (NMR) and Magnetic Resonance Imaging (MRI) are two high-end techniques that exploit the dependence of the spin-lattice relaxation rate $R_1=1/T_1$ on the $B_0$ magnetic field experienced by the sample, to highlight information about molecular dynamics otherwise invisible to standard NMR or MRI. This eventually allows a more complete characterization of the sample and a better classification of healthy and diseased tissues.FFC experiments are characterized by a fast switching of the $B_0$ field, whose magnitude cycles over three levels [1, 2]:

• a high polarization field $B_0=B_{pol}$, to pre-polarize the sample;

• a low relaxation magnetic field $B_0=B_{rel}$, whose intensity is changed at every repetition to observe relaxation at different field strengths;

• an acquisition field $B_0=B_{acq}$, to guarantee a sufficient Signal-to-noize Ratio (SNR) for signal acquisition;

As magnetic resonance techniques, FFC-NMR and MRI require a very precise and stable acquisition field. Due to the tight bound between magnetic field strength and resonance frequency, each magnetic field disturbance results in a perturbation of the resonance frequency and, ultimately, in noise affecting the experimental data. In addition, the FFC experimental design requires the desired level of field accuracy to be guaranteed as soon as possible, after the relaxation/acquisition magnetic field switch. As a matter of fact, the later the actual signal acquisition starts after the magnetic field reaches the acquisition value, the less information about the dependence of the spin-lattice relaxation rate on the magnetic field magnitude is encoded in the acquired signal [1, 2].

1.1 The Challenge of Field Stabilization in Fast Field Cycling Magnetic Resonance

In standard FFC setups, a magnetic field control loop, based on direct magnetic field measurements, takes care of the tracking of the field reference profile, but may not provide the desired field regulation and disturbance rejection performances during the acquisition phase [3, 4]. The main issue of this approach resides in the lack of a proper magnetic field sensor, which should be able to provide high resolution and quick response over a wide range of measured values, while being sufficiently compact and suitable to be placed very close to (virtually inside) the measured NMR sample [5, 6]. Furthermore, the need for field cycling capabilities does not allow for the application of the typical approaches adopted to generate stable magnetic fields, such as the use of permanent or superconducting magnets [7, 8]. The NMR Field-Frequency Lock (FFL) is another common approach to reduce magnetic field oscillations in NMR experiments [5, 6, 9, 10, 11, 12, 13, 14]. FFL systems exploit the dependence of the NMR signal on the magnetic field, and obtain an indirect but very precise measurement of magnetic field fluctuations from a parallel NMR experiment, called the lock experiment. To avoid cross-talk between main and lock experiments, the two are performed targeting different nuclear species. Very often, it is possible to construct samples containing the nuclei of interest for both the main and the lock experiments, obtaining measurements of the magnetic field at the exact position of the sample [9, 15, 16, 17]. The standard implementation of the FFL is the phase Locked Loop (PLL) [8, 10, 18]: the lock signal is first processed to extract its main frequency, which is compared with the reference one to generate an error signal. The error eventually feeds into a regulator that computes the necessary magnetic field adjustment to steer the field error, and thus the frequency error, to zero. However, the PLL control scheme is only effective for the compensation of slow magnetic field drifts, such as thermal drift effects, and does not allow for the rapid field stabilization [5] required in the FFC context. A reliable estimation of the frequency of the lock signal requires in fact a sufficient number of samples, as well as a sufficient Signal to Noise (SNR) ratio. Consequently, the control action can be computed and applied to the system only at a relatively low frequency, resulting in long closed-loop settling times and poor high frequency disturbance rejection capabilities [19, 20].

1.2 State-of-the-Art Solutions for Field Stabilization in Fast Field Cycling Magnetic Resonance

To overcome the above limitation, the FFL approach can be adapted as discussed in some recent works. References [5, 6] demonstrate that a series of low power, high repetition rate Radio Frequency (RF) pulses, which bring the sample in a Steady State Free Precession (SSFP) regime ([15, 21, 22, 23, 24]), generate a continuous NMR signal measuring the field deviation from the resonant one. In the reminder of this work, the SSFP NMR signal will be denoted as $M_y\left(t\right)$; the magnetic field deviation from the value resulting in perfect resonance will be denoted as $\Delta B\left(t\right)$. The $M_y\left(t\right)$ signal can be effectively adopted as feedback signal in a continuous-time control loop [5, 6, 11]. Furthermore, [5, 6], characterize the lock experiment as a sensor, both in term of static and dynamic response, by means of simulations and real experiments. The analysis underlines that the static response of the sensor is linear and bijective in a symmetric interval centered in $\Delta B\left(t\right)=0$, with $\Delta B=0$ corresponding to $M_y=0$ at steady state. Moreover, the analysis underlines that the sensor dynamic response can be approximated in this region as that of a linear dynamic system. In addition, both works stress the impact of field homogeneity on both static and dynamic responses, and provide further insight on how the sample spin-lattice and spin-spin time constants, $T_1$ and $T_2$, could affect the sensor dynamics. Finally, [6, 25], propose a methodology for the synthesis of a linear regulator, based on the linear model of the NMR lock experiment, providing robust field regulation to the desired value within a specified time deadline, as well as field disturbance rejection capabilities. Reference [25] also demonstrates the effectiveness of the approach by means of experiments performed on a complete FFC-NMR setup, based on Stelar [26] (magnets, probes, firmware and software) and IECO [27] equipment (power supplies) [27]. The FFL setup tested in [25] provides regulation of magnetic field to the setpoint in about $0.015\hspace{0.17em}s$, while the effects of sinusoidal disturbances at $10\hspace{0.17em}Hz$, $25\hspace{0.17em}Hz$ and $50\hspace{0.17em}Hz$ can be reduced by $14\hspace{0.17em}dB$, $8\hspace{0.17em}dB$, and $2\hspace{0.17em}dB$, respectively. The effect of the FFL system on the main FFC-NMR experiment (S1P sequences, generating a standard decay) is quantified as the power of the imaginary NMR signal component, which should be null when the experiment runs in perfect resonance. The best FFL setup tested in [25] allows reduction of the imaginary signal power to $24\%$ and $63\%$ of the original, open-loop values in presence of $10\hspace{0.17em}Hz$ and $50\hspace{0.17em}Hz$ current sinusoidal disturbances, respectively.

While delivering promising results, a more specific analysis of the experiments presented in [25] can highlight a series of issues that may act as limiting factors for the FFC-FFL performances. Therefore, this perspective paper aims at discussing such issues and proposing possible research directions, based on preliminary simulated experiments. Moreover, the final goal of this research is the integration of a FFL into a novel FFC-MRI scanner, as the one described in [28]. Field stabilization of standard MRI scanners represents a great challenge itself, due to the spatial distribution of the magnetic field and the presence of field-encoding gradients. Only few works address this problem, adopting both feedforward [29, 30, 31, 32] or feedback control methods [13, 33, 34, 35]. However, none of them is currently examining solutions for FFC-MRI scanners. Therefore, this work also aims at discussing possible approaches to adapt the state-of-the-art field stabilization strategies for FFC to handle the presence of field-encoding gradients characterizing FFC-MRI scanners, thus moving a step forward toward the design of a suitable FFL system for FFC-MRI.

2 Discussion

The Discussion section of this work addresses the key issues in the implementation of a FFL system for FFC-NMR and MRI, as well as possible ways to face them. In particular, Figure 1A depicts the overall FFL scheme for FFC-MRI proposed in this work. The main enhancements to its components are analyzed in the reminder of this Section, by means of simulated experiments. The simulation environment models all the main components of the NMR lock experiment, consisting of magnet and power supply, NMR physics, transmission and acquisition chains, linear regulator. The simulation environment is discussed in detail in [6, 25].

FIGURE 1

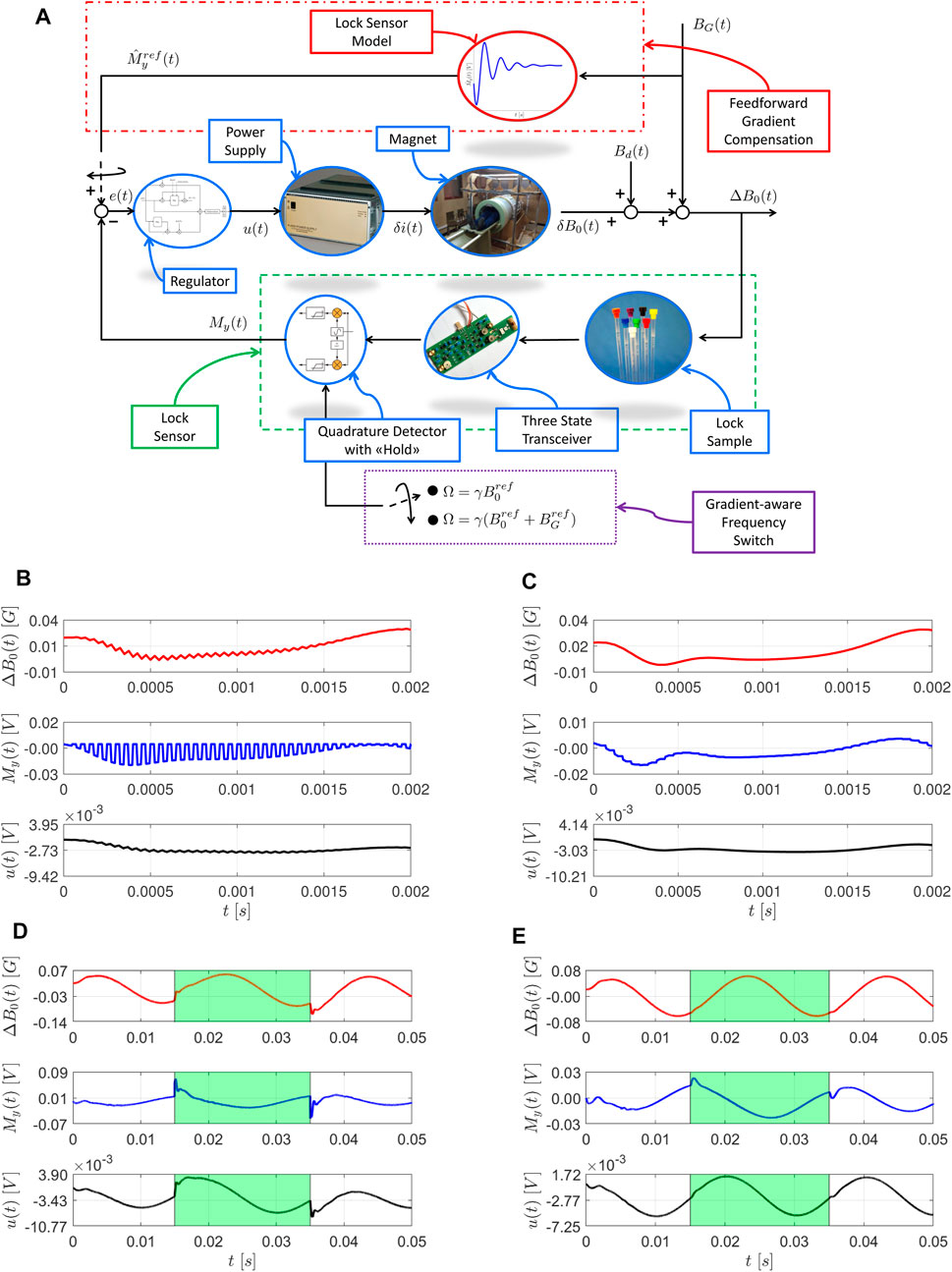
FIGURE 1. Enhanced FFL control scheme for MRI and preliminary closed-loop simulations. Simulations are performed with a virtual version of the Copper Sulfate sample from [25]. (A) The control loop, including power supply, magnet, lock sample, three state transceiver, quadrature detector with hold procedure and a linear regulator. The cascade sample-transceiver-detector plays the role of lock magnetic field sensor (green, dashed box). The main signals in the loop are the voltage control action $u\left(t\right)$, the current correction $\delta i\left(t\right)$, the magnetic field correction $\delta B_0\left(t\right)$, the magnetic field disturbance $\Delta B_d\left(t\right)$, the overall magnetic field deviation $\Delta B_0\left(t\right)$, the gradient magnetic field contribution $B_G\left(t\right)$, the measured lock signal $M_y\left(t\right)$, the error signal $e\left(t\right)=0-M_y\left(t\right)$. Additionally, two different field encoding gradient compensation strategies can be implemented, according to the gradient intensity in the lock sample volume. When the gradient intensity is small, a Feedforward Gradient Compensation strategy (red, dotted-dashed box) exploits a dynamical model of the lock sensor to compute and adapt in real time the closed-loop reference ${\widehat{M}}_y\left(t\right)$ and require regulation to the correct field intensity. With high intensity gradients, a Gradient-Aware Frequency Dwitch policy (purple, dotted box) adapts the receiver working frequency to account for the presence of the gradient, thus obtaining a lock signal measuring the field deviation from the new resonance condition. (B) Closed-loop simulation with sinusoidal field disturbance: a standard receiver gate procedure during the receiver blank time $T_{rb}=20\hspace{0.17em}\mu s$ (repetition time $T=100\hspace{0.17em}\mu s$) results in chattering of the control action and, in turn, in chattering of the magnetic field. (C) Closed-loop simulation with sinusoidal field disturbance: the proposed receiver hold procedure during the receiver blank time $T_{rb}=20\hspace{0.17em}\mu s$ (repetition time $T=100\hspace{0.17em}\mu s$) avoids chattering and helps improving the FFL regulation performances. (D) Closed-loop simulation with sinusoidal field disturbance and high intensity field gradient active from $t=15\hspace{0.17em}ms$ to $t=35\hspace{0.17em}ms$: the GAFS procedure restores the correct FFL operation after a short transient phase characterized by underdamped oscillations. (E) Closed-loop simulation with sinusoidal field disturbance and low intensity field gradient active from $t=15\hspace{0.17em}ms$ to $t=35\hspace{0.17em}ms$: the FGC procedure quickly restores the correct FFL operation with almost no oscillations after gradient switch on and off.

2.1 Field Frequency Lock Hardware and Firmware Improvements

The proposed FFL can benefit from the hardware and firmware enhancements described in the reminder of this Section, in case of application to both FFC-NMR and MRI setups.

2.1.1 Receiver Hold Procedure

As previously introduced, the main step allowing to overcome the use of PLLs and improve the FFL performance is the generation of a continuous NMR signal, acting as magnetic field disturbance measure. To this end, the lock sample must be stimulated with low power RF pulses, with a repetition time T such that $T<T_2^{\ast }$. In this way, a SSFP is enforced [15, 21, 22, 23, 24], and the resulting NMR signal provides high sensitivity to magnetic field disturbances [5, 6]. However, it must be noted that the signal is not actually acquired during the RF pulse (with a receiver gate procedure, the signal is typically set to zero), as well as immediately before and after it, to avoid measuring noise related to transmitter operations (polarization, transmission and discharge) [9, 15, 16, 17]. This interval of time will be denoted as receiver blank time, $T_{rb}$. The temporary lack of significant lock signal represents a (typically high frequency) measurement disturbance acting on the FFL closed-loop. While linear regulators can be tuned to provide rejection of high frequency measurement noise [19, 20], as well as some degree of robustness, the temporary lack of feedback signal inevitably results in chattering of the control action and in degraded regulation performance. Simulations (as an example, see Figures 1B,C) suggest that, when the receiver is not operating, holding the last meaningful lock signal sample during $T_{rb}$ represents a simple but effective improvement with respect to setting the missing samples to zero. This modification can be implemented in the firmware or hardware receiver chain in a straightforward way.

2.1.2 Three-State Transceiver Design

Even when applying low power pulses, due to field inhomogeneity, the sample $T_2^{\ast }$ limit may require the RF pulse repetition time T to be so short that $T_{rb}$ may constitute a significant portion of T. In this scenario, the hold procedure described above may not be sufficient to guarantee correct and effective operation of the lock control loop. The analysis performed in [5, 6] suggests that a longer T may results in poor sensitivity of the lock signal to field disturbances. On the other hand, improving the field homogeneity, e.g, by means of a local shimming setup, has the effect of increasing the lock signal sensitivity, but, at the same time, shrinking the field disturbance region where the lock signal response is approximately linear. The proposed linear regulator can guarantee robust field regulation and disturbance rejection, provided that the magnetic field deviation from the resonance condition does not exceed the linear region characterizing the lock experiment [6, 25]. Therefore, local shimming may not be a viable solution.The design of a high-power RF transmitter would allow reducing the time needed to deliver the required energy, but may require a much longer time for discharge, thus delaying the start of signal acquisition. To overcome this trade-off, a novel transceiver design is proposed in this work, with the goal of combining high power transmission capabilities, fast damping of the associated spurious, discharge signal, and high SNR during signal acquisition. In addition, the new transceiver should be compact and shielded against external RF pulses, since it must be included in an existing NMR/MRI instrument. The proposed design is based on the online adaptation of the probe Q factor, according to three operating states on the transceiver:

1.transmit: a high Q factor is engaged to handle high transmission power $\left(>\hspace{0.17em}\hspace{0.17em}1\hspace{0.17em}\hspace{0.17em}W\right)$;

2.Q-damping: a low Q factor is engaged to quickly discharge the coil;

3.receive: a high Q factor is engaged again to provide high SNR.

As depicted in Figure 2A, online adaptation of the probe Q factor is obtained by connecting the probe to a damping resistor during the Q-damping state. The three-state transceiver operation state is determined by a three-way switch that connects the probe to the transmitter, the damping resistor and the receiver, respectively. An example of logic circuit to control the state of the transceiver is depicted in Figure 2B. Note that, while in the example the logic circuit is designed to be driven by three lines, it can be straightforwardly adapted to a two lines framework. Finally, to protect the receiver during the high power transmission, the circuit includes protection diodes and preamp disabling during transmit and Q damping states. The proposed three-state transceiver design allows for impedance matching and adjustable gain, and provides filtering of out-band noise and overall low noise amplification, as underlined by preliminary simulations performed with models of commercially available discrete components. In particular, the plots reported in Figures 2C–E, which depict the current through the RF coil for a $1\hspace{0.17em}V$, AC input, the voltage gain of the LC network during receive oration and return loss (S11 in dB), in case of impedance matching with $50\hspace{0.17em}\Omega$, respectively.

FIGURE 2

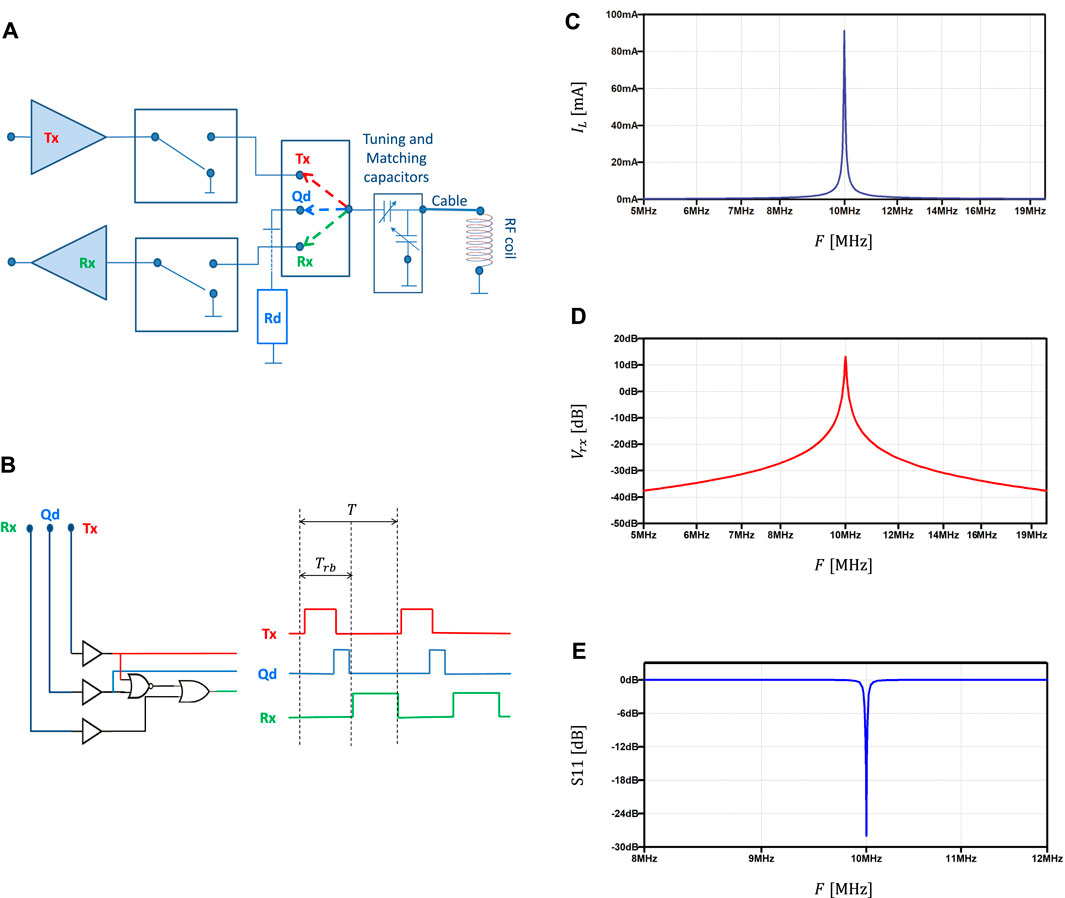
FIGURE 2. Three state transceiver. (A) Conceptual block scheme including transmitter, receiver, Q damping resistor, three way switch, tuning and matching capacitors and RF coil. (B) Example of logic circuit (three command lines) driving the three state transceiver over transmit, Q-damping and receive states at each RF pulse repetition time T. The receiver blank time $T_{rb}$ spans over transmit and Q-damping states. (C) Current through the RF coil $I_L\hspace{0.17em}\left[mA\right]$ for a $1\hspace{0.17em}V$, AC input, as function of the working frequency $F\hspace{0.17em}\left[MHz\right]$. (D) Voltage gain of the LC network during receive operation $V_{rx}\hspace{0.17em}\left[dB\right]$, as function of the working frequency $F\hspace{0.17em}\left[MHz\right]$. (E) Return loss $S11\hspace{0.17em}\left[dB\right]$, in case of impedance matching with $50\hspace{0.17em}\Omega$, as function of the working frequency $F\hspace{0.17em}\left[MHz\right]$.

2.2 Handling of MRI Field Encoding Gradients

Despite the enhancements discussed in the previous section, the application of the FFL system to a FFC-MRI scanner unavoidably requires explicit handling of field gradients. From the FFL perspective, each magnetic field moving the resonance condition from the original, resonance one represents a disturbance to be rejected. In case of field gradients, the lock sensor would detect a field disturbance and try to restore the resonance condition corresponding to no gradient active, possibly spoiling the results of the encoding procedure. In a worst case scenario, this may spoil the results of the whole experiment. Preliminary simulations suggest two possible ways to mitigate this problem, and retain some of the benefits of the FFL system during the application of field gradients: the Gradient-Aware Frequency Switch (GAFS) and the Feedforward Gradient Compensation (FGC) procedures. Both techniques are based on the hypothesis that the field deviation introduced with gradients is known (with sufficient precision) at the lock sensor site. Since gradient generation is controlled by the MRI equipment, this hypothesis is typically reasonable.

2.2.1 Gradient-Aware Frequency Switch Procedure

The GAFS procedure, depicted in Figure 1A, consists in the online switch of the lock sensor receiver frequency, $\Omega$, from its original value $\Omega =\gamma B_0^{ref}$, to the gradient dependent value $\Omega =\gamma \left(B_0^{ref}+B_G^{ref}\right)$, with γ the gyromagnetic ratio of the lock target nucleus, $B_0^{ref}$ the magnetic field value corresponding to perfect resonance without gradients, and $B_G^{ref}$ the magnetic field value corresponding to perfect resonance with the current gradient configuration. This approach requires a preliminary, offline phase to determine the value of $B_G^{ref}$ for each possible gradient configuration and construct a look-up table for online consultation, at the benefit of negligible online computational effort. Simulations (see Figure 1D for an example) suggest that GAFS can effectively restore the FFL functioning after a short time transient, where the magnetic field may undergo some oscillations. The duration of the transient is related to the closed-loop settling time of the main FFL control loop. This behavior can also be interpreted as a step change in the closed-loop reference.

2.2.2 Feedforward Gradient Compensation Procedure

The FGC procedure, depicted in Figure 1A, aims at reducing the impact of such sudden reference change, by dynamically adapting the closed-loop reference according to a dynamic model of the lock sensor response. Note that, as a first approximation, this model can coincide with the linear model used for the model based tuning of the FFL regulator, and is therefore available at no additional effort. While preliminary simulations (see Figure 1E for an example) highlight the benefit of the approach, it must be remarked that, due to the use of a linear model for the dynamic lock sensor response, FGC can only be applied for gradients whose intensity, $B_0^{ref}$, allows the lock sensor to work in its linear operating region [25]. On the contrary, the GAFS procedure can be straightforwardly applied regardless of the gradient intensity, therefore the two solutions can be considered as complementary, rather than alternatives.

2.3 Concluding Remarks and Open Issues

Based on the results presented in the recent literature regarding FFL systems for FFC-NMR, this perspective article highlighted and discussed some key problems and possible ways to improve the FFC-FFL performances, and allow its implementation on a FFC-MRI scanner. Since preliminary simulations suggested that the proposed approaches can provide promising results, the future work will focus on their practical implementation and experimental evaluation. Moreover, while this work focused more on issues related to hardware and firmware enhancements, it is worth mentioning in this concluding section that room for further improvement can also be found in the engineering of a control sample whose characteristic time constants and dynamic behavior could allow for even faster regulation of the magnetic field [5, 25]. Finally, the tuning of the regulator could be optimized and automatized, by adapting optimization-based procedures suitable to handle systems characterized by very complex high frequency behavior [36].

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization: GG, LM and GF; writing—original draft preparation: GG writing—review and editing: LM and GF All authors have read and agreed to the published version of the manuscript.

Funding

This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 668119 (project “IDentIFY”).

Conflict of Interest

Author GF is company director of Stelar s.r.l.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The Authors would like to thank the whole Stelar group for providing great insight and expertize in the development of this research.

References

1. Ferrante G, Sykora S. Technical Aspects of Fast Field Cycling. Adv Inorg Chem (2005) 57:405–70. doi:10.1016/s0898-8838(05)57009-0

CrossRef Full Text | Google Scholar

2. Kimmich R. Field-cycling NMR Relaxometry: Instrumentation, Model Theories and Applications. London, UK: Royal Society of Chemistry) (2018).

3. Roque A, Maia J, Margato E, Sousa DM, Marques G. Control and Dynamic Behaviour of a Ffc Nmr Power Supply. In: IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society (IEEE), 10-13 November, Vienna, Austria (2013). p. 5945–50.

Google Scholar

4. Roque A, Sousa DM, Sebastião P, Margato E, Marques G. Ffc Nmr Relaxometer with Magnetic Flux Density Control. Jlpea (2019) 9:22. doi:10.3390/jlpea9030022

CrossRef Full Text | Google Scholar

5. Samra J. A Field-Frequency Lock Implemented with a Sampled-Data Feedback Control Algorithm Derived from a Small-Signal NMR Model. Master’s thesis. University Park, PA: The Pennsylvania State University (2008).

6. Galuppini G, Toffanin C, Raimondo DM, Provera A, Xia Y, Rolfi R, et al. Towards a Model-Based Field-Frequency Lock for Nmr. IFAC-PapersOnLine (2017) 50:13020–5. doi:10.1016/j.ifacol.2017.08.1999

CrossRef Full Text | Google Scholar

7. Maly T, Bryant J, Ruben D, Griffin RG. A Field-Sweep/field-Lock System for Superconducting Magnets-Application to High-Field EPR. J Magn Reson (2006) 183:303–7. doi:10.1016/j.jmr.2006.09.012

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hoult DI, Richards RE, Styles P. A Novel Field-Frequency Lock for a Superconducting Spectrometer. J Magn Reson (1969) (1978) 30:351–65. doi:10.1016/0022-2364(78)90106-3

CrossRef Full Text | Google Scholar

9. Keeler J. Understanding NMR Spectroscopy. Hoboken, NJ: John Wiley & Sons (2011).

10. Jiang D, Chen H, Chen Z, Zheng Z. The Digital Field-Frequency Lock System of High-Resolution Nmr Spectrometer. In: Electrical and Control Engineering (ICECE), 2010 International Conference on IEEE, 25-27 June, Wuhan, China (2010). p. 2328–31.

Google Scholar

11. Li M, Schiano JL, Samra JE, Shetty KK, Brey WW. Reduction of Magnetic Field Fluctuations in Powered Magnets for Nmr Using Inductive Measurements and Sampled-Data Feedback Control. J Magn Reson (2011) 212:254–64. doi:10.1016/j.jmr.2011.05.010

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Yanagisawa Y, Nakagome H, Hosono M, Hamada M, Kiyoshi T, Hobo F, et al. Towards Beyond-1 GHz Solution NMR: Internal 2H Lock Operation in an External Current Mode. J Magn Reson (2008) 192:329–37. doi:10.1016/j.jmr.2008.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Henry P-G, van de Moortele P-Fo., Giacomini E, Nauerth A, Bloch G. Field-frequency Locked In Vivo Proton Mrs on a Whole-Body Spectrometer. Magn Reson Med (1999) 42:636–42. doi:10.1002/(sici)1522-2594(199910)42:4<636::aid-mrm4>3.0.co;2-i

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chen S, Xu L, Wang H, Dai S. Field-frequency Lock Approach for 21.3-mhz High-Performance Nmr Relaxation Analyzer. AIP Adv (2018) 8:075327. doi:10.1063/1.5038138

CrossRef Full Text | Google Scholar

15. Elster A. Questions and Answers in Magnetic Resonance Imaging. Maryland Heights, Missouri: Mosby Inc (1994).

16. Hornak JP. The Basics of NMR. Rochester, NY: Rochester Institute of Technology, Center for Imaging Science (1997).

17. Jacobsen NE. NMR Spectroscopy Explained: Simplified Theory, Applications and Examples for Organic Chemistry and Structural Biology. Hoboken, New Jersey: John Wiley & Sons (2007).

18. Kan S, Gonord P, Fan M, Sauzade M, Courtieu J. Automatic NMR Field‐frequency Lock-Pulsed Phase Locked Loop Approach. Rev Scientific Instr (1978) 49:785–9. doi:10.1063/1.1135615

CrossRef Full Text | Google Scholar

19. Seborg DE, Mellichamp DA, Edgar TF, Doyle FJ. Process Dynamics and Control. Hoboken, NJ: John Wiley & Sons (2010).

20. Magni L, Scattolini R. Advanced and Multivariable Control. Bologna, Italy: Pitagora (2014).

21. Carr HY. Steady-state Free Precession in Nuclear Magnetic Resonance. Phys Rev (1958) 112:1693–701. doi:10.1103/physrev.112.1693

CrossRef Full Text | Google Scholar

22. Patz S. Some Factors that Influence the Steady State in Steady-State Free Precession. Magn Reson Imaging (1988) 6:405–13. doi:10.1016/0730-725x(88)90477-8

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Gyngell ML. The Steady-State Signals in Short-Repetition-Time Sequences. J Magn Reson (1969) (1989) 81:474–83. doi:10.1016/0022-2364(89)90083-8

CrossRef Full Text | Google Scholar

24. Bagueira de Vasconcelos Azeredo R, Colnago LA, Engelsberg M. Quantitative Analysis Using Steady-State Free Precession Nuclear Magnetic Resonance. Anal Chem (2000) 72:2401–5. doi:10.1021/ac991258e

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Galuppini G, Toffanin C, Raimondo D, Provera A, Xia Y, Rolfi R, et al. Towards a Model-Based Field-Frequency Lock for Fast-Field Cycling Nmr. Appl Magn Reson (2019) 1–23.

Google Scholar

26.[Dataset] Stelar Website. Available from: https://www.stelar.it/ (Accessed 14 June 2021).

27.[Dataset] Ieco Website. Available from: http://www.ieco.fi/ (Accessed 14 June 2021).

28. Broche LM, Ross PJ, Davies GR, MacLeod MJ, Lurie DJ. A Whole-Body Fast Field-Cycling Scanner for Clinical Molecular Imaging Studies. Sci Rep (2019) 9:10402–11. doi:10.1038/s41598-019-46648-0

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Juchem C, Nixon TW, Diduch P, Rothman DL, Starewicz P, De Graaf RA. Dynamic Shimming of the Human Brain at 7 T. Concepts Magn Reson (2010) 37B:116–28. doi:10.1002/cmr.b.20169

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Bhogal A, Versluis M, Koonen J, Siero JCW, Boer VO, Klomp D, et al. Image-based Method to Measure and Characterize Shim-Induced Eddy Current fields. Concepts Magn Reson (2013) 42:245–60. doi:10.1002/cmr.a.21290

CrossRef Full Text | Google Scholar

31. Fillmer A, Vannesjo SJ, Pavan M, Scheidegger M, Pruessmann KP, Henning A. Fast Iterative Pre‐emphasis Calibration Method Enabling Third‐order Dynamic Shim Updated fMRI. Magn Reson Med (2016) 75:1119–31. doi:10.1002/mrm.25695

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Vannesjo SJ, Dietrich BE, Pavan M, Brunner DO, Wilm BJ, Barmet C, et al. Field Camera Measurements of Gradient and Shim Impulse Responses Using Frequency Sweeps. Magn Reson Med (2014) 72:570–83. doi:10.1002/mrm.24934

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Sinanna A, Bermond S, Donati A, Gros P, Hugon C, Jacquinot J-F, et al. Field Stabilization of an Mri Magnet Operating in Driven Mode. IEEE Trans Appl Supercond (2009) 19:2301–4. doi:10.1109/tasc.2009.2018105

CrossRef Full Text | Google Scholar

34. Dürst Y, Wilm BJ, Dietrich BE, Vannesjö S, Pruessmann KP. Real-time Shim Feedback for Field Stabilization in Human Mri Systems. Melbourne, Australia: Scientific Meeting of the International Society for Magnetic Resonance in Medicine (2012).

35. Duerst Y, Wilm BJ, Dietrich BE, Vannesjo SJ, Barmet C, Schmid T, et al. Real-time Feedback for Spatiotemporal Field Stabilization in Mr Systems. Magn Reson Med (2015) 73:884–93. doi:10.1002/mrm.25167

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Galuppini G, Creaco E, Magni L. Bi-objective Optimisation Based Tuning of Pressure Control Algorithms for Water Distribution Networks. Control Eng Pract (2020) 104:104632. doi:10.1016/j.conengprac.2020.104632

CrossRef Full Text | Google Scholar