Generation and Detection of Structured Light: A Review

Structured light beams have rapidly advanced over the past few years, from specific spatial-transverse/longitudinal structure to tailored spatiotemporal structure. Such beams with diverse spatial structures or spatiotemporal structures have brought various breakthroughs to many fields, including optical communications, optical sensing, micromanipulation, quantum information processing, and super-resolution imaging. Thus, plenty of methods have been proposed, and lots of devices have been manufactured to generate structured light beams by tailoring the structures of beams in the space domain and the space–time domain. In this paper, we firstly give a brief introduction of different types of structured light. Then, we review the recent research progress in the generation and detection of structured light on different platforms, such as free space, optical fiber, and integrated devices. Finally, challenges and perspectives are also discussed.

Introduction

Different from electrons, photons feature multiple degrees of freedom, including frequency/wavelength, time, complex amplitude (amplitude, phase), polarization, and spatial structure. Manipulating these physical dimensions of photons enables a diversity of light-related applications. Beyond the traditional attention to frequency, time, complex amplitude, and polarization, the spatial structure, which is another known physical dimension of photons, has attracted increasing interest. Tailoring the spatial structures and even the spatiotemporal structures of light waves enables the generation of various special light beams, such as helically phased beams, Bessel beams, vector beams, Airy beams, and spatiotemporal beams. Such beams, namely structured light in a broad sense, have grown into a significant research field, giving rise to many developments in optical communications [1–3], optical sensing [4, 5], micromanipulation [6], quantum information processing [7, 8], and super-resolution imaging [9, 10].

In recent years, structured light beams with distinct spatial structures or spatiotemporal structures have been needed more and more in different applications. For all these applications, the first and important thing is to generate and detect structured light beams. The generation and detection of diverse structured light beams on different platforms, such as free space, optical fiber, and integrated devices, have become a necessary part of structured light-enabled applications. On one hand, generating and detecting structured light beams help to facilitate emerging applications, which are not available with conventional Gaussian beams; on the other hand, the increasing demands of some special applications also promote new methods and techniques for generating and detecting structured light beams.

In this paper, we focus on the generation and detection of different structured light beams. In section Different Types of Structured Light, we firstly introduce different types of structured light beams. Then, we present the recent research progress in the generation and detection of spatial-structured light beams in sections Generation of Spatial-Structured Light and Detection of Spatial-Structured Light. We also discuss the generation and detection of spatiotemporal light beams in section Generation and Detection of Spatiotemporal Light Beams. Finally, upcoming challenges and prospects are underlined in section Prospect and Discussion.

Different Types of Structured Light

Structured light beams can be divided into two categories due to their different structures. One is spatial-structured light beams, and the other is spatiotemporal light beams. Shown in Figure 1 are illustrations of different types of structured light beams.

FIGURE 1

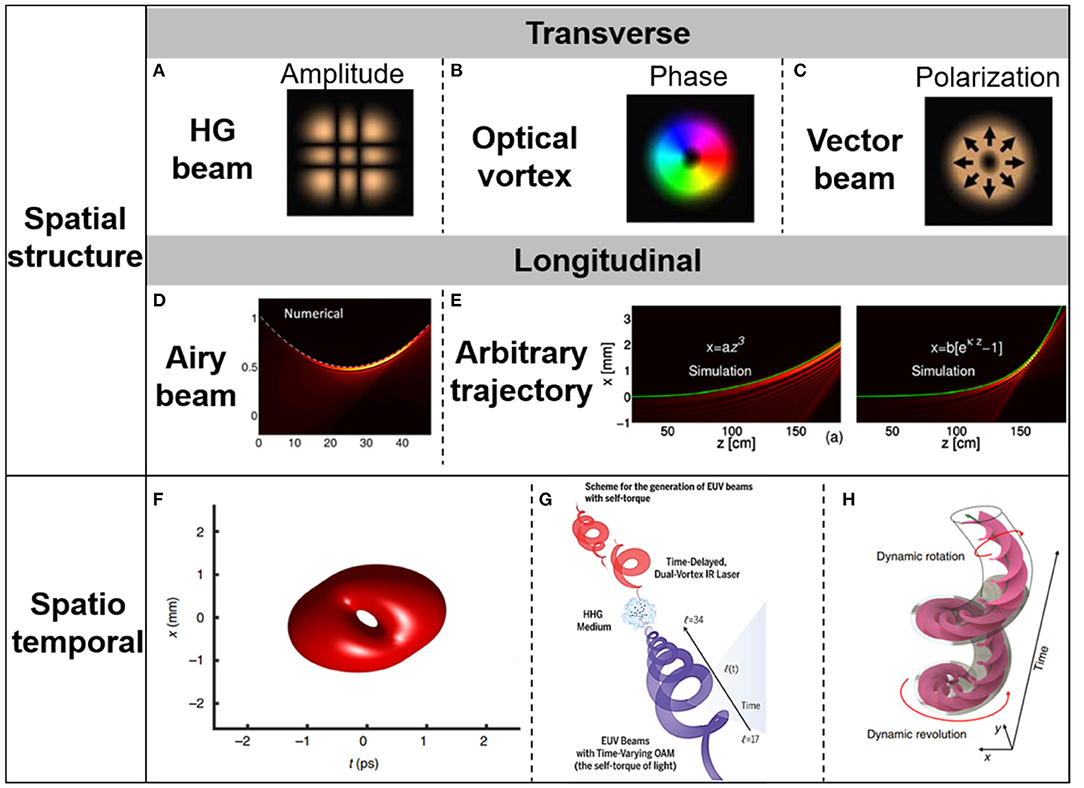
Figure 1. Introduction of different types of structured light beams. (A–C) Structured light with transverse amplitude inhomogeneities, phase inhomogeneities, and polarization inhomogeneities. (D) An Airy beam with a parabolic trajectory. Reprinted from Froehly et al. [11]. (E) Longitudinal structured light with arbitrary trajectories. Reprinted from Greenfield et al. [12]. (F–H) Spatiotemporal structured light. Reprinted from Chong et al. [13], Rego et al. [14], and Zhao et al. [15].

Spatial-structured light beams are, obviously, light fields with spatially inhomogeneous distributions/trajectories. For spatial-structured light beams, according to at which plane these spatial inhomogeneities exist, they can be divided into two types: transverse structured light beams and longitudinal structured light beams. Transverse structured light beams refer to beams with inhomogeneous amplitude, phase, and polarization distribution at the plane perpendicular to the direction of beam propagation, such as Hermite–Gaussian (HG)/Laguerre–Gaussian (LG)/Bessel beams [16–18], optical vortex beams with a helical phase front carrying orbital angular momentum [19–21], and radially/azimuthally polarized vector beams [22, 23]. Longitudinal structured light beams with spatial inhomogeneities, along the transmission direction, can be divided into several types according to different trajectories, including Airy beam with a parabolic trajectory [24], Mathieu beam and winding light, along an elliptical trajectory [25], a frozen wave with a snake-like trajectory [26], and beams along quartic trajectories, logarithmic trajectories, and even arbitrary trajectories [11, 12, 27].

In the last few years, spatiotemporal-structured light beams with inhomogeneous structures in space–time domain have become a significant field due to their unique nature [28–30], although these kinds of beams were proposed a long time ago [31, 32]. By tailoring the spatiotemporal property of light beams, spatiotemporal-structured light beams with specific nature can be generated and adopted in many applications in a frontier. For example, spatiotemporal optical vortices, with controllable transverse orbital angular momentum, are proposed and experimentally demonstrated [13], which may be used in research fields of spin Hall effect, quantum entanglement of the spatiotemporal vortex by parametric down conversion, second-harmonic generation, propagation in a Kerr medium, spatiotemporal spin–orbit angular momentum coupling, and so on. Pulse with time-varying orbital angular momentum has been successfully demonstrated in the process of high-harmonic generation [14], providing the ability for controlling magnetic, topological, and quantum excitations and for manipulating molecules and nanostructures on their natural time and length scales. Dynamic spatiotemporal beams, with two independent orbital angular momentum, are also proposed [15]. In addition, the study of group velocities [33] and anomalous refraction [34] of spatiotemporal beams paves the way to fabricate a new free-space optical delay line [35].

Generation of Spatial-Structured Light

In this section, we highlight methods and devices for generating spatial-structured light beams on different platforms, including generating free-space structured light, using discrete devices, producing structured light in fiber and emitting structured light, utilizing integrated devices. We summarize the commonly used methods and devices, as displayed in Figure 2. We divide these methods into passive devices and active structured light lasers. Passive devices modulate the spatial structure of input Gaussian beams. Thus, they can be considered as mode converters, which convert input Gaussian beams into structured light beams. For a structured light laser, a structure-modulating part in the laser cavity or at the output of the cavity is introduced, compared with traditional Gaussian beam lasers. Obviously, passive devices can be applied to establish active structured light lasers as a structure-modulating part.

FIGURE 2

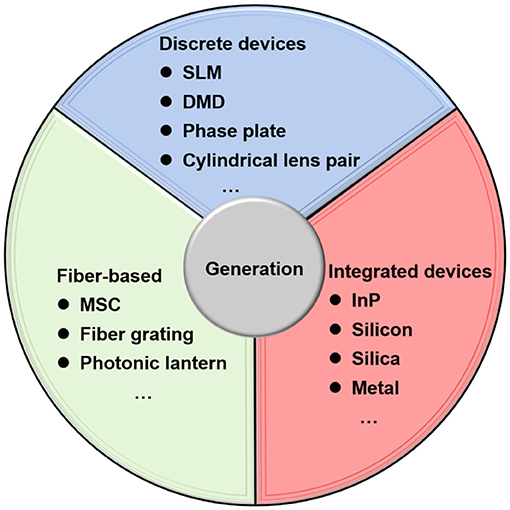
Figure 2. Methods and devices for generation of spatial-structured light beams. SLM, spatial light modulator; DMD, digital micro-mirror device; MSC, mode selective coupler.

Discrete Devices

In order to generate diverse spatial-structured light beams in free space, several methods utilizing discrete devices are proposed and experimentally demonstrated. For transverse-structured light beams, they can be generated by shaping the transverse amplitude, phase, and polarization of a fundamental Gaussian beam. For longitudinal spatial-structured light beams, their trajectories can be thought as the result of changing wave vector k, are related to the transverse phase gradient. Therefore, longitudinal structured light beams can also be produced by designing and shaping the transverse phase of beams [3, 11, 12].

Shown in Figure 3 are some typical methods for generating spatial-structured light beams, using discrete devices. A phase-only spatial light modulator (SLM) modulates the two-dimensional transverse phase of an input Gaussian beam. Optical vortex beams can be generated by loading a spiral phase pattern or a forked hologram (a superposition of a spiral phase pattern and a linear phase grating) onto a phase-only SLM [40]. Even multiple optical vortex beams and an optical vortex beams array can be produced, using a phase-only SLM [37, 41]. Moreover, transverse amplitude and polarization modulation of beams can be accomplished by propagating beams through two holograms [42, 43]. Longitudinal beams can also be generated by loading a computed hologram related to their trajectories, utilizing a caustic method [3, 11, 12]. Here, Figure 3B illustrates the experimental setup for generating vector beams (transverse polarization) by loading two different holograms onto a single phase-only SLM [43]. Transverse polarization modulation is achieved by a concatenation of two holograms. Figure 3C displays the experimental setup for generating Airy beams [3]. The phase hologram for generating an Airy beam is computed, using the caustic method. A digital micro-mirror device (DMD) can also shape the two-dimensional transverse phase distribution of a beam by controlling the optical path, using the micro-mirror array. DMD is another device for generating optical vortex beams, vector beams, and HG beams. Figure 3A illustrates the experimental setup for generating vector beams, using DMD, in which vector beams are formed by the superposition of two optical vortex beams [36].

FIGURE 3

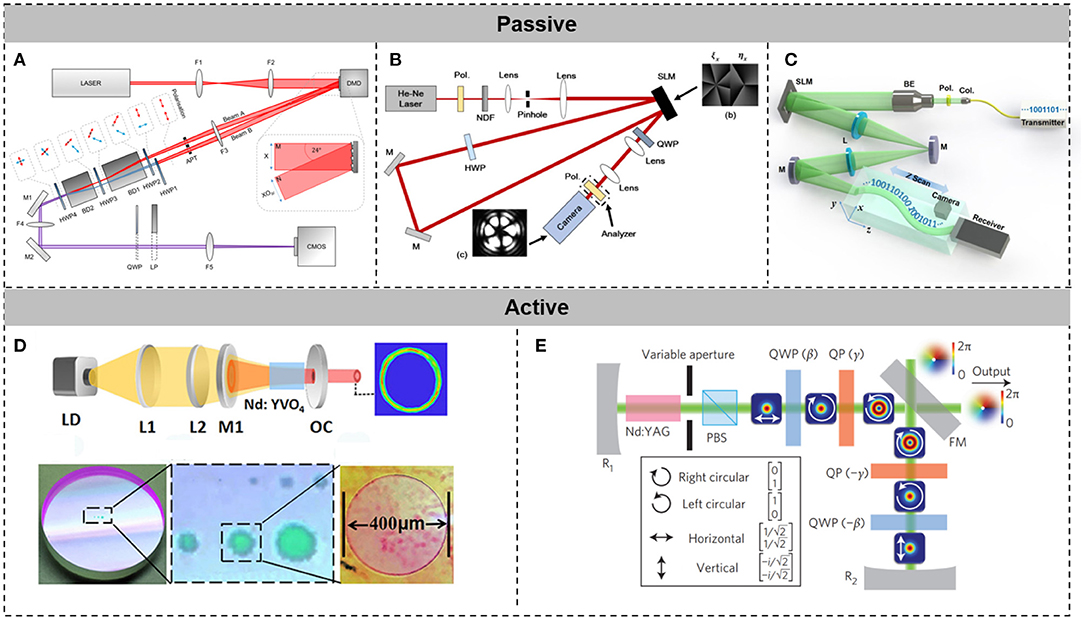
Figure 3. Generation of spatial-structured light beams, utilizing discrete devices. (A) An experimental setup for generating vector beams, using a single DMD. Reprinted from Mitchell et al. [36]. (B) An experimental setup for generating vector beams, utilizing a single phase-only SLM. Reprinted from Li and Wang [43]. (C) An experimental setup for generating Airy beams, utilizing a single phase-only SLM. Reprinted from Zhu et al. [3]. (D) A schematic of optical vortex laser, applying a cylindrical lens pair. Reprinted from Qiao et al. [38]. (E) A schematic of a vector beam laser, employing a Q plate. Reprinted from Naidoo et al. [39].

Figures 3D,E are schematics of structured light beam lasers. By placing a pair of cylindrical lenses in the resonant cavity of a laser, optical vortex beams with topological charges up to 288 can be directly produced from the laser [38, 44]. Placing a Q plate into an interferometric setup, one can establish a vector beam laser, which produces vector beams by combining two optical vortex beams with opposite topological charges and orthogonal circular polarization [39].

Fiber-Based Devices

Optical vortex beams and vector beams are both supporting modes in an optical fiber and are widely used in fiber-based space-division multiplexing (SDM) communications [2, 45, 46] and fiber endoscopes [47]. Thus, generating these two types of structured light beams with high purity is required in many fiber-based applications. In addition to the traditional approach, i.e., generating structured light beams in free space with discrete devices and coupling them into the optical fiber, many other methods have also been proposed to directly produce and propagate structured light beams in fiber, including the fiber-based structured-light-beams laser.

Figure 4 outlines several approaches for generating optical vortex beams and vector beams in fiber. Figure 4A shows the process of converting a fundamental Gaussian beam into an optical vortex beam by applying a helical fiber grating [48]. Figure 4B refers to the generation of optical vortex beams, using long-period fiber gratings [49, 53]. Long-period fiber gratings enable effective index matching between the fundamental mode and higher-order linearly polarized (LP) modes in few mode fibers (FMF). Thus, higher-order LP modes can be generated by long-period fiber gratings. Optical vortex beams are produced by the superposition of higher-order LP modes. Shown in Figure 4C is another way to generate optical vortex beams in fiber. A standard single-mode fiber (SMF) is stuck to a two-mode fiber (TMF), with specific offsets and tilt angles to realize high-order fiber mode conversion [50]. High-purity (extinction ratio >20 dB) generation of OAM modes within a wide wavelength range from 1,480 to 1,640 nm is achieved. The mode selective coupler, manufactured by taping and coupling an SMF with an FMF, converts the input Gaussian beam from the SMF into output higher-order optical vortex beams in the FMF based on the principle of effective index matching of different modes [54]. Figure 4D displays the schematic of a femtosecond optical vortex laser, using such a mode selective coupler [51]. Two hundred and seventy-three fs and 140 fs pulses of OV_±1 and OV_±2 beams are generated from such a mode-locked fiber laser. Figure 4E illustrates the schematic of a reconfigurable multicore fiber-structured light laser for generating optical vortex beams and vector beams. By appropriately controlling the phase and polarization of beam output from each core of the multicore fiber, optical vortex beams and vector beams with changeable orders can be generated [52].

FIGURE 4

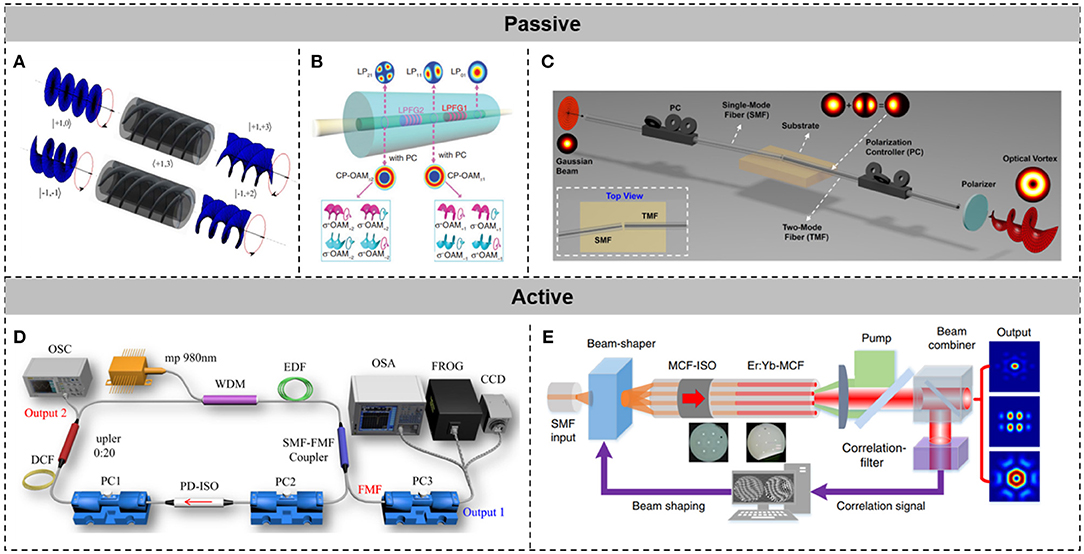
Figure 4. Generation of spatial-structured light beams, utilizing fiber-based devices. (A) A helical fiber grating for generating optical vortex beams. Reprinted from Fang and Wang [48]. (B) Generating optical vortex beams, using long-period fiber gratings. Reprinted from Han et al. [49]. (C) Fiber-to-fiber butt coupling for generating optical vortex beams. Reprinted from Li et al. [50]. (D) A schematic of an optical vortex laser, using a mode selective coupler. Reprinted from Wang et al. [51]. (E) A reconfigurable multicore fiber laser for generating optical vortex beams and vector beams. Reprinted from Lin et al. [52].

Integrated Devices

Integrated devices with small volumes for generating various structured light beams are, remarkably, showing a promise prospect. Here, we present different types of integrated devices for generating structured light beams based on diverse materials, including silicon [55–60], silica [61–63], metals [64–66], crystal [67], InP [68–71], and so on. Among them, the active material InP can be used to build a structured light beam laser.

Figure 5 displays some typical integrated devices and integrated lasers for emitting structured light beams. Shown in Figure 5A is the miniature optical vortex emitter based on silicon microring with angular gratings [55]. For the clockwise (or anticlockwise) Nth order whispering gallery mode (WGM), supported in a silicon microring, its energy gets scattered by the angular grating sidewall (M equidistant scatters), resulting in optical vortex-scattered light as output with a topological charge of ℓ, where ℓ = N-M. Despite its compact footprint and accuracy in phase control, the resonance feature of WGM causes intrinsic narrowband operation. An ultra-broadband OAM emitter is proposed and experimentally demonstrated to overcome this limitation, as displayed in Figure 5B [58]. Coaxial OV beams are emitted across the entire telecommunication band from 1,450 to 1,650 nm. Such an OV beams emitter enables an OV beam communication with a data rate of 1.2 Tbit/s, assisted by 30-channel optical frequency combs. In addition to silicon waveguides, metal-based metasurface can also be used to generate structured light beams. Figure 5C illustrates the structure of a reflection-enhanced plasmonic metasurface for efficient generation of structured light with the phase helix and intensity helix at 2 μm [64]. Such a plasmonic metasurface is formed by a V-shaped optical antenna array. V-shaped antenna cells with different arm lengths and angles allow one to flexibly achieve different localized abrupt phase shifts. Therefore, a phase helix (optical vortex) can be generated with such a plasmonic metasurface. In addition, the intensity helix is generated by a metasurface-assisted self-referenced interferometric method.

FIGURE 5

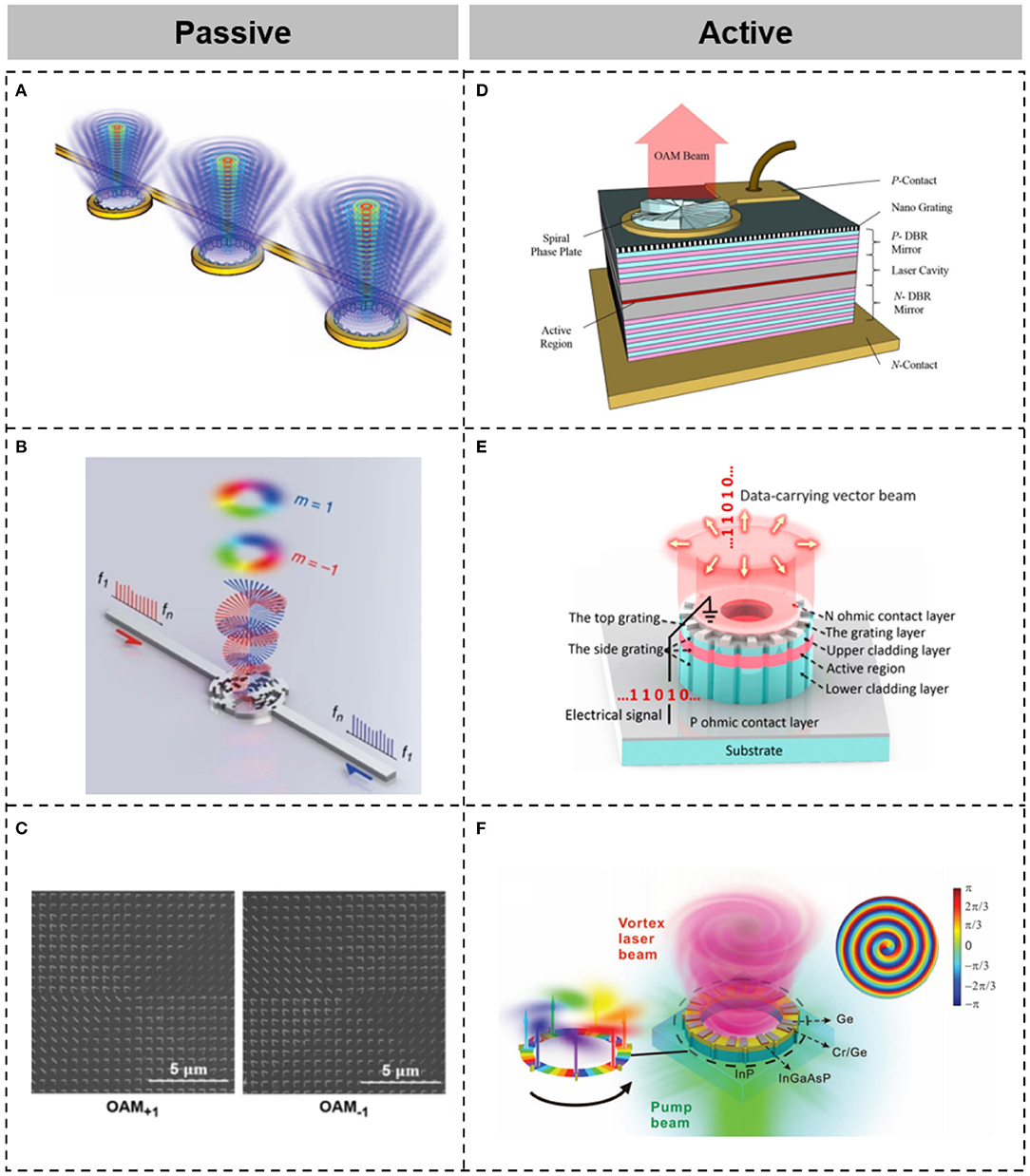
Figure 5. Generation of spatial-structured light beams, utilizing integrated devices. (A) Schematic of an optical vortex emitter based on silicon microring with angular gratings. Reprinted from Cai et al. [55]. (B) Schematic of a broadband optical vortex emitter. Reprinted from Xie et al. [58]. (C) Schematic of reflection-enhanced plasmonic metasurface for generating a phase helix and an intensity helix. Reprinted from Zhao et al. [64]. (D) Schematic of a vertical-cavity surface-emitting laser with an integrated spiral phase plate at the output port. Reprinted from Li et al. [68]. (E) Schematic of a high-speed directly modulated cylindrical vector beam laser. Reprinted from Ma et al. [70]. (F) Schematic of an optical vortex microlaser on an InGaAsP/InP platform. Reprinted from Miao et al. [69].

Beyond integrated structured light beam emitters, there are also integrated structured light beam lasers. Figure 5D displays the schematic of a micro vortex laser, implemented by placing a micro spiral phase plate on the output port of a vertical cavity surface emitting laser (VCSEL) [68]. A beam out from the VCSEL is converted to a higher-order optical vortex beam by such a spiral phase plate. Shown in Figure 5E is a high-speed directly modulated cylindrical vector beam laser, enabling single cylindrical vector beam lasing and efficient emission, assisted by ion implantation, which is manufactured by placing two sets of optimized second-order gratings in InP-based microring cavities [70, 71]. Eight to 20 Gbit/s cylindrical vector beam lasing is achieved with >1 mW output power and a ~50 dBside-mode suppression ratio. Figure 5F illustrates the structure of an optical vortex microlaser on an InGaAsP/InP platform [69]. The on-top Ge and Cr/Ge introduce different loss and gain modulation, forming an exceptional point operation with unidirectional power circulation in the microring laser. Thus, the microring with angular gratings allows for only one direction of light circulation, resulting in integrated optical vortex laser emission.

Additionally, we may also classify these integrated devices based on different working principles, such as metasurface [63–66], bounded in the continuum [72, 73], and WGM waveguides [55, 69, 70].

Detection of Spatial-Structured Light

Remarkably, many passive devices mentioned above for generating structured light beams can be reversely applied to detect spatial-structured light. For example, loading a spiral phase pattern of -lth order onto the SLM enables the demodulation of the lth optical vortex beam. The MSC converting fundamental Gaussian beam in the SMF into structured light in the FMF can also be used to detect structured light in an opposite way. Here, in this section, we review some other efficient methods and devices for the detection of spatial-structured light, even the superposition of spatial-structured light beams. For longitudinal structured light beams, beam trajectories can be easily reconstructed by moving a charge coupled device (CCD), along the optical axis. Thus, here, we focus on the detection of transverse-structured light beams. For transverse-structured light beams, most of these methods and devices, generally, sort or detect spatial-structured light beams based on three kinds of principles: propagating structured light beams with different orders to different spatial positions, converting structured light beams to other easily measured physical parameters, or analyzing the light field to reconstruct a structured light beam spectrum. We summarize some frequently utilized methods and devices in Figure 6.

FIGURE 6

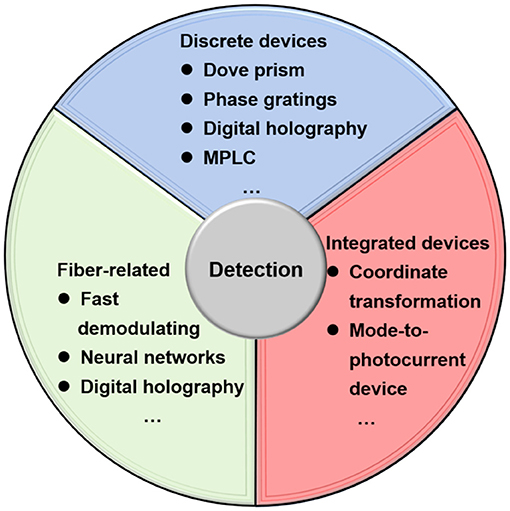
Figure 6. Methods and devices for detection of spatial-structured light beams. MPLC, multiplane light conversion.

Discrete Devices

Various discrete devices have been proposed, fabricated, and applied to efficiently demultiplex/sort structured light beams, like a Dove prism [74], Dammann gratings [75], gradually changing gratings [76], annular gratings [77], and multiplane light conversion (MPLC) devices [78]. Moreover, an approach to decomposing the orbital angular momentum spectrum based on the rotational Doppler effect converts different topological charges of optical vortex beams into frequency shifts in the frequency domain [79]. The digital holography method [80] and the neural network approach [81] can also be utilized to analyze the light field and decompose structured light beam superposition states.

Displayed in Figure 7 are the typical methods for the detection of spatial-structured light beams, using discrete devices. Placing a Dove prism into an interferometric setup enables propagating optical vortex beams with different orders to different output ports, as shown in Figure 7A [74]. Optical vortex beams in two arms are rotated with respect to each other through a rotation angle due to the Dove prism. The phase shift of the two arms is determined by the rotation angle and topological charge. Adjusting the rotation angle so that the phase shift takes the form of lα, odd- and even-order optical vortex beams has different phase shifts. Thus, odd- and even-order optical vortex beams are sorted at two different ports. Cascading such interferometric setups enables sorting of more optical vortex beams by carefully setting the rotation angle of each interferometric setup. Dammann gratings translating optical vortex beams with different orders to Gaussian beams with diverse output directions can be employed to efficiently multiplex/demultiplex optical vortex beams in optical communication applications [75], as displayed in Figure 7B. It enables 10 channel OV beams (de)multiplexing so that 80/160 Tbit/s optical communication is accomplished. Figure 7C shows the detection results of optical vortex beams, employing annular gratings [77]. The magnitude of the topological charge value is determined by the number of dark fringes after diffraction, and the sign of the topological charge value is distinguished by the orientation of the diffraction pattern. Shown in Figure 7D is a newly proposed MPLC device for efficiently sorting HG/LG modes [78]. Propagating HG/LG beams superposition state through multiple phase planes—this superposition state can be decomposed into a Cartesian grid of identical Gaussian spots, each containing a single HG/LG component. Over 210 modes are demonstrated, using an MPLC device. Such phase planes are holograms loaded onto a single SLM or phase masks written on plates. Another method for the detection of optical vortex beams is digital holography. Figure 7E displays the experimental setup for decomposing optical vortex superposition states, utilizing on-axis digital holography [80]. Capturing the intensity profiles of measured light fields, a reference beam, and interference of measured beam with the reference beam at different phase shifts, one can compute the complex amplitude distribution of a measured light field. Then the final optical vortex spectrum is calculated, using the reconstructed complex amplitude distribution.

FIGURE 7

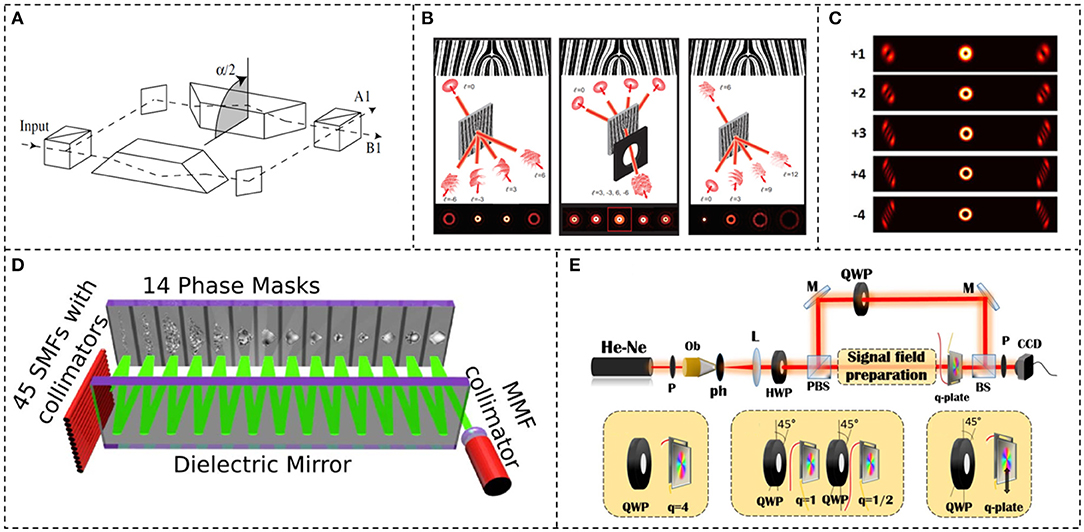
Figure 7. Detection of spatial-structured light beams, utilizing discrete devices. (A) Sorting optical vortex beams, using a Dove prism. Reprinted from Leach et al. [74]. (B) Demultiplexing optical vortex superposition states, utilizing Dammann gratings. Reprinted from Lei et al. [75]. (C) Detection of optical vortex beams, using annular gratings. Reprinted from Zheng et al. [77]. (D) The MPLC device for HG/LG superposition state decomposition. Reprinted from Fontaine et al. [78]. (E) An experimental setup for decomposing optical vortex superposition state, using on-axis digital holography. Reprinted from D'Errico et al. [80].

Detection of Fiber-Guided Structured Light

Optical vortex beams and vector beams are supported in a multimode fiber (MMF). In the last decade, lots of efforts have been devoted to SDM based on MMF to improve the traffic of optical communications and increase the pixel resolution of fiber imaging. The most useful characterization of such a multimode system is the mode transfer matrix. It can quantitatively evaluate how each input mode couples to each output mode, which is also the state-of-the-art technology for fiber-guided structured light beam detection.

Here, we introduce several methods to detect fiber-guided structured light beams. Figure 8A shows a method for intelligent recognition of different mode bases in a ring-core fiber based on deep learning [82]. Using a camera to capture intensity profiles of different mode bases as training and testing data sets of the neural networks, the convolutional neural network-based deep learning successfully recognizes different mode bases with an overall recognition rate of close to 100%. In addition, a 1 × 5 PD array can perfectly recognize different mode bases with a recognition rate of close to 100%. Even a 1 × 2 PD array with only two PDs can obtain a high recognition rate of close to 93.3%. This work gives a method to qualitatively recognize different fiber-guided structured light beams. Besides, quantitative characterization of fiber-guided structured light beams in MMF, i.e., mode transfer matrix measurement mentioned above, is required in order to see through the chaos in MMF [83]. Several approaches have been proposed to fast characterize the mode transfer matrix of MMF. By quickly switching the input vortex modes of the MMF and, at the same time, changing the demodulation phase hologram and recording the power of different modes at the output, a 110 ×110 mode transfer matrix of 2 m MMF is measured through 110 ×110 times rapid demodulating and measurements [84], as shown in Figure 8B. Such a system enables the mode transfer matrix characterization of both optical vortex modes and vector modes in MMF. Despite its high efficiency in MMF characterization, it suffers from too many measurements. To overcome this limitation, many other methods are proposed to simplify the characterization process, such as measuring the mode transfer matrix of MMF, utilizing the neural network method [85], on-axis digital holography [86], and off-axis digital holography [78, 87, 88]. Displayed in Figure 8C is the schematic for measuring the 45 × 45 mode transfer matrix of 26.5 km MMF [87]. With specific mode input, the beam propagates through MMF and then outputs and interferes with a reference beam with a small tilt angle off the axis. By applying two-dimensional fast Fourier transform to captured off-axis interference intensity profiles, the spatial frequency domain is obtained. Then, the autocorrelation term is filtered out and the cross-correlation term is kept in the spatial frequency domain. Implementing the two-dimensional reversal fast Fourier transforms to the cross-correlation term, the complex amplitude distribution of the output beam can be computed to calculate the mode spectrum of the output light field [89]. A 45 × 45 mode transfer matrix of MMF can be fast characterized, using only 45 measurements within 0.3 s [87].

FIGURE 8

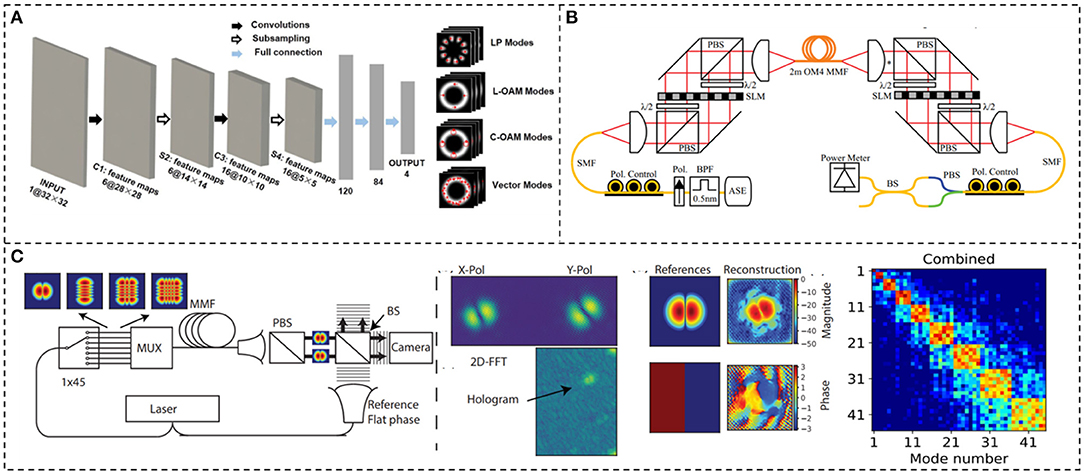
Figure 8. Methods for detection of fiber-guided spatial-structured light beams. (A) Intelligent recognition of different mode bases in a ring-core fiber based on deep learning. Reprinted from Wang et al. [82]. (B) A fast modulation method for characterization of a 110 × 110 mode transfer matrix of 2 m MMF. Reprinted from Carpenter et al. [84]. (C) Efficient characterization of a 45 × 45 mode transfer matrix of 26.5 km MMF based on off-axis digital holography. Reprinted from Mazur et al. [87].

Integrated Devices

Many passive integrated devices mentioned above can also be used in an opposite way to detect structured light beams [60–62]. Here, we introduce three other integrated devices to efficiently detect structured light beams. Coordinate transformation, shaping optical vortex beams with different topological charges into Gaussian-like beams at different spatial locations, is frequently used as an optical vortex mode sorter. According to different transformation principles and formulas, there are two transformation methods: log-polar transformation [90–92] and spiral transformation [93, 94]. These approaches usually use two phase masks to achieve the transformation. The first phase mask is applied to unwrap the optical vortex beam with topological charge land translate it into a rectangle beam with phase distribution from 0 to 2lπ along the rectangular. The rectangle beam formed at the second plane is a caustic, so the second plane called “compensate plane” is employed to shape the caustic into a collimated beam. Then, the collimated beam propagates through a cylindrical lens and is translated to Gaussian-like beam at specific spatial position due to phase distribution from 0 to 2lπ along the rectangular. Different l determines different spatial position. The phase mask of the first plane is calculated by obtaining the relationship between the coordinates of the first plane and the second plane and deriving the phase gradient at the first plane required for such coordinate transformation [95]. The phase mask of the second plane is calculated based on the principle of shaping the caustic into a collimated beam by calculating the phase gradient of the second plane [95]. These two-phase masks can be loaded onto two SLMs or integrated into a small dielectric slab. An integrated device for spiral transformation, which is more convenient, is displayed in Figure 9A. Intermodal crosstalk is <13 dB for all the seven OAM modes and the two circular polarization states. Moreover, by introducing the Pancharatnam–Berry optical element manufacturing technology, integrated devices, utilizing a spin-dependent optical geometric transformation for efficiently sorting vector beams, are fabricated with photoaligned liquid crystal [96, 97]. In addition to transforming different structured light beams to different spatial positions, approaches converting different modes into other easily measured physical parameters are also proposed and experimentally demonstrated, such as converting different modes into different photocurrents. Figure 9B indicates such a photodetector based on tungsten ditelluride (WTe2) with carefully fabricated electrode geometries to facilitate direct characterization of the topological charge of orbital angular momentum of optical vortex beams [98]. This orbital photogalvanic effect, driven by the helical phase gradient, is distinguished by a current winding around the optical beam axis, with a magnitude proportional to its quantized orbital angular momentum mode number. Shown in Figure 9C is a dielectric metasurface demultiplexer formed by TiO₂ for detecting optical vortex beams with different spin and orbital angular momentum. Coaxial optical vortex superposition state with different spin angular momentum (different circular polarizations) and diverse orbital angular momentum (various topological charges) can be converted into fundamental Gaussian beams with different diffractive directions [99]. By carefully designing the phase distribution of metasurface, a different optical vortex beam diffracts along different direction, and the optical vortex beam can be converted into a fundamental Gaussian beam only at a specific direction. Such a demultiplexer supports 22 different modes, including topological charges from −5 to +5 and two orthogonal circular polarizations. Moreover, the diffraction pattern of the dielectric metasurface with a fundamental Gaussian beam input is also displayed in Figure 9C.

FIGURE 9

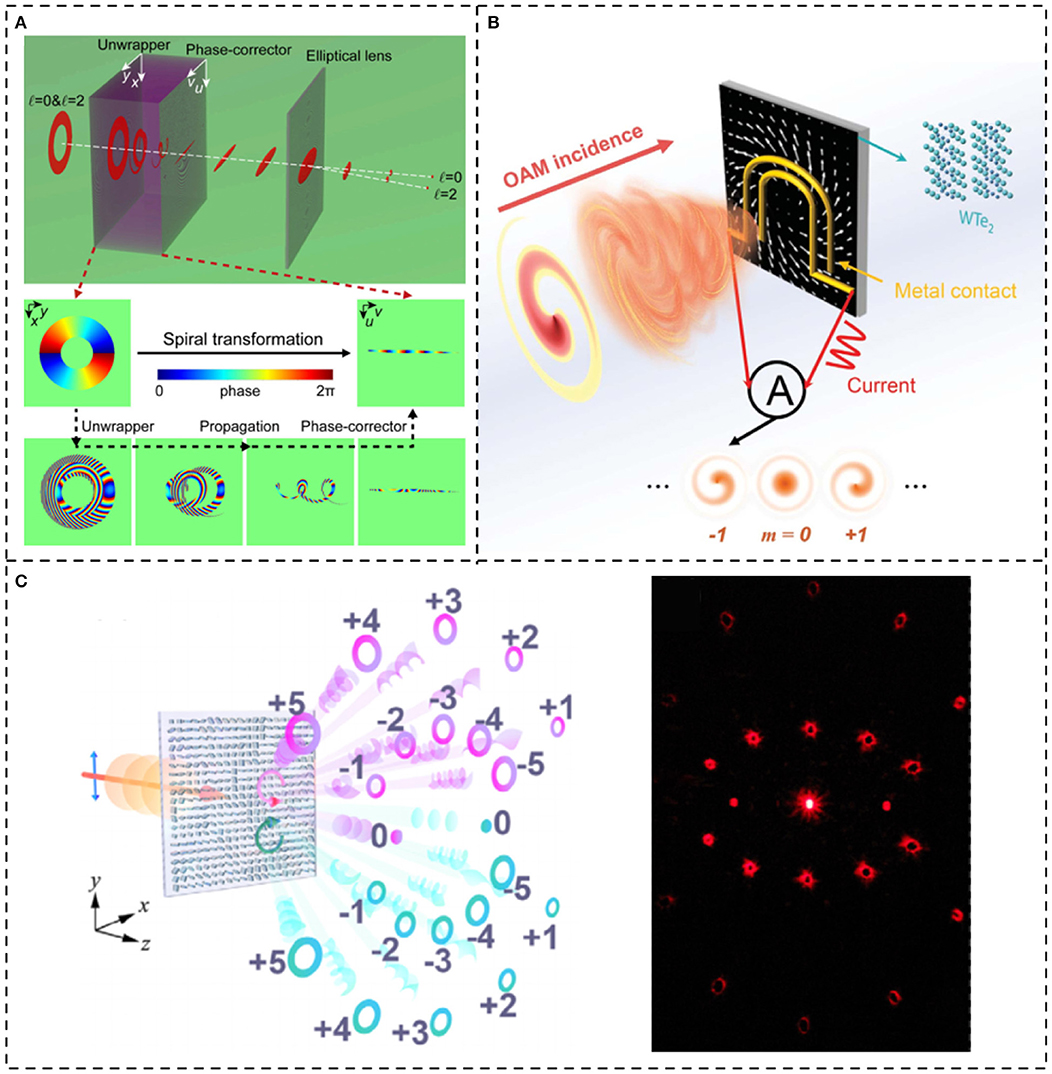
Figure 9. Integrated devices for detection of spatial-structured light beams. (A) A spiral transformation device integrated on a dielectric slab for efficient sorting of optical vortex beams. Reprinted from Wen et al. [94]. (B) An integrated device converting different topological charges of optical vortex beams into different magnitudes of photocurrent. Reprinted from Ji et al. [98]. (C) Dielectric metasurface for multiple optical vortex beams detection. Reprinted from Zhang et al. [99].

Generation and Detection of Spatiotemporal Light Beams

In the last few years, spatiotemporal light beams with inhomogeneous structures in the spatiotemporal domain have become a frontier research field. Various spatiotemporal light beams have been proposed and demonstrated in the experiment [13–15, 33–35]. However, tailoring the spatiotemporal structure of light beams is not that easy due to the ultrahigh value of light speed. Here, we introduce several commonly used methods for the generation and detection of spatiotemporal light beams.

In order to shape the spatial structure of light beams in an ultrashort time scale, light sources for generating ultrashort pulse or optical-frequency-comb lines are applied. Spatiotemporal light beams can be produced by applying distinguished spatial structures to different pulses. Figure 10A illustrates the schematic for generating extreme-ultraviolet beams with time-varying orbital angular momentum [14]. Two time-delayed, collinear IR pulses with the same wavelength (800 nm), but different OAM values, are focused on an argon gas target (HHG medium) to produce harmonic beams with self-torque [14]. Shown in Figure 10B is a powerful setup for the generation of arbitrary vector spatiotemporal light fields with arbitrary amplitude, phase, and polarization at every point in space and time [100]. First, the light output from a swept-wavelength laser with two orthogonal polarizations propagates through a pulse shaper so that it is redistributed among the spatial and spectral/temporal domains. Such a pulse shaper is proposed to shape different pulses into different spatial positions, similar to the shaper device in Weiner [101]. The shaped light then propagates through an MPLC device and is converted into different HG modes at the output port of MPLC due to input beams steering to different spatial positions. Thus, arbitrary spatiotemporal beams can be generated by a designed combination of different HG beams at different times. Remarkably, such a method with the principle that disperses the light beams at different moments to different spatial positions and converts them into different spatial structures is a universal approach to generating many kinds of spatiotemporal light beams. Figure 10C introduces a convenient method to produce a spatiotemporal optical vortex wave packet [13]. Since the x–y plane of the SLM is, in fact, k_x − λ plane, loading a spiral phase hologram of an optical vortex beam with topological charge l onto the SLM equals to applying a spiral phase of optical vortex beam with topological charge –l in k_x − ω plane. Such an optical vortex in k_x − ω plane is then converted into an optical vortex beam in the x–t plane by the two-dimensional Fourier transform of cylindrical lens and diffraction gratings. Thus, the spatiotemporal optical vortex beam with transverse orbital angular momentum is successfully generated.

FIGURE 10

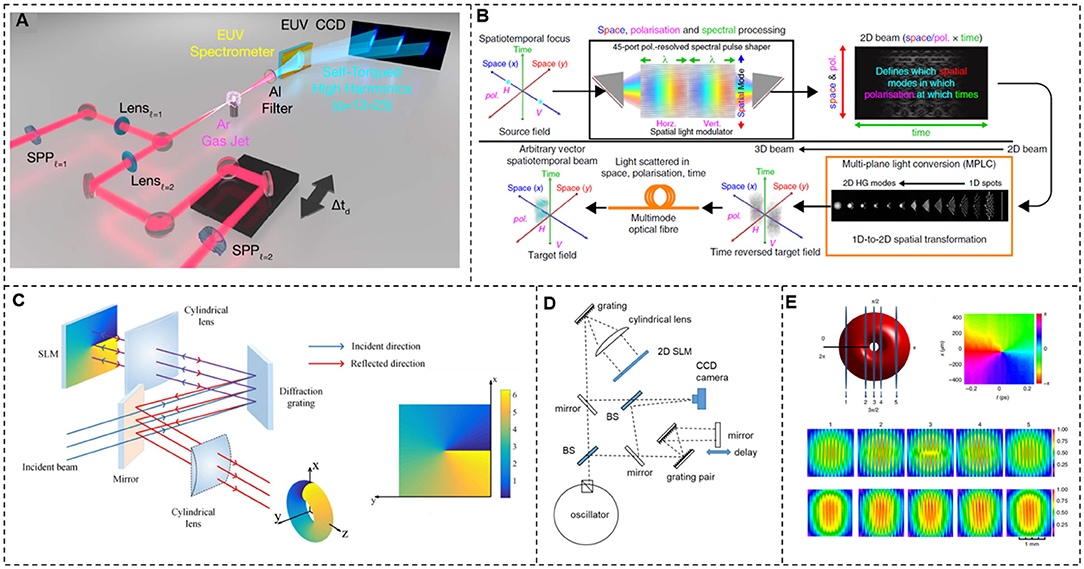
Figure 10. Generation and detection of spatiotemporal light beams. (A) Schematic of generating extreme-ultraviolet beams with time-varying orbital angular momentum. Reprinted from Rego et al. [14]. (B) Schematic of generating vector spatiotemporal light fields with arbitrary amplitude, phase, and polarization at every point in space and time. Reprinted from Mounaix et al. [100]. (C) An experimental setup for the generation of a spatiotemporal optical vortex beam with transverse orbital angular momentum. Reprinted from Chong et al. [13]. (D,E) Detection of spatiotemporal optical vortex beams. Reprinted from Chong et al. [13].

Detection of spatiotemporal light beams requires reconstruction of the spatial structure at different times. It is like slicing a space–time beam along the time axis, reconstructing the structure (amplitude and phase) of each slice to retrieve its entire envelope. Figure 10D displays the experimental setup for the generation and detection of spatiotemporal optical vortex beams. Mode-locked pulses from a fiber oscillator are positively chirped (~3 ps). While a chirped spatiotemporal vortex is formed by the spiral phase on the pulse-shaper two-dimensional SLM, a short reference pulse (~90 fs) is prepared by compressing the pulse with a grating pair. The spatiotemporal vortex and the short reference pulse are off-axis overlapped with a delay, in order to form a spatial fringe intensity profile. Such a fringe intensity profile is captured to retrieve the phase front at a specific time. As the reference pulse advancing from the beginning to the end of the wave packet along the time axis, the whole envelope is reconstructed, as shown in Figure 10E.

Prospect and Discussion

Despite the rapid development of structured light in recent years, it is still full of challenges and opportunities. Here, we briefly discuss the challenges for the generation and detection of structured light beams and outline different application fields of structured light beams.

Shown in Figure 11 are challenges and prospects. For example, implementing a reconfigurable structure light laser with high efficiency for selective generation of HG beams, optical vortex beams, vector beams, and even longitudinal structured light beams is still a great challenge. Similarly, simultaneous detection of diverse structured light beams is also required. Very recently, an optical vortex generator with an almost homogenous structure has been proposed and fabricated [73]. Such a device without a real-space center is alignment free for generating any even-order optical vortex beams. This flexible optical vortex beam generator greatly reduces the difficulty of coupling. It is expected that alignment-free devices for other structured light beams could be of great interest. In addition, ultracompact integrated devices for generating broadband and polarization diversity orbital angular momentum beams have been reported [56]. With future improvement, ultracompact generation and detection of diverse structured light beams are highly desired. In SDM communications and other applications with multiple modes, a laudable goal would be to employ as many spatial modes as possible with low-level insertion loss and crosstalk. The key device is the high-performance scalable spatial mode (de)multiplexer, very similar to the arrayed waveguide grating (AWG), serving as the wavelength (de)multiplexer. Besides, generating new types of spatiotemporal light beams enables researchers to know more unique nature of an optical field and may facilitate more and more emerging applications [34]. It is attractive to produce application-specified spatiotemporal light beams with unique nature. Moreover, the generation and detection of structured light beams with an ultrahigh order is of great significance for studying the limit and finding applications in high-dimensional quantum entanglement of photons. Remarkably, spiral phase mirrors for generating an optical vortex with a topological charge of 10,010 have been fabricated and applied in quantum optics [102]. The future prospects for robust generation and detection of structured light beams would be reconfigurable, alignment free, ultracompact, multiple modes, unique nature, higher order, etc.

FIGURE 11

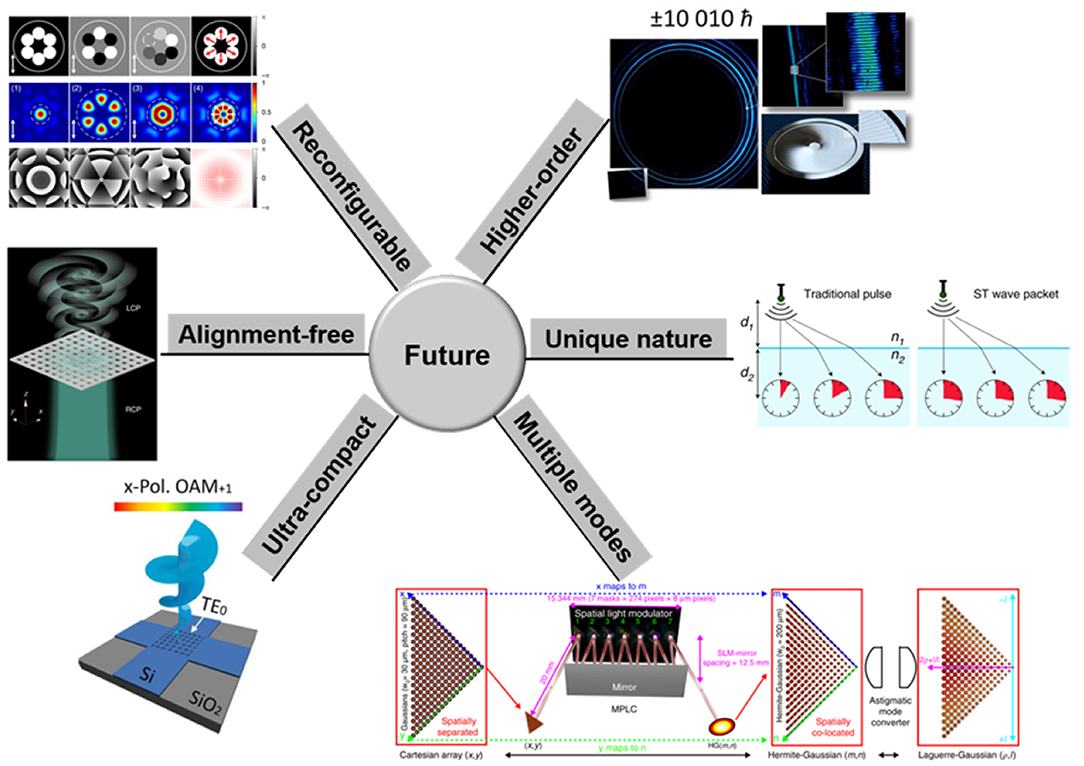
Figure 11. Future challenges and prospects for generation and detection of structured light beams. Reprinted from Bhaduri et al. [34], Lin et al. [52], Zhou et al. [56], Wang et al. [73], Fontaine et al. [78], and Fickler et al. [102].

In this paper, we review the generation and detection of structured light beams (transverse structured light beams, longitudinal structured light beams, and spatiotemporal structured light beams). These structured light beams have already been widely used in diverse applications, as shown in Figure 12. Utilizing multiple transverse structured light beams as independent data channels for multiplexing can greatly expand the transmission capacity and spectral efficiency of optical communications [1, 103–105]. Longitudinal structured light beams with bendable trajectories provide a new way to avoid obstacles in a free-space line-of-sight communication system [3, 106]. Due to the specific spatial structure, spatially structured light beams can be used in optical sensing applications. For example, measuring the rotation of objects and particles is achievable by employing the rotational Doppler effect [4, 5]. In addition, high-order structured light beams may also find potential applications in high-dimensional quantum entanglement [8]. Structured light beams with distinct phase structures and intensity profiles are also used in imaging applications, e.g., super-resolution imaging by structured light beams with singularities [9, 10, 107] and fiber endoscopes [83, 108–110]. Moreover, micromanipulation based on optical vortex beams carrying orbital angular momentum enables the twisting of trapped particles [6, 111].

FIGURE 12

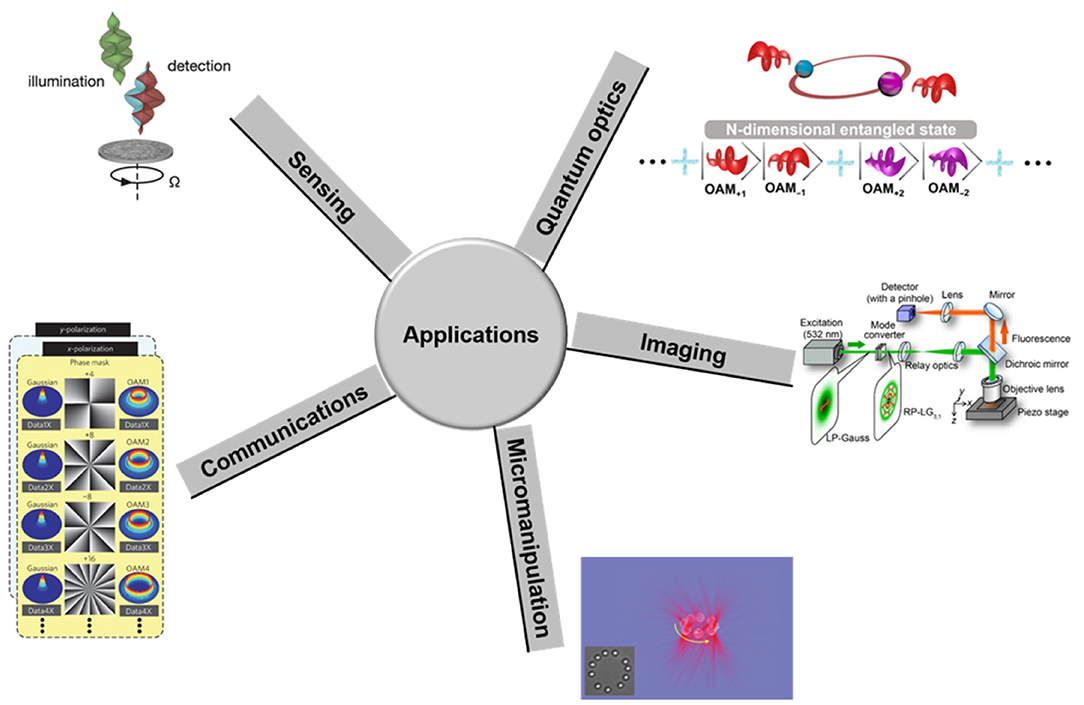
Figure 12. Diverse applications of structured light beams. Reprinted from Wang et al. [1], Lavery et al. [4], Padgett and Bowman [6], Liu et al. [8], and Kozawa et al. [9].

Structured light is a young and cutting-edge field. It accesses the new degrees of freedom and tailors the spatial-transverse/spatial-longitudinal/spatiotemporal structure of photons, leading to attractive properties and interesting applications. With future improvement, more robust generation, detection, and manipulation methods and devices of structured light are highly desired. Meanwhile, more advanced applications of structured light are also highly expected.

Author Contributions

JW supervised the project. All authors contributed to writing the paper and finalized the paper.

Funding

This work was supported by the National Key R&D Program of China (2018YFB1801803), the Key R&D Program of Guangdong Province (2018B030325002), the National Natural Science Foundation of China (NSFC) (11774116), the Key R&D Program of Hubei Province of China (2020BAB001), the Science and Technology Innovation Commission of Shenzhen (JCYJ20200109114018750), the Open Fund of IPOC (BUPT) (IPOC2018A002), the Open Program from State Key Laboratory of Advanced Optical Communication Systems and Networks (2020GZKF009), and the Fundamental Research Funds for the Central Universities (2019kfyRCPY037).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Wang J, Yang JY, Fazal IM, Ahmed N, Yan Y, Huang H, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat Photon. (2012) 6:488–96. doi: 10.1038/nphoton.2012.138

CrossRef Full Text | Google Scholar

2. Liu J, Li SM, Zhu L, Wang AD, Chen S, Klitis C, et al. Direct fiber vector eigenmode multiplexing transmission seeded by integrated optical vortex emitters. Light Sci Appl. (2018) 7:17148. doi: 10.1038/lsa.2017.148

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zhu L, Wang AD, Wang J. Free-space data-carrying bendable light communications. Sci Rep. (2019) 9:14969. doi: 10.1038/s41598-019-51496-z

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lavery MP, Speirits FC, Barnett SM, Padgett MJ. Detection of a spinning object using light's orbital angular momentum. Science. (2013) 341:537–40. doi: 10.1126/science.1239936

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Fang L, Padgett MJ, Wang J. Sharing a common origin between the rotational and linear Doppler effects. Laser Photon Rev. (2017) 11:1700183. doi: 10.1002/lpor.201700183

CrossRef Full Text | Google Scholar

6. Padgett MJ, Bowman R. Tweezers with a twist. Nat Photon. (2011) 5:343–8. doi: 10.1038/nphoton.2011.81

CrossRef Full Text | Google Scholar

7. Zhang Y, Agnew M, Roger T, Roux FS, Konrad T, Faccio D, et al. Simultaneous entanglement swapping of multiple orbital angular momentum states of light. Nat Commun. (2017) 8:632. doi: 10.1038/s41467-017-00706-1

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Liu J, Nape I, Wang QK, Valles A, Wang J, Forbes A. Multidimensional entanglement transport through single-mode fiber. Sci Adv. (2020) 6:eaay0837. doi: 10.1126/sciadv.aay0837

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Kozawa Y, Matsunaga D, Sato S. Superresolution imaging via superoscillation focusing of a radially polarized beam. Optica. (2018) 5:86–92. doi: 10.1364/OPTICA.5.000086

CrossRef Full Text | Google Scholar

10. Yoshida M, Kozawa Y, Sato S. Subtraction imaging by the combination of higher-order vector beams for enhanced spatial resolution. Opt Lett. (2019) 44:883–6. doi: 10.1364/OL.44.000883

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Froehly L, Courvoisier F, Mathis A, Jacquot M, Furfaro L, Giust R, et al. Arbitrary accelerating micron-scale caustic beams in two and three dimensions. Opt Express. (2011) 19:16455–65. doi: 10.1364/OE.19.016455

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Greenfield E, Segev M, Walasik W, Raz O. Accelerating light beams along arbitrary convex trajectories. Phys Rev Lett. (2011) 106:213902. doi: 10.1103/PhysRevLett.106.213902

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chong A, Wan C, Chen J, Zhan QW. Generation of spatiotemporal optical vortices with controllable transverse orbital angular momentum. Nat Photon. (2020) 14:350–4. doi: 10.1038/s41566-020-0587-z

CrossRef Full Text | Google Scholar

14. Rego L, Dorney KM, Brooks NJ, Nguyen QL, Liao CT, Román JS, et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science. (2019) 364:eaaw9486. doi: 10.1126/science.aaw9486

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhao Z, Song H, Zhang RZ, Pang K, Liu C, Song HQ, et al. Dynamic spatiotemporal beams that combine two independent and controllable orbital-angular-momenta using multiple optical-frequency-comb lines. Nat Commun. (2020) 11:1–10. doi: 10.1038/s41467-020-17805-1

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Restuccia S, Giovannini D, Gibson G, Padgett MJ. Comparing the information capacity of Laguerre–Gaussian and Hermite–Gaussian modal sets in a finite-aperture system. Opt Express. (2016) 24:27127–36. doi: 10.1364/OE.24.027127

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Du J, Wang J. High-dimensional structured light coding/decoding for free-space optical communications free of obstructions. Opt Lett. (2015) 40:4827–30. doi: 10.1364/OL.40.004827

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhu L, Wang J. Demonstration of obstruction-free data-carrying N-fold Bessel modes multicasting from a single Gaussian mode. Opt Lett. (2015) 40:5463–6. doi: 10.1364/OL.40.005463

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A. (1992) 45:8185. doi: 10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Yao AM, Padgett MJ. Orbital angular momentum: origins, behavior and applications. Adv Opt Photon. (2011) 3:161–204. doi: 10.1364/AOP.3.000161

CrossRef Full Text | Google Scholar

21. Shen Y, Wang X, Xie Z, Min CJ, Fu X, Liu Q, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci Appl. (2019) 8:1–29. doi: 10.1038/s41377-019-0194-2

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhan QW. Cylindrical vector beams: from mathematical concepts to applications. Adv Opt Photon. (2009) 1:1–57. doi: 10.1364/AOP.1.000001

CrossRef Full Text | Google Scholar

23. Milione G, Lavery MPJ, Huang H, Ren YX, Xie GD, Nguyen TA, et al. 4× 20 Gbit/s mode division multiplexing over free space using vector modes and a q-plate mode (de) multiplexer. Opt Lett. (2015) 40:1980–3. doi: 10.1364/OL.40.001980

CrossRef Full Text | Google Scholar

24. Siviloglou GA, Broky J, Dogariu A, Christodoulides DN. Observation of accelerating Airy beams. Phys Rev Lett. (2007) 99:213901. doi: 10.1103/PhysRevLett.99.213901

CrossRef Full Text | Google Scholar

25. Wen YH, Chen YJ, Zhang YF, Chen H, Yu SY. Winding light beams along elliptical helical trajectories. Phys Rev A. (2016) 94:013829. doi: 10.1103/PhysRevA.94.013829

CrossRef Full Text | Google Scholar

26. Dorrah AH, Zamboni-Rached M, Mojahedi M. Frozen waves following arbitrary spiral and snake-like trajectories in air. Appl Phys Lett. (2017) 110:051104. doi: 10.1063/1.4975593

CrossRef Full Text | Google Scholar

27. Zannotti A, Denz C, Alonso MA, Dennis MR. Shaping caustics into propagation-invariant light. Nat Commun. (2020) 11:1–7. doi: 10.1038/s41467-020-17439-3

CrossRef Full Text | Google Scholar

28. Kondakci HE, Abouraddy AF. Diffraction-free space–time light sheets. Nat Photon. (2017) 11:733–40. doi: 10.1038/s41566-017-0028-9

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Jhajj N, Larkin I, Rosenthal EW, Zahedpour S, Wahlstrand JK, Milchberg HM. Spatiotemporal optical vortices. Phys Rev X. (2016) 6:031037. doi: 10.1103/PhysRevX.6.031037

CrossRef Full Text | Google Scholar

30. Hancock SW, Zahedpour S, Goffin A, Milchberg HM. Free-space propagation of spatiotemporal optical vortices. Optica. (2019) 6:1547–53. doi: 10.1364/OPTICA.6.001547

CrossRef Full Text | Google Scholar

31. Dallaire M, McCarthy N, Piché M. Spatiotemporal bessel beams: theory and experiments. Opt Express. (2009) 17:18148–64. doi: 10.1364/OE.17.018148

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Faccio D, Averchi A, Couairon A, Kolesik M, Moloney JV, Dubietis A. Spatio-temporal reshaping and X Wave dynamics in optical filaments. Opt Express. (2007) 15:13077–95. doi: 10.1364/OE.15.013077

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Kondakci HE, Abouraddy AF. Optical space-time wave packets having arbitrary group velocities in free space. Nat Commun. (2019) 10:1–8. doi: 10.1038/s41467-019-08735-8

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Bhaduri B, Yessenov M, Abouraddy AF. Anomalous refraction of optical spacetime wave packets. Nat Photon. (2020) 14:416–421. doi: 10.1038/s41566-020-0645-6

CrossRef Full Text | Google Scholar

35. Yessenov M, Bhaduri B, Delfyett PJ, Abouraddy AF. Free-space optical delay line using space-time wave packets. Nat Commun. (2020) 11:1–10. doi: 10.1038/s41467-020-19526-x

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Mitchell KJ, Turtaev S, Padgett MJ, Cižmár T, Phillips DB. High-speed spatial control of the intensity, phase and polarisation of vector beams using a digital micro-mirror device. Opt Express. (2016) 24:29269–82. doi: 10.1364/OE.24.029269

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Li SH, Wang J. Simultaneous demultiplexing and steering of multiple orbital angular momentum modes. Sci Rep. (2015) 5:1–8. doi: 10.1038/srep15406

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Qiao Z, Xie GQ, Wu YH, Yuan P, Ma JG, Qian LJ, et al. Generating high-charge optical vortices directly from laser up to 288th order. Laser Photon Rev. (2018) 12:1800019. doi: 10.1002/lpor.201800019

CrossRef Full Text | Google Scholar

39. Naidoo D, Roux FS, Dudley A, Litvin I, Piccirillo B, Marrucci L, et al. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat Photon. (2016) 10:327–32. doi: 10.1038/nphoton.2016.37

CrossRef Full Text | Google Scholar

40. Forbes A, Dudley A, McLaren M. Creation and detection of optical modes with spatial light modulators. Adv Opt Photon. (2016) 8:200–27. doi: 10.1364/AOP.8.000200

CrossRef Full Text | Google Scholar

41. Zhu L, Wang J. Simultaneous generation of multiple orbital angular momentum (OAM) modes using a single phase-only element. Opt Express. (2015) 23:26221–33. doi: 10.1364/OE.23.026221

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Zhu L, Wang J. Arbitrary manipulation of spatial amplitude and phase using phase-only spatial light modulators. Sci Rep. (2014) 4:1–7. doi: 10.1038/srep07441

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Zhao YF, Wang J. High-base vector beam encoding/decoding for visible-light communications. Opt Lett. (2015) 40:4843–6. doi: 10.1364/OL.40.004843

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Qiao Z, Wan ZY, Xie GQ, Wang J, Qian LJ, Fan DY. Multi-vortex laser enabling spatial and temporal encoding. PhotoniX. (2020) 1:1–4. doi: 10.1186/s43074-020-00013-x

CrossRef Full Text | Google Scholar

45. Bozinovic N, Yue Y, Ren YX, Tur M, Kristensen P, Huang H, et al. Terabit-scale orbital angularmomentum mode division multiplexing in fibers. Science. (2013) 340:1545–8. doi: 10.1126/science.1237861

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Wang HY, Liang YZ, Zhang X, Chen S, Shen L, Zhang L, et al. Low-loss orbital angular momentum ring-core fiber: design, fabrication and characterization. J Lightwave Technol. (2020) 38:6327–33. doi: 10.1109/JLT.2020.3012285

CrossRef Full Text | Google Scholar

47. Nicholson JW, Yablon AD, Ramachandran S, Ghalmi S. Spatially and spectrally resolved imaging of modal content in large-mode-area fibers. Opt Express. (2008) 16:7233–43. doi: 10.1364/OE.16.007233

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Fang L, Wang J. Flexible generation/conversion/exchange of fiber-guided orbital angular momentum modes using helical gratings. Opt Lett. (2015) 40:4010–3. doi: 10.1364/OL.40.004010

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Han Y, Liu YG, Wang Z, Huang W, Chen L, Zhang HW, et al. Controllable all-fiber generation/conversion of circularly polarized orbital angular momentum beams using long period fiber gratings. Nanophotonics. (2018) 7:287–93. doi: 10.1515/nanoph-2017-0047

CrossRef Full Text | Google Scholar

50. Li SH, Xu Z, Zhao RX, Shen L, Du C, Wang J. Generation of orbital angular momentum beam using fiber-to-fiber butt coupling. IEEE Photon J. (2018) 10:1–7. doi: 10.1109/JPHOT.2018.2856263

CrossRef Full Text | Google Scholar

51. Wang T, Wang F, Shi F, Pang FF, Huang SJ, Wang TY, et al. Generation of femtosecond optical vortex beams in all-fiber mode-locked fiber laser using mode selective coupler. J Lightwave Technol. (2017) 35:2161–6. doi: 10.1109/JLT.2017.2676241

CrossRef Full Text | Google Scholar

52. Lin D, Carpenter J, Feng Y, Jain S, Jung Y, Feng Y, et al. Reconfigurable structured light generation in a multicore fibre amplifier. Nat Commun. (2020) 11:1–9. doi: 10.1038/s41467-020-17809-x

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Li S, Mo Q, Hu X, Du C, Wang J. Controllable all-fiber orbital angular momentum mode converter. Opt Lett. (2015) 40:4376–9. doi: 10.1364/OL.40.004376

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Yan Y, Wang J, Zhang L, Yang JY, Fazal IM, Ahmed N, et al. Fiber coupler for generating orbital angular momentum modes. Optics Lett. (2011) 36:4269–71. doi: 10.1364/OL.36.004269

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Cai XL, Wang JW, Strain MJ, Morris BJ, Zhu JB, Sorel M, et al. Integrated compact optical vortex beam emitters. Science. (2012) 338:363–6. doi: 10.1126/science.1226528

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Zhou N, Zheng S, Cao XP, Zhao YF, Gao SQ, Zhu YT, et al. Ultra-compact broadband polarization diversity orbital angular momentum generator with 3.6× 3.6 μm² footprint. Sci Adv. (2019) 5:eaau9593. doi: 10.1126/sciadv.aau9593

CrossRef Full Text | Google Scholar

57. Zhu Y, Tan H, Zhou N, Chen LF, Wang J, Cai XL. Compact high-efficiency four-mode vortex beam generator within the telecom C-band. Opt Lett. (2020) 45:1607–10. doi: 10.1364/OL.385878

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Xie Z, Lei T, Li F, Qiu H, Zhang Z, Wang H, et al. Ultra-broadband on-chip twisted light emitter for optical communications. Light Sci Appl. (2018) 7:18001. doi: 10.1038/lsa.2018.1

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Zhou N, Zheng S, Cao XP, Gao SQ, Li SM, He MB, et al. Generating and synthesizing ultrabroadband twisted light using a compact silicon chip. Opt Lett. (2018) 43:3140–3. doi: 10.1364/OL.43.003140

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Zheng S, Wang J. On-chip orbital angular momentum modes generator and (de) multiplexer based on trench silicon waveguides. Opt Express. (2017) 25:18492–501. doi: 10.1364/OE.25.018492

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Guan B, Scott RP, Qin C, Fontaine NK, Su T, Ferrari C, et al. Free-space coherent optical communication with orbital angular, momentum multiplexing/demultiplexing using a hybrid 3D photonic integrated circuit. Opt Express. (2014) 22:145–56. doi: 10.1364/OE.22.000145

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Beresna M, Gecevičius M, Kazansky PG, Gertus T. Radially polarized optical vortex converter created by femtosecond laser nanostructuring of glass. Appl Phys Lett. (2011) 98:201101. doi: 10.1063/1.3590716

CrossRef Full Text | Google Scholar

63. He Y, Wang P, Wang C, Liu J, Ye H, Zhou X, et al. All-optical signal processing in structured light multiplexing with dielectric meta-optics. ACS Photon. (2020) 7:135–46. doi: 10.1021/acsphotonics.9b01292

CrossRef Full Text | Google Scholar

64. Zhao YF, Du J, Zhang JR, Shen L, Wang J. Generating structured light with phase helix and intensity helix using reflection-enhanced plasmonic metasurface at 2 μ m. Appl Phys Lett. (2018) 112:171103. doi: 10.1063/1.5024433

CrossRef Full Text | Google Scholar

65. Zhao YF, Zhang JR, Du J, Wang J. Meta-facet fiber for twisting ultra-broadband light with high phase purity. Appl Phy Lett. (2018) 113:061103. doi: 10.1063/1.5043268

CrossRef Full Text | Google Scholar

66. Zhao Z, Wang J, Li SH, Willner AE. Metamaterials-based broadband generation of orbital angular momentum carrying vector beams. Opt Lett. (2013) 38:932–4. doi: 10.1364/OL.38.000932

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Wei B, Hu W, Ming Y, Xu F, Rubin S, Wang JG, et al. Generating switchable and reconfigurable optical vortices via photopatterning of liquid crystals. Adv Mater. (2014) 26:1590–5. doi: 10.1002/adma.201305198

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Li H, Phillips DB, Wang X, Daniel YL, Chen LF, Zhou XQ, et al. Orbital angular momentum vertical-cavity surface-emitting lasers. Optica. (2015) 2:547–52. doi: 10.1364/OPTICA.2.000547

CrossRef Full Text | Google Scholar

69. Miao P, Zhang Z, Sun J, Walasik W, Longhi S, Litchinitser NM, et al. Orbital angular momentum microlaser. Science. (2016) 353:464–7. doi: 10.1126/science.aaf8533

CrossRef Full Text | Google Scholar

70. Ma X, Zheng S, Chen Q, Tan S, Zhang PF, Lu QY, et al. High-speed directly modulated cylindrical vector beam lasers. ACS Photon. (2019) 6:3261–70. doi: 10.1021/acsphotonics.9b01244

CrossRef Full Text | Google Scholar

71. Zheng S, Ma X, Chen QA, Lu QY, Guo WH, Wang J. Concentric microcavities for cylindrical vector beam lasers. Opt Lett. (2020) 45:2211–4. doi: 10.1364/OL.388974

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Huang C, Zhang C, Xiao SM, Wang YH, Fan YB, et al. Ultrafast control of vortex microlasers. Science. (2020) 367:1018–21. doi: 10.1126/science.aba4597

CrossRef Full Text | Google Scholar

73. Wang B, Liu W, Zhao M, Wang J, Zhang Y, Chen A, et al. Generating optical vortex beams by momentum-space polarization vortices centred at bound states in the continuum. Nat Photon. (2020) 14:623–8. doi: 10.1038/s41566-020-0658-1

CrossRef Full Text | Google Scholar

74. Leach J, Padgett MJ, Barnett SM, Arnold S, Courtial J. Measuring the orbital angular momentum of a single photon. Phys Rev Lett. (2002) 88:257901. doi: 10.1103/PhysRevLett.88.257901

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Lei T, Zhang M, Li Y, Jia P, Liu G, Xu X, et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci Appl. (2015) 4:e257. doi: 10.1038/lsa.2015.30

CrossRef Full Text | Google Scholar

76. Dai K, Gao C, Zhong L, Na Q, Wang Q. Measuring OAM states of light beams with gradually-changing-period gratings. Opt Lett. (2015) 40:562–5. doi: 10.1364/OL.40.000562

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Zheng S, Wang J. Measuring orbital angular momentum (OAM) states of vortex beams with annular gratings. Sci Rep. (2017) 7:1–9. doi: 10.1038/srep40781

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Fontaine N K, Ryf R, Chen H, Neilson DT, Kim K, Carpenter J. Laguerre-Gaussian mode sorter. Nat Commun. (2019) 10:1–7. doi: 10.1038/s41467-019-09840-4

CrossRef Full Text | Google Scholar

79. Zhou HL, Fu DZ, Dong JJ, Zhang P, Chen DX, Cai XL, et al. Orbital angular momentum complex spectrum analyzer for vortex light based on the rotational Doppler effect. Light Sci Appl. (2017) 6:e16251. doi: 10.1038/lsa.2016.251

PubMed Abstract | CrossRef Full Text | Google Scholar

80. D'Errico A, D'Amelio R, Piccirillo B, Cardano F, Marrucci L. Measuring the complex orbital angular momentum spectrum and spatial mode decomposition of structured light beams. Optica. (2017) 4:1350–7. doi: 10.1364/OPTICA.4.001350

CrossRef Full Text | Google Scholar

81. Wang Z, Dedo MI, Guo K, Zhou K, Shen F, Sun Y, et al. Efficient recognition of the propagated orbital angular momentum modes in turbulences with the convolutional neural network. IEEE Photon J. (2019) 11:1–4. doi: 10.1109/JPHOT.2019.2916207

CrossRef Full Text | Google Scholar

82. Wang L, Ruan Z, Wang H, Shen L, Zhang L, Luo J, et al. Deep learning based recognition of different mode bases in ring-core fiber. Laser Photon Rev. (2020) 14:2000249. doi: 10.1002/lpor.202000249

CrossRef Full Text | Google Scholar

83. Plöschner M, Tyc T, Cižmár T. Seeing through chaos in multimode fibres. Nat Photon. (2015) 9:529–35. doi: 10.1038/nphoton.2015.112

CrossRef Full Text | Google Scholar

84. Carpenter J, Eggleton B, Schröder J. 110x110 optical mode transfer matrix inversion. Opt Express. (2014) 22:96–101. doi: 10.1364/OE.22.000096

PubMed Abstract | CrossRef Full Text | Google Scholar

85. An Y, Huang Y, Li J, Leng J, Yang L, Zhou P. Learning to decompose the modes in few-mode fibers with deep convolutional neural network. Opt Express. (2019) 27:10127–37. doi: 10.1364/OE.27.010127

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Zhu G, Chen Y, Liu Y, Zhang Y, Yu S. Characterizing a 14× 14 OAM mode transfer matrix of a ring-core fiber based on quadrature phase-shift interference. Opt Lett. (2017) 42:1257–60. doi: 10.1364/OL.42.001257

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Mazur M, Fontaine NK, Ryf R, Chen H, Neilson DT, Bigot-Astruc M, et al. Characterization of long multi-mode fiber links using digital holography. In: 2019 Optical Fiber Communication Conference (OFC); 3-7 March 2019. San Diego, CA. Optical Society of America (2019). Available online at: https://www.osapublishing.org/abstract.cfm?uri=OFC-2019-W4C.5

Google Scholar

88. Alvarado-Zacarias JC, Fontaine NK, Ryf R, Chen H, Heide S, Enrique J, et al. Assembly and characterization of a multimode EDFA using digital holography. In: Optical Fiber Communication Conference (OFC); 8-12 March 2020. San Diego, CA. Optical Society of America (2020). Available online at: https://www.osapublishing.org/abstract.cfm?uri=ofc-2020-Th1H.6

Google Scholar

89. Shaked NT, Micó V, Trusiak M, Kuś A, Mirsky SK. Off-axis digital holographic multiplexing for rapid wavefront acquisition and processing. Adv Opt Photon. (2020) 12:556–611. doi: 10.1364/AOP.384612

CrossRef Full Text | Google Scholar

90. Berkhout GCG, Lavery MPJ, Courtial J, Beijersbergen MW, Padgett MJ. Efficient sorting of orbital angular momentum states of light. Phys Rev Lett. (2010) 105:153601. doi: 10.1103/PhysRevLett.105.153601

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Lavery MPJ, Robertson DJ, Sponselli A, Courtial J, Steinhoff NK, Tyler GA, et al. Efficient measurement of an optical orbital-angular-momentum spectrum comprising more than 50 states. New J Phys. (2013) 15:013024. doi: 10.1088/1367-2630/15/1/013024

CrossRef Full Text | Google Scholar

92. Ruffato G, Girardi M, Massari M, Mafakheri E, Sephton B, Capaldo P, et al. A compact diffractive sorter for high-resolution demultiplexing of orbital angular momentum beams. Sci Rep. (2018) 8:1–2. doi: 10.1038/s41598-018-28447-1

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Wen Y, Chremmos I, Chen Y, Zhu J, Zhang Y, Yu S. Spiral transformation for high-resolution and efficient sorting of optical vortex modes. Phys Rev Lett. (2018) 120:193904. doi: 10.1103/PhysRevLett.120.193904

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Wen Y, Chremmos I, Chen Y, Zhu G, Zhang J, Zhu J, et al. Compact and high-performance vortex mode sorter for multi-dimensional multiplexed fiber communication systems. Optica. (2020) 7:254–62. doi: 10.1364/OPTICA.385590

CrossRef Full Text | Google Scholar

95. Hossack WJ, Darling AM, Dahdouh A. Coordinate transformations with multiple computer-generated optical elements. J Mod Opt. (1987) 34:1235–50. doi: 10.1080/09500348714551121

CrossRef Full Text | Google Scholar

96. Fang J, Xie Z, Lei T, Min C, Du L, Li Z, et al. Spin-dependent optical geometric transformation for cylindrical vector beam multiplexing communication. ACS Photon. (2018) 5:3478–84. doi: 10.1021/acsphotonics.8b00680

CrossRef Full Text | Google Scholar

97. Lei T, Fang J, Xie Z, Yuan X. High-resolution cylindrical vector beams sorting based on spin-dependent fan-out optical geometric transformation. Opt Express. (2019) 27:20901–9. doi: 10.1364/OE.27.020901

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Ji Z, Liu W, Krylyuk S, Fan X, Zhang Z, Pan A, et al. Photocurrent detection of the orbital angular momentum of light. Science. (2020) 368:763–7. doi: 10.1126/science.aba9192

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Zhang S, Huo P, Zhu W, Zhang C, Chen P, Liu M, et al. Broadband detection of multiple spin and orbital angular momenta via dielectric metasurface. Laser Photon Rev. (2020) 14:2000062. doi: 10.1002/lpor.202000062

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Mounaix M, Fontaine NK, Neilson DT, Ryf R, Chen H, Alvarado-Zacarias JC, et al. Time reversed optical waves by arbitrary vector spatiotemporal field generation. Nat Commun. (2020) 11:1–7. doi: 10.1038/s41467-020-19601-3

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Weiner AM. Femtosecond pulse shaping using spatial light modulators. Rev Sci Instrum. (2000) 71:1929–60. doi: 10.1063/1.1150614

CrossRef Full Text | Google Scholar

102. Fickler R, Campbell G, Buchler B, Lam PY, Zeilinger A. Quantum entanglement of angular momentum states with quantum numbers up to 10,010. Proc Natl Acad Sci USA. (2016) 113:13642–7. doi: 10.1073/pnas.1616889113

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Wang J. Advances in communications using optical vortices. Photon Res. (2016) 4:B14–28. doi: 10.1364/PRJ.4.000B14

CrossRef Full Text | Google Scholar

104. Wang J. Data information transfer using complex optical fields: a review and perspective. Chin Opt Lett. (2017) 15:030005. doi: 10.3788/COL201715.030005

CrossRef Full Text | Google Scholar

105. Wang J. Twisted optical communications using orbital angular momentum. Sci China Phys Mech Astron. (2019) 62:1–21. doi: 10.1007/s11433-018-9260-8

CrossRef Full Text | Google Scholar

106. Zhu G, Wen Y, Wu X, Chen Y, Liu J, Yu S. Obstacle evasion in free-space optical communications utilizing Airy beams. Opt Lett. (2018) 43:1203–6. doi: 10.1364/OL.43.001203

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Youngworth KS, Brown TG. Focusing of high numerical aperture cylindrical-vector beams. Opt Express. (2000) 7:77–87. doi: 10.1364/OE.7.000077

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Gataric M, Gordon GSD, Renna F, Ramos AG, Alcolea MP, Bohndiek SE. Reconstruction of optical vector-fields with applications in endoscopic imaging. IEEE TransMed Imaging. (2018) 38:955–67. doi: 10.1109/TMI.2018.2875875

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Carpenter J, Eggleton BJ, Schröder J. Maximally efficient imaging through multimode fiber. In: 2014 Conference on Lasers Electro-Optics (CLEO): Science Innovations; 8-13 June 2014. San Jose CA. Optical Society of America (2014). Available online at: https://www.osapublishing.org/abstract.cfm?uri=CLEO_SI-2014-STh1H.3

Google Scholar

110. Choudhury D, McNicholl DK, Repetti A, Gris-Sánchez I, Li S, Philips DB, et al. Computational optical imaging with a photonic lantern. Nat Commun. (2020) 11:1–9. doi: 10.1038/s41467-020-18818-6

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Gao D, Ding W, Nieto-Vesperinas M, Ding X, Rahman M, Zhang T, et al. Optical manipulation from the microscale to the nanoscale: fundamentals, advances and prospects. Light Sci Appl. (2017) 6:e17039. doi: 10.1038/lsa.2017.39

PubMed Abstract | CrossRef Full Text | Google Scholar