Photon-Assisted Seebeck Effect in a Quantum Dot Coupled to Majorana Zero Modes

The Seebeck effect is investigated within the framework of a non-equilibrium Green's function technique in a quantum dot (QD) sandwiched between the left and right leads held at different temperatures. We consider that the QD is shelled by a photon field and is side-coupled to a topological superconductor nanowire hosting Majorana zero modes (MZMs). It is found that the thermopower (Seebeck coefficient) can be obviously enhanced by weak QD-MZMs coupling at low temperatures, in addition to its sign reversion that may be used for detecting the existence of MZMs. In the presence of a photon field, the thermopower can be further enhanced due to decreased electrical conductance when electrons' transport probability through each channel is reduced by photon-assisted tunneling (PAT). The hybridization between the MZMs will also induce sign reversion of the thermopower in the absence of a photon field, whereas it has less impact on the thermopower when the QD is shelled by the photon field.

Introduction

Majorana zero modes (MZMs) [1, 2] are zero-energy excitations that have been extensively studied in the condensed matter physics community for much of the last decade. They are massless and of their own antiparticles, which are analogous to the electron-hole pair in superconductors. A pair of spatially separated MZMs obeys non-Abelian statistics and is robust against local sources of decoherence. This enables them to be used as quantum bits for fault-tolerant topological quantum computation [2–4]. The MZMs also play important roles in some other research subjects, such as spintronics [5] and thermoelectricity [6, 7].

Due to the similarities between MZMs and electron-hole pairs, researchers have been naturally trying to prepare MZMs in superconductors. Indeed, Kitaev has theoretically demonstrated that MZMs can be formed at the two ends of a p-wave superconductor chain [8]. However, it can hardly be realized in experiments as the p-wave superconductors are rare in nature. In 2008, Fu and Kane proved the theory that it is possible to induce MZMs in vortices by the means of the proximity effect between an s-wave superconductor and the surface states of a strong topological insulator. It was subsequently demonstrated in experiments and has led to numerous studies [9, 10]. Along with this kind of scheme, a variety of other platforms have been proposed as hosts of MZMs and intensively studied, including heavy metal surfaces [11], semiconductor nanowires [12, 13], magnetic atom chains [14], planar Josephson junctions in 2D electron gas [15] and iron superconductors [16, 17]. Owing to the unique properties of MZMs as mentioned above, the detection of it is very challenging. In early years, one of the signatures most likely to be induced by MZMs is the zero-bias anomaly (ZBA) of conductance in semiconductor superconductor nanowires [18–20]. However, ZBA cannot be solely attributed to the existence of MZMs in that an ordinary localized state can also give rise to this phenomenon, such as the Kondo effect [21]. In 2011, Liu and Baranger proposed to detect the MZMs by measuring the electrical conductance through a quantum dot (QD) attached to the edge of a topological nanowire [22]. In such a scheme, the MZMs at one end of the nanowire leak into the QD [22, 23] and reduce the zero-bias conductance through the dot to be half of its quantum value, i.e., G(0) = e²/2h. Recently, hybridized topological nanowire-QD junctions have been successfully realized in experiments [24, 25], providing an excellent platform for the preparation, manipulation, and detection of MZMs. The introduction of QD offers a non-invasive measurement technique for the MZMs as there is no direct charge transfer between them and the QD. In addition, the origin of the ZBA in the conductance can also be excluded from the Kondo effect, even if the experiment is performed at temperatures below the Kondo temperature [26, 27]. Along with the preparation and detection of MZMs in tunneling experiments, thermoelectric effect in QD mediated by MZMs has also been studied in recent years. The previous research subject of thermoelectric effect concerned energy conversion between electrical and thermal energies, which has reacquired recognitions because of the significantly enhanced thermoelectric efficiency and thermopower [28]. In thermoelectricity, the most common studied issue is the Seebeck effect, which refers to the generation of an electrical voltage ΔV in response to a temperature difference ΔT applied across the two ends of the system. The thermopower (Seebeck coefficient) is then defined as S = −ΔV/ΔT which is directly measured in experiments. It has been proved that thermopower in hybridized QD-superconductor nanowire hosting MZMs satisfies the Mott formula, and can be used for inferring the temperature of the Majorana edge state by measuring the differential conductance [29]. The enhancement and sign change of the thermopower in such a system have also been reported [30–34]. The optical techniques are widely used in manipulating particles' transportation in nanostructures, and were also proved to be promising in the study of MZMs [35, 36]. In [37], Chen and Zhu found that in the presence of the QD-MZMs interaction, if a strong pump laser is applied at the QD, the single peak in the probe absorption spectrum will be split into two. In [38, 39], as the photon-assisted tunneling (PAT) occurs, the PAT peaks are developed and the original zero-bias peak is suppressed to zero due to the MZMs, which turn to non-zero mode by emitting (absorbing) photons. Based on the features of MZMs in the PAT process, it is worthy to investigate the affection of MZMs on the thermoelectricity by the optical techniques.

In the present paper, we study the Seebeck effect in a hybridized QD-topological superconductor nanowire with a photon field shelled on the QD (see Figure 1). The dot is connected to the left and right leads at different temperatures. We calculate the electrical conductance and thermopower through the dot interacting with one mode of the MZMs prepared at the ends of the topological superconductor nanowire. Our numerical results show that the magnitude of the thermopower can be obviously enhanced by the combined effect of the MZMs and PAT. When the two modes of the MZMs are strongly overlapped with each other, the thermopower is less influenced by the MZMs in the presence of the photon field because the photon energy absorbed by one mode of the MZMs is subsequently emitted by the other one. We also find a sign change of the thermopower induced by changing either dot-MZMs coupling or temperature.

FIGURE 1

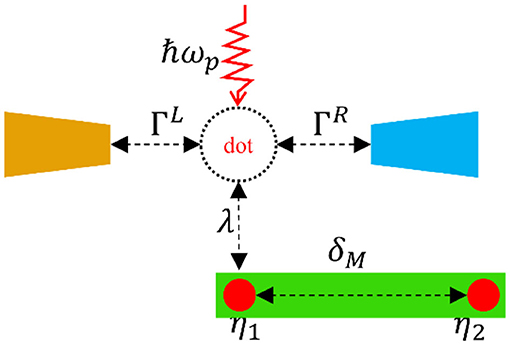
Figure 1. Schematic plot of the scheme composing a quantum dot connected to the left and right leads at different temperatures of T_L and T_R, respectively. The dot is shelled by a microwave field with frequency ω_p and intensity Δ_d, and is side-coupled to a topological superconductor nanowire hosting a pair of MZMs (red circles). Here we consider that only one mode of the MZMs denoted by the operator of is coupled to the dot with strength λ. The hybridization amplitude between the MZMs is δ_M.

Model and Methods

The Hamiltonian of the system illustrated in Figure 1 is written as the following [22, 40]

$\begin{array}{l}H={\displaystyle \sum _{k\alpha }}{\epsilon }_{k\alpha }{c}_{k\alpha }^{+}{c}_{k\alpha }+{\epsilon }_d(t)d^{+}d+{\displaystyle \sum _{k,\alpha }}(V_{\alpha }{c}_{k\alpha }^{+}d+H.c)\\ +i{\delta }_M{\eta }_1{\eta }_2+(\lambda d-\lambda d^{+}){\eta }_1,& (1)\end{array}$

in which the first term describes the left and right (α = L, R) leads at temperatures of T_L and T_R, respectively. The annihilation (creation) operator $c_{k\alpha }(c_{k\alpha }^{+})$ is for the electrons on the leads with wave-vector k and energy ε_kα. The second term is for the electrons on the QD with annihilation (creation) operator d(d⁺), time-varying dot level ε_d(t) = ε_d + Δ_d cos(ωt) [40, 41], in which ε_d is the dot level in the absence of the photon field, Δ_d the field intensity applied on the dot, and ω_p the photon frequency. The third term represents the tunneling between the QD and the leads, with tunnel amplitude V_α. The last two terms in Equation (1) are for the MZMs and their interaction to the QD. Following previous work [22], we transform the Majorana fermions into the regular ones by ${\eta }_1=\frac{1}{\sqrt{2}}\left(f^{+}+f\right)$, ${\eta }_2=\frac{i}{\sqrt{2}}\left(f^{+}-f\right)$ and then the Hamiltonian is rewritten as

$\begin{array}{l}H={\displaystyle \sum _{k\alpha }}{\epsilon }_{k\alpha }{c}_{k\alpha }^{+}{c}_{k\alpha }+{\epsilon }_d(t)d^{+}d+{\displaystyle \sum _{k,\alpha =L,R}}(V_{\alpha }{c}_{k\alpha }^{+}d+H.c)\\ +{\delta }_M\left(f^{+}f-\frac{1}{2}\right)+\frac{1}{\sqrt{2}}(\lambda d-\lambda d^{+})(f+f^{+})& (2)\end{array}$

The electrical and heat currents from lead-α to the dot are individually calculated from the time rate of the electrons' average occupation number and the associated energy [41], i.e., J_α = −ed〈N_α〉/dt and $Q_{\alpha }=-ed\langle {\sum }_k({\epsilon }_{k\alpha }-{\mu }_{\alpha })c_{k\alpha }^{+}{c}_{k\alpha }\rangle /dt$, in which $N_{\alpha }={\sum }_k{c}_{k\alpha }^{+}{c}_{k\alpha }$ is the electrons' occupation number and μ_α the chemical potential in the lead. In the present paper, we focus the linear response regime with infinitesimal bias voltage ΔV and temperature difference ΔT between the two leads. The total electrical and heat currents through the dot are then given by [30, 31, 42]

$\begin{array}{ll}J=e{L}_0\Delta V+\frac{e}{T}{L}_1\Delta T,& (3)\end{array}$

$\begin{array}{ll}Q=L_1\Delta V+\frac{1}{T}{L}_2\Delta T,& (4)\end{array}$

where the integral L_n (n = 0, 1, 2) is defined by [31, 42]

$\begin{array}{ll}{L}_n=-\frac{1}{\hslash }{\displaystyle \int }d\epsilon (\epsilon -\mu {)}^n\frac{\partial f(\epsilon )}{\partial \epsilon }T(\epsilon )& (5)\end{array}$

in which the Fermi distribution function is $f(\epsilon )\mathrm{\text{=}}[exp\left[(\epsilon -\mu )/k_{B}T\right]+1{]}^{-1}$, with the chemical potential μ = μ_L = μ_R in the linear response regime. By setting J = 0 and Q = 0, the electrical conductance and thermopower are given by $G=e^2{L}_0$ and S = −L₁/(eTL₀), respectively. The remaining task is to calculate the transmission coefficient T(ε) in Equation (5). In the framework of non-equilibrium Green's function technique, its expression is given by [39–41],

$\begin{array}{ll}T(\epsilon )=\frac{{\Gamma }_L{\Gamma }_R}{{\Gamma }_L+{\Gamma }_R}{\displaystyle \sum _k}{\tilde{G}}_{dd;k}^r(\epsilon )J_k^2,& (6)\end{array}$

in which ${\Gamma }_{\alpha }=2\pi {\left|V_{k\alpha }\right|}^2{\rho }_{\alpha }$ is the line-width function with ρ_α being the local density of states in lead-α. In the above equation, J_k is the k-th order Bessel function with argument Δ_d/ω_p, and ${\tilde{G}}_{dd;k}^r(\epsilon )$ the retarded Green's function given by [39–41]

$\begin{array}{l}{\tilde{G}}_{dd;k}^r(\epsilon )\\ ={\left[g_{dd;k}^{r-1}(\epsilon )-{\displaystyle {\sum }_n}{J}_{k+n}^2{\Sigma }_{nn}^r(\epsilon )-{\displaystyle {\sum }_{k^{\prime }}}\frac{{\tilde{\Sigma }}_{k{k}^{\prime }}^{r2}(\epsilon )}{{\tilde{g}}_{dd;k^{\prime }}^{r-1}(\epsilon )-{\tilde{\Sigma }}_{k^{\prime }}^r(\epsilon )}\right]}^{-1},& (7)\end{array}$

where the dot free Green's function in the absence of coupling to the leads and MZMs is $g_{dd;k}^r(\epsilon )={\left[\epsilon -{\epsilon }_d-k{\omega }_p+i({\Gamma }_L+{\Gamma }_R)/2\right]}^{-1}$, and the associated hole free Green's function ${\tilde{g}}_{dd;k}^r(\epsilon )={\left[\epsilon +{\epsilon }_d+k{\omega }_p+i({\Gamma }_L+{\Gamma }_R)/2\right]}^{-1}$. The self-energies in Equation (7) are individually given by${\Sigma }_{nn}^r(\epsilon )={\lambda }^2(\epsilon +n{\omega }_p)/\left[{(\epsilon +n{\omega }_p)}^2+{\delta }_M^2\right]$,${\tilde{\Sigma }}_{k^{\prime }}^r(\epsilon )={\sum }_{k^{\prime }}{J}_{k^{\prime }-n}{\Sigma }_{nn}^r(\epsilon )$, and ${\tilde{\Sigma }}_{k{k}^{\prime }}^r(\epsilon )={\sum }_{k^{\prime }}{J}_{k+n}{J}_{k^{\prime }-n}{\Sigma }_{nn}^r(\epsilon )$. One can check that in the absence of the photon field, i.e., Δ_d = 0, the Green's function ${\tilde{G}}_{dd;k}^r(\epsilon )$ reduces to that in [22].

Results and Discussion

In the following numerical calculations, the photon frequency ω_p is set as the energy unit, and the equilibrium chemical potential in the leads is fixed at μ_L = μ_R = μ = 0 as the energy zero point. Throughout the paper we fix the value of line-width functions Γ_L = Γ_R = 0.05ω_p. Figure 2 shows the conductance and thermopower as functions of the dot level without the photon field shelled on the dot (Δ_d = 0). For λ = 0 as indicated by the black solid in Figure 2A, the conductance G develops a resonant peak when the dot level ε_d is aligned to the chemical potential μ, where the maximum of the conductance reaches its quantum value G(μ = 0) = e²/h. Turning on the coupling between the dot and MZMs (λ ≠ 0), the value of conductance around the leads' chemical potentials μ reduces to half of its quantum value, i.e., G = e²/2h due to the half fermionic property of MZMs. This is regarded as a signature of the existence of MZMs in QD [22, 23]. Note that at ultra-low temperature, the half fermionic property of MZMs (G = e²/2h) is independent of the dot's level [31]. At a rather high temperature, however, we find that only the conductance near the chemical potential is half of its quantum value, as shown in Figure 2A. This is because the interaction between the MZMs and electrons on the dot is weakened by increased thermal motion of the electrons.

FIGURE 2

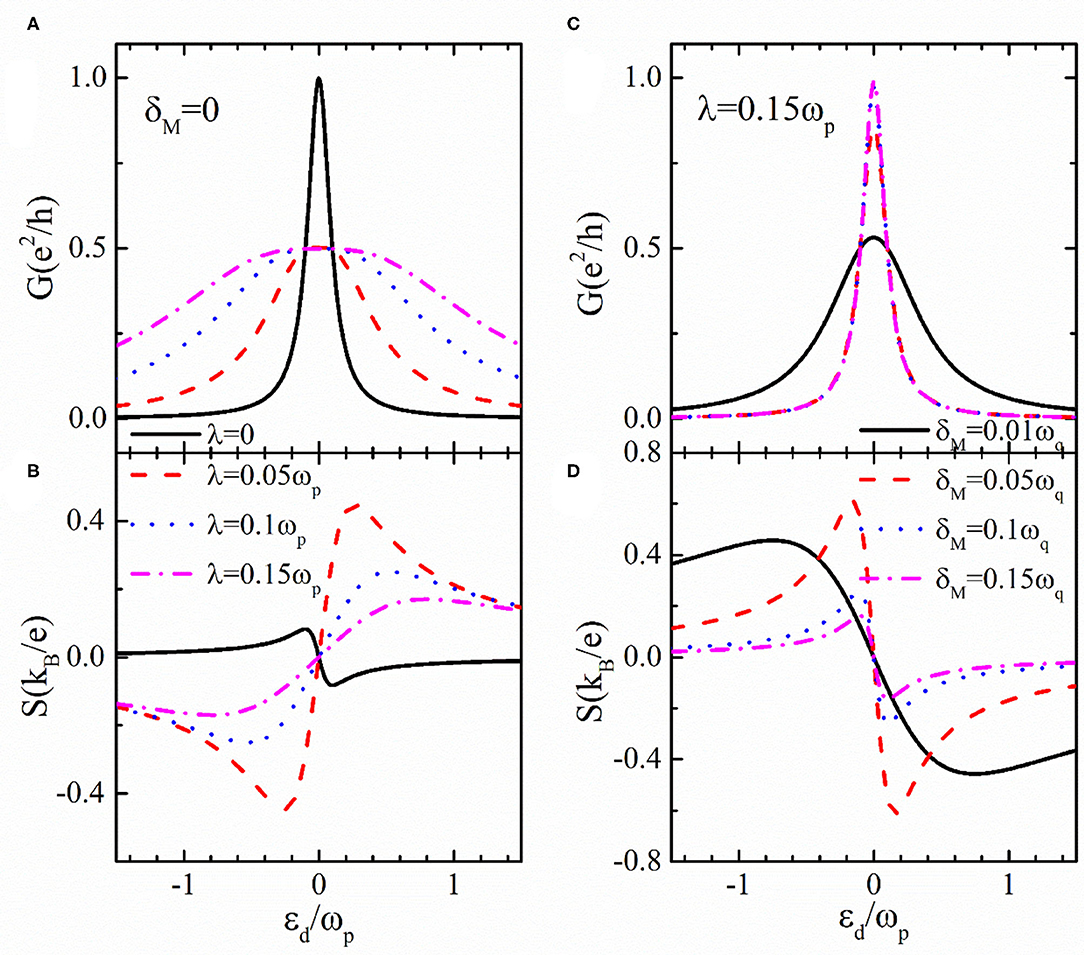
Figure 2. Conductance and thermopower as functions of the dot level for different values of dot-MZMs coupling strength λ in (A), (B) with a fixed value of δ_M = 0, and for different δ_M in (C), (D) with fixed λ = 0.15ω_p. The other parameters are T_e = 0.0025ω_p, Δ_d = 0.

The most prominent change of the thermopower is the sign reversion induced by dot-MZMs coupling, as shown in Figure 2B. For λ = 0 as indicated by the black solid line, the thermopower is positive (negative) when the dot level is below (above) the chemical potential μ = 0. The reason is that in the presence of thermal gradient ΔT between the two leads that induces the thermoelectric effect, there are more electrons flowing from the left hotter lead to the right cooler one as ε_d > μ. This will induce a positive voltage drop ΔV and correspondingly a negative thermopower S = −ΔV/ΔT [42]. When ε_d = μ, tunneling of electrons through the dot are compensated by that of holes and thus the thermopower is zero. In other words, there are the same amounts of electrons flowing in opposite directions and then the voltage drop is zero accordingly [42]. Just in the same way, one can explain the origin of the positive thermopower when ε_d < μ. The dependence of thermopower on the dot-MZMs coupling λ can be derived by Sommerfeld expansion of the Fermi function f(ε) up to second order in temperature, and its analytical expression when the dot level is near the chemical potential is [31, 34]

$\begin{array}{ll}S=\frac{{\pi }^2{k}_B^{2}T}{3e}\frac{{\epsilon }_d}{2{\lambda }^2}& (8)\end{array}$

Note that this result applies only to the case of finite dot-MZMs coupling, and clearly shows the sign reversion of the thermopower as compared to the case of zero λ. From Equation (8), one can also expect the magnitude of the thermopower to be enhanced by a small λ, as has been shown in previous works [6, 33].

The two modes of the MZMs at opposite ends of the topological nanowire interact with each other with strength of ${\delta }_M~e^{-\zeta /L}$, where L is the length of the topological superconductor wire and ζ is the superconducting coherence length [29, 30]. Figure 2C shows that when the hybridization strength between the MZMs is strong enough δ_M > 0.01ω_q, the property of G(μ) = e²/2h is destroyed. For a sufficiently large value of δ_M ≥ 0.1ω_q, the conductance reduces to the result of resonant level model G(μ) = e²/h because the transportation is dominated by regular fermions as demonstrated in [22, 31]. As for the thermopower with finite δ_M, its analytical expression when the dot level is near the chemical potential can also be obtained by the Sommerfeld expansion as [31]

$\begin{array}{ll}S=-\frac{{\pi }^2{k}_B^{2}T}{3e}\frac{{\epsilon }_d}{4{\Gamma }^2+{\epsilon }_d^2}\frac{8({\delta }_M^2+{\lambda }^2)}{{\delta }_M^2}& (9)\end{array}$

By comparing Equations (8) and (9), one finds that the hybridization between the MZMs will also induce a sign reversion of the thermopower as seen from Figure 2D. The peaks at the two sides of the zero point become sharper and lower with increasing δ_M due to the increased level renormalization by coupling between the MZMs [22, 31, 33].

Figure 3 presents the conductance and thermopower varying as functions of the system equilibrium temperature T_e for different values of δ_M and a fixed value of λ = 0.05. The dot level is fixed at ε_d = −0.2ω_p where the thermopower develops a peak. With increasing temperature, the conductance for δ_M = 0 in Figure 3A is essentially decreased and finally reaches a constant value at high temperature (solid line). The absolute value of the thermopower in Figure 3B is first enhanced, reaching a maximum, and then decreases with increasing temperature. With further increased temperature, the thermopower experiences a sign reversion and then increases. The sign change of the thermopower by temperature in the absence of dot-MZMs coupling has been previously found to be induced by the Kondo effect in single QD [43], and by interdot Coulomb interaction in double-QD [44]. In the presence of δ_M, both the conductance and thermopower depend on the temperature in a non-monotonous way. The sign reversion of the thermopower by δ_M can be clearly seen in Figure 3B, which agrees with the results in [31, 33].

FIGURE 3

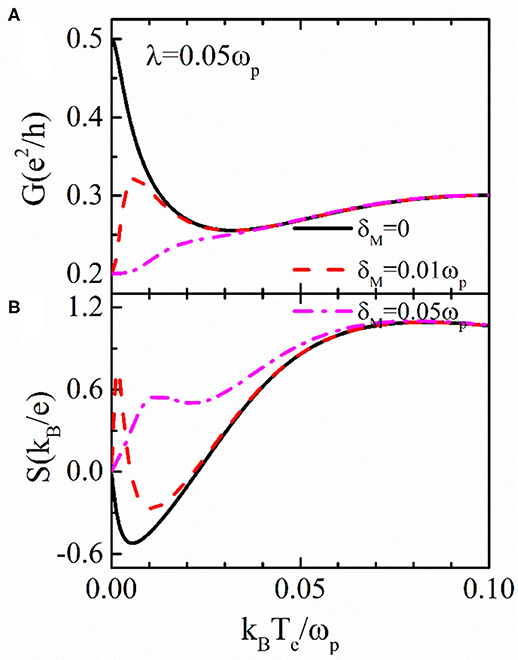
Figure 3. (A) Conductance and (B) thermopower as functions of the temperature T_e for ε_d = −0.2ω_p and different values of the overlap amplitude between the MZMs δ_M. Other parameters are λ = 0.05ω_p and Δ_d = 0.

We now study the case of finite photon field shelled on the dot, i.e., Δ_d ≠ 0. As has been demonstrated in previous works, the conductance develops a series of photon-assisted side peaks at ε_d = μ + nω_p with n = 0, ±1, ±2⋯, due to the additional transport channels induced by photon absorption and emission processes [39–41]. Since now electrons can transport through the dot via more states, the tunneling probability through each channel is weakened and then the conductance's peak height is lowered, as shown by the solid line in Figure 4A. The thermopower in Figure 4B is zero at these photon-induced additional side bands ε_d = μ + nω_p (black solid line) correspondingly. The peaks' height of the conductance is further lowered by the dot-MZMs coupling as indicated by the dashed and dash-dotted lines in Figure 4A, which is consistent with the results in Figure 2A. For λ = 0.15ω_p, the conductance is negligibly small. As a result of it, the thermopower in Figure 4B is significantly enhanced in addition to the sign reversion. This can be understood by the definition of the thermopower of S = −eL₁/(TG). We find in Figure 4C that the magnitude of the conductance is slightly increased by the overlap between the MZMs as shown in Figure 2C. Such a change is amplified by the thermopower in Figure 4D, in which it shows the typical sawtooth configuration with weakened strength. By comparing Figures 4B,D, one can find that the sign reversion of the thermopower by δ_M is retained in the presence of the photon field.

FIGURE 4

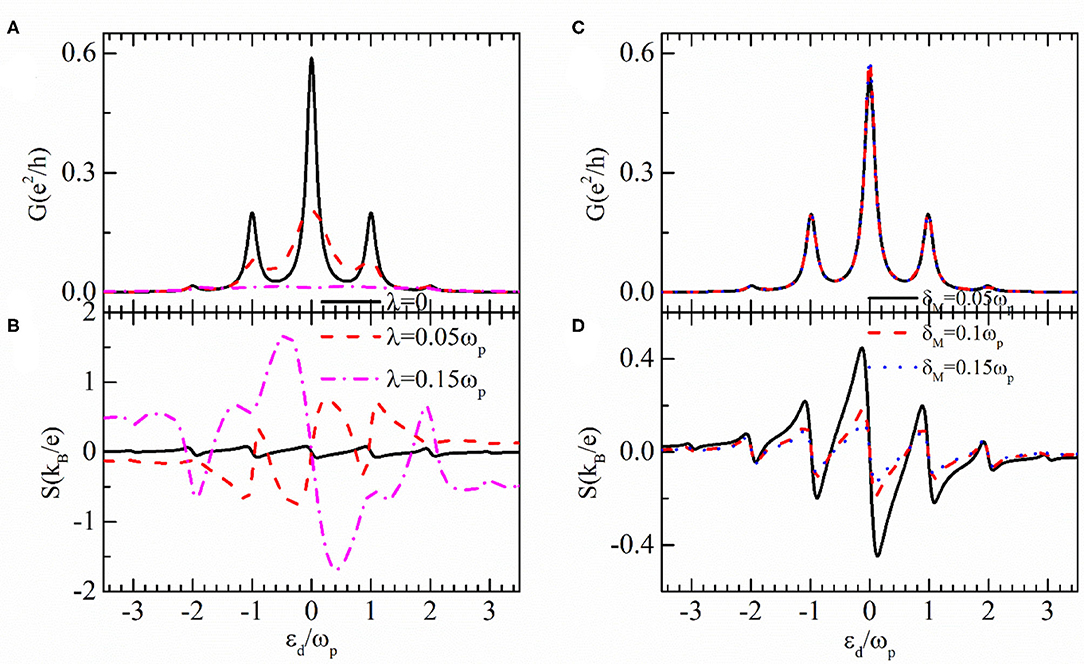
Figure 4. Conductance and thermopower in the presence of the microwave field with Δ_d = ω_p as functions of the dot level for different values of dot-MZMs coupling strength λ in (A), (B) with δ_M = 0, and for different δ_M in (C), (D) with λ = 0.05ω_p. The equilibrium temperature is chosen as T_e = 0.0025ω_p.

Finally, in Figure 5 we study the properties of thermopower varying as a function of the temperature. For zero δ_M and λ as indicated by the black solid line in Figure 5A, the magnitude of the thermopower is first increased with increasing temperature, reaching a maximum at about k_BT_e = 0.05ω_p and then decreases to a constant value. As compared to Figure 3B, one can see that the sign change of the thermopower induced by the varying temperature is eliminated in the presence of photon field. For non-zero λ, however, the thermopower changes sign by the varying of both temperature and λ, as shown in Figure 5A. At a lower temperature, the thermopower develops a peak, whose sign depends on the magnitude of λ. To show this more clearly, we present in Figure 5B the blow-up of the case of k_BT_e < 0.01ω_p. For λ < 0.05ω_p represented by the red-dashed line, the thermopower is positive at k_BT_e ~ 0, whereas those for λ < 0.1ω_p and λ < 0.15ω_p are negative. In these three cases, the thermopower develops positive peaks at higher temperatures and then becomes negative with further increasing temperature. At sufficiently high temperature, the thermopower reaches a positive value regardless of the existence of MZMs. Behaviors of the thermopower in Figure 5C essentially resemble those in Figure 3B in which Δ_d = 0. The reason can be attributed to the fact that when the MZMs are overlapped [39], the photon energy absorbed by one mode of the MZMs is subsequently emitted by the other mode, and then the electron transport through the dot is less influenced.

FIGURE 5

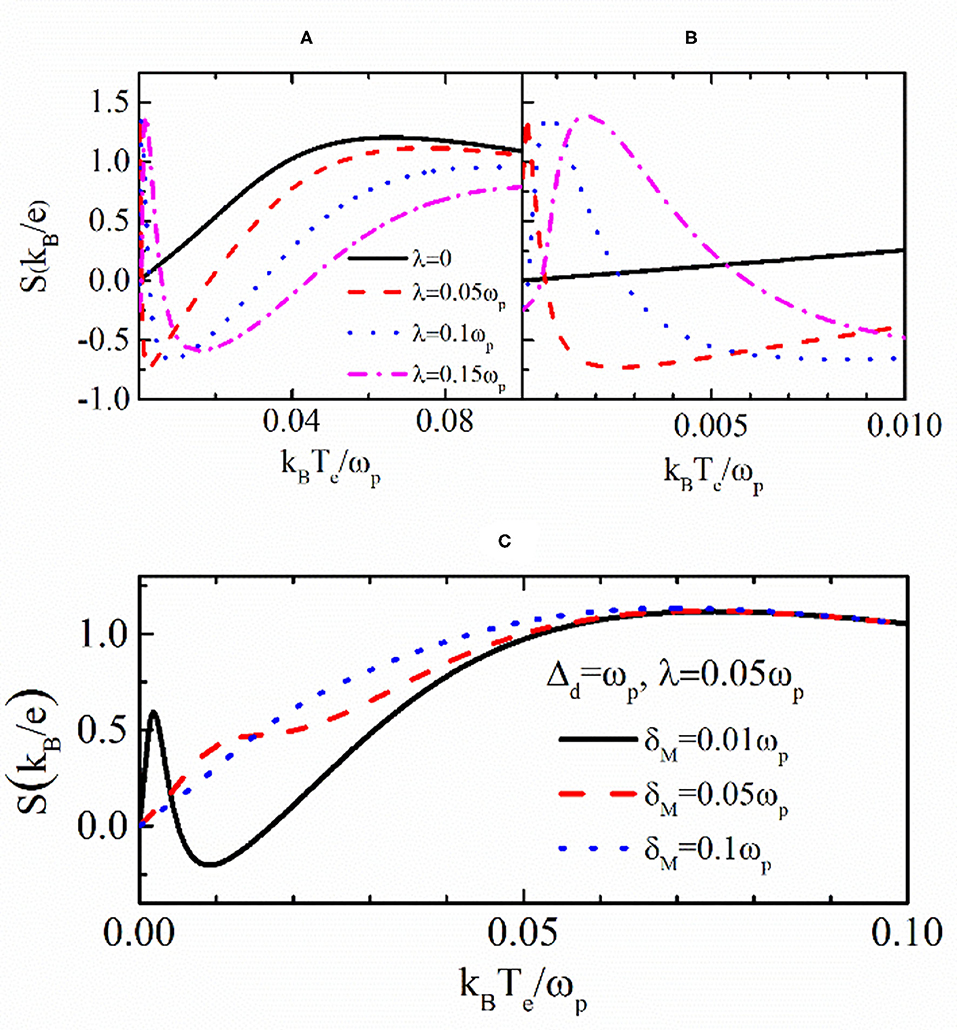
Figure 5. Thermopower varying with the equilibrium temperature for ε_d = −0.2ω_p and different values of λ in (A), and varying δ_M in (C). (B) is the blow-up of (A) at lower temperatures.

Conclusions

In conclusion, we have studied the properties of electrical conductance and thermopower in a quantum dot coupled to MZMs under the irradiation of a photon field. Our numerical results show that the conductance is fixed at half of its quantum value as the QD-MZMs coupling increases. The thermopower can be obviously enhanced by the combined effect of the MZMs and PAT. This mainly occurs in a low temperature regime, under which the MZMs are prepared at the two ends of a topological superconductor nanowire. When the two modes of the MZMs are strongly overlapped with each other, the thermopower is less influenced by the MZMs in the presence of the photon field because the photon energy absorbed by one mode of the MZMs is subsequently emitted by the other one. We also find a sign change of the thermopower induced by changing either dot-MZMs coupling or temperature.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

HS and GZ contributed the ideas equally. HS and T-YH derived the formulae, performed the numerical calculations, and wrote the original manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by Science and Technology Program of Guangzhou (No. 2019050001), Program for Guangdong Innovative and Entrepreneurial Teams (No. 2019BT02C241), Program for Chang Jiang Scholars and Innovative Research Teams in Universities (No. IRT_17R40), Key-Area Research and Development Program of Guangdong Province (No. 2019B010924005), Guangdong Provincial Key Laboratory of Optical Information Materials and Technology (No. 2017B030301007), and Guangzhou Key Laboratory of Electronic Paper Displays Materials and Devices (201705030007) and the 111 Project.

Conflict of Interest

GZ is employed by Shenzhen Guohua Optoelectronics Tech. Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Read N, Green D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect N. Phys Rev B. (1999) 61:10267–97. doi: 10.1103/PhysRevB.61.10267

CrossRef Full Text | Google Scholar

2. Nayak C, Simon SH, Stern A, Freedman M, Das Sarma S. Non-Abelian anyons and topological quantum computation. Rev Mod Phys. (2008) 80:1083–159. doi: 10.1103/RevModPhys.80.1083

CrossRef Full Text | Google Scholar

3. Alicea J, Oreg Y, Refael G, Von Oppen F, Fisher MPA. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat Phys. (2011) 7:412–7. doi: 10.1038/nphys1915

CrossRef Full Text | Google Scholar

4. Karzig T, Knapp C, Lutchyn RM, Bonderson P, Hastings MB, Nayak C, et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys Rev B. (2017) 95:1–32. doi: 10.1103/PhysRevB.95.235305

CrossRef Full Text | Google Scholar

5. Liu X, Li X, Deng DL, Liu XJ, Das Sarma S. Majorana spintronics. Phys Rev B. (2016) 94:1–13. doi: 10.1103/PhysRevB.94.014511

CrossRef Full Text | Google Scholar

6. Chi F, Fu ZG, Liu J, Li KM, Wang Z, Zhang P. Thermoelectric effect in a correlated quantum dot side-coupled to Majorana bound states. Nanoscale Res Lett. (2020) 15:79. doi: 10.1186/s11671-020-03307-y

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Smirnov S. Universal Majorana thermoelectric noise. Phys Rev B. (2018) 97:1–14. doi: 10.1103/PhysRevB.97.165434

CrossRef Full Text | Google Scholar

8. Kitaev AYu. Fault-tolerant quantum computation by anyons. Ann Phys (N Y). (2003) 303:2–30. doi: 10.1016/S0003-4916(02)00018-0

CrossRef Full Text | Google Scholar

9. Fu L, Kane CL. Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys Rev Lett. (2008) 100:1–4. doi: 10.1103/PhysRevLett.100.096407

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Qi XL, Zhang SC. Topological insulators and superconductors. Rev Mod Phys. (2011) 83:1057–110. doi: 10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

11. Potter AC, Lee PA. Topological superconductivity and Majorana fermions in metallic surface states. Phys Rev B. (2012) 85:1–9. doi: 10.1103/PhysRevB.85.094516

CrossRef Full Text | Google Scholar

12. Lutchyn RM, Sau JD, Das Sarma S. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys Rev Lett. (2010) 105:1–4. doi: 10.1103/PhysRevLett.105.077001

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Lutchyn RM, Bakkers EPAM, Kouwenhoven LP, Krogstrup P, Marcus CM, Oreg Y. Majorana zero modes in superconductor-semiconductor heterostructures. Nat Rev Mater. (2018) 3:52–68. doi: 10.1038/s41578-018-0003-1

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Nadj-Perge S, Drozdov IK, Bernevig BA, Yazdani A. Proposal for realizing Majorana fermions in chains of magnetic atoms on a superconductor. Phys Rev B. (2013) 88:1–5. doi: 10.1103/PhysRevB.88.020407

CrossRef Full Text | Google Scholar

15. Pientka F, Keselman A, Berg E, Yacoby A, Stern A, Halperin BI. Topological superconductivity in a planar Josephson junction. Phys Rev X. (2017) 7:1–17. doi: 10.1103/PhysRevX.7.021032

CrossRef Full Text | Google Scholar

16. Wang Z, Zhang P, Xu G, Zeng LK, Miao H, Xu X, et al. Topological nature of the FeSe0.5Te0.5 superconductor. Phys Rev B. (2015) 92:1–7. doi: 10.1103/PhysRevB.92.115119

CrossRef Full Text | Google Scholar

17. Wu X, Qin S, Liang Y, Fan H, Hu J. Topological characters in Fe(Te1-xSex) thin films. Phys Rev B. (2016) 93:1–13. doi: 10.1103/PhysRevB.93.115129

CrossRef Full Text | Google Scholar

18. Mourik V, Zuo K, Frolov SM, Plissard SR, Bakkers EPAM, Kouwenhoven LP. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science. (2012) 336:1003–7. doi: 10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Das A, Ronen Y, Most Y, Oreg Y, Heiblum M, Shtrikman H. Zero-bias peaks and splitting in an Al-InAs nanowire topological superconductor as a signature of Majorana fermions. Nat Phys. (2012) 8:887–95. doi: 10.1038/nphys2479

CrossRef Full Text | Google Scholar

20. Deng MT, Yu CL, Huang GY, Larsson M, Caroff P, Xu HQ. Anomalous zero-bias conductance peak in a Nb-InSb nanowire-Nb hybrid device. Nano Lett. (2012) 12:6414–9. doi: 10.1021/nl303758w

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Lee EJH, Jiang X, Aguado R, Katsaros G, Lieber CM, De Franceschi S. Zero-bias anomaly in a nanowire quantum dot coupled to superconductors. Phys Rev Lett. (2012) 109:1–5. doi: 10.1103/PhysRevLett.109.186802

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Liu DE, Baranger HU. Detecting a Majorana-fermion zero mode using a quantum dot. Phys Rev B. (2011) 84:1–4. doi: 10.1103/PhysRevB.84.201308

CrossRef Full Text | Google Scholar

23. Vernek E, Penteado PH, Seridonio AC, Egues JC. Subtle leakage of a Majorana mode into a quantum dot. Phys Rev B. (2014) 89:1–5. doi: 10.1103/PhysRevB.89.165314

CrossRef Full Text | Google Scholar

24. Deng MT, Vaitiekenas S, Hansen EB, Danon J, Leijnse M, Flensberg K, et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science. (2016) 354:1557–62. doi: 10.1126/science.aaf3961

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Deng MT, Vaitiekenas S, Prada E, San-Jose P, Nygård J, Krogstrup P, et al. Nonlocality of Majorana modes in hybrid nanowires. Phys Rev B. (2018) 98:1–10. doi: 10.1103/PhysRevB.98.085125

CrossRef Full Text | Google Scholar

26. Górski G, Barański J, Weymann I, Domański T. Interplay between correlations and Majorana mode in proximitized quantum dot. Sci Rep. (2018) 8:1–12. doi: 10.1038/s41598-018-33529-1

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Silva JF, Da Silva LGGVD, Vernek E. Robustness of the Kondo effect in a quantum dot coupled to Majorana zero modes. Phys Rev B. (2020) 101:1–10. doi: 10.1103/PhysRevB.101.075428

CrossRef Full Text | Google Scholar

28. Dubi Y, Di Ventra M. Colloquium: heat flow and thermoelectricity in atomic and molecular junctions. Rev Mod Phys. (2011) 83:131–55. doi: 10.1103/RevModPhys.83.131

CrossRef Full Text | Google Scholar

29. Hou CY, Shtengel K, Refael G. Thermopower and Mott formula for a Majorana edge state. Phys Rev B. (2013) 88:1–8. doi: 10.1103/PhysRevB.88.075304

CrossRef Full Text | Google Scholar

30. Leijnse M. Thermoelectric signatures of a Majorana bound state coupled to a quantum dot. New J Phys. (2014) 16:1–13. doi: 10.1088/1367-2630/16/1/015029

CrossRef Full Text | Google Scholar

31. López R, Lee M, Serra L, Lim JS. Thermoelectrical detection of Majorana states. Phys Rev B. (2014) 89:1–7. doi: 10.1103/PhysRevB.89.205418

CrossRef Full Text | Google Scholar

32. Ricco LS, Dessotti FA, Shelykh IA, Figueira MS, Seridonio AC. Tuning of heat and charge transport by Majorana fermions. Sci Rep. (2018) 8:1–8. doi: 10.1038/s41598-018-21180-9

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Hong L, Chi F, Fu ZG, Hou YF, Wang Z, Li KM, et al. Large enhancement of thermoelectric effect by Majorana bound states coupled to a quantum dot. J Appl Phys. (2020) 127:1–10. doi: 10.1063/1.5125971

CrossRef Full Text | Google Scholar

34. Bin NP, Liu L, Su X, Dong L, Shi Y, Luo HG. Spin Seebeck effect induced by a Majorana zero mode in a nanomagnet. Phys E Low Dimensional Syst Nanostruct. (2020) 124:1–7. doi: 10.1016/j.physe.2020.114313

CrossRef Full Text | Google Scholar

35. Li Y, Kundu A, Zhong F, Seradjeh B. Tunable Floquet Majorana fermions in driven coupled quantum dots. Phys Rev B. (2014) 90:1–5. doi: 10.1103/PhysRevB.90.121401

CrossRef Full Text | Google Scholar

36. Väyrynen JI, Rastelli G, Belzig W, Glazman LI. Microwave signatures of Majorana states in a topological Josephson junction. Phys Rev B. (2015) 92:1–5. doi: 10.1103/PhysRevB.92.134508

CrossRef Full Text | Google Scholar

37. Chen HJ, Zhu KD. All-optical scheme for detecting the possible Majorana signature based on QD and nanomechanical resonator systems. Sci China Phys Mech Astron. (2015) 58:1–14. doi: 10.1007/s11433-014-5637-4

CrossRef Full Text | Google Scholar

38. Tang HZ, Zhang YT, Liu JJ. Photon-assisted tunneling through a topological superconductor with Majorana bound states. AIP Adv. (2015) 5:1–8. doi: 10.1063/1.4939096

CrossRef Full Text | Google Scholar

39. Chi F, He TY, Wang J, Fu ZG, Liu LM, Liu P, et al. Photon-assisted transport through a quantum dot side-coupled to Majorana bound states. Front Phys. (2020) 8:8–13. doi: 10.3389/fphy.2020.00254

CrossRef Full Text | Google Scholar

40. Sun QF, Lin TH, Wang J. Photon-assisted andreev tunneling through a mesoscopic hybrid system. Phys Rev B. (1999) 59:13126–38. doi: 10.1103/PhysRevB.59.13126

CrossRef Full Text | Google Scholar

41. Jauho AP, Wingreen NS, Meir Y. Time-dependent transport in interacting and noninteracting resonant-tunneling systems. Phys Rev B. (1994) 50:5528–44. doi: 10.1103/PhysRevB.50.5528

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Liu J, Sun QF, Xie XC. Enhancement of the thermoelectric figure of merit in a quantum dot due to the Coulomb blockade effect. Phys Rev B. (2010) 81:1–6. doi: 10.1103/PhysRevB.81.245323

CrossRef Full Text | Google Scholar

43. Krawiec M, Wysokiński KI. Thermoelectric phenomena in a quantum dot asymmetrically coupled to external leads. Phys Rev B. (2007) 75:155330–5. doi: 10.1103/PhysRevB.75.155330

CrossRef Full Text | Google Scholar

44. Rajput G, Ahluwalia PK, Sharma KC. Thermoelectric properties of correlated double quantum dot system in Coulomb blockade regime. Phys B Condens Matter. (2011) 406:3328–34. doi: 10.1016/j.physb.2011.05.054

CrossRef Full Text | Google Scholar