Zhaohui Chen1,2*†
Miao Li1,3†Caixing Liu1,2Zongwei Ma1Yuyan Han1Jianhua Gao1
Wensen Wei1Zhigao Sheng1Haifeng Du1,4- 1Anhui Key Laboratory of Condensed Matter Physics at Extreme Conditions, High Magnetic Field Laboratory, Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei, China
- 2University of Science and Technology of China, Hefei, China
- 3School of Physics and Electronic Information, Huaibei Normal University, Huaibei, China
- 4Institutes of Physical Science and Information Technology, Anhui University, Hefei, China
Two types of magnetic domains, that is, type-I domain belt domain and type-II new stripe domain, are observed in a kagome metal DyMn6Sn6 by microscopic magneto-optic Kerr imaging technique. From 255 to 235 K, the spin reorientation is observed directly in DyMn6Sn6. We analyze the structure of two types of domains through brightness distribution of the images. The type-II domain exists from 235 to 160 K by zero-field cooling (ZFC). At the same time, type-I domain and type-II domain coexist and transform into each other with variation of temperature. Type-II domains can easily transform into type-I domains when the temperature and magnetic field changes, and this process is irreversible. These results demonstrate that the type-I domain is more stable than the type-II domain. The phase diagram of magnetic domains in DyMn6Sn6 is obtained.
Introduction
Novel magnetic domain structure, which is observed in various magnetic materials, is the consequence of competition among various magnetic interactions that are executed on the materials both from intrinsic and extrinsic circumstances [1–4]. In particular, the intrinsic magnetic interactions that occur in materials with kagome crystal is of great complexity and results in complicated magnetic domains, for example, a frustrated circumstance would occur and lead to noncollinear magnetic spin structure [5–10]. Recently, topologically nontrivial skyrmions have been predicted to generate in kagome crystal when the crystal owns both Heisenberg and Dzyaloshinskii–Moriya interactions [11–13], and finally, the skyrmion bubbles are experimented and reported in Fe3Sn2 without any Dzyaloshinskii–Moriya interaction [14–17], showing that the uniaxial magnetic anisotropy in kagome crystal can play a vital role in stabilized novel spin structure. On the other hand, the magnetic and electronic structures in kagome crystals are highly entangled, making them show both fruitful spin-orbit and electronic corrected effects. Consequently, the conduction electrons show both an intrinsic anomalous Hall effect which links to reciprocal band structure and a topological Hall effect which related to real space nontrivial spin textures [18–22]. The exotic phenomena are confirmed in many kagome crystals like Fe3Sn2 [23, 24], Co3Sn2S2 [25, 26], YMn6Sn6 [27], etc. Evenly, the kagome lattices may also host Dirac electronic states, which leads to topological and Chern insulating phases, which have been confirmed both by theoretical and experimental investigation on Fe3Sn2 [23, 24] and TbMn6Sn6 [28]. Recently, not only TbMn6Sn6 but also RMn6Sn6 (R = Y, Dy, Ho, etc.) have been reported to show a very large anomalous Hall effect and a large topological Hall effect [27, 29, 30], stimulating vast investigations in the field and materials of kagome lattices.
DyMn6Sn6 is a member of kagome metal RMn6Sn6 family (R = rare element) which consists of a two-dimensional (2D) Mn layer kagome lattice. It has a hexagonal HfFe6Ge6-type structure with P6/mmm space group [31]. It has a ferrimagnetic behavior below TC = 393 K with Dy and Mn sublattices ordering simultaneously due to the strong Mn-Dy antiferromagnetic coupling [32]. Neutron diffraction study shows that above room temperature, it possesses a planar anisotropy for the Mn sublattice but with a negative value for Dy, resulting in a partial spin reorientation below Tt ∼ 240 K [31]. Considering both the spontaneous magnetization with kagome lattice in DyMn6Sn6, a conical arrangement of the spin magnetic moment is inferred in the previous report. Recently, the transport, and therefore the electronic structure, has been intensively studied to uncover the possible Dirac and Chern insulating state nature [28]; however, the directional observation of the spin texture has not been reported. The relationship between the complex electronic correlated novel state and the novel spin structure, in other words, the link between the degrees of charge and spin for the electrons in kagome lattices, is highly elusive.
Microscopic magneto-optical Kerr effect (micro-MOKE), which refers to the polarization rotation of a linearly polarized light when reflected by magnetized materials, is widely used to map the magnetic domain patterns and magnetic phase transitions in various materials [33–35]. In this study, the magnetic domain in DyMn6Sn6 crystal and its evolution with temperature and magnetic field was investigated using the micro-MOKE imaging technique. We evidenced that the spin reorientation occurs between 255 and 235 K. In addition, we observed two types of magnetic domain structures that coexist and compete with each other simultaneously in DyMn6Sn6. Our results can provide a platform to understand the novel magnetic domain structure in the kagome metal family.
Materials and Methods
DyMn6Sn6 single crystals were grown by the flux method [36]. The constituent elements Dy, Mn, and Sn of better than 3N purity were weighed in the mole ratio of Dy:Mn:Sn = 1:6:30. The sample was placed in an alumina crucible and sealed in an evacuated silica ampoule. The ampoule was heated to 1,273 K and kept at the temperature for 24 h, and then slowly cooled to 1,223 K. It was heated again up to 1,263 K and finally cooled down slowly to 873 K at a rate of 6 K/h. The ampoule was quickly removed from the furnace. Sn flux was removed using a centrifuge. After cooling down to room temperature, the ampoule was broken by tools, and plate-like DyMn6Sn6 single crystals of about 2 × 2 × 0.5 mm3 in size were obtained from the alumina crucible. The quality of the crystals was checked by X-ray diffraction (XRD). Magnetization was carried out using the quantum design magnetic property measurement system (MPMS-XL5) for 1.8 K < T < 400 K and the H < 7 T.
The crystal was exfoliated using Torr seal glue to get smooth sample surface. Then micro-MOKE images of the surface magnetic domains were obtained at several temperatures using a polarizing microscope (Olympus, BX53M) equipped with a homemade option which could provide low temperature circumstances with liquid nitrogen. The magnetic fields executed on the sample during measurements were generated by calibrated permanent magnets.
Results and Discussions
Figure 1A shows the crystal structure of DyMn6Sn6. It has an hexagonal HfFe6Ge6-type structure with P6/mmm space group with two-dimensional (2D) Mn layer kagome lattice. Figure 1B shows the XRD pattern of a DyMn6Sn6 single crystal. The DyMn6Sn6 single crystal is high quality due to the very sharp diffraction peaks. Temperature-dependent magnetization (M–T) curves with B//c and B//ab plane and magnetic field-dependent magnetization (M–H) curves with B//c are shown in Figure 1C,D, respectively. There is an obvious spin reorientation transition in DyMn6Sn6, the same as that in TbMn6Sn6 and HoMn6Sn6 [32]. The curve at 300 K in Figure 1D is obviously different from the curve at 250 K. It means that the spin reorientation happens between 250 and 300 K.
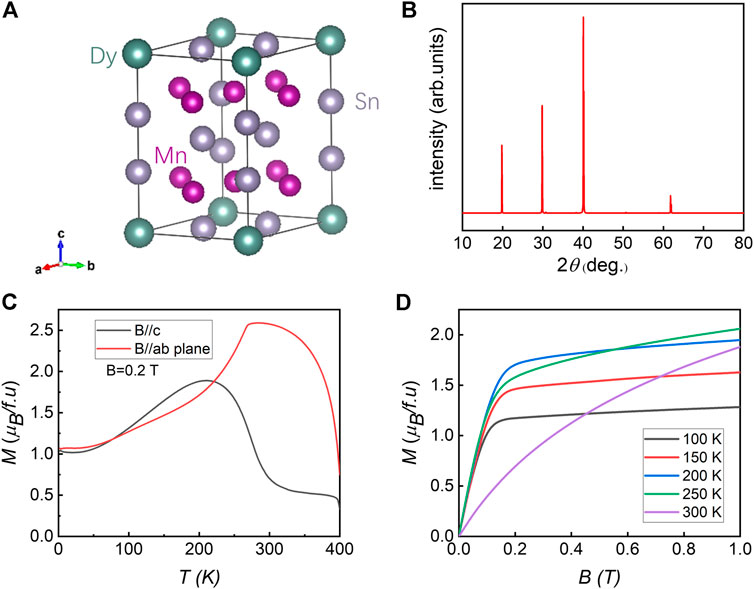
FIGURE 1. (A) Crystal structure of DyMn6Sn6. (B) XRD pattern of a DyMn6Sn6 single crystal. (C) Temperature-dependent magnetization (M–T) curve with B//c and B//ab plane. (D) Magnetic field-dependent magnetization (M–H) curve with B//c.
In order to understand the material behavior of magnetic materials, the direct visualization of the domain structure is required. Figure 2A is a MOKE image of the magnetic domain of DyMn6Sn6 crystal at 173 K. In Figure 2A, we discover that there are two types of magnetic domains in DyMn6Sn6. Type-I domain is the belt domain, while type-II domain is the new stripe domain with complex construction, as shown in Figure 2B,C, respectively. The type-I domain shows that there are many white elliptic domains in the black belt domains. The type-II domain shows that the main part is a wide and long domain and the other part is a thin, short domain with the same direction. The thin, short domain locates in the middle of the black main domain and the white main domain. Figure 2D,E shows the line profile of the brightness distribution as marked by the dotted lines in Figure 2B,C. The intensity of black elliptic domains is stronger than the black belt domains in Figure 2D. Inferred from the theory of two-phase branching [37], the elliptic domains could be considered as floating on the belt domains, as shown in Figure 2F. Similar to the type-I domains, the intensity of black stripe domains is stronger than the black main domains in Figure 2E. It is quite likely that the stripe domains float on the main domains as shown in Figure 2G. From the brightness of the magnetic domains, the magnetic structure in DyMn6Sn6 is reasonably clear, where the sketch map of two types of magnetic domain structures are shown in Figure 2F,G, respectively.
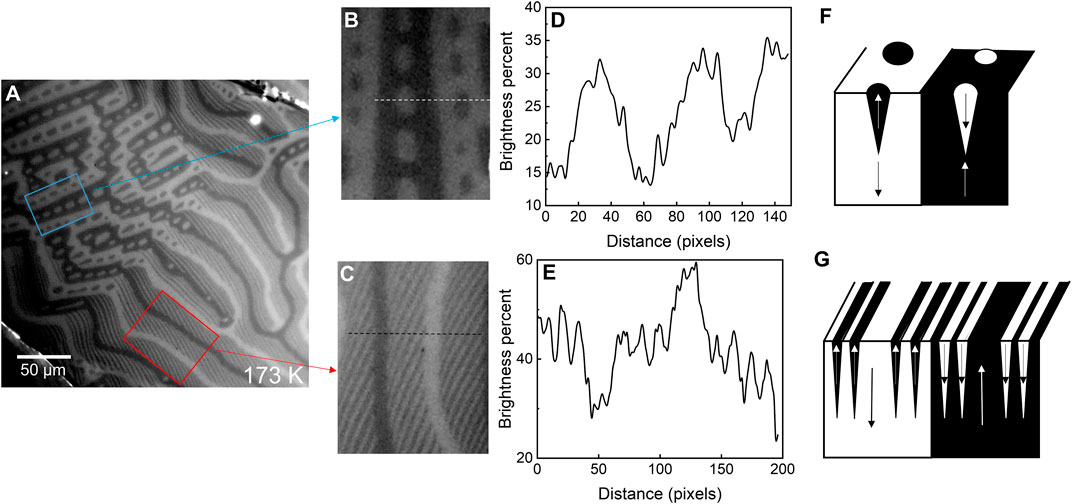
FIGURE 2. (A) Represented image of the magnetic domains of DyMn6Sn6 crystal at 173 K. (B) Type-I domains in DyMn6Sn6. (C) Type-II domains in DyMn6Sn6. (D,E) Corresponding map of the brightness distribution in two types of magnetic domains. (F,G) Corresponding sketch map of two types of magnetic domains structure.
From the above observation, one can note that for DyMn6Sn6, the domain shows refinement structure, reminiscent of the domain branching phenomenon in very large crystals with strongly misoriented surfaces. For DyMn6Sn6, it shows three-dimensional branching, as shown in Figure 2. Based on the theory of two-phase branching, the refinement structure that occurs in DyMn6Sn6 could be understood when one takes the uniaxial magnetic anisotropy. Usually, the theory of two-phase branching consists of three energy terms [37]: 1) the wall energy that increases toward the surface with increasing wall density, 2) the generalized closure energy depending only on the domain width of the last generation, and 3) the energy connected with the internal stray fields. It is rather complicated and difficult to extract explicit calculation, especially for the three-dimensional structure, as in the case of DyMn6Sn6. However, the theory applies to both Co- and Dy-modified NdFeB crystals with thickness of about several hundred micrometers. The theory and experimental result confirmed that the occurrence of domain branching has the relationship to both sample thickness and strong enough uniaxial magnetic anisotropy. Based on these previous results, we propose that the branching phenomenon observed in DyMn6Sn6 has the same mechanism with Dy-modified NdFeB, since DyMn6Sn6 is a strong uniaxial ferromagnet.
Figure 3 displays the magnetic domain structure as a function of temperature. From 255 to 235 K, the spin reorientation (SR) is observed and shown in Figure 3A–C. The magnetic domain is not clear until the temperature decreases to 245 K. When the temperature is below 245 K, the domain appears but is misty. It becomes obvious when the temperature continues decreasing. It is also shown that the spin reorientation in DyMn6Sn6 occurs gradually.
FIGURE 3. (A–C) Appearance of the magnetic domain of DyMn6Sn6 crystal from 255 to 235 K. (D–H) Magnetic domains of DyMn6Sn6 crystal from 230 to 110 K. (D–G) Type-II domains transform into type-I domains from 230 to 140 K. (I,J) Type-II domains of DyMn6Sn6 crystal from 180 to 160 K.
For investigating these two types of domains, we study the magnetic domains in DyMn6Sn6 with the temperature decrease. In Figure 3D–G, we observe the coexistence of two types of magnetic domains from 230 to 140 K. At the beginning, the type-II domains are in the vast majority at 230 K. When the temperature keeps decreasing, the type-II domains transform into type-I domains. The type-I domain also changes, in which the white elliptic domain in the black belt domain becomes little and disappears with the temperature decrease. At 140 K, all the type-II domains disappear and only a few white elliptic domains are left. The white elliptic domains disappear and the type-I domain does not show any edges nor branches at 110 K. As the temperature continues decreasing, the magnetic domain does not change any more. As shown above, the magnetic domain structure at 110 K is a kind of stripe domain due to the strong perpendicular anisotropy. At the beginning, the type-II domains are in the vast majority due to the weak perpendicular anisotropy. When the temperature decreases, the perpendicular anisotropy becomes strong making the magnetic moment apt to move along the perpendicular plane. We find that type-I domain is less affected than the type-II domain. The domains floating on other domains may reverse under the influence of the perpendicular anisotropy. It is obvious that the type-II domain is more sensitive to the perpendicular anisotropy than that of type-I domain. Consequently, the type-II domains transform into type-I domain when the temperature continues decreasing. The type-I domain also changes because of the perpendicular anisotropy. At last, the perpendicular anisotropy only makes the stripe domain left. The stripe domain is affected by the demagnetizing field.
For investigating the type-II domain in detail, from 180 to 160 K, the structure of the type-II domains is observed. In Figure 3I,J, we find that our description of the type-II domains is the same as the domain in Figure 2A. It is shown that the structure of the type-II domains changes with temperature. As the temperature decreases, the main domain becomes wider, but the other part keeps the same width. The temperature changes the number of the other part domain. The lower the temperature is, the lower the number is. It is the main reason that the perpendicular anisotropy is enhanced as the temperature decreases. The perpendicular anisotropy can make the magnetic moment apt to move along the perpendicular plane. So, the main domain becomes wider and the number of the other stripe domains decreases. The type-I domain is a kind of manifestation of the branch domain at low temperature [37]. As the temperature increases, the branch structure grows on the type-I domain. The physics behind the domain transformation is the temperature dependence of magnetic anisotropy, especially in kagome lattice with strong uniaxial anisotropy. When the temperature decreases, the coefficients for anisotropy changes, leading to spin reorientation and domain variations, as shown in Figure 3.
To make sense of the domains clearly, we perform the experiment with the various magnetic fields at two representative temperatures, 223 and 173 K, as shown in Figure 4. The variable magnetic field of 0 or 510 Oe pointing up (+) or down (−) was applied by a permanent magnet. At 223 K, type-I domains sparsely appear while type-II domains are in the vast majority. One side of the white stripe domains flip to the black domain with the magnetic field increase and the other side of space between the white stripe domains becomes wider. With the magnetic field on, some of the type-II domains transform into the type-I domains. When the magnetic field is removed, the domain recovers. However, the type-I domain to the type-II domain transform does not recover, showing very strong irreversible effect. With the magnetic field reverse, a similar phenomenon happens. One side of the black stripe domains flips to the white domains and the other side of space between the black stripe domains becomes wider. Some type-II domains transform into type-I domain and do not recover without magnetic field assistance. At 173 K, we discover that the type-II domains in Figure 4F are far less than the type-II domains in Figure 2A. This is because the image in Figure 2A is obtained during zero field cooling (ZFC) process, but the image in Figure 4F is obtained during cooling process from the state in Figure 4E. Both the magnetic field and the temperature can make the type-II domain transform into type-I domain. At 173 K, we observe the same phenomenon. After a loop in the magnetic field, the area of the type-II domain decreases. From the above results, we can conclude that the type-I domain is more stable than the type-II domain.
FIGURE 4. (A–E) Magnetic domains of DyMn6Sn6 with varying magnetic field at 223 K. (F–G) Magnetic domains of DyMn6Sn6 with varying magnetic field at 173 K. (H) Phase diagram of magnetic domain distribution in DyMn6Sn6.
The phase diagram of magnetic domains is obtained in Figure 4H. At T > 235 K, the spin reorientation happens. There is no domain in the gray area. Type-II domain appears, as the temperature decreases, as shown in the light blue part. Type-II domain transforms into type-I domain under the influence of temperature and magnetic field. Type-I domain is shown in the yellow part. Type-II domain and type-I domain coexist locating at the intermediate region, as shown in the figure. As the temperature continues decreasing, only stripe domains are left, as marked by red color in the figure.
Conclusion
In summary, the magnetic domains in kagome lattice metal DyMn6Sn6 are observed using the micro-MOKE technique. Spin reorientation in DyMn6Sn6 is observed directly by the micro-MOKE technique from 255 to 235 K. There are two types of magnetic domains in DyMn6Sn6. Type-I domain is the belt domain. Type-II domain is the new stripe domain. The type-II domain exists from 160–235 K (ZFC). We analyze the structure of two types of domains. As the temperature decreases, the perpendicular anisotropy becomes strong, making the type-II domain transform into the type-I domain and even disappear. With a varying magnetic field experiment, we find that the type-II domain is less stable than the type-I domain. The phase diagram of magnetic domains in DyMn6Sn6 is obtained. However, the formation mechanism of new stripe domain in DyMn6Sn6 needs to be further investigated in the future.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
Author Contributions
ZC and WW grew the single crystal and wrote the paper. YH and ZC did the experiment about the magnetic curves and corrected the paper. ZC, ML, and CL did the experiment about micro-MOKE. ZM and JG corrected the paper and discussed. HD and ZS provided the funding and supervised the research. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the Natural Science Foundation of China (Grants No. 11904368) and the Natural Science Foundation of Anhui Province (Grants No. 2008085QA32).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Takagi R, White JS, Hayami S, Arita R, Honecker D, Rønnow HM, et al. Multiple-q Noncollinear Magnetism in an Itinerant Hexagonal Magnet. Sci Adv (2018) 4:eaau3402. doi:10.1126/sciadv.aau3402
2. Nagaosa N, Tokura Y. Topological Properties and Dynamics of Magnetic Skyrmions. Nat Nanotech (2013) 8:899–911. doi:10.1038/NNANO.2013.243
3. Nayak AK, Kumar V, Ma T, Werner P, Pippel E, Sahoo R, et al. Magnetic Antiskyrmions above Room Temperature in Tetragonal Heusler Materials. Nature (2017) 548:561–6. doi:10.1038/nature23466
4. Liu YZ, Zang JD. Overview and Outlook of Magnetic Skyrmions. Acta Physica Sinica (2018) 67:131201. doi:10.7498/aps.67.20180619
5. Fert A, Cros V, Sampaio J. Skyrmions on the Track. Nat Nanotech (2013) 8:152–6. doi:10.1038/nnano.2013.29
6. Balents L. Spin Liquids in Frustrated Magnets. Nature (2010) 464:199–208. doi:10.1038/nature08917
7. Jo G-B, Guzman J, Thomas CK, Hosur P, Vishwanath A, Stamper-Kurn DM. Ultracold Atoms in a Tunable Optical Kagome Lattice. Phys Rev Lett (2012) 108:045305. doi:10.1103/PhysRevLett.108.045305
8. Zhou Y, Kanoda K, Ng T-K. Quantum Spin Liquid States. Rev Mod Phys (2017) 89:89. doi:10.1103/RevModPhys.89.025003
9. Han T-H, Helton JS, Chu S, Nocera DG, Rodriguez-Rivera JA, Broholm C, et al. Fractionalized Excitations in the Spin-Liquid State of a Kagome-Lattice Antiferromagnet. Nature (2012) 492:406–10. doi:10.1038/nature11659
10. Li Y, Che HL, Sun XF. Syntheses and Magnetic Properties of RE3Sb3Zn2O (14)(RE=Tb,Dy and Ho) with a New 2D Kagome Structure. Chin J Rare Met (2020) 44(3):333–6. doi:10.13373/j.cnki.cjrm.XY18110010.html
11. Liu C, Zang Y, Ruan W, Gong Y, He K, Ma X, et al. Dimensional Crossover-Induced Topological Hall Effect in a Magnetic Topological Insulator. Phys Rev Lett (2017) 119:176809. doi:10.1103/PhysRevLett.119.176809
12. Kurumaji T, Nakajima T, Hirschberger M, Kikkawa A, Yamasaki Y, Sagayama H, et al. Skyrmion Lattice with a Giant Topological Hall Effect in a Frustrated Triangular-Lattice Magnet. Science (2019) 365:914–8. doi:10.1126/science.aau0968
13. Batista CD, Lin S-Z, Hayami S, Kamiya Y. Frustration and Chiral Orderings in Correlated Electron Systems. Rep Prog Phys (2016) 79:084504. doi:10.1088/0034-4885/79/8/084504
14. Hou Z, Ren W, Ding B, Xu G, Wang Y, Yang B, et al. Observation of Various and Spontaneous Magnetic Skyrmionic Bubbles at Room Temperature in a Frustrated Kagome Magnet with Uniaxial Magnetic Anisotropy. Adv Mater (2017) 29:1701144. doi:10.1002/adma.201701144
15. Tang J, Wu Y, Kong L, Wang W, Chen Y, Wang Y, et al. Two-dimensional Characterization of Three-Dimensional Magnetic Bubbles in Fe3Sn2 Nanostructures. Natl Sci Rev (2020) nwaa200. doi:10.1093/nsr/nwaa200
16. Tang J, Kong L, Wu Y, Wang W, Chen Y, Wang Y, et al. Target Bubbles in Fe3Sn2 Nanodisks at Zero Magnetic Field. ACS Nano (2020) 14:10986–92. doi:10.1021/acsnano.0c04036
17. Heritage K, Bryant B, Fenner LA, Wills AS, Aeppli G, Soh YA. Images of a First‐Order Spin‐Reorientation Phase Transition in a Metallic Kagome Ferromagnet. Adv Funct Mater (2020) 30:1909163. doi:10.1002/adfm.201909163
18. Xu G, Lian B, Zhang S-C. Intrinsic Quantum Anomalous Hall Effect in the Kagome LatticeCs2LiMn3F12. Phys Rev Lett (2015) 115:186802. doi:10.1103/PhysRevLett.115.186802
19. Mazin II, Jeschke HO, Lechermann F, Lee H, Fink M, Thomale R, et al. Theoretical Prediction of a Strongly Correlated Dirac Metal. Nat Commun (2014) 5:4261. doi:10.1038/ncomms5261
20. Tang E, Mei J-W, Wen X-G. High-temperature Fractional Quantum Hall States. Phys Rev Lett (2011) 106:236802. doi:10.1103/PhysRevLett.106.236802
21. Kida T, Fenner LA, Dee AA, Terasaki I, Hagiwara M, Wills AS. The Giant Anomalous Hall Effect in the Ferromagnet Fe3Sn2-A Frustrated Kagome Metal. J Phys Condens Matter (2011) 23:112205. doi:10.1088/0953-8984/23/11/112205
22. Wang X-L, Liu Y, Chen X. Tailoring Magnetostriction and Magnetic Domains of -oriented Fe80Ga16Al4 alloy by Magnetic Field Annealing. Rare Met (2020) 40:563–9. doi:10.1007/s12598-020-01590-3
23. Baidya S, Mallik AV, Bhattacharjee S, Saha-Dasgupta T. Interplay of Magnetism and Topological Superconductivity in Bilayer Kagome Metals. Phys Rev Lett (2020) 125:026401. doi:10.1103/PhysRevLett.125.026401
24. Ye L, Kang M, Liu J, von Cube F, Wicker CR, Suzuki T, et al. Massive Dirac Fermions in a Ferromagnetic Kagome Metal. Nature (2018) 555:638–42. doi:10.1038/nature25987
25. Morali N, Batabyal R, Nag PK, Liu E, Xu Q, Sun Y, et al. Fermi-arc Diversity on Surface Terminations of the Magnetic Weyl Semimetal Co3Sn2S2. Science (2019) 365:1286–91. doi:10.1126/science.aav2334
26. Jiao L, Xu Q, Cheon Y, Sun Y, Felser C, Liu E, et al. Signatures for Half-Metallicity and Nontrivial Surface States in the Kagome Lattice Weyl Semimetal Co3Sn2S2. Phys Rev B (2019) 99:245158. doi:10.1103/PhysRevB.99.245158
27. Zhang H, Feng X, Heitmann T, Kolesnikov AI, Stone MB, Lu Y-M, et al. Topological Magnon Bands in a Room-Temperature Kagome Magnet. Phys Rev B (2020) 101:100405. doi:10.1103/PhysRevB.101.100405
28. Yin J-X, Ma W, Cochran TA, Xu X, Zhang SS, Tien H-J, et al. Quantum-limit Chern Topological Magnetism in TbMn6Sn6. Nature (2020) 583:533–6. doi:10.1038/s41586-020-2482-7
29. Asaba T, Thomas SM, Curtis M, Thompson JD, Bauer ED, Ronning F Anomalous Hall Effect in the Kagome Ferrimagnet GdMn6Sn6. Phys Rev B (2020) 101:174415. doi:10.1103/PhysRevB.101.174415
30. Ma W, Xu X, Yin JX, Zhou H, Huang Y, Hasan MZ, et al. Rare Earth Engineering in RMn6Sn6 Topological Kagome Magnets. arXiv:2007.09913.
31. Fruchart D, Venturini G, Malaman B. Incommensurate MagneticStructures of RMn6Sn6(R = Sc, Y, Lu) Compounds from Neutron Diffraction Study. J Appl Phys (1996) 236:102–10. doi:10.1016/0925-8388(95)01998-7
32. Clatterbuck DM, Gschneidner KA. Magnetic Properties of RMn6Sn6 (R=Tb, Ho, Er, Tm, Lu) Single Crystals. J Magnetism Magn Mater (1999) 207:78–94. doi:10.1016/s0304-8853(99)00571-5
33. McCord J. Progress in Magnetic Domain Observation by Advanced Magneto-Optical Microscopy. J Phys D Appl Phys (2015) 48:333001. doi:10.1088/0022-3727/48/33/333001
34. Kustov M, Grechishkin R, Gusev M, Gasanov O, McCord J. A Novel Scheme of Thermographic Microimaging Using Pyro-Magneto-Optical Indicator Films. Adv Mater (2015) 27:5017–22. doi:10.1002/adma.201501859
35. Stupakiewicz A, Chizhik A, Tekielak M, Zhukov A, Gonzalez J, Maziewski A Direct Imaging of the Magnetization Reversal in Microwires Using All-MOKE Microscopy. Rev Scientific Instr (2014) 85:103702. doi:10.1063/1.4896758
Keywords: kagome metal, magnetic domain, microscopic magneto-optical kerr effect technique, perpendicular anisotropy, spin reorientation
Citation: Chen Z, Li M, Liu C, Ma Z, Han Y, Gao J, Wei W, Sheng Z and Du H (2021) Magnetic Domain Structure in Ferromagnetic Kagome Metal DyMn6Sn6. Front. Phys. 9:685510. doi: 10.3389/fphy.2021.685510
Received: 25 March 2021; Accepted: 17 May 2021;
Published: 09 June 2021.
Edited by:
Xichao Zhang, Shinshu University, JapanReviewed by:
Shilei Zhang, ShanghaiTech University, ChinaFarhad Sattari, University of Mohaghegh Ardabili, Iran
Copyright © 2021 Chen, Li, Liu, Ma, Han, Gao, Wei, Sheng and Du. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhaohui Chen, Y3poMTc3QG1haWwudXN0Yy5lZHUuY24=
†These authors have contributed equally to this work and share first authorship