- 1Institut für Theoretische Physik, Technische Universität Braunschweig, Braunschweig, Germany
- 2Space Research Institute, Austrian Academy of Sciences, Graz, Austria
- 3Institut für Geophysik und Extraterrestrische Physik, Technische Universität Braunschweig, Braunschweig, Germany
- 4DLR Institute of Planetary Research, Berlin, Germany
The error propagation of Capon’s minimum variance estimator resulting from measurement errors and position errors is derived within a linear approximation. It turns out, that Capon’s estimator provides the same error propagation as the conventionally used least square fit method. The shape matrix which describes the location depence of the measurement positions is the key parameter for the error propagation, since the condition number of the shape matrix determines how the errors are amplified. Furthermore, the error resulting from a finite number of data samples is derived by regarding Capon’s estimator as a special case of the maximum likelihood estimator.
1 Introduction
The reconstruction of model parameters from a given set of measurements is one of the most important tasks in geophysical and space science studies. The measurements are always affected by measurement errors which result in estimation errors for the wanted model parameters. The Capon method [1–3], also known as minimum variance distortionless response estimator (MVDR), is currently being considered as a robust inversion method for the analysis of planetary magnetic fields. In the past, the method has successfully been applied to the analysis of waves [1, 4] and therefore, specific attention has been paid to errors of the spectrum resulting from random perturbations in the amplitude and phase of sensor arrays [5]. Since Capon’s method is based on the evaluation of statistically averaged data, the spectrum is also affected by errors resulting from a finite number of samples [6]. Within the estimation of the frequency-wavenumber spectrum, the difference between static structures and waves or their combination can be discerned through dispersion relation analysis [7–12]. Concerning the application of the Capon method for the analysis of planetary magnetic fields, the error propagation of Capon’s estimator itself is of major importance for assessing the quality of the reconstructed model parameters. In general, two essential types of errors are expectable. On the one hand, the measured magnetic field data are affected by e.g., offsets, gains resulting from thermal variations and spacecraft magnetic disturbances [13]. On the other hand, the determination of the spacecraft’s positions can be defective (measurement position errors), which results in a defective shape matrix. As a follow-up of the generalized derivation of Capon’s method [3] and the error estimation of the power spectrum [6], in this work the effects of measurement errors, measurement position errors as well as finite sample sizes on Capon’s estimator are considered.
2 Capon’s Method
Before deducing the error propagation of Capon’s method, the main ideas of the method are shortly revisited [2, 3]. Due to the complexity of several physical problems, the entire parametrization of experimental data is unrealizable. Thus, it is useful to decompose the measurements
is valid. The measurement noise is assumed to be Gaussian with variance
with respect to the distortionless constraint
where
The robustness of the method can be improved by the diagonal loading technique
3 Error Propagation
In the following, the error propagation of Capon’s estimator is deduced. Since it is expectable that the errors are much smaller than the measurements themselves, the error propagation is derived by making use of a linearization. For the approximation of the matrix inversions that are necessary for calculating Capon’s estimator, the Neumann series bears of essential meaning for which reason we discuss it in a seperate section.
3.1 Neumann Series
The Neumann series is a special case of the functional calculus for linear operators or matrices, respectively, [14] and enables the approximation of matrix inversions.
Let
where
As a direct consequence it follows that
For the estimation of Capon’s error propagation a generalized formulation of the Neumann series is required. To expand the inverse of the sum of a matrix
If
3.2 Measurement Errors
In the following, the error of Capon’s estimator resulting from measurement errors is derived. The model for the (temporal) statistically averaged accurate data
where
where
denotes the accurate filter matrix composed of the shape matrix
The perturbed measurements
where
where
where
denotes the perturbed filter matrix. Thus, the difference between the accurate and the perturbed estimator results in
Within the practical application only the perturbed measurements
where
In the case of
as well as
for the unknown coefficient matrix
it follows that
where
Inserting this approximation into Eq. 16 delivers
where
within the linear approximation. Further transformation for estimating the relative error of the estimator delivers
Making use of the Cauchy-Schwarz inequality yields
where
or equivalently
for the relative error. When the measurements are adequately described by the underlying model, i.e.,
Comparing this expression with the relative error of the least square fit estimator [15].
where
delivers
where
where
Thus, Capon’s estimator propagates the measurement errors in the same way as the least square fit estimator. This mathematical property can be interpreted as follows: These two methods differ in the filter matrices
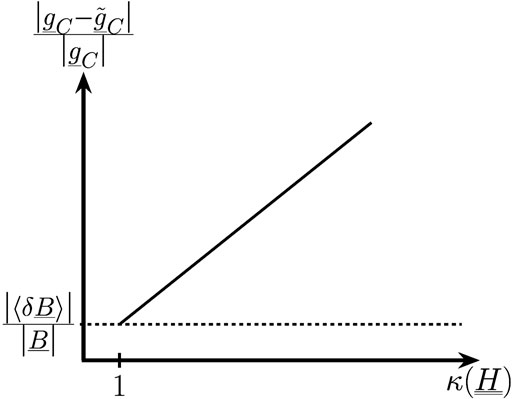
FIGURE 1. Sketch of the upper bound for the relative estimation error resulting from measurement errors with respect to the condition number
Furthermore, it should be noted that the condition number of the shape matrix determines how the measurement errors are amplified. Thereby, the condition number depends on the underlying model and the measurement positions, whereas the measurement error is produced by the sensor. For a given underlying model, the condition number solely depends on the measurement positions. Thus, the estimation errors can be reduced by analyzing measurements from suitable data points. Considering the analysis of Mercury’s magnetic field, the underlying model describes the geometry of the magnetic field, for example the internal dipole and quadrupole field [2, 3]. For the estimation of the corresponding Gauss coefficients [16, 17], the data points have to cover the geometry of the field properly. For example, the superposition of Mercury’s internal dipole field with the quadrupole field can equivalently be described as a northward shifted dipole field. When only measurement positions in the northern hemisphere are available, the condition number of the shape matrix increases, resulting in large estimation errors so that the internal field can be misinterpreted as a strong dipole field. The analysis of measurement points covering the southern and the northern hemisphere symmetrically, like that of the BepiColombo mission, decreases the condition number and enables a more detailed characterization of the geometry of Mercury’s internal magnetic field [18]. The smaller the condition number of the shape matrix becomes, the better the geometry of the field is covered by the data points [18].
Before discussing the errors resulting from the perturbed determination of the measurement positions, let us make a general comment about the error of Capon’s estimator resulting from measurement errors. The perturbed data can be rewritten in the form
where
it does not follow that
3.3 Measurement Position Errors
The model for the correctly determined measurement positions is given by
The corresponding accurate estimator results in
where
The perturbed determination of the sensor’s positions transfers onto a perturbed shape matrix
and the corresponding perturbed estimator results in
where
The deviation between the accurate and the perturbed estimator results in
As discussed above, only the perturbed filter matrix
which describes the magnetic field of a current sheet superposed with Mercury’s internal dipolar field [6], where
Assuming that
by making use of a Taylor series expansion. It should be noted that the shape matrix can be linearized for any underlying model by performing a Taylor series expansion for the functions within the model. Linearization of the error terms for the estimation of the unknown accurate filter matrix delivers
Making use of the Neumann series results in
so that
or equivalently
Thus, the deviation of the estimator can be approximated via
By
and therefore
Within the application of Capon’s method to Mercury’s magnetic field analysis, the first summand on the right hand side of Eq. 54 is of the order of about
The relative error results in
where
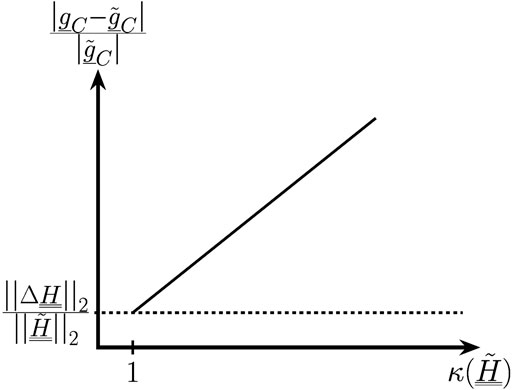
FIGURE 2. Sketch of the upper bound for the relative estimation error resulting from measurement position errors with respect to the condition number
3.4 Measurement Errors and Measurement Position Errors
Within the former sections the influences of measurement errors and measurement position errors have been discussed separately. Within the practical application it is expectable that both errors occur simultanously. The relative error resulting from the noisy measurements and the perturbed measurement positions is given by the quadratic sum of the two cases discussed above
This can be derived as follows:
The accurate model is given by
so that the corresponding accurate estimator results in
where
The measured data are not affected by the perturbed determination of the sensor’s positions. The data are solely affected by measurement errors
The corresponding perturbed estimator results in
where
and
By making use of the Neumann series, the unknown filter matrix
Using
and again making use of the Neumann series delivers
Taking into account that
within the linear approximation as well as
the deviation between the estimators can be approximated by
Using
and thus,
Assuming that
It is important to note that the right sides of Eqs. 35, 56 and 73 represent upper bounds for the error of the estimator. These bounds can be much larger than the true errors. The great advantage of the bounds lies in the fact that they solely depend on known quantities, wheras the accurate estimator for calculating the true estimation error is unknown within the practical application of the method. Thus, the above derived upper bounds are conservative and guarantee that the true estimation errors cannot exceed these bounds as long as the measurement errors as well as the measurement position errors are much smaller than the measurements themselves so that the linear approximation is valid.
4 Finite Sample Averaging
For the calculation of Capon’s estimator, averaged magnetic field data
are required [3]. Here, Q denotes the number of measurements at a fixed set of data points. Within the practical application of the method only a finite number
In the vicinity of its maximum value the likelihood function can be approximated as
where
For most practical applications, the noise matrix
The weighted difference between the model and the data can be rewritten as
As discussed above, the data covariance matrix
Insertion into Eq. 76 yields
or equivalently
The m’th component of Capon’s estimator
where
Since
where
yielding
Because of
and therefore,
which is in agreement with the estimator resulting from the linear algebraic formulation of Capon’s method [3]. The second derivative results in
Using the definition of the coefficient matrix [3].
or equivalently
delivers
Thus, the error of the m’th component of Capon’s estimator results in
which declines as
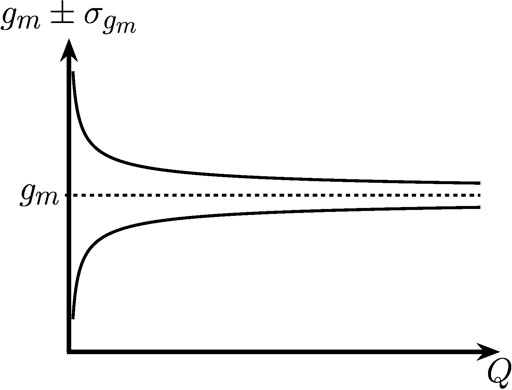
FIGURE 3. Sketch of the m’the component of Capon’s estimator and the corresponding
5 Summary and Outlook
The analysis of the error propagation is of major importance for the application of linear inversion methods. Within a linear approximation, upper bounds for the errors of Capon’s estimator resulting from measurement errors and measurement position errors are derived. These upper bounds solely depend on known quantities, i.e., measurements and measurement positions, whereas the true estimation error cannot be calculated within the practical application of the method, since the accurate estimator is unavailable. It turns out that Capon’s method provides the same error propagation as the least square fit method. These two methods differ in the filter matrices which weight or eliminate parts of the data in different ways. Since these matrices are applied to the same set of measurements, the different weighting of the data or the elimination of subsets does not reduce the errors. The condition number of the shape matrix is the key parameter for the error propagation, since it determines how the errors are amplified. The measurement errors as well as the measurement position errors have to be estimated from the measurements. For a given underlying model, the condition number of the shape matrix solely depends on the measurement positions. Thus, the amplification of the errors can be reduced by choosing preferred data points.
Furthermore, Capon’s method is based on the evaluation of statistically averaged data. For the practical application of the method only a finite number Q of samples is available. This limited number of samples results in an error of Capon’s estimator which can be derived by regarding Capon’s method as a special case of the maximum likelihood estimator. The more samples are available, the smaller the error becomes, since the error declines as
As a follow-up of the generalized derivation of Capon’s method, the present work establishes the mathematical basis of Capon’s error propagation for the practical application of the method.
Appendix: Matrix Power of the Data Covariance Matrix
For the calculation of Capon’s estimator the inverse data covariance matrix
Furthermore, there exists a unitary transformation
where
is a diagonal matrix that contains the eigenvalues of
where
Further transformation delivers
so that the square root of the inverse data covariance matrix is defined as
where
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors contributed conception and design of the study; ST and UM wrote the first draft of the manuscript; All authors contributed to manuscript revision, read and approved the submitted version.
Funding
We acknowledge support by the German Research Foundation and the Open Access Publication Funds of the Technische Universität Braunschweig. The work by YN is supported by the Austrian Space Applications Program at the Austrian Research Promotion Agency under contract 865967. DH was supported by the German Ministerium für Wirtschaft und Energie and the German Zentrum für Luft-und Raumfahrt under contract 50 QW1501.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer LZ declared a past collaboration with one of the authors YN to the handling editor.
Acknowledgments
The authors are grateful for stimulating discussions and helpful suggestions by Karl-Heinz Glassmeier, Patrick Kolhey and Alexander Schwenke.
References
1. Capon J. High-resolution Frequency-Wavenumber Spectrum Analysis. Proc IEEE (1969) 57:1408–18. doi:10.1109/PROC.1969.7278
2. Toepfer S, Narita Y, Heyner D, Motschmann U. The Capon Method for Mercury's Magnetic Field Analysis. Front Phys (2020) 8:249. doi:10.3389/fphy.2020.00249
3. Toepfer S, Narita Y, Heyner D, Kolhey P, Motschmann U. Mathematical Foundation of Capon's Method for Planetary Magnetic Field Analysis. Geosci Instrum Method Data Syst (2020) 9:471–81. doi:10.5194/gi-9-471-2020
4. Motschmann U, Woodward TI, Glassmeier KH, Southwood DJ, Pinçon JL. Wavelength and Direction Filtering by Magnetic Measurements at Satellite Arrays: Generalized Minimum Variance Analysis. J Geophys Res (1996) 101:4961–5. doi:10.1029/95JA03471
5. Su W, Gu H, Ni J, Liu G. Performance Analysis of MVDR Algorithm in the Presence of Amplitude and Phase Errors. IEEE Trans Antennas Propagat (2001) 49(12):1875–7. doi:10.1109/8.982472
6. Narita Y. A Note on Capon’s Minimum Variance Projection for Multi-Spacecraft Data Analysis. Front Phys (2019) 7:121. doi:10.3398/fphy.2019.00008
7. Sahraoui F, Belmont G, Rezeau L, Cornilleau-Wehrlin N, Pinçon JL, Balogh A. Anisotropic Turbulent Spectra in the Terrestrial Magnetosheath as Seen by the Cluster Spacecraft. Phys Rev Lett (2006) 96:7. doi:10.1103/PhysRevLett.96.075002
8. Huang SY, Zhou M, Sahraoui F, Deng XH, Pang Y, Yuan ZG, et al. Wave Properties in the Magnetic Reconnection Diffusion Region with Highβ: Application of Thek-Filtering Method to Cluster Multispacecraft Data. J Geophys Res (2010) 115:17–9. doi:10.1029/2010JA015335
9. Narita Y, Comişel H, Motschmann U. Spatial Structure of Ion-Scale Plasma Turbulence. Front Phys (2014) 2:13. doi:10.3389/fphy.2014.00013
10. Roberts OW, Li X, Jeska L. A Statistical Study of the Solar Wind Turbulence at Ion Kinetic Scales Using the K-Filtering Technique and Cluster Data. ApJ (2015) 802:1. doi:10.1088/0004-637X/802/1/2
11. Wang T, Cao J, Fu H, Meng X, Dunlop M. Compressible Turbulence with Slow-Mode Waves Observed in the Bursty Bulk Flow of Plasma Sheet. Geophys Res Lett (2016) 43(5):1854–61. doi:10.1002/2016GL068147
12. Zhang L, He J, Narita Y, Feng X. Reconstruction Test of Turbulence Power Spectra in 3D Wavenumber Space with at Most 9 Virtual Spacecraft Measurements. J Geophys Res Space Phys (2021) 126:e2019JA027413. doi:10.1029/2019JA027413
13. Narita Y, Plaschke F, Magnes W, Fischer D, Schmid D. Error Estimate for Fluxgate Magnetometer In-Flight Calibration on a Spinning Spacecraft. Geosci Instrum Method Data Syst (2021) 10:13–24. doi:10.5194/gi-10-13-202
15. Belsley DA, Kuh E, Welsch RE. The Condition Number, Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. New York: Wiley (1980). p. 100–4.
16. Gauß CF. (1839) Allgemeine Theorie des Erdmagnetismus: Resultate aus den Beobachtungen des magnetischen Vereins im Jahre 1838, editorsCF Gauss, and W Weber. Leipzig: Weidmannsche Buchhandlung (1839). p. 1–57.
17. Glassmeier K-H, Tsurutani BT. Carl Friedrich Gauss—General Theory of Terrestrial Magnetism—A Revised Translation of the German Text. Hist Geo Space Sci (2014) 5:11–62. doi:10.5194/hgss-5-11-2014
Keywords: Capon’s method, error propagation, least-squares method, maximum likelihood, condition number
Citation: Toepfer S, Narita Y, Heyner D and Motschmann U (2021) Error Propagation of Capon’s Minimum Variance Estimator. Front. Phys. 9:684410. doi: 10.3389/fphy.2021.684410
Received: 23 March 2021; Accepted: 20 May 2021;
Published: 09 June 2021.
Edited by:
Jiansen He, Peking University, ChinaReviewed by:
Tieyan Wang, Rutherford Appleton Laboratory, United KingdomLei Zhang, China Academy of Space Technology (CAST), China
Copyright © 2021 Toepfer, Narita, Heyner and Motschmann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: S. Toepfer, cy50b2VwZmVyQHR1LWJyYXVuc2Nod2VpZy5kZQ==
 S. Toepfer
S. Toepfer Y. Narita
Y. Narita D. Heyner3
D. Heyner3