- 1School of Materials Science and Engineering, Dongguan University of Technology, Dongguan, China
- 2Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai, China
- 3Guangdong Provincial Key Laboratory of Optical Information Materials and Technology and Institute for Advanced Materials, South China Academy of Advanced Optoelectronics, South China Normal University, Guangzhou, China
Reorientation of skyrmion crystal (SkX) with respect to crystallographic axes is believed to be insensitive to anisotropies of fourth order in spin-orbit coupling, for which sixth order terms are considered for explanation. Here, we show that this is wrong due to an oversimplified assumption that SkX possesses hexagonal symmetry. When the deformation of SkX is taken into account, fourth order anisotropies such as exchange anisotropy and magnetocrystalline anisotropy have pinning (in this work, the word ‘pinning’ refers to the reorientation effects of intrinsic anisotropy terms) effects on SkX. In particular, we reproduce some experiments of MnSi and Fe1−xCoxSi by considering the effect of fourth order magnetocrystalline anisotropy alone. We reproduce the
1 Introduction
Helimagnets have attracted extensive interest since the first observation of magnetic skyrmions in 2009 [1]. Magnetic skyrmions in helimagnets are nontrivial spin textures, in which the spins point in all of the directions wrapping a sphere. Their topological protection [2] and facile current driven motion [3, 4] make them possible to be applied in novel spintronic and information storage devices [5, 6].
In helimagnets such as MnSi, Fe1−xCoxSi, and Cu2OSeO3, the ferromagnetic exchange interaction (for Cu2OSeO3, the exchange interaction consists of ferromagnetic and antiferromagnetic interactions, but the field-induced ground state is closer to ferromagnetic than antiferromagnetic [7, 8]) and the Dzyaloshinsky-Moriya interaction (DMI), which arises due to the broken of space inversion symmetry [9, 10], dominate the free energy when studying bulk material free from any external magnetic field. The former favors parallel spin alignment, while the latter favors the twist of the spins. They compete with each other and result in SkX at appropriate magnetic field just below the Curie temperature [1, 11–14]. In experiments, when the magnetic field is along directions with high symmetry, such as the [001], [111] and [110] directions, the wave vectors of SkX are orientated with respect to the crystallographic axes [1, 12, 15, 16]. This indicates the existence of anisotropy energy. The anisotropies of fourth order in spin-orbit coupling, such as the exchange anisotropy and fourth order magnetocrystalline anisotropy, are widely used to explain the pinning of helical phase, the transition from helical to conical phase and the appearance of tilted conical phase [1, 17–20]. However, according to the perturbation theory [1, 12, 16, 21], which treats the anisotropies perturbatively and approximates SkX by a triple-Q structure with three equivalent wave vectors forming a regular triangle, they are insensitive to the pinning of SkX. As a consequence, anisotropies with higher order are proposed. In our opinion, ignoring the deformation of SkX is oversimplified, because many experiments show that the structure of SkX is sensitive to anisotropy of the system which destroys its hexagonal symmetry [22–24].
In this work, we study the pinning effects of the exchange anisotropies and the fourth order magnetocrystalline anisotropy on deformable SkX. We apply a rescaled free-energy-density model for T point group and describe Bloch SkX by a three-order Fourier expansion with deformation-related degrees of freedom. Firstly, we study four anisotropies (three types of exchange anisotropies and a fourth order magnetocrystalline anisotropy in helimagnets with T symmetry) separately. It is found that they have different pinning effects on SkX. Then, by plotting the deformation-related parameters as functions of one exchange anisotropy, we figure out that the deformation of SkX is characterized by the change of amplitudes, lengths and azimuth angles of wave vectors. Next, we compare our results with some experiments, the fourth order magnetocrystalline anisotropy may explain the pinning of SkX in MnSi [1, 25, 26] and Fe1−xCoxSi [12, 27–29]. To reproduce the
2 Model
Based on the continuum spin model established by Bak and Jensen [17], we write the rescaled free-energy density [30] for helimagnets with the symmetry of T point group in the following form:
Here,
where
For bulk B20 materials, the skyrmion plane rotates with respect to the applied magnetic field. To describe the configuration of SkX under magnetic field with different direction, we should choose an appropriate cartesian coordinates system O-
In the cartesian coordinates system O-
Here,
In reciprocal space,
where
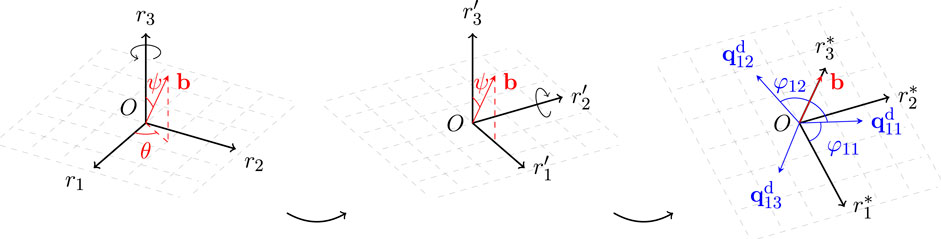
FIGURE 1. Rotations of coordinates system. θ and ψ are the azimuthal and polar angles of the magnetic field
According to Eqs. (1) and (2), the free energy density is a functional of
the free-energy density can be rewritten as, after averaging over a magnetic unit cell
At certain temperature t, magnetic field
Our analytical method can only deal with periodic magnetization structure. For the cases where the periodicity of skyrmions is broken, e.g., the thermal-induced disorder or the pinning from impurities, the review [33] and references therein are good to refer to.
3 Results and Discussion
We first investigate the pinning effects of anisotropies
We change the rotation-related parameter
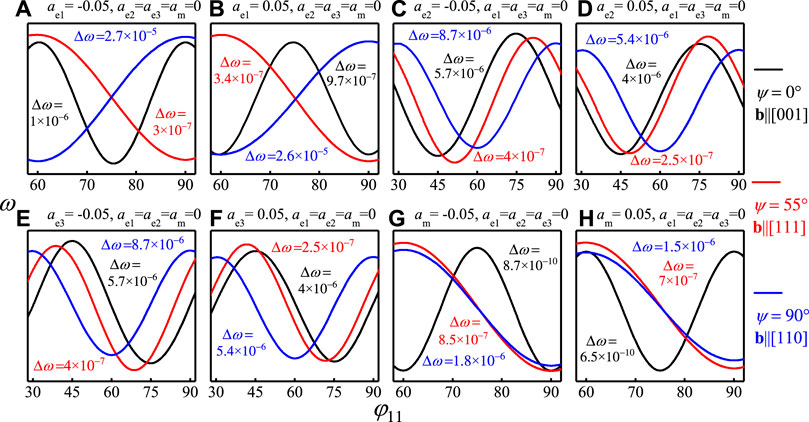
FIGURE 2. ω as a function of
In Figure 2, we give the values of
SkX is treated as a deformable structure. To reveal how anisotropy energy deforms SkX, we take
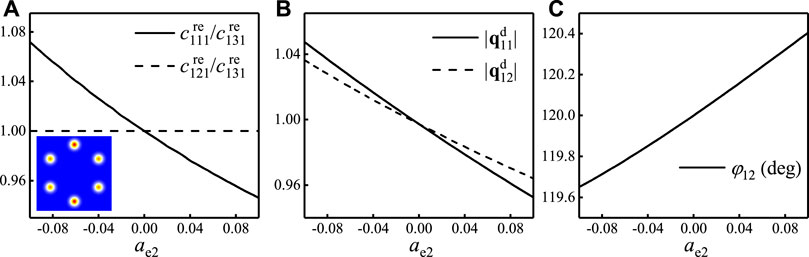
FIGURE 3. Deformation of SkX induced by
We now compare our results with some experiments. The SANS experiments of
Cu2OSeO3 is another helimagnet hosting SkX, a peculiar experimental phenomenon about it is that for
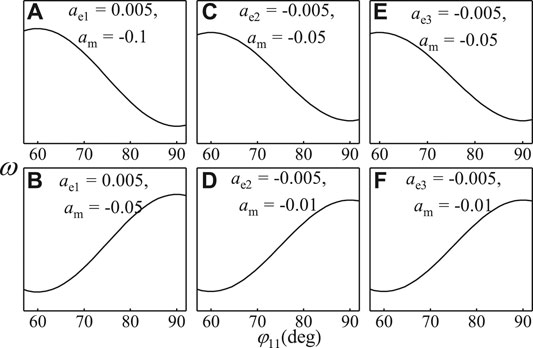
FIGURE 4. Combined effects of the exchange and fourth order magnetocrystalline anisotropies on SkX. The absolute value of exchange anisotropy coefficient is fixed to be 0.005, the value of magnetocrystalline anisotropy coefficient is fixed to be −0.1 or −0.05 or −0.01. The results are calculated at
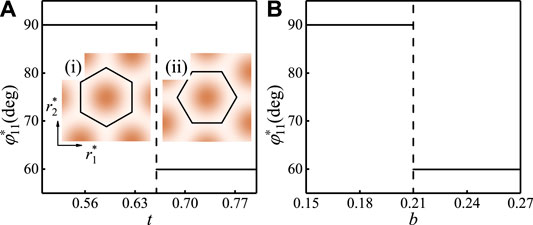
FIGURE 5.
In another published work [41], we explain the electric-field-induced continuous rotation of SkX [42] by extending the present model. Unlike a previous theory [42] which explains the phenomenon by considering both the fourth and sixth order magnetocrystalline anisotropies, we find that a combination of fourth order exchange anisotropies and magnetocrystalline anisotropies dominates the phenomena. This is because the theory used in [42] obtains a positive coefficient of the fourth order magnetocrystalline anisotropy
In polar magnets with
Here, we have ignored the terms
For
For
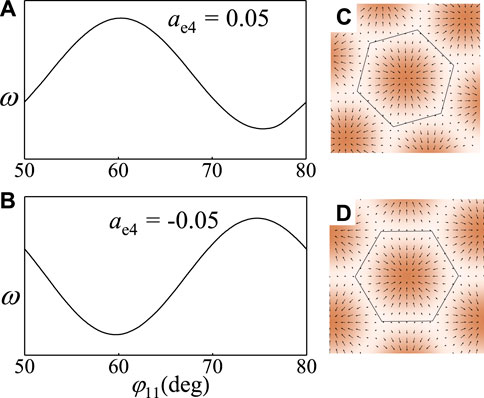
FIGURE 6. ω as a function of
4 Conclusion
In conclusion, the exchange and fourth order magnetocrystalline anisotropies deform SkX by changing the amplitudes of, the lengths of, and the angles between wave vectors and thus show pinning effects on SkX. The results of magnetocrystalline anisotropy [exchange anisotropy] may explain some experiments of MnSi and Fe1−xCoxSi [VOSe2O5]. By considering the exchange and magnetocrystalline anisotropies at the same time, the
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
XW and YH conceived the idea. XW finished the analytical deduction, and performed all the calculations. XW, YH, ZH, and BW discussed the results for revision and co-wrote the manuscript.
Funding
This work was supported by the NSFC (National Natural Science Foundation of China) through fund Nos. 11772360, 11832019, 11572355 and 51901081, the National Key Research and Development Program of China (Grant No. 2020YFA0309300), the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2019A1515012016), and the Pearl River Nova Program of Guangzhou (Grant No. 201806010134).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Mühlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, et al. Skyrmion Lattice in a Chiral Magnet. Science (2009) 323:915–9. doi:10.1126/science.1166767
2. Nagaosa N, Tokura Y. Topological Properties and Dynamics of Magnetic Skyrmions. Nat Nanotech (2013) 8:899–911. doi:10.1038/nnano.2013.243
3. Jonietz F, Mühlbauer S, Pfleiderer C, Neubauer A, Münzer W, Bauer A, et al. Spin Transfer Torques in Mnsi at Ultralow Current Densities. Science (2010) 330:1648–51. doi:10.1126/science.1195709
4. Yu XZ, Kanazawa N, Zhang WZ, Nagai T, Hara T, Kimoto K, et al. Skyrmion Flow Near Room Temperature in an Ultralow Current Density. Nat Commun (2012) 3:988. doi:10.1038/ncomms1990
5. Zhang X, Ezawa M, Zhou Y. Magnetic Skyrmion Logic gates: Conversion, Duplication and Merging of Skyrmions. Sci Rep (2015a) 5:9400. doi:10.1038/srep09400
6. Zhang X, Zhao GP, Fangohr H, Liu JP, Xia WX, Xia J, et al. Skyrmion-skyrmion and Skyrmion-Edge Repulsions in Skyrmion-Based Racetrack Memory. Sci Rep (2015b) 5:7643. doi:10.1038/srep07643
7. Janson O, Rousochatzakis I, Tsirlin AA, Belesi M, Leonov AA, Rößler UK, et al. The Quantum Nature of Skyrmions and Half-Skyrmions in Cu2oseo3. Nat Commun (2014) 5:5376–11. doi:10.1038/ncomms6376
8. Yang JH, Li ZL, Lu XZ, Whangbo M-H, Wei S-H, Gong XG, et al. Strong Dzyaloshinskii-Moriya Interaction and Origin of Ferroelectricity inCu2OSeO3. Phys Rev Lett (2012) 109:107203. doi:10.1103/physrevlett.109.107203
9. Dzyaloshinsky I. A Thermodynamic Theory of "weak" Ferromagnetism of Antiferromagnetics. J Phys Chem Sol (1958) 4:241–55. doi:10.1016/0022-3697(58)90076-3
10. Moriya T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys Rev (1960) 120:91–8. doi:10.1103/physrev.120.91
11. Wilhelm H, Baenitz M, Schmidt M, Rößler UK, Leonov AA, Bogdanov AN. Precursor Phenomena at the Magnetic Ordering of the Cubic Helimagnet Fege. Phys Rev Lett (2011) 107:127203. doi:10.1103/physrevlett.107.127203
12. Münzer W, Neubauer A, Adams T, Mühlbauer S, Franz C, Jonietz F, et al. Skyrmion Lattice in the Doped Semiconductor Fe1-Xcoxsi. Phys Rev B (2010) 81:041203. doi:10.1103/physrevb.81.041203
13. Ruff E, Widmann S, Lunkenheimer P, Tsurkan V, Bordács S, Kézsmárki I, et al. Multiferroicity and Skyrmions Carrying Electric Polarization in Gav4s8. Sci Adv (2015) 1:e1500916. doi:10.1126/sciadv.1500916
14. Omrani A, White J, Prša K, Živković I, Berger H, Magrez A, et al. Exploration of the Helimagnetic and Skyrmion Lattice Phase Diagram in Cu2oseo3 Using Magnetoelectric Susceptibility. Phys Rev B (2014) 89:064406. doi:10.1103/physrevb.89.064406
15. Moskvin E, Grigoriev S, Dyadkin V, Eckerlebe H, Baenitz M, Schmidt M, et al. Complex Chiral Modulations in Fege Close to Magnetic Ordering. Phys Rev Lett (2013) 110:077207. doi:10.1103/PhysRevLett.110.077207
16. Seki S, Kim J-H, Inosov DS, Georgii R, Keimer B, Ishiwata S, et al. Formation and Rotation of Skyrmion crystal in the Chiral-Lattice Insulator Cu2oseo3. Phys Rev B (2012) 85:220406. doi:10.1103/physrevb.85.220406
17. Bak P, Jensen MH. Theory of Helical Magnetic Structures and Phase Transitions in Mnsi and Fege. J Phys C: Solid State Phys (1980) 13:L881–L885. doi:10.1088/0022-3719/13/31/002
18. Park J-H, Han JH. Zero-temperature Phases for Chiral Magnets in Three Dimensions. Phys Rev B (2011) 83:184406. doi:10.1103/physrevb.83.184406
19. Halder M, Chacon A, Bauer A, Simeth W, Mühlbauer S, Berger H, et al. Thermodynamic Evidence of a Second Skyrmion Lattice Phase and Tilted Conical Phase in Cu2oseo3. Phys Rev B (2018) 98:144429. doi:10.1103/physrevb.98.144429
20. Chacon A, Heinen L, Halder M, Bauer A, Simeth W, Mühlbauer S, et al. Observation of Two Independent Skyrmion Phases in a Chiral Magnetic Material. Nat Phys (2018) 14:936–41. doi:10.1038/s41567-018-0184-y
21. Luo Y, Lin S-Z, Fobes DM, Liu Z, Bauer ED, Betts JB, et al. Anisotropic Magnetocrystalline Coupling of the Skyrmion Lattice in Mnsi. Phys Rev B (2018) 97:104423. doi:10.1103/physrevb.97.104423
22. Shibata K, Iwasaki J, Kanazawa N, Aizawa S, Tanigaki T, Shirai M, et al. Large Anisotropic Deformation of Skyrmions in Strained crystal. Nat Nanotech (2015) 10:589–92. doi:10.1038/nnano.2015.113
23. Wang C, Du H, Zhao X, Jin C, Tian M, Zhang Y, et al. Enhanced Stability of the Magnetic Skyrmion Lattice Phase under a Tilted Magnetic Field in a Two-Dimensional Chiral Magnet. Nano Lett (2017) 17:2921–7. doi:10.1021/acs.nanolett.7b00135
24. Makino K, Reim JD, Higashi D, Okuyama D, Sato TJ, Nambu Y, et al. Thermal Stability and Irreversibility of Skyrmion-Lattice Phases in Cu2oseo3. Phys Rev B (2017) 95:134412. doi:10.1103/physrevb.95.134412
25. Grigoriev SV, Potapova NM, Moskvin EV, Dyadkin VA, Dewhurst C, Maleyev SV. Hexagonal Spin Structure of A-phase in Mnsi: Densely Packed Skyrmion Quasiparticles or Two-Dimensionally Modulated Spin Superlattice?. Jetp Lett (2014) 100:216–21. doi:10.1134/s0021364014150065
26. Bannenberg LJ, Qian F, Dalgliesh RM, Martin N, Chaboussant G, Schmidt M, et al. Reorientations, Relaxations, Metastabilities, and Multidomains of Skyrmion Lattices. Phys Rev B (2017a) 96:184416. doi:10.1103/physrevb.96.184416
27. Adams T, Mühlbauer S, Neubauer A, Münzer W, Jonietz F, Georgii R, et al. Skyrmion Lattice Domains in Fe1−xCoxSi. J Phys Conf Ser (2010) 200:032001. doi:10.1088/1742-6596/200/3/032001
28. Bannenberg LJ, Kakurai K, Qian F, Lelièvre-Berna E, Dewhurst CD, Onose Y, et al. Extended Skyrmion Lattice Scattering and Long-Time Memory in the Chiral magnetFe1−xCoxSi. Phys Rev B (2016) 94:104406. doi:10.1103/physrevb.94.104406
29. Bannenberg LJ, Kakurai K, Falus P, Lelièvre-Berna E, Dalgliesh R, Dewhurst CD, et al. Universality of the Helimagnetic Transition in Cubic Chiral Magnets: Small Angle Neutron Scattering and Neutron Spin echo Spectroscopy Studies of Fecosi. Phys Rev B (2017b) 95:144433. doi:10.1103/physrevb.95.144433
30. Wan X, Hu Y, Wang B. Exchange-anisotropy-induced Intrinsic Distortion, Structural Transition, and Rotational Transition in Skyrmion Crystals. Phys Rev B (2018) 98:174427. doi:10.1103/physrevb.98.174427
31. Hu Y. Wave Nature and Metastability of Emergent Crystals in Chiral Magnets. Commun Phys (2018) 1:82. doi:10.1038/s42005-018-0071-y
33. Reichhardt C, Reichhardt C, Milosevic M. Statics and Dynamics of Skyrmions Interacting with Pinning: A Review. arXiv:2102.10464 (2021).
34. Hu Y, Wang B. Unified Theory of Magnetoelastic Effects in B20 Chiral Magnets. New J Phys (2017) 19:123002. doi:10.1088/1367-2630/aa9507
35. Ehlers D, Stasinopoulos I, Kézsmárki I, Fehér T, Tsurkan V, von Nidda H-AK, et al. Exchange Anisotropy in the Skyrmion Host Gav4s8. J Phys Condens Matter (2016) 29:065803. doi:10.1088/1361-648x/aa4e7e
36. Adams T, Mühlbauer S, Pfleiderer C, Jonietz F, Bauer A, Neubauer A, et al. Long-range Crystalline Nature of the Skyrmion Lattice in Mnsi. Phys Rev Lett (2011) 107:217206. doi:10.1103/physrevlett.107.217206
37. Grigoriev S, Maleyev S, Dyadkin V, Menzel D, Schoenes J, Eckerlebe H. Principal Interactions in the Magnetic System Fe1-Xcoxsi: Magnetic Structure and Critical Temperature by Neutron Diffraction and Squid Measurements. Phys Rev B (2007) 76:092407. doi:10.1103/physrevb.76.092407
38. Takeda M, Endoh Y, Kakurai K, Onose Y, Suzuki J, Tokura Y. Nematic-to-smectic Transition of Magnetic Texture in Conical State. J Phys Soc Jpn (2009) 78:093704. doi:10.1143/jpsj.78.093704
39. Bannenberg LJ, Wilhelm H, Cubitt R, Labh A, Schmidt MP, Lelièvre-Berna E, et al. Multiple Low-Temperature Skyrmionic States in a Bulk Chiral Magnet. Npj Quan Mater. (2019) 4:11. doi:10.1038/s41535-019-0150-7
40. Qian F, Bannenberg LJ, Wilhelm H, Chaboussant G, Debeer-Schmitt LM, Schmidt MP, et al. New Magnetic Phase of the Chiral Skyrmion Material Cu2oseo3. Sci Adv (2018) 4:eaat7323. doi:10.1126/sciadv.aat7323
41. Wan X, Hu Y, Wang B. First and Second Order Rotational Transitions of Skyrmion crystal in Multiferroic Cu2oseo3 under Electric Field. Appl Phys Lett (2020) 116:182403. doi:10.1063/5.0003880
42. White JS, Prša K, Huang P, Omrani AA, Živković I, Bartkowiak M, et al. Electric-Field-Induced Skyrmion Distortion and Giant Lattice Rotation in the Magnetoelectric InsulatorCu2OSeO3. Phys Rev Lett (2014) 113:107203. doi:10.1103/physrevlett.113.107203
43. Leonov AO, Kézsmárki I. Skyrmion Robustness in Noncentrosymmetric Magnets with Axial Symmetry: The Role of Anisotropy and Tilted Magnetic fields. Phys Rev B (2017) 96:214413. doi:10.1103/physrevb.96.214413
44. Kézsmárki I, Bordács S, Milde P, Neuber E, Eng LM, White JS, et al. Néel-type Skyrmion Lattice with Confined Orientation in the Polar Magnetic Semiconductor GaV4S8. Nat Mater (2015) 14:1116–22. doi:10.1038/nmat4402
Keywords: skyrmion crystal, pinning effect, exchange anisotropy, magnetocrystalline anisotropy, helimagnet
Citation: Wan X, Hu Y, Hou Z and Wang B (2021) Pinning Effects of Exchange and Magnetocrystalline Anisotropies on Skyrmion Lattice. Front. Phys. 9:684346. doi: 10.3389/fphy.2021.684346
Received: 23 March 2021; Accepted: 27 May 2021;
Published: 21 June 2021.
Edited by:
Cynthia Reichhardt, Los Alamos National Laboratory (DOE), United StatesReviewed by:
Carles Navau, Universitat Autònoma de Barcelona, SpainAnjan Soumyanarayanan, National University of Singapore, Singapore
Charles Reichhardt, Los Alamos National Laboratory (DOE), United States
Copyright © 2021 Wan, Hu, Hou and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yangfan Hu, aHV5ZkBkZ3V0LmVkdS5jbg==; Biao Wang, d2FuZ2JpYW9AbWFpbC5zeXN1LmVkdS5jbg==
 Xuejin Wan1
Xuejin Wan1 Zhipeng Hou
Zhipeng Hou