M. Bellingeri
M. Turchetto2
D. Bevacqua
F. Scotognella
Q. Nguyen- 1Dipartimento di Fisica, Politecnico di Milano, Piazza Leonardo da Vinci, Milano, Italy
- 2Dipartimento di Scienze Matematiche, Fisiche e Informatiche, Parma, Italy
- 3PSH, UR 1115, INRAE, Avignon, France
- 4Center for Nano Science and Technology@PoliMi, Istituto Italiano di Tecnologia, Via Giovanni Pascoli, Milan, Italy
- 5Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh, Vietnam
- 6Faculty of Finance and Banking, Ton Duc Thang University, Ho Chi Minh, Vietnam
In this perspective, we describe how the link removal (LR) analysis in social complex networks may be a promising tool to model non-pharmaceutical interventions (NPIs) and social distancing to prevent epidemics spreading. First, we show how the extent of the epidemic spreading and NPIs effectiveness over complex social networks may be evaluated with a static indicator, that is, the classic largest connected component (LCC). Then we explain how coupling the LR analysis and type SIR epidemiological models (EM) provide further information by including the temporal dynamics of the epidemic spreading. This is a promising approach to investigate important aspects of the recent NPIs applied by government to contain SARS-CoV-2, such as modeling the effect of the social distancing severity and timing over different network topologies. Further, implementing different link removal strategies to halt epidemics spreading provides information to individuate more effective NPIs, representing an important tool to offer a rationale sustaining policies to prevent SARS-CoV-2 and similar epidemics.
Introduction
The prominent role of networks in epidemiology has been recognized in last 2 decades [1–7]. In fact, a spreading disease can be modeled as a network where nodes represent the individuals (i.e., the hosts) and links (edges) represent the social contacts between the individuals. One of the major issues in epidemiology is to determine the most efficient way to halt an epidemic.
When a vaccine is available, one must take into account resource limitations (vaccine doses, doctors, time, costs, etc.) and optimize vaccine administrations [3, 4, 8–11]. This is equivalent to remove some nodes from the network and there is extensive literature about how to rank nodes to be first removed in order to efficiently halt a spreading epidemic [3, 4, 8]. Classic results showed that the random vaccination of a fraction of individuals is not the most efficient way to protect the population [1, 3, 4]. The best strategy consists in obtaining a targeted immunization, where the most central nodes/individuals of the system are immunized in decreasing order of centrality importance [3, 4, 8, 12–17].
On the other hand, when a vaccine is not available, control policies must rely upon non-pharmaceutical interventions (NPIs), which mainly consist in policies reducing the chances to disease transmission by imposing the so called “social distancing” [18]. In terms of network, this is equivalent to remove links, and in the network science research, rich literature exists on the most efficient link removal strategies to disentangle network connectivity (see, e.g., [19–23]). Although the link removal (LR) analyses can help model the consequences of NPIs policies and evaluate their efficacy [9], it has been rarely used for this purpose.
In this perspective article, we define possible ways to model the consequences of social distancing in complex social networks by LR analysis. First, we focus on the network fragmentation triggered by LR strategies through a topological and static representation of the effect of NPIs to reduce the epidemic spreading entity [2, 4]. Second, we propose a dynamical representation of the effect of NPIs by coupling LR and classical, dynamical, epidemiological type SIR models (EM) [6, 24, 25]. A similar framework combining EM and LR has been proposed with the aim to minimize the spreading of computer viruses [26, 27] and to halt epidemic in airport networks [28, 29]. Here, we show that the proposed approach has the advantage to investigate important aspects of the NPIs, such as modeling how the social distancing affects the temporal dynamic of the infection. Eventually, we discuss our findings with respect to the control of the SARS-CoV-2.
Modeling Epidemics Spread on Social Networks Affected by Link Removal
Network Topology and Link Removal
In the present perspective, we will provide simulations for different kind of networks. We will use two “virtual” networks with different characteristics and a real one. The virtual networks have N = 1,000 nodes, that is, a network size sufficiently large to avoid significant size effect in the topological structure of the model networks [30], and average node degree <k> 8, that is, each node has eight links on average, modeling the individual real range of daily social interactions [31].
We will use the Erdős–Rényi (ER) random network [32]. The ER network is the simplest, oldest, and widely used network model, and it is generated by adding links between nodes with an independent probability p for each node pair [33]. The ER model presents a Poissonian distribution of the node degree and nodes deviating from the average are extremely rare; it generates a “small-world network,” that is, the distance between nodes increases very slowly (usually logarithmically) as a function of the number of nodes in the network [32, 33].
The Watts–Strogatz (WS) [34] network has been proposed as a small-world network model encoding the clustering property, that is, it presents high density of links among groups (clusters) of nodes. The clustering property makes WS more suitable to reproduce the “community structure” of real-world networks, and it is widely used to model epidemic spreading [6]. Last, we process the United Kingdom faculty real-world social network (UK) that represents the friendship among academic staff (81 nodes/individuals) in a United Kingdom university [35].
Any link removal policy is characterized by its “severity,” that is, the fraction of links removed and its “rule” to select the links that will be removed first. In fact, one can randomly remove links (RAN) or start from those with higher importance in the network, for example, measured by the link betweenness centrality (BC) [20, 36].
A Static Approach Based on LCC
High network connectivity has been demonstrated to be positively correlated to disease incidence [6]. Thus, the reduction of network connectivity, which can be described by the largest connected component (LCC), can be seen as the target of NPIs. The LCC, also named giant or spanning cluster, accounting the highest number of connected nodes in the network [4, 14, 20, 21] provides a static indicator of the spreading magnitude. When assuming the absence of link/interaction rewiring, that is, no new interactions may be formed among individuals, the LCC represents the maximum number of individuals that may be infected following a primary infection.
When considering an ER network, the effect of link removal becomes effective (i.e., it halves the LCC) only when removing more than 80% of original links, whatever the strategy is—random removal (RAN) or based on BC (Figure 1A). On the other hand, when considering a WS network, 55% of links removed according to a BC strategy becomes effective to dismantle the LCC, while if one removes randomly it should remove more than 80% of the links to obtain a similar result (Figure 1B). Results obtained for UK faculty real-world network are close to those obtained with the WS network (Figure 1C).
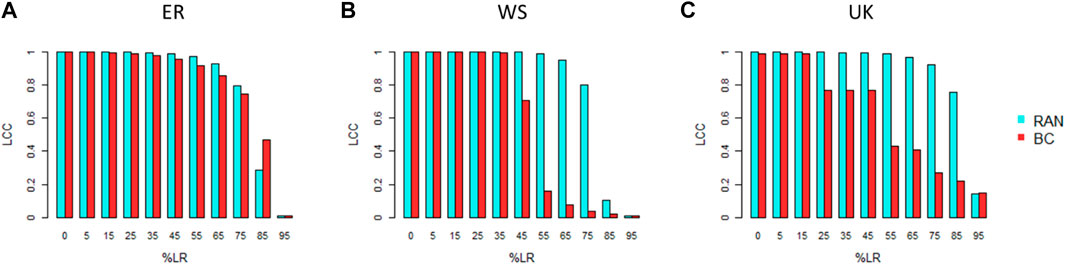
FIGURE 1. Static epidemic spreading indicators largest connected component (LCC) as a function of the fraction of the links removed (%LR) for the three networks analyzed. Blue bars indicate the LCC subjected to random link removal (RAN), whereas red bars indicate the LCC under link betweenness centrality removal (BC). The outcomes are the average of 103 simulations. Panel (A): LCC as a function of %LR over the ER N = 1,000, p = 0.008 model network; panel (B): LCC as a function of %LR for the WS N = 1,000, p = 0.3 model networks; panel (C): LCC as a function of the %LR for the United Kingdom faculty real-world social network.
A Dynamic Approach Based on Solving an Epidemiological SIR Model on a Social Network
The analysis of the topological changes over the network consequent to link removal provides interesting insight on how much the network is suited for epidemic spreading but does not provide information over the temporal dynamics of the epidemic spreading. Such dynamics is captured by classical susceptible-infected-recovered (SIR) models [see [37] for an overview].
Network topology has been successfully incorporated into SIR models which could then be analytically [1, 2] or numerically [31] solved according to the complexity of the considered network. In order to solve a SIR model on a social network, one should assume that a given society is composed by N individuals connected by social links. Hereinafter, we will refer to those individuals that are connected by a social link with the term “neighbors.”
At any time, an individual is in one of three possible compartments: susceptible (S), infected (I), and recovered (R). If an individual is infected, the individual will infect susceptible neighbors with a transmission rate, β. An infected individual stays infectious on average for γ −1 consecutive days, that is, recovers with a rate equal to γ. Recovered individuals can no longer infect others and their state will no longer change, which is equivalent to assume that immunization does not vanish in the considered time horizon. The system is initialized by fixing all nodes as susceptible except one, randomly chosen, whose state is set as infected. The system dynamics can then be solved and permit to model the epidemics evolution over time. Note that a fraction of links can be removed, randomly or following a given rule, at any time to simulate the implementation of social distancing. Also, in a temporal dynamic model, the time at which links are removed plays a key role. We model this time of intervention by removing a certain fraction of links at different times, that is, the first day at which an infected node appears in the system, 20 and 40 days later. This permits to evidence the consequences of a delay in applying control measures.
The entity of the epidemic spreading can be quantified by 1) the total number of individuals that have been infected (TI) (i.e., the cumulative sum of new cases, which is equivalent to the number of recovered nodes at the end of the dynamics, where, by model construction, no more nodes can be infected) and 2) the maximum value of infected nodes in a given day (Peak). The first indicator provides an estimate of the spread of the disease within a population, and it is likely to correlate with the number of severe, and possible fatal, cases. The second indicator provides an estimate of the pressure over the sanitary system which might collapse, thus causing higher mortality probabilities of infected individuals, when a critical threshold is exceeded.
In order to provide explicative results via simulations, we use the NDlib Python library presented in Rossetti et al. [38] by keeping the default SIR parameter of β and γ equals to 0.06 and 0.04 (see [38] for details).
Results are reported in Figure 2. For the ER model network, the RAN and BC strategies show similar effect to curb Peak and TI, and if NPIs are implemented with a delay of 20 days, the NPIs become useless to halt epidemic spreading (Figures 2A–C). Differently, in the WS model network, the BC strategy is more effective to curb Peak and TI; however, in the case NPIs are implemented at t = 40 (or after), the NPIs become useless to halt epidemic spreading (Figures 2D–F). Last, similar to the WS for the UK faculty real-world network, the BC strategy is more effective to curb Peak and PI but even more pronounced than we observe for WS network; to delay the NPIs implementation may impair their effectiveness, that is, already for t = 20, the LR did not curb Peak and PI (Figures 2G–I).
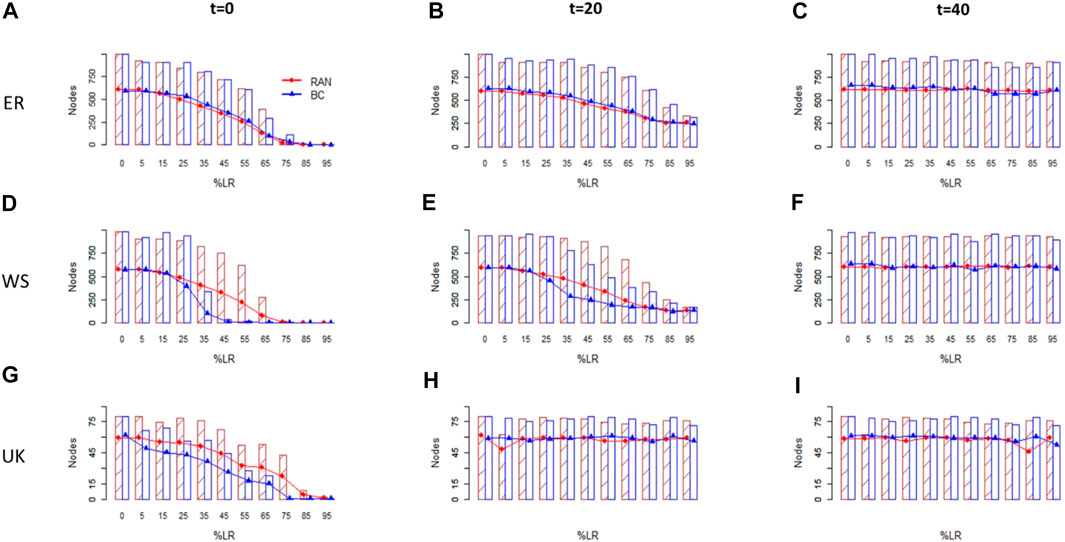
FIGURE 2. Indicators of the dynamic epidemic spreading infected peak (Peak) and total infected (TI) of the SIR model over three networks analyzed as a function of the fraction of the links removed (%LR). Bar plots indicate the TI; lines/points indicate the Peak. Red bar plots with diagonal lines indicate the spreading indicators of the network subjected to random link removal (RAN), whereas blue empty bar plots indicate the spreading indicators under link betweenness centrality removal (BC). Red/circle describes the spreading indicators of the network subjected to random link removal (RAN), whereas blue/triangle indicates the spreading indicators under link betweenness centrality removal (BC). The SIR model has per-day transmission probability β = 0.04 and per-day recovery probability γ = 0.06. The outcomes are the average of 103 simulations. 1th row: Panels (A–C) spreading indicators as a function of %LR over the ER N = 1,000, p = 0.008 model network; 2nd row: Panels (D–F) spreading indicators as a function of %LR for the WS N = 1,000, p = 0.3 model network; and 3rd row: Panels (G–I) spreading indicators as a function of %LR for the United Kingdom faculty real-world social network. 1th column: Panels (A,D, and G) the social distancing represented by the LR is implemented at t = 0; 2nd column: Panels (B,E, and H) the LR is implemented at t = 20; 3rd column: Panels (C,F, and I) the LR is implemented at t = 40.
SIR-type models have been recently used for SARS-CoV-2 [7, 31]; we therefore decided to combine LR analyses and the SIR model. Nonetheless, other epidemiological models, such as the SEIRS [24], have been proposed to describe SARS-CoV-2 spreading. The network approach proposed here can be easily adapted to other epidemiological models.
Discussion
In the following, we discuss ideas combining LR and EM to model important aspects of the recent NPIs applied by government to contain SARS-CoV-2.
Social Distancing Severity
When establishing social distancing, one should first decide the severity of such an action which, in network analysis, translates to the fraction of links to be removed. The preliminary outcomes presented here show that to remove less than 25% of the links would be useless to curb epidemic spreading whatever the network type, giving us information to evaluate the minimum value of the severity to perform effective NPIs. To note, %LR > 45% triggers an increase of the spreading slowdown, and this would indicate that to tighten up the NPIs toward higher level would produce an increase of the marginal efficacy to halt the epidemic spreading. This kind of results from LR analyses may be particularly important, since they furnish information about the opportunity to implement more severe NPIs, with the possibility to verify preliminary results showing that the adoption of multiple NPIs would achieve a stronger effect [39]. Noteworthy, the LCC start to significantly decrease only for %LR > 55%; this would indicate how the LCC is not able to detect the epidemic slowdown indicated by EM indicators for lower LR percentage. In fact, one can remove many links and yet leave the nodes connected and the LCC size constant. In this case, the LCC may be a coarse indicator underestimating the NPIs effectiveness to curb the spreading.
Social Distancing Rules
To understand which NPIs to implement is a fundamental problem for policy containing the epidemic spreading. Good NPIs should present 1) high efficacy while 2) minimizing the detrimental social effects. With the first aim, we have to find the LR strategy producing the fastest epidemic spreading slowdown in the network. To do this, it is possible to adopt different LR methods [19–22, 26, 27, 40] and testing their efficacy to slowdown EM epidemic. With the aim to curb epidemic spreading in computers network models, Nandi and Medal [19] showed that LR producing the complete isolation of susceptible nodes from infected nodes is the most effective method in reducing the average number of new infections.
The BC strategy, based on link betweenness, is more effective to halt epidemic spreading than randomly removing links, especially for real-world UK faculty and model network with community structure (WS). Betweenness centrality accounts the number of shortest paths that must go through link, and it is able to identify bridge links connecting different communities of individuals [20]. For this reason, our outcomes would advise against to reduce social links/interactions at random, outlining the necessity to perform highly targeted NPIs with the aim to isolate social network communities by breaking bridges links, and this can be done in real situations at different levels, such as implementing policies reducing the interactions between families, school classes, cities, or regions.
Social Distancing Timing
The use of an epidemiological dynamical model permits to evaluate the role of the time of application of control measure, an aspect otherwise ignored by classical network analysis based on network topology.
The timing which NPIs are imposed is thought to be important to determine the size of the epidemic spreading [31, 41]. Assessing the effects of early NPIs on SARS-CoV-2 spread is crucial for understanding and planning future control measures to combat the pandemic [41]. It is possible to model the effect of NPIs timing by performing LR for increasing time values from the epidemic starting. The simulations show that the LR time delay results in higher Peak and TI, thus reproducing the efficacy in halting the epidemic by imposing NPIs early [41]. To note, if the LR are performed for t > 20, they are no longer able to reduce the Peak and TI in the three types of networks tested here (Figure 2). This would indicate that in case NPIs are imposed too late and the disease covers a sufficient part of the population, the NPIs can result useless to contain epidemic.
This phenomenon has a simple explanation: when performing LR with delay, the epidemic may have already infected a large fraction of individuals, and even removing enough links to fragment the network in many isolated clusters, each cluster will own with high probability of some infected individuals and the epidemic spreading will continue within the clusters.
It is also worthy to note that to perform immediate intervention would permit to hold the NPIs for a reduced window of time, thus minimizing the inevitable detrimental social effects.
The Cost of Social Distancing
Although NPIs, including lockdown, have been shown to reduce the SARS-CoV-2 spread, they implicate detrimental impact on population health and economies [42], such as physical inactivity [43], increased depression [44], increased domestic violence [45], and reduced access to health care [46].
To find highly efficient LR that can curb an epidemic may be useful to minimize these negative social effects, given that it is possible to implement less severe social distancing (less link removed) yet inducing a significant spreading slowdown. A similar idea can be found in the study by Nishi et al. [47] that propose network interventions by removing and rewiring links to form specific subgroups of individuals (e.g., customer groups can only go to the grocery store in the morning or in the afternoon) showing that the strategy may curb the epidemic spreading while preserving economic activities. We can translate this idea in our framework, performing LR while maintaining a quota of links to preserve desired social interactions, such as family, work, or school interactions. This problem can be reframed: once selected the groups that have to be preserved in the social network, and thus defining the links set to hold, to find the most efficient LR strategies acting over the complementary set of links.
Social Distancing on Different Types of Social Network Model
The structure of the interpersonal relationships forming the social networks may differ among society and different society may present different dynamics of the epidemic spreading. For these reasons, a fundamental problem to simulate NPIs using LR methodology is to choose the proper network structure. The easiest approach is to use a synthetic network mimicking desired social system characteristic. The ER is the simplest and the more commonly model used, due to the ease of analysis allowed by its random structure [32, 33]. The ER is able to reproduce the small-world property of real-world social systems, that is, individuals are separated by small number of link/connections [48] but fails to mimic other features, such as the presence of “hubs,” individuals with higher than average number of interactions [32], and the “community structure” in which individuals are joined together in tightly knit groups, between which there are only looser connections [20, 49, 50]. Other social network models are the Barabasi–Albert scale-free network [51], the Watts–Strogatz (WS) small-world network [34], and the Poissonian small-world network (PSWN) which generalizes the WS with a Poissonian degree distribution of the nodes [31]. The WS and PSWN seem promising models to analyze SARS-CoV-2 epidemic [31], since they allow to describe transmission in a social network owing both community structure (with local groups of individuals) and highly connected individuals that may act as a “superspreaders” [52]. Comparing ER and WS with equal number of nodes and links under BC, we find that the BC strategy is clearly more effective to halt the epidemic spreading over the WS network. This seminal outcome would indicate that real-world social networks with a pronounced community structure may experience faster spreading decrease under NPIs.
Social Distancing on Real-World Social Networks
The simulation of control strategies for SARS-CoV-2 epidemic transmission in real-world social networks is an optimal framework to investigate NPIs effectiveness [53].
We show the LR outcomes from the United Kingdom faculty social network (UK) that represents the friendship among academic staff (81 nodes/individuals) in a United Kingdom faculty [35]. We can see how the BC strategy is clearly more effective than RAN to curb SIR epidemic spreading (Figure 2G), showing how the United Kingdom response to LR is similar to the WS and different with respect to the ER model. This would outline how real-world social networks present a non-random community structure that affects the epidemic spreading [54] and may influence the efficacy of the NPIs [31].
The use of real-world networks seems particularly promising because recent technological progress made easier to collect massive social interactions data, such as the high-resolution GPS, the longitudinal data on the physical proximity, and face-to-face contacts of individuals. This made available to build social networks in numerous real-world environments of epidemics importance, such as schools, museums, and hospitals [53]1. Such new technologies represent strong tools to develop real-world networks to investigate the transmission of infectious diseases and implement reliable LR analyses.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
Author Contributions
All the authors conceived the papers. MT and RA wrote the Python code. MB, MT, RA, and DC performed the analyses. All the authors wrote the papers.
Funding
This project has received funding from the Executive Programme of Scientific and Technological Cooperation between the Socialist Republic of Vietnam and the Italian Republic for the years 2021–2023. MB and FS acknowledges financial support from Fondazione Cariplo, grant n° 2018–0979. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 816313).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1http://www.sociopatterns.org/ (accessed 2021-03-10)
References
1. Pastor-Satorras R, Vespignani A. Immunization of Complex Networks. Phys Rev E (2002) 65:036104. doi:10.1103/PhysRevE.65.036104
2. Newman MEJ. Spread of Epidemic Disease on Networks. Phys Rev E (2002) 66:016128. doi:10.1103/PhysRevE.66.016128
3. Cohen R, Havlin S, ben-Avraham D. Efficient Immunization Strategies for Computer Networks and Populations. Phys Rev Lett (2003) 91:247901. doi:10.1103/PhysRevLett.91.247901
4. Gallos LK, Liljeros F, Argyrakis P, Bunde A, Havlin S. Improving Immunization Strategies. Phys Rev E (2007) 75:1–4. doi:10.1103/PhysRevE.75.045104
5. Sun Y, Liu C, Zhang C-X, Zhang Z-K. Epidemic Spreading on Weighted Complex Networks. Phys Lett A (2014) 378:635–40. doi:10.1016/j.physleta.2014.01.004
6. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic Processes in Complex Networks. Rev Mod Phys (2015) 87:925–79. doi:10.1103/RevModPhys.87.925
7. Amaral MA, Oliveira MMd., Javarone MA. An Epidemiological Model with Voluntary Quarantine Strategies Governed by Evolutionary Game Dynamics. Chaos, Solitons & Fractals (2021) 143:110616. doi:10.1016/j.chaos.2020.110616
8. Holme P. Efficient Local Strategies for Vaccination and Network Attack. Europhys Lett (2004) 68:908–14. doi:10.1209/epl/i2004-10286-2
9. Bellingeri M, Bevacqua D, Scotognella F, Alfieri R, Nguyen Q, Montepietra D, et al. Link and Node Removal in Real Social Networks: A Review. Front Phys (2020) 8:8. doi:10.3389/fphy.2020.00228
10. Hadidjojo J, Cheong SA. Equal Graph Partitioning on Estimated Infection Network as an Effective Epidemic Mitigation Measure. PLoS One (2011) 6:e22124. doi:10.1371/journal.pone.0022124
11. Bellingeri M, Agliari E, Cassi D. Optimization Strategies with Resource Scarcity: from Immunization of Networks to the Traveling Salesman Problem. Mod Phys Lett B (2015) 29:1550180. doi:10.1142/S0217984915501808
12. Chen Y, Paul G, Havlin S, Liljeros F, Stanley HE. Finding a Better Immunization Strategy. Phys Rev Lett (2008) 101:058701. doi:10.1103/PhysRevLett.101.058701
13. Bellingeri M, Cassi D, Vincenzi S. Efficiency of Attack Strategies on Complex Model and Real-World Networks. Physica A: Stat Mech its Appl (2014) 414:174–80. doi:10.1016/j.physa.2014.06.079
14. Iyer S, Killingback T, Sundaram B, Wang Z. Attack Robustness and Centrality of Complex Networks. PLoS One (2013) 8:e59613. doi:10.1371/journal.pone.0059613
15. Schneider CM, Mihaljev T, Herrmann HJ. Inverse Targeting -An Effective Immunization Strategy. Epl (2012) 98:46002. doi:10.1209/0295-5075/98/46002
16. Wandelt S, Sun X, Feng D, Zanin M, Havlin S. A Comparative Analysis of Approaches to Network-Dismantling. Sci Rep (2018) 8:1–15. doi:10.1038/s41598-018-31902-8
17. Wang Z, Zhao D-W, Wang L, Sun G-Q, Jin Z. Immunity of Multiplex Networks via Acquaintance Vaccination. Epl (2015) 112:48002. doi:10.1209/0295-5075/112/48002
18. Flaxman S, Mishra S, Mishra S, Gandy A, Unwin HJT, Mellan TA, et al. Estimating the Effects of Non-pharmaceutical Interventions on COVID-19 in Europe. Nature (2020) 584:257–61. doi:10.1038/s41586-020-2405-7
19. Nandi AK, Medal HR. Methods for Removing Links in a Network to Minimize the Spread of Infections. Comput Operations Res (2016) 69:10–24. doi:10.1016/j.cor.2015.11.001
20. Bellingeri M, Bevacqua D, Scotognella F, Alfieri R, Cassi D. A Comparative Analysis of Link Removal Strategies in Real Complex Weighted Networks. Sci Rep (2020) 10:1–15. doi:10.1038/s41598-020-60298-7
21. Bellingeri M, Bevacqua D, Scotognella F, Cassi D. The Heterogeneity in Link Weights May Decrease the Robustness of Real-World Complex Weighted Networks. Sci Rep (2019) 9:1–13. doi:10.1038/s41598-019-47119-2
22. Hao Y, Jia L, Wang Y. Edge Attack Strategies in Interdependent Scale-free Networks. Physica A: Stat Mech its Appl (2020) 540:122759. doi:10.1016/j.physa.2019.122759
23. Javarone MA, Marinazzo D. Dilution of Ferromagnets via a Random Graph-Based Strategy. Complexity (2018) 2018:11. doi:10.1155/2018/2845031
24. Gatto M, Bertuzzo E, Mari L, Miccoli S, Carraro L, Casagrandi R, et al. Spread and Dynamics of the COVID-19 Epidemic in Italy: Effects of Emergency Containment Measures. Proc Natl Acad Sci USA (2020) 117:10484–91. doi:10.1073/pnas.2004978117
25. Allen LJS. Some Discrete-Time SI, SIR, and SIS Epidemic Models. Math Biosciences (1994) 124:83–105. doi:10.1016/0025-5564(94)90025-6
26. Kimura M, Saito K, Motoda H. Blocking Links to Minimize Contamination Spread in a Social Network. ACM Trans Knowl Discov Data (2009) 3:1–23. doi:10.1145/1514888.1514892
27. Kimura M, Saito K, Motoda H. Minimizing the Spread of Contamination by Blocking Links in a Network. Proc Natl Conf Artif Intell (2008) 2:1175–80.
28. Marcelino J, Kaiser M. Reducing Influenza Spreading over the Airline Network. Plos Curr (2009) 1–14. doi:10.1371/currents.RRN1005
29. Matamalas JT, Arenas A, Gómez S. Effective Approach to Epidemic Containment Using Link Equations in Complex Networks. Sci Adv (2018) 4:1–10. doi:10.1126/sciadv.aau4212
30. Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D. Complex Networks: Structure and Dynamics. Phys Rep (2006) 424:175–308. doi:10.1016/j.physrep.2005.10.009
31. Thurner S, Klimek P, Hanel R. A Network-Based Explanation of Why Most COVID-19 Infection Curves Are Linear. Proc Natl Acad Sci USA (2020) 117:22684–9. doi:10.1073/pnas.2010398117
32. Erdos P, Renyi A. On the Evolution of Random Graphs. Publ Math Inst Hung Acad Sci (1960) 5:17–60.
33. Bollobás B, Riordan O. Robustness and Vulnerability of Scale-free Random Graphs. Internet Math (2004) 1:1–35. doi:10.1080/15427951.2004.10129080
34. Watts DJ, Strogatz SH. Collective Dynamics of 'small-World' Networks. Nature (1998) 393:440–2. doi:10.1038/30918
35. Nepusz T, Petróczi A, Négyessy L, Bazsó F. Fuzzy Communities and the Concept of Bridgeness in Complex Networks. Phys Rev E (2008) 77:1–12. doi:10.1103/PhysRevE.77.016107
36. Freeman HE. A Set of Measures of Centrality Based on Betweenness. Sociometry (1977) 40:35–41. Available at: http://unesdoc.unesco.org/images/0002/000208/020885eb.pdf. doi:10.2307/3033543
37. Matt K, Pejman R. Modeling Infectious Diseases in Humans and Animals. Oxfordshire: Princeton University Press (2008).
38. Rossetti G, Milli L, Rinzivillo S, Sîrbu A, Pedreschi D, Giannotti F. NDlib: a python Library to Model and Analyze Diffusion Processes over Complex Networks. Int J Data Sci Anal (2018) 5:61–79. doi:10.1007/s41060-017-0086-6
39. Lai S, Ruktanonchai NW, Zhou L, Prosper O, Luo W, Floyd JR, et al. Effect of Non-pharmaceutical Interventions to Contain COVID-19 in China. Nature (2020) 585:410–3. doi:10.1038/s41586-020-2293-x
40. Holme P, Kim BJ, Yoon CN, Han SK. Attack Vulnerability of Complex Networks. Phys Rev E (2002) 65:056109. doi:10.1103/physreve.65.056109
41. Pei S, Kandula S, Shaman J. Differential Effects of Intervention Timing on COVID-19 Spread in the United States. medRxiv (2020) 2020:1–10. doi:10.1101/2020.05.15.20103655
42. Bavel JJV, Baicker K, Boggio PS, Capraro V, Cichocka A, Cikara M, et al. Using Social and Behavioural Science to Support COVID-19 Pandemic Response. Nat Hum Behav (2020) 4:460–71. doi:10.1038/s41562-020-0884-z
43. Lippi G, Henry BM, Bovo C, Sanchis-Gomar F. Health Risks and Potential Remedies during Prolonged Lockdowns for Coronavirus Disease 2019 (COVID-19). Diagnosis (Berlin) (2020) 7:85–90. doi:10.1515/dx-2020-0041
44. Brooks SK, Webster RK, Smith LE, Woodland L, Wessely S, Greenberg N, et al. The Psychological Impact of Quarantine and How to Reduce it: Rapid Review of the Evidence. The Lancet (2020) 395:912–20. doi:10.1016/S0140-6736(20)30460-8
45. Bradbury-Jones C, Isham L. The Pandemic Paradox: The Consequences of COVID-19 on Domestic Violence. J Clin Nurs (2020) 29:2047–9. doi:10.1111/jocn.15296
46. Thornton J. Covid-19: A&E Visits in England Fall by 25% in Week after Lockdown. BMJ (2020) 369:m1401. doi:10.1136/bmj.m1401
47. Nishi A, Dewey G, Endo A, Neman S, Iwamoto SK, Ni MY, et al. Network Interventions for Managing the COVID-19 Pandemic and Sustaining Economy. Proc Natl Acad Sci USA (2020) 117:30285–94. doi:10.1073/pnas.2014297117
48. Schnettler S. A Structured Overview of 50 Years of Small-World Research. Social Networks (2009) 31:165–78. doi:10.1016/j.socnet.2008.12.004
50. Kumpula JM, Onnela J-P, Saramäki J, Kertész J, Kaski K. Model of Community Emergence in Weighted Social Networks. Comp Phys Commun (2009) 180:517–22. doi:10.1016/j.cpc.2008.12.016
51. Albert R, Barabási A. Statistical Mechanics of Complex Networks. Rev Mod Phys (2002) 74:47–97. Available at: http://rmp.aps.org/abstract/RMP/v74/i1/p47_1. doi:10.1103/RevModPhys.74.47 Accessed December 5, 2013).
52. Wong F, Collins JJ. Evidence that Coronavirus Superspreading Is Fat-Tailed. Proc Natl Acad Sci USA (2020) 117:29416–8. doi:10.1073/pnas.2018490117
53. Firth JA, Hellewell J, Hellewell J, Klepac P, Kissler S, Kucharski AJ, et al. Using a Real-World Network to Model Localized COVID-19 Control Strategies. Nat Med (2020) 26:1616–22. doi:10.1038/s41591-020-1036-8
Keywords: complex network, social networks, epidemic, SARS-CoV-2, link (node) removal
Citation: Bellingeri M, Turchetto M, Bevacqua D, Scotognella F, Alfieri R, Nguyen Q and Cassi D (2021) Modeling the Consequences of Social Distancing Over Epidemics Spreading in Complex Social Networks: From Link Removal Analysis to SARS-CoV-2 Prevention. Front. Phys. 9:681343. doi: 10.3389/fphy.2021.681343
Received: 16 March 2021; Accepted: 10 May 2021;
Published: 28 May 2021.
Edited by:
Roy Cerqueti, Sapienza Università di Roma, ItalyReviewed by:
Marco Alberto Javarone, University College London, United KingdomJie Cao, Nanjing University of Finance and Economics, China
Copyright © 2021 Bellingeri, Turchetto, Bevacqua, Scotognella, Alfieri, Nguyen and Cassi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. Bellingeri, michele.bellingeri@polimi.it