
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 17 June 2021
Sec. Social Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.681268
 Xiaoyan Wang1
Xiaoyan Wang1 Junyuan Yang2*
Junyuan Yang2*In this paper, we propose a degree-based mean-field SIS epidemic model with a saturated function on complex networks. First, we adopt an edge-compartmental approach to lower the dimensions of such a proposed system. Then we give the existence of the feasible equilibria and completely study their stability by a geometric approach. We show that the proposed system exhibits a backward bifurcation, whose stabilities are determined by signs of the tangent slopes of the epidemic curve at the associated equilibria. Our results suggest that increasing the management and the allocation of medical resources effectively mitigate the lag effect of the treatment and then reduce the risk of an outbreak. Moreover, we show that decreasing the average of a network sufficiently eradicates the disease in a region or a country.
Mathematical modeling plays a crucial role in fighting against large scale infectious disease such as Tuberculosis, HIV, COVID-19, etc., Compartment models have been used to anticipate the progression of diseases and evaluate the effect of interventions on disease spread [1]. One of such models separates the total population into two distinct categories with respect to disease status. People who have not gotten the disease are labeled “susceptibles”; while those who have been infected by a certain disease are called “infectives”. This kind of compartment model is denoted by “an SIS epidemic model” [2–7], which has been extensively used to address the dynamics of those diseases, describing an individual infected by a disease as having no immunity, thus becoming a susceptible again.
Most of the existing models assume that all the individuals are well-mixed and they have homogeneous mixing of surfaces, which implies that each individual has the same probability to contact other individuals and ignores the degree of social heterogeneity induced by age, household, spatial structures, and social spheres, etc. Generally, the social interactions of individuals generate a certain pattern based on social preferences, which contributes to transmission heterogeneity. Indeed, such factors may play a decisive role in the disease transmission and they also may help health policymakers to take more effective control measures for curbing the disease spread [7, 8]. Epidemic models on complex networks incorporate such contact heterogeneity and take account for how the structures of the networks affect the disease prevalence. A popular degree-based SIS epidemic model has been built [9] and it exhibits threshold dynamics [4, 5]. Since then, many factors including vector-borne [10, 11], infective media [12], awareness reaction [13], and the gene diversity of pathogens [14], etc., have been incorporated into the study of the co-evolution of networks and epidemics.
In epidemiology, the basic reproduction number,
with transmission rate β and treatment rate
where α denotes a hysteretic effect due to medical limitations. Apparently,
In view of such epidemiological models incorporating a saturated treatment function, it is not hard to find that most of them enable such models, essentially changing their dynamics. Once a saturated function has been introduced, there always exists a backward bifurcation, which implies that even if some certain control measures make
There are three main contributions in this paper. First, we propose a degree-based SIS epidemic model with a saturated function to study its long-term behaviors. Second, to overcome the difficulty of high dimensions for a network, we adopt an edge-based compartmental approach to lower the dimensions of an SIS epidemic model. Such an approach changes a complete degree-based model to a degree-edge-mixed model, and hence, it lowers the dimension of such a model from
The organization of this paper is as follows: In Section 2, a degree-based SIS epidemic model on complex networks with a saturated function is proposed. Furthermore, we adopt an edge-compartmental approach to rewrite it as a degree-edge-mixed model. Section 3 gives a geometric approach to study the local stability of each equilibrium. In Section 4, we conducted some numerical simulations to illustrate our theoretical results. We give a brief discussion in the last section.
In this paper, we focus on the complete stability of each equilibrium by a novel approach. Let us assume that the maximum contact number of an individual is n and then the degree set is
where β denotes the transmission rate and γ represents the treatment rate; α stands for the lag effect of the treatment due to the limitation of medical resources. From epidemiological view of points, the term
denotes the probability of a given node connecting to an infected node at time t. Hence, it can be considered as a density of an
with initial condition
Lemma 2.1. If
where
Obviously,
This leads to a contradiction with the claim. Therefore,
Remark 2.1. Lemma 2.1 ensures that the solution of system (2) is strictly positive if
Therefore, for all
is positively invariant associate with system (2) and
In this section, we will consider the local stability of system (2) by a novel-geometric approach, which resolves such a matter once and for all. First, we try to give the basic reproduction number
Solving Eq. 5 by a constant variation method, one drives a renew equation
So that the basic reproduction number is calculated in form of
The epidemiological meaning of
Theorem 3.1. If
Let us assume that system (8) has the solution with exponential forms, i.e,
If
Theorem 3.2. If
Differentiating V along the solution of system (2) leads to
here we have used the fact that
The equality holds if and only if
From the first equation of (10), we get
Substituting Eq. 11 into the second equation of (10) and canceling
Apparently, if
Consequently, we conclude the following theorem on the existence of system (2).
Theorem 3.3 If
Proof If
From Theorem 3.3, we assert that system (2) has the existence of the endemic equilibrium, but it does not guarantee the uniqueness of the positive solution when
Now, we are concerned with the endemic curve which bifurcates backwards at
Calculating the derivative of Eq. 14 with respect to
where
After a simple computation, we have that
Lemma 3.4. Suppose
Proof This is a direct result from Section 2.3 [26].Next, let us move our attention on to the local stability of equilibria if they exist, which is a challenge issue for a degree-based epidemic model due to the complex structure. We will propose a geometric approach to deal with such an issue.Linearising system (2) around
If
Replacing
Recall that
and hence,
Alternatively, taking the derivative of F with respect to
Plugging Eq. 23 into Eq. 22, we have that
If
Theorem 3.5. Let
(1) If
(2) If
Proof To address the stability of case (1), we rewrite
where
Hence, if
This, together with the Intermediate Value Theorem, ensures that Eq. 21 has at least one positive real solution. Hence, the endemic equilibrium
Theorem 3.6. If
Theorem 3.7. Suppose
Proof Let us pick up a candidate Lyapunov function by
where
where
Taking the derivative of
On the contrary, differentiating
Adding Eqs 30, 31 together, one derives that
If
here we have used the fact that
Consequently, the largest invariant set of
In this section, we will proceed with some numerical experiments to validate our theoretical results. We account for an epidemic spreading on a scale-free network. Hence, we assume that the degree distribution of that network is
First, we fix
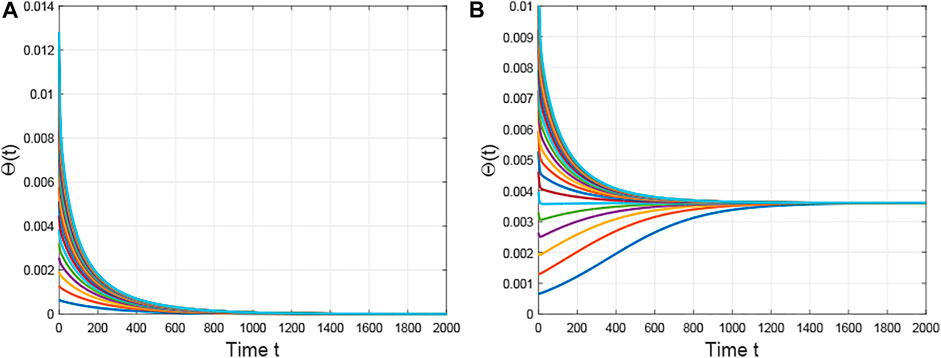
FIGURE 1. The evolution of the densities of infected edges with different initial values
Second, we fix
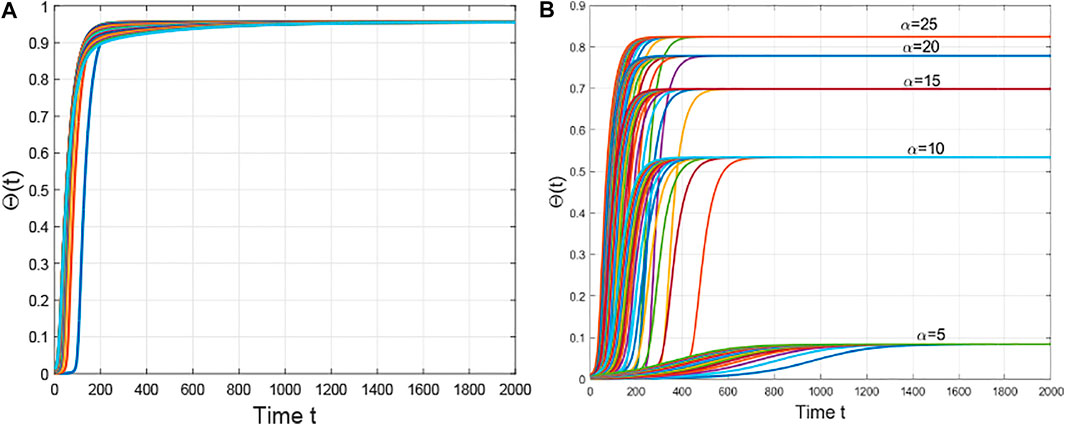
FIGURE 2. The evolution of the densities of infected edges with different initial values
Third, if we fix the structure of the network, then a key value
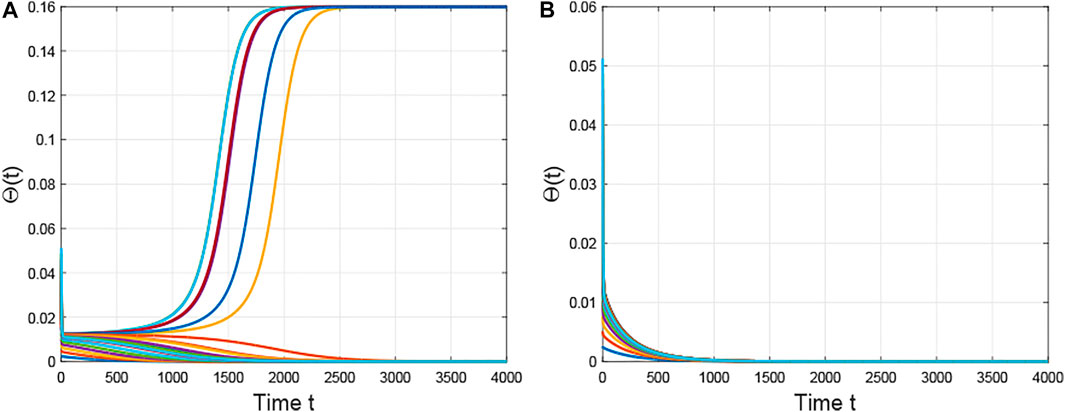
FIGURE 3. The evolution of the densities of infected edges with different initial values
Finally, we want further insight into the existence of endemic equilibria when
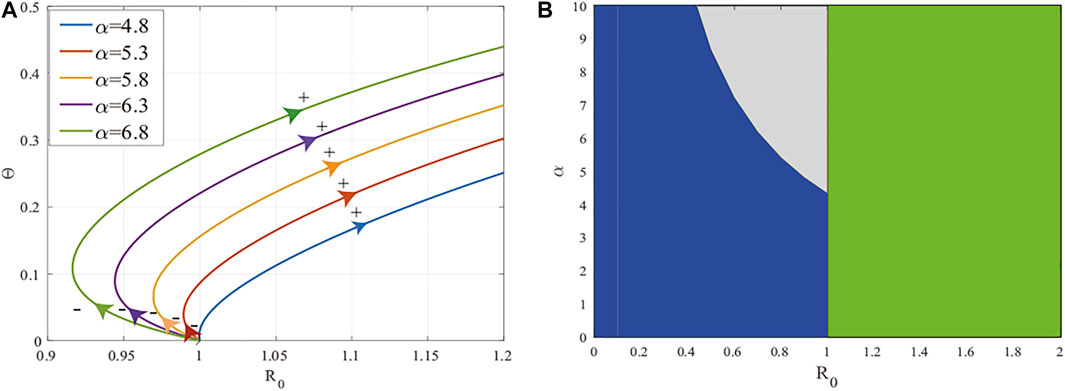
FIGURE 4. Backward bifurcation in system (2). (A) The figure of function
In this paper, we considered a mean-field degree-based SIS epidemic model with a saturated treatment function. First, we adopted an edge-compartmental approach to simplify a pure degree-based model to a degree-edge-mixed model. Second, we proposed a novel method-a geometric approach to completely study the stability of each feasible equilibrium. The proposed model exhibits a backward bifurcation, i.e,
Compared with the results in [5, 25], a degree-based SIS epidemic model on complex networks shows a threshold dynamic, in the sense that, if
The basic reproduction number
Generally, the contact magnitude of an outbreak is characterized by the average degree
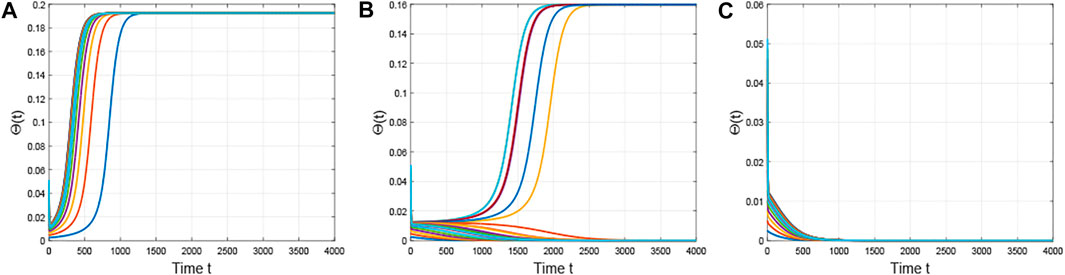
FIGURE 5. Time series of the densities of
From an epidemiological viewpoint, the occurrence of a backward bifurcation implies that those control measures enabling
However, there are some limitations of this paper. First, we do not incorporate the population demography into the modeling process because introducing birth and death nodes essentially changes the topology of a network [27, 28]. This makes the model become too complex and then it has been become an unresolved issue to analyze its dynamical behaviors from mathematical view of points. Second, we do not couple individual contact data with some reported data for a realistic disease to study its evolutionary behaviors [29]. Third, we do not consider the convolution of information spread and epidemic transmission on multi-layered networks [30]. To carry out such a project, it may provide some valuable control suggestions for policymakers and public health government. We leave these for our future works.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
JY and XW conceived of the presented idea. JY developed the theory and performed the computations. XW verified the analytical methods. All authors discussed the results and contributed to the final manuscript. JY designed the modeling process and analyzed theoretical results. XW conceived of the study and helped to draft the manuscript. All the authors read and approved the final manuscript.
This work is partially supported by the National Natural Science Foundation of China (No.12001339, No.61573016), and the Shanxi Province Science Foundation for Youths (No. 201901D211413). Shanxi University of Finance and Economics Youth Research Fund Project (QN-2019017).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. Kermack W, McKendrick A. A Contribution to the Mathematical Theory of Epidemics. Proc R Soc Lond A (1927) 115:700–21. doi:10.1098/rspa.1927.0118
2. van den Driessche P, Watmough J. A Simple Sis Epidemic Model with a Backward Bifurcation. J Math Biol (2000) 40:525–40. doi:10.1007/s002850000032
3. Kribs-Zaleta CM, Velasco-Hernández JX. A Simple Vaccination Model with Multiple Endemic States. Math Biosciences (2000) 164:183–201. doi:10.1016/s0025-5564(00)00003-1
4. Wang L, Dai G-z. Global Stability of Virus Spreading in Complex Heterogeneous Networks. SIAM J Appl Math (2008) 68:1495–502. doi:10.1137/070694582
5. d’Onofrio A. A Note on the Global Behaviour of the Network-Based Sis Epidemic Model. Nonlinear Anal Real World Appl (2008) 9:1567–72. doi:10.1016/j.nonrwa.2007.04.001
6. Zhu L, Guan G, Li Y. Nonlinear Dynamical Analysis and Control Strategies of a Network-Based Sis Epidemic Model with Time Delay. Appl Math Model (2019) 70:512–31. doi:10.1016/j.apm.2019.01.037
7. Xie Y, Wang Z, Lu J, Li Y. Stability Analysis and Control Strategies for a New Sis Epidemic Model in Heterogeneous Networks. Appl Math Comput (2020) 383:125381. doi:10.1016/j.amc.2020.125381
8. Lau MSY, Dalziel BD, Funk S, McClelland A, Tiffany A, Riley S, et al. Spatial and Temporal Dynamics of Superspreading Events in the 2014-2015 West Africa Ebola Epidemic. Proc Natl Acad Sci USA (2017) 114:2337–42. doi:10.1073/pnas.1614595114
9. Pastor-Satorras R, Vespignani A. Epidemic Spreading in Scale-free Networks. Phys Rev Lett (2001) 86:3200–3. doi:10.1103/physrevlett.86.3200
10. Wang X, Yang J. Dynamical Analysis of a Mean-Field Vector-Borne Diseases Model on Complex Networks: An Edge Based Compartmental Approach. Chaos (2008) 30:013103. doi:10.1063/1.5116209
11. Wang Y, Jin Z, Yang Z, Zhang Z-K, Zhou T, Sun G-Q. Global Analysis of an Sis Model with an Infective Vector on Complex Networks. Nonlinear Anal Real World Appl (2012) 13:543–57. doi:10.1016/j.nonrwa.2011.07.033
12. Yang M, Chen G, Fu X. A Modified Sis Model with an Infective Medium on Complex Networks and its Global Stability. Physica A: Stat Mech its Appl (2011) 390:2408–13. doi:10.1016/j.physa.2011.02.007
13. Wu Q, Fu X, Small M, Xu X-J. The Impact of Awareness on Epidemic Spreading in Networks. Chaos (2012) 22:013101. doi:10.1063/1.3673573
14. Yang J, Kuniya T, Luo X. Competitive Exclusion in a Multi-Strain Sis Epidemic Model on Complex Networks. Electron J Differ Equat (2019) 2019:1–30.
15. van den Driessche P, Watmough J. Reproduction Numbers and Sub-threshold Endemic Equilibria for Compartmental Models of Disease Transmission. Math Biosciences (2002) 180:29–48. doi:10.1016/s0025-5564(02)00108-6
16. Keeling MJ, Grenfell BT. Individual-based Perspectives on R0. J Theor Biol (2000) 203:51–61. doi:10.1006/jtbi.1999.1064
17. Diekmann O, Heesterbeek JA, Metz JA. On the Definition and the Computation of the Basic Reproduction Ratio R0 in Models for Infectious Diseases in Heterogeneous Populations. J Math Biol (1990) 28:365–82. doi:10.1007/BF00178324
18. Wang W. Backward Bifurcation of an Epidemic Model with Treatment. Math Biosciences (2006) 201:58–71. doi:10.1016/j.mbs.2005.12.022
19. Cui J, Mu X, Wan H. Saturation Recovery Leads to Multiple Endemic Equilibria and Backward Bifurcation. J Theor Biol (2008) 254:275–83. doi:10.1016/j.jtbi.2008.05.015
20. Buonomo B, Lacitignola D. On the Backward Bifurcation of a Vaccination Model with Nonlinear Incidence. Namc (2011) 16:30–46. doi:10.15388/na.16.1.14113
21. Garba SM, Gumel AB, Abu Bakar MR. Backward Bifurcations in Dengue Transmission Dynamics. Math Biosciences (2008) 215:11–25. doi:10.1016/j.mbs.2008.05.002
22. Gumel AB. Causes of Backward Bifurcations in Some Epidemiological Models. J Math Anal Appl (2012) 395:355–65. doi:10.1016/j.jmaa.2012.04.077
23. Li C-H, Yousef AM. Bifurcation Analysis of a Network-Based Sir Epidemic Model with Saturated Treatment Function. Chaos (2019) 29:033129. doi:10.1063/1.5079631
24. Huang Y-J, Li C-H. Backward Bifurcation and Stability Analysis of a Network-Based Sis Epidemic Model with Saturated Treatment Function. Physica A: Stat Mech its Appl (2019) 527:121407. doi:10.1016/j.physa.2019.121407
25. Yang J, Xu F. The Computational Approach for the Basic Reproduction Number of Epidemic Models on Complex Networks. IEEE Access (2019) 7:26474–9. doi:10.1109/access.2019.2898639
26. Martcheva M. Methods for Deriving Necessary and Sufficient Conditions for Backward Bifurcation. J Biol Dyn (2019) 13:538–66. doi:10.1080/17513758.2019.1647359
27. Jin Z, Sun G, Sun G, Zhu H. Epidemic Models for Complex Networks with Demographics. Math Biosci Engin (2014) 11:1295–317. doi:10.3934/mbe.2014.11.1295
28. Yin Q, Wang Z, Xia C, Dehmer M, Emmert-Streib F, Jin Z. A Novel Epidemic Model Considering Demographics and Intercity Commuting on Complex Dynamical Networks. Appl Math Comput (2020) 386:125517. doi:10.1016/j.amc.2020.125517
29. Yang J, Wang G, Wang G, Zhang S. Impact of Household Quarantine on SARS-Cov-2 Infection in mainland China: A Mean-Field Modelling Approach. Math Biosci Engin (2020) 17:4500–12. doi:10.3934/mbe.2020248
Keywords: complex networks, an edge-compartmental approach, a geometric approach, backward bifurcation, global stability
Citation: Wang X and Yang J (2021) A Bistable Phenomena Induced by a Mean-Field SIS Epidemic Model on Complex Networks: A Geometric Approach. Front. Phys. 9:681268. doi: 10.3389/fphy.2021.681268
Received: 17 March 2021; Accepted: 03 May 2021;
Published: 17 June 2021.
Edited by:
Mahdi Jalili, RMIT University, AustraliaReviewed by:
Gui-Quan Sun, North University of China, ChinaCopyright © 2021 Wang and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Junyuan Yang, eWp5YW5nNjZAc3h1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.