Coarse-Grained Modeling of Coronavirus Spike Proteins and ACE2 Receptors

We developed coarse-grained models of spike proteins in SARS-CoV-2 coronavirus and angiotensin-converting enzyme 2 (ACE2) receptor proteins to study the endocytosis of a whole coronavirus under physiologically relevant spatial and temporal scales. We first conducted all-atom explicit-solvent molecular dynamics simulations of the recently characterized structures of spike and ACE2 proteins. We then established coarse-grained models using the shape-based coarse-graining approach based on the protein crystal structures and extracted the force field parameters from the all-atom simulation trajectories. To further analyze the coarse-grained models, we carried out normal mode analysis of the coarse-grained models to refine the force field parameters by matching the fluctuations of the internal coordinates with the original all-atom simulations. Finally, we demonstrated the capability of these coarse-grained models by simulating the endocytosis of a whole coronavirus through the host cell membrane. We embedded the coarse-grained models of spikes on the surface of the virus envelope and anchored ACE2 receptors on the host cell membrane, which is modeled using a one-particle-thick lipid bilayer model. The coarse-grained simulations show the spike proteins adopt bent configurations due to their unique flexibility during their interaction with the ACE2 receptors, which makes it easier for them to attach to the host cell membrane than rigid spikes.

Introduction

Although a significant amount of research effort has been conducted to understand the SARS-CoV-2 coronaviruses and vaccines have been developed the exact infection mechanisms remain unclear [1]. Coronaviruses are spherical viruses with unique surface spikes [2]. The average diameter is about 80–120 nm. The virus is protected by the envelope and nucleocapsid when it is outside the host cell [3]. The RNAs of the virus are enclosed in an envelope with a diameter of roughly 85 nm [1]. The envelope consists of a lipid bilayer and the membrane (M), envelope (E), and spike (S) structural proteins embedded in the bilayer. While membrane proteins, envelope proteins, and the lipid bilayer shape the viral envelope and maintain its size, spike proteins interact with the host cells by binding with surface receptors such as angiotensin-converting enzyme 2 (ACE2) receptors. Cryo-electron microscopy (cryo-EM) and x-ray crystallographic techniques have been applied to reveal the new structures of viral proteins [4–16]. Due to their significance, computational modeling was employed alongside experimental studies to investigate the properties of these proteins [17], but most of these existing computational studies are limited to atomistic length and time scales. In this study, we will investigate the endocytosis of the whole virus under physiologically relevant spatial and temporal scales by constructing coarse-grained models of the spike proteins and ACE2 receptors.

On the one hand, multiscale coarse-grained models of the whole coronavirus have been developed [15], but they have not been applied to study the endocytosis. In addition, to build a minimal model with enough molecular details, we adopted a more aggressive coarse-graining approach than that used in [15] for both proteins and membranes. On the other hand, the endocytosis of nanoparticles has been extensively studied by computational modeling [18–24], but the endocytosis of coronavirus has not been explored computationally with sufficient molecular details. In the current study, we will explicitly take into account the detailed molecular structures of the spikes and ACE2 rather than modeling them as abstract binding points.

We will focus on establishing the coarse-grained models of the spike proteins and ACE2 receptors. The spikes are unique structures of coronaviruses and are responsible for their distinguishing halo-like surface. A coronavirus particle typically has about 70 spikes on its surface [25]. Each spike consists of three spike proteins (a trimer) and its length is about 20 nm. Each spike protein is made of an S1 head subunit and an S2 stem subunit. The S1 head subunit includes the receptor-binding domain (RBD). Although one spike has three RBDs, only one of them is in the up position for binding [26]. The S2 stem subunit anchors the spike in the viral envelope. Recently, the crystal structure of the SARS-CoV-2 spike protein has been characterized using cryo-EM [PDB ID: 6Vestigial sideband (VSB)] [6], which is responsible for binding to the cell membrane via the extracellular domain of the ACE2 receptor (PDB ID: 6M17) [27]. ACE2 receptor is a membrane-bound carboxypeptidase that forms a dimer and serves as the cellular receptor for SARS-CoV-2 [27]. Molecular dynamics (MD) simulations revealed that the spike protein polybasic cleavage sites, which are distributed approximately 10 nm away from the RBD, can enhance the binding affinity between the SARS-CoV-2 RBD and ACE2 [28]. We took this into consideration by using the enhanced binding energy (−177 kcal/mol) between RBD and ACE2 among the predicted values of −50 kcal/mol ∼ −177 kcal/mol [28–32].

During the infection, the viral spike proteins first attach to their complementary host cell receptors such as ACE2. Then the host cell protease activates the receptor-attached spike proteins. The virus enters the host cell by either endocytosis or membrane fusion of the viral envelope with the host membrane, depending on the availability of the host cell proteases [33]. One of our goals is to simulate the endocytosis by coarse-grained modeling and explicit consideration of the structures of spike and receptor proteins. We will focus on the endocytosis simulation in this study and extend the model to study membrane fusion in the future.

Since the coronavirus is more than 80 nm, all-atom molecular dynamics simulation is prohibitively expensive, not to mention the long-time scale of the endocytosis. Instead, we will apply a multiscale modeling approach. We will conduct all-atom MD simulations of the spike protein and the ACE2 receptors based on their recently characterized crystal structures. Then we will build coarse-grained models of these proteins using the all-atom simulation trajectories. After we demonstrate that the coarse-grained model share similar structural properties with the original all-atom proteins by matching fluctuations, we will construct a whole virus model with a realistic number of spike proteins, and conduct simulations of the endocytosis process of the virus to investigate the cell entry mechanisms. In addition, we developed automated scripts and MATLAB code for establishing these CG models and conducting normal mode analysis. We made them publicly available so that other users can repeat and modify these models.

Materials and Methods

All-Atom Molecular Dynamics Simulations

All-atom MD simulations of the spike protein and ACE2 receptor were conducted using Nanoscale Molecular Dynamics (NAMD) [34]. Explicit solvent is used in order to capture the accurate fluctuations of the structure in equilibrium. A standard protocol is applied. Minimization and annealing processes were carried out first and then equilibrium simulation with the backbone fixed were done before production MD simulations were run. Both the fully-glycosylated full-length spike protein model (Supplementary Figure S1 in the Supplementary Material) and spike protein head S1 subunit model (Figure 1A) were conducted by following the procedure described in [35]. The simulation of the S1 subunit model is used to extract the force field parameters of the bonds and angles in the S1 subunit, and the simulation of the full-length spike protein model is used to estimate the bond and angle coefficients for the stem S2 subunit. A typical simulation box is 25 by 25 by 38 nm and about 2.3 million atoms were simulated for 20 ns. All-atom MD and CG simulations were conducted on the supercomputer Theta in Argonne Leadership Computing Facility (ALCF) in the Argonne National Lab.

FIGURE 1

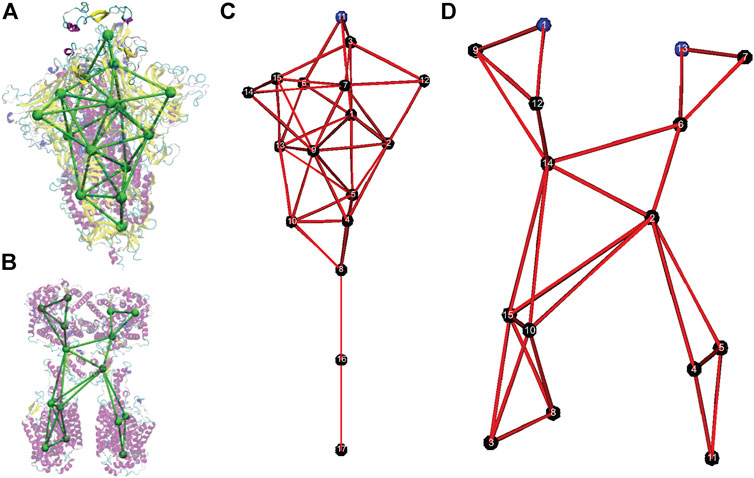
FIGURE 1. Coarse-grained models of the spike protein and the Angiotensin-Converting Enzyme 2 (ACE2) receptor. (A) Overlap of the original all-atom structure of the head unit of spike protein (PDB ID: 6VSB) with the CG model. (B) Overlap of the original all-atom structure of the head unit of ACE2 protein (PDB ID: 6M18) with the CG model. (C) Numbering of CG sites of the spike CG model. (D) Numbering of CG sites of the ACE2 CG model.

Shape-Based Coarse-Graining and Coarse Grained Simulations

We utilized a technique called the Shape-Based Coarse Graining (SBCG) approach to develop the CG models, where large-scale motions of organic/biological molecules are represented using as few spherical CG sites (beads) as possible [36]. This decreases computational demand significantly when performing molecular dynamics simulations. When it comes to the force-field equation, atoms are substituted with CG beads. “Intramolecular” bonds between CG beads are established if the CG beads are within a certain distance of each other, or if the all-atom domains that comprise the CG beads are contiguously connected by intramolecular bonds.

We applied the SBCG tool in Visual Molecular Dynamics (VMD) to construct the coarse-grained model [37]. First, the CG sites and bonded interactions (bonds and angles) were established based on the original all-atom structures. The coefficients of Lennard-Jones (LJ) potential and the bonded interactions were extracted based on all-atom MD simulation trajectories. Specifically, an initial guess of the coefficients of bonded interactions was made by matching the root mean square displacement (RMSD) of internal coordinates, such as bond lengths and angles. Then iterations of refinements were made through CGMD simulations and normal mode analysis [38]. Detailed steps are shown in the Supplementary Material. In addition, we also developed an automated Tool Command Language (TCL) script for this procedure (“To-CG-File.tcl”) within the Supplementary Material. The following classical intramolecular and intermolecular interactions without dihedrals were used

$V={\displaystyle \sum }_{bonds k} \frac{K_{b,k}}{2}{(R_k-R_{0,k})}^2+{\displaystyle \sum }_{angles k} \frac{K_{\theta ,k}}{2}{({\theta }_k-{\theta }_{0,k})}^2+{\displaystyle \sum }_{beads i,j} 4E_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]+{\displaystyle \sum }_{beads i,j} \frac{q_i{q}_j}{4\pi \mathit{ϵ}{\mathit{ϵ}}_0{r}_{i,j}}(1)$

where E_ij= (E_i × E_j)^½, σ_ij = (σ_i + σ_j)/2.0. The first term in Eq. 1 represents the energy associated with the harmonic oscillation of a bond connecting two beads. K_b,k is the proportionality constant for the harmonic oscillator, and R_0,k is the equilibrium distance of the bond, or, the distance where the elastic force is zero for bond k. The 2nd term represents the energy associated with the harmonic oscillation of an angle between the position vectors of two beads that are bonded to a common bead. K_{θ, k} is the proportionality constant, and θ_{0, k} is the equilibrium angle between the three beads for angle k. Energy arising from electrostatic interactions is modeled through Coulombic potential energy and the Van der Waals interaction is modeled using the 6–12 LJ potential. r_ij is the distance between beads i and j, and q_i and q_j are the charges of beads i and j, respectively. ε₀ is the vacuum permittivity constant and ε is the relative permittivity of the medium that beads i and j exist in. σ_ij represents the Van der Waals radius of the pair of beads i and j, or, the distance where the LJ potential is zero. E_ij is a proportionality constant representing the minima of the LJ potential energy graph for the paired beads i and j, and is proportional to the maximum strength of the attraction between beads i and j. LJ potentials prevent the overlapping or penetrating of neighboring CG sites. The equation sums up all of the individual energies obtained from every intramolecular bond, intramolecular bond angle, and every combinatorial pair of beads that exist in the molecule. In addition to the force field approximations, the following Langevin equation is used to describe the motions of the CG beads

$m\frac{{\partial }^2\mathit{r}}{\partial {\mathit{t}}^2}=F-m\gamma \frac{\partial \mathit{r}}{\partial \mathit{t}}+\chi \psi \left(t\right)(2)$

where F is the force imparted on the bead by other beads in the system, r is the position of the bead, m is the mass of the bead, γ is the damping coefficient of the solvent the bead is in, and χ is a fluctuation-dissipation theorem function of the form χ = (2γk_BT/m)^½, where k_B is the Boltzmann constant. ψ(t) is a Gaussian process used to simulate Brownian motion. As ∂²r/∂t² would represent the acceleration of the bead, then this Langevin equation describes the motion of the bead after accounting for fluid viscous friction and thermal fluctuations. The CG simulations of individual spike proteins and ACE2 receptors were carried out in NAMD for refinement of the force field parameters.

The detailed procedure is given in the Supplementary Material for building the CG model based on all-atom MD simulations in VMD and converting it to the format of molecule files that can be used in CG simulations of endocytosis using Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [39].

Normal Mode Analysis

We also wrote a Matlab code to conduct the normal mode analysis (NMA) [38] of the two CG models. We constructed the Hessian matrix ${\nabla }^{2}E$ ($E$ is the total energy) based on bond and angle interactions

$\begin{array}{c}\left|{\nabla }^{2}E - \lambda \mathit{M}\right|=0\end{array}(3)$

where $\mathit{M}$ is the mass matrix and $\lambda ={\omega }^2$ is the eigenvalue ($\omega$ is the vibration frequency). We diagonalized the mass weighted Hessian matrix to obtain eigenvalues and eigenvectors. The fluctuations of the CG bead coordinates are given as

$\begin{array}{c}\langle \Delta x_k^2\rangle ={\displaystyle \sum }_{i=1 }^{3N-6}\frac{k_{B}T}{M_k{\omega }^2}{\left| y_{ki}\right|}^2\end{array}(4)$

The mean square displacement (MSD) of the internal coordinates can be written as function of eigenvalues and eigenvectors as [38].

$\begin{array}{c}\langle \Delta {\varphi }_j^2\rangle ={\displaystyle \sum }_{i=1 }^{3N-6}\frac{k_{B}T}{{\omega }^2}{\displaystyle \sum }_{k=1 }^{3N}{\left|B_{jk} M_k^{-1/2}{y}_{kj}\right|}^2\end{array}(5)$

where ${\omega }^2=\lambda$ and $\mathit{y}$ is the eigenvector and $\mathit{B}$ is the Wilson matrix relating the CG bead coordinates to the internal coordinate as $\mathbf{\Delta }\mathit{\varphi }=\mathit{B}\mathbf{\Delta }\mathit{x}$[38].

Setup of Endocytosis Coarse-Grained Simulations

We modeled the envelope of the virus as a rigid sphere with a diameter of 85 nm. Seventy-two spikes are embedded in the envelope in our model. The end CG sites (CG site 17 in Figure 1C) of the spike stems are anchored to the envelope. Morse bonds are formed between the receptor binding site (CG site 11 Figure 1C) of the spike and the binding sites (CG sites 1 and 13 in Figure 1D) of the ACE2 protein when they get close to each other. Only one receptor binding site is modeled on each spike, as the crystal structure of the spike has only one receptor binding site up [26]. Two binding sites on each ACE2 receptor were modeled. The virus is given an initial small velocity towards the cell membrane to initiate the endocytosis process. Body temperature is used for all simulations, and a simulation box of 800 by 800 by 1600 nm is applied with the periodic boundary condition. While there is no direct measurement of absolute ACE2 surface densities and only relative ACE2 expressions were measured [40, 41], Chen et al. measured a density of 480–640/μm² for receptors of various species [42]. We used a surface density of 300/μm² which is about 1/10 of the surface density of the spike on the envelope (3,260/μm²). This value was also used in a recent study to quantify the adhesive strength between the SARS-CoV-2 spike proteins and the human receptor ACE2 [43].

We applied the one-particle-thick lipid bilayer model [44], which we developed as a LAMMPS package [45], to simulate a flat cell membrane patch with ACE2 proteins embedded. It gives a bending rigidity of 50 k_BT, and ACE2 proteins can diffuse freely on the surface of the fluctuating cell membrane. All the CG simulations of endocytosis were carried out in LAMMPS.

We used the Berendsen thermostat and barostat to control the temperature and membrane tension. The temperature is set to T = 0.23 $\mathit{\epsilon }/{\mathit{k}}_{\mathit{B}}$ for all the particles in the simulations, where $\mathit{\epsilon }$ is the energy depth in the one-particle-thick lipid bilayer. We controlled the membrane tension to zero by setting the coupled XYZ pressure to zero. Because the out-of-plane stress of the membrane is always zero, and the membrane is curved in 3D due to deformation, the coupled XYZ pressure is linearly proportional to the membrane tension.

The binding energy between the spike RBD and ACE2 is modeled using the Morse breakable bond as

$\begin{array}{c}E=D{\left[1-e^{-\alpha (r-r_0)}\right]}^2\end{array}(6)$

with an energy well depth of D = 68 $\mathit{\epsilon }$, which gives a physical value of 177 kcal/mol obtained from all-atom simulations [28], and $\alpha =1.0$, $r_0$ = 1 nm. We used Morse breakable bonds instead of Morse pair interactions because pair interactions can cause clustering of ACE2 receptors, as many ACE2 receptors can bind to the same spike at the same time [18]. This unphysical problem can be solved by using LAMMPS commands “fix bond/create” and “fix bond/break”. We set the maximum number of bonds that can be formed for the spike RBD from ACE2 to be one. The cutoff for Morse bond formation in “fix bond/create” is set to 20 nm, and the cutoff for Morse bond break in “fix bond/break” is set to 28 nm. By using the command “fix bond/break”, we not only make the simulation of binding/unbinding more realistic, but also avoid numerical instability due to excessive bond stretch. Because the attraction branch of Morse potential near the cutoff distance is weak, after the bond is formed the bond can be stretched beyond the ghost atom cutoff length in LAMMPS in some cases, leading to errors of missing atoms in multiple CPU simulations. With “fix_bond/break”, the bond will break if it is longer than 28 nm before it reaches the ghost atom cutoff length, which is set to 30 nm in the simulations.

Results

Overview of the Coarse-Grained Models

Although different resolutions of coarse-graining can be developed by using the SBCG approach, we focused on the minimal model with a small number of CG sites. The CG models for the SARS-CoV-2 spike protein and the ACE2 receptor are shown in Figure 1B. In Figure 1A and Figure 2B, the CG models are superimposed on top of their respective all-atom structures, and only the head S1 subunit is shown for the spike protein. The all-atom systems are colored based on their secondary structures.

FIGURE 2

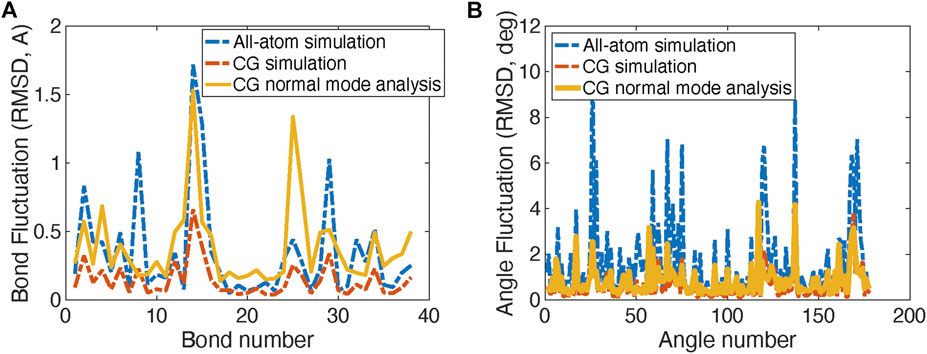
FIGURE 2. Comparison of Root Mean Square Displacement (RMSD) fluctuations of bond lengths (A) and angles (B) obtained from the original all-atom simulations, the CG simulations, and the normal mode analysis of the CG model of the spike protein head S1 unit.

The CG model of the spike protein has 17 CG sites. Sites 1–15 represent the S1 head subunit and sites 16 and 17 present the S2 stem subunit. Within the S1 subunit, CG site 11 represents the receptor binding domain (RBD) in the original crystal structure (PDB: 6VSB), and CG sites 3 and 15 present the hidden RBDs. CG sites 6, 12, and 14 represent the outer beta sheets domains of each spike protein in the trimer. In the S2 subunit, CG site 17 is anchored in the viral envelope, and CG site eight is the connecting region between S1 and S2 subunits.

The CG model of the ACE2 receptor has 15 CG sites. CG sites 3, 4, 5, 8, 10, 11, and 15 represent the transmembrane domains, while CG sites 1 and 13 represent two binding sites for the spike protein.

Parameters of the Coarse-Grained Model

The CG parameters in Eq. 1, such as bond coefficients and initial lengths, are listed as Supplementary Tables S1–S8 in the Supplementary Material for the SARS-CoV-2 spike protein and the ACE2 receptor. Note that only bond and angle interactions are used as shown in Eq. 1, while dihedral angles are not included in this shape-based coarse-graining approach.

Note that the bonded coefficients of the S1 head subunit are obtained from the all-atom simulations of the S1 head subunit, while the bonded coefficients of S2 subunits are obtained from the fully-glycosylated full-length spike protein model (Supplementary Figure S1 in the Supplementary Material).

The comparison RMSDs of the original all-atom simulations with the CG models for bond length and angles are shown in Figure 2A. Figure 2B shows the fluctuation magnitudes of the CG model match well with the original all-atom model.

Normal mode analysis of the coarse-grained model

Normal mode analysis (NMA) is also applied to calculate the fluctuations and vibration modes of the CG models. In Figure 2B, the fluctuations (yellow curves) obtained by NMA match well with the all-atom model. The fluctuations calculated from NMA are different from the fluctuations obtained from direction CG simulation of the same model due to the anharmonic effect in the direct CG simulations. In addition, the first three vibration modes of the spike S1 head unit are shown in Figure 3. The 1st and 2nd modes involve the motions of the RBD site in two horizontal directions, respectively, and the 3rd mode involves the motion of one of the three exterior beta sheet domains.

FIGURE 3

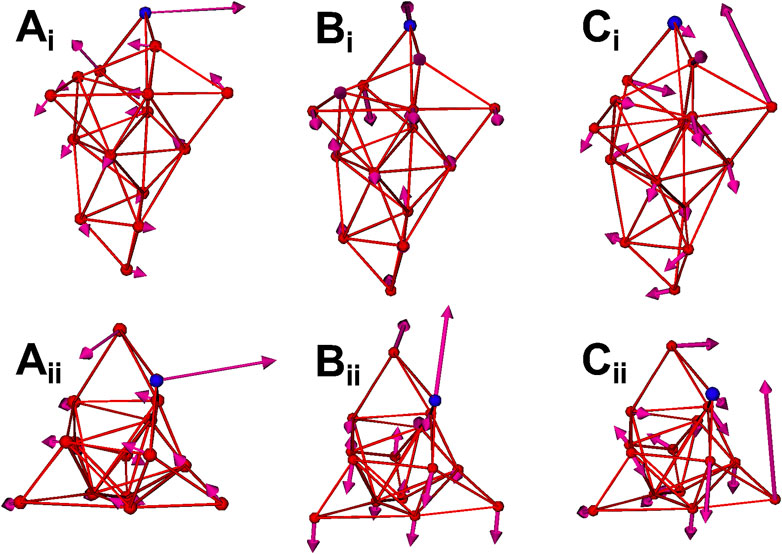
FIGURE 3. The first three normal modes of the spike CG model. (Ai) 1st mode (side view). (Aii) 1st mode (top view). (Bi) 2nd mode (side view). (Bii) 2nd mode (top view). (Ci) 3rd mode (side view). (Cii) 3rd mode (top view). The RBD site (CG site 11) is highlighted as blue.

Modeling of the Endocytosis of the Coronavirus.

After we established the CG models of the spike protein and ACE2 protein, we applied them to simulate the endocytosis of a whole coronavirus. As shown in Figure 4A, we modeled the virus envelope as a rigid sphere with a diameter of 85 nm. The CG models of the spike proteins (red) are distributed on the surface of the virus with the stems embedded in the viral envelope (grey). The RBD binding sites of the spike proteins (CG site 11 in Figure 1A) are highlighted as blue. The transmembrane domain CG sites of the ACE2 proteins (green) are embedded in the host cell membrane (orange). The host cell membrane is modeled by using the one-particle-thick bilayer model [44, 45]. The same interaction is applied between the cell membrane particles and the CG particles of the transmembrane domains of ACE2 so that the ACE2 proteins are anchored in the cell membrane with the right orientation as shown in Figure 4A. The binding sites of the ACE2 proteins are also shown as blue. The depth of the energy well $\mathit{\epsilon }$ of the pair interaction in the one-particle-thick model is set to about 5.0 times thermal energy (k_B T) and the characteristic length and the cutoff length are set to 4 and 10.4 nm so that the membrane self-assembled into a one-particle-thick layer with the fluid behavior and bending rigidity of 50 k_B T. The attraction and repulsive parameters $\eta =2$ and $\zeta =4$, and the bending parameter $\mu =3$ (see Fu et al. [45]).

FIGURE 4

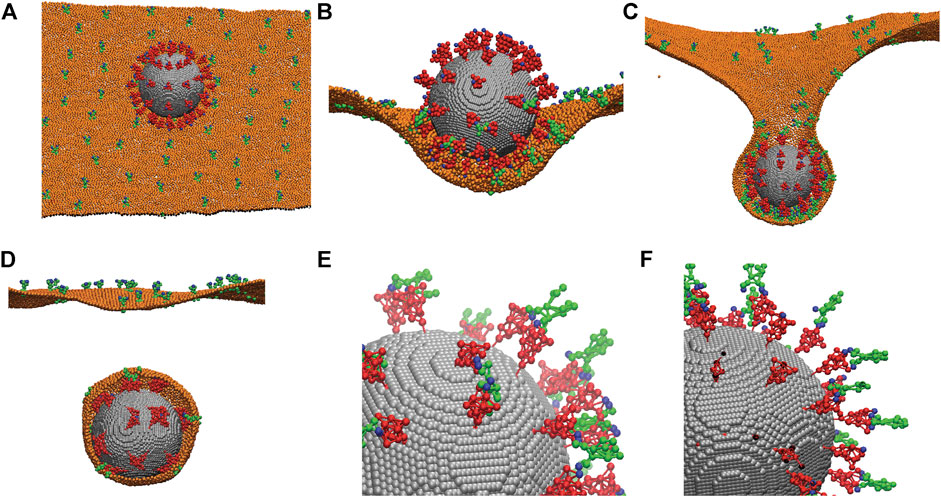
FIGURE 4. Simulations of the endocytosis of a whole virus by incorporating the CG models of the spike protein and the ACE2 receptor. (A) A CG model of the whole virus with 72 distributed spike proteins (red) anchored on its viral envelope (grey). The spike proteins are modeled using the CG model described in Figure 1. ACE2 proteins (green) are anchored in the host cell membrane (orange). Both the binding sites of the spike proteins and ACE2 proteins are marked as blue. (B) The initial attachment of the virus to the fluctuating cell membrane. (C) The progress of the endocytosis due to spike-ACE2 interaction. (D) Separation of the membrane-bounded virus from the host cell membrane. Only half of the cell membrane is shown in (B, C, D) for revealing the interior virus and interactions. (E) A close view of the interactions between the spike proteins (red) and ACE2 receptors (green) through their binding sites (blue). Most ACE2 receptors bind to two spikes. Membrane is not shown. (F) The same as (E) except the ACE2 receptors and spikes are modeled as rigid bodies without flexibility. All ACE2 bind to one spike only. Membrane is not shown.

As shown in Figures 4C,D, the ACE2 proteins can diffuse on the fluctuating cell membrane with the correct orientations. The Berendsen thermostat and barostat are used to maintain a constant membrane temperature and zero membrane tension. The rigid body dynamics in LAMMPS is employed for the viral envelope, and the NVE integrator with Langevin thermostats is employed for the dynamics of spike and ACE2 proteins under the same temperature as the membrane. The interaction between the spike RBD sites and the ACE2 binding sites is simulated by breakable Morse bonds. The binding energy between the spike and ACE2 is set to −177 kcal/mol, obtained from the literature for spike-ACE2 interaction [28–32].

When the virus is initially attached to the cell membrane, the spike proteins at the bottom surface of the virus bind to the ACE2 proteins and are deformed due to their structure flexibility as shown in Figure 4B, while the spike proteins on the top surface remain much less deformed, although they vibrate due to thermal fluctuations. After more ACE2 proteins bind to the spikes, the virus is engulfed by the cell membrane. This eventually leads to the necking and rupture of the cell membrane as shown in Figures 4C,D. Our simulations show that due to the flexibility of the spike proteins and their actual surface density, it is possible for the two spikes to bend significantly to bind to the same ACE2 receptor as shown in Figure 4E. Our simulations show that this is not possible if the spike and ACE2 proteins are modeled as rigid structures, and one spike can only bind to one ACE2 as shown in Figure 4F. Therefore, it is critical to consider the realistic flexibility of the spike and ACE2 proteins in the simulations, as also demonstrated in all-atom MD simulations [46–48].

Conclusions and Discussions

We developed the CG models of the spike proteins and ACE2 receptors using the shape-based coarse-graining approach. The force field parameters are obtained from the all-atom simulations by matching the fluctuations. Then these CG models are incorporated into LAMMPS to simulate the binding of the spike proteins with the ACE2 receptors during the endocytosis of a whole virus. We found that the realistic structure flexibility of the spike proteins and ACE2 proteins is critical for better interaction between these two proteins. For example, our results showed that two spike proteins can easily bind to one ACE2 receptor due to significant bending deformation.

Besides endocytosis, the coronavirus can enter the host cell by membrane fusion. To model the membrane fusion process in a future study, we will need to consider the viral envelope as a flexible membrane using the one-particle-thick lipid bilayer model. As the connection between the S1 and S2 subunits is cleaved and the S1 head subunit is removed from the virus during the membrane fusion process, we also need to refine the CG model to incorporate this breakable bond mechanism.

In summary, we simulated the endocytosis of the whole coronavirus with minimal atomistic details of its spike proteins and corresponding ACE2 receptors. Although the resolution is coarse and the coarse-graining is aggressive, it can help us understand the biophysical behavior of the coronavirus at large temporal and spatial scales beyond typical atomistic simulations. Furthermore, the CG resolutions can be refined if needed through the same procedure by using the scripts provided in the Supplementary Material.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

ZP constructed the cell membrane CG model, the CG virus using the SARS-CoV-2 and ACE2 CG models, and performed MD simulations with the aforementioned CG models in LAMMPS. TL designed the coarse-graining program to convert the all-atom SARS-CoV-2 and ACE2 proteins into their CG models, and designed the program to extract the bonding parameters from the CG models and convert them into a LAMMPS-compatible format. TL was also responsible for patching a technical issue that impeded CG model creation. CV designed the normal mode analysis program and performed normal mode analyses on all aforementioned CG models.

Funding

ZP acknowledge the funding support from NSF Grant No. CBET-1948347. TL is supported through the Research Experiences for Undergraduates (REU) supplement of NSF CBET-1948347. CV is supported by the Guaranteed Paid Internship Program (GPIP) from University of Illinois at Chicago. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

All-atom MD and CG simulations were conducted on the supercomputer Theta in Argonne Leadership Computing Facility (ALCF) in the Argonne National Lab under Director’s Discretionary (DD) allocation Modeling Corona Virus.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.680983/full#supplementary-material

References

1. He F, Deng Y, Li W. Coronavirus Disease 2019: What We Know? J Med Virol (2020). 92(7):719–25. doi:10.1002/jmv.25766

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Goldsmith CS, Tatti KM, Ksiazek TG, Rollin PE, Comer JA, Lee WW, et al. Ultrastructural Characterization of SARS Coronavirus. Emerg Infect Dis (2004). 10(2):320–6. doi:10.3201/eid1002.030913

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Godet M, L'Haridon R, Vautherot J-F, Laude H. TGEV corona Virus ORF4 Encodes a Membrane Protein that Is Incorporated into Virions. Virology (1992). 188(2):666–75. doi:10.1016/0042-6822(92)90521-p

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Andersson R. University Decentralization as Regional Policy: the Swedish experiment. J Econ Geogr (2004). 4(4):371–88. doi:10.1093/jeg/4.4.371

CrossRef Full Text | Google Scholar

5. Berman H, Henrick K, Nakamura H. Announcing the Worldwide Protein Data Bank. Nat Struct Mol Biol (2003). 10(12):980. doi:10.1038/nsb1203-980

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Berman HM. The Protein Data Bank. Nucleic Acids Res (2000) 28(1):235–42. doi:10.1093/nar/28.1.235

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Frick DN, Virdi RS, Vuksanovic N, Dahal N, Silvaggi NR. Molecular Basis for ADP-Ribose Binding to the Mac1 Domain of SARS-CoV-2 Nsp3. Biochemistry (2020) 59(28):2608–15. doi:10.1021/acs.biochem.0c00309

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hillen HS, Kokic G, Farnung L, Dienemann C, Tegunov D, Cramer P. Structure of Replicating SARS-CoV-2 Polymerase. Nature (2020) 584(7819):154–6. doi:10.1038/s41586-020-2368-8

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Kern DM, Sorum B, Mali SS, Hoel CM, Sridharan S, Remis JP, et al. Cryo-EM Structure of the SARS-CoV-2 3a Ion Channel in Lipid Nanodiscs. bioRxiv (2020) [Preprint]. doi:10.1101/2020.06.17.156554

CrossRef Full Text

10. Rut W, Lv Z, Zmudzinski M, Patchett S, Nayak D, Snipas SJ, et al. Activity Profiling and Structures of Inhibitor-Bound SARS-CoV-2-PLpro Protease Provides a Framework for Anti-COVID-19 Drug Design. bioRxiv (2020)[Preprint]. doi:10.1101/2020.04.29.068890

11. Shang J, Ye G, Shi K, Wan Y, Luo C, Aihara H, et al. Structural Basis of Receptor Recognition by SARS-CoV-2. Nature (2020) 581(7807):221–4. doi:10.1038/s41586-020-2179-y

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Yan R, Zhang Y, Li Y, Xia L, Guo Y, Zhou Q. Structural basis for the recognition of SARS-CoV-2 by full-length human ACE2. Science (2020) 367(6485):1444–1448. doi:10.1126/science.abb2762

CrossRef Full Text

13. Surya W, Li Y, Torres J. Structural Model of the SARS Coronavirus E Channel in LMPG Micelles. Biochim Biophys Acta (Bba) - Biomembranes (2018) 1860(6):1309–17. doi:10.1016/j.bbamem.2018.02.017

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Walls AC, Park Y-J, Tortorici MA, Wall A, McGuire AT, Veesler D. Structure, Function, and Antigenicity of the SARS-CoV-2 Spike Glycoprotein. Cell (2020) 183(6):1735. doi:10.1016/j.cell.2020.11.032

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Yu A, Pak AJ, He P, Monje-Galvan V, Casalino L, Gaieb Z, et al. A Multiscale Coarse-Grained Model of the SARS-CoV-2 Virion. Biophys J (2021) 120(6):1097–1104. doi:10.1016/j.bpj.2020.10.048

16. Zhang L, Lin D, Sun X, Curth U, Drosten C, Sauerhering L, et al. Crystal Structure of SARS-CoV-2 Main Protease Provides a Basis for Design of Improved α-ketoamide Inhibitors. Science (2020) 368(6489):409–12. doi:10.1126/science.abb3405

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Jaimes JA, André NM, Chappie JS, Millet JK, Whittaker GR. Phylogenetic Analysis and Structural Modeling of SARS-CoV-2 Spike Protein Reveals an Evolutionary Distinct and Proteolytically Sensitive Activation Loop. J Mol Biol (2020) 432(10):3309–25. doi:10.1016/j.jmb.2020.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Shen Z, Ye H, Yi X, Li Y. Membrane Wrapping Efficiency of Elastic Nanoparticles during Endocytosis: Size and Shape Matter. ACS Nano (2018) 13(1):215–28. doi:10.1021/acsnano.8b05340

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Shen Z, Ye H, Li Y. Understanding Receptor-Mediated Endocytosis of Elastic Nanoparticles through Coarse Grained Molecular Dynamic Simulation. Phys Chem Chem Phys (2018) 20(24):16372–85. doi:10.1039/c7cp08644j

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Shen Z, Ye H, Kröger M, Li Y. Aggregation of Polyethylene Glycol Polymers Suppresses Receptor-Mediated Endocytosis of PEGylated Liposomes. Nanoscale (2018) 10(9):4545–60. doi:10.1039/c7nr09011k

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Richards DM, Endres RG. Target Shape Dependence in a Simple Model of Receptor-Mediated Endocytosis and Phagocytosis. Proc Natl Acad Sci USA (2016) 113(22):6113–8. doi:10.1073/pnas.1521974113

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Li Y, Kröger M, Liu WK. Endocytosis of PEGylated Nanoparticles Accompanied by Structural and Free Energy Changes of the Grafted Polyethylene Glycol. Biomaterials (2014) 35(30):8467–78. doi:10.1016/j.biomaterials.2014.06.032

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Gao H, Shi W, Freund LB. From the Cover: Mechanics of Receptor-Mediated Endocytosis. Proc Natl Acad Sci (2005) 102(27):9469–74. doi:10.1073/pnas.0503879102

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Doherty GJ, McMahon HT. Mechanisms of Endocytosis. Annu Rev Biochem (2009) 78(1):857–902. doi:10.1146/annurev.biochem.78.081307.110540

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Neuman BW, Kiss G, Kunding AH, Bhella D, Baksh MF, Connelly S, et al. A Structural Analysis of M Protein in Coronavirus Assembly and Morphology. J Struct Biol (2011) 174(1):11–22. doi:10.1016/j.jsb.2010.11.021

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wrapp D, Wang N, Corbett KS, Goldsmith JA, Hsieh C-L, Abiona O, et al. Cryo-EM Structure of the 2019-nCoV Spike in the Prefusion Conformation. Science (2020) 367(6483):1260–3. doi:10.1126/science.abb2507

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yan R, Zhang Y, Li Y, Xia L, Guo Y, Zhou Q. Structural Basis for the Recognition of SARS-CoV-2 by Full-Length Human ACE2. Science (2020) 367(6485):1444–8. doi:10.1126/science.abb2762

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Qiao B, Olvera de la Cruz M. Enhanced Binding of SARS-CoV-2 Spike Protein to Receptor by Distal Polybasic Cleavage Sites. ACS Nano (2020) 14(8):10616–23. doi:10.1021/acsnano.0c04798

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ali A, Vijayan R. Dynamics of the ACE2–SARS-CoV-2/sars-CoV Spike Protein Interface Reveal Unique Mechanisms. Scientific Rep (2020) 10(1). doi:10.1038/s41598-020-71188-3

PubMed Abstract | CrossRef Full Text | Google Scholar

30. He J, Tao H, Yan Y, Huang S-Y, Xiao Y. Molecular Mechanism of Evolution and Human Infection with SARS-CoV-2. Viruses (2020) 12(4):428. doi:10.3390/v12040428

31. Mercurio I, Tragni V, Busto F, De Grassi A, Pierri CL. Protein Structure Analysis of the Interactions between SARS-CoV-2 Spike Protein and the Human ACE2 Receptor: from Conformational Changes to Novel Neutralizing Antibodies. Cell. Mol. Life Sci. (2020) 78(4):1501–22. doi:10.1007/s00018-020-03580-1

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Spinello A, Saltalamacchia A, Magistrato A. Is the Rigidity of SARS-CoV-2 Spike Receptor-Binding Motif the Hallmark for Its Enhanced Infectivity? Insights from All-Atom Simulations. J Phys Chem Lett (2020)11(12):4785–4790. doi:10.1021/acs.jpclett.0c01148

33. Simmons G, Zmora P, Gierer S, Heurich A, Pöhlmann S. Proteolytic Activation of the SARS-Coronavirus Spike Protein: Cutting Enzymes at the Cutting Edge of Antiviral Research. Antiviral Res (2013) 100(3):605–14. doi:10.1016/j.antiviral.2013.09.028

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Phillips JC, Hardy DJ, Maia JDC, Stone JE, Ribeiro JV, Bernardi RC, et al. Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD. J Chem Phys (2020) 153(4):044130. doi:10.1063/5.0014475

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Woo H, Park S-J, Choi YK, Park T, Tanveer M, Cao Y, et al. Developing a Fully Glycosylated Full-Length SARS-CoV-2 Spike Protein Model in a Viral Membrane. J Phys Chem B (2020) 124(33):7128–37. doi:10.1021/acs.jpcb.0c04553

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Arkhipov A, Schulten K, Freddolino P, Ying Y, Shih A, Chen Z. Coarse-Graining of Condensed Phase and Biomolecular Systems. Boca Raton, FL: CRC Press (2008). p. 299–315. doi:10.1201/9781420059564 ch20 Application of Residue-Based and Shape-Based Coarse-Graining to Biomolecular Simulations.

CrossRef Full Text | Google Scholar

37. Humphrey W, Dalke A, Schulten K. VMD: Visual Molecular Dynamics. J Mol Graphics (1996) 14(1):33–8. doi:10.1016/0263-7855(96)00018-5

CrossRef Full Text | Google Scholar

38. Brooks BR, Jane?i? Da., Karplus M. Harmonic Analysis of Large Systems. I. Methodology. J Comput Chem (1995) 16(12):1522–42. doi:10.1002/jcc.540161209

CrossRef Full Text | Google Scholar

39. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J Comput Phys (1995) 117(1):1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

40. Al-Benna S. Association of High Level Gene Expression of ACE2 in Adipose Tissue with Mortality of COVID-19 Infection in Obese Patients. Obes Med (2020) 19:100283. doi:10.1016/j.obmed.2020.100283

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Zhang L, Han X, Shi Y. Comparative Analysis of SARS-CoV-2 Receptor ACE2 Expression in Multiple Solid Tumors and Matched Non-diseased Tissues. Infect Genet Evol (2020) 85:104428. doi:10.1016/j.meegid.2020.104428

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Chen Y, Munteanu AC, Huang Y-F, Phillips J, Zhu Z, Mavros M, et al. Mapping Receptor Density on Live Cells by Using Fluorescence Correlation Spectroscopy. Chem Eur J (2009) 15(21):5327–36. doi:10.1002/chem.200802305

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ponga M. Quantifying the Adhesive Strength between the SARS-CoV-2 S-Proteins and Human Receptor and its Effect in Therapeutics. Scientific Rep (2020) 10(1). doi:10.1038/s41598-020-74189-4

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Yuan H, Huang C, Li J, Lykotrafitis G, Zhang S. One-particle-thick, Solvent-free, Coarse-Grained Model for Biological and Biomimetic Fluid Membranes. Phys Rev E (2010) 82(1). doi:10.1103/physreve.82.011905

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Fu S-P, Peng Z, Yuan H, Kfoury R, Young Y-N. Lennard-Jones Type Pair-Potential Method for Coarse-Grained Lipid Bilayer Membrane Simulations in LAMMPS. Computer Phys Commun (2017) 210:193–203. doi:10.1016/j.cpc.2016.09.018

CrossRef Full Text | Google Scholar

46. Barros EP, Casalino L, Gaieb Z, Dommer AC, Wang Y, Fallon L, et al. The Flexibility of ACE2 in the Context of SARS-CoV-2 Infection. Biophys J (2020) 120(6):1072–1084. doi:10.1101/2020.09.16.300459

47. Pierri CL. SARS-CoV-2 Spike Protein: Flexibility as a New Target for Fighting Infection. Signal Transduction Targeted Ther (2020) 5(1). doi:10.1038/s41392-020-00369-3

CrossRef Full Text | Google Scholar

48. Römer RA, Römer NS, Wallis AK. Flexibility and Mobility of SARS-CoV-2-Related Protein Structures. Scientific Rep (2021) 11(1). doi:10.1038/s41598-021-82849-2

CrossRef Full Text | Google Scholar