Control of Néel-type Magnetic Kinks Confined in a Square Nanostructure by Spin-Polarized Currents

Magnetic skyrmion in chiral magnet exhibits a variety of unique topological properties associated with its innate topological structure. This inspires a number of ongoing searching for new topological magnetic textures. In this work, we used micromagnetic simulations and Monte Carlo simulations to investigate an exotic Néel-type magnetic kinks in square-shaped nanostructures of chiral magnets, which performs rather stably in the absence of magnetic field. The individual magnetic kink can reside in one of the four possible corners, and carry possibly upward or downward core polarity, constituting eight degenerate states. In addition, these kinks also exhibit unique behaviors of generation, stability and dynamics, as revealed by micromagnetic simulations. It was found that such kinks can be created, annihilated, displaced, and polarity-reversed on demand by applying a spin-polarized current pulse, and are easily switchable among the eight degenerate states. In particularly, the kinks can be switched toward the ferromagnetic-like states and backward reversibly by applying two successive current pulses, indicating the capability of writing and deleting the kink structures. These findings predict the existence of Néel-type magnetic kinks in the square-shaped nanostructures, as well as provide us a promising approach to tailor the kinks by utilizing the corners of the nanostructures, and control these states by spin-polarized currents. The present work also suggests a theoretical guide to explore other chiral magnetic textures in nanostructures of polygon geometries.

1 Introduction

A magnetic skyrmion is a topologically stable configuration often observed in chiral magnets with broken inversion symmetry. The nanoscale skyrmion shows particle-like behavior, as it can be moved, created, and annihilated. These characters make it promising candidate as information carrier for future memory devices and logic devices [1–6]. It has thus aroused intense research efforts in recent years, leading to a series of breakthrough achievements in manipulation of skyrmion states, via injected spin-polarized currents, external electric-field, and so on [7–14]. For the application of skyrmions in spintronic devices, many feasible designs have been proposed for confining the skyrmions in geometric nanostructures, such as nanostripes and nanodisks, which may allow the precise control of individual skyrmions [8–10]. These achievements pave the way towards all-electrical manipulation schemes [2, 3], and underpin the skyrmion-based information storage concepts, such as the skyrmion-based racetrack memory, high density magnetic random access memory, and logic gates, etc. [2–6, 8, 9].

These fascinating physical properties also inspired an ongoing search for new types of magnetic topological textures, for instance, fractional skyrmion emerging in various chiral and frustrated magnets [15–21], which exhibit some unusual physical phenomena distinctly different from skyrmion-host chiral magnetic materials such as MnSi and Fe_1-xCo_xSi systems [22, 23]. Moreover, some recent observations indicated that fractional skyrmions also emerge in geometric nanostructures due to the effects of geometric confinement and shape anisotropy [24–28]. For example, it was observed in Lorentz transmission electron microscopy (TEM) images of FeGe nanostripes that, the skyrmions survive when the width of the nanostripe much larger than the single skyrmion size, whereas some merons form at the edges that are not large enough for accommodating a complete skyrmion [24, 25].

Generally, the presence of edges and corners in nanostructures can be utilized to tailor the magnetic textures and modify their dynamics behaviors. For the skyrmion confined in ultrathin film nanostructures with Dzyaloshinskii-Moriya (DM) interaction, the boundary constrictions naturally make the magnetization orientation undergo the 180° rotation at the edges, forming the so-called kink or π domain wall configurations [2, 15, 29–32]. Depending on the crystal symmetry of chiral magnets, two distinct types of chiral kinks, namely, Néel-type and Bloch-type kinks, are favorable in interfacial and bulk DM interaction systems respectively [29, 30]. It had been theoretically proposed in chiral magnets that the skyrmions, antiskyrmions, and other magnetic configurations can be naturally interpreted in terms of chiral kinks. These kinks carry a topological charge and allow to construct new topological particle-like states [15, 31, 32]. In addition, the previous studies demonstrated that some special magnetic textures often appear in the corners of the polygon geometries like triangles, squares, rectangles, in which the corners may also act as pinning sites for the domain wall motion [33–36]. This indicates that the nanostructure with polygon geometries may provide a unique platform for studying the kink structures, favoring the control of the magnetic states, by utilizing their edges and corners. Certainly, there are more open questions to be explored along this line. For instance, is it possible to realize some new kink structures beyond the skyrmions and merons in nanostructures? Is it possible the kink structures stable in nanostructures without the assistance of external magnetic field? Is it possible to manipulate these kinks by pure electric currents? These issues are very critical for our understanding the physical properties of the new type chiral magnetic structures in confined nanostructures.

Inspired by this motivation, the purpose of our work is to explore new kink structures in nanostructures by using micromagnetic simulations and Monte Carlo simulations. In this work, we aimed at studying the square-shaped nanostructures with width smaller than the single skyrmion size. We demonstrated an exotic Néel-type kink structure, which can stably exist in the corners of the square-shaped nanostructures in the absence of external magnetic field. Such kinks possess eight switchable degenerate states and can be created, annihilated, displaced, and polarity-reversed by applying spin-polarized currents.

2 Model and Simulation Methods

In this work, the magnetic state in an ultrathin square nanostructure of chiral magnets is described by a classical Heisenberg model. The Hamiltonian consists of ferromagnetic exchange interaction $\left(J_{FM}\right)$, DM interaction $\left(D\right)$, anisotropy $\left(A\right)$, and Zeeman term $\left(B_z\right)$ [8, 37, 38]:

$\begin{array}{c}\mathrm{\mathscr{H}}=-J_{FM}{\displaystyle \sum _i{\mathbf{m}}_i\cdot \left({\mathbf{m}}_{i+\widehat{x}}+{\mathbf{m}}_{i+\widehat{y}}\right)}-D{\displaystyle \sum _i\left({\mathbf{m}}_i\times {\mathbf{m}}_{i+\widehat{x}}\cdot \widehat{y}+{\mathbf{m}}_i\times {\mathbf{m}}_{i+\widehat{y}}\cdot \widehat{x}\right)}\\ -A{\displaystyle \sum _i{\left({\mathbf{m}}_i\cdot \widehat{z}\right)}^2}-{\mathit{B}}_z\cdot {\displaystyle \sum _i{\mathbf{m}}_i},\end{array}(1)$

where the magnetic moments are imposed on a two-dimensional $L\times L$ square lattice with free boundary conditions. ${\mathbf{m}}_i$ denotes the magnetic moment at site i in the xy-plane, with fixed length $\left|{\mathbf{m}}_i\right|=\mathrm{1.0.}$ The magnetic field ${\mathit{B}}_z=B_z{\mathit{e}}_z$ is applied normal to the xy-plane and easy-axis anisotropy ($A$ > 0) is along the ± z-axis. In the simulations, we have neglected the dipole-dipole interactions. This treatment is suitable for chiral magnets with strong DM interaction and weak dipole-dipole interactions such as Pd/Fe bilayers on Ir(111) substrate [39, 40]. For Pd/Fe/Ir(111) the magnetic dipolar energy is very weak in energy scale in comparison with the ferromagnetic exchange energy and DM interaction, and thus it can be effectively included into the anisotropy energy. We choose typical parameters for Pd/Fe/Ir(111) as $J_{FM}\equiv 2.95$ meV, $\mathit{D}/J_{FM}=0.27$, $A/J_{FM}=0.05$, and a typical lattice constant $a=$ 5 Å [39, 40].

To investigate the dynamics of the magnetic structures driven by the spin-polarized current, we numerically solved the Landau-Lifshitz-Gilbert (LLG) equation by using fourth-order Runge-Kutta method [8, 10, 41, 42]:

$\begin{array}{c}\frac{d{\mathbf{m}}_i}{dt}=-\gamma {\mathbf{m}}_i\times {\mathit{B}}_i^{eff}+\alpha {\mathbf{m}}_i\times \frac{d{\mathbf{m}}_i}{dt}+\mathbf{T},\end{array}(2)$

with the effective field ${\mathit{B}}_i^{eff}=-\left(1/\hslash \gamma \right)\left(\partial \mathrm{\mathscr{H}}/\partial {\mathbf{m}}_i\right)$, the gyromagnetic ratio $\gamma =g_{\text{s}}{\mu }_{\text{B}}/\hslash$ (here $g_{\text{s}}$ is the electron spin g-factor, and ${\mu }_{\text{B}}$ is the Bohr magneton), and Gilbert damping $\alpha$. The first and second terms describe respectively the gyromagnetic precession and the Gilbert damping, and the third term $\mathbf{T}$ denotes the spin transfer torque (STT) due to the spin-polarized current.

The skyrmion motion can be driven by spin-polarized current flowing in the nanostructure along either the in-plane or out-of-plane direction. For simulations of the skyrmion dynamics induced by the current-in-plane (CIP) injection, the corresponding torque ${\mathbf{T}}_{\text{CIP}}$ is given by the following form [41]:

$\begin{array}{c}{\mathbf{T}}_{\text{CIP}}=\frac{{\text{P}}_e{a}^3}{2e{\text{M}}_{\text{s}}}\left({\mathit{j}}_{\text{CIP}}\cdot \nabla \right){\mathbf{m}}_i-\frac{{\text{P}}_e{a}^3\beta }{2e{\text{M}}_{\text{s}}}\left[{\mathbf{m}}_i\times \left({\mathit{j}}_{\text{CIP}}\cdot \nabla \right){\mathbf{m}}_i\right],\end{array}(3)$

where the first and second terms represent the coupling between magnetic moments and spin-polarized current ${\mathit{j}}_{\text{CIP}}$ via the spin transfer torque and via the non-adiabatic effects, with $\beta$ the non-adiabaticity factor. ${\text{M}}_{\text{s}}$ is the saturation magnetization, ${\text{P}}_e$ is the polarization rate of the electric current, and $e$ is the elementary charge.

For the current-perpendicular-to-plane (CPP) injection, the current-induced spin transfer torque ${\mathbf{T}}_{\text{CPP}}$ includes an in-plane Slonczewski torque and an out-of-plane field-like torque [8, 42, 43]:

$\begin{array}{c}{\mathbf{T}}_{\text{cpp}}=\gamma u({\mathbf{m}}_i\times {\mathbf{m}}_{\text{p}}\times {\mathbf{m}}_i)-\gamma \xi u({\mathbf{m}}_i\times {\mathbf{m}}_{\text{p}}),\end{array}(4)$

where $u=\left|\frac{\hslash }{e}\right|\frac{j_{\text{CPP}}{\text{P}}_e}{2d{\text{M}}_{\text{s}}}$ is the Slonczewski torque coefficient, $d$ the film thickness of FM layer, $j_{\text{CPP}}$ the current density, ${\mathbf{m}}_{\text{p}}$ is the electron polarization direction, and $\xi$ is the amplitude of the out-of-plane torque relative to the in-plane one. In the simulations, we fixed the coefficient$\xi =0.2$, the polarization rate${\text{P}}_e=0.4$, gyromagnetic ratio $\gamma =1.0$, Gilbert damping $\alpha =0.3$, and non-adiabaticity factor $\beta =0.1$, as the typical parameters for studying the current-induced skyrmion dynamics [8, 10, 41]. The simulated time t is measured in the units of $\tau \equiv \hslash /J_{\text{FM}}\sim$0.2 ps, and current density $j$ are scaled by ${\text{κ}}_{\text{CIP}}\equiv 2e{J}_{\text{FM}}/{\text{P}}_e{a}^2\hslash \sim$ 1.4 × 10¹³ Am⁻² for the CIP case, and ${\text{κ}}_{\text{CPP}}\equiv 2ed{\text{M}}_{\text{s}}{J}_{\text{FM}}/{\hslash }^2{\text{P}}_e\gamma \sim$ 8.5 × 10¹³ Am⁻² for the CPP case, respectively [41]. Here we chose the typical parameters for Pd/Fe/Ir(111) as $d=$0.4 nm and ${\text{M}}_{\text{s}}=$ 1.1 MA/m, and used these values to estimate the units of simulated time and current density.

To get the zero-temperature equilibrium state, we adopted a specific simulation scheme: the lattice was initialized as a paramagnetic phase at sufficiently high temperature, and annealed for obtaining the state at a low temperature, by using the Metropolis Monte Carlo simulation combined with over-relaxation algorithm [17, 18, 44]. Then the configuration was further relaxed for the equilibrium state, by solving the LLG equation under $\mathbf{T}=0$ with long enough equilibration time.

In addition, the kink dynamics is controlled by injecting a CIP-type or CPP-type spin-polarized current pulse on demand. We introduced the schemes in our simulations for setting the amplitude and duration of current pulses as follows: 1) First, we tested the effect of amplitude of current density on the kink dynamics and chose the suitable amplitude of current pulses for control (generation, creation, annihilation, displacement or polarity reversal) of the kink states. 2) Then we carefully tracked its dynamics and turned off the current once the germinal kink appears or kink shifts (in this procedure, the current duration is determined), and further relaxed the system by solving LLG equation under zero-current condition to get an equilibrium kink state.

3 Simulation Results

3.1 Size Effect of Nanostructures on the Magnetic Structures

We first investigated the size effect of the nanostructures on magnetic structures. The simulations were carried out on a $L\times L$ square lattice with free boundary conditions. The zero-temperature equilibrium states for the lattices with different sizes were obtained, and some of the typical configurations were presented in Figure 1. Here a magnetic field $B_z=-0.008J_{FM}$ (corresponding to ∼ −0.1 Tesla, as estimated with the magnetic moment ∼3.0${\mu }_{\text{B}}$ obtained from density functional theory for Pd/Fe/Ir(111) in Ref. [40]) is applied along the −z-axis, which is sufficient for creating the skyrmion states here. In the following, we used an external magnetic field to generate the exotic magnetic kink textures in the nanostructures, and then we demonstrated an alternative way for creating kink by applying spin-polarized current.

FIGURE 1

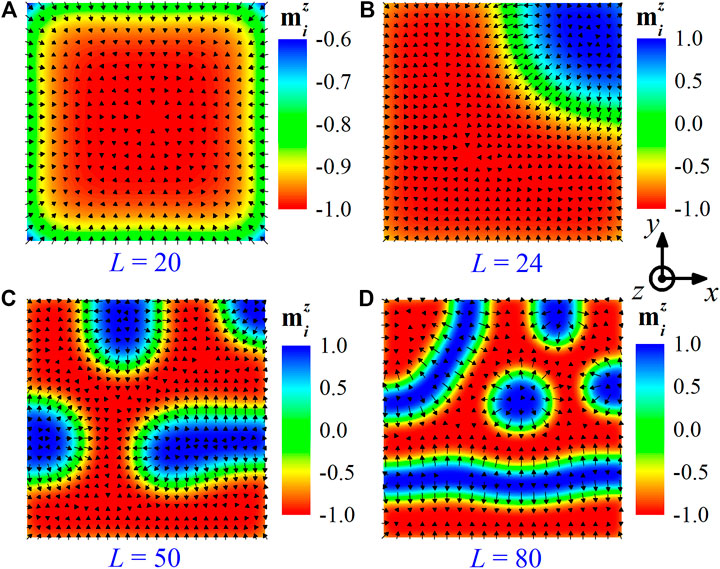
FIGURE 1. Size effect of nanostructures on the equilibrium magnetic states. Some typical magnetic configurations are shown for square-shaped nanostructures with lateral sizes of (A)$L=$ 20 (∼10 nm), (B)$L=$24 (∼12 nm) (C)$L=$50 (∼25 nm), and (D)$L=$ 80 (∼40 nm). Here the magnetic field $B_z=-0.008J_{FM}$ (∼−0.1 T) is applied along the −z-axis. To illustrate the magnetic configurations, we used the color map to scale the magnetization components along z-axis (out-of-plane)${\text{m}}_i^z$, and used the arrows to describe the on-plane xy components${\text{\hspace{0.17em}m}}_i^{xy}$.

As one may see in Figure 1A, a bubble domain arises in the square nanostructure at small lateral size $L=$ 20 (∼10 nm). As the size increases to $L=$ 24 (∼12 nm), a kink-like structure forms in the corner of the square nanostructure, surrounded by the ferromagnetic domain, as will be discussed below. For $L=$ 50 (∼25 nm), it was observed that some half-skyrmion-like (meron-like) structures with topological charge $\left|Q\right|$ ≈ 1/2 and elongated stripes (fractional skyrmion) with topological charge 0 < $\left|Q\right|$ < 1 emerges at the edge of the lattice, together with a kink-like structure that appears in the corner. Further increasing the size, the magnetic states evolve into multi-domains composed of spiral domains, edge-merons, and skyrmion as seen in Figure 1D for the relatively large size $L=$ 80 (i.e., ∼40 nm). It is interesting that the kink-like, meron-like, and skyrmion states tend to nucleate in the corner, the edge, and the inner region of the nanostructure, respectively. These are reasonable likely due to the different boundary constrictions on the formation of magnetic structures, which manifests the strong boundaries and geometric confinement effects in the nanostructures. It is noted that some similar edge states are also found experimentally and theoretically in diverse magnetic materials that host skyrmions with constricted geometry, as a consequence of the effects of geometric boundaries and confinements [37, 45].

3.2 Néel-Type Magnetic Kinks

Now we focus on the intriguing features of kink-like structures and analyzing their current-induced dynamics in this paper. For this, we adopted a small square shaped nanomagnet consisting of 24 × 24 square lattices (∼12 × 12 nm) for studying the kink-like structure, in the rest part of this work. We first tested the stability of the kink-like structure in Figure 1B once the magnetic field was removed. For this, the magnetic structure was relaxed for the equilibrium state by solving the LLG equation, in which we used the kink-like state shown in Figure 1B as the initial state, and set $B_z$ = 0 in the calculation. It was found that the kink-like structure remains stable without the assistance of an external magnetic field, as presented in Figure 2A. Note that the magnetic structure enclosed by the dash lines in Figure 2A is called Néel-type magnetic kink in this work, in which the magnetic moments undergo 180° rotation from the upward direction at its center to the downward direction in the periphery. The schematic magnetic configuration for a Néel-type kink is displayed in Figure 2D. For simplicity, we call the kink-like state as the kink state hereafter.

FIGURE 2

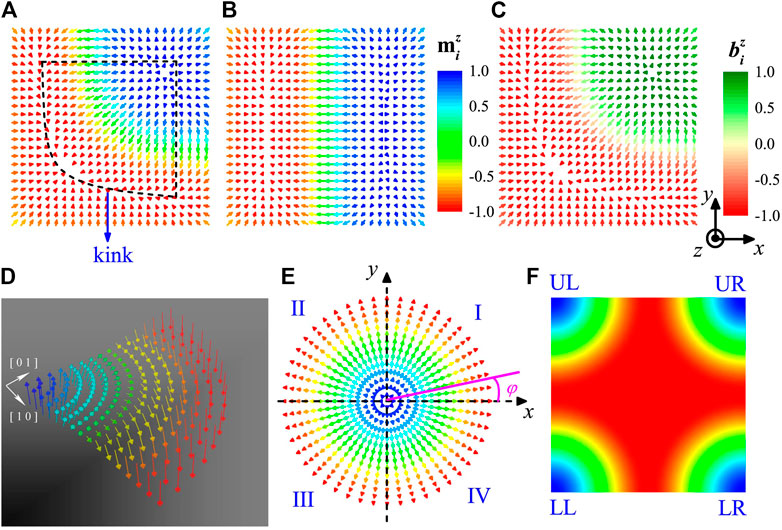
FIGURE 2. (A) The magnetic structure obtained from the above state in Figure 1B after withdrawal of magnetic field. A kink structure is enclosed by the dash lines. (B) A spiral structure, as the possible ground state of nanostructure with a size of 24 × 24 square lattices (i.e., ∼12 × 12 nm) in the absence of magnetic field.(C) The reduced effective field ${\mathit{b}}_i$profile corresponding to the magnetic structure in (A). (D) Schematic illustrations of the kink structure (E) Schematic illustrations of an isolated skyrmion configuration, which can be divided into four quadrants along the dash lines, denoted as kink I, II, III, and IV. (F) These kinks may appear in one of the four possible corners (i.e., LL, LR, UR or UL corner) in the nanostructure, corresponding to kinks residing in the four possible quadrants (i.e., quadrant I, II, III or IV).

To explore the possible ground state for the nanomagnet of 24 × 24 square lattices at $B_z$ = 0, the system was initialized from a the paramagnetic state at sufficiently high temperature T, and cooled down gradually until it reaches a very low T under $B_z$ = 0, using Monte Carlo simulations with simulated annealing technique [17, 18, 44]. Then the system was further relaxed for the zero-temperature equilibrium state by solving LLG equation. As a result, a spiral structure forms as shown in Figure 2B. The numerical calculations indicate that the total energy of the spiral structure is a little smaller than that of the Néel-type kink structure. These results suggest the spiral structure to be the possible zero-field ground state, while the Néel-type kink structure to be a metastable state at $B_z$ = 0, other than the minimum-energy state.

To further estimate the stability of the metastable Néel-type kink state under $B_z$ = 0, we calculated the reduced local effective field ${\mathit{b}}_i\equiv {\mathit{B}}_i^{eff}/\left|{\mathit{B}}_i^{eff}\right|$ acting on the i-th magnetic moment ${\mathbf{m}}_i$. Interestingly, it was found in Figure 2C that the ${\mathit{b}}_i$ distribution and the magnetic kink state in Figure 2A are similar in spatial profile, and almost all the magnetic moments in the kink structure are oriented in parallel to the local field ${\mathit{b}}_i$, making the metastable kink structure self-sustaining. In addition, it was noted that the anisotropy energy ${\mathrm{\mathscr{H}}}_{ani}=-A{\displaystyle {\sum }_i{\left({\mathbf{m}}_i\cdot \widehat{z}\right)}^2}$ contributes to the effective field in terms of $-\left(1/\hslash \gamma \right)\left(\partial {\mathrm{\mathscr{H}}}_{ani}/\partial {\mathbf{m}}_i\right)=\left(2/\hslash \gamma \right)A{\mathrm{m}}_i^z{\mathit{e}}_z$. This suggests that the anisotropy plays an important role in guaranteeing the robustness of the metastable kink state, since the effective field $\left(2/\hslash \gamma \right)A{\text{m}}_i^z{\mathit{e}}_z$makes the stabilization of the out-of-plane magnetization component ${\text{m}}_i^z$ [46, 47]. In this regard, we reckon that the kink structure is a robust state after the withdrawal of the magnetic field, due to the kink state is trapped in an energy valley in the configurational energy landscape [47].

In fact, one may take account of the kink structures from the prototypical Néel skyrmion, whose configuration can be viewed as a coplanar spiral with magnetic moments lying in a plane perpendicular to the xy plane [1, 38]:

$\begin{array}{c}\{\begin{array}{cc}\mathbf{m}\left(\mathbf{r}\right)=\sin \left(\mathbf{q}\cdot \mathbf{r}\right){\mathit{e}}_q+\cos \left(\mathbf{q}\cdot \mathbf{r}\right){\mathit{e}}_z& |\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}-\mathrm{u}\mathrm{p},p=1\\ \mathbf{m}\left(\mathbf{r}\right)=\sin \left(\mathbf{q}\cdot \mathbf{r}+\pi \right){\mathit{e}}_q+\cos \left(\mathbf{q}\cdot \mathbf{r}+\pi \right){\mathit{e}}_z& |\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}-\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n},p=-1\end{array},\end{array}(5)$

where the spatial variables of magnetization are defined in polar coordinates $\mathbf{r}=\left(\mathrm{r}\cos \phi ,\mathrm{r}\sin \phi \right)$, and the magnitude of spiral wave vector is $\left|\mathbf{q}\right|=\pi /R$, with the direction denoted by unit vector ${\mathit{e}}_q=\cos \phi {\mathit{e}}_x+\sin \phi {\mathit{e}}_y$. For the isolated Néel skyrmion configuration, the core magnetization points upward or downward, and smoothly changes to the opposite direction in the peripheral circle with radius $R$. We considered skyrmion structure with core-up (core-down) magnetization carries core polarity $p=$ 1 ($p=$ −1), as the skyrmion with $p=$ 1 depicted in Figure 2E. Here, $R$ is used to define the radius of skyrmion, with $0\le \mathrm{r}\le R$ and the azimuthal angle $0\le \phi \le 2\pi$ for a single skyrmion.

To proceed, one may divide an isolated skyrmion configuration into four quadrants along the dash lines, as illustrated in Figure 2E. The magnetic structures in quadrant I, II, III, and IV can be described by Eq. 5, with the azimuthal angle 0$\le {\phi }_{\text{I}}\le$π/2, π/2$\le {\phi }_{\text{II}}\le$π, π $\le {\phi }_{\text{III}}\le$3π/2, 3π/2$\le {\phi }_{\text{IV}}\le$2π, respectively. The kink may appear in one of the four possible corners, i.e., the upper left (UL), upper right (UR), lower left (LL) or lower right (LR) corner of the nanostructure in the simulations, as shown in Figure 2F. The LL, LR, UR, and UL kink structures correspond to the well-defined kinks residing in the quadrant I, II, III, and IV, respectively. In addition, we define the polarity of the kink with core-up (core-down) as $p=$ 1 ($p=$ −1). Therefore, the kinks in the nanostructure can carry the core polarity $p=$ ± 1, and can reside in one of the four possible corners, constituting 8 degenerate kink states. By comparison, the single skyrmion often appears in circular shaped nanodisks, and possesses only two degenerate states with core polarity $p=$ ±1 [8, 48–50]. In this sense, the kinks in the square shaped nanostructure have the special feature of multiple degenerate states.

3.3 Generation and Switching of Kinks by In-Plane Current Pulse

In this section, we studied the generation of kinks by injecting into the nanostructure an in-plane spin-polarized current pulse. Here, the direction of the CIP injection is defined by the angle φ with respect to the x-axis (see in Figure 3B), and $\phi$ is tunable. Note that in the following study, no external magnetic field was applied.

FIGURE 3

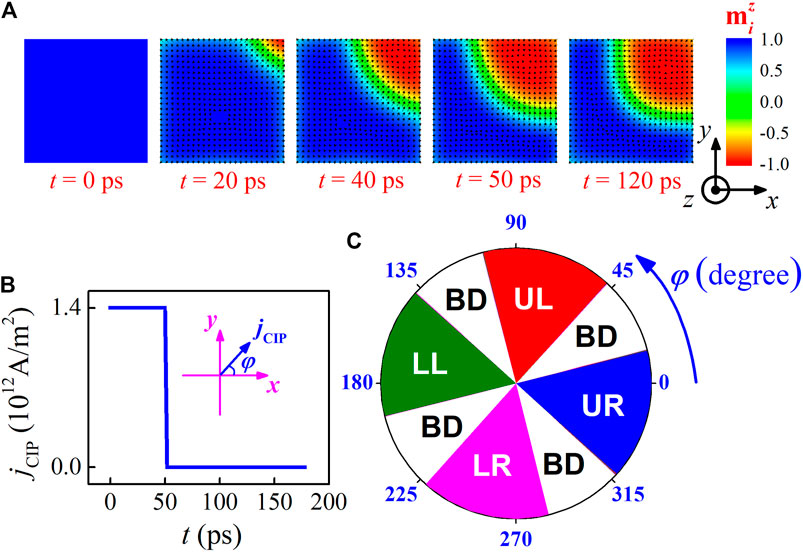
FIGURE 3. The generation of kink from the initial ferromagnetic state, by injecting into the nanostructure an in-plane spin-polarized current pulse. (A) Snapshots show the formation process of the UR kink, driven by the current pulse with injection angle $\phi$ = 10°. (B) A current pulse with current density $j_{\text{CIP}}=$ 1.4 × 10¹² Am⁻² and duration$t_{dur}=$ 50 ps. The insert shows the direction of the CIP injection, defined by the angle $\phi$ with respect to the x-axis. (C) A pie chart shows four colored sections, with the sections colored red, green, pink and blue representing the angle conditions for generation of UL, LL, LR, and UR kinks, respectively. The white region on the pie chart corresponds to angle conditions for the formation of bubble domain (abbreviated to “BD”) like that shown in Figure 1A. Here the pie chart is generated from a set of data points for $\phi$ = 2, 4, …, 360° at intervals of 2°.

The simulations start from the initial ferromagnetic phase, with all magnetic moments aligning along z-axis at $t=$ 0.0 ps (see Figure 3A). We first tested the effect of CIP on the kink dynamics, using a moderate current density $j_{\text{CIP}}=0.1{\text{κ}}_{\text{CIP}}$ ∼ 1.4 × 10¹² Am⁻² with current duration $t_{dur}=$ 250$\tau$ ∼ 50 ps. Figure 3A shows the formation process of the UR kink for a typical case of $\phi$ = 10°. At the beginning ($t=$ 20 ps) of the current duration, the embryo of kink pattern emerges in the UR corner of the nanostructures. This pattern gradually enlarges, and becomes a rough kink at $t=$ 50 ps. Subsequently, the current is turned off and the system evolves into an equilibrated kink state at t = 120 ps.

Further simulations demonstrated that the generation of kinks is sensitive to injection angle φ, with the simulated results summarized in Figure 3C. It was found that the UR, UL, LL, and LR quarters can also be created respectively for −42° ≤ $\phi$ ≤ 14°, 48° ≤ $\phi$ ≤ 104°, 138° ≤ $\phi$ ≤ 194°, and 228° ≤ $\phi$ ≤ 284°, while some bubble domain states form beyond these angles $\phi$ (see the while region in the Figure 3C). Note that the kinks with $p=$ −1 presented here are generated from the initial ferromagnetic phase with magnetization along the z-axis. If the initial ferromagnetic phase is magnetized along the −z-axis, the lattices will evolve to the kinks with $p=$ 1. Therefore, all the eight degenerate kink states can be created by tuning the direction of CIP injection with two different initial ferromagnetic orientations.

Next, we investigated the switching between these kinks using in-plane current pulse, which is fundamental to understand their dynamics properties. The current pulse ($j_{\text{CIP}}=$ 1.4 × 10¹² Am⁻², current duration $t_{dur}=$ 50 ps) with varying angle $\phi$ is exerted on the initial UR kink state with $p=$ −1. Simulated results reveal that the kink can transfer from UR corner to the LR corner in a clockwise (CW) direction, driven by current with 116° ≤ $\phi$ ≤ 178°. However, it was noted that the UR kink cannot move to LL corner in a counterclockwise (CCW) direction or to diagonal UL corner with the adopted simulation parameters. Figures 4A–H show the dynamic process for the typical case of $\phi$ = 135°. We can see clearly that the upper part of the UR kink is pushed towards the right-edge of the nanostructures, and the lower part is simultaneously dragged to the bottom of the nanostructures (see Figures 4A–D). Although the entire kink pattern deforms largely in this process, it gradually turns in a CW direction and eventually moves to the LR corner at $t=$ 50 ps (see Figures 4E,F). After that the current is switched off to zero for reaching the equilibrated kink state in the relaxation procedure. Moreover, simulations for the kinks with $p=$ −1 indicate that their switching sequences can be summarized as follows: UR kink → LR kink → LL kink → UL kink with suitable angle $\phi$, as shown schematically in Figure 4I. In this procedure, the switching sequences is in a CW direction, and the kink polarity has not been reversed by the CIP injection.

FIGURE 4

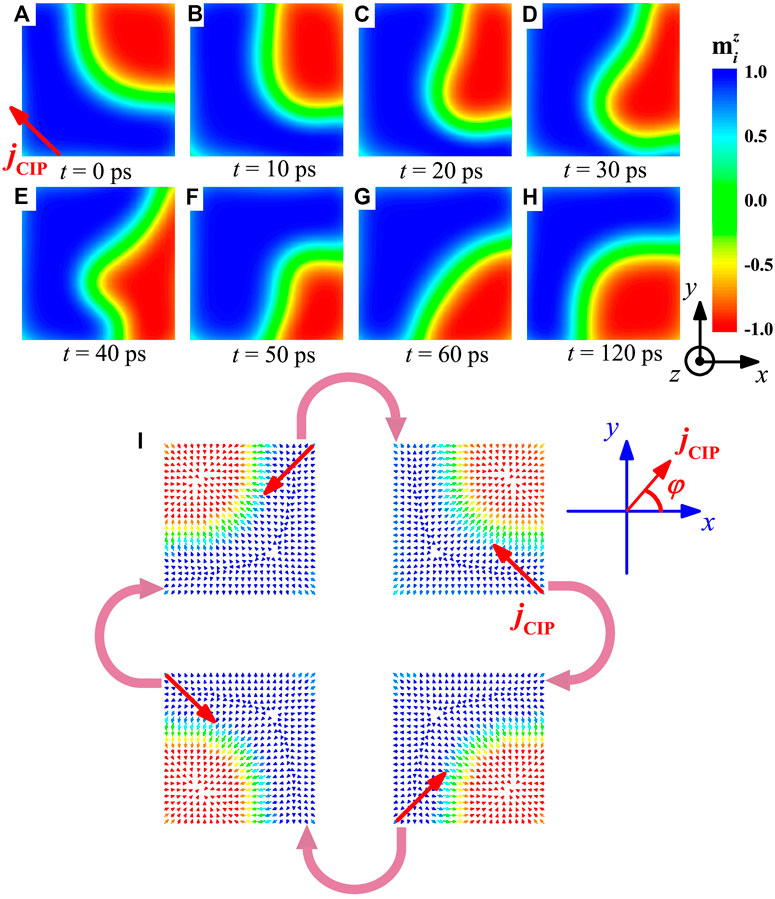
FIGURE 4. (A)–(H) The gradual shift of kink from UR to LR corner, driven by in-plane current pulse with current density $J_{\text{CIP}}=$ 1.4 × 10¹² Am⁻², current duration $t_{dur}=$50 ps, and injection angle $\phi =$ 135°. (I) Schematic illustrations of switching sequences for the kinks driven by in-plane current pulse. Here we used the straight red arrows to mark the injection direction of current $J_{\text{CIP}}$, and the curved pink arrows to denote the switching sequences of magnetic kinks.

3.4 Annihilation and Creation of Kinks by In-Plane Current Pulses

In this section, we presented an effective way to annihilate and create the kink by applying two successive CIP pulses, as the results shown in Figure 5. Our simulations start from the initial UR kink state with $p=$ –1 in Figure 5A. We first found that the kink can be annihilated by applying a CIP current pulse, with a larger current density$j_{\text{CIP}}=$ 2.8 × 10¹² Am⁻² and an appropriate injection angle ${\phi }_1$ = 135°. Here two successive current pulses are used to annihilate and create the kink states respectively, with injection angle ${\phi }_1$= 135° for the first pulse, and tunable injection angle ${\phi }_2$for the second one. The current duration $t_{dur}=$ 200  ps is considered for both two pulses, as shown in Figure 5C. Figure 5A displays the annihilation of the kink driven by the first current pulse with angle ${\phi }_1$, whose pattern rotates along a CW direction and disappears at the LR corner of the nanostructure, forming the ferromagnetic-like state at $t=$ 40 ps. The ferromagnetic-like state remains at 40 ps ≤ $t$ ≤ 200 ps, and we may see that most magnetic moments orientate along the z-axis in the ferromagnetic-like state, though some remaining magnetic moments align in the xy-plane at the LR and LL corners of the nanostructure.

FIGURE 5

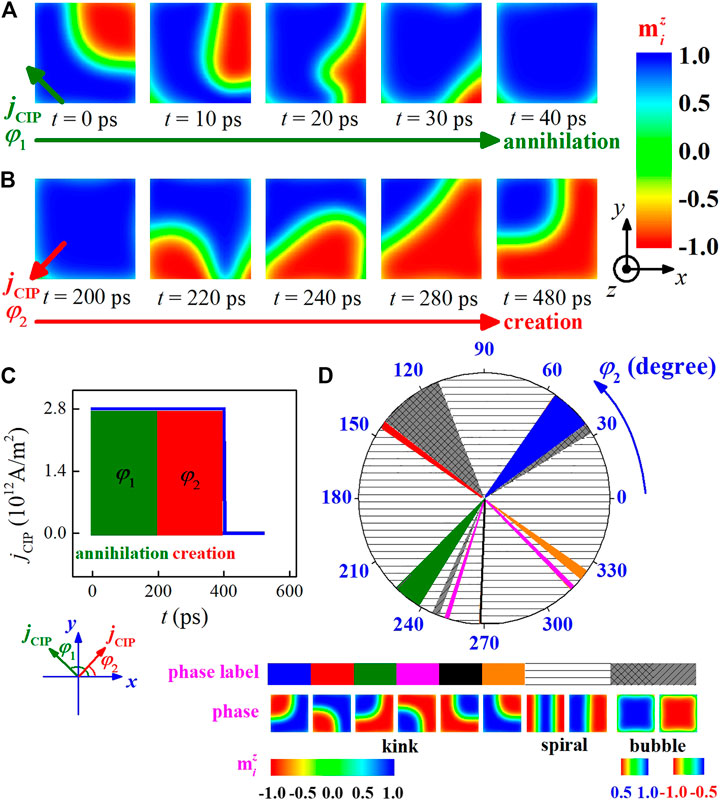
FIGURE 5. The annihilation and creation of kink is achieved by applying CIP current pulses. (A) and (B) Snapshots show a typical case for the annihilation and creation process of kink induced by two successional current pulses with injection angle ${\phi }_1=$ 135° and ${\phi }_2=$ 230°. Simulations start from the initial UR kink state with $p=$−1. (C) Here two successional current pulses with injection angle ${\phi }_1=$135° and tunable injection angle ${\phi }_2$, current density $j_{\text{CIP}}=$ 2.8 × 10¹² Am⁻² and duration $t_{dur}=$ 20 ps is considered. These two pulses are used to annihilate and create the kink state, respectively. (D) The phase diagram for the equilibrated states at $t=$ 520 ps after relaxation as a function of angle ${\phi }_2$was summarized. The various kinks, spiral states, and bubble states are marked by the colored pieces, striped pattern and grid pattern, respectively. The color map below is used to scale the magnetization components along z-axis ${\text{m}}_i^z$. Here the pie chart is generated from a set of data points for ${\phi }_2$ = 1, 2, …, 360° at intervals of 1°.

More interestingly, the simulated results reveal that some other kink states can be created from the ferromagnetic-like state, by applying the second current pulse with varying injection angle ${\phi }_2$. The typical case for ${\phi }_2$ = 230° is presented in Figure 5B, in which the domains first appear and gradually grow in the LL, and LR corners during 200 ps ≤ $t$ ≤ 240 ps. The new embryonic kink forms at $t=$ 280 ps and remains during 280 ps ≤ $t$ ≤ 400 ps, and it finally evolves into a core-up kink in the UL corners after the relaxation with $j_{\text{CIP}}=$ 0. In this process, the kink has been annihilated and created by two successive current pulses, in which the switching between the kink and ferromagnetic-like states is reversible. This indicates the capability of reversible writing and deleting the kink states.

Further simulations generate the phase diagram for the equilibrated states at $t=$ 520 ps as a function of ${\phi }_2$, as summarized in Figure 5D. It was noted that current pulses with 37° ≤ ${\phi }_2$ ≤ 55°, 143° ≤ ${\phi }_2$ ≤ 145°, and 320° ≤ ${\phi }_2$ ≤ 325° may create the kinks with $p=$−1 in the UL, LL, and UR corners of the nanostructure, while current pulses with 226° ≤ ${\phi }_2$ ≤ 238°, 252° ≤ ${\phi }_2$ ≤ 253° $\cup$ 314° ≤ ${\phi }_2$ ≤ 315°, and ${\phi }_2$ = 268° generate the kinks with $p=$ 1 in the UL, LL, and UR corners, respectively. In addition, some bubble or spiral states form beyond these angles $\phi$ (see the striped-pattern and grid-pattern region in Figure 5D), with some typical configurations shown at the bottom of Figure 5D. Regarding early investigations on magnetic vortex, it was demonstrated that the vortex polarity reversal may be triggered by a CIP pulse through the formation of a vortex-antivortex pair [51], or by an alternating CIP through the resonant dynamics [52]. However, for the skyrmion in chiral magnets, CIP is usually used for displacing the skyrmion, while cannot change the skyrmion polarity in the dynamics [8, 41, 42]. In this sense, the core polarity reversal of kink can be achieved by CIP pulse, which is analogous to that of vortex system [51, 52]. From the simulation results and analyses in Generation and Switching of Kinks by In-Plane Current Pulse and Annihilation and Creation of Kinks by In-Plane Current Pulses, one may create, annihilate, displace, and reverse the kink on demand by adjusting the CIP pulse injections.

3.5 Manipulation of Kinks by Out-of-Plane Current Pulse

In this section, we investigated the core polarity reversal of the kinks with out-of-plane current, which is also a fundamental issue for understanding their dynamics properties. One may build a magnetic tunnel junction (MTJ) or spin valve to locally address the kinks [5, 53]. As schematically shown in Figure 6A, a typical MTJ structure consists of the top and bottom two layers of ferromagnet, which is separated by an ultrathin spacer of insulator. The top ferromagnetic layer is a free layer which presents a kink state, while the bottom one is a fixed layer with the magnetization ${\mathbf{M}}_{\text{fix}}$ fixed along the z direction. When a spin current is injected into the bottom fixed layer along the z direction, the spin is polarized along z direction. The polarized spin current then flows through the insulating layer to the free layer, acting on its magnetizations with CPP-type STT, described by Eq. 4. One may reverse the polarization direction of the spin current, by injecting the spin current into the top free layer along the −z direction. Here we defined the current density$j_{\text{CPP}}$ > 0 and$j_{\text{CPP}}$ < 0 in Eq. 4 corresponding to the injection of spin current flowing along z and −z direction, respectively. Our simulations start from an initial UR kink with polarity $p=$ −1 as a general representative. Note that the CPP-type STT induced by current $j_{\text{cpp}}$ < 0 tends to align the magnetic moments in the free layer along the −z direction, thus the kink may be reversed to its image structure with polarity $p=$ 1. Contrarily, the kink with polarity $p=$ 1 can be reversed, once the spin current is injected along the z direction.

FIGURE 6

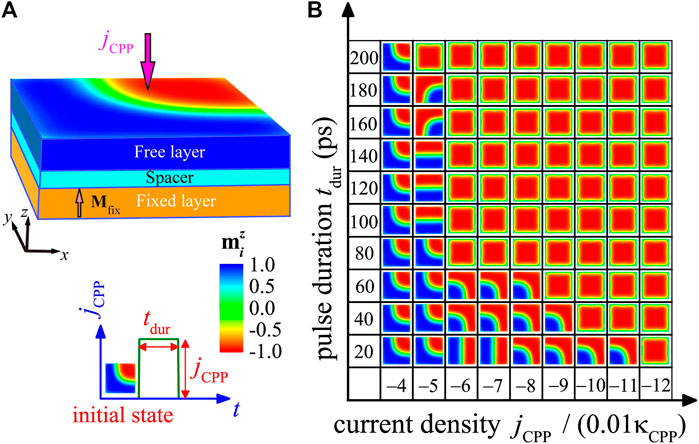
FIGURE 6. (A) Sketch of a MTJ nanopillar consisting of the top and bottom layers of ferromagnet, and the spacer layer of insulator. (B) Simulations for the evolutions of kink driven by a CPP pulse, starting from an initial kink with $p=$ −1 in UR corner of the nanostructure. A phase diagram for the equilibrated states obtained after the current pulses, as a function of current density $j_{\text{CPP}}$ and duration time $t_{dur}$.

We first studied the dynamics of the kink driven by various current densities $j_{\text{CPP}}$ and duration time $t_{dur}$, and the phase diagram for the equilibrated states obtained after the current pulses was summarized in Figure 6B. The results show that the kink is immovable under low current densities $\left|j_{\text{CPP}}\right|<0.04{\text{κ}}_{\text{CPP}}$ (∼3.4 × 10¹² Am⁻²), due to the weak STT strength. It was seen that the kink may be pulled at current densities larger than the critical value $\left|j_{\text{CPP}}\right|=0.05{\text{κ}}_{\text{CPP}}$ (∼4.3 × 10¹² Am⁻²). At an intermediate current density $j_{\text{CPP}}$∼ −4.3 × 10¹² Am⁻² and duration time$t_{dur}$ = 160 ps − 180 ps, the kink moves in a CW direction to near LR corner of the nanostructure, accompanying with the kink polarity reverse. For the current pulse with a relatively large current density 0.06κ_CPP ≤ $\left|j_{\text{CPP}}\right|$ ≤ 0.11${\text{κ}}_{\text{CPP}}$ (i.e., 5.1 × 10¹² Am⁻² ≤ $\left|j_{\text{CPP}}\right|$ ≤ 9.4 × 10¹² Am⁻²) and duration ∼20 ps ≤ $t_{dur}$ ≤ ∼ 60 ps, it was found that the kink polarity is also reserved, while the UR kink shifts diagonally to the LL corner of the nanostructure. It was also seen in the phase diagram that the large$j_{\text{CPP}}$ and large $t_{dur}$ usually lead to the bubble domains, and some spiral states appear at 0.06κ_CPP ≤ $\left|j_{\text{CPP}}\right|$≤ 0.07κ_CPP with a short pulse duration.

To further investigate the repeatability of polarity reversals of kink driven by CPP pulses, we took an examination on injecting some discontinuous current pulses to the system, as presented in Figure 7A. The insert shows the kink states at some typical time before and after the pulse injections in the evolutions. It was observed that all the four CPP pulses reverse the kink polarity, and the pulse with spin current $j_{\text{CPP}}$ < 0 ($j_{\text{CPP}}$ > 0) is used to reverse the kink with polarity $p$ = −1 ($p$ = 1). The first and second CPP pulses with $j_{\text{CPP}}$= ± 4.3 × 10¹² Am⁻² and $t_{dur}$ = 160 ps rotate the kink in CW and CCW directions respectively (see state transitions $\mathrm{①}\to \mathrm{②}\to \mathrm{③}$), which is a reversible switching. Note that the CW and CCW rotational directions here depend on the core polarity of the pre-evolutionary kink. The third and fourth CPP pulses with $j_{\text{CPP}}=\pm 0.07{\text{κ}}_{\text{CPP}}$ ∼ ± 6.0 × 10¹² Am⁻² and $t_{dur}$= 40 ps move the kink to the diagonal corner of the nanostructure (see state transitions $\mathrm{③}\to \mathrm{④}\to \mathrm{⑤}$), which is also repeatable. For tracking the variations of the magnetic structures, the out-of-plane magnetization ${\text{M}}_z={\sum }_i{\text{m}}_i^z/N$ is used to characterize the reversal of kink, where N is the total number of magnetic moments. Although some fluctuant variations appear in the ${\text{M}}_z-t$ curve in Figure 7B, it is clear that ${\text{M}}_z$ flips to the opposite direction after every current pulse, in response to the core polarity reversal of the kinks. Therefore, we may use the CPP current to reverse the kink polarity and displace their position.

FIGURE 7

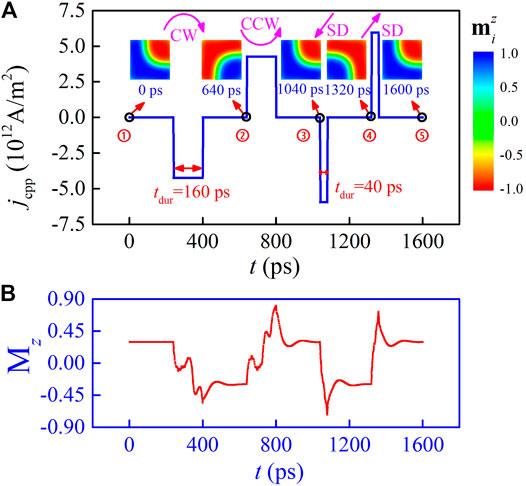
FIGURE 7. (A) The polarity reversal of kinks induced by CPP pulses, accompanying with the displacements of kinks. The first and second CPP pulses with $j_{\text{CPP}}=$ ±0.05${\text{κ}}_{\text{CPP}}$ ∼ ±4.3 × 10¹² Am⁻² and $t_{dur}$= 160 ps result in the rotation of kink along CW and CCW directions respectively, while the third and fourth CPP pulses with $j_{\text{CPP}}=$ ±0.07${\text{κ}}_{\text{CPP}}$ ∼ ±6.0 × 10¹² Am⁻² and $t_{dur}$= 40 ps shifts diagonally (SD) the kink to the diagonal corner of the nanostructure. Snapshots show the kink states (①−⑤) at some typical time before and after the pulses in the evolutions. (B) Plots of variations of out-of-plane magnetization ${\text{M}}_z$as a function of time $t$, responding to the polarity reversal of kinks.

4 Discussion and Conclusion

Before concluding this work, we briefly discuss the experimental observations and thermal stability of the kink states. The X-ray holography allow the imaging of ultrafast magnetization dynamics in magnetic nanostructure with sub-10 nm spatial resolution time-resolved [6]. Using time-resolved X-ray microscopy, a number of experimental studies reported the direct observation of nanoscale skyrmions, current-driven skyrmions dynamics, and the detailed evolution of magnetic configuration during the writing and deleting a skyrmion process [54, 55].

On the other hand, all simulations in present study were calculated under zero temperature in which the thermal effect is neglected. However, the thermal stability of magnetic kink structure is also a crucial issue for a detailed understanding of their underlying physical properties. For this, we tested the effect of thermal fluctuation on the magnetic structure by using Monte Carlo simulation with ladder cooling protocol [44]. It was found that the magnetic structure may forms at a very low-temperature T ≤ 1.2$J_{FM}/k_B$ ($k_B$ is the Boltzmann constant), under a magnetic field $B_z=-0.008J_{FM}$. Note that temperature T in Monte Carlo simulations is scaled in the unit of $J_{FM}/k_B$. Thus the kink structures are estimated to be stable below a critical temperature of ∼ 40 K, with a typical exchange constant $J_{FM}=$2.95 meV adopted for Pd/Fe/Ir(111). This suggests that the kink structures in nanostructures can only exist at cryogenic temperatures, in agreement with the latest experimental investigations on Néel skyrmion in Pd/Fe/Ir(111) [56]. In this regard, the previous studies on skyrmions [57–60] may provide us an enlightened approach to enhance the thermal stability of kinks, which would be an interesting challenge for our further studies.

In summary, we used micromagnetic simulations and Monte Carlo simulations to investigate an exotic Néel-type kink texture in square-shaped nanostructures, which may stably exist in the absence of magnetic field. It was interesting to find that individual kinks hold eight degenerate states as they can reside in one of the four possible corners of a nanostructure, and carry upward or downward polarity. In addition, we proposed some effective schemes to control their dynamics by means of injecting spin-polarization current pulses. It was found that kinks can be created, annihilated, displaced and reversed polarity on demand by applying an in-plane or an out-of-plane spin-polarized current pulse, and are facile switchable among the degenerate kink states. In particularly, the kinks can be switched toward the ferromagnetic-like states and backward reversibly by applying two successive current pulses, indicating the capability of writing and deleting the kink states. These findings predict the existence of Néel-type kinks in the square-shaped nanostructures, as well as provide us a promising approach to tailor the kinks by utilizing the corners of the nanostructures, and control these states by spin-polarized currents. This study also suggests a theoretical guide to explore other chiral magnetic textures in nanostructures of polygon geometries.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

J-PC and X-SG conceived the research project, and J-PC performed the computations. J-PC, J-QL, XS, YC, Z-FC, W-AL, M-HQ, Z-PH, X-SG, and J-ML commented the modeling and discussed the results. J-PC and X-SG wrote the manuscript.

Funding

This work was supported by the Natural Science Foundation of China (11604059), the Natural Science Foundation of Guangdong Province, China (2017A030313020), Scientific Research Project of Guangzhou Municipal Colleges and Universities (1201630455) and the Guangzhou University’s Training Program for Excellent New-recruited Doctors (YB201715).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Nagaosa N, Tokura Y. Topological Properties and Dynamics of Magnetic Skyrmions. Nat Nanotech (2013) 8:899–911. doi:10.1038/nnano.2013.243

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fert A, Reyren N, Cros V. Magnetic Skyrmions: Advances in Physics and Potential Applications. Nat Rev Mater (2017) 2:17031. doi:10.1038/natrevmats.2017.31

CrossRef Full Text | Google Scholar

3. Wiesendanger R. Nanoscale Magnetic Skyrmions in Metallic Films and Multilayers: a New Twist for Spintronics. Nat Rev Mater (2016) 1:16044. doi:10.1038/natrevmats.2016.44

CrossRef Full Text | Google Scholar

4. Jiang W, Chen G, Liu K, Zang J, te Velthuis SGE, Hoffmann A. Skyrmions in Magnetic Multilayers. Phys Rep (2017) 704:1–49. doi:10.1016/j.physrep.2017.08.001

CrossRef Full Text | Google Scholar

5. Kang W, Huang Y, Zhang X, Zhou Y, Zhao W. Skyrmion-electronics: an Overview and Outlook. Proc IEEE (2016) 104:2040–61. doi:10.1109/JPROC.2016.2591578

CrossRef Full Text | Google Scholar

6. Zhang X, Zhou Y, Mee Song K, Park T-E, Xia J, Ezawa M, et al. Skyrmion-electronics: Writing, Deleting, reading and Processing Magnetic Skyrmions toward Spintronic Applications. J Phys Condens Matter (2020) 32:143001. doi:10.1088/1361-648X/ab5488

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Romming N, Hanneken C, Menzel M, Bickel JE, Wolter B, von Bergmann K, et al. Writing and Deleting Single Magnetic Skyrmions. Science (2013) 341:636–9. doi:10.1126/science.1240573

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Sampaio J, Cros V, Rohart S, Thiaville A, Fert A. Nucleation, Stability and Current-Induced Motion of Isolated Magnetic Skyrmions in Nanostructures. Nat Nanotech (2013) 8:839–44. doi:10.1038/nnano.2013.210

CrossRef Full Text | Google Scholar

9. Fert A, Cros V, Sampaio J. Skyrmions on the Track. Nat Nanotech (2013) 8:152–6. doi:10.1038/nnano.2013.29

CrossRef Full Text | Google Scholar

10. Iwasaki J, Mochizuki M, Nagaosa N. Current-induced Skyrmion Dynamics in Constricted Geometries. Nat Nanotech (2013) 8:742–7. doi:10.1038/nnano.2013.176

CrossRef Full Text | Google Scholar

11. Hsu P-J, Kubetzka A, Finco A, Romming N, von Bergmann K, Wiesendanger R. Electric-field-driven Switching of Individual Magnetic Skyrmions. Nat Nanotech (2017) 12:123–6. doi:10.1038/nnano.2016.234

CrossRef Full Text | Google Scholar

12. Jiang W, Upadhyaya P, Zhang W, Yu G, Jungfleisch MB, Fradin FY, et al. Blowing Magnetic Skyrmion Bubbles. Science (2015) 349:283–6. doi:10.1126/science.aaa1442

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang Y, Wang L, Xia J, Lai Z, Tian G, Zhang X, et al. Electric-field-driven Non-volatile Multi-State Switching of Individual Skyrmions in a Multiferroic Heterostructure. Nat Commun (2020) 11:3577. doi:10.1038/s41467-020-17354-7

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Yao X, Chen J, Dong S. Controlling the Helicity of Magnetic Skyrmions by Electrical Field in Frustrated Magnets. New J Phys (2020) 22:083032. doi:10.1088/1367-2630/aba1b3

CrossRef Full Text | Google Scholar

15. Göbel B, Mertig I, Tretiakov OA. Beyond Skyrmions: Review and Perspectives of Alternative Magnetic Quasiparticles. Phys Rep (2021) 895:1–28. doi:10.1016/j.physrep.2020.10.001

CrossRef Full Text | Google Scholar

16. Lin S-Z, Saxena A, Batista CD. Skyrmion Fractionalization and Merons in Chiral Magnets with Easy-Plane Anisotropy. Phys Rev B (2015) 91:224407. doi:10.1103/PhysRevB.91.224407

CrossRef Full Text | Google Scholar

17. Chen JP, Zhang D-W, Liu J-M. Exotic Skyrmion Crystals in Chiral Magnets with Compass Anisotropy. Sci Rep (2016) 6:29126. doi:10.1038/srep29126

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Chen JP, Zhang D-W, Chen Y, Gao XS, Liu J-M. Compass-anisotropy-modulated Helical States and Skyrmion Crystals in Chiral Magnets. Phys Lett A (2018) 382:2944–51. doi:10.1016/j.physleta.2018.06.035

CrossRef Full Text | Google Scholar

19. Kanazawa N, Kim J-H, Inosov DS, White JS, Egetenmeyer N, Gavilano JL, et al. Possible Skyrmion-Lattice Ground State in theB20chiral-Lattice Magnet MnGe as Seen via Small-Angle Neutron Scattering. Phys Rev B (2012) 86:134425. doi:10.1103/PhysRevB.86.134425

CrossRef Full Text | Google Scholar

20. Yu XZ, Koshibae W, Tokunaga Y, Shibata K, Taguchi Y, Nagaosa N, et al. Transformation between Meron and Skyrmion Topological Spin Textures in a Chiral Magnet. Nature (2018) 564:95–8. doi:10.1038/s41586-018-0745-3

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gao S, Rosales HD, Gómez Albarracín FA, Tsurkan V, Kaur G, Fennell T, et al. Fractional Antiferromagnetic Skyrmion Lattice Induced by Anisotropic Couplings. Nature (2020) 586:37–41. doi:10.1038/s41586-020-2716-8

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yu XZ, Onose Y, Kanazawa N, Park JH, Han JH, Matsui Y, et al. Real-space Observation of a Two-Dimensional Skyrmion crystal. Nature (2010) 465:901–4. doi:10.1038/nature09124

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Mühlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, et al. Skyrmion Lattice in a Chiral Magnet. Science (2009) 323:915–9. doi:10.1126/science.1166767

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Du H, Che R, Kong L, Zhao X, Jin C, Wang C, et al. Edge-mediated Skyrmion Chain and its Collective Dynamics in a Confined Geometry. Nat Commun (2015) 6:8504. doi:10.1038/ncomms9504

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Jin C, Li Z-A, Kovács A, Caron J, Zheng F, Rybakov FN, et al. Control of Morphology and Formation of Highly Geometrically Confined Magnetic Skyrmions. Nat Commun (2017) 8:15569. doi:10.1038/ncomms15569

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Xing X, Pong PWT, Zhou Y. Current-controlled Unidirectional Edge-Meron Motion. J Appl Phys (2016) 120:203903. doi:10.1063/1.4968574

CrossRef Full Text | Google Scholar

27. Leonov AO, Mostovoy M. Edge States and Skyrmion Dynamics in Nanostripes of Frustrated Magnets. Nat Commun (2017) 8:14394. doi:10.1038/ncomms14394

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhou Y, Ezawa M. A Reversible Conversion between a Skyrmion and a Domain-wall Pair in a junction Geometry. Nat Commun (2014) 5:4652. doi:10.1038/ncomms5652

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Rohart S, Thiaville A. Skyrmion Confinement in Ultrathin Film Nanostructures in the Presence of Dzyaloshinskii-Moriya Interaction. Phys Rev B (2013) 88:184422. doi:10.1103/PhysRevB.88.184422

CrossRef Full Text | Google Scholar

30. Heinonen O, Jiang W, Somaily H, te Velthuis SGE, Hoffmann A. Generation of Magnetic Skyrmion Bubbles by Inhomogeneous Spin Hall Currents. Phys Rev B (2016) 93:094407. doi:10.1103/PhysRevB.93.094407

CrossRef Full Text | Google Scholar

31. Kuchkin VM, Barton-Singer B, Rybakov FN, Blügel S, Schroers BJ, Kiselev NS. Magnetic Skyrmions, Chiral Kinks, and Holomorphic Functions. Phys Rev B (2020) 102:144422. doi:10.1103/PhysRevB.102.144422

CrossRef Full Text | Google Scholar

32. Cheng R, Li M, Sapkota A, Rai A, Pokhrel A, Mewes T, et al. Magnetic Domain wall Skyrmions. Phys Rev B (2019) 99:184412. doi:10.1103/PhysRevB.99.184412

CrossRef Full Text | Google Scholar

33. Zheng Y, Chen WJ. Characteristics and Controllability of Vortices in Ferromagnetics, Ferroelectrics, and Multiferroics. Rep Prog Phys (2017) 80:086501. doi:10.1088/1361-6633/aa5e03

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Cowburn RP, Welland ME. Micromagnetics of the Single-Domain State of Square Ferromagnetic Nanostructures. Phys Rev B (1998) 58:9217–26. doi:10.1103/PhysRevB.58.9217

CrossRef Full Text | Google Scholar

35. Jaafar M, Yanes R, Perez de Lara D, Chubykalo-Fesenko O, Asenjo A, Gonzalez EM, et al. Control of the Chirality and Polarity of Magnetic Vortices in Triangular Nanodots. Phys Rev B (2010) 81:054439. doi:10.1103/PhysRevB.81.054439

CrossRef Full Text | Google Scholar

36. Yao J, Song X, Gao X, Tian G, Li P, Fan H, et al. Electrically Driven Reversible Magnetic Rotation in Nanoscale Multiferroic Heterostructures. ACS Nano (2018) 12:6767–76. doi:10.1021/acsnano.8b01936

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Keesman R, Leonov AO, van Dieten P, Buhrandt S, Barkema GT, Fritz L, et al. Degeneracies and Fluctuations of Néel Skyrmions in Confined Geometries. Phys Rev B (2015) 92:134405. doi:10.1103/PhysRevB.92.134405

CrossRef Full Text | Google Scholar

38. Banerjee S, Rowland J, Erten O, Randeria M. Enhanced Stability of Skyrmions in Two-Dimensional Chiral Magnets with Rashba Spin-Orbit Coupling. Phys Rev X (2014) 4:031045. doi:10.1103/PhysRevX.4.031045

CrossRef Full Text | Google Scholar

39. Romming N, Kubetzka A, Hanneken C, von Bergmann K, Wiesendanger R. Field-dependent Size and Shape of Single Magnetic Skyrmions. Phys Rev Lett (2015) 114:177203. doi:10.1103/PhysRevLett.114.177203

PubMed Abstract | CrossRef Full Text | Google Scholar

40. von Malottki S, Dupé B, Bessarab PF, Delin A, Heinze S. Enhanced Skyrmion Stability Due to Exchange Frustration. Sci Rep (2017) 7:12299. doi:10.1038/s41598-017-12525-x

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Iwasaki J, Mochizuki M, Nagaosa N. Universal Current-Velocity Relation of Skyrmion Motion in Chiral Magnets. Nat Commun (2013) 4:1463. doi:10.1038/ncomms2442

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Zhang X, Zhou Y, Ezawa M. Magnetic Bilayer-Skyrmions without Skyrmion Hall Effect. Nat Commun (2016) 7:10293. doi:10.1038/ncomms10293

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Zhang S, Levy PM, Fert A. Mechanisms of Spin-Polarized Current-Driven Magnetization Switching. Phys Rev Lett (2002) 88:236601. doi:10.1103/PhysRevLett.88.236601

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Chen JP, Wang ZQ, Gong JJ, Qin MH, Zeng M, Gao XS, et al. Stripe-vortex Transitions in Ultrathin Magnetic Nanostructures. J Appl Phys (2013) 113:054312. doi:10.1063/1.4790483

CrossRef Full Text | Google Scholar

45. Hagemeister J, Iaia D, Vedmedenko EY, von Bergmann K, Kubetzka A, Wiesendanger R. Skyrmions at the Edge: Confinement Effects in Fe/Ir(111). Phys Rev Lett (2016) 117:207202. doi:10.1103/PhysRevLett.117.207202

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Wilson MN, Butenko AB, Bogdanov AN, Monchesky TL. Chiral Skyrmions in Cubic Helimagnet Films: The Role of Uniaxial Anisotropy. Phys Rev B (2014) 89:094411. doi:10.1103/PhysRevB.89.094411

CrossRef Full Text | Google Scholar

47. Chen JP, Xie YL, Chu P, Wang ZQ, Wang YL, Gao XS, et al. Manipulation of Magnetic State in Nanostructures by Perpendicular Anisotropy and Magnetic Field. J Appl Phys (2014) 115:243910. doi:10.1063/1.4885158

CrossRef Full Text | Google Scholar

48. Büttner F, Moutafis C, Schneider M, Krüger B, Günther CM, Geilhufe J, et al. Dynamics and Inertia of Skyrmionic Spin Structures. Nat Phys (2015) 11:225–8. doi:10.1038/nphys3234

CrossRef Full Text | Google Scholar

49. Liu Y, Du H, Jia M, Du A. Switching of a Target Skyrmion by a Spin-Polarized Current. Phys Rev B (2015) 91:094425. doi:10.1103/PhysRevB.91.094425

CrossRef Full Text | Google Scholar

50. Kim J-V, Garcia-Sanchez F, Sampaio J, Moreau-Luchaire C, Cros V, Fert A. Breathing Modes of Confined Skyrmions in Ultrathin Magnetic Dots. Phys Rev B (2014) 90:064410. doi:10.1103/PhysRevB.90.064410

CrossRef Full Text | Google Scholar

51. Liu Y, Gliga S, Hertel R, Schneider CM. Current-induced Magnetic Vortex Core Switching in a Permalloy Nanodisk. Appl Phys Lett (2007) 91:112501. doi:10.1063/1.2780107

CrossRef Full Text | Google Scholar

52. Yamada K, Kasai S, Nakatani Y, Kobayashi K, Kohno H, Thiaville A, et al. Electrical Switching of the Vortex Core in a Magnetic Disk. Nat Mater (2007) 6:270–3. doi:10.1038/nmat1867

CrossRef Full Text | Google Scholar

53. Finocchio G, Büttner F, Tomasello R, Carpentieri M, Kläui M. Magnetic Skyrmions: from Fundamental to Applications. J Phys D: Appl Phys (2016) 49:423001. doi:10.1088/0022-3727/49/42/423001

CrossRef Full Text | Google Scholar

54. Büttner F, Lemesh I, Schneider M, Pfau B, Günther CM, Hessing P, et al. Field-free Deterministic Ultrafast Creation of Magnetic Skyrmions by Spin-Orbit Torques. Nat Nanotech (2017) 12:1040–4. doi:10.1038/nnano.2017.178

CrossRef Full Text | Google Scholar

55. Woo S, Song KM, Han H-S, Jung M-S, Im M-Y, Lee K-S, et al. Spin-orbit Torque-Driven Skyrmion Dynamics Revealed by Time-Resolved X-ray Microscopy. Nat Commun (2017) 8:15573. doi:10.1038/ncomms15573

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Lindner P, Bargsten L, Kovarik S, Friedlein J, Harm J, Krause S, et al. Temperature and Magnetic Field Dependent Behavior of Atomic-Scale Skyrmions in Pd/Fe/Ir(111) Nanoislands. Phys Rev B (2020) 101:214445. doi:10.1103/PhysRevB.101.214445

CrossRef Full Text | Google Scholar

57. Büttner F, Lemesh I, Beach GSD. Theory of Isolated Magnetic Skyrmions: From Fundamentals to Room Temperature Applications. Sci Rep (2018) 8:4464. doi:10.1038/s41598-018-22242-8

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Boulle O, Vogel J, Yang H, Pizzini S, de Souza Chaves D, Locatelli A, et al. Room-temperature Chiral Magnetic Skyrmions in Ultrathin Magnetic Nanostructures. Nat Nanotech (2016) 11:449–54. doi:10.1038/nnano.2015.315

CrossRef Full Text | Google Scholar

59. Desplat L, Suess D, Kim J-V, Stamps RL. Thermal Stability of Metastable Magnetic Skyrmions: Entropic Narrowing and Significance of Internal Eigenmodes. Phys Rev B (2018) 98:134407. doi:10.1103/PhysRevB.98.134407

CrossRef Full Text | Google Scholar

60. Varentcova AS, von Malottki S, Potkina MN, Kwiatkowski G, Heinze S, Bessarab PF. Toward Room-Temperature Nanoscale Skyrmions in Ultrathin Films. npj Comput Mater (2020) 6:193. doi:10.1038/s41524-020-00453-w

CrossRef Full Text | Google Scholar