Abstract
The product vague graph (PVG) is one of the most significant issues in fuzzy graph theory, which has many applications in the medical sciences today. The PVG can manage the uncertainty, connected to the unpredictable and unspecified data of all real-world problems, in which fuzzy graphs (FGs) will not conceivably ensue into generating adequate results. The limitations of previous definitions in FGs have led us to present new definitions in PVGs. Domination is one of the highly remarkable areas in fuzzy graph theory that have many applications in medical and computer sciences. Therefore, in this study, we introduce distinctive concepts and properties related to domination in product vague graphs such as the edge dominating set, total dominating set, perfect dominating set, global dominating set, and edge independent set, with some examples. Finally, we propose an implementation of the concept of a dominating set in medicine that is related to the COVID-19 pandemic.
Mathematics Subject Classification: 05C99, 03E72
1 Introduction
Graph theory began its adventure from the well-known “Konigsberg bridge problem.” This problem is frequently believed to have been the beginning of graph theory. In 1739, Euler finally elucidated this problem using graphs. Even though graph theory is an extraordinarily old concept, its growing utilization in operations research, chemistry, genetics, electrical engineering, geography, and so forth has reserved its freshness. In graph theory, it is highly considered that the nodes, edges, weights, and so on are definite. To be exact, there may be no question concerning the existence of these objects. However, the real world sits on a plethora of uncertainties, indicating that in some situations, it is believed that the nodes, edges, and weights may be additional or may not be certain. For instance, the vehicle travel time or vehicle capacity on a road network may not be exactly identified or known. To embody such graphs, Rosenfeld [1] brought up the idea of the “fuzzy graph” in 1975. FG-models are advantageous mathematical tools for handling different domains of combinatorial problems embracing algebra, topology, optimization, computer science, social sciences, and physics (e.g., vulnerability of networks: fractional percolation on random graphs). The VS theory was defined by Gau and Buehrer [2]. Using Zadeh’s fuzzy relation [3], Kauffman [4] illustrated FGs. Mordeson et al. [5–7] evaluated some results in FGs. Pal et al. [8–10] investigated some remarks on bipolar fuzzy graphs and competition graphs. Akram et al. [11, 12] epitomized new definitions in FGs. Ramakrishna [13] described the VG concepts and examined the properties. Rashmanlou et al. [14] defined PVGs and studied new concepts such as the complete-PVG, complement of a PVG, and the edge regular PVG with several examples. Shao et al. [15–20] proposed new concepts in vague graph structures and vague incidence graphs such as the maximal product, residue product, irregular vague graphs, valid degree, isolated vertex, vague incidence irredundant set, Laplacian energy, adjacency matrix, and Laplacian matrix in VGs and investigated their properties with several examples. Also, they described several applications of these concepts in the medical sciences. Borzooei et al. [21–24] analyzed several concepts of VGs. Ore [25] defined “domination” for undirected graphs and studied its properties. Somasundaram [26] defined the DS and IDS in FGs. Nagoorgani et al. [27, 28] represented the fuzzy DS and IDS notions using strong arcs. Parvathi and Thamizhendhi [29] represented the domination number, independent set, independent domination number, and total domination number in intuitionistic fuzzy graphs [29]. Cockayne [30] and Hedetniemi [31, 32] introduced fundamentals of domination in graphs.
Fuzzy graph theory has a wide range of applications in various fields. Since indeterminate information is an essential real-life problem, mostly uncertain, modeling those problems based on fuzzy graphs (FGs) is highly demanding for an expert. A PVG is an indiscriminately comprehensive structure of an FG that offers higher precision, adaptability, and compatibility to a system when coordinated with systems running on FGs. PVGs are a very useful tool for examining many issues such as networking, social systems, geometry, biology, clustering, medical science, and traffic plans. Domination is one of the most important issues in graph theory and has found numerous applications in formulating and solving many problems in several domains of science and technology exemplified by computer networks, artificial intelligence, combinatorial analyses, etc. Domination of PVGs is an interesting and powerful concept and can play an important role in applications. Thus, in this study, we introduce different kinds of domination in PVGs, such as the EDS, TDS, PDS, GDS, and EIS, with some examples and also discuss the properties of each of them. Today, almost every country in the world is inflicted by a dangerous disease called Covid-19. Unfortunately, many people have lost their lives due to contracting this dangerous virus and the lack of necessary medical equipment for treatment. So, we have tried to identify a suitable hospital for a person infected with the coronavirus that has more appropriate medical facilities and equipment and is in the most favorable conditions in terms of distance and amount of traffic, so that time and money are saved, with the help of the DS in the VG. Some basic notations introduced in Table 1
TABLE 1
| Notation | Meaning |
|---|---|
| FG | Fuzzy graph |
| VS | Vague set |
| VG | Vague graph |
| DS | Dominating set |
| PVG | Product vague graph |
| IDS | Independent dominating set |
| EDS | Edge dominating set |
| GDS | Global dominating set |
| GDN | Global dominating number |
| MI-EDS | Minimal edge dominating set |
| EIS | Edge independent set |
| MA-EIS | Maximal edge independent set |
| EIN | Edge independent number |
| MA-EDS | Maximal edge dominating set |
| TDS | Total dominating set |
| MI-TDS | Minimal total dominating set |
| PDS | Perfect dominating set |
| PDN | Perfect dominating number |
| IDN | Independent dominating number |
Some basic notations.
2 Preliminaries
A (crisp) graph consists of two sets called the vertices (V) and the edge (E). The elements of V are called vertices and the elements of E are called edges. An FG has the form of , so that and , as is defined as , , and φ is a symmetric fuzzy relation on σ and denotes the minimum.
Definition 2.1: [2] A VS A is a pairwhereandare considered as real-valued functions that can be described on, such that,.
Definition 2.2: [13] A pairis named as a VG on, such thatis a VS on V andis a VS onso that for all, we have, and.
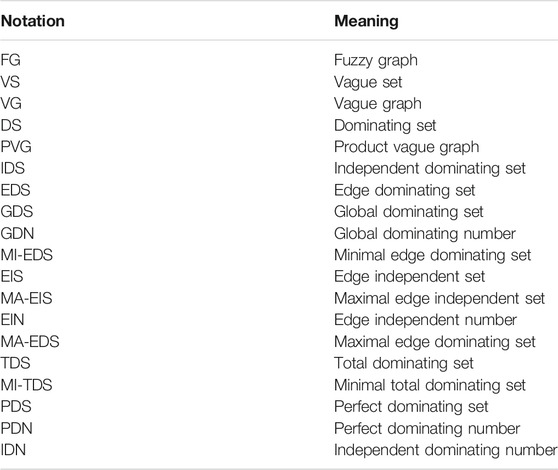
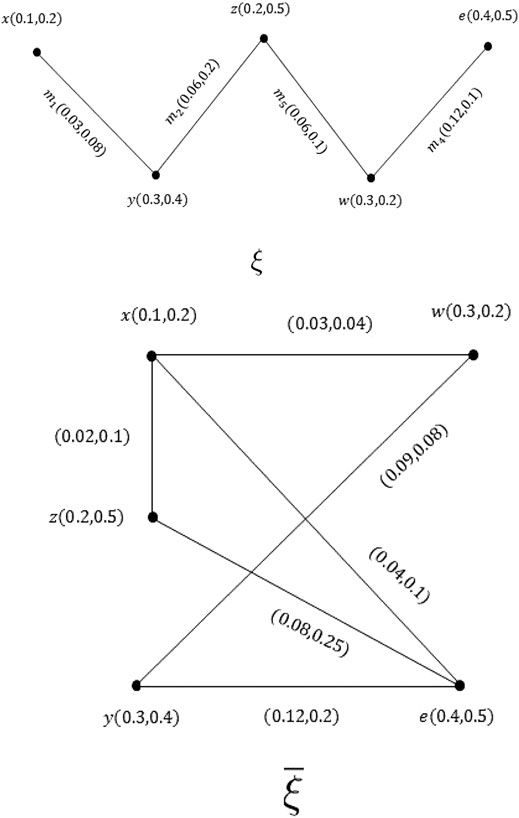
Example 2.3: Consider a VG ξ asFigure 1, so thatand. Clearly, ξ is a VG.
FIGURE 1
Definition 2.4:
[
23]
Letbe a VG. The cardinality, vertex cardinality, and edge cardinality of ξ are defined as follows:(1)
(2) ,.
(3) ,.
Definition 2.5: [24] Consideras a VG. Provided that, the connectedness t-strength betweenandis termed asand the connectedness f-strength betweenandis termed as.
Definition 2.6: [22] An edgein a VGwill be a strong edge provided thatand.
Definition 2.7: [23] A VGis called complete provided thatand,.A VG ξ is called strong provided that and , .
Definition 2.8: [22] Consider ξ as a VG. Assuming, we state that x dominates y in ξ, provided that there is a strong edge between them.A subset will be named a DS in ξ provided that for every , there exists so that x dominated y. A DS K of a VG ξ is referred to as an MI-DS, provided that no proper subset of K is a DS.
Definition 2.9: [14] Letbe a VG. Ifand,, then the VG ξ is called a PVG. Note that a PVG ξ is not necessarily a VG. A PVG ξ is called complete-PVG ifand,.The complement of a PVG is , where and so that and .
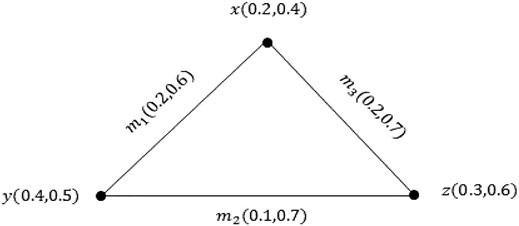
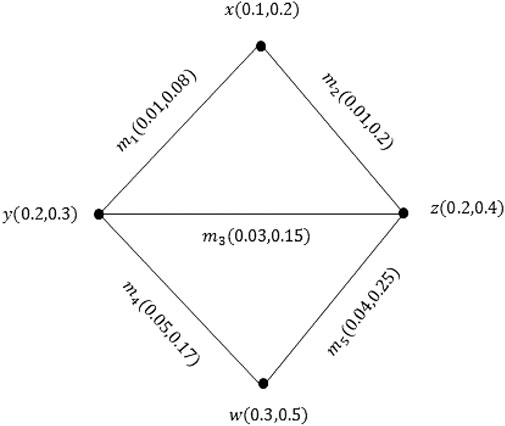
Example 2.10: Consider the PVG ξ asFigure 2.For the edge, we have the following:In the same way, we can show that both conditions of Definition 2.9 are true for other edges. So, ξ is a PVG.
FIGURE 2
Definition 2.11: [14] An edgein a PVG ξ is named an effective edge ifand.
Definition 2.12: [14] If ξ is a PVG, then the vertex cardinality ofis described as follows:
Definition 2.13: [14] Letbe a PVG; then the edge cardinality ofis defined as follows:
Definition 2.14: [14] Two edgesandin a PVG ξ are named adjacent if they are neighbors. Also, they are independent if they are not adjacent.
Definition 2.15: [22] Let ξ be a PVG.is called a DS of ξ if, and there exists a vertexso that the following occurs:A DS K of a PVG ξ is said to be a minimal-DS if no proper subset of K is a DS.
Definition 2.16: [5] Letbe a PVG. Then we have, whereand, for.Two vertices, and , are said to be strong neighbors if and .
Definition 2.17: [22] Two vertices,and, are said to be independent vertices if there is no strong arc among them.is called an independent set if every two vertices of K are independent.
3 New Kinds of Domination in Product Vague Graphs
Definition 3.1: Letbe a PVG andandbe two adjacent edges of ξ. We say thatdominatesifis an effective edge in ξ.
Definition 3.2: is named an EDS in ξ if for every, there is an, so thatdominates.
Definition 3.3: An EDS D of a PVG ξ is named an MI-EDS if no proper subset of D is an EDS.
Definition 3.4: Minimum cardinality between all MI-EDSs is named an EDN of ξ and is denoted by.
Definition 3.5: The strong neighborhood of an edgein a PVG ξ is defined as.
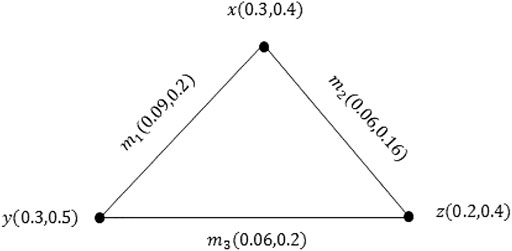
Example 3.6: Consider a PVGon, as shown inFigure 3.Here, , , , and are EDSs and .
FIGURE 3
Definition 3.7: Letbe a PVG. Two edges,and, are called edge independent, ifand
Definition 3.8: Letbe a PVG. A subset S of E is called an EIS of ξ if any two edges in S are edge independent.
Definition 3.9: An EIS S of a PVG ξ is called an MA-EIS if for every edge, the setis not independent. The minimum cardinality between all MA-EISs is called an EIN of ξ and is denoted by.
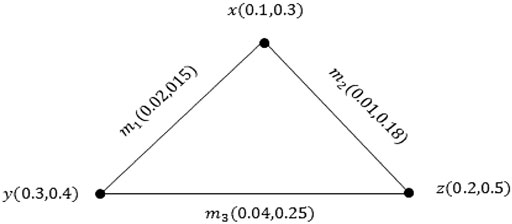
Example 3.10: Consider the example of a PVGas shown inFigure 4. Clearly,andare MA-EISs of ξ and.
FIGURE 4
Definition 3.11: If all the edges are effective edges in a PVG ξ, then it is called an effective-PVG.
Definition 3.12: Assume thatis a subset of edge set E. Then, the node cover ofis defined as the set of all nodes incident to every edge in.
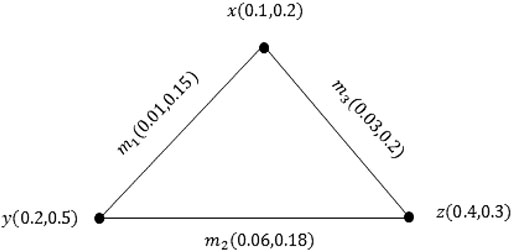
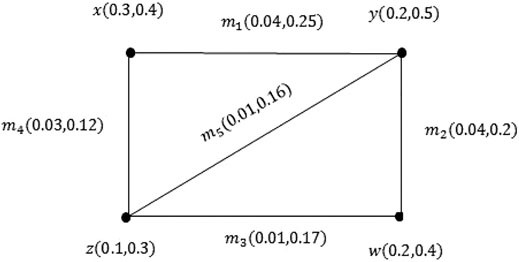
Example 3.13: Consider the PVG ξ as shown inFigure 5. Obviously, ξ is an effective-PVG.
FIGURE 5
Node cover of an EDS of a PVG ξ is a DS of ξ.
Proof: Let ξ be a PVG. Suppose that S is a node cover of an EDS K. We prove that S is a DS. Let , since K is an EDS; then there is a strong edge such that m is incident to y. Since S is a node cover of K, there is an so that x dominated y or x covers m. Hence, S is a DS of ξ.
Definition 3.15: An edge in a PVG ξ is called an isolated edge if it is not a neighbor to any effective edge in ξ.
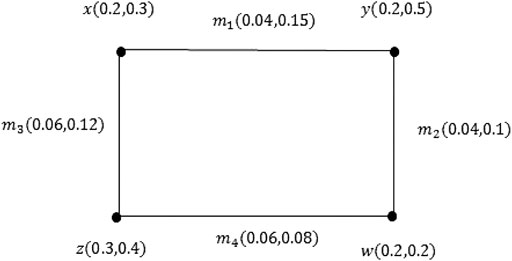
Example 3.16: Consider the PVG ξ as shown inFigure 6. It is obvious thatis an isolated edge.
FIGURE 6
Let ξ be a PVG without isolated edges, and there exists no edgeso that. If S is an MI-EDS, thenis an EDS where K is the set of all effective edges in ξ.
Proof: Let S be an MI-EDS of a PVG ξ. Suppose that is not an EDS. Then, there exists at least one edge that is not dominated by . Because ξ has no isolated edges and there is no edge so that , neighbors at least one effective edge in K. Since is not an EDS of ξ, . So . Hence, . Therefore, is an EDS that is a contradiction of the fact that S is an MI-EDS. Hence, each edge in is dominated by an edge in . Thus, is an EDS.
An EIS of a PVG ξ having only effective edges is an MA-EIS if and only if it is edge independent and an EDS.
Proof: Suppose that S is an EIS of a PVG ξ having only effective edges. Consider that S is an MA-EIS of ξ. Then, , and the set is not an EIS, that is, for every , there is an edge so that . Hence, S is an EDS of ξ. Conversely, suppose that S is both edge independent and an EDS of ξ. We have to prove that S is an MA-EIS having only effective edges. Because S is an EDS of ξ, it has only effective edges. Assume that S is not an MA-EIS. Then, there is an edge so that is an EIS, and there is no edge in S belonging to and hence, is not dominated by S. So, S cannot be an EDS of ξ; that is a contradiction. Therefore, we conclude that for every edge , the set is not independent. Thus, S is an MA-EIS of ξ having only effective edges.
Node cover of an MA-EIS of a PVG ξ having only effective edges is a DS of ξ.
Proof: Let S be an MA-EIS of a PVG ξ having only effective edges. Let be the node cover of S. We know that each MA-EDS having only effective edges is a minimal DS of ξ. Then, is a node cover of a PVG ξ. According to Theorem 3.14, the node cover of an EDS of a PVG ξ is a DS of ξ. Hence, is a DS of ξ.
Definition 3.20: Consideras a PVG on V without isolated nodes. A subsetis a TDS provided that for each node,a node,, so that x dominates y.
Definition 3.21: A TDS S of a PVG ξ is called an MI-TDS if no proper subset of S is a TDS. The minimum cardinality of an MI-TDS is named a lower-TDN of ξ and is shown by.
Example 3.22: InFigure 7,,,, andare TDSs and.
FIGURE 7
Letbe a PVG without isolated nodes and S is a minimal-DS of ξ; thenis a DS of ξ.
Proof: Let S be a minimal-DS and . Since ξ has no isolated nodes, there is a node so that y must be dominated by at least one node in , that is, is a DS and . Thus, each node in S is dominated by at least one node in , and so is a DS.
Definition 3.24: A DS S in a PVG ξ is called a PDS if for each node, there is exactly one nodeso that x dominates y.
Definition 3.25: A PDS S in a PVG ξ is said to be an MI-PDS if for every,is not a PDS in ξ. The minimum cardinality among all MI-PDSs is called a PDN of ξ and is denoted by.
Example 3.26: InFigure 8,,,, andare MI-PDSs and.
FIGURE 8
Every DS in a complete PVG ξ is a PDS.
Proof: Let S be a minimal-DS of a PVG ξ. Since ξ is complete, every edge in ξ is an effective edge and every node is exactly neighboring one node . Hence, every DS in ξ is a PDS.
ξ
is an MI-PDS if and only if for each node, one of the following conditions is present:(i) ,
(ii) a nodeso that.
Proof: Let S be an MI-PDS and . Then, is not a DS and hence a node so that x is not dominated by an element of S. If , we get and if , we get . On the contrary, suppose that S is a PDS and for every vertex , one of the two conditions is met. We prove that S is an MI-PDS. Assume that S is not an MI-PDS. So, there exists a vertex such that is a PDS. Thus, x is a perfect dominated by exactly one vertex in . Therefore, condition (i) is not held. Also, if is a PDS, then every vertex in is dominated by exactly one vertex in . So, condition (ii) is not held and this is a contradiction.
Letbe a connected PVG and S be an MI-PDS of ξ. Then,is a DS of ξ.
Proof: Let S be an MI-PDS of ξ, and is not a DS. Then, a node so that y is not dominated by any node in . Since ξ is connected, y is a strong neighbor of at least one node in . Then, is a DS, which contradicts the minimality of S. Thus, for each node b in S, there is at least one node x in so that and . Hence, is a DS.
Definition 3.30: A DS S of a PVG ξ is named a GDS if S is a DS of, too. The minimum cardinality between all GDSs is called a GDN, and is described by.
Example 3.31: Let ξ andbe PVGs inFigure 9.It is obvious that and are GDSs and .
FIGURE 9
A DS S in a PVG ξ is called a GDS if and only if,a vertexsuch that x and y are not dominating each other.
Proof: Suppose that S is a GDS in a PVG ξ. Let x in S be dominated by y in ; then S is not a DS, contradicting S which is a DS of ξ. Conversely, let , so that x and y will not be dominating each other; then S is a DS in both ξ and , which indicates that S is a GDS of ξ and so the result.
4 Application of Domination in Medical Sciences
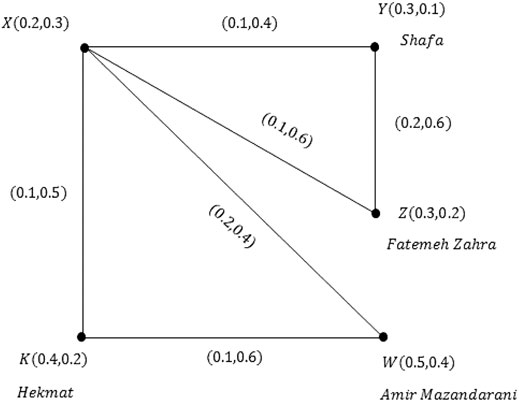
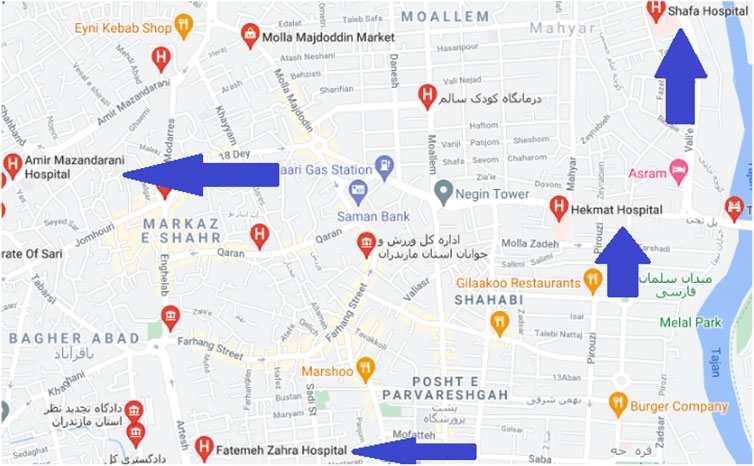
Today, almost every country in the world is affected by a dangerous disease called COVID-19, which is also commonly referred to as Corona. COVID-19 is an infectious disease caused by the coronavirus of acute respiratory syndrome. Its common symptoms are fever, cough, shortness of breath, and, most recently, infertility. Although the majority of cases of the disease cause mild symptoms, some cases progress to pneumonia and multiple sclerosis. The mortality rate is appraised at 2–5% but varies with age and other health conditions. The pathogenicity of the virus touches the respiratory system and instigates symptoms similar to those of the common cold, which can be very precarious for a patient because the patient assumes that the condition is not very serious. Over time, the disease progresses and can easily derail the patient and lead to poor health. But the issue that can be very important is how to find out when a person is infected with this dangerous virus (with the help of medical diagnostic kits) and what medical facilities and equipment should be used to treat this patient. Considering that this virus has appeared in just one year, most countries are not equipped with the necessary facilities to treat it, and this point can be very critical and threatening for a patient. Accordingly, in this study, we have tried to locate a suitable hospital for a person infected with the coronavirus, which has more appropriate medical facilities and equipment and is in the most favorable condition in terms of distance and amount of traffic, so that the patient can regain his or her health faster and also save time and money. To do so, we consider four hospitals in Iran (Sari city) named Shafa, Fatemeh Zahra, Amir Mazandarani, and Hekmat, which are shown in the graph with the symbols Y, Z, W, and K. The patient’s home is located at point X. In this vague graph, one vertex illustrates the patient’s home and other vertices represent the hospitals in the city. The edges specify the accumulation of cars in the city. The location of hospitals is shown in Figure 11. Weight of nodes and edges defined in Table 2 and Table 3.
TABLE 2
| ξ | X | Y | Z | W | K |
|---|---|---|---|---|---|
Weight of nodes in a VG ζ.
TABLE 3
| ξ | |||
| ξ | |||
Weight of edges in a VG ζ.
The vertex asserts that it involves 40% of the prerequisite amenities and services for curing the patient and unfortunately is short of 20% of the necessary tools. The edge indicates that simply 10% of the patient’s transport route to the hospital is not obstructed by any traffic if taken by ambulance, and unfortunately, 60% of the route between these two points is congested with cars, especially during the rush hours. The DSs for Figure 10 will be as follows:After calculating the cardinality of , we have the following:
FIGURE 10
Clearly, holds the smallest proportions among other DSs, so it is concluded that it serves as the best selection since first, the free space for the ambulance from the patient’s home to the Amir Mazandarani hospital is higher; therefore, the patient cannot be taken to the desired location faster, leading to the saving of money and time. Second, considering the medical services in all the hospitals in the region, the Amir Mazandarani hospital is the most equipped and supplied. Therefore, we conclude that the government should, first, allocate more funds to hospitals and medical staff so that they can purchase respirators and diagnostic kits for coronary heart disease from rich countries and, second, cooperate with the roads and transportation organization to improve the road quality, especially the routes leading to hospitals.
5 Conclusion
Product vague graphs are used in many sciences today, including computers, artificial intelligence, fuzzy social networks, physics, chemistry, and biology. Since all the data in the problem can be considered on it, researchers use it to display the theories in their research work well. Domination is one of the most important issues in graph theory and has found many uses and functions in terms of formulating and solving many problems in different domains of technology and science exemplified by computer networks, artificial intelligence, combinatorial analyses, etc. Domination helps consider the best way to save time and money. Hence, in this study, we introduced different concepts and properties related to domination in product vague graphs, such as the edge dominating set, total dominating set, perfect dominating set, global dominating set, and edge independent set, and studied their properties by giving some examples. Finally, an application of domination in the field of medical sciences that is related to COVID-19 has been introduced. In our future work, we will introduce vague incidence graphs and study the concepts of the connected perfect dominating set, regular perfect dominating set, inverse perfect dominating set, and independent perfect dominating set on the vague incidence graph.
FIGURE 11
Statements
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Key R&D Program of China (No. 2019YFA0706402) and the National Natural Science Foundation of China under Grant 61772376 and 62072129.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
RosenfeldA. FUZZY GRAPHS††The Support of the Office of Computing Activities, National Science Foundation, under Grant GJ-32258X, Is Gratefully Acknowledged, as Is the Help of Shelly Rowe in Preparing This Paper. In: ZadehLAFuKSShimuraM, editors. Fuzzy Sets and Their Applications. New York, NY, USA: Academic Press (1975). p. 77–95. 10.1016/b978-0-12-775260-0.50008-6
2.
GauW-LBuehrerDJ. Vague Sets. IEEE Trans Syst Man Cybern (1993) 23:610–4. 10.1109/21.229476
3.
ZadehLA. The Concept of a Linguistic Variable and its Application to Approximate Reasoning-I. Inf Sci (1975) 8:199–249. 10.1016/0020-0255(75)90036-5
4.
KaufmannA. Introduction a la Theorie des Sour-Ensembles Flous. Paris, France: Masson et Cie (1973).
5.
MordesonJNMathewS. Fuzzy End Nodes in Fuzzy Incidence Graphs. New Math Nat Comput (2017) 13(3):13–20. 10.1142/s1793005717500028
6.
MordesonJNMathewS. Human Trafficking: Source, Transit, Destination, Designations. New Math Nat Comput (2017) 13(3):209–18. 10.1142/s1793005717400063
7.
MordesonJNMathewSBorzooeiRA. Vulnerability and Government Response to Human Trafficking: Vague Fuzzy Incidence Graphs. New Math Nat Comput (2018) 14(2):203–19. 10.1142/s1793005718500138
8.
SamantaSPalM. Fuzzy K-Competition Graphs and P-Competition Fuzzy Graphs. Fuzzy Inf Eng (2013) 5:191–204. 10.1007/s12543-013-0140-6
9.
SamantaSAkramMPalM. m-Step Fuzzy Competition Graphs. J Appl Math Comput (2014) 47(1-2):461–72. 10.1007/s12190-s12014-s10785-s10782
10.
SamantaSPalM. Irregular Bipolar Fuzzy Graphs. Int J Appl Fuzzy Sets (2012) 2:91–102.
11.
AkramMNazS. Energy of Pythagorean Fuzzy Graphs with Applications. Mathematics (2018) 6:136. 10.3390/math6080136
12.
AkramMSitaraM. Certain Concepts in Intuitionistic Neutrosophic Graph Structures. Information (2017) 8:154. 10.3390/info8040154
13.
RamakrishnaN. Vague Graphs. Int J Comput Cogn (2009) 7:51–8.
14.
RashmanlouHBorzooeiRA. Product Vague Graphs and its Applications. J Intell Fuzzy Syst (2016) 30:371–82. 10.3233/ifs-162089
15.
KosariSRaoYJiangHLiuXWuPShaoZ. Vague Graph Structure with Application in Medical Diagnosis. Symmetry (2020) 12(10):1582. 10.3390/sym12101582
16.
RaoYKosariSShaoZ. Certain Properties of Vague Graphs with a Novel Application. Mathematics (2020) 8:1647. 10.3390/math8101647
17.
RaoYKosariSShaoZCaiRXinyueL. A Study on Domination in Vague Incidence Graph and its Application in Medical Sciences. Symmetry (2020) 12:1885. 10.3390/sym12111885
18.
RaoYChenRWuPJiangHKosariS. A Survey on Domination in Vague Graphs with Application in Transferring Cancer Patients between Countries. Mathematics (2021) 9(11):1258. 10.3390/math9111258
19.
ShaoZKosariSRashmanlouHShoaibM. New Concepts in Intuitionistic Fuzzy Graph with Application in Water Supplier Systems. Mathematics (2020) 8:1241. 10.3390/math8081241
20.
ShaoZKosariSShoaibMRashmanlouH. Certain Concepts of Vague Graphs with Applications to Medical Diagnosis. Front Phys (2020) 8:357. 10.3389/fphy.2020.00357
21.
BorzooeiRARashmanlouH. Semi Global Domination Sets in Vague Graphs with Application. J Intell Fuzzy Syst (2015) 7:16–31. 10.3233/IFS-162110
22.
BorzooeiRRashmanlouH. Domination in Vague Graphs and its Applications. Ifs (2015) 29:1933–40. 10.3233/ifs-151671
23.
BorzooeiRARashmanlouH. Degree of Vertices in Vague Graphs. J Appl Math Inform (2015) 33:545–57. 10.14317/jami.2015.545
24.
BorzooeiRARashmanlouHSamantaSPalM. Regularity of Vague Graphs. Ifs (2016) 30:3681–9. 10.3233/ifs-162114
25.
OreO. Theory of Graphs, Vol. 38. Providence: American Mathematical Society Publications (1962).
26.
SomasundaramASomasundaramS. Domination in Fuzzy Graphs - I. Pattern Recognition Lett (1998) 19(9):787–91. 10.1016/s0167-8655(98)00064-6
27.
NagoorganiAMohamedSYHussainRJ. Point Set Domination of Intuitionistic Fuzzy Graphs. Int J Fuzzy Math Archive (2015) 7(1):43–9.
28.
NagoorganiAChandrasekaranVT. Domination in Fuzzy Graphs. Adv Fuzzy Sets Syst (2006) I(1):17–26. 10.1016/S0167-8655(98)00064-6
29.
ParvathiRThamizhendhiG. Domination in Intuitionistic Fuzzy Graph. Proc 14th Int Conf Intuiyionistic Fuzzy Graphs, Notes Intuitionistic Fuzzy Sets (2010) 16(2):39–49. 10.1007/S12190-015-0952-0
30.
CockayneEJFavaronOPayanCThomasonAG. Contributions to the Theory of Domination, independence and Irredundance in Graphs. Discrete Math (1981) 33(3):249–58. 10.1016/0012-365x(81)90268-5
31.
HaynesTWHedetniemiSSlaterP. Fundamentals of Domination in Graphs. Boca Raton: CRC Press (2013).
32.
ZadehLA. Fuzzy Sets. Inf Control (1965) 8:338–53. 10.1016/s0019-9958(65)90241-x
Summary
Keywords
fuzzy graph, vague set, vague graph, dominating set, medicine
Citation
Shi X and Kosari S (2021) Certain Properties of Domination in Product Vague Graphs With an Application in Medicine. Front. Phys. 9:680634. doi: 10.3389/fphy.2021.680634
Received
15 March 2021
Accepted
24 June 2021
Published
23 July 2021
Volume
9 - 2021
Edited by
Jinjin Li, Shanghai Jiao Tong University, China
Reviewed by
Haci Mehmet Baskonus, Harran University, Turkey
Hossein Rashmanlou, University of Mazandaran, Iran
Updates
Copyright
© 2021 Shi and Kosari.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saeed Kosari, saeedkosari38@gzhu.edu.cn
This article was submitted to Mathematical and Statistical Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.