Larval Zebrafish Exhibit Collective Circulation in Confined Spaces

Collective behavior may be elicited or can spontaneously emerge by a combination of interactions with the physical environment and conspecifics moving within that environment. To investigate the relative contributions of these factors in a small millimeter-scale swimming organism, we observed larval zebrafish, interacting at varying densities under circular confinement. If left undisturbed, larval zebrafish swim intermittently in a burst and coast manner and are socially independent at this developmental stage, before shoaling behavioral onset. Our aim was to explore the behavior these larvae as they swim together inside circular confinements. We report here our analysis of a new observation for this well-studied species: in circular confinement and at sufficiently high densities, the larvae collectively circle rapidly alongside the boundary. This is a new physical example of self-organization of mesoscale living active matter driven by boundaries and environment geometry. We believe this is a step forward toward using a prominent biological model system in a new interdisciplinary context to advance knowledge of the physics of social interactions.

Introduction

The emergence of complex collective behavior of natural and artificial motile agents has long been a question of interest to scientists in many disciplines. The transition from disordered to ordered collective motion can be seen across scales, from micron long bacteria and colloids, to millimeter long ants and bees, to centimeter long crickets and bristle-bots, and even to meter-long fish and humans [1–3]. The complex behavior of flocks of birds, colonies of ants, swarms of bees and schools of fish emerges from the interactions of the constituent parts of the respective systems. While similarities in the patterns that such groups produce have suggested general principles governing the self-organization [4], it is also becoming clear that the specific patterns depend on the type of motile agent, scale, and also the type of interaction. For example, for fluid-immersed micro-scale units such as motile bacteria and colloids, it has become clear that mechanical interactions often mediated through the liquid are paramount to the type of eventual patterns [5, 6]. For larger animals such as birds, mechanics are not the only factor as others may become more prominent, e.g., visual input for birds [7], environmental factors for bees [8], sensory stimuli or social cues for humans [9].

Despite the large effort in studying the emergence of collective motion for various motile agents, little has been done to study how this behavior changes when the agents are confined, whether by hard walls or soft impediments. Recent work has shown that when swimming bacteria, colloids, spermatozoa, and even bristle-bots are placed in circular or racetrack dishes, then they will spontaneously start to circulate [5, 6, 10–13]. Even soft confinement can lead to locust milling [4] and human mosh pits [14]. Our approach was motivated by the need to develop a model where behavior can be observed easily, which is amenable to neurobiological perturbations, and which generates interesting and quantifiable individual and collective behavior. In the popular biological model organism Danio rerio, the zebrafish, swimming is influenced by fluid mechanics as well as by sensory stimuli [15–18]. Adult zebrafish have been studied extensively in both individual and collective contexts [19–24]. However, at the 5 days post-fertilization larval life stage, when zebrafish are approximately 4 mm in length, before the onset of social shoaling behavior [25, 26], they utilize different movement patterns from adult fish. Larval zebrafish, a millimeter with 2 Ls swimmer move in what is often termed a beat-and-glide or burst-and-coast discontinuous manner; they swim in bouts of movement followed by pauses [27]. This species has been extensively studied in terms of their kinematics, neurobiology, development, and behavior [28–32] but the individual or collective motion of larvae in confinement has not been explored previously.

At this life stage, larval zebrafish placed in low density have a usual social avoidance area of approximately 50 mm² surrounding their body and will initiate escape responses to avoid contact [33]. However, the set of observations we report here included confinement and a range of densities where larvae were forced to interact with others and did not permit them to maintain their preferred social avoidance area. These “escape” responses are short duration, high velocity movements, and can be directed away from noxious stimuli [34, 35, 36]. Here, we observed that when in confined environments at sufficiently high densities, larval zebrafish may spontaneously collectively perform a novel circling behavior or short duration “panic waves” along the confining dish. We report conditions under which the phenomenon of collective circling behavior may be elicited in larval zebrafish by use of confinement. Confined collective motion is a new and developing area of interest in the field of living active matter, where experiments at this scale and intermediate Reynolds number remain rare [36].

Materials and Methods

Animals

Larval zebrafish used in these experiments were 5 days post-fertilization (dpf) AB wild-type (origin: ZIRC stock center, Eugene, Oregon) reared in an incubator at 28.5°C with a 14L:10D light cycle. Larvae were generated from an adult colony maintained at NJIT in the Severi lab under Rutgers University-Newark IACUC oversight, PROTO201800041.

Acquisition

High-speed videos were collected on a custom-built setup (Figure 1A, Supplemental Table S1). A high-speed camera (Mikrotron GmbH, Germany) attached to a rail (ThorLabs) fitted with a 35 mm F1.4 lens (Fujinon) and an 850 nm bandpass filter (Midwest Optical) were used to acquire images to a Dell Precision 5820 computer fitted with a frame grabber (National Instruments) and running custom-written LabView software (National Instruments, available upon request) saving TIFF image stacks for each trial. Larvae were illuminated with 850 nm IR LEDs which are not within their visible spectra (Waveform Lighting) under an acrylic platform stabilized by Thorlabs components covered with light diffusers (Pro Gel, B&H Photo) within a custom-built enclosure (MiniTec Framing Systems, LLC) which was left open to room light. Videos were acquired at 200 Hz with 1,423 μs shutter speed at 648 × 648 pixel resolution, and trials were 6,000 frames or 30 s in duration. The same larvae were used for each trial. Videos were captured approximately 1–5 min after larvae were placed in the behavior enclosure to allow time for acclimation following handling. Animals were counted and added to the arena group before trial repeats occurred at each density stage (Table 1). Animals were recorded at room temperature during daytime in round petri dishes with 5.4 cm diameter.

FIGURE 1

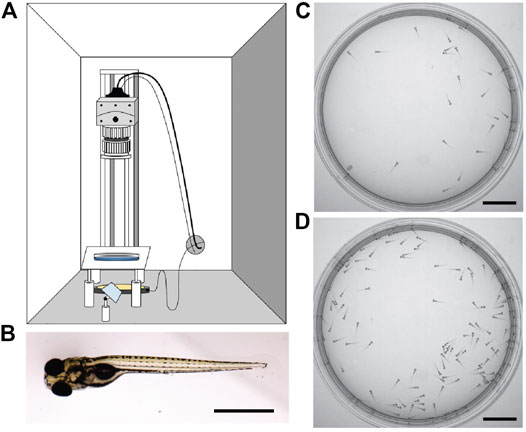
FIGURE 1. Experimental observation of larval zebrafish swimming collectively at various densities. (A) Schematic of experimental set-up. (B) Image of a larval zebrafish at 6 days post-fertilization, scale bar 1 mm. Rostral (head) is to the left. (C) 30 larval zebrafish in the arena as captured by the camera. (D) 130 larval zebrafish in the arena. Scale bar for C-D 1 cm.

TABLE 1

TABLE 1. Table of density across trial noting when circling behavior was observed.

Tracking and Trajectories

To generate tracks from raw videos, we utilized trackR, an R package written by Dr. Simon Garnier [38]. trackR is an object tracker for R allowing users to perform multi-object video tracking by background subtraction and adaptive thresholding. trackR outputted object trajectories as .csv files however with discontinuities, i.e. we could not assign particular tracks to individual larvae. These tracks were imported to MATLAB and plotted. To determine the distance traveled over tracks in separate regions within the dish, tracks were imported to MATLAB and the arena boundary and center were determined using a custom function, with a radius of 310 pixels. The inner circle was 70% of the radius (217 pixels) with the same center coordinates Figures 2A,B. Tracks within those regions were segregated and distances across all tracks for a given trial were calculated for three trials with 30 larvae and three trials with 130 larvae over 1,497 frames of the trial. Each trial and the means were plotted along with the standard error of the mean Figure 2C. A standard t-test was applied between groups (ttest2 function in MATLAB) and p-values < 0.05 were considered significant. The mean tangential velocities and circulating order parameter were calculated using the trajectories from trackR with MATLAB custom code (Figures 2D,E).

FIGURE 2

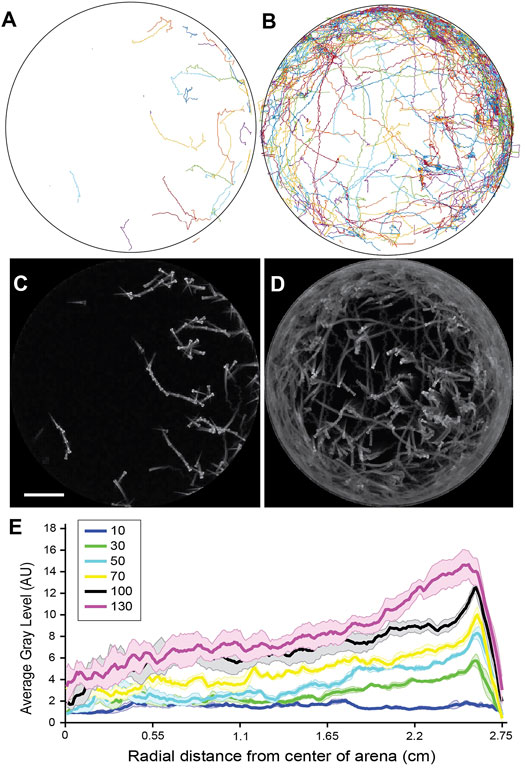
FIGURE 2. Distribution of larval positions varies as a function of distance from the arena wall. (A) Tracked trajectories for a single trial with 30 larvae. (B) Tracked trajectories for a single trial with 130 larvae. (C) Standard deviation z-projection for the frames corresponding to A. (D) Standard deviation z-projection for the frames corresponding to B. (E) Average gray area of standard deviation z-projections plotted from the center of the arena to the border of the arena for 5 trials at each density. The mean is shown in bold and the standard error of the mean is shaded in a color corresponding to the density. Densities tested were: 10 larvae, 30 larvae, 50 larvae, 70 larvae, 100 larvae, and 130 larvae, in the same arena. Scale bar for A-D 1 cm.

Radial Distance Measure

To determine how position varied with radial distance Figure 3E using FIJI (NIH) and MATLAB, videos were reduced by ¼ in FIJI and cropped to exclude the pixels outside the arena. A standard deviation z-projection was applied to the image stacks to create a single image using FIJI. This process outputs a single image where each pixel represents the standard deviation value over all images in the stack at that particular pixel location (https://imagejdocu.tudor.lu/gui/image/stacks#zproject). Using the MATLAB function average_radial_profile_2 (Image Analyst, Mathworks author id:31,862) the average radial profile was calculated from a center location of each image and plotted.

FIGURE 3

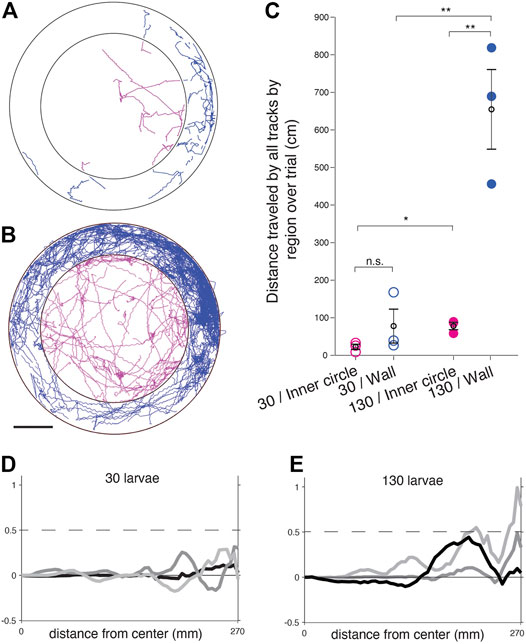
FIGURE 3. Larval zebrafish traverse space differently at different densities when bordering the arena wall in comparison to in the center of the arena. (A) Trajectories for a trial with 30 larvae segregated into an outer ring adjacent to the wall (blue) and the arena center (magenta). (B) Trajectories for a trial with 130 larvae segregated into an outer ring adjacent to the wall (blue) and the arena center (magenta). Scale bar for A-B 1 cm. (C) Summed distance traveled in cm for all tracks in a trial. Trials with 30 larvae (open circles) were compared to trials of 130 larvae (filled circles) and wall-adjacent regions (blue) were compared to the inner circle of the arena (magenta). Means per group are in black open circles and error bars are the SEM. n.s. = not significant, *p < 0.05, **p < 0.01. (D–E). Mean tangential velocity <v> versus the radial distance from the dish center for 3 trials each of n = 30 (D) and n = 130 (E) larvae.

Qualitative Assessment

For determination of the circling behavior (Table 1), a pair of qualitative assessments of the captured videos were used. First, when watching the videos at 30 Hz playback and paying attention to the region just inside the arena boundary, some collective circling instances were immediately obvious based on easily discernible rotational movement. When many conspecifics began moving in a coordinated manner around the edge of the dish in a single major direction, we took this to be circling behavior. A second qualitative identifier of circling motion was a correlate of the behavior that arises due to fluid flow. When a significant number of the larvae are circling near the boundary of the dish, a radial region of the larvae within the circling ring will exhibit larvae in counter-rotation, moving in the opposite circular direction to the major circling direction of the outer ring. This is characterized through the obvious lack of self-propelled movement (the larvae themselves are static), and oftentimes a drifting motion in a backward direction which is not a gait present in this species. Based on our understanding of fluid motion [6], this is strongly indicative of coordinated circling in one major direction. With either or both of these qualifications met, we could categorize a captured video to have circling behavior.

Results

We set out to observe larval zebrafish behaving spontaneously under confinement at various densities and to determine whether collective behavior emerged. Observing larval zebrafish behaving spontaneously at varying densities, from 5 to 130 individuals, in a 5.4 cm diameter arena (Figure 1), we found the animals moved freely within the arena in short bouts of swimming. We systematically tested a range of densities (Table 1) and found that at low densities the animals behaved relatively independently of each other, though the circular wall affected their motion as they tended to swim or stop by it more often. At high densities however the animals exhibited a high-speed circling behavior, with incidence increasing alongside density. At this density the larvae are forced to interact with other larvae as well as the boundary. The circling behavior appeared to initiate on occasions when larvae came close to each other, producing a response in the contacted larvae, and that the size and shape of the arena and the interaction with the wall produced a group of larvae circling near the edge of the arena (Figure 2, Supplementary Movie S1).

Tracking the positions of the animals confirmed there was a propensity to spend time in the outer region of the arena in proximity to the arena walls (Figures 2A,B). While a preference for the arena edges is well noted and was found at densities of 30 or greater larvae, the distribution in spatial position was highly biased toward the outer circumference of the arena at higher densities (Figures 2C–E). These higher densities of 100 larvae and greater 5.4 cm dish correlated with more frequent observation of the circling behavior (Table 1). We observed instances where the collective circulation slowed down, stopped, or initiated in competing directions with one direction of flow emerging as the dominant direction. This needs to be explored in future work investigating the factors that determine initiation, stopping, and direction of motion, keeping in mind that the fish can interact with others and the boundary not just through direct contact but also through fluid-mediated mechanical forces.

Indeed, when the traveled distances of each tracked position were plotted and separated into the wall-adjacent boundary region of the arena and compared to the central inner circle away from the boundary (Figures 3A,B), there were significant differences in the distance traveled when comparing high and low densities, and when comparing the two spatial regions at high densities (Figure 3C).

We quantify the active swimming bouts of the larvae by examining the azimuthal flow profile ${\mathbf{v}}_{\mathbf{t}}= <\mathbf{v}\cdot \mathbf{t}{>}_{\text{θ}}$ where v is the instantaneous larva velocity measured from the trajectories, and t is the tangential direction at the larval position. Figures 3D,E show the profiles of ${\mathbf{v}}_{\mathbf{t}}$ as a function of the distance from the dish center for three experiments each at n = 30 larvae (Figure 3D) and n = 130 larvae (Figure 3E). The positive direction is taken to be one with the dominant circulation direction (clock-wise or counter-clockwise). We notice higher ${\mathbf{v}}_{\mathbf{t}}$, especially closer to the edge, for the higher density, meaning the larvae are moving tangentially, i.e., alongside the boundary especially since ${\mathbf{v}}_{\mathbf{t}}$ is highest there. Negative ${\mathbf{v}}_{\mathbf{t}}$ means counter-rotating movement, which matches the observations. We also calculate the vortex order parameter

$\mathbf{\Phi }=\frac{{{\displaystyle \sum }}_i\left|v_i\cdot t_i\right| / {{\displaystyle \sum }}_i\left|\right| v_i \left|\right| -2/ \pi }{1-2/\pi }$

This parameter is used in many studies of confined collective motion to quantify collective circulation [6, 39]. $\mathbf{\Phi }=1$means the motion is perfectly tangential/azimuthal, $\mathbf{\Phi }=0$ means the motion is disordered, and $\mathbf{\Phi }<0$ means the motion is radial. For our examples with n = 30 larvae, we get $\mathbf{\Phi }= 0.0759,0.0580,0.0898$, whereas for n = 130 larvae we get $\mathbf{\Phi }=0.1295,0.1327,0.1120$. We note that $\mathbf{\Phi }$ is higher for the higher density cases, meaning there is more circulation in those cases. While this is not as stong a signal as in the examples of bacteria [39], note that larval zebrafish do not have constant swimming speed and move in bouts.

Discussion

The collective motion of animals and other active agents in enclosed areas is an evolving but promising area of study, as is collective motion at the mesoscale [6, 37]. We see similarities but also differences in the self-organization of larval zebrafish to other types of motile agents under circular confinement. Here we refer to collective motion simply as an emergent group behavior that only occurs as a function of the interactions of the conspecifics and their environment and would not occur if a single larva were in isolation or in free space. At high densities the larval fish transition to short bouts of circulation alongside the dish boundary and tend to be found swimming closer to the walls than at low densities. A largely similar circulating collective motion pattern is seen across scales from single-cell organisms to humans when the motile units are placed in hard or soft circular enclosures. And yet the specific physical and neurobiological capabilities of larval fish give rise to distinct behavior. Their individual non-uniform speeds and preference for social avoidance may be influencing the non-uniform circulation or “panic wave” which at times may stop or even reverse direction. Their preferred social distancing, possible visual cues, and fluidic interactions may influence why they can mostly be found at a certain distance from the confining wall that increases with density.

Unlike smaller swimmers like bacteria, algae or spermatozoa [40], these relatively larger larval fish have more complex individual motion patterns. They are well-studied however, and much is known about their biology, locomotion, individual, and social behavior. Groneberg et al., 2020 shows that the preferred distance between animals changes due to early life social interaction, and that these responses are driven by vision and by the sensory lateral line, which senses water flow around fishes [33]. While thigmotaxis or “wall-hugging” as a response to anxiety-inducing stimuli has been well documented in larval zebrafish [41], it is interesting to consider this emergent circling behavior in the context of social anxiety caused by crowding and confinement. It was observed in work involving small groups of zebrafish at the same life stage with much smaller arenas housing seven larvae at a time, that one larva in the group could set off chain reactions of escape responses: if one animal escaped it would collide with another setting off a domino effect [42]. It’s possible this emergent collective circling results from these same chains of escapes, created by the interaction with the confinement of walls and the high density of conspecifics, which then catalyze this circling behavior. In future work we are interested in identifying mechanistic drivers of transitions between states, as has been identified in other species [43].

Another interesting observation was noted just inside the extreme edges of the arena, where immobile larvae can be seen drifting rearwards, in counter-rotation with the adjacent larvae circling at the dish circumference. We presume this can be attributed to fluid flow as the animals do not appear to be oscillating their tail or actively moving, and larval zebrafish have not been observed to swim backward. This is reminiscent of the collective behavior of bacteria in circular chambers where the fluid flow disturbed by the edge-swimming bacteria pushed back the middle-swimming ones [6]. The interaction between water flow generated by the circling proportion of animals and the diameter and shape of the confinement is a point of interest which we will model and further test experimentally in the future. The study of individual or collective animal motion at intermediate Reynolds numbers remains underexplored. A better understanding of the mechanisms and interactions that give rise to the confined zebrafish collective motion will allow us to optimally direct their behavior by designing appropriate confining boundaries.

In future work, we hope to experimentally manipulate these various sensory inputs and systematically study the triggers for collective circling. It is highly advantageous to develop collective motion paradigms in a model system with an extensive genetic and optical toolkit to allow experimenters to observe and manipulate neural circuits [44–53]. Insects are also known to display a transition from disordered to ordered movement with increasing density, most famously in locusts [4]. Zebrafish sit in an advantageous space between invertebrate models where sensory systems may be easily perturbed to investigate mechanisms [54], and humans which display complex behavior but inaccesssible neurobiological underpinnings, although techniques like fMRI permit some measurement of individual human neural activity during complex social decision making [9].

Here we share a new paradigm where collective motion can be induced by confinement in a model system amenable to genetic and neurobiological tools to investigate the underlying neural circuits. By understanding what influences this collective behavior and manipulating the enclosure scales and shapes in the future, we can determine fundamental interaction rules that could be widely applicable to other organisms and systems.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by Rutgers-Newark IACUC protocol # PROTO201800041.

Author Contributions

All the authors conceived of the project, analyzed the data, and wrote the article. HZ and KS collected the data.

Funding

New Jersey Institute of Technology startup funds to EL and KS. Simons Foundation for EL.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Dr. Simon Garnier and the Swarm lab for insightful suggestions and mentorship throughout the project, as well as Rafael Asfour from the Swarm lab for assistance implementing trackR. Mahathi Mohan Gowda built the behavior rig setup utilized for the experiments, along with members of the Severi lab and Dr. Christoph Gebhardt assisted in designing and building the behavior rig and gave input on analysis. We thank all members of the Severi lab past and present for excellent animal care and useful discussions throughout the project. Hassan Elsaid contributed through the NJIT Research @Home program. KS acknowledges support from NJIT startup funds. EL acknowledges support from the Simons Foundation as well as NJIT startup and seed funds.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.678600/full#supplementary-material

Supplemental Table 1 | Components for custom-built behavioral recording setup.

References

1. Vicsek T, Zafeiris A. Collective Motion. Phys Rep (2012) 517(3–4):71–140. doi:10.1016/j.physrep.2012.03.004

CrossRef Full Text | Google Scholar

2. Cavagna A, Cimarelli A, Giardina I, Parisi G, Santagati R, Stefanini F, et al. Scale-free Correlations in Starling Flocks. Proc Natl Acad Sci (2010) 107(26):11865–70. doi:10.1073/pnas.1005766107

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Katz Y, Tunstrom K, Ioannou CC, Huepe C, Couzin ID. Inferring the Structure and Dynamics of Interactions in Schooling Fish. Proc Natl Acad Sci (2011) 108(46):18720–5. doi:10.1073/pnas.1107583108

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Buhl J, Sumpter DJT, Couzin ID, Hale JJ, Despland E, Miller ER, et al. From Disorder to Order in Marching Locusts. Science (2006) 312(5778):1402–6. doi:10.1126/science.1125142

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bricard A, Caussin J-B, Desreumaux N, Dauchot O, Bartolo D. Emergence of Macroscopic Directed Motion in Populations of Motile Colloids. Nature (2013) 503(7474):95–8. doi:10.1038/nature12673

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lushi E, Wioland H, Goldstein RE. Fluid Flows Created by Swimming Bacteria Drive Self-Organization in Confined Suspensions. Proc Natl Acad Sci USA (2014) 111(27):9733–8. doi:10.1073/pnas.1405698111

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Pearce DJG, Miller AM, Rowlands G, Turner MS. Role of Projection in the Control of Bird Flocks. Proc Natl Acad Sci (2014) 111(29):10422–6. doi:10.1073/pnas.1402202111

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Peleg O, Peters JM, Salcedo MK, Mahadevan L. Collective Mechanical Adaptation of Honeybee Swarms. Nat Phys (2018) 14(12):1193–8. doi:10.1038/s41567-018-0262-1

CrossRef Full Text | Google Scholar

9. Charpentier CJ, Moutsiana C, Garrett N, Sharot T. The Brain's Temporal Dynamics from a Collective Decision to Individual Action. J Neurosci (2014) 34(17):5816–23. doi:10.1523/jneurosci.4107-13.2014

CrossRef Full Text | Google Scholar

10. Wioland H, Lushi E, Goldstein RE. Directed Collective Motion of Bacteria under Channel Confinement. New J Phys (2016) 18(7). doi:10.1088/1367-2630/18/7/075002

CrossRef Full Text | Google Scholar

11. Giomi L, Hawley-Weld N, Mahadevan L. Swarming, Swirling and Stasis in Sequestered Bristle-Bots. Proc R Soc A (2013) 469(2151):20120637. doi:10.1098/rspa.2012.0637

CrossRef Full Text | Google Scholar

12. Creppy A, Plouraboué F, Praud O, Druart X, Cazin S, Yu H, et al. Symmetry-breaking Phase Transitions in Highly Concentrated Semen. J R Soc Interf (2016) 13(123):20160575. doi:10.1098/rsif.2016.0575

CrossRef Full Text | Google Scholar

13. Tsang ACH, Kanso E. Density Shock Waves in Confined Microswimmers. Phys Rev Lett (2016) 116(4):48101. doi:10.1103/physrevlett.116.048101

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Silverberg JL, Bierbaum M, Sethna JP, Cohen I. Collective Motion of Humans in Mosh and circle Pits at Heavy Metal Concerts. Phys Rev Lett (2013) 110(22):228701–5. doi:10.1103/PhysRevLett.110.228701

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ehrlich DE, Schoppik D. Control of Movement Initiation Underlies the Development of Balance. Curr Biol [Internet] (2017) 27(3):334. Available at: http://linkinghub.elsevier.com/retrieve/pii/S096098221631449X.doi:10.1016/j.cub.2016.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Danos N. Locomotor Development of Zebrafish (Danio Rerio) under Novel Hydrodynamic Conditions. J Exp Zool (2012) 317(2):117–26. doi:10.1002/jez.1002

CrossRef Full Text | Google Scholar

17. Orger MB, Smear MC, Anstis SM, Baier H. Perception of Fourier and Non-fourier Motion by Larval Zebrafish. Nat Neurosci (2000) 3(11):1128–33. doi:10.1038/80649

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Oteiza P, Odstrcil I, Lauder G, Portugues R, Engert F. A Novel Mechanism for Mechanosensory-Based Rheotaxis in Larval Zebrafish. Nature (2017) 547(7664):445–8. doi:10.1038/nature23014

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Kim C, Ruberto T, Phamduy P, Porfiri M. Closed-loop Control of Zebrafish Behaviour in Three Dimensions Using a Robotic Stimulus. Sci Rep (2018) 8(1):1–15. doi:10.1038/s41598-017-19083-2

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Heras FJH, Romero-Ferrero F, Hinz RC, De Polavieja GG. Deep Attention Networks Reveal the Rules of Collective Motion in Zebrafish. Plos Comput Biol (2019) 15(9):e1007354–23. doi:10.1371/journal.pcbi.1007354

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Romero-Ferrero F, Bergomi MG, Hinz RC, Heras FJH, de PolaviejaAi GG. idtracker.ai: Tracking All Individuals in Small or Large Collectives of Unmarked Animals. Nat Methods (2019) 16(2):179–82. doi:10.1038/s41592-018-0295-5

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Spinello C, Yang Y, Macrì S, Porfiri M. Zebrafish Adjust Their Behavior in Response to an Interactive Robotic Predator. Front Robot AI (2019) 6(MAY):1–14. doi:10.3389/frobt.2019.00038

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yang Y, Clément RJG, Ghirlanda S, Porfiri M. A Comparison of Individual Learning and Social Learning in Zebrafish through an Ethorobotics Approach. Front Robot AI (2019) 6(August):1–13. doi:10.3389/frobt.2019.00071

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Nunes AR, Carreira L, Anbalagan S, Blechman J, Levkowitz G, Oliveira RF. Perceptual Mechanisms of Social Affiliation in Zebrafish. Sci Rep (2020) 10(1):1–14. doi:10.1038/s41598-020-60154-8

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Engeszer RE, Da Barbiano LA, Ryan MJ, Parichy DM. Timing and Plasticity of Shoaling Behaviour in the Zebrafish, Danio rerio. Anim Behav (2007) 74(5):1269–75. doi:10.1016/j.anbehav.2007.01.032

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Buske C, Gerlai R. Shoaling Develops with Age in Zebrafish (Danio rerio). Prog Neuro-Psychopharmacology Biol Psychiatry (2011) 35(6):1409–15. doi:10.1016/j.pnpbp.2010.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Budick SA, O’Malley DM. Locomotor Repertoire of the Larval Zebrafish: Swimming, Turning and Prey Capture. J Exp Biol [Internet] (2000) 203(Pt 17):2565–79. Available at: http://www.ncbi.nlm.nih.gov/pubmed/10934000. doi:10.1242/jeb.203.17.2565

CrossRef Full Text | Google Scholar

28. Wolman M, Granato M. Behavioral Genetics in Larval Zebrafish: Learning from the Young. Devel Neurobio (2012) 72:366–72. doi:10.1002/dneu.20872

CrossRef Full Text | Google Scholar

29. Portugues R, Engert F. The Neural Basis of Visual Behaviors in the Larval Zebrafish. Curr Opin Neurobiol (2009) 19(6):644–7. Available at: http://www.ncbi.nlm.nih.gov/pubmed/19896836. doi:10.1016/j.conb.2009.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Portugues R, Severi KE, Wyart C, Ahrens MB. Optogenetics in a Transparent Animal: Circuit Function in the Larval Zebrafish. Curr Opin Neurobiol (2013) 23(1):119–26. Available at: http://www.ncbi.nlm.nih.gov/pubmed/23246238. doi:10.1016/j.conb.2012.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Bollmann JH. The Zebrafish Visual System: From Circuits to Behavior. Annu Rev Vis Sci (2019) 5:269–93. doi:10.1146/annurev-vision-091718-014723

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Sakai C, Ijaz S, Hoffman EJ. Zebrafish Models of Neurodevelopmental Disorders: Past, Present, and Future. Front Mol Neurosci (2018) 11(August):294. doi:10.3389/fnmol.2018.00294

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Groneberg AH, Marques JC, Martins AL, Diez del Corral R, de Polavieja GG, Orger MB. Early-Life Social Experience Shapes Social Avoidance Reactions in Larval Zebrafish. Curr Biol (2020) 30(20):4009–21. doi:10.1016/j.cub.2020.07.088

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Foreman MB, Eaton RC. The Direction Change Concept for Reticulospinal Control of Goldfish Escape. J Neurosci (1993) 13(October):4101–13. doi:10.1523/jneurosci.13-10-04101.1993

CrossRef Full Text | Google Scholar

35. Dunn TW, Gebhardt C, Naumann EA, Riegler C, Ahrens MB, Engert F, et al. Neural Circuits Underlying Visually Evoked Escapes in Larval Zebrafish. Neuron (2016) 89:613–28. Available at: http://linkinghub.elsevier.com/retrieve/pii/S089662731501123X. doi:10.1016/j.neuron.2015.12.021

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Hale ME, Katz HR, Peek MY, Fremont RT. Neural Circuits That Drive Startle Behavior, With a Focus on the Mauthner Cells and Spiral Fiber Neurons of Fishes J Neurogenet. (2016) 30(2):89–100. doi:10.1080/01677063.2016.1182526

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Klotsa D. As above, So below, and Also in between: Mesoscale Active Matter in Fluids. Soft Matter (2019) 15(44):8946–50. doi:10.1039/C9SM01019J

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Garnier S. TrackR - Multi-Object Tracking with R. [Internet] (2021). Available at: https://swarm-lab.github.io/trackR/(Accessed Mar 5, 2021).

Google Scholar

39. Wioland H, Woodhouse FG, Dunkel J, Kessler JO, Goldstein RE. Confinement Stabilizes a Bacterial Suspension into a Spiral Vortex. Phys Rev Lett (2013) 110(26):268102–5. doi:10.1103/PhysRevLett.110.268102

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Ostapenko T, Schwarzendahl FJ, Böddeker TJ, Kreis CT, Cammann J, Mazza MG, et al. Curvature-Guided Motility of Microalgae in Geometric Confinement. Phys Rev Lett (2018) 120(6):68002. doi:10.1103/physrevlett.120.068002

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Schnörr SJ, Steenbergen PJ, Richardson MK, Champagne DL. Measuring Thigmotaxis in Larval Zebrafish. Behav Brain Res (2012) 228(2):367–74. doi:10.1016/j.bbr.2011.12.016

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Mirat O, Sternberg JR, Severi KE, Wyart C. ZebraZoom: an Automated Program for High-Throughput Behavioral Analysis and Categorization. Front Neural Circuits (2013) 7:107. Available at: http://www.ncbi.nlm.nih.gov/pubmed/23781175.

Google Scholar

43. Tunstrøm K, Katz Y, Ioannou CC, Huepe C, Lutz MJ, Couzin ID. Collective States, Multistability and Transitional Behavior in Schooling Fish. Plos Comput Biol (2013) 9(2):e1002915. doi:10.1371/journal.pcbi.1002915

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Arrenberg AB, Del Bene F, Baier H. Optical Control of Zebrafish Behavior with Halorhodopsin. Proc Natl Acad Sci U S A (2009) 106(42):17968–73. Available at: http://www.ncbi.nlm.nih.gov/pubmed/19805086. doi:10.1073/pnas.0906252106

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Wyart C, Del Bene F, Warp E, Scott EK, Trauner D, Baier H, et al. Optogenetic Dissection of a Behavioural Module in the Vertebrate Spinal Cord. Nature (2009) 461(7262):407–10. Available at: http://www.ncbi.nlm.nih.gov/pubmed/19759620. doi:10.1038/nature08323

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ahrens MB, Orger MB, Robson DN, Li JM, Keller PJ. Whole-brain Functional Imaging at Cellular Resolution Using Light-Sheet Microscopy. Nat Methods (2013) 10(5):413–20. Available at: http://www.ncbi.nlm.nih.gov/pubmed/23524393. doi:10.1038/nmeth.2434

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Satou C, Kimura Y, Hirata H, Suster ML, Kawakami K, Higashijima S-i. Transgenic Tools to Characterize Neuronal Properties of Discrete Populations of Zebrafish Neurons. Development (2013) 140(18):3927–31. doi:10.1242/dev.099531

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Kimura Y, Hisano Y, Kawahara A, Higashijima S-i. Efficient Generation of Knock-In Transgenic Zebrafish Carrying Reporter/driver Genes by CRISPR/Cas9-mediated Genome Engineering. Sci Rep (2014) 4:6545. doi:10.1038/srep06545

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Portugues R, Feierstein CE, Engert F, Orger MB. Whole-brain Activity Maps Reveal Stereotyped, Distributed Networks for Visuomotor Behavior. Neuron [Internet] (2014) 81(6):1328–43. Available at: http://www.ncbi.nlm.nih.gov/pubmed/24656252. doi:10.1016/j.neuron.2014.01.019

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Fidelin K, Djenoune L, Stokes C, Prendergast A, Gomez J, Baradel A, et al. State-Dependent Modulation of Locomotion by GABAergic Spinal Sensory Neurons. Curr Biol (2015) 25(23):3035–47. doi:10.1016/j.cub.2015.09.070

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Sternberg JR, Severi KE, Fidelin K, Gomez J, Ihara H, Alcheikh Y, et al. Optimization of a Neurotoxin to Investigate the Contribution of Excitatory Interneurons to Speed Modulation In Vivo. Curr Biol (2016) 26(17):2319–28. doi:10.1016/j.cub.2016.06.037

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Kishore S, Cadoff EB, Agha MA, McLean DL. Orderly Compartmental Mapping of Premotor Inhibition in the Developing Zebrafish Spinal Cord. Science (2020) 370(6515):431–6. doi:10.1126/science.abb4608

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Marques JC, Li M, Schaak D, Robson DN, Li JM. Internal State Dynamics Shape Brainwide Activity and Foraging Behaviour. Nature (2020) 577(7789):239–43. doi:10.1038/s41586-019-1858-z

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Jiang L, Cheng Y, Gao S, Zhong Y, Ma C, Wang T, et al. Emergence of Social Cluster by Collective Pairwise Encounters in Drosophila. Elife (2020) 9:e51921. doi:10.7554/eLife.51921

PubMed Abstract | CrossRef Full Text | Google Scholar