Olbert’s Kappa Fermi and Bose Distributions

The quantum version of Olbert’s kappa distribution applicable to fermions is obtained. Its construction is straightforward but requires recognition of the differences in the nature of states separated by Fermi momenta. Its complement, the bosonic version of the kappa distribution is also given, as is the procedure of how to construct a hypothetical kappa-anyon distribution. At very low temperature the degenerate kappa Fermi distribution yields a kappa-modified version of the ordinary degenerate Fermi energy and momentum. We provide the Olbert-generalized expressions of the Olbert-Fermi partition function and entropy which may serve determining all relevant statistical mechanical quantities. Possible applications are envisaged to condensed matter physics, possibly quantum plasmas, and dense astrophysical objects like the interior state of terrestrial planets, neutron stars, magnetars where quantum effects come into play and dominate the microscopic scale but may have macroscopic consequences.

1 Introduction

The classical (nonrelativistic) kappa distribution was introduced by Stan Olbert in 1966 [1] and first applied in the PhD thesis of Binsack [2].¹ Its first refereed version [3], applied to electron fluxes in Earth’s plasma sheet (acknowledging Olbert), is usually taken as its origin [for an account of its history, see Chapter 1 in Ref. 4]. In the honor of Olbert, we call it “Olbert’s kappa distribution,” while for simplicity shall speak of kappa distributions below.

The kappa distribution occurred almost permanently when dealing with particle distributions in high-temperature plasmas encountered in space [4–10]. It was also inferred from cosmic ray [11] spectra [12], extended into the relativistic domain, in the solar wind [13–17], near shocks [18–20], and in the heliosphere in general [21]. Various applications to statistical probabilities in correlated systems have been reviewed as well [see Refs. 22, 23, for collections]. It thus seems to represent a general distribution function in physical systems which in theory have been identified as obeying some kind of internal correlations. Conventionally, their evolution under nonstationary conditions, in particular in application to particle acceleration, is attributed to a Fokker–Planck description which naturally generates tails on the distribution function via momentum space diffusion. More basic theories have also been developed based on nonequilibrium statistical mechanics where they arise as stationary states far from thermal equilibrium [24–28]. In the asymptotic limit, nonlinear plasma theories [29–31] provide classical distributions of this kind. To some extent, kappa distributions are relatives of Tsallis’ nonextensive distributions in Tsallis’ thermostatistics [32] as in both formulations, the entropy turns out not to be simply extensive. Tsallis’ theory calls it nonextensive. Recently, the analytical form of the classical (nonquantum) kappa entropy has been constructed [33], which shows that it is super-extensive while being different from its thermo-statistical cousin, indicating that the fields of application in physics and statistics presumably refer to different domains.

The appearance of nonequilibrium distributions is physically no surprise. In classical physics, they arise as nonstationary distributions in quasi-linear (Fokker–Planck) theory where they can be made stationary by balancing particle injection and losses from the volume under consideration [11]. What, however, is unusual is that so far the attempts failed to construct a quantum equivalent of the classical kappa distribution. Formally, it seems very simple to obtain it from the partition function, but the distributions found [26, 34] were rather inconvenient versions of the classical Olbertian and no real quantum distributions as they did not allow for the presence of particles with energy below Fermi energy.² As an explanation, it was concluded that quantum theory at low temperatures suppresses correlations of the Fokker–Planck kind, which cause the evolution of non-Gaussian tails on the distribution. However, such a conclusion is rather unsatisfactory because there is no obvious way to demonstrate that correlations are indeed excluded by quantum effects. Motivation for constructing a kappa quantum distribution can thus be found in the wish to correct this mismatch in order to complete and generalize the Olbertian statistical mechanical theory by extending it into the quantum domain. In the Discussion section, we also provide some hints on possible applications. An application to nonideal gases which the former version was given [38, 38] should, for consistency, probably be adapted to the correct kappa Fermi version of the distribution obtained below. One would expect that it improves the interpretation of the experimentally obtained results. Here, we identify the crucial step that was missed in those attempts and subsequently provide the correct kappa quantum distributions. We first restrict to the Fermi-Olbertian as this one is more important in view of the wide range of quantum problems to that it may possibly be applied to some particularly suited problems.

2 Classical Kappa Distribution

There are several ways of deriving the classical kappa distribution. Consider an ideal gas of indistinguishable particles. The simplest is to start from the classical either micro-canonical or canonical Gibbs partition function [27], which is just the sum of all micro-canonical probabilities, and replacing the Boltzmann factor with the Olbert factor:

$\exp \left(-\beta {\epsilon }_{\alpha }\right)\to {\left[1+\beta {\epsilon }_{\alpha }/\kappa \right]}^{-\kappa -s}.(1)$

Here, ${\mathit{ϵ}}_{\alpha }$ is particle energy in state α, $\beta =T^{-1}$ with temperature T in energy units, $0<\kappa \in \mathrm{ℛ}$ Olberts parameter, and $0<s$ a constant power which is eventually needed in adjusting for thermodynamical reasons. (Note that there is no restriction on $\kappa >0$ except that it has to be positive. The analyticity of the distribution, its character of a distribution, and its correct thermodynamic properties are taken care of by s in the exponent, a fixed constant number whose particular nonrelativistic and relativistic values are determined by the thermodynamic constraints [for proof, see, e.g., 23, 26, 35] and are given below.) It is not a problem to include a high-energy cutoff $\text{exp}\left(-{\mathit{ϵ}}_{\alpha }/{\mathit{ϵ}}_c\right)$ with $\beta {\mathit{ϵ}}_c\gg 1$, which truncates the Olbertian at high energies. For the distribution, this is not required as it converges by itself. It is, however, needed when calculating moments higher than the second in fluid theory [15, 16, 22, 26]. Then on the usual way of finding the probability distribution, the kappa distribution becomes of course trivially

$p_{\kappa }\left({\epsilon }_{\alpha }\right)=e^{-{\epsilon }_{\alpha }/{\epsilon }_c}{\left[1+\frac{\beta {\epsilon }_{\alpha }}{\kappa }\right]}^{-\kappa -s},\beta =T^{-1}.(2)$

One easily shows that this choice with $\kappa \to \infty$ reproduces Boltzmann’s classical distribution where the artificial truncation is superficial and can be dropped. Summation of all occupations of states α yields the partition function which serves as normalization factor in the Olbert–Gibbs distribution and other purposes. Of course, as usual, though the partition function just remains the sum of the Olbert factors, the summation still poses a major problem.

3 The Kappa Fermi Distribution

This same procedure fails in the quantum case in application to the Fermi or Bose distributions. One can, however, give it a different start when, for simplicity, referring to the slightly more lucid canonical so-called thermodynamic Gibbs potential [37, 38] defined as the form $d\text{Ω}=-SdT-\mathcal{N}d\mu$ dual to energy conservation in the first law of thermodynamics with entropy S, temperature T, particle number $\mathcal{N}$, and chemical potential μ. It is of course closely related to the canonical Gibbs partition function from which it is derived to become the following:

$\beta {\Omega }_{\alpha }=-\log {\displaystyle \sum }_{n_{\alpha }}{\left[\exp \beta \left(\mu -{\epsilon }_{\alpha }\right)\right]}^{n_{\alpha }},(3)$

where $n_{\alpha }$ is the exact occupation number of states α, and the sum is to be taken over all occupations. In the Fermi case, there are only two possibilities: $n_{\alpha }=\mathrm{0,1}$, while the Bose case allows for arbitrary occupations. The advantage of using the thermodynamic potential is that the average occupation number simply follows from the partial derivative with respect to the chemical potential μ as

$\langle n_{\alpha }\rangle =-\frac{\partial {\Omega }_{\alpha }}{\partial \mu }\equiv p\left({\epsilon }_{\alpha }\right).(4)$

This is the prescription for constructing the wanted distribution. However, simply substituting the Olbert factor for the Boltzmann factor in the above expression turns out to be wrong. Sometimes, a very small move is necessary to progress a bit. Before proceeding, the potential must be inverted by resolving the logarithm:

$\exp \left(-\beta {\Omega }_{\alpha }\right)={\displaystyle \sum }_{n_{\alpha }}{\left[\exp \beta \left(\mu -{\epsilon }_{\alpha }\right)\right]}^{n_{\alpha }},(5)$

which yields a form that contains exponentials on both sides of the equation, and thus the substitution has to be done for both exponentials. Moreover, inspecting the exponential on the right one realizes that at $\mu ={\mathit{ϵ}}_{\alpha }$ the character of the Boltzmann factor changes as the argument of the exponential changes sign. Physically, this means that for positive chemical potential μ, the exponentials of states with energy below μ behave differently from those with energy larger than μ. They belong to different physical states. In Fermi theory, this is automatically taken care of by the smooth behavior of the exponential. However, in the Olbertian, this smoothness is destroyed by the properties of the rational function and, as in our previous approaches [26, 35] who did not take this difference into account, results in non-physical distributions either forbidding occupation of any states with energy less than μ or requiring that $\mu \le 0$ which eliminates any quantum properties. Hence, in the substitution, the sign of the argument of the exponential must be adapted. This yields the following expressions:

${\left[1+\beta {\Omega }_{\alpha }/\kappa \right]}^{-\left(\kappa +s\right)}=\{\begin{array}{ccc}{\displaystyle {\sum }_{n_{\alpha }}{\left[1-\beta \left(\mu -{\epsilon }_{\alpha }\right)/\kappa \right]}^{-n_{\alpha }\left(\kappa +s\right)}},& & {\epsilon }_{\alpha }>\mu \\ & & \\ {\displaystyle {\sum }_{n_{\alpha }}{\left[1+\beta \left(\mu -{\epsilon }_{\alpha }\right)/\kappa \right]}^{-n_{\alpha }\left(\kappa +s\right)}},& & {\epsilon }_{\alpha }<\mu \end{array}(6)$

which with $\mu >0$ positive, applicable to the Fermi distribution, can be written as follows:

${\left[1+\beta {\Omega }_{\alpha }/\kappa \right]}^{-\left(\kappa +s\right)}={\displaystyle \sum }_{n_{\alpha }}{\left[1+\beta \left|\mu -{\epsilon }_{\alpha }\right|/\kappa \right]}^{-n_{\alpha }\left(\kappa +s\right)}.(7)$

Application of the Pauli principle in order to specify to the quantum exclusions which the Fermi distribution takes care of then produces

${\left[1+\beta {\Omega }_{\alpha }/\kappa \right]}^{-\left(\kappa +s\right)}=1+{\left[1+\beta \left|\mu -{\epsilon }_{\alpha }\right|/\kappa \right]}^{-\left(\kappa +s\right)},(8)$

which must be differentiated with respect to μ keeping β and ${\mathit{ϵ}}_{\alpha }$ constant. This gives after some algebra the wanted (most probable) Olbert κ Fermi distribution

${\langle n_{\alpha }\left(\beta \right)\rangle }_{\mathrm{O}\mathrm{F}}={\left\{{\left[1+\left|\mu -{\epsilon }_{\alpha }\right|\beta /\kappa \right]}^{\kappa +s}+1\right\}}^{-\left[1+1/\left(\kappa +s\right)\right]},(9)$

for the average occupation number of states. It applies to both nonrelativistic as well as relativistic ${\mathit{ϵ}}_{\alpha }=m{c}^2{\gamma }_{\alpha }$ gases with ${\mathbf{p}}_{\alpha }$ momentum and ${\gamma }_{\alpha }=\sqrt{1+p_{\alpha }^2/m^2{c}^2}$. Clearly, this is not the same as if in the Fermi distribution, the exponential would have been replaced with the Olbert factor. In particular, the plus sign in the bracket is important as it warrants that the state of zero particle energy ${\mathit{ϵ}}_{\alpha }=0$ is not forbidden at low temperature and $\mu >0$, which would be nonphysical as there will always be electrons of zero energy (except in a magnetic field where the lowest state has energy ${\mathit{ϵ}}_0=\frac{1}{2}\hslash {\omega }_{ce})$. As in the ordinary Fermi distribution, the total number of particles $\mathcal{N}$ and total energy $\mathrm{ℰ}$ are just the respective sums of all occupations and all energies:

${\displaystyle \sum _{\alpha }\langle n_{\alpha }\rangle }=\mathcal{N},{\displaystyle \sum _{\alpha }{\epsilon }_{\alpha }\langle n_{\alpha }\rangle ={\rm E}}(10)$

For a gas of particles with momenta p, the above discrete Olbert κ Fermi distribution becomes a continuous function of particle energy ${\mathit{ϵ}}_{\mathbf{p}}$, and the Olbert κ Fermi distribution function is given as follows:

$f_{\mathrm{O}\mathrm{F}}\left(p\right)={\left\{{\left[1+\left|\mu -{\epsilon }_{\mathrm{p}}\right|\beta /\kappa \right]}^{\kappa +s}+1\right\}}^{-\left[1+1/\left(\kappa +s\right)\right]},(11)$

which for practical purposes when integrating over momentum and configuration space has to be properly normalized to the total number of particles in the volume, as indicated above, using the transition from summation over discrete states to continuous integration over space and momentum ${\displaystyle {\sum }_{\alpha }\to 2\mathcal{V}{\left(2\pi \hslash \right)}^{-3}}{{\displaystyle \int }}^{\text{}}{d}^3\mathbf{p},$ where one accounts for the presence of two independent electron spin directions, and the density integral is normalized to the above total particle number $\mathcal{N}$. However, while the Olbert parameter κ accounts for deviations of the distribution, normalization by itself becomes a formidable task already for the complicated analytical form of the distribution and the subtlety of its different behavior below and above the chemical potential μ. Applying L’Hôpital’s rule, it is straightforward to show that both distributions Eq. 9 and Eq. 11 for $\kappa \to \infty$ turn into their ordinary Fermi forms.

The kappa Fermi distribution obtained in this way maintains the quantum properties of the gas which become most important at low temperature. For large $\kappa \gg 1$, the distribution approaches the ordinary Fermi distribution. At moderate $\kappa >1$, the effective temperature in the distribution is kept at a higher value, thus even for low temperatures enlarging the domain of finite temperature. However, with small $\kappa <1$, this effect becomes reversed as fractional values of κ reduce the temperature and extend the domain of low temperature into the warmer domain. Interpreting $\kappa T$ as physical temperature would be as wrong as it was in the classical case [3]. It has been demonstrated elsewhere [cf., e.g., 23, 25, 26, 31, 35] that T remains the real physical temperature in the classical case, a conclusion which is not violated in the quantum domain as its physical meaning is not changed by the transition from classical to quantum physics. For ideal nonrelativistic and relativistic gases, one in addition has $s=5/2$ and $s=4$ [12, 35], respectively.

Asking for the shape of the kappa Fermi distribution at finite temperature, one excludes large $\kappa \gg 1$ because it just reproduces the Fermi distribution. Medium $\kappa \sim s$ and small $\kappa \ll s$ distributions are the only interesting cases. The shape of the distribution is essentially determined by the quantities $X\equiv \beta \mu /\kappa$ and $Y=\beta {\mathit{ϵ}}_{\alpha }/\kappa$ suppressing the index α on Y. One may note that for the values of interest $\kappa =z-s>0$ is positive, and z is a finite number the order of a few. Moreover, the only interesting case is that of comparably large chemical potentials μ, as they correspond to non-negligible Fermi energies. The limiting case $T\equiv 0$ is that of a degenerate gas which is considered below separately. In that case, all states α below μ are occupied. For finite though small temperatures, this is also the case up to a short distance $-\frac{1}{2}\text{Δ}\mathit{ϵ}$ from μ. One may expand the above distribution with respect to the difference $\text{Δ}\mathit{ϵ}=\left|\mu -{\mathit{ϵ}}_{\alpha }\right|$. This then yields that the distribution deviates from its value at ${\mathit{ϵ}}_{\alpha }=\mu$, which is $\langle n_{\alpha }\left(\text{Δ}\mathit{ϵ}\right)\rangle {|}_{\text{Δ}\mathit{ϵ}=0}=2^{-\left(1+1/z\right)}$, by the amount $-\frac{1}{2}\left(1+\kappa +s\right)\text{Δ}\mathit{ϵ}$, the energy gap, before, at larger energies ${\mathit{ϵ}}_{\alpha }>\mu +\frac{1}{2}\text{Δ}\mathit{ϵ}$ changing into a power law ${\mathit{ϵ}}_{\alpha }^{-\left(1+\kappa +s\right)}$ and decreasing further on.

Figure 1 shows a schematic of the shape of the kappa Fermi distribution for the two cases of zero $\beta \to \infty$ and finite $\beta \ll \infty$ temperatures.

FIGURE 1

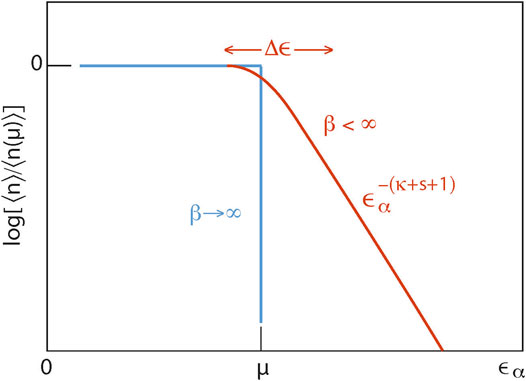
FIGURE 1. Schematic of Olbert’s kappa Fermi distribution as function of energy ${\mathit{ϵ}}_{\alpha }$ in state α for the cases of zero temperature $\beta \to \infty$ (the degenerate case, shown in blue color) and finite temperature $\beta \ll \infty$ (given in red). In the latter case of finite temperature, an energy gap $\text{Δ}\mathit{ϵ}$ appears as indicated around energies ${\mathit{ϵ}}_{\alpha }=\mu$ which to higher energy turns into a power law decay of the distribution. The power is a function of Olbert parameter κ and the thermodynamic constant s. Note that the distribution converges for infinite energy but must be truncated in order to maintain convergence by adding an exponential cutoff factor at some energy ${\mathit{ϵ}}_c\gg \mu$, if higher moments than mean energy $\mathrm{ℰ}$ are required. Note the obvious similarity to the Fermi distribution which identifies Olbert’s kappa Fermi distribution as the relevant analytical generalization of the quantum mechanical Fermi distribution. The main difference is in the natural occurrence of the power law tail and the related stretching of the gap.

4 Thermodynamic Potential and Partition Function

In order to find a representation of the Olbert-Fermi thermodynamic Gibbs potential of an ideal gas, one must invert the above distribution and insert it into the expression for $\text{Ω}$ which yields the equivalent expressions:

$\frac{\beta {\text{Ω}}_{\alpha }^{\text{OF}}}{\kappa }={\left(1-{\langle n_{\alpha }\rangle }^{\frac{\kappa +s}{\kappa +s+1}}\right)}^{1/\left(\kappa +s\right)}-1,(12)$

$={\left\{1+{\left[1+\beta \left|\mu -{\mathit{ϵ}}_{\alpha }\right|/\kappa \right]}^{-\left(\kappa +s\right)}\right\}}^{-1/\left(\kappa +s\right)}-1,(13)$

which may serve to calculate the properties of the ideal Olbert-Fermi gas. The first part gives ${\text{Ω}}_{\alpha }$ in terms of the average occupation number, that is, the distribution function, the second in terms of energy ${\mathit{ϵ}}_{\alpha }$. This enables to obtain the entropy which is defined as the negative derivative $S=-{\partial }_T\text{Ω}$ with respect to temperature at constant volume $\mathcal{V}$ and μ or

$S_{\alpha }={\beta }^2\frac{\partial {\text{Ω}}_{\alpha }}{\partial \beta }=\beta \left(\frac{\partial \beta {\text{Ω}}_{\alpha }}{\partial \beta }-{\text{Ω}}_{\alpha }\right),(14)$

which gives for the (dimensionless) entropy of state α the expression

$\frac{S_{\alpha }^{\text{OF}}}{\kappa }=1-{\displaystyle \sum }_{\pm }{\left\{{\left(1+\beta \left|\mu -{\mathit{ϵ}}_{\alpha }\right|/\kappa \right)}^{\pm \left(\kappa +s\right)}+1\right\}}^{-1-1/\left(\kappa +s\right)}.(15)$

One would like to have a representation of the entropy solely in terms of the mean occupation number $\langle n\rangle$. This is obtained after substantial simple though tedious algebra in the following form:

$\frac{S_{\alpha }^{\mathrm{O}\mathrm{F}}}{\kappa }=1-\frac{{\langle n_{\alpha }\left(\beta \right)\rangle }_{\mathrm{O}\mathrm{F}}}{1-{\langle n_{\alpha }\left(\beta \right)\rangle }_{\mathrm{O}\mathrm{F}}^{\left(\kappa +s\right)/\left(\kappa +s+1\right)}},(16)$

which replaces the well-known logarithmic form [38] of the Fermi entropy. The total entropy $\mathcal{S}$ is obtained when summing up Eq. 15 over α respectively integrating over momentum space. Similarly, summing or integrating ${\text{Ω}}_{\alpha }$Eq. 13 generates the equation of state $\mathcal{PV}=-{\displaystyle {\sum }_{\alpha }{\text{Ω}}_{\alpha }}$ with $\mathcal{P}$ pressure and $\mathcal{V}$ volume. Moreover, the consistent physical temperature $T\equiv {\beta }^{-1}$ (in energy units) is defined in the usual way as the partial derivative ${\partial }_{\mathrm{ℰ}}\mathcal{S}=\beta$ of the total entropy with respect to the total energy $\mathrm{ℰ}$.

Knowing the kappa Fermi distribution, the corresponding partition function can be written down. We here give it the canonical version which of course is identical with the above normalization condition with unspecified particle number

$Z_{\mathrm{O}\mathrm{F}}\equiv {\displaystyle \sum }_{\alpha }{\langle n_{\alpha }\rangle }_{\mathrm{O}\mathrm{F}}={\displaystyle \sum }_{\alpha }{\left\{{\left[1+\left|\mu -{\epsilon }_{\alpha }\right|\beta /\kappa \right]}^{\kappa +s}+1\right\}}^{-\left[1+1/\left(\kappa +s\right)\right]}.(17)$

As usual, it can be used to evaluate all thermodynamically interesting quantities.

5 The Kappa Bose Distribution

For completeness, we note in passing that the same procedure allows obtaining the complementary Olbert-Bose potential summing up the right-hand side of Eq. 13 for $0\le n_{\alpha }<\infty$. Summation yields

$\beta {\Omega }_{\alpha }^{\mathrm{O}\mathrm{B}}/\kappa ={\left\{1-{\left[1-\beta \left(\mu -{\epsilon }_{\alpha }\right)/\kappa \right]}^{-\left(\kappa +s\right)}\right\}}^{1/\left(\kappa +s\right)}-1,\mu \le 0,(18)$

which has to be differentiated with respect to μ holding ${\mathit{ϵ}}_{\alpha }$ constant in order to obtain the average occupation number ${\langle n_{\alpha }\rangle }_{\text{OB}}$ of states of an Olbert-Bose gas. This gives immediately

${\langle n_{\alpha }\rangle }_{\text{OB}}={\left\{{[1-\beta \left(\mu -{\mathit{ϵ}}_{\alpha }\right)/\kappa ]}^{\left(\kappa +s\right)}-1\right\}}^{-1+1/\left(\kappa +s\right)}{[1-\beta \left(\mu -{\mathit{ϵ}}_{\alpha }\right)/\kappa ]}^{-2},(19)$

which must be normalized to the total particle number. Clearly, the chemical potential $\mu \le 0$ must be negative as follows from the requirement that the occupation of the ground state ${\mathit{ϵ}}_{\alpha }=0$ is not forbidden. Like in the Fermi case, its entropy and equation of state can be obtained straightforwardly. We do not pursue this case here in any detail. We just point out that in contrast to ordinary quantum statistics, the kappa Fermi and Bose distributions are not mirror symmetrical versions of each other.

Again, the Olbert-Bose partition function is the sum of all the un-normalized Olbert κ Bose distributions in states α

$Z_{\text{OB}}\equiv {\displaystyle \sum }_{\alpha }{\langle n_{\alpha }\rangle }_{\text{OB}}={\displaystyle \sum }_{\alpha }{\left\{{[1-\beta \left(\mu -{\mathit{ϵ}}_{\alpha }\right)/\kappa ]}^{\left(\kappa +s\right)}-1\right\}}^{-1+1/\left(\kappa +s\right)}{[1-\beta \left(\mu -{\mathit{ϵ}}_{\alpha }\right)/\kappa ]}^{-2}.(20)$

One may, in addition, note that the thermodynamic Gibbs potential is an energy. It thus remains additive, (extensive) independent of any other properties of the gas. Hence, on the way of fractionally adding the Olbert-Fermi and Bose potentials ${\text{Ω}}_{\alpha }=q{\text{Ω}}_{\alpha }^{\text{OF}}+\left(1-q\right){\text{Ω}}_{\alpha }^{\text{OB}}$ with $q<1$ and differentiating with respect to μ and β, one also can construct the mixed Olbert κ anyon distribution and entropy of Olbert anyon gases, applicable to the fractional quantum-Hall effect, for instance, where correlations are known to exist even at the quantum level.

6 Degenerate Olbert-Fermi Gas

The most interesting is the degenerate electron gas with temperature $T\approx 0$, more generally with $T\ll {\mathrm{ℰ}}_{\text{OF}}$, where ${\mathrm{ℰ}}_{\text{OF}}$ is the Olbert-Fermi energy defined below. With $\kappa \to \infty$, Eqs 9, 11 are of course the usual degenerate Fermi distributions. Leaving $\kappa \ll \infty$ and $T\approx 0$, Eqs 9, 11 become the degenerate Olbert κ Fermi distributions. Like in the Fermi distribution, for $T\to 0$, all energy levels α become confined below μ, the Fermi energy. Here, this gives for the total particle density, when interpreting the sum as an integral with respect to the particle momentum p and integrating the kappa Fermi distribution Eq. 11 up to $\mu =p_{\text{OF}}^2/2m$ counting two spins per state,

$N=\frac{1}{{\pi }^2{\hslash }^3{A}_{\kappa }}\underset{0}{\overset{p_{\text{OF}}}{{\displaystyle \int }}}{p}^{2}dp=\frac{p_{\text{OF}}^3}{3A_{\kappa }{\pi }^2{\hslash }^3},A_{\kappa }=2^{1/\left(\kappa +s\right)}.(21)$

This yields the expressions for $p_{\text{OF}}$, the Olbert-Fermi moment, and ${\mathit{ϵ}}_{\text{OF}}$, the Olbert-Fermi energy

$p_{\text{OF}}=A_{\kappa }^{\frac{1}{3}}{p}_F,{\mathit{ϵ}}_{\text{OF}}=\frac{p_F^2}{2m}{A}_{\kappa }^{\frac{2}{3}},\text{where}{p}_F=\hslash k_F,(22)$

and $k_F={\left(3{\pi }^{2}N\right)}^{1/3}$ is the Fermi wavenumber. As one observes, the effects of the Olbertian transformation on the properties of the degenerate Fermi gas are moderate. They become susceptible only at small $\kappa <1$ and those numbers are determined mainly by the value of $s=5/2$, thus being practically constant. Following Eq. 21, when κ approaches zero and $s=5/2$, $A_{\kappa }$ approaches 1.36 (roughly 1.4). Therefore, the effect of κ is to stretch or shrink the quantum domain of the ideal gas. For large $\kappa \gg 1$, there is no change as this becomes the Fermi case. These expressions can be used to calculate

${{\rm E}}_{\mathrm{O}\mathrm{F}}=\frac{A_{\kappa }^{2/3}{p}_{\mathrm{F}}^{5/3}}{5{\pi }^2{\hslash }^3},and{\mathcal{P}}_{\mathrm{O}\mathrm{F}}=\frac{2}{15}\frac{A_{\kappa }^{2/3}{p}_{\mathrm{F}}^{5/3}}{{\pi }^2{\hslash }^2}.(23)$

The mean energy $\mathrm{ℰ}$ and degeneracy pressure $\mathcal{P}$ of the electron gas in the usual way, which turn out to become simple $A_{\kappa }$-modifications of the usual properties of a degenerate Olbert-Fermi gas. At small but finite temperatures, the distribution bents down from its constant value below ${\mathit{ϵ}}_{\alpha }=\mu$ at distance $-\frac{1}{2}\text{Δ}\mathit{ϵ}$ from the Fermi boundary to cross the Fermi boundary until at $+\frac{1}{2}\text{Δ}\mathit{ϵ}$ becoming power law $\propto {\mathit{ϵ}}_{\alpha }^{-\left(1+\kappa +s\right)}$ and decaying to low values. This is similar to the ordinary Fermi case though without the common exponential decay of the distribution. The latter is replaced by the power law decay causing an interesting substantial increase of the gap. One may note that the distribution converges at large ${\mathit{ϵ}}_{\alpha }$. However when moments larger than the mean energy are required, then the distribution has to be truncated through introducing an exponential high-energy cut-off $\text{exp}\left(-{\mathit{ϵ}}_{\alpha }/{\mathit{ϵ}}_c\right)$ with ${\mathit{ϵ}}_c\gg \mu$, as indicated in the section on the classical Olbertian. On the other hand, the distribution function of the Olbert-Fermi gas can be used in the calculation of the modified thermal and magnetic properties of the Olbert-Fermi gas and in any other application like degenerate stars.

7 Summary

In this brief communication, we generalized, based on physical arguments, the classical kappa distribution to fermions and bosons, the quantum Fermi and Bose cases. We also noted how this can be extended to mixed fermion-boson anyon states. The distributions, Gibbs potentials, and partition functions can be used to derive all relevant thermodynamic and statistical mechanical quantities for quantum and classical systems. In principle, this completes and rounds up the task of a generalized Olbertian statistical mechanics which turns out in all cases to be the analytical generalization of Boltzmann-Gibbs statistical mechanics into the Lorentzian and quantum domains. It results in well-defined distributions, Gibbs potentials, partition functions, and entropies. If required, it can, under appropriate conditions, serve as the thermodynamic theory for both classical and quantum systems. As such, it does apply to any system, not being restricted to plasmas. In fact, plasmas may not be the most interesting of such systems. It seems that the main field of application could be envisaged in some kinds of solid state physics, condensed matter physics, suitable astrophysical object, and possibly also, if relevant, high-energy physics. It should be noted that even under quantum conditions, the thermodynamic definition of temperature is maintained, which is a satisfactory physical fact.

For finite temperatures, the kappa Fermi distribution yields a substantial modification which, however, in the degenerate case of near-zero temperature, that is, environmental temperature much below Fermi temperature $\beta {\mathrm{ℰ}}_{\text{OF}}\gg 1$, which in solid state physics and astrophysical applications is the most interesting case, just leads to some more or less slight modifications of the well-known expressions of Fermi energy and momentum. The Olbert parameter κ accounts for deviations of the distribution from fermionic standard, indicating the presence of either internal correlations or degrees of freedom if applicable. These affect the low temperature behavior though, as it seems, only weakly and, preferably for small κ, increase the quantum domain a bit into the higher energy/temperature range by shifting the Fermi energy. Investigation of the higher temperature properties is more complicated by the analytical form of the kappa Fermi distribution. This has to be done case by case if required as it might have some effect, for instance, in the generation of the gap in the superconductivity theory.

We should, however, note at this occasion that the above investigation of the finite temperature behavior of the kappa Fermi distribution with increase of the gap around Fermi energy might be of interest in superconductivity theory. It still awaits an extension of the BCS theory [44] to the application of the Olbert-Fermi statistical mechanics.

For completeness, the complementary Olbert-Bose thermodynamic potential and distribution have also been given. The thermodynamic potential may serve to obtain the Olbert-Bose entropy, and equation of state. In this case, there is no indication of any presence of a Bose-Einstein condensation such that one would conclude that internal quantum correlations hidden in a finite value of κ destroy the formation of a bosonic quantum condensate at zero physical temperature.

Classical Olbertian statistical mechanics, as by now known (for reference the reader is referred to the literature cited in the introduction) applies to high-temperature collisionless plasmas as encountered in dilute near-Earth space, the heliosphere, and probably also environments of stars and planetary systems. Kappa distributions of particles have in the past been inferred in a multitude of space plasmas. In dilute high temperature plasma, similar to ordinary quantum physics, quantum effects are wiped out. Application of Fermi and Bose Olbertians and the corresponding Olbertian physics there becomes clearly obsolete. Quantum plasmas, on the other hand, may provide a promising field of application but require the transition from the currently practiced fluid approach based on the Madelung–Bohm theory to an appropriate statistical mechanics. Quantum plasmas are dense enough in this case, have very high Fermi temperature which by far exceeds the physical temperature ${\beta }^{-1}$. Physical examples are found in compact astrophysical objects like neutron stars, pulsars, magnetars, active galactic nuclei, and also black holes (if anything can be inferred about their interior state other than collapse). Electrons in the overlapping energy bands of the compact objects become, say, asymptotically free in the sense that they can freely move, resembling an electron fluid which may be subject to Olbert-Fermi statistics.

In similar sense system closer-by and of large interest are terrestrial planetary interiors, for instance, Earth’s outer core. Its temperature is some 3500 K, corresponding to an energy of ${\beta }^{-1}\sim 0.3$ eV and Fermi energy of conduction electrons (assuming ⁵⁶Fe ions as the basic constituent) of ${\mathit{ϵ}}_F>$ few eV. Hence, either Fermi or Olbert-Fermi physics applies. It may have consequences in planetary dynamo theory taking into account statistical microphysics in the excitation of the magnetic field, and if generating superconductivity, may presumably lead to the generation of a Ginzburg–Landau–Meissner effect of chains of magnetic bubbles/depletions in the magnetized outer core medium, an effect that should affect the interior structure of planetary magnetic fields.

This research was driven by curiosity, not by any applicational needs. It just presents a generalization of known classical statistical mechanics into the quantum domain. It may await application to the above indicated fields.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was part of a brief Visiting Scientist Programme at the International Space Science Institute, Bern. RT acknowledges the interest of the ISSI directorate as well as the generous hospitality of the ISSI staff, in particular the assistance of the librarians Andrea Fischer and Irmela Schweitzer, and the Systems Administrator Saliba F. Saliba. We acknowledge valuable discussions with M. Leubner, R. Nakamura, and Z. Vörös.

Footnotes

¹We thank C. Tsallis for kindly bringing this reference to our attention and G. Livadiotis for the access to the thesis.

²It was brought to our attention by the Associate Editor, G. Livadiotis, that in the framework of Tsallis’ nonextensive statistics, Fermi and Bose distributions had been derived already [cf. e.g., 35–37]. Since they arise from different propositions, they differ from Olbert’s kappa quantum distributions.

References

1. Olbert S. Summary of Experimental Results from M.I.T. Detector on IMP-1. In: Physics of the Magnetosphere, Proceedings of a Conference at Boston College, June 19-28, 1967 (RDL Carovillano, JF McClayAstrophysics and Space Science Library 40. Dordrecht: Reidel Publ. (1968). p. 641.

CrossRef Full Text

2. Binsack JH. Plasma Studies with the Imp-2 Satellite. Boston: PhD-Thesis, MIT (1966). p. 200. April 2, 2021.https://core.ac.uk/download/pdf/18321836.pdf.

3. Vasyliunas VM. A Survey of Low-Energy Electrons in the Evening Sector of the Magnetosphere with OGO 1 and OGO 3. J Geophys Res (1968) 73:2839–84. doi:10.1029/JA073i009p02839

CrossRef Full Text | Google Scholar

4. Livadiotis G. In: G Livadiotis, editor. Kappa Distributions, Theory and Applications in Plasmas. Amsterdam, NL: Elsevier (2017).

5. Christon SP, Mitchell DG, Williams DJ, Frank LA, Huang CY, Eastman TE. Energy spectra of plasma sheet ions and electrons from 50 eV/e to 1 MeV during plasma temperature transitions. J Geophys Res (1988) 93:2562–72. doi:10.1029/JA093iA04p02562

CrossRef Full Text | Google Scholar

6. Christon SP, Williams DJ, Mitchell DG, Frank LA, Huang CY. Spectral Characteristicds of Plasma Sheet Ion and Electron Populations during Undisturbed Geomagnetic Conditions. J Geophys Res (1989) 94:13409–24. doi:10.1029/JA094iA19p13409

CrossRef Full Text | Google Scholar

7. Christon SP, Williams DJ, Mitchell DG, Huang CY, Frank LA. Spectral Characteristicds of Plasma Sheet Ion and Electron Populations during Disturbed Geomagnetic Conditions. J Geophys Res (1991) 96:1–22. doi:10.1029/90JA01633

CrossRef Full Text | Google Scholar

8. Espinoza CM, Stepanova M, Moya PS, Antonova EE, Valdivia JA. Ion and Electron Distribution Functions along the Plasma Sheet. Geophys Res Lett (2018) 45:6362–70. doi:10.1029/2018GL078631

CrossRef Full Text | Google Scholar

9. Kirpichev IP, Antonova EE. Dependencies of Kappa Parameter on the Core Energy of Kappa Distributions and Plasma Parameter in the Case of the Magnetosphere of the Earth. Astrophysical J (2020) 891:ID 35. doi:10.3847/1538-4365/abdec9

CrossRef Full Text | Google Scholar

10. Eyelade AV, Stepanova M, Espinoza CM, Moya PS. On the Relation between Kappa Distribution Functions and the Plasma Beta Parameter in the Earth’s Magnetosphere: THEMIS Observations. Astrophysical JournalSupplement Ser (2021) 253:ID 34. doi:10.3847/1538-4357/ab700f

CrossRef Full Text | Google Scholar

11. Schlickeiser R. Cosmic Ray Astrophysics. Berlin: Astronomy & Astrophysics Library, Springer (2002).

12. Treumann RA, Baumjohann W. The Differential Cosmic ray Energy Flux in the Light of an Ultrarelativistic Generalized Lorentzian Thermodynamics. Astrophysics Space Sci (2018) 363:37. doi:10.1007/s10509-018-3255-8

CrossRef Full Text | Google Scholar

13. Goldstein ML, Eastwood JP, Treumann RA, Lucek EA, Pickett J, Décréau P. The Near-Earth Solar Wind. Space Sci Rev (2005) 118:7–39. doi:10.1007/s11214-005-3823-4

CrossRef Full Text | Google Scholar

14. Pierrard V, Lazar M, Poedts S, Štervák Š, Maksimovic M, Trávníček PM. The Electron Temperature and Anisotropy in the Solar Wind. Comparison of the Core and Halo Populations. Solar Phys (2016) 291:2165–79. doi:10.1209/0295-5075/120/50002

CrossRef Full Text | Google Scholar

15. Lazar M, Pierrard V, Poedts S, Fichtner H. Characteristics of Solar Wind Suprathermal Halo Electrons. Astron Astrophys (2020) 642:ID A130. doi:10.1051/0004-6361/2020038830

CrossRef Full Text | Google Scholar

16. Yoon PH, Lazar M, Scherer K, Fichtner H, Schlickeiser R. Modified Kappa-Distribution of Solar Wind Electrons and Steady-State Langmuir Turbulence. Astrophysical J (2018) 868:111131. doi:10.3847/1538-4357/aaeb94

CrossRef Full Text | Google Scholar

17. Livadiotis G, Desai MI, Wilson LB. Generation of kappa distributions in solar wind at 1 au. Astrophysical J (2018) 853:ID 142. doi:10.3847/1538-4357/aaa713

CrossRef Full Text | Google Scholar

18. Eastwood JP, Lucek EA, Mazelle C, Meziane K, Narita Y, Pickett J, et al. The Foreshock. Space Sci Rev (2005) 118:41–94. doi:10.1007/s11214-005-3824-3

CrossRef Full Text | Google Scholar

19. Lucek EA, Constantinescu D, Goldstein ML, Pickett J, Pinçon JL, Sahraoui F, et al. The Magnetosheath. Space Sci Rev (2005) 118:95–152. doi:10.1007/s11214-005-3825-2

CrossRef Full Text | Google Scholar

20. Balogh A, Treumann RA. Physics of Collisionless Shocks. New York: Springer Media (2013). doi:10.1007/978-1-4614-6099-2

CrossRef Full Text

21. Fichtner H, Kleimann J, Yoon PH, Scherer K, Oughton S, Engelbrecht NE. On the Generation of Compressible Mirror-Mode Fluctuations in the Inner Heliosheath. Astrophysical J (2020) 901:76. doi:10.3847/1538-4357/abaf52

CrossRef Full Text | Google Scholar

22. Livadiotis G, McComas DJ. Understanding Kappa Distributions: A Toolbox for Space Science and Astrophysics. Space Sci Rev (2013) 175:183–214. doi:10.1007/s11214-013-9982-9

CrossRef Full Text | Google Scholar

23. Scherer K, Husidic E, Lazar M, Fichtner H. The κ-cookbook: a Novel Generalizing Approach to Unify κ-like Distributions for Plasma Particle Modelling. Monthly Notices R Astronomical Soc (2020) 497:1738–56. doi:10.1093/mnras/staa1969

CrossRef Full Text | Google Scholar

24. Treumann RA. Kinetic Theoretical Foundation of Lorentzian Statistical Mechanics. Physica Scripta (1999) 59:19–26. doi:10.1238/Physica.Regular.059a00019

CrossRef Full Text | Google Scholar

25. Treumann RA, Jaroschek CH, Scholer M. Stationary Plasma States Far from Equilibrium. Phys Plasmas (2004) 11:1317–25. doi:10.1063/1.1667498

CrossRef Full Text | Google Scholar

26. Treumann RA, Jaroschek CH. Gibbsian Theory of Power Law Distributions. Phys Rev Lett (2008) 100:155005. doi:10.1103/PhysRevLett.100.155005

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Livadiotis G. Kappa Distributions: Thermodynamic Origin and Generation in Space Plasmas. J Phys Conf Ser (2018) 1100:ID 012017. doi:10.1088/1742-6596/1100/1/012017

CrossRef Full Text | Google Scholar

28. Livadiotis G. Kappa Distributions. Stat Phys Thermodynamics Space Astrophysical PlasmasUniverse (2018) 4:ID 144. doi:10.3390/universe4120144

CrossRef Full Text | Google Scholar

29. Hasegawa A, Mima K, Duong-van M. Plasma Distribution Function in a Superthermal Radiation Field. Phys Rev Lett (1985) 54:2608–10. doi:10.1103/PhysRevLett.54.2608

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yoon PH, Rhee T, Ryu CM. Self-consistent Generation of Superthermal Electrons by Beam-Plasma Interaction. Phys Rev Lett (2005) 95:215003. doi:10.1103/PhysRevLett.95.215003

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Yoon PH, Rhee T, Ryu CM. Self-consistent Generation of Electron κ Distribution: 1. Theory. J Geophys Res (2006) 111:A09106. doi:10.1029/2006JA011681

CrossRef Full Text | Google Scholar

32. Tsallis C. Possible Generalization of Boltzmann-Gibbs Statistics. J Stat Phys (1988) 52:479–87. doi:10.1007/BF01016429

CrossRef Full Text | Google Scholar

33. Treumann RA, Baumjohann W. Lorentzian Entropies and Olbert’s κ-distribution. Front Phys (2020) 8:221. doi:10.3389/fphy.2020.00221

CrossRef Full Text | Google Scholar

34. Treumann RA, Baumjohann W. Beyond Gibbs-Boltzmann-Shannon: General Entropies – the Gibbs-Lorentzian Example. Front Phys (2014) 2:49. doi:10.3389/fphys.2014.00049

CrossRef Full Text | Google Scholar

35. Aragão-Rêgo HH, Soares DJ, Lucena LS, da Silva LR, Lenzi EK, et al. Bose-Einstein and Fermi-Dirac Distributions in Nonextensive Tsallis Statistics: an Exact Study. Phys A: Stat Mech its Appl (2003) 317:199–208. doi:10.1016/50378-4371(02)01330-4

CrossRef Full Text | Google Scholar

36. Christianto V, Smarandache F. A Note on Unified Statistics Including Fermi-Dirac, Bose-Einstein, and Tsallis Statistics, and Plausible Extension to Anisotropic Effect. Prog Phys (2007) 2:61–4. Available at: https://www.ptep-online.com/2007/PP-09-12.PDF.

Google Scholar

37. Obregón O, Ortega-Cruz M. Generalizes Entropies Depending Only on the Probability and Their Quantum Statistics. Proceedings (2018) 2:169–75. doi:10.3390/ecea-4-05020

CrossRef Full Text | Google Scholar

38. Domenech-Garret JL, Tierno SP, Conde L. Non-equilibrium Thermionic Electron Emission for Metals at High Temperatures. J Appl Phys (2015) 118:074904. doi:10.1063/1.49929150

CrossRef Full Text | Google Scholar

39. Domenech-Garret JL. Transmission through potential barriers with a generalizsed Fermi-Dirac curren. J. Statis. Mech. Theory Exp. 2020:053102. doi:10.1088/172-5468/ab7af1

CrossRef Full Text | Google Scholar

40. Scherer K, Fichtner H, Lazar M. Regularized κ-distributions with Non-diverging Moments. Europhysics Lett EPL (2017) 120:50002. doi:10.1209/0295-5075/120/50002

CrossRef Full Text | Google Scholar

41. Lazar M, Scherer K, Fichtner H, Pierrard V. Toward a Realistic Macroscopic Parametrization of Space Plasmas with Regularized κ-distribution. Astron Astrophysics (2020) 643:A20. doi:10.1051/0004-6361/201936861

CrossRef Full Text | Google Scholar

42. Kittel C, Kroemer H. Thermal Physics. New York: W. H. Freeman (1980).

43. Landau LD, Lifshitz EM. Statistical Physics Part 1. In: Course of Theoretical Physics, 5. Oxford UK: Pergamon Press (1980).

44. Bardeen J, Cooper LN, Schrieffer JR. Theory of Superconductivity. Phys Rev (1957) 108:1175–204. doi:10.1103/PhysRev.108.1175

CrossRef Full Text | Google Scholar