Complexity and Entropy in Legal Language

We study the language of legal codes from different countries and legal traditions, using concepts from physics, algorithmic complexity theory and information theory. We show that vocabulary entropy, which measures the diversity of the author’s choice of words, in combination with the compression factor, which is derived from a lossless compression algorithm and measures the redundancy present in a text, is well suited for separating different writing styles in different languages, in particular also legal language. We show that different types of (legal) text, e.g. acts, regulations or literature, are located in distinct regions of the complexity-entropy plane, spanned by the information and complexity measure. This two-dimensional approach already gives new insights into the drafting style and structure of statutory texts and complements other methods.

1 Introduction

The complexity of the law has been the topic of both scholarly writing and scientific investigation, with the main challenge being the proper definition of “complexity”. Historically, articles in law journals took a conceptual and non-technical approach toward the “complexity of the law”, motivated by practical reasons, such as the ever increasing amount of legislation produced every year and the resulting cost of knowledge acquisition, e.g. [1, 2]. Although this approach is important, it remains technically vague and not accessible to quantitative analysis and measurement. Over the past decade, with the increasing availability of digitized (legal) data and the steady growth of computational power, a new type of literature has emerged within legal theory, the authors of which use various mathematical notions that come from areas as diverse as physics and information theory or graph theory, to analyze the complexity of the law, cf. e.g. [3–5]. The complexity considered results mainly from the exogenous structure of the positive law, i.e. the tree-like hierarchical organization of the legal texts in a forest consisting of codes (root nodes), chapters, sections, etc., but also from the associated reference network.

According to the dichotomy introduced by [6]; one can distinguish between structure-based measures and content-based measures of complexity, with the former pertaining to the field of knowledge representation (knowledge engineering) and the latter relating to the complexity of the norms, which includes, e.g. the (certainty of) legal commands, their efficiency and socio-economic impact.

In this article, we advance the measurement of legal complexity by focusing on the language using a method originating in the physics literature, cf. [7]. So, we map legal documents from several major legal systems into a two-dimensional complexity-entropy plane, spanned by the (normalized) vocabulary entropy and the compression factor, cf. Section 2.1. Using an abstract and rigorous measurement of the complexity of the law, should have significant practical benefits for policy, as discussed previously by, e.g. [1, 2]. For example, it could potentially identify parts of the law that need to be rewritten in order to remain manageable, thereby reducing the costs for citizens and firms who are supposed to comply. Most notably, the French Constitutional Court has ruled that articles of unjustified “excessive-complexity” are unconstitutional¹. However, in order to render the notion of “excessive complexity” functional, quantitative methods are needed such as those used by [5, 8]; and which our version of the complexity-entropy plane ideally complements.

2 Complexity and Entropy

A non-trivial question that arises in several disciplines is how the complexity of a hierarchical structure, i.e. of a multi-scale object, can be measured. Different areas of human knowledge are coded as written texts that are organized hierarchically, e.g. each book’s Table of Contents reflects its inherent hierarchical organization as a tree, and all books together form a forest. Furthermore, a tree-like structure appears again at the sentence level in the form of the syntax tree and its semantics as an additional degree of freedom. Although various measures of complexity have been introduced that are specially adapted to a particular class of problems, there is still no unified theory. The first concept we consider is Shannon entropy, [9]; which is a measure of information. It is an observable on the space of probability distributions with values in the non-negative real numbers. For a discrete probability distribution $P:=\left\{p_1,\dots ,p_N\right\}$, with $p_i>0$, for all i, and ${{{\displaystyle \sum }}^{\text{}}}_{i=1}^N{p}_i=1$, the Shannon entropy $H\left(P\right)$, is defined as:

$H\left(P\right):=-{\displaystyle \sum _{i=1}^N{p}_i{\log }_2\left(p_i\right)},(1)$

with ${\log }_2$, the logarithm with base 2. The normalized Shannon entropy $H_n\left(P\right)$, is given by

$H_n\left(P\right):=\frac{H\left(P\right)}{{\text{log}}_2\left(N\right)},(2)$

i.e. by dividing $H\left(P\right)$ by the entropy $H\left(P_N\right)$ of the discrete uniform distribution $P_N:=\left\{1/N,\dots ,1/N\right\}$, for N different outcomes. We shall use the normalized entropy in order to measure the information content of the vocabulary of individual legal texts, for details cf. Section 6.3. Word entropies have previously been used by various authors. In the legal domain [5], calculated the word entropy, after removing stop words, for the individual Titles of the U.S. Code. [10] used word entropies to gauge Shakespeare’s and Jin Yong’s writing capacity, based on the 100 most frequent words in each text.

The second concept we consider is related to Kolmogorov complexity (cf. [11, 12] and references therein), which is the prime example of algorithmic (computational) complexity. Heuristically, the complexity of an object is defined as the length of the shortest of all possible descriptions. Further fundamental examples of algorithmic complexity include Lempel-Ziv complexity $C_{76}$, [13]; or Wolfram’s complexity measure of a regular language, [14]. The latter is defined as (logarithm of) the minimal number of nodes of a deterministic finite automaton (DFA) that recognizes the language (Meyhill-Nerode theorem). In order to facilitate the discussion, let us propose a set of axioms for a complexity measure. This measure is basically a general form of an outer measure.

Let X be (at least) a monoid $\left(X,\circ ,\epsilon \right)$, with binary composition $\circ :X\times X\to X$, and identity element $\epsilon$, and additionally, let $\ge$ be a partial order on X.

A complexity measure C on X, is a functional $C:X\to {ℝ}_{+}$, such that for all $a,b\in X$, we have

pointed:

$C\left(\epsilon \right)=0,(3)$

monotone:

$\text{if} a\le b\text{then} C\left(a\right)\le C\left(b\right),(4)$

sub-additive:

$C\left(a\circ b\right)\le C\left(a\right)+C\left(b\right).(5)$

Examples satisfying the above axioms include tree structures, with the (simple) complexity measure given by the number of levels, i.e. the depth from the baseline. Then the empty tree has zero complexity, the partial order being given by being a sub-tree and composition being given by grafting trees. Further, the Lempel-Ziv complexity $C_{76}$, and Wolfram’s complexity measure for regular languages, if slightly differently defined via recognizable series, satisfy the axioms. However, plain Kolmogorov complexity does not satisfy, e.g. sub-additivity, cf. the discussion by [12].

2.1 Compression Factor

A derived complexity measure is the compression factor, which we consider next, and which is obtained from a lossless compression algorithm, such as, [15, 16].

A lossless compression algorithm, i.e. a compressor γ, reversibly transforms an input string s into a sequence $\gamma \left(s\right)$ which is shorter than the original one, i.e. $\left|\gamma \left(s\right)|\le |s\right|$, but contains exactly the same information as s, cf. e.g. [17, 18].

For a string s, the compression factor $r=r\left(s\right)$, is defined as

$r\left(s\right):=\frac{\left|s\right|}{\left|\gamma \left(s\right)\right|}.(6)$

The inverse $r^{-1}$, is called the compression ratio. These derived complexity measures quantify the relative amount of redundancy or structure present in a string, or more generally data.

The compression factor, as the entropy rate, is a relative quantity which permits to directly compare individual data items, independently of their size.

Let us illustrate this for the Lempel-Ziv complexity measure $C_{76}$, cf. [13]; and the following strings of length 20:

$s_1:=00000000000000000000,$

$s_2:=01010101010101010101,$

$s_3:=01001010100110101101.$

Then we have $C_{76}\left(s_1\right)=2$, $C_{76}\left(s_2\right)=3$ and $C_{76}\left(s_3\right)=7$, from which one immediately obtains the respective compression factors. [19]; showed that a generic string of length n has complexity close to n, i.e. it is “random”, however the meaningful strings for humans, i.e. representing text, images etc., are not random and have a structure between the completely uniform and the random string, cf. [18, 19]. [20] introduced a quantity related to the compression factor, called the “computable information density”, which is a measure of order and correlation in (physical) systems in and out of equilibrium. Compression factors (ratios) were previously used by [21]; who measured the complexity of mulitple languages by compressing texts and their shuffled versions to measure the inherent linguistic order. [22]; additionally to a neural language model, utilized compression ratios to measure the complexity of the language used by the Supreme Courts of the U.S. (USSC) and Germany (BGH). [23]; using the Lempel-Ziv complexity measure $C_{76}$, took into account not only the order inherent in a grammatically correct sentence, but also the larger organization of a text document, e.g. sections, by selectively shuffling the data belonging to each level of the hierarchy.

3 Some Remarks on Complexity, Entropy and Language

[24] (pp. 10–11) intuitively describe the broad difference between classical information theory and algorithmic complexity, which we summarize next. Whereas information theory (entropy), as conceived by Shannon, determines the minimal number of bits needed to transmit a set of messages, it does not provide the number of bits necessary to transmit a particular message from the set. Kolmogorov complexity on the other hand, focuses on the information content of an individual finite object, e.g. a play by Shakespeare, accounting for the (empirical) fact that strings which are meaningful to humans, are compressible, cf. [19]. In order to relate entropy, Kolmogorov complexity or Ziv-Lempel compression to one another, various mathematical assumptions such as stationarity, ergodicity or infinity are required, cf. [11, 17, 25]. Also, the convergence of various quantities found in natural languages, e.g. entropy estimates, [26]; are based on some of these assumptions. Despite the fact that the different approximations and assumptions proved valuable for language models, natural language is not necessarily generated by a stationary ergodic process, cf. [11]; as e.g., cf. [25]; the probability of upcoming words can depend on words which are far away. But, as argued by [27]; it is precisely due to the non-ergodic nature of natural language that one can empirically distinguish different topics, e.g. by determining the uneven distribution of keywords in texts, cf. also [28]. [29] considered a model of a random languages and showed how structure emerges as a result of the competition between energy and entropy.

Finally, let us comment on the relation between relative frequencies and probabilities in the context of entropy. Given a standard n-simplex, ${\Delta }_n$, i.e. $\left(x_0,\dots ,x_n\right)\in {ℝ}^{n+1}$, ${{{\displaystyle \sum }}^{\text{}}}_{i=0}^n{x}_i=1$, and $x_i\ge 0$, for $i=0,\dots ,n$, its points can either be interpreted as discrete probability distributions on $\left(n+1\right)$ elements or as the set of relative frequencies of $\left(n+1\right)$ elements. The distinction between the two concepts is relevant as the Shannon entropy H, provides in both cases a functional (observable) $H:{\Delta }_n\to {\mathbf{ℝ}}_{+},$ which, in our context, has two possible interpretations. Namely, as a component of a coordinate system on (law) texts, which is the interpretation in the present study, but also as an estimate of the Shannon entropy of the language used if considered as a sample from the space of all (law) texts of a certain type. In the latter case, it is known that the “naive” estimation of the Shannon entropy Eq. 1 from finite samples is biased. Therefore, several estimators have been developed to solve this problem. We utilize the entropy estimator introduced by [30]; in order to reexamine some of our results in the light of a probabilistic interpretation, and find that it has no qualitative effect on the outcome, cf. Supplementary Material.

4 The Complexity-Entropy Plane

Complex systems, e.g. biological, physical or social ones, are high-dimensional multi-scale objects. [31]; and [32] realized that in order to describe them, entropy is not enough, and an independent complexity measure is needed. Guided by the insight that the intuitive notion of complexity for patterns, when ordered by the degree of disorder, is at odds with its algorithmic description, the notion of the physical complexity of a system emerged, cf. [7, 31, 33]. The corresponding physical complexity measure, pioneered by [33]; should not be a monotone function of the disorder or the entropy, but should attain its maximum between complete order (perfect crystal) and total disorder (isolated ideal gas). [7]; introduced the excess Shannon entropy as a statistical complexity measure for physical systems, and later [34] introduced another physical complexity measure, the product of a system’s entropy with its disequilibrium measure. [35]; introduced a novel approach to handle the complexity of patterns on multiple scales using a multi-level renormalization technique to quantify the complexity of a (two- or three-dimensional) pattern by a scalar quantity that should ultimately better fit the intuitive notion of complexity.

[7]; paired both the entropy and the physical complexity measure into what has become a complexity-entropy diagram, in order to describe non-linear dynamical systems; for a review cf. [36]. Remarkably, these low-dimensional coordinates are often sufficient to characterize such systems (in analogy to principal component analysis), since they capture the inherent randomness, but also the degree of organization. Several variants of entropy-complexity diagrams are now widely used, even outside the original context. [37]; by combining the normalized word entropy, cf. Eq. 7, with a version of a statistical complexity measure, quantitatively study Shakespeare and other English Renaissance authors. [23]; used for the complexity-entropy plane the entropy rate and the entropy density and studied the organization of literary texts (Shakespeare, Abbott and Doyle) at different levels of the hierarchy. In order to calculate the entropy rate and density, which are asymptotic quantities, they used the Lempel-Ziv complexity $C_{76}$. Strictly speaking this approach would require the source to be stationary and ergodic, cf. [11].

We introduce a new variant $\Gamma$ of the complexity-entropy plane, spanned by the normalized word entropy and the compression factor, in order to study text data. So, every text t, can be represented by a point in $\Gamma$, via the map $t\mapsto \left(H_n\left(t\right),r\left(t\right)\right)$, with coordinates $H_n$, the normalized Shannon entropy of the underlying vocabulary, and r, the compression factor. Let us note, that $\Gamma$ is naturally a metric space, e.g. with the Euclidean metric, but other metrics may be more appropriate, depending on the particular question at hand.

5 The Norm Hierarchy and Boundaries of Natural Language

Let us now motivate some of our research questions from the perspective of Legal Theory.

[38] and his school introduced and formalized the notion of the “Stufenbau der Rechtsordnung”,² which led to the concept of the hierarchy of norms. The hierarchy starts with the Constitution (often originating in a revolutionary charter written by the “pouvoir constituant”), which governs the creation of statutes or acts, which themselves govern the creation (by delegation) of regulations, administrative actions, and also the judiciary. At the national level these (abstract) concepts are taken into account, e.g. Guide de légistique [39]; when drafting positive law. This is valid for, e.g. Austria, France, Germany, Italy, Switzerland and the European Union, although strictly speaking, it does not have a formal Constitution. Every new piece of legislation has to fit the preexisting order, so at each level, the content outlined at an upper level, has to be made more precise, which leads to the supposed linguistic gradient of abstraction. A new phenomenon can be observed for regulations, namely that the legislature, or more precisely its drafting agencies, is being forced to abandon the realm of natural language and take an approach that is common to all scientific writing, namely the inclusion of images, figures and formulae. The purpose of figures, tables and formulae is not only the ability to succinctly visualize or summarize large amounts of abstract information, but most often it is the only mean to convey complex scientific information at all. As regulations increasingly leave the domain of jurisprudence, novel methods should be adopted. For example [2], advocated the inclusion of mathematical formulae in a statute if this statue contains a computation that is based on this formula. Ultimately, a natural scientific approach (including the writing style) to law would be beneficial, however, this might be at odds with the idea of law being intelligible to a wide audience.

Our hypothesis is that these functional differences between the levels of the hierarchy of legal norms should manifest themselves as differences in vocabulary entropy or in the compression factor.

6 Materials and Methods

6.1 Data

Our analysis is based on the valid (in effect) and online available national codes from Canada, Germany, France, Switzerland, the United States, Great Britain and Shakespeare’s collected works, for a summary statistics, cf. Table 1. We also included the online available constitutions of Canada, Germany, and Switzerland in the analysis, cf. Table 2. In addition, we use the online available German EuroParl corpus from [40] and its aligned English and French translations (proceedings of the European Parliament from 1996 to 2006) to measure language-specific effects for German, English and French.

TABLE 1

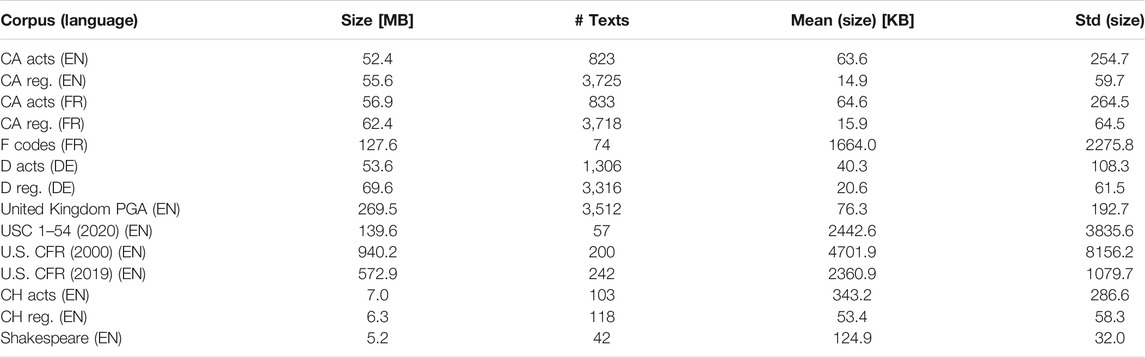
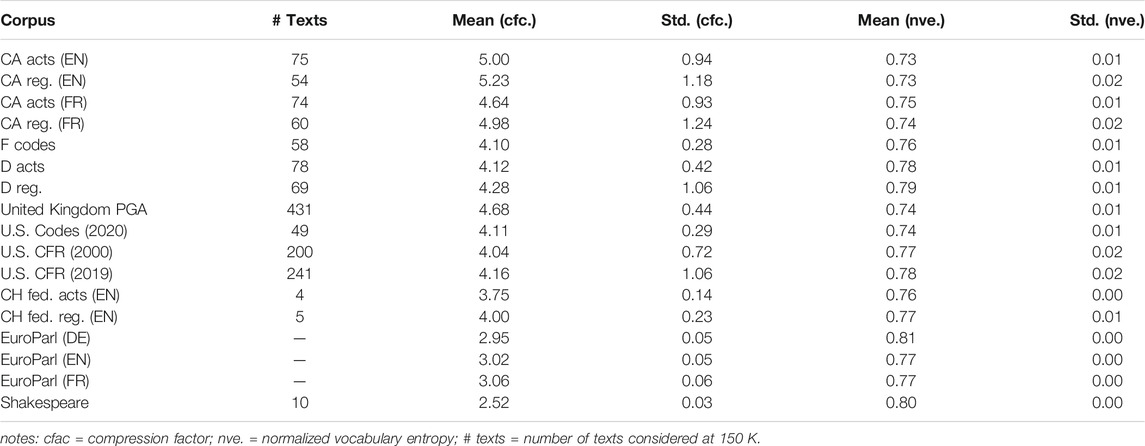
TABLE 1. Summary statistics on acts, regulations and English literature showing the language used and size (in MB) of the respective corpora, the number of items, the mean size (in KB) and the standard deviation.

TABLE 2

TABLE 2. Summary statistics for the Constitutions of Canada (EN), Germany (DE), Switzerland (DE,EN,FR), showing the language used, the original size (in KB), the compression factor and the normalized vocabulary entropy (after cutoff at 150 K).

In detail, we use all Consolidated Canadian Acts and Regulations in English and French (2020); all Federal German acts (Gesetze) and Federal regulations (Verordnungen) in German (2020); all French Codes (en vigueur) (2020); all Swiss Internal Laws (Acts and Ordinances) which have been translated into English, containing the following areas: 1 State - People - Authorities; 2 Private law - Administration of civil justice - Enforcement; Criminal law - Administration of criminal justice - Execution of sentences; 4 Education - Science - Culture; 5 National defense; 6 Finance; 7 Public works - Energy - Transport; 8 Health - Employment - Social security; 9 Economy - Technical cooperation (2020); the United Kingdom Public General Acts (partial dataset 1801–1987 and complete dataset 1988–2020); U.S. Code Titles 1–54 (Title 53 is reserved, including the appendices) (2020); U.S. Code of Federal Regulations for (2000) and (2019).

The collected works of Shakespeare are obtained from “The Folger Shakespeare - Complete Set, June 2, 2020”, https://shakespeare.folger.edu/download/

6.2 Pre-Processing

For our analysis we use Python 3.7. If available, we downloaded the bulk data as XML-files, from which we extracted the legal content (without any metadata), and saved it as a TXT-file, after removing multiple white spaces or line breaks. If no XML-files were available, we extracted the texts from the PDF versions, removed multiple white spaces or line breaks, and saved it as TXT-files.

6.3 Measuring Vocabulary Entropy

For an individual text t, let $V:=V\left(t\right):=\left\{v_1,\dots ,v_{\left|V\right|}\right\}$, be the underlying vocabulary, and $\left|V\right|$ the size of V. Let $f_i$ be the frequency (total number of occurrences) of a unique word $v_i\in t$, and let $\left|t\right|$ be the total number of words in t (with repetitions), i.e. $\left|t\right|={\displaystyle {\sum }_{i=1}^{\left|V\right|}{f}_i}$. The relative frequency is given by ${\widehat{p}}_i:=f_i/\left|t\right|$, which can also be interpreted as the empirical probability distribution ${\widehat{p}}_i$. The word entropy $H\left(t\right)$ of a text t (but cf. Section 3), is then given by

$H\left(t\right):=-{\displaystyle \sum _{i=1}^{\left|V\right|}{\widehat{p}}_i{\log }_2\left({\widehat{p}}_i\right)},(7)$

and correspondingly, the normalized word entropy $H_n\left(t\right)$, cf. Eq. 2. Let us remark, that the word entropy is invariant under permutation of the words in a sentence.

First we read the individual TXT-files, then filter the punctuation or special characters out and then split the remaining text into a list of items. In order to account for prefixes in French, the splitting separates expressions which are written with an apostrophe into separate entities. However, we do not lowercase letters, lemmatize or stem the remaining text, nor do we consider any bi- or trigrams. Keeping the original case-sensitivity, allows us to capture some syntactic or semantic information. Then we determine the relative frequencies (empirical probability values) of all unique items, from which we calculate the normalized entropy values according to Eq. 2. We truncate each text file at 150,000 characters, and discard files which are smaller than the cutoff value. For the EuroParl corpus we sampled 400 strings, consisting of 150 K characters each (with a gap of 300 K characters between consecutive strings) from the English, German and French texts, in order to calculate the corresponding normalized vocabulary entropy.

6.4 Measuring Compression Factors Using Gzip

In order to compute the compression factor as our derived complexity measure, we use as lossless compressor gzip.³ After reading the individual TXT-files as strings, we compress them using Python’s gzip compression module, with the compression level set to its maximum value (= 9). The individual compression factors are calculated according to Eq. 6. After analyzing all of our data, we choose 150,000 characters as the cutoff in order to minimize the effects of the overhead generated by the compression algorithm for very small text sizes. For the EuroParl corpora (English, French, German), we calculated the compression factors based on 400 samples each, as described above. Note that in the future it might make sense to also consider other (e.g. language specific) lossless compression algorithms in order to deal with short strings.

7 Results

Our first analysis, cf. Table 1, is a summary of the sizes of the different corpora, the languages used, the number of individual items, the mean text sizes and standard deviations. The analysis shows different approaches to the organization of national law, namely either by thousands of small texts of around 50 KB (Canada, Germany, United Kingdom) or less than a hundred large codes, several MB in size (France, United States), with the regulations significantly exceeding the number of acts. Note that the French codes contain both the law and the corresponding regulation in the same text. The size of a corpus within the same category, i.e. act or regulation, differs from country to country by an order of magnitude or even two, which is noteworthy as broadly similar or even identical areas are regulated within the law, e.g. banking, criminal, finance or tax law. This begs the question of what an efficient codification should ideally look like. The Swiss Federal codification is remarkably compact, despite the fact that the English version does not contain all acts or regulations available in German, French or Italian (which are the official languages); nevertheless all important and recent ones are included, cf. Section 6.1.

7.1 Normalized Entropy and Compression Factor

The normalized vocabulary entropies per corpus, cf. Table 3, have a standard deviation of approximately 0.01, and average entropy values that are distributed as follows: English in $\left[0.73,0.80\right]$, German in $\left[0.78,0.81\right]$ and French in $\left[0.74,0.77\right]$. The analysis of the mean compression factors, based on the individual texts truncated at 150 K, reveals three regions where the values accumulate, cf. Table 3. So, Shakespeare’s works have a mean compression factor of 2.52 (std = 0.03), the EuroParl corpora in English, French and German of around 3.01 (std = 0.06 approximately), whereas the national codifications are located in the interval $\left[3.75,5.23\right]$, with the standard deviations being in the interval $\left[0.14,1.24\right]$. On average, all national acts have a lower compression factor and a lower standard deviation than the corresponding national regulations. The (French), German, Swiss and United States acts are in the sub-interval $\left[3.75,4.12\right]$, and the respective regulations in $\left[4.00,4.28\right]$, but with a large standard deviation (1.06), for Germany and the United States. Based on the mean compression factor, the variance, the number of acts and the total size of the corpus, the French and the US codes are most similar. The acts of Canada (English and French) and of the United Kingdom are located at the upper end of the interval, namely in $\left[4.68,5.0\right]$, as are the Canadian regulations with 4.98 and 5.23, for French and English, respectively. The values for the constitutions can be found in the interval $\left[3.57,3.88\right]$ (compression factors), and $\left[0.75,0.79\right]$ (normalized vocabulary entropy). The value of the compression factor of the Canadian and German Constitution is smaller than the corresponding mean value of the acts or regulations, but larger than that of EuroParl (DE, EN, FR) or Shakespeare. In the case of the Swiss Federal Constitution and its aligned translations into English, French and German, the compression factor is significantly higher than the corresponding EuroParl average values, but between the mean of the acts (EN) and the mean of the regulations (EN), cf. Tables 2,3.

TABLE 3

TABLE 3. Summary statistics on acts, regulations (reg.) and English literature.$\#$

7.2 Complexity-Entropy Plane

The general picture of all texts analyzed in this study, cf. Figure 1, reveals, that the literary works of Shakespeare occupy a region to the left and are well separated from all the other data points. The three points corresponding to the English, French and German EuroParl samples are also well separated from the vast majority of legal texts and Shakespeare’s collected works. This indicates that legal texts are much more redundant than classic literary texts or parliamentary speeches. The picture for the constitutions is heterogeneous for the data considered.

FIGURE 1

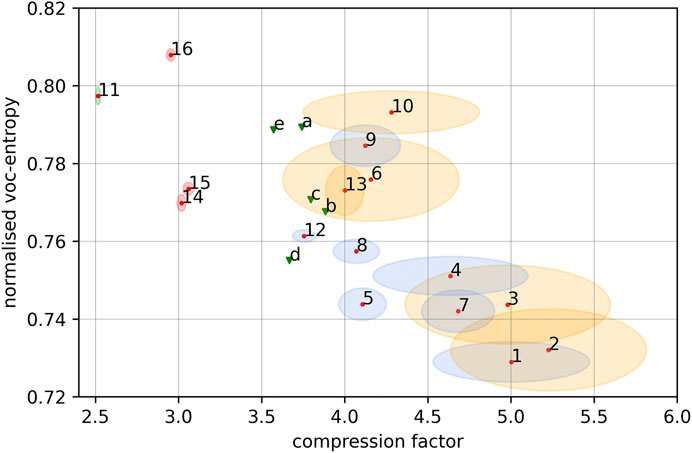
FIGURE 1. Figure showing the mean compression factor and mean normalized vocabulary entropy for: 1 = Canadian acts (EN), 2 = Canadian regulations (EN), 3 = Canadian regulations (FR), 4 = Canadian acts (FR), 5 = U.S. Code Titles 1–54, 6 = U.S. CFR 2019, 7 = United Kingdom acts, 8 = French acts (FR), 9 = German Federal acts (DE), 10 = German Federal regulations (DE), 11 = Shakespeare’s collected works, 12 = Swiss Federal acts (EN), 13 = Swiss Federal regulations (EN) 14 = EuroParl speeches (EN), 15 = EuroParl speeches (FR), 16 = EuroParl speeches (DE); and the compression factor and normalized vocabulary entropy (green marker) for: a = Swiss Federal Constitution (DE), b = Swiss Federal Constitution (EN), c = Swiss Federal Constitution (FR), d = Canadian Constitution (EN), e = German Constitution (Grundgesetz) (DE). The ellipses are centered around the mean values and have half-axes corresponding to $\sigma /2$ of the standard deviation of the compression factor and the normalized vocabulary entropy, respectively. Colors of ellipses correspond to: red = speeches (EuroParl), green = literature (Shakespeare), light blue = acts, orange = regulations; all texts truncated at 150 K.

The German (DE) and Canadian (EN) Constitution are located on the left border of the region, which contains the respective national acts and ordinances, while the Swiss Federal Constitution lies between the averages of the acts and ordinances, but is much closer to the mean of the acts.

The plot for U.S. Code (USC), Titles 1–54 for the year 2020, and U.S. Code of Federal Regulations (CFR) for the years 2000 and 2019, cf. Figure 2, shows that the Federal acts occupy a distinguishable region which is located below the domain populated by the Federal regulations. This is in line with the values from Table 3, as the mean vocabulary entropy for USC is 0.74, as compared to 0.77, for CFR 2000, and 0.78, for CFR 2019. On the other hand, the distribution pattern of the regulations in 2000 and 2019 is similar (small changes in the region around the means), but several points are more spread out in the 2019 data, which is in line with the larger standard deviation of 1.06 in 2019 vs. 0.72 in 2000. However, the overall size of CFR 2000 is 940 MB, vs. 572,9 MB, for CFR 2019, which is a quite substantial difference.

FIGURE 2

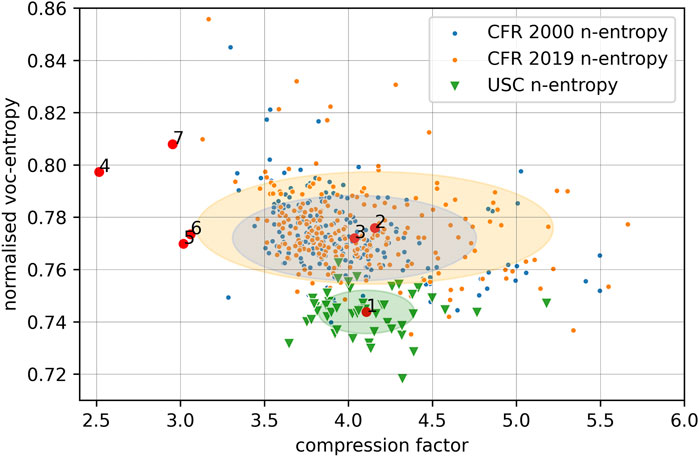
FIGURE 2. Figure showing the mean compression factor and mean normalized vocabulary entropy for: 1 = U.S. Code Titles 1–54, 2 = U.S. CFR 2019, 3 = U.S. CFR 2000, 4 = Shakespeare’s collected works, 5 = EuroParl speeches (EN), 6 = EuroParl speeches (FR), 7 = EuroParl speeches (DE). The ellipses are centered around the mean values and have axes corresponding to $1\sigma$ of the standard deviation of the compression factor and the normalized vocabulary entropy, respectively. Colors of ellipses correspond to: green = U.S. Federal acts (2020), orange = U.S. Federal regulations (2019), light blue = U.S. Federal regulations (2000); all texts truncated at 150 K.

We have already noted the similarity of the U.S. Titles and the French Codes. As Figure 3 shows, the French Codes (in French), German Federal acts (in German) and the U.S. Titles (in English) are situated in the complexity-entropy plane, almost as vertical, non-overlapping, translations of each other, with the German acts being highest up. The order of the average normalized vocabulary entropies appears to be language specific, although in this case we are not considering (aligned) translations, cf. Section 7.3.

FIGURE 3

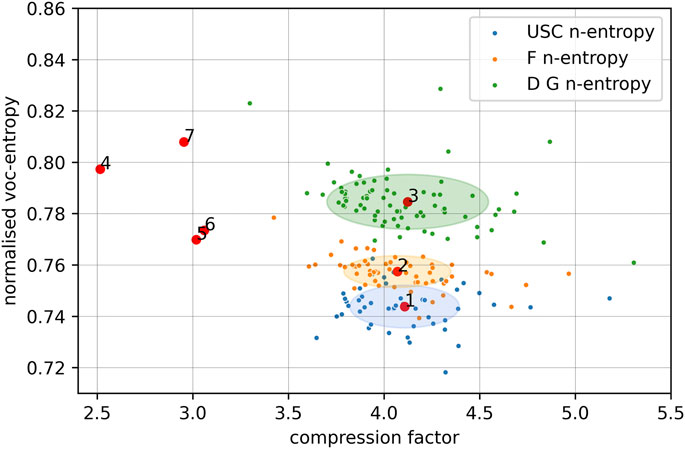
FIGURE 3. Figure showing the mean compression factor and mean normalized vocabulary entropy for: 1 = U.S. Code Titles 1–54, 2 = French Codes (FR), 3 = German Federal acts (DE), 4 = Shakespeare’s collected works, 5 = EuroParl speeches (EN), 6 = EuroParl speeches (FR), 7 = EuroParl speeches (DE). The ellipses are centered around the mean values and have axes corresponding to $1\sigma$ of the standard deviation of the compression factor and the normalized vocabulary entropy, respectively. Colors of ellipses correspond to: light blue = U.S. Code (2020), orange = French Codes, green = German Federal acts; all texts truncated at 150 K.

The picture for the aligned translations of the Canadian acts and regulations into English and French, cf. Figure 4, reveals that the acts are located, depending on the language, in separated regions which are bounded by ellipses of the same size around the respective means. For both English and French, the regulations are more dispersed than the acts (in particular the French) and the regulations in French are more widespread than those in English. The mean normalized entropy of the regulations in French is below the mean of the acts in French, but above the mean of the acts and regulations in English. The slightly odd position of the regulations in French could be due to the fact that after being truncated at 150 K, 60 (FR) vs. 54 (EN) regulations remain, while for the acts the number of texts remaining is the same. As we are dealing with aligned translations, the observed language specific pattern is quite meaningful, cf. Section 7.3. On the other hand, Canadian acts and regulations in the same language are not easily separable, i.e. they show a distribution pattern that differs from the U.S. Titles and U.S. Federal regulations, cf. Figure 2.

FIGURE 4

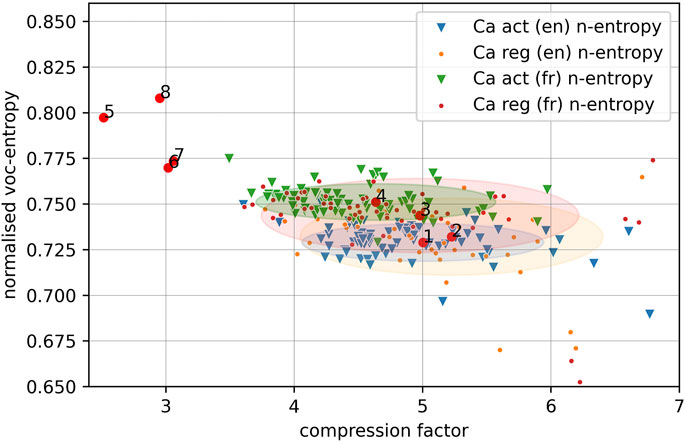
FIGURE 4. Figure showing the mean compression factor and mean normalized vocabulary entropy for: 1 = Canadian acts (EN), 2 = Canadian regulations (EN), 3 = Canadian regulations (FR), 4 = Canadian acts (FR), 5 = Shakespeare’s collected works, 6 = EuroParl speeches (EN), 7 = EuroParl speeches (FR), 8 = EuroParl speeches (DE). The ellipses are centered around the mean values and have axes corresponding to $1\sigma$ of the standard deviation of the compression factor and the normalized vocabulary entropy, respectively. Colors of ellipses correspond to: light blue = Canadian acts (EN), orange = Canadian regulations (EN), green = Canadian acts (FR), red = Canadian regulations (FR); all texts truncated at 150 K.

The German Federal acts and regulations accumulate in nearby and overlapping areas of the plane, and cannot be clearly separated from each other, with the laws being more compactly grouped around the mean. The acts of Canada (EN), the United States and the United Kingdom are close to each other, but far below the German acts and regulations, cf. Figure 5. Indeed, this seems to reflect language-specific characteristics common to all genres.

FIGURE 5

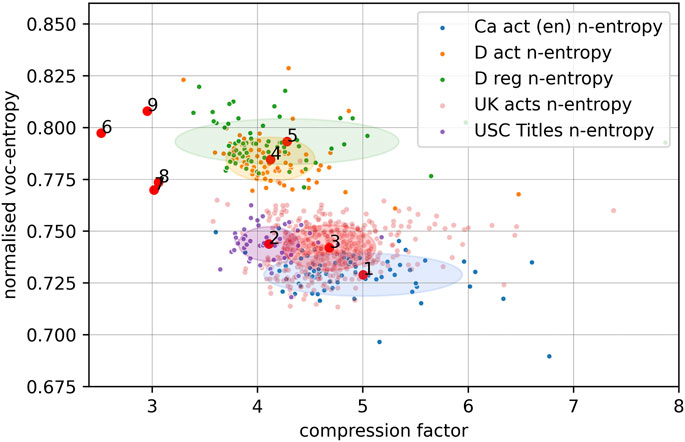
FIGURE 5. Figure showing the mean compression factor and mean normalized vocabulary entropy for: 1 = Canadian acts (EN), 2 = U.S. Code, Titles 1–54 (USC), 3 = United Kingdom General Public Acts (PGA), 4 = German Federal acts (DE), 5 = German Federal regulations (DE), 6 = Shakespeare’s collected works, 7 = EuroParl speeches (EN), 8 = EuroParl speeches (FR), 9 = EuroParl speeches (DE). The ellipses are centered around the mean values and have axes corresponding to $1\sigma$ of the standard deviation of the compression factor and the normalized vocabulary entropy, respectively. Colors of ellipses correspond to: light blue = Canadian acts (EN), orange = German Federal acts (DE), green = German Federal regulations (DE), red = United Kingdom PGA, purple = USC; all texts truncated at 150 K.

The fact that the United States Code, unlike for Canada, Germany and Switzerland, is fairly well separated in the plane from its associated regulations could reflect differences in the way laws and regulations are drafted in the United States as compared to the countries mentioned above.

7.3 Distinguishing Different Languages

From the above discussion it can be seen that different languages can be distinguished by the normalized vocabulary entropy if the genre is kept constant. In order to further investigate the language effect on the position of the corpora in the complexity-entropy plane, we specifically considered aligned translations. So, additionally to the Swiss Federal Constitution (English, French and German), the German EuroParl corpus and its translation into English and French, we processed the nine largest Swiss Federal acts in English, French and German. However, in order to have enough Swiss Federal acts, we had to lower the cutoff to 100K, and correspondingly had to recalculate the EuroParl values. Additionally we added the collected works of Shakespeare (in English), with a cutoff of 100 K. Further, we have the Canadian acts and regulations, and their aligned translations into English and French. The results imply that (aligned) translations of the same collection of texts into different languages are primarily not distinguished by the compression factor but rather by the (normalized) vocabulary entropy, cf. Figure 6 and Figure 1.

FIGURE 6

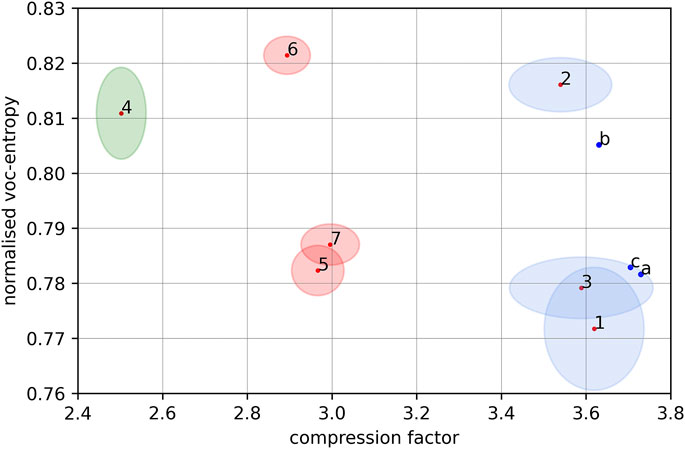
FIGURE 6. Figure showing the mean compression factor and mean normalized vocabulary entropy for: 1 = Swiss Federal acts (EN), 2 = Swiss Federal acts (DE), 3 = Swiss Federal acts (FR), 4 = Shakespeare’s collected works (EN), 5 = EuroParl speeches (EN), 6 = EuroParl speeches (DE), 7 = EuroParl speeches (FR), and the compression factor and normalized vocabulary entropy for: a = Swiss Federal Constitution (EN), b = Swiss Federal Constitution (DE), c = Swiss Federal Constitution (FR). The ellipses are centered around the mean values, and have axes corresponding to $1\sigma$ of the standard deviation of the compression factor and the normalized vocabulary entropy, respectively. Color code: red = EuroParl speeches, green = literature, light blue = acts; all texts truncated at 100 K.

8 Conclusion

We introduced a tool that is new to the legal field but has already served other areas of scientific research well. Its main strength is the ability to simultaneously capture and visualize independent and fundamental information, namely entropy and complexity, of large collections of data, and to track changes over time. By devising a novel variant of the complexity-entropy plane, we were not only able to show that legal texts of different types and languages are located in distinguishable regions, but also to identify different drafting approaches with regard to laws and regulations. In addition, we have taken the first steps to follow the spatial evolution of the legislation over time. Although we observe that constitutions tend to have lower compression factors than acts and regulations, and regulations on average have higher compression factors than acts, which corresponds to the hierarchy of norms, we could not fully capture the assumed abstraction gradient. This suggests that other language-specific methods should also be used to investigate (possible) differences. On the other hand, the high(er) redundancy of the regulations reflects the increasing need to leave the realm of natural language and to borrow tools from the natural sciences. The analysis we perform can be modified in a number of ways to provide even more specific information. So, one might include n-grams, or perform additional pre-processing steps, or choose different compression algorithms. Also, one might add a third coordinate for even more visual information. In combination with other quantitative methods such as citation networks or the consideration of additional (internal) degrees of freedom such as local entropy, new types of quantitative research questions could be formulated, which may lead to more efficient and manageable legislation. In summary, we expect a broad range of further applications of complexity-entropy diagrams within the legal domain.

Data Availability Statement

Publicly available datasets were analyzed in this study. The data can be found at: https://uscode.house.gov, https://www.govinfo.gov/bulkdata/CFR, https://www.legislation.gov.uk/ukpga, https://open.canada.ca/data/en/dataset/eb0dee21-9123-4d0d-b11d-0763fa1fb403, https://www.fedlex.admin.ch/en/cc/internal-law/, https://www.gesetze-im-internet.de/aktuell.html, https://www.legifrance.gouv.fr/liste/code?etatTexte=VIGUEUR&page=1#code, https://www.statmt.org/europarl/.

Author Contributions

RF contributed to the methods, analyzed the data and wrote the article.

Funding

The author received funding from the Max Planck Institute for the Physics of Complex Systems (MPIPKS).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

RF thanks Elliott Ash (ETH Zurich) and Holger Spamann (Harvard University) for numerous stimulating discussions. He thanks the condensed matter physics group at the Max Planck Institute for the Physics of Complex Systems in Dresden for its hospitality during his stay in 2020, and its support. Finally, he thanks the anonymous referees for their constructive comments and suggestions which helped to improve this article.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.671882/full#supplementary-material

Footnotes

¹Conseil Constitutionnel, Décision n 2005–530 DC du 29 décembre 2005 (Loi de Finances pour 2006) 77–89, available at https://www.conseil-constitutionnel.fr/decision/2005/2005530DC.htm.

²This could be translated with “hierarchy of the legal order” or “hierarchy of norms”.

³Note that we do not consider quantities in the limit or issues like the convergence of entropy estimates.

References

1. Schuck PH. Legal Complexity: Some Causes, Consequences, and Cures. Duke L J (1992) 42:1–52. doi:10.2307/1372753

CrossRef Full Text | Google Scholar

2. Rook LW. Laying Down the Law: Canons for Drafting Complex Legislation. Or L Rev (1993) 72:663.

Google Scholar

3. Mazzega P, Bourcier D, Boulet R. Proceedings of the 12th International Conference on Artificial Intelligence and Law. New York, NY: Association for Computing Machinery) (2009). p. 236–7. The Network of French Legal Codes.

Google Scholar

4. Bommarito MJ, Katz DM. A Mathematical Approach to the Study of the united states Code. Physica A: Stat Mech its Appl (2010) 389:4195–200. doi:10.1016/j.physa.2010.05.057

CrossRef Full Text | Google Scholar

5. Katz DM, Bommarito MJ. Measuring the Complexity of the Law: the united states Code. Artif Intell L (2014) 22:337–74. doi:10.1007/s10506-014-9160-8

CrossRef Full Text | Google Scholar

6. Bourcier D, Mazzega P. Toward Measures of Complexity in Legal Systems. Proceedings of the 11th International Conference on Artificial Intelligence and Law (2007). p. 211–5.

Google Scholar

7. Crutchfield JP, Young K. Inferring Statistical Complexity. Phys Rev Lett (1989) 63:105–8. doi:10.1103/physrevlett.63.105

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ruhl J, Katz DM. Measuring, Monitoring, and Managing Legal Complexity. Iowa L Rev (2015) 101:191–244.

Google Scholar

9. Shannon CE. A Mathematical Theory of Communication. Bell Syst Tech J (1948) 27:379–423. doi:10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

10. Chang M-C, Yang AC-C, Eugene Stanley H, Peng C-K. Measuring Information-Based Energy and Temperature of Literary Texts. Physica A: Stat Mech its Appl (2017) 468:783–9. doi:10.1016/j.physa.2016.11.106

CrossRef Full Text | Google Scholar

11. Cover TM, Thomas JA. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing). USA: Wiley-Interscience (2006).

12. Li M, Vitányi PM. An Introduction to Kolmogorov Complexity and its Applications. 4 edn. Incorporated: Springer Publishing Company (2019).

13. Lempel A, Ziv J. On the Complexity of Finite Sequences. IEEE Trans Inform Theor (1976) 22:75–81. doi:10.1109/TIT.1976.1055501

CrossRef Full Text | Google Scholar

14. Wolfram S. Computation Theory of Cellular Automata. Commun.Math Phys (1984) 96:15–57. doi:10.1007/bf01217347

CrossRef Full Text | Google Scholar

15. Ziv J, Lempel A. A Universal Algorithm for Sequential Data Compression. IEEE Trans Inform Theor (1977) 23:337–43. doi:10.1109/tit.1977.1055714

CrossRef Full Text | Google Scholar

16. Ziv J, Lempel A. Compression of Individual Sequences via Variable-Rate Coding. IEEE Trans Inform Theor (1978) 24:530–6. doi:10.1109/tit.1978.1055934

CrossRef Full Text | Google Scholar

17. Hansel G, Perrin D, Simon I. Compression and Entropy. Annual Symposium on Theoretical Aspects of Computer Science. Berlin, Heidelberg: Springer (1992).

18. Salomon D. Data Compression: The Complete Reference. 4 edn. London: Springer-Verlag (2007). doi:10.1007/978-1-84628-959-0

CrossRef Full Text

19. Chaitin GJ. Algorithmic Information Theory. IBM J Res Dev (1977) 21:350–9. doi:10.1147/rd.214.0350

CrossRef Full Text | Google Scholar

20. Martiniani S, Lemberg Y, Chaikin PM, Levine D. Correlation Lengths in the Language of Computable Information. Phys Rev Lett (2020) 125:170601. doi:10.1103/physrevlett.125.170601

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Montemurro MA, Zanette DH. Universal Entropy of Word Ordering across Linguistic Families. PLoS ONE (2011) 6:e19875. doi:10.1371/journal.pone.0019875

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Friedrich R, Luzzatto M, Ash E. Entropy in Legal Language. 2nd Workshop on Natural Legal Language Processing (NLLP, Collocated with KDD 2020) CEUR Workshop Proceedings. Vol. 2645, (virtual) (2020). Available at: http://ceur-ws.org/Vol-2645/.

23. Estevez-Rams E, Mesa-Rodriguez A, Estevez-Moya D. Complexity-entropy Analysis at Different Levels of Organisation in Written Language. PloS one (2019) 14:e0214863. doi:10.1371/journal.pone.0214863

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Grunwald P, Vitányi P. Shannon Information and Kolmogorov Complexity. arXiv preprint cs/0410002. (2004).

Google Scholar

25. Jurafsky D, Martin JH. Speech and Language Processing. 2nd ed. USA: Prentice-Hall (2009). doi:10.1109/asru.2009.5373494

CrossRef Full Text

26. Shannon CE. Prediction and Entropy of Printed English. Bell Syst Tech J (1951) 30:50–64. doi:10.1002/j.1538-7305.1951.tb01366.x

CrossRef Full Text | Google Scholar

27. Debowski Ł. Is Natural Language a Perigraphic Process? the Theorem about Facts and Words Revisited. Entropy (2018) 20:85.

Google Scholar

28. Schürmann T, Grassberger P. Entropy Estimation of Symbol Sequences. Chaos (1996) 6:414–27. doi:10.1063/1.166191

PubMed Abstract | CrossRef Full Text | Google Scholar

29. DeGiuli E. Random Language Model. Phys Rev Lett (2019) 122:128301. doi:10.1103/physrevlett.122.128301

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Grassberger P. Entropy Estimates from Insufficient Samplings (2003) (arXiv preprint physics/0307138.

31. Grassberger P. Toward a Quantitative Theory of Self-Generated Complexity. Int J Theor Phys (1986) 25:907–38. doi:10.1007/bf00668821

CrossRef Full Text | Google Scholar

32. Crutchfield JP. Between Order and Chaos. Nat Phys (2012) 8:17–24. doi:10.1038/nphys2190

CrossRef Full Text | Google Scholar

33. Huberman BA, Hogg T. Complexity and Adaptation. Physica D: Nonlinear Phenomena (1986) 22:376–84. doi:10.1016/0167-2789(86)90308-1

CrossRef Full Text | Google Scholar

34. López-Ruiz R, Mancini HL, Calbet X. A Statistical Measure of Complexity. Phys Lett A (1995) 209:321–6. doi:10.1016/0375-9601(95)00867-5

CrossRef Full Text | Google Scholar

35. Bagrov AA, Iakovlev IA, Iliasov AA, Katsnelson MI, Mazurenko VV. Multiscale Structural Complexity of Natural Patterns. Proc Natl Acad Sci USA (2020) 117:30241–51. doi:10.1073/pnas.2004976117

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Feldman DP, McTague CS, Crutchfield JP. The Organization of Intrinsic Computation: Complexity-Entropy Diagrams and the Diversity of Natural Information Processing. Chaos: Interdiscip J Nonlinear Sci (2008) 18:043106. doi:10.1063/1.2991106

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Rosso OA, Craig H, Moscato P. Shakespeare and Other English Renaissance Authors as Characterized by Information Theory Complexity Quantifiers. Physica A: Stat Mech its Appl (2009) 388:916–26. doi:10.1016/j.physa.2008.11.018

CrossRef Full Text | Google Scholar

38. Kelsen H. Reine Rechtslehre: Mit einem Anhang: Das Problem der Gerechtigkeit. Tübingen: Mohr Siebeck (2017). doi:10.33196/9783704683991

CrossRef Full Text

39. General S. Guide de légistique (3 édition mise à jour 2017). 3 edn. France: La documentation Française (2017).

40. Koehn P. Conference Proceedings: The Tenth Machine Translation Summit. AAMT. Phuket, Thailand: AAMT (2005). p. 79–86. Europarl: A Parallel Corpus for Statistical Machine Translation.

Google Scholar